A Review on the Modelling of Aligned Discontinuous Fibre Composites
Abstract
1. Introduction
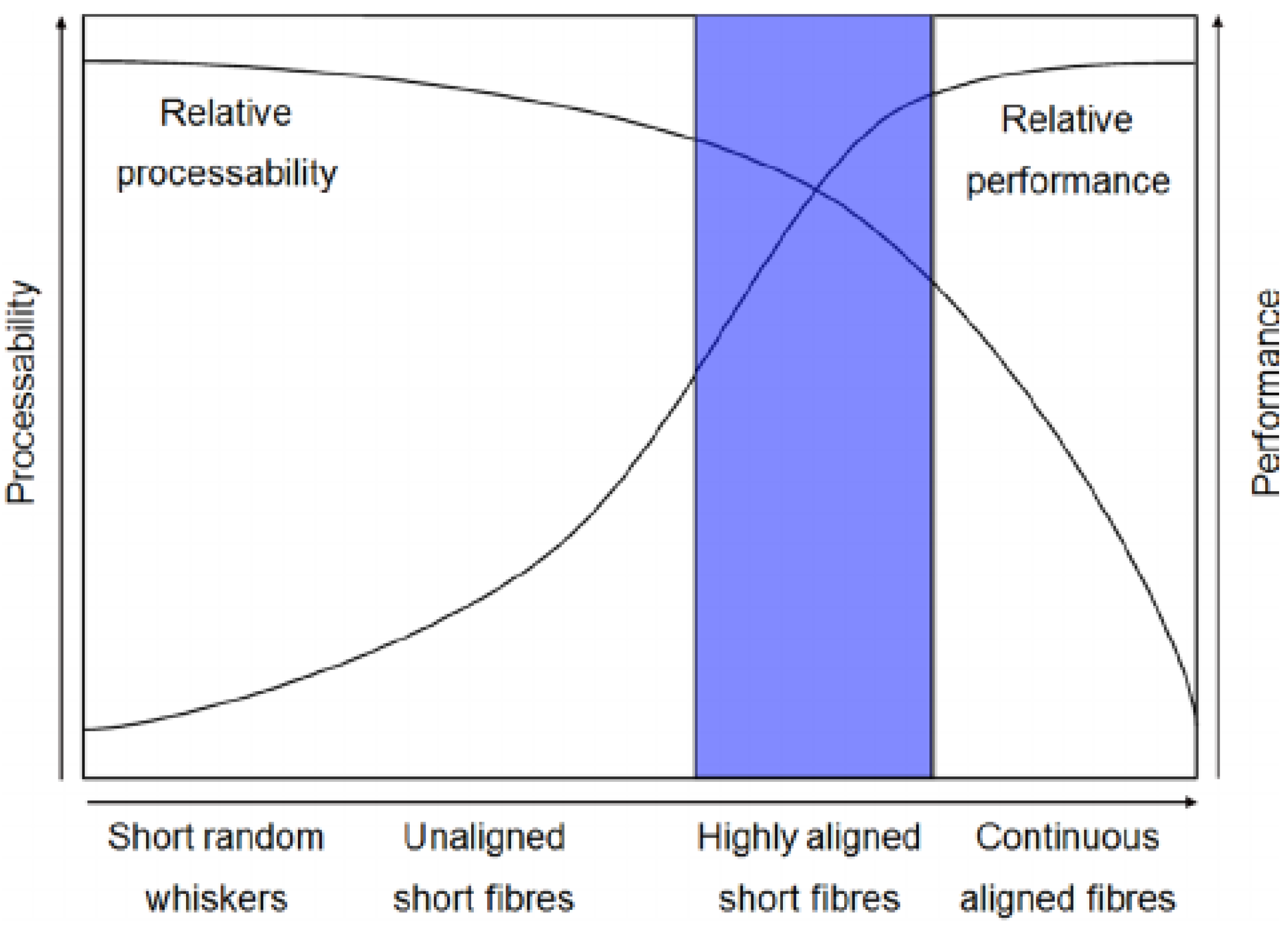
2. Performance of Discontinuous Fibre Systems
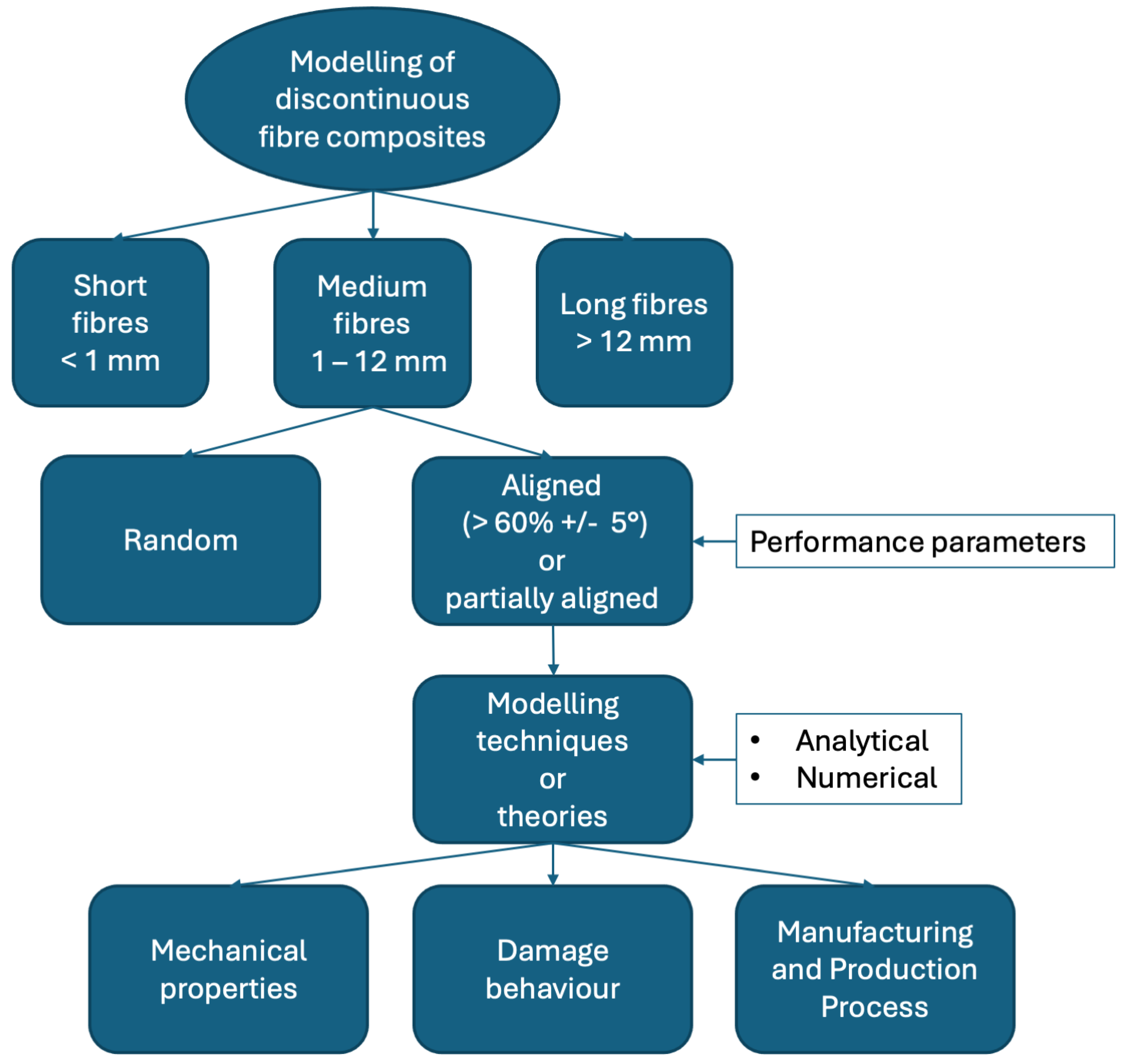
3. Performance Modelling of Discontinuous Fibre Systems
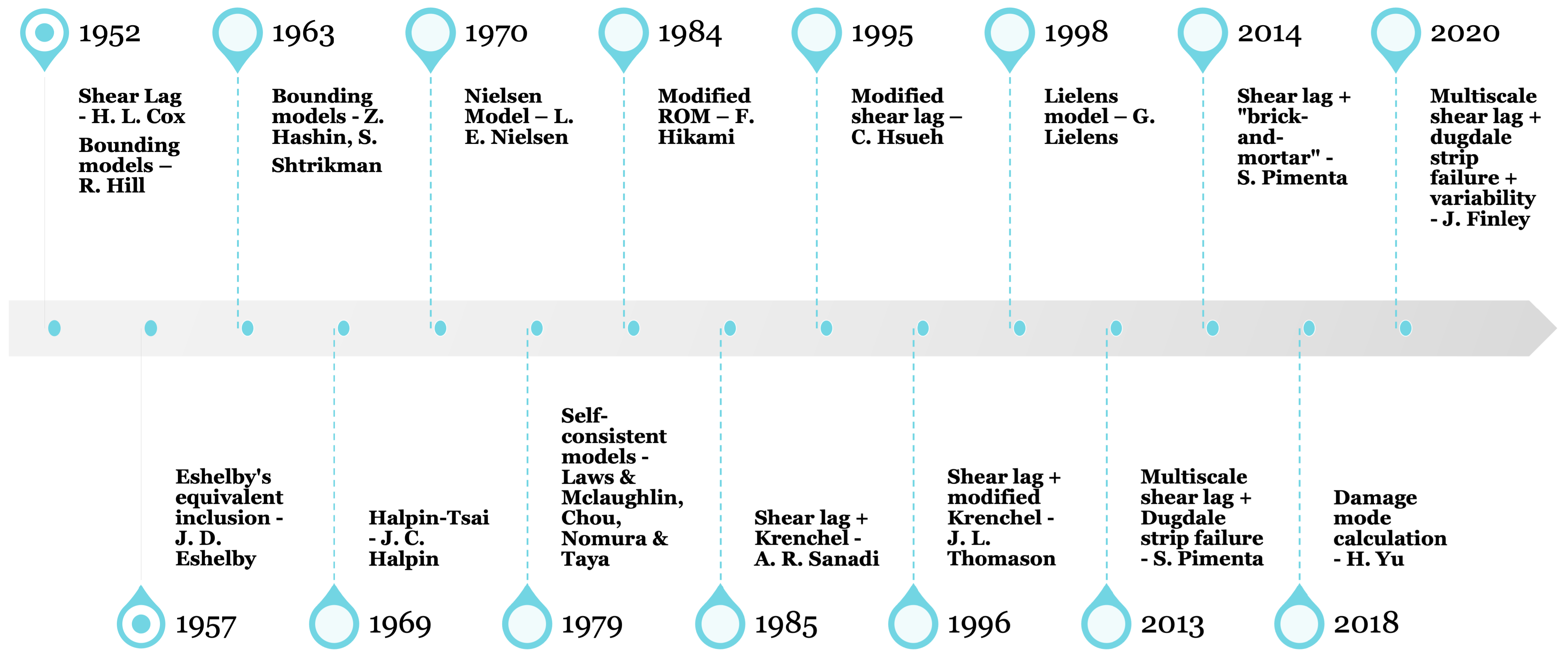
3.1. Analytical Modelling
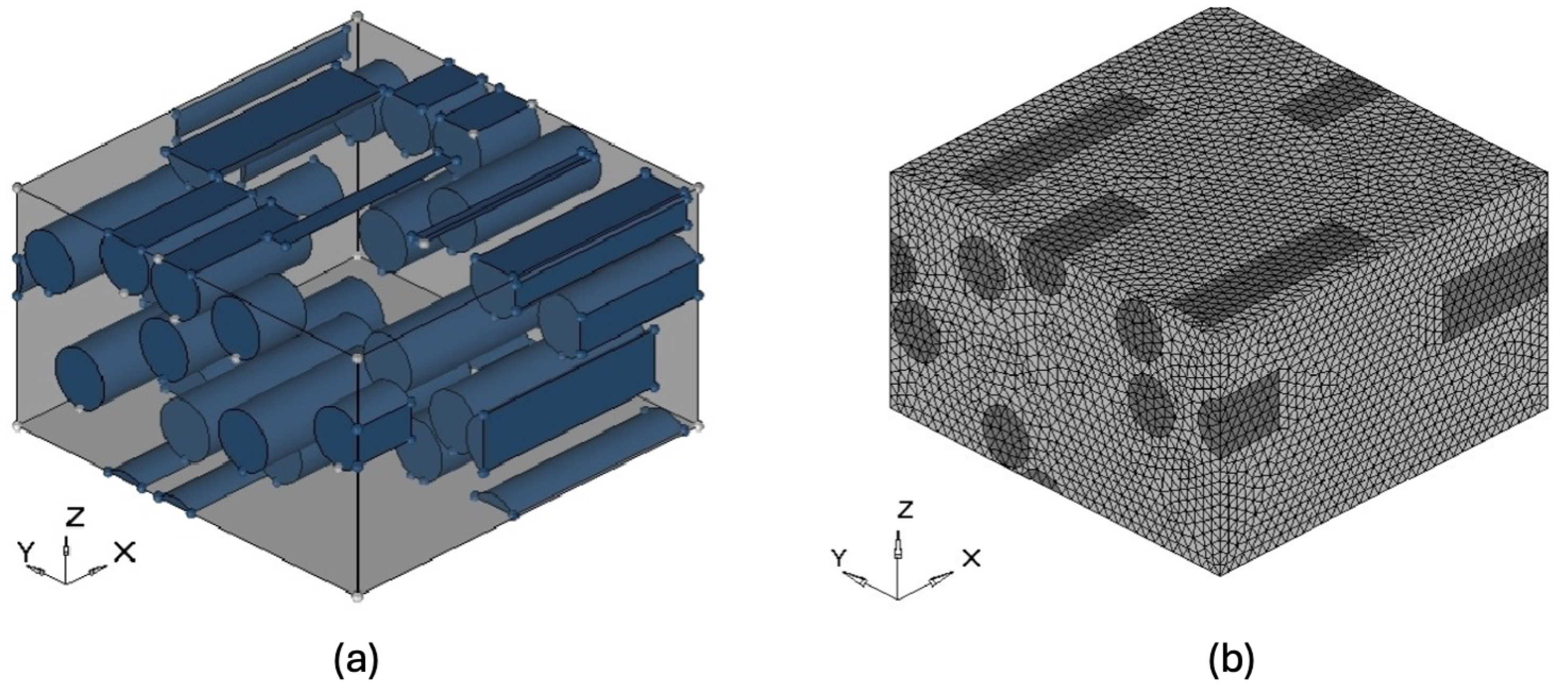
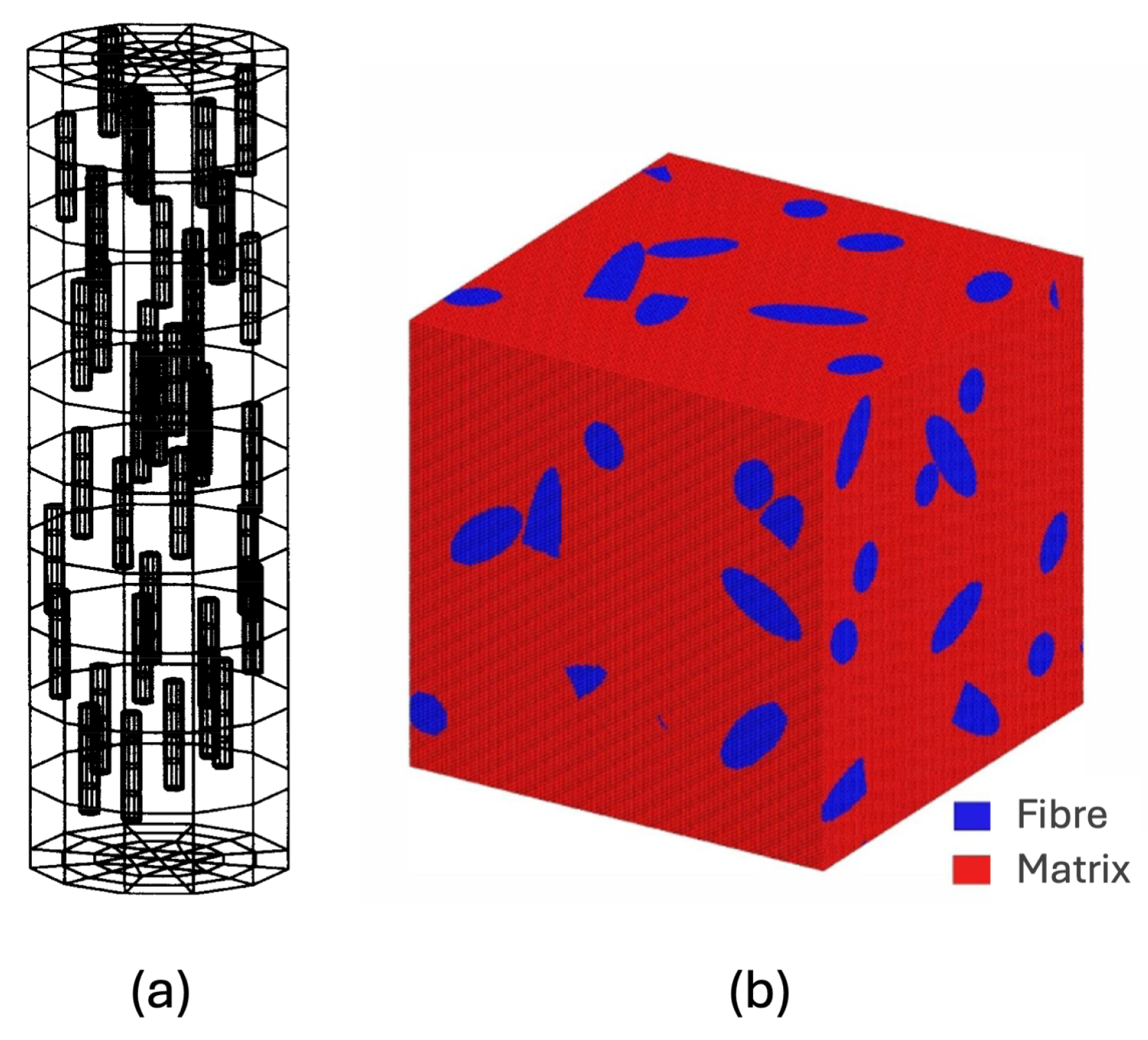
3.2. Numerical Modelling
| Numerical Model | Parameter | Description | Limitations | Experimental Validation |
|---|---|---|---|---|
| boundary element metho (1995–1997) [119,120,121,122] | Stiffness | Flexible | Low volume fraction | Hydrodynamic alignment [121] |
| Simple mesh generation | Use of shorter fibres | |||
| Low alignment | ||||
| Periodic unit cell simulation (2009) [127] | Strength | Analyses failure modes | High computational cost | - |
| Includes stress concentration at fibre ends | Difficulty scaling up specimen size | |||
| Includes fibre end gap | Shorter fibre lengths | |||
| Considers matrix stresses and fibre breaking | ||||
| FE-based models (2011–2020) [47,109,111,116] | Stiffness | RVE analysis | Low fibre volume fraction | - |
| Ability to scale up specimen size | Simplified geometry | |||
| Low number of fibres | ||||
| Layer wise (2012) [126] | Strength | Analyses failure modes | Variation in fibre length and orientation not considered | Random thermoplastic press moulded composites [126] |
| Uniform fibre angle | ||||
| Includes viscoelastic response of matrix | Data | |||
| Data | Considers fibre failure | |||
| Spring element (2014) [128] | Strength | Analyses failure modes | Variation in fibre orientation not considered | Random thermoplastic press moulded composites [126] |
| Damage progression | 3D SEM suitable only for longer fibres | Unable to combine failure modes (only includes fibre breaks) | ||
| Considers fibre length variations | ||||
| Peridynamic technique (2018–2021) [124,125] | Strength | Particulate macro scale model | Difficulty scaling up specimen size Variation in fibre length | - |
| Damage progression | not considered | |||
| Wrinkling or voids not considered | ||||
| Inconsistency in modelling | ||||
| Mainly for damage progression |
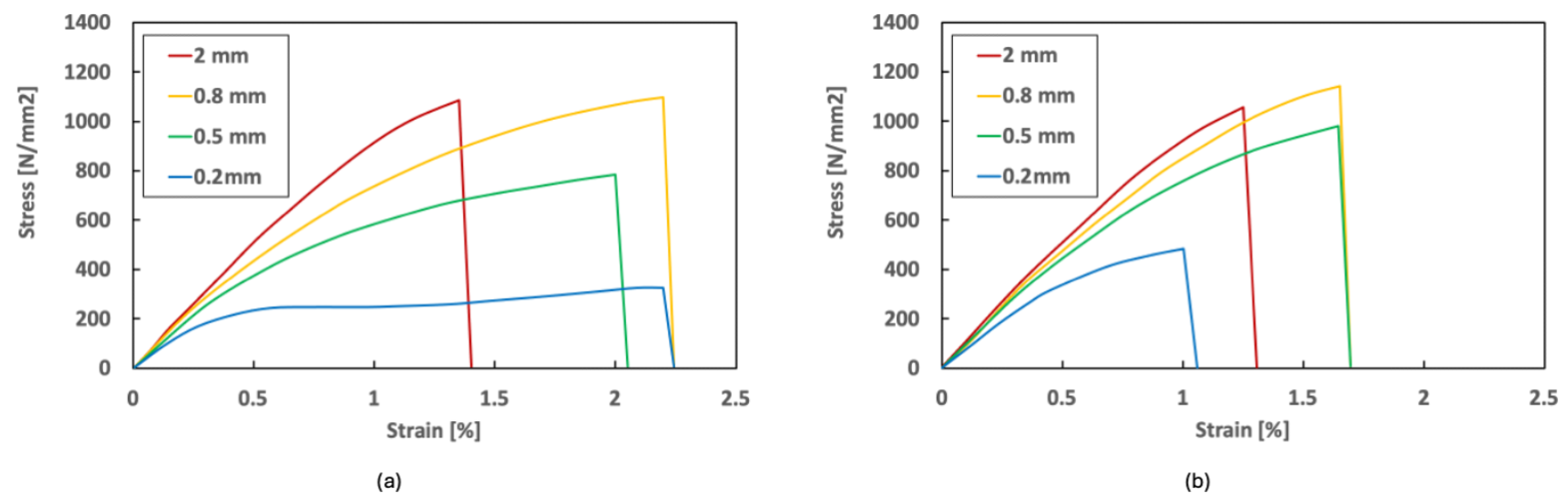
3.3. Recent Works on Modelling Predictions Using ADFRCs
4. Process Modelling of ADFRC
- The alignment stage—to understand how the fibres behave in a fluid in order to optimise the alignment quality.
- The forming stage—to predict the behaviour of the matrix and fibres during tape placement, as well as understand defect formation.
- The curing stage—to understand how the matrix and fibres behave when heat is applied.
4.1. Fibre Alignment Modelling
4.2. Towards Forming Predictive Capabilities
5. Conclusions
- Analytical models so far seem capable of predicting trends for the mechanical properties of ADFRC.
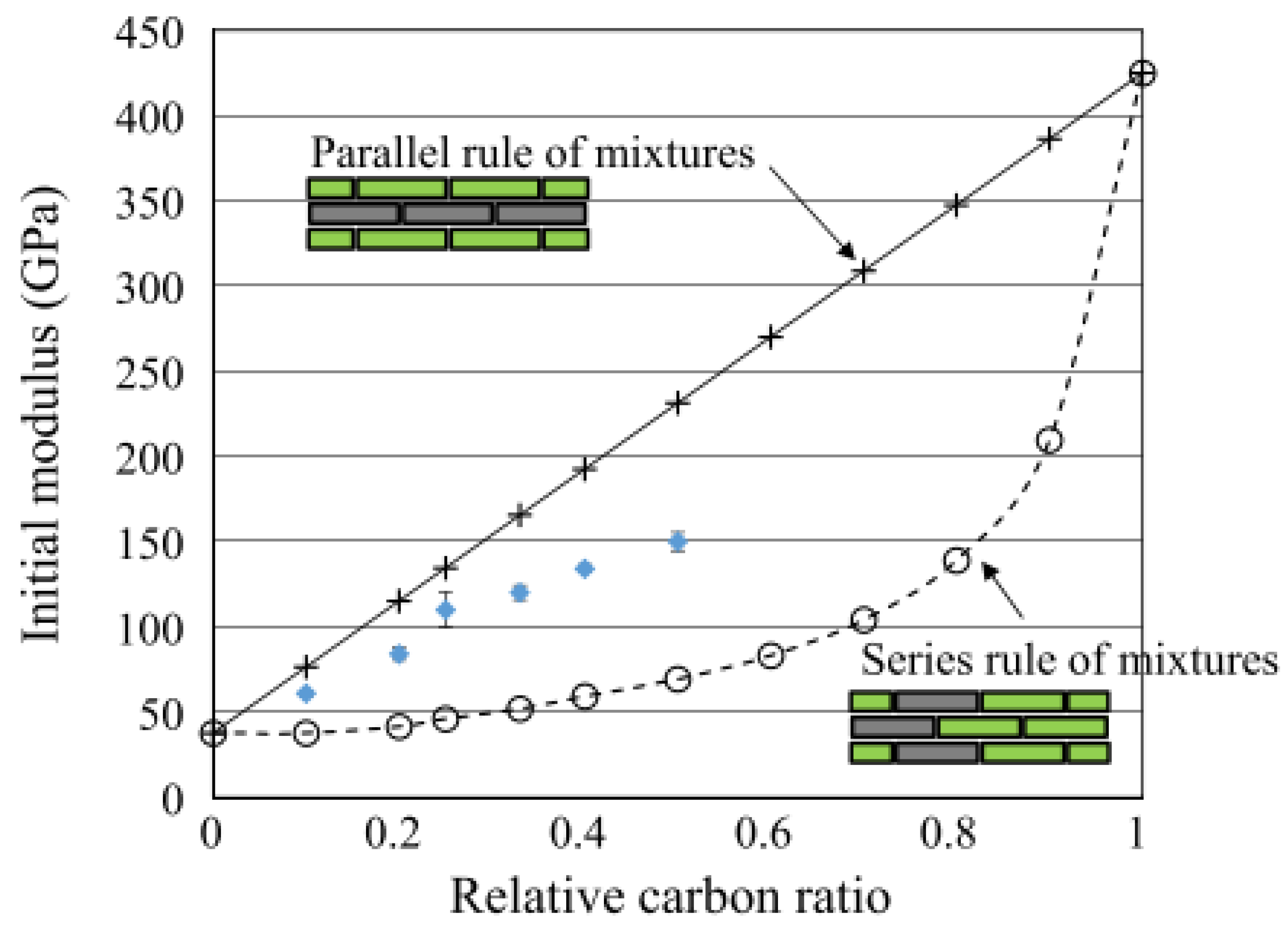
- Techniques derived from the ROM and shear lag theory show a good prediction for modulus when compared with experimental data.
- Processing parameters as well as the stochastic nature of the microstructure affect the overall quality of ADFRC and this aspect should be explored further in future models.
- Movement in the ply layers leads to delaminations and wrinkles during forming, and this is difficult to simulate using current process modelling techniques.
- Cure parameters are linked to the type of matrix used and have an effect on the overall mechanical response. These variables will need to be considered in future performance models.
- Combining statistical approaches with experimental validation using experimental data from highly aligned composites is necessary to progress more realistic modelling frameworks.
- Forming capabilities are demonstrated with possible routes to follow, and the preliminary work performed on tensile properties supports the possibility.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fukuda, H.; Chou, T.W. A probabilistic theory of the strength of short-fibre composites with variable fibre length and orientation. J. Mater. Sci. 1982, 17, 1003–1011. [Google Scholar] [CrossRef]
- Chin, W.K.; Liu, H.T.; Lee, Y.D. Effects of fiber length and orientation distribution on the elastic modulus of short fiber reinforced thermoplastics. Polym. Compos. 1988, 9, 27–35. [Google Scholar] [CrossRef]
- Chou, T.W. Microstructural Design of Fiber Composites; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar] [CrossRef]
- Piggott, M.R. Expressions governing stress–strain curves in short fibre reinforced polymers. J. Mater. Sci. 1978, 13, 1709–1716. [Google Scholar] [CrossRef]
- Kuriger, R.J.; Alam, M.K.; Anderson, D.P. Strength prediction of partially aligned discontinuous fiber-reinforced composites. J. Mater. Res. 2001, 16, 226–232. [Google Scholar] [CrossRef]
- Yu, H.; Potter, K.D.; Wisnom, M.R. Aligned short fibre composites with high performance. In Proceedings of the ICCM International Conferences on Composite Materials, Montréal, QC, Canada, 28 July–2 August 2013; pp. 2583–2590. [Google Scholar]
- Yu, H.; Potter, K.D.; Wisnom, M.R. A novel manufacturing method for aligned discontinuous fibre composites (High Performance-Discontinuous Fibre method). Compos. Part A Appl. Sci. Manuf. 2014, 65, 175–185. [Google Scholar] [CrossRef]
- Yarlagadda, S.; Deitzel, J.; Heider, D.; Tierney, J.; Gillespie, J.W. Tailorable Universal Feedstock for Forming (TUFF): Overview and performance. In Proceedings of the International SAMPE Technical Conference, Charlotte, NC, USA, 20 May 2019; p. 12. [Google Scholar] [CrossRef]
- Such, M.; Ward, C.; Potter, K. Aligned discontinuous fibre composites: A short history. J. Multifunct. Compos. 2014, 2, 1995–1998. [Google Scholar] [CrossRef]
- Yu, H.; Potter, K.D.; Wisnom, M.R. A novel manufacturing method foraligned short fibre composite. In Proceedings of the ECCM15-15th European Conference on Composite Materials, Venice, Italy, 24–28 June 2012. [Google Scholar]
- Heider, D.; Tierney, J.; Henchir, M.A.; Gargitter, V.; Yarlagadda, S.; Gillespie, J.W.; Sun, J.; Sietins, J.M.; Knorr, D. Microstructural evaluation of aligned, short fiber Tuff material. In Proceedings of the International SAMPE Technical Conference, Charlotte, NC, USA, 20–23 May 2019; p. 11. [Google Scholar] [CrossRef]
- Yarlagadda, S.; Advani, S.; Deitzel, J.; Heider, D.; Molligan, D.; Simacek, P.; Tierney, J.; Gillespie, J.W. Formability of TUFF Composite Blanks. In Proceedings of the International SAMPE Technical Conference, Charlotte, NC, USA, 20–23 May 2019; p. 12. [Google Scholar] [CrossRef]
- Pickering, S.J.; Liu, Z.; Turner, T.A.; Wong, K.H. Applications for carbon fibre recovered from composites. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 139, p. 012005. [Google Scholar] [CrossRef]
- Bagg, G.E.; Evans, M.E.; Pryde, A.W. The glycerine process for the alignment of fibres and whiskers. Composites 1969, 1, 97–100. [Google Scholar] [CrossRef]
- Wong, K.H.; Turner, T.A.; Pickering, S.J.; Warrior, N.A. The potential for fibre alignment in the manufacture of polymer composites from recycled carbon fibre. SAE Int. J. Aerosp. 2010, 2, 225–231. [Google Scholar] [CrossRef]
- Liu, Z.; Turner, T.A.; Wong, K.H.; Pickering, S.J. Development of high performance recycled carbon fibre composites with an advanced hydrodynamic fibre alignment process. J. Clean. Prod. 2021, 278, 123785. [Google Scholar] [CrossRef]
- Kacir, L.; Narkis, M.; Ishai, O. Oriented short glass-fiber composites. I. Preparation and statistical analysis of aligned fiber mats. Polym. Eng. Sci. 1975, 15, 525–531. [Google Scholar] [CrossRef]
- Vyakarnam, M.N.; Drzal, L.T. Novel processing and performance of aligned discontinuous fiber polymer composites. J. Eng. Appl. Sci. 1996, 2, 2531–2535. [Google Scholar] [CrossRef]
- Flemming, T.; Kress, G.; Flemming, M. A new aligned short-carbon-fiber-reinforced thermoplastic prepreg. Adv. Compos. Mater. 1996, 5, 151–159. [Google Scholar] [CrossRef]
- Ferabolu, P.; Gasco, F.; Wade, B.; Maier, S.; Kwan, R.; Masini, A.; Deoto, L.; Reggiani, M. Lamborghini forged composite technology for the suspension arms of the Sesto Elemento. In Proceedings of the 26th Annual Technical Conference of the American Society for Composites, Montreal, QC, Canada, 26–28 September 2011; pp. 1012–1036. [Google Scholar]
- Okine, R.; Edison, D.; Little, N. Properties and formability of an aligned discontinuous fiber thermoplastic composite sheet. J. Reinf. Plast. Compos. 1990, 9, 70–90. [Google Scholar] [CrossRef]
- Eguemann, N.; Giger, L.; Roux, M.; Dransfeld, C.; Thiebaud, F.; Perreux, D. Compression moulding of complex parts for the aerospace with discontinuous novel and recycled thermoplastic composite materials. In Proceedings of the 19th International Conference on Composite Materials, Montreal, QC, Canada, 28 July–2 August 2013; pp. 1–11. [Google Scholar]
- Dodwell, T.J.; Butler, R.; Hunt, G.W. Out-of-plane ply wrinkling defects during consolidation over an external radius. Compos. Sci. Technol. 2014, 105, 151–159. [Google Scholar] [CrossRef]
- Yu, H.; Longana, M.L.; Jalalvand, M.; Wisnom, M.R.; Potter, K.D. Pseudo-ductility in intermingled carbon/glass hybrid composites with highly aligned discontinuous fibres. Compos. Part A Appl. Sci. Manuf. 2015, 73, 35–44. [Google Scholar] [CrossRef]
- Czél, G.; Pimenta, S.; Wisnom, M.R.; Robinson, P. Demonstration of pseudo-ductility in unidirectional discontinuous carbon fibre/epoxy prepreg composites. Compos. Sci. Technol. 2015, 106, 110–119. [Google Scholar] [CrossRef]
- Finley, J.M.; Yu, H.; Longana, M.L.; Pimenta, S.; Shaffer, M.S.; Potter, K.D. Exploring the pseudo-ductility of aligned hybrid discontinuous composites using controlled fibre-type arrangements. Compos. Part A Appl. Sci. Manuf. 2018, 107, 592–606. [Google Scholar] [CrossRef]
- Tang, J.; Swolfs, Y.; Longana, M.L.; Yu, H.N.; Wisnom, M.R.; Lomov, S.V.; Gorbatikh, L. Hybrid composites of aligned discontinuous carbon fibers and self-reinforced polypropylene under tensile loading. Compos. Part A Appl. Sci. Manuf. 2019, 123, 97–107. [Google Scholar] [CrossRef]
- Yu, H.N.; Longana, M.L.; Jalalvand, M.; Wisnom, M.R.; Potter, K.D. Hierarchical pseudo-ductile hybrid composites combining continuous and highly aligned discontinuous fibres. Compos. Part A Appl. Sci. Manuf. 2018, 105, 40–56. [Google Scholar] [CrossRef]
- Longana, M.L.; Yu, H.N.; Jalavand, M.; Wisnom, M.R.; Potter, K.D. Aligned discontinuous intermingled reclaimed/virgin carbon fibre composites for high performance and pseudo-ductile behaviour in interlaminated carbon-glass hybrids. Compos. Sci. Technol. 2017, 143, 13–21. [Google Scholar] [CrossRef]
- Longana, M.L.; Yu, H.; Lee, J.; Pozegic, T.R.; Huntley, S.; Rendall, T.; Potter, K.D.; Hamerton, I. Quasi-isotropic and pseudo-ductile highly aligned discontinuous fibre composites manufactured with the HiPerDiF (High Performance Discontinuous Fibre) technology. Materials 2019, 12, 1794. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.N.; Longana, M.L.; Grail, G.; Pimenta, S.; Robinson, P.; Wisnom, M.R.; Potter, K.D. Aligned short fibre composites with nonlinear behaviour. In Proceedings of the ICCM International Conferences on Composite Materials, Montreal, QC, Canada, 19–24 July 2015; pp. 19–24. [Google Scholar]
- Heider, D.; Yarlagadda, S.; Blackwell, C.; Crane, R.; Davis, M.; Emmerich, R.; Deitzel, J.; Ozdemir, T. Carbon Fiber Composites Recycling Technology Enabled By the Tuff Technology. Int. SAMPE Tech. Conf. 2022, 58, 1–14. [Google Scholar] [CrossRef]
- Aravindan, P.; Becagli, F.; Longana, M.L.; Blok, L.G.; Pozegic, T.R.; Huntley, S.J.; Rendall, T.; Hamerton, I. Remanufacturing of woven carbon fibre fabric production waste into high performance aligned discontinuous fibre composites. J. Compos. Sci. 2020, 4, 68. [Google Scholar] [CrossRef]
- Hecker, M.D.; Longana, M.L.; Eloi, J.C.; Thomsen, O.; Hamerton, I. Recycling end-of-life sails by carbon fibre reclamation and composite remanufacture using the HiPerDiF fibre alignment technology. Compos. Part A Appl. Sci. Manuf. 2023, 173, 107651. [Google Scholar] [CrossRef]
- Kandemir, A.; Longana, M.L.; Panzera, T.H.; del Pino, G.G.; Hamerton, I.; Eichhorn, S.J. Natural fibres as a sustainable reinforcement constituent in aligned discontinuous polymer composites produced by the HiPerDiF method. Materials 2021, 14, 1885. [Google Scholar] [CrossRef] [PubMed]
- Messmer, L.L.; Kandemir, A.; Yavuz, B.O.; Longana, M.L.; Hamerton, I. Mechanical Behaviour of As-Manufactured and Repaired Aligned Discontinuous Basalt Fibre-Reinforced Vitrimer Composites. Polymers 2024, 16, 1089. [Google Scholar] [CrossRef] [PubMed]
- Naqvi, S.R.; Prabhakara, H.M.; Bramer, E.A.; Dierkes, W.; Akkerman, R.; Brem, G. A critical review on recycling of end-of-life carbon fibre/glass fibre reinforced composites waste using pyrolysis towards a circular economy. Resour. Conserv. Recycl. 2018, 136, 118–129. [Google Scholar] [CrossRef]
- Tapper, R.J.; Longana, M.L.; Hamerton, I.; Potter, K.D. A closed-loop recycling process for discontinuous carbon fibre polyamide 6 composites. Compos. Part B Eng. 2019, 179, 107418. [Google Scholar] [CrossRef]
- Heider, D.; Tierney, J.; Deitzel, J.; Kubota, M.; Thiravong, J.; Gargitter, V.; Burris, W.; Morris, J.; Shevchenko, N.; Yarlagadda, S.; et al. Closed loop recycling of CFRP into highly aligned high performance short fiber composites using the tuff process. In Proceedings of the International SAMPE Technical Conference, Charlotte, NC, USA, 20–23 May 2019; p. 11. [Google Scholar] [CrossRef]
- Zhang, J.; Chevali, V.S.; Wang, H.; Wang, C.H. Current status of carbon fibre and carbon fibre composites recycling. Compos. Part B Eng. 2020, 193, 108053. [Google Scholar] [CrossRef]
- Legenstein, A.; Füssel, L.; Tierney, J.; Gillespie, J.W., Jr.; Heider, D.; Cender, T. Stretch-Steering of Aligned Discontinuous Fiber Tapes on Highly Curved Paths using Automated Fiber Placement. In Proceedings of the Paper presented at SAMPE North America, Seattle, WA, USA, 17–20 May 2023; pp. 992–1005. [Google Scholar]
- Krajangsawasdi, N.; Longana, M.L.; Hamerton, I.; Woods, B.K.; Ivanov, D.S. Batch production and fused filament fabrication of highly aligned discontinuous fibre thermoplastic filaments. Addit. Manuf. 2021, 48, 102359. [Google Scholar] [CrossRef]
- Composites Automation LLC. Available online: https://www.compositesautomationllc.com/ (accessed on 26 June 2024).
- Lineat. Available online: https://lineat.co.uk/ (accessed on 5 June 2024).
- FAIRMAT. Available online: https://www.fairmat.tech/ (accessed on 26 June 2024).
- Feraboli, P.; Cleveland, T.; Stickler, P.; Halpin, J. Stochastic laminate analogy for simulating the variability in modulus of discontinuous composite materials. Compos. Part A Appl. Sci. Manuf. 2010, 41, 557–570. [Google Scholar] [CrossRef]
- Luchoo, R.; Harper, L.T.; Warrior, N.A.; Dodworth, A. Three-dimensional numerical modelling of discontinuous fibre composite architectures. Plast. Rubber Compos. 2011, 40, 356–362. [Google Scholar] [CrossRef]
- Nakashima, Y.; Yamashita, S.; Zhang, X.; Suganuma, H.; Takahashi, J. Analytical modelling of the behaviour and scatter of the flexural modulus of randomly oriented carbon fibre strand thermoplastic composites. Compos. Struct. 2017, 178, 217–224. [Google Scholar] [CrossRef]
- Zhang, J.J.; Qin, Q.; Zhang, J.J.; Yuan, H.; Du, J.; Li, H. Low-velocity impact on square sandwich plates with fibre-metal laminate face-sheets: Analytical and numerical research. Compos. Struct. 2021, 259, 113461. [Google Scholar] [CrossRef]
- CMH-17 Composite Materials Handbook Volume 3—Revision G; SAE International: Warrendale, PA, USA, 2012.
- Ravindran, A.R.; Ladani, R.B.; Wu, S.; Kinloch, A.J.; Wang, C.H.; Mouritz, A.P. The electric field alignment of short carbon fibres to enhance the toughness of epoxy composites. Compos. Part A Appl. Sci. Manuf. 2018, 106, 11–23. [Google Scholar] [CrossRef]
- Aruan Efendy, M.G.; Pickering, K.L. Comparison of strength and young’s modulus of aligned discontinuous fibre PLA composites obtained experimentally and from theoretical prediction models. Compos. Struct. 2019, 208, 566–573. [Google Scholar] [CrossRef]
- Huntley, S.; Rendall, T.; Longana, M.; Pozegic, T.; Potter, K.; Hamerton, I. Validation of a smoothed particle hydrodynamics model for a highly aligned discontinuous fibre composites manufacturing process. Compos. Sci. Technol. 2020, 196, 108152. [Google Scholar] [CrossRef]
- Thompson, A.J.; Belnoue, J.P.; Hallett, S.R. Modelling defect formation in textiles during the double diaphragm forming process. Compos. Part B Eng. 2020, 202, 108357. [Google Scholar] [CrossRef]
- Pimenta, S.; Pinho, S.T. Recycling carbon fibre reinforced polymers for structural applications: Technology review and market outlook. Waste Manag. 2011, 31, 378–392. [Google Scholar] [CrossRef]
- Tapper, R.J.; Longana, M.L.; Yu, H.; Hamerton, I.; Potter, K.D. Development of a closed-loop recycling process for discontinuous carbon fibre polypropylene composites. Compos. Part B Eng. 2018, 146, 222–231. [Google Scholar] [CrossRef]
- Longana, M.L.; Ondra, V.; Yu, H.; Potter, K.D.; Hamerton, I. Reclaimed carbon and flax fibre composites: Manufacturing and mechanical properties. Recycling 2018, 3, 52. [Google Scholar] [CrossRef]
- Campbell, F.C. Structural Composite Materials; ASM International: Materials Park, OH, USA, 2010; pp. 285–305. ISBN 978-1-62708-314-0. [Google Scholar]
- Kacir, L.; Narkis, M.; Ishai, O. Oriented short glass fiber composites. III. Structure and mechanical properties of molded sheets. Polym. Eng. Sci. 1977, 17, 234–241. [Google Scholar] [CrossRef]
- Berthelot, J.M. Effect of fibre misalignment on the elastic properties of oriented discontinuous fibre composites. Fibre Sci. Technol. 1982, 17, 25–39. [Google Scholar] [CrossRef]
- Fara, S.; Pavan, A. Fibre orientation effects on the fracture of short fibre polymer composites: On the existence of a critical fibre orientation on varying internal material variables. J. Mater. Sci. 2004, 39, 3619–3628. [Google Scholar] [CrossRef]
- Harper, L.T.; Turner, T.A.; Martin, J.R.; Warrior, N.A. Fiber alignment in directed carbon fiber preforms—A feasibility study. J. Compos. Mater. 2009, 43, 57–74. [Google Scholar] [CrossRef]
- Edwards, H.; Evans, N.P. Method for the Production of High Quality Aligned Short Fibre Mats and Their Composites.; Pergamon Press Ltd.: Oxford, UK, 1980; Volume 2, pp. 1620–1635. [Google Scholar] [CrossRef]
- Yu, F.; Chen, S.; Viisainen, J.V.; Sutcliffe, M.P.; Harper, L.T.; Warrior, N.A. A macroscale finite element approach for simulating the bending behaviour of biaxial fabrics. Compos. Sci. Technol. 2020, 191, 108078. [Google Scholar] [CrossRef]
- Ge, H.; Li, S.; Liu, H.; Wang, D.; Chen, J. Preparation and properties of water-soluble-type sizing agents for carbon fibers. J. Appl. Polym. Sci. 2014, 131, 39843. [Google Scholar] [CrossRef]
- Pozegic, T.R.; Huntley, S.; Longana, M.L.; He, S.; Bandara, R.M.; King, S.G.; Hamerton, I. Improving dispersion of recycled discontinuous carbon fibres to increase fibre throughput in the HiPerDiF process. Materials 2020, 13, 1544. [Google Scholar] [CrossRef]
- Lei, H.F.; Zhang, Z.Q.; Liu, B. Effect of fiber arrangement on mechanical properties of short fiber reinforced composites. Compos. Sci. Technol. 2012, 72, 506–514. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chen, P.Y.; Lin, A.Y.M.; Seki, Y. Biological materials: Structure and mechanical properties. Prog. Mater. Sci. 2008, 53, 1–206. [Google Scholar] [CrossRef]
- Pimenta, S.; Robinson, P. An analytical shear-lag model for composites with `brick-and-mortar’ architecture considering non-linear matrix response and failure. Compos. Sci. Technol. 2014, 104, 111–124. [Google Scholar] [CrossRef]
- Finley, J.M.; Shaffer, M.S.; Pimenta, S. Data-driven intelligent optimisation of discontinuous composites. Compos. Struct. 2020, 243, 112176. [Google Scholar] [CrossRef]
- Chou, T.W.; Nomura, S.; Taya, M. A self-consistent approach to the elastic stiffness of short-fiber composites. J. Compos. Mater. 1980, 14, 178–188. [Google Scholar] [CrossRef]
- Tucker, C.L.; Liang, E. Stiffness predictions for unidirectional short-fiber composites: Review and evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Jules, E.J.; Tsujikami, T.; Lomov, S.V.; Verpoest, I. Effect of fibres length and fibres orientation on the predicted elastic properties of long fibre composites. Macromol. Symp. 2004, 17, 1–109. [Google Scholar]
- Affdl, J.C.H.; Kardos, J.L.; Patterson, W.; Force, A. The Halpin-Tsai Equations: A Review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Piggott, M.R.; Ko, M.; Chuang, H.Y. Aligned short-fibre reinforced thermosets: Experiments and analysis lend little support for established theory. Compos. Sci. Technol. 1993, 48, 291–299. [Google Scholar] [CrossRef]
- Vignoli, L.L.; Savi, M.A.; Pacheco, P.M.; Kalamkarov, A.L. Comparative analysis of micromechanical models for the elastic composite laminae. Compos. Part B Eng. 2019, 174, 106961. [Google Scholar] [CrossRef]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Houshyar, S.; Shanks, R.A.; Hodzic, A. The effect of fiber concentration on mechanical and thermal properties of fiber-reinforced polypropylene composites. J. Appl. Polym. Sci. 2005, 96, 2260–2272. [Google Scholar] [CrossRef]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube-polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Karsli, N.G.; Aytac, A.; Deniz, V. Effects of initial fiber length and fiber length distribution on the properties of carbon-fiber-reinforced-polypropylene composites. J. Reinf. Plast. Compos. 2012, 31, 1053–1060. [Google Scholar] [CrossRef]
- Halpin, J.; Jerine, K.; Whitney, J. The Laminate Analogy for 2 and 3 Dimensional Composite Materials. J. Compos. Mater. 2016, 5, 36–49. [Google Scholar] [CrossRef]
- Halpin, J. Stiffness and expansion estimates for oriented short fiber composites. J. Compos. Mater. 2016, 3, 732–734. [Google Scholar] [CrossRef]
- Sanadi, A.R.; Piggott, M.R. Interfacial effects in carbon-epoxies. J. Mater. Sci. 1985, 20, 431–437. [Google Scholar] [CrossRef]
- Kelly, A.; Tyson, W.R. Tensile properties of fibre-reinforced metals: Copper/tungsten and copper/molybdenum. J. Mech. Phys. Solids 1965, 13, 329–350. [Google Scholar] [CrossRef]
- Fu, S.Y.; Lauke, B. Effects of fiber length and fiber orientation distributions on the tensile strength of short-fiber-reinforced polymers. Compos. Sci. Technol. 1996, 56, 1179–1190. [Google Scholar] [CrossRef]
- Petersen, R.C. Discontinuous fiber-reinforced composites above critical length. J. Dent. Res. 2005, 84, 365–370. [Google Scholar] [CrossRef]
- Kim, H.G.; Kwac, L.K. Evaluation of elastic modulus for unidirectionally aligned short fiber composites. J. Mech. Sci. Technol. 2009, 23, 54–63. [Google Scholar] [CrossRef]
- Thomason, J.L.; Vlug, M.A.; Schipper, G.; Krikor, H.G. Influence of fibre length and concentration on the properties of glass fibre-reinforced polypropylene: Part 3. Strength and strain at failure. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1075–1084. [Google Scholar] [CrossRef]
- Hikami, F.; Chou, T.W. A probabilistic theory for the strength of discontinuous fibre composites. J. Mater. Sci. 1984, 19, 1805–1817. [Google Scholar] [CrossRef]
- Hsueh, C.H. A modified analysis for stress transfer in fibre-reinforced composites with bonded fibre ends. J. Mater. Sci. 1995, 30, 219–224. [Google Scholar] [CrossRef]
- Hsueh, C.H. Young’s modulus of unidirectional discontinuous-fibre composites. Compos. Sci. Technol. 2000, 60, 2671–2680. [Google Scholar] [CrossRef]
- Hsueh, C.H. Analytical analyses of stress transfer in fibre-reinforced composites with bonded and debonded fibre ends. J. Mater. Sci. 1989, 24, 4475–4482. [Google Scholar] [CrossRef]
- Fukuda, H.; Chou, T.W. A probabilistic theory for the strength of short fibre composites. J. Mater. Sci. 1981, 16, 1088–1096. [Google Scholar] [CrossRef]
- Visweswaraiah, S.B.; Selezneva, M.; Lessard, L.; Hubert, P. Mechanical characterisation and modelling of randomly oriented strand architecture and their hybrids-A general review. J. Reinf. Plast. Compos. 2018, 37, 548–580. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Lei, Z.; Zhu, P. An innovative computational framework for the analysis of complex mechanical behaviors of short fiber reinforced polymer composites. Compos. Struct. 2021, 277, 114594. [Google Scholar] [CrossRef]
- Babu, K.P.; Mohite, P.M.; Upadhyay, C.S. Development of an RVE and its stiffness predictions based on mathematical homogenization theory for short fibre composites. Int. J. Solids Struct. 2018, 130–131, 80–104. [Google Scholar] [CrossRef]
- Gusev, A.A. Representative volume element size for elastic composites: A numerical study. J. Mech. Phys. Solids 1997, 45, 1449–1459. [Google Scholar] [CrossRef]
- Gusev, A.A.; Heggli, M.; Lusti, H.R.; Hine, P.J. Orientation averaging for stiffness and thermal expansion of short fiber composites. Adv. Eng. Mater. 2002, 4, 931–933. [Google Scholar] [CrossRef]
- Hine, P.J.; Rudolf Lusti, H.; Gusev, A.A. Numerical simulation of the effects of volume fraction, aspect ratio and fibre length distribution on the elastic and thermoelastic properties of short fibre composites. Compos. Sci. Technol. 2002, 62, 1445–1453. [Google Scholar] [CrossRef]
- Lusti, H.R.; Hine, P.J.; Gusev, A.A. Direct numerical predictions for the elastic and thermoelastic properties of short fibre composites. Compos. Sci. Technol. 2002, 62, 1927–1934. [Google Scholar] [CrossRef]
- Fliegener, S.; Luke, M.; Gumbsch, P. 3D microstructure modeling of long fiber reinforced thermoplastics. Compos. Sci. Technol. 2014, 104, 136–145. [Google Scholar] [CrossRef]
- Sasagawa, T.; Tanaka, M.; Omote, R.; Balzani, D. Numerical material testing for discontinuous fiber composites using statistically similar representative volume elements. Sci. Rep. 2020, 10, 10608. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Iorga, L.; Pelegri, A.A. Numerical generation of a random chopped fiber composite RVE and its elastic properties. Compos. Sci. Technol. 2008, 68, 2792–2798. [Google Scholar] [CrossRef]
- Pan, Y.; Iorga, L.; Pelegri, A.A. Analysis of 3D random chopped fiber reinforced composites using FEM and random sequential adsorption. Comput. Mater. Sci. 2008, 43, 450–461. [Google Scholar] [CrossRef]
- Harper, L.T.; Qian, C.; Turner, T.A.; Li, S.; Warrior, N.A. Representative volume elements for discontinuous carbon fibre composites—Part 2: Determining the critical size. Compos. Sci. Technol. 2012, 72, 204–210. [Google Scholar] [CrossRef]
- Harper, L.T.; Qian, C.; Turner, T.A.; Li, S.; Warrior, N.A. Representative volume elements for discontinuous carbon fibre composites—Part 1: Boundary conditions. Compos. Sci. Technol. 2012, 72, 225–234. [Google Scholar] [CrossRef]
- Liu, H.; Zeng, D.; Li, Y.; Jiang, L. Development of RVE-embedded solid elements model for predicting effective elastic constants of discontinuous fiber reinforced composites. Mech. Mater. 2016, 93, 109–123. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Velmurugan, R.; Srinivasulu, G.; Jayasankar, S. Influence of fiber waviness on the effective properties of discontinuous fiber reinforced composites. Comput. Mater. Sci. 2014, 91, 339–349. [Google Scholar] [CrossRef]
- Koley, S.; Mohite, P.M.; Upadhyay, C.S. A micromechanical study and uncertainty quantification for effective properties of unidirectional fibre reinforced composites. Compos. Struct. 2019, 225, 111141. [Google Scholar] [CrossRef]
- Cai, H.; Ye, J.; Wang, Y.; Saafi, M.; Huang, B.; Yang, D.; Ye, J. An effective microscale approach for determining the anisotropy of polymer composites reinforced with randomly distributed short fibers. Compos. Struct. 2020, 240, 112087. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Zhou, J.; Liang, J.; Ma, Y. Representative volume element for composites reinforced by spatially randomly distributed discontinuous fibers and its applications. Compos. Struct. 2015, 131, 366–373. [Google Scholar] [CrossRef]
- Pahr, D.H.; Arnold, S.M. The applicability of the generalized method of cells for analyzing discontinuously reinforced composites. Compos. Part B Eng. 2002, 33, 153–170. [Google Scholar] [CrossRef]
- Sertse, H.; Zhang, L.; Yu, W.; Ye, Z. A comprehensive evaluation of the predictive capabilities of several advanced micromechanics approaches. In Proceedings of the 55th AIAA/ASMe/ASCE/AHS/SC Structures, Structural Dynamics, and Materials Conference, National Harbour, MD, USA, 13–17 January 2014; pp. 1–23. [Google Scholar] [CrossRef]
- Sertse, H.; Yu, W. A micromechanical approach to static failure prediction of heterogeneous materials. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015; pp. 1–27. [Google Scholar] [CrossRef]
- Bouhala, L.; Koutsawa, Y.; Makradi, A.; Belouettar, S. An advanced numerical method for predicting effective elastic properties of heterogeneous composite materials. Compos. Struct. 2014, 117, 114–123. [Google Scholar] [CrossRef]
- Sertse, H.M.; Goodsell, J.; Ritchey, A.J.; Pipes, R.B.; Yu, W. Challenge problems for the benchmarking of micromechanics analysis: Level I initial results. J. Compos. Mater. 2018, 52, 61–80. [Google Scholar] [CrossRef]
- Mirkhalaf, S.M.; Eggels, E.H.; van Beurden, T.J.; Larsson, F.; Fagerström, M. A finite element based orientation averaging method for predicting elastic properties of short fiber reinforced composites. Compos. Part B Eng. 2020, 202, 108388. [Google Scholar] [CrossRef]
- Papathanasiou, T.D.; Ingber, M.S.; Guell, D.C. Stiffness enhancement in aligned, short-fibre composites: A computational and experimental investigation. Compos. Sci. Technol. 1995, 54, 1–9. [Google Scholar] [CrossRef]
- Ingber, M.S.; Papathanasiou, T.D. A parallel-supercomputing investigation of the stiffness of aligned, short-fiber-reinforced composites using the boundary element method. Int. J. Numer. Methods Eng. 1997, 40, 3477–3491. [Google Scholar] [CrossRef]
- Gun, H.; Kose, G. Prediction of longitudinal modulus of aligned discontinuous fiber-reinforced composites using boundary element method. Sci. Eng. Compos. Mater. 2014, 21, 219–221. [Google Scholar] [CrossRef]
- Papathanasiou, T.D.; Ingber, M.S.; Mondy, L.A.; Graham, A.L. The effective elastic modulus of fiber-reinforced composites. J. Compos. Mater. 1994, 28, 288–304. [Google Scholar] [CrossRef]
- Hu, Y.L.; Wang, J.Y.; Madenci, E.; Mu, Z.; Yu, Y. Peridynamic micromechanical model for damage mechanisms in composites. Compos. Struct. 2022, 301, 116182. [Google Scholar] [CrossRef]
- Qu, P.; Wan, Y.; Bao, C.; Sun, Q.; Fang, G.; Takahashi, J. A new numerical method for the mechanical analysis of chopped carbon fiber tape-reinforced thermoplastics. Compos. Struct. 2018, 201, 857–866. [Google Scholar] [CrossRef]
- Zhang, D.; Qu, P.; Jia, Y. A new numerical method for the tensile property analysis of discontinuous fiber-reinforced thermoplastics. Compos. Adv. Mater. 2021, 30, 2633366X2097749. [Google Scholar] [CrossRef]
- Hashimoto, M.; Okabe, T.; Sasayama, T.; Matsutani, H.; Nishikawa, M. Prediction of tensile strength of discontinuous carbon fiber/polypropylene composite with fiber orientation distribution. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1791–1799. [Google Scholar] [CrossRef]
- Nishikawa, M.; Okabe, T.; Takeda, N. Periodic-cell simulations for the microscopic damage and strength properties of discontinuous carbon fiber-reinforced plastic composites. Adv. Compos. Mater. 2009, 18, 77–93. [Google Scholar] [CrossRef]
- Okabe, T.; Sasayama, T.; Koyanagi, J. Micromechanical simulation of tensile failure of discontinuous fiber-reinforced polymer matrix composites using Spring Element Model. Compos. Part A Appl. Sci. Manuf. 2014, 56, 64–71. [Google Scholar] [CrossRef]
- Pimenta, S.; Robinson, P. An analytical model for the mechanical response of discontinuous composites. In Proceedings of the 19th International Conference on Composite Materials, Montréal, QC, Canada, 28 July–2 August 2013; pp. 2881–2889. [Google Scholar]
- Henry, J.; Pimenta, S. Semi-analytical simulation of aligned discontinuous composites. Compos. Sci. Technol. 2017, 144, 230–244. [Google Scholar] [CrossRef]
- Henry, J.; Pimenta, S. Modelling hybrid effects on the stiffness of aligned discontinuous composites with hybrid fibre-types. Compos. Sci. Technol. 2017, 152, 275–289. [Google Scholar] [CrossRef]
- Henry, J.; Pimenta, S. Virtual testing framework for hybrid aligned discontinuous composites. Compos. Sci. Technol. 2018, 159, 259–272. [Google Scholar] [CrossRef]
- Wang, L.; Nygren, G.; Karkkainen, R.L.; Yang, Q. A multiscale approach for virtual testing of highly aligned short carbon fiber composites. Compos. Struct. 2019, 230, 111462. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length and concentration on the properties of glass fibre reinforced polypropylene: 5. Injection moulded long and short fibre PP. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1641–1652. [Google Scholar] [CrossRef]
- Capela, C.; Oliveira, S.E.; Pestana, J.; Ferreira, J.A. Effect of fiber length on the mechanical properties of high dosage carbon reinforced. Procedia Struct. Integr. 2017, 5, 539–546. [Google Scholar] [CrossRef]
- Sadabadi, H.; Ghasemi, M. Effects of some injection molding process parameters on fiber orientation tensor of short glass fiber polystyrene composites (SGF/PS). J. Reinf. Plast. Compos. 2007, 26, 1729–1741. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, H.; Kuang, T.; Jiang, Q.; Chen, Z.; Li, W. Simulation and optimization of short fiber circumferential orientation in short-fiber-reinforced composites overflow water-assisted injection molded tube. Adv. Polym. Technol. 2019, 2019. [Google Scholar] [CrossRef]
- Liu, Z.; Turner, T.A.; Wong, K.H.; Pickering, S.J. Effect of fiber suspension jet stability on alignment quality of discontinuous carbon fiber tapes. Int. J. Multiph. Flow 2019, 120, 103102. [Google Scholar] [CrossRef]
- Oumer, A.N.; Mamat, O. A study of fiber orientation in short fiber-reinforced composites with simultaneous mold filling and phase change effects. Compos. Part B Eng. 2012, 43, 1087–1094. [Google Scholar] [CrossRef]
- Borzacchiello, D.; Abisset-Chavanne, E.; Chinesta, F.; Keunings, R. Orientation kinematics of short fibres in a second-order viscoelastic fluid. Rheol. Acta 2016, 55, 397–409. [Google Scholar] [CrossRef]
- Huntley, S.; Rendall, T.; Longana, M.; Pozegic, T.; Potter, K.; Hamerton, I. SPH simulation for short fibre recycling using water jet alignment. Int. J. Comput. Fluid Dyn. 2021, 35, 129–142. [Google Scholar] [CrossRef]
- Lipscomb, G.G.; Denn, M.M.; Hur, D.U.; Boger, D.V. The flow of fiber suspensions in complex geometries. J. Non–Newton. Fluid Mech. 1988, 26, 297–325. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. Flow and Rheology in Polymer Composites Manufacturing; Chapter 4; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Advani, S.G. A numerical simulation of short fibrer orientation in compression molding. Polym. Compos. 1990, 11, 164–173. [Google Scholar] [CrossRef]
- Azaiez, J.; Chiba, K.; Chinesta, F.; Poitou, A. State-of-the-art on numerical simulation of fiber-reinforced thermoplastic forming processes. Arch. Comput. Methods Eng. 2002, 9, 141–198. [Google Scholar] [CrossRef]
- Kim, H.S.; Chang, S.H. Simulation of compression moulding process for long-fibre reinforced thermoset composites considering fibre bending. Compos. Struct. 2019, 230, 111514. [Google Scholar] [CrossRef]
- Boisse, P.; Hamila, N.; Madeo, A. The difficulties in modeling the mechanical behavior of textile composite reinforcements with standard continuum mechanics of Cauchy. Some possible remedies. Int. J. Solids Struct. 2018, 154, 55–65. [Google Scholar] [CrossRef]
- Lin, H.; Wang, J.; Long, A.C.; Clifford, M.J.; Harrison, P. Predictive modelling for optimization of textile composite forming. Compos. Sci. Technol. 2007, 67, 3242–3252. [Google Scholar] [CrossRef]
- Boisse, P.; Hamila, N.; Vidal-Sallé, E.; Dumont, F. Simulation of wrinkling during textile composite reinforcement forming. Influence of tensile, in-plane shear and bending stiffnesses. Compos. Sci. Technol. 2011, 71, 683–692. [Google Scholar] [CrossRef]
- Harrison, P.; Gomes, R.; Curado-Correia, N. Press forming a 0/90 cross-ply advanced thermoplastic composite using the double-dome benchmark geometry. Compos. Part A Appl. Sci. Manuf. 2013, 54, 56–69. [Google Scholar] [CrossRef]
- Harrison, P. Modelling the forming mechanics of engineering fabrics using a mutually constrained pantographic beam and membrane mesh. Compos. Part A Appl. Sci. Manuf. 2016, 81, 145–157. [Google Scholar] [CrossRef]
- Harrison, P.; Alvarez, M.F.; Anderson, D. Towards comprehensive characterisation and modelling of the forming and wrinkling mechanics of engineering fabrics. Int. J. Solids Struct. 2018, 154, 2–18. [Google Scholar] [CrossRef]
- Mulye, P.D.; Hemmer, J.; Morançay, L.; Binetruy, C.; Leygue, A.; Comas-Cardona, S.; Pichon, P.; Guillon, D. Numerical modeling of interply adhesion in composite forming of viscous discontinuous thermoplastic prepregs. Compos. Part B Eng. 2020, 191, 107953. [Google Scholar] [CrossRef]
- Yu, F.; Chen, S.; Harper, L.T.; Warrior, N.A. Simulating the effect of fabric bending stiffness on the wrinkling behaviour of biaxial fabrics during preforming. Compos. Part A Appl. Sci. Manuf. 2021, 143, 106308. [Google Scholar] [CrossRef]
- Yu, F.; Chen, S.; Harper, L.T.; Warrior, N.A. Double diaphragm forming simulation using a global-to-local modelling strategy for detailed defect detection in large structures. Compos. Part A Appl. Sci. Manuf. 2021, 147, 106457. [Google Scholar] [CrossRef]
- Charmetant, A.; Vidal-Sallé, E.; Boisse, P. Hyperelastic modelling for mesoscopic analyses of composite reinforcements. Compos. Sci. Technol. 2011, 71, 1623–1631. [Google Scholar] [CrossRef]
- Pipes, R.B.; Hearle, J.W.S.; Beaussart, A.J.; Okine, R.K. Influence of Fiber Length on the Viscous Flow of an Oriented Fiber Assembly. J. Compos. Mater. 1991, 25, 1379–1390. [Google Scholar] [CrossRef]
- Pipes, R.B.; Hearle, J.W.; Beaussart, A.J.; Sastry, A.M.; Okine, R.K. A Constitutive Relation for the Viscous Flow of an Oriented Fiber Assembly. J. Compos. Mater. 1991, 25, 1204–1217. [Google Scholar] [CrossRef]
- Šimáček, P.; Advani, S.G. A micromechanics model to predict extensional viscosity of aligned long discontinuous fiber suspensions. Int. J. Mater. Form. 2019, 12, 777–791. [Google Scholar] [CrossRef]
- Wang, Y.; Chea, M.K.; Belnoue, J.P.; Kratz, J.; Ivanov, D.S.; Hallett, S.R. Experimental characterisation of the in-plane shear behaviour of UD thermoset prepregs under processing conditions. Compos. Part A Appl. Sci. Manuf. 2020, 133, 105865. [Google Scholar] [CrossRef]
- Guzman-Maldonado, E.; Hamila, N.; Naouar, N.; Moulin, G.; Boisse, P. Simulation of thermoplastic prepreg thermoforming based on a visco-hyperelastic model and a thermal homogenization. Mater. Des. 2016, 93, 431–442. [Google Scholar] [CrossRef]
- Dörr, D.; Joppich, T.; Kugele, D.; Henning, F.; Kärger, L. A coupled thermomechanical approach for finite element forming simulation of continuously fiber-reinforced semi-crystalline thermoplastics. Compos. Part A Appl. Sci. Manuf. 2019, 125, 105508. [Google Scholar] [CrossRef]
- Yavuz, B.O.; Hamerton, I.; Longana, M.L.; Belnoue, J.P. Tensile characterisation of HiPerDiF PLA/carbon fibre tape under processing conditions. In Proceedings of the 20th European Conference on Composite Materials ECCM20, Lausanne, Switzerland, 26–30 June 2022; pp. 26–30. [Google Scholar] [CrossRef]
- Yavuz, B.O.; Hamerton, I.; Longana, M.L.; Belnoue, J.P. In forming s of a HiPerDiF PLA/Carbon fibre tape with a micromechanical model. In Proceedings of the American Society for Composites (ASC) 38th Annual Technical Conference, Boston, MA, USA, 17–20 September 2023. [Google Scholar]
- Franck, A. Viscoelasticity and Dynamic Mechanical Testing AN004. Available online: https://www.tainstruments.com/applications-notes/ (accessed on 5 June 2024).






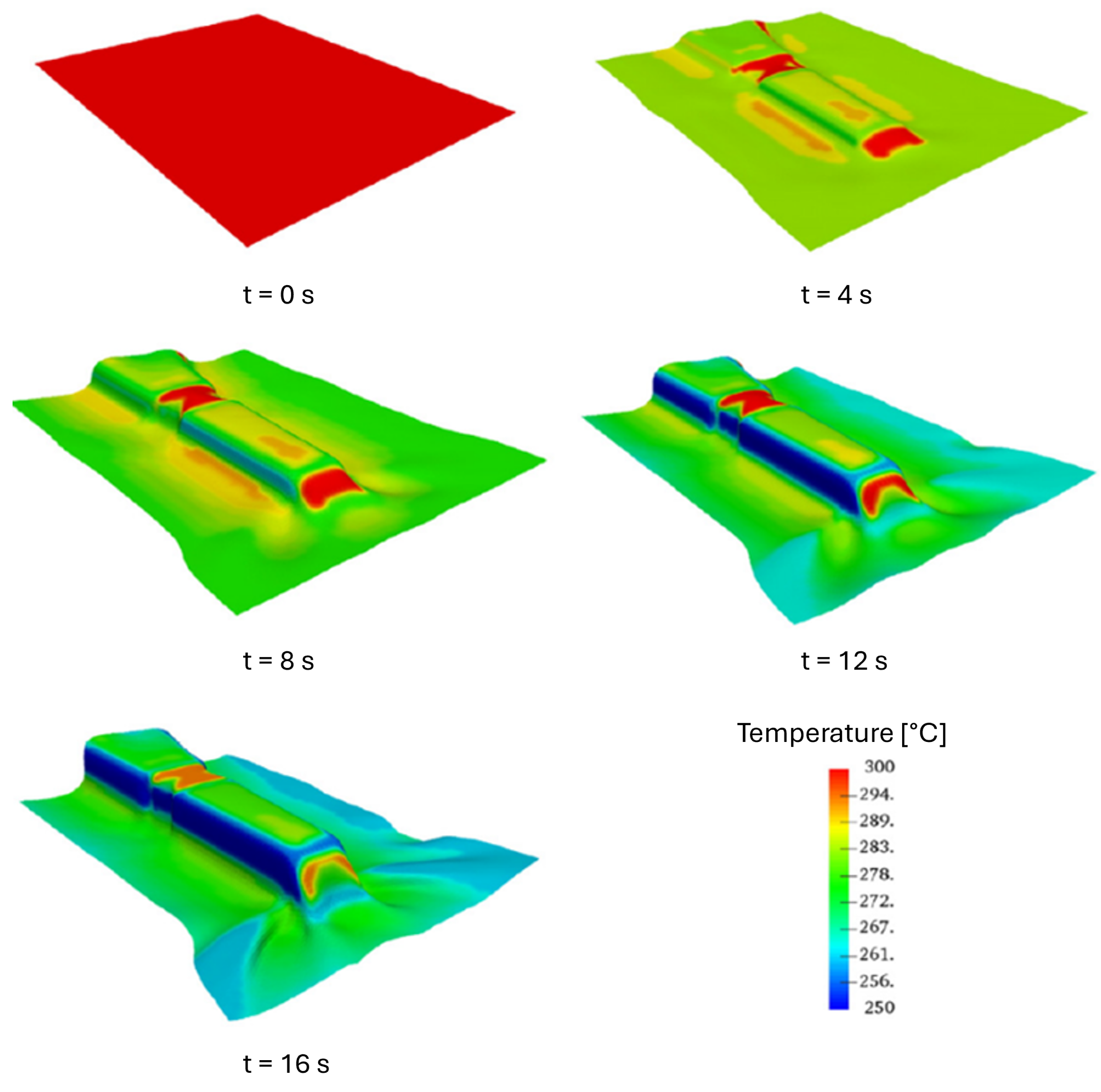
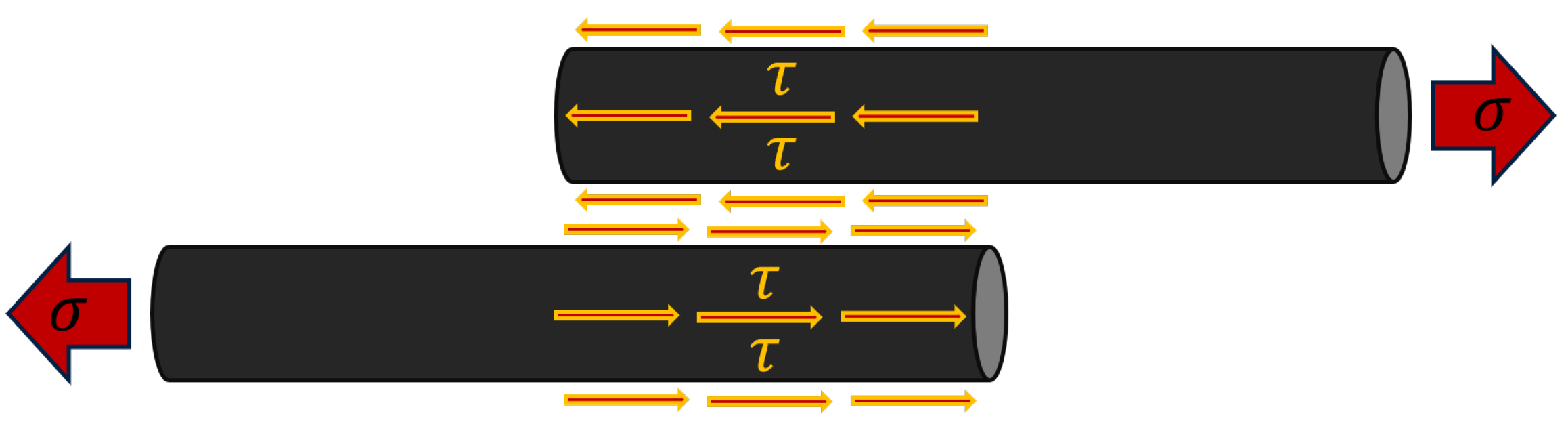
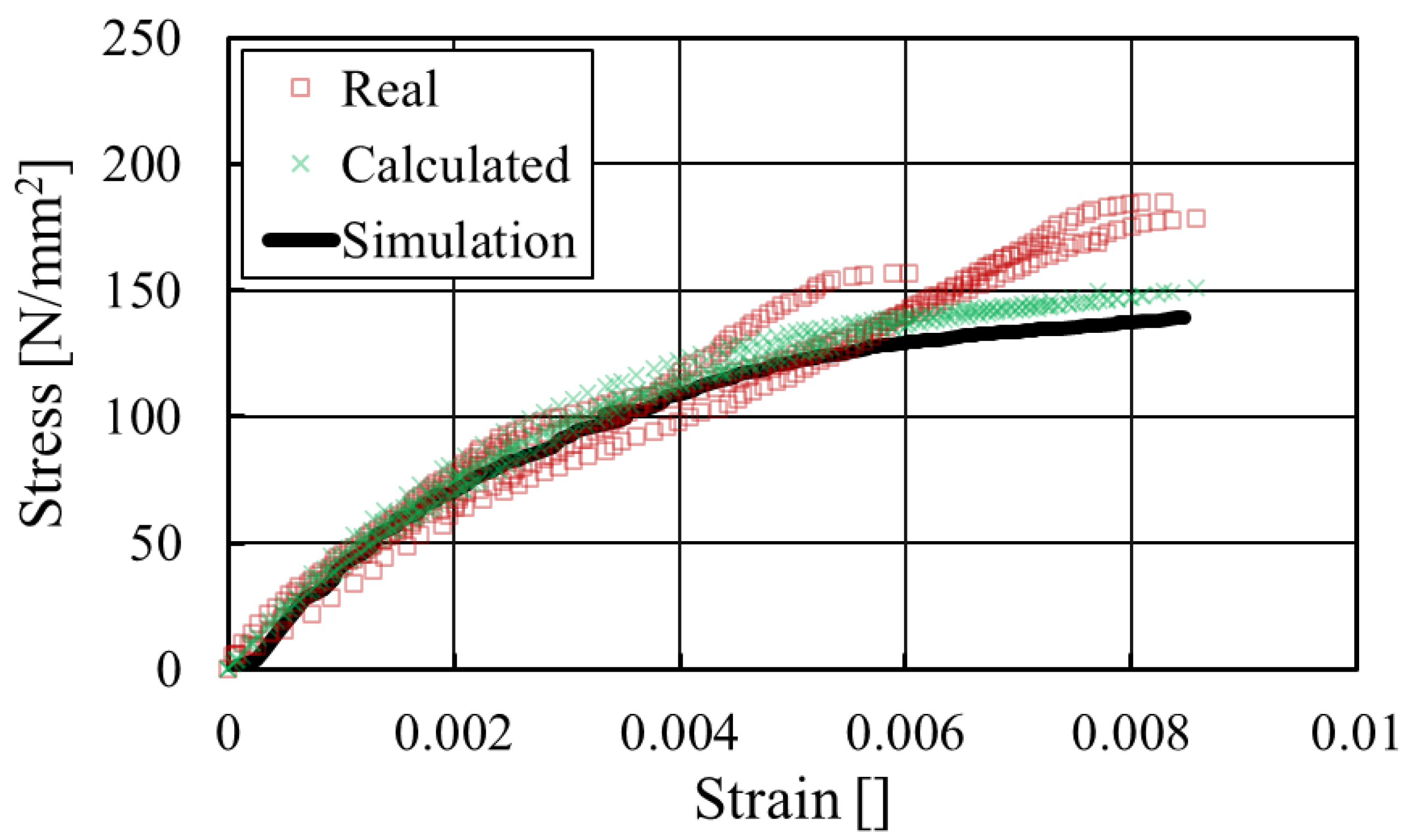
| Method | Year | Materials 1 | Fibre Volume Fraction (%) | Alignment (°) | Stiffness (GPa) | Strength (MPa) |
|---|---|---|---|---|---|---|
| Converging flow [17] | 1978 | GF/EP | 50 | ±15 (95%) | 31 | 290 |
| Electrical [18] | 1996 | GF/Nylon-12 | 40 | ±20 (70%) | 17 | 225 |
| Centrifugal flow—ERDE [19] | 1996 | CF/EP/PA/PI | 55 | ±4 (80%) | 100 | 1100 |
| HiPerDiF [7,10] | 2012 | CF/EP | 55 | ±3 (80%) | 115 | 1509 |
| Rotating drum [13] | 2016 | CF/EP | 46 | ±10 (94%) | 85 | 620 |
| TuFF [12] | 2019 | CF/PEI | 58 | ±5 (87%) | 162 | 2105 |
| Analytical Theory | Parameter | Considerations | Not Considered | Experimental Validation |
|---|---|---|---|---|
| Shear lag-modified (1989–2000) [90,91,92] | Stiffness | Perfect bonding between fibre and matrix | Stresses at the fibre ends | Wet deposition [88] |
| Load transfer along the fibre | Variation in fibre and matrix properties | Wet alignment method [83] | ||
| Matrix transfers only shear force | Variation in fibre length and alignment | |||
| Shear lag-modified (1981–1984) [89,93] | Strength | Stress transfer at the fibre ends | Variation in fibre and matrix properties | - |
| Stress distribution | Variation in fibre end gap size | Defects like wrinkling or voids | ||
| Effect of matrix stress transfer | ||||
| Shear lag-modified (1989–2000) [90,91,92] | Stiffness | RVE includes bonded fibre ends | Variation in fibre and matrix properties | Squeeze casting |
| Stress distribution | Imaginary fibres added to bonded ends | Multiple fibres in RVE | Metal matrix composites [91] | |
| Stress transfer at the fibre ends | Defects like wrinkling or voids | |||
| The effect of matrix stress transfer |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewis, C.; Yavuz, B.O.; Longana, M.L.; Belnoue, J.P.-H.; Ramakrishnan, K.R.; Ward, C.; Hamerton, I. A Review on the Modelling of Aligned Discontinuous Fibre Composites. J. Compos. Sci. 2024, 8, 318. https://doi.org/10.3390/jcs8080318
Lewis C, Yavuz BO, Longana ML, Belnoue JP-H, Ramakrishnan KR, Ward C, Hamerton I. A Review on the Modelling of Aligned Discontinuous Fibre Composites. Journal of Composites Science. 2024; 8(8):318. https://doi.org/10.3390/jcs8080318
Chicago/Turabian StyleLewis, Chantal, Burak Ogun Yavuz, Marco L. Longana, Jonathan P.-H. Belnoue, Karthik Ram Ramakrishnan, Carwyn Ward, and Ian Hamerton. 2024. "A Review on the Modelling of Aligned Discontinuous Fibre Composites" Journal of Composites Science 8, no. 8: 318. https://doi.org/10.3390/jcs8080318
APA StyleLewis, C., Yavuz, B. O., Longana, M. L., Belnoue, J. P.-H., Ramakrishnan, K. R., Ward, C., & Hamerton, I. (2024). A Review on the Modelling of Aligned Discontinuous Fibre Composites. Journal of Composites Science, 8(8), 318. https://doi.org/10.3390/jcs8080318








