Mechanical and Thermal Properties of the Hf–Si System: First-Principles Calculations
Abstract
1. Introduction
2. Computation Methods
3. Results and Discussion
3.1. Structural Properties
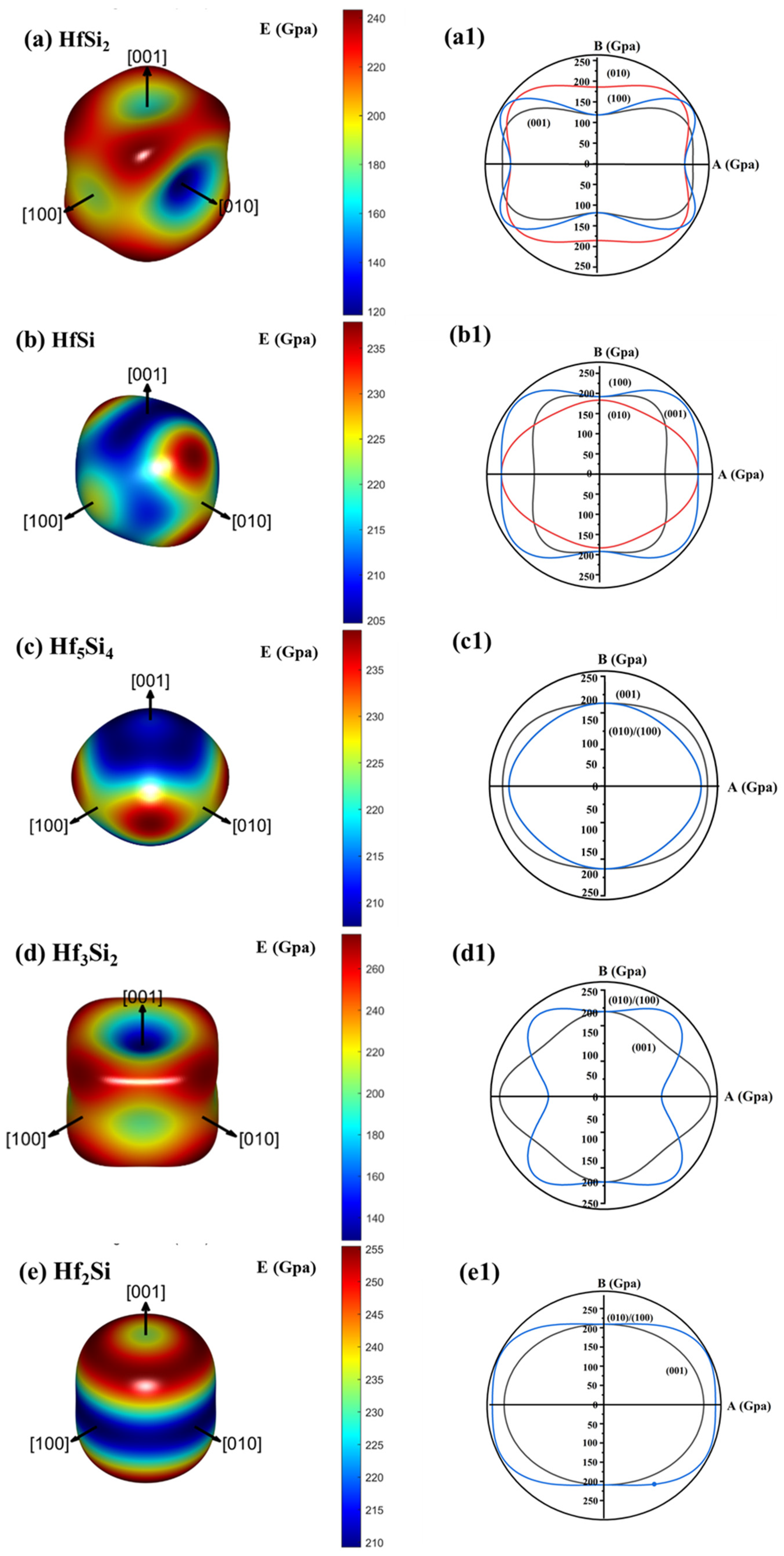
3.2. Elastic and Mechanical Properties
3.3. Thermal Conductivity
4. Conclusions
- (1)
- The Hf-Si system has improved plasticity and hardness as compared to Si, and reduced G/B value, which benefits in minimizing the thermal stress on the substrate, and increases their thermal shock resistance. In addition, the Young’s modulus of Hf-Si system is higher than that of Si.
- (2)
- The addition of the Hf element to Si forming silicide can increase the sound velocities and reduce the Debye temperature, and thus reduce the thermal conductivity. Compared with Si, the theoretical minimum thermal conductivity of the Hf-Si system was substantially small, which was only 0.63 W m−1 K−1 for Hf2Si with improved heat insulation ability than that of Si.
- (3)
- The calculation results show that HfSi2 in the Hf-Si system has the lowest Young’s modulus and good plasticity, making it a good candidate as a bond layer for EBCs used at a high temperature.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raj, R. Fundamental research in structural ceramics for service near 2000 °C. J. Am. Ceram. Soc. 1993, 76, 2147–2174. [Google Scholar] [CrossRef]
- Smialek, J.L.; Robinson, R.C.; Opila, E.J.; Fox, D.S.; Jacobson, N.S. SiC and Si3N4 recession due to SiO2 scale volatility under combustor conditions. Adv. Compos. Mater. 1999, 8, 33–45. [Google Scholar] [CrossRef]
- Klemm, H.; Taut, C.; Wötting, G. Long-term stability of nonoxide ceramics in an oxidative environment at 1500 °C. J. Eur. Ceram. Soc. 2003, 23, 619–627. [Google Scholar] [CrossRef]
- Lee, K.N.; Fox, D.S.; Bansal, N.P. Rare earth silicate environmental barrier coatings for SiC/SiC composites and Si3N4 ceramics. J. Eur. Ceram. Soc. 2005, 25, 1705–1715. [Google Scholar] [CrossRef]
- Tejero-Martin, D.; Bennett, C.; Hussain, T. A review on environmental barrier coatings: History, current state of the art and future developments. J. Eur. Ceram. Soc. 2021, 41, 1747–1768. [Google Scholar] [CrossRef]
- Zhang, Z.; Park, Y.; Xue, Z.; Zhang, S.; Byon, E.; Koo, B.-H. Research status of bond coats in environmental barrier coatings. Int. J. Appl. Ceram. Technol. 2022, 19, 1841–1859. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, X.; Chang, Z.; Tian, Y.; Zhang, X.; Han, G.; Li, J.; Zhang, J. Si-HfO2 composite powders fabricated by freeze drying for bond layer of environmental barrier coatings. Ceram. Int. 2022, 48, 19266–19273. [Google Scholar] [CrossRef]
- Ding, S.; Zeng, Y.; Jiang, D. Oxidation bonding of porous silicon nitride ceramics with high strength and low dielectric constant. Mater. Lett. 2007, 61, 2277–2280. [Google Scholar] [CrossRef]
- Kamino, T.; Saka, H. Newly developed high-resolution hot stage and its application to materials science. Microsc. Microanal. Microstruct. 1993, 4, 127–135. [Google Scholar] [CrossRef]
- Zhuang, M.A.; Ling, L.; Wei, Z. Environmental Barrier Coating for Aeroengines:Materials and Properties. Adv. Ceram. 2019, 40, 331–344. [Google Scholar]
- Sullivan, R.M. Reformulation of Oxide Growth Equations for Oxidation of Silicon Bond Coat in Environmental Barrier Coating Systems. J. Eur. Ceram. Soc. 2019, 39, 5403–5409. [Google Scholar] [CrossRef]
- Damby, D.E.; Llewellin, E.W.; Horwell, C.J.; Williamson, B.J.; Najorka, J.; Cressey, G.; Carpenter, M. The α–β phase transition in volcanic cristobalite. J. Appl. Crystallogr. 2014, 47, 1205–1215. [Google Scholar] [CrossRef] [PubMed]
- Theil, J.A.; Tsu, D.V.; Watkins, M.W.; Kim, S.S.; Lucovsky, G. Local bonding environments of Si–OH groups in SiO2 deposited by remote plasma-enhanced chemical vapor deposition and incorporated by postdeposition exposure to water vapor. J. Vac. Sci. Technol. A Vac. Surf. Film. 1990, 8, 1374–1381. [Google Scholar] [CrossRef]
- Deijkers, J.A.; Wadley, H.N. Hafnium silicate formation during oxidation of a permeable silicon+ HfO2 powder composite system. Acta Mater. 2020, 201, 448–461. [Google Scholar] [CrossRef]
- Harder, B.J. Oxidation performance of Si-HfO2 environmental barrier coating bond coats deposited via plasma spray-physical vapor deposition. Surf. Coat. Technol. 2020, 384, 125311. [Google Scholar] [CrossRef]
- Yuan, J.; Zhou, X.; Dong, S.; Jiang, J.; Deng, L.; Song, W.; Dingwell, D.B.; Cao, X. Plasma sprayed 18 mol% YO1. 5 stabilized hafnia as potential thermal barrier coating. Ceram. Int. 2021, 47, 14515–14526. [Google Scholar] [CrossRef]
- Pi, N.-W.; Zhang, M.; Jiang, J.; Belosludtsev, A.; Vlček, J.; Houška, J.; Meletis, E.I. Microstructure of hard and optically transparent HfO2 films prepared by high-power impulse magnetron sputtering with a pulsed oxygen flow control. Thin Solid Film. 2016, 619, 239–249. [Google Scholar] [CrossRef]
- Zhu, D. Development and performance evaluations of HfO2-Si and rare earth-Si based environmental barrier bond coat systems for SiC/SiC ceramic matrix composites. In Proceedings of the International Conference on Metallurgical Coatings and Thin Films, San Diego, CA, USA, 28 April–2 May 2014. [Google Scholar]
- Xiao, S.; Li, J.; Liu, X.; Chang, Z.; Huang, P.; Zhang, A.; Tian, Y.; Zhang, X.; Zhang, J.; Han, G. Exploration of the oxidation behavior and doping ratio of the Si–HfO2 bond layer used in environmental barrier coatings. Int. J. Appl. Ceram. Technol. 2023, 20, 1753–1763. [Google Scholar] [CrossRef]
- Gigolotti, J.C.J.; Nunes, C.A.; Suzuki, P.A.; Coelho, G.C. Evaluation of Phase Equilibria Involving the Liquid Phase in the Hf-Si System. J. Phase Equilibria Diffus. 2014, 35, 622–630. [Google Scholar] [CrossRef]
- Gao, J.; Li, C.; Guo, C.; Du, Z. Thermodynamic re-assessment of the Hf-Si binary system. J. Phys. Conf. Ser. 2018, 1074, 012074. [Google Scholar] [CrossRef]
- Kato, Y.; Kakamu, K.; Hironaka, Y.; Arai, N.; Kobayashi, N.; Pierre, G.R.S. Improvement of high-temperature endurance of C/C composites by double coating with SiC and glass materials. J. Chem. Eng. Jpn. 1996, 29, 669–674. [Google Scholar] [CrossRef]
- Engström, I.; Lönnberg, B. Thermal expansion studies of the group IV-VII transition-metal disilicides. J. Appl. Phys. 1988, 63, 4476–4484. [Google Scholar] [CrossRef]
- Clarke, D.R. Materials selection guidelines for low thermal conductivity thermal barrier coatings. Surf. Coat. Technol. 2003, 163, 67–74. [Google Scholar] [CrossRef]
- Liu, B.; Wang, J.; Li, F.; Zhou, Y. Theoretical elastic stiffness, structural stability and thermal conductivity of La2T2O7 (T=Ge, Ti, Sn, Zr, Hf) pyrochlore. Acta Mater. 2010, 58, 4369–4377. [Google Scholar] [CrossRef]
- Slack, G.A. Nonmetallic crystals with high thermal conductivity. J. Phys. Chem. Solids 1973, 34, 321–335. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B Condens. Matter 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Hill, R. The elastic behavior of crystalline aggregate. Proc. Phys. Society. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Teubner-Leipzig: Macmillan, NY, USA, 1928. [Google Scholar]
- Reuss, A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Green, D.J. An Introduction to the Mechanical Properties of Ceramics; Cambridge University Press: Cambridge, UK, 1998; Volume 1, pp. 1–12. [Google Scholar]
- Nazipov, D.V. First-Principles Study of Elastic Properties of Rare-Earth Oxyorthosilicates R2SiO5. Phys. Status Solidi (B) 2021, 258, 2100181. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Sanditov, B.D.; Tsydypov, S.B.; Sanditov, D.S. Relation between the Grüneisen constant and Poisson’s ratio of vitreous systems. Acoust. Phys. 2007, 53, 594–597. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yip, S.; Phillpot, S.; Wolf, D. Mechanical instabilities of homogeneous crystals. Phys. Rev. B 1995, 52, 12627–12635. [Google Scholar] [CrossRef] [PubMed]
- Beckstein, O.; Klepeis, J.E.; Hart, G.; Pankratov, O. First-principles elastic constants and electronic structure of α-Pt2Si and PtSi. Phys. Rev. B 2001, 13, 134112. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. 2007, 76, 054115. [Google Scholar]
- Liu, Q.-J.; Tian, H.; Liu, Z.-T. Mechanical properties and electronic structures of the Hf–Si system: First-principles calculations. Solid State Commun. 2015, 205, 39–45. [Google Scholar] [CrossRef]
- Makishima, A.; Mackenzie, J.D. Calculation of bulk modulus, shear modulus and Poisson’s ratio of glass. J. Non-Cryst. Solids 1975, 17, 147–157. [Google Scholar] [CrossRef]
- Lee, B.; Rudd, R.E. First-principles calculation of mechanical properties of Si⟨001⟩ nanowires and comparison to nanomechanical theory. Phys. Rev. B 2007, 75, 195328. [Google Scholar] [CrossRef]
- Mattesini, M.; Magnuson, M.; Tasnadi, F.; Höglund, C.; Abrikosov, I.A.; Hultman, L. Elastic properties and electrostructural correlations in ternary scandium-based cubic inverse perovskites: A first-principles study. Phys. Rev. B 2009, 79, 125122. [Google Scholar] [CrossRef]
- Robertson, J.H. Physical properties of crystals: Their representation by tensors and matrices by J. F. Nye. Acta Crystallogr. 2014, 41, 624. [Google Scholar] [CrossRef]
- Brantley, W.A. Calculated Elastic Constants for Stress Problems Associated with Semiconductor Devices. J. Appl. Phys. 1973, 44, 534–535. [Google Scholar] [CrossRef]
- Mohapatra, H.; Eckhardt, C.J. Elastic constants and related mechanical properties of the monoclinic polymorph of the carbamazepine molecular crystal. J. Phys. Chem. B 2008, 112, 2293–2298. [Google Scholar] [CrossRef] [PubMed]
- Shanks, H.; Maycock, P.; Sidles, P.; Danielson, G. Thermal conductivity of silicon from 300 to 1400 K. Phys. Rev. 1963, 130, 1743. [Google Scholar] [CrossRef]
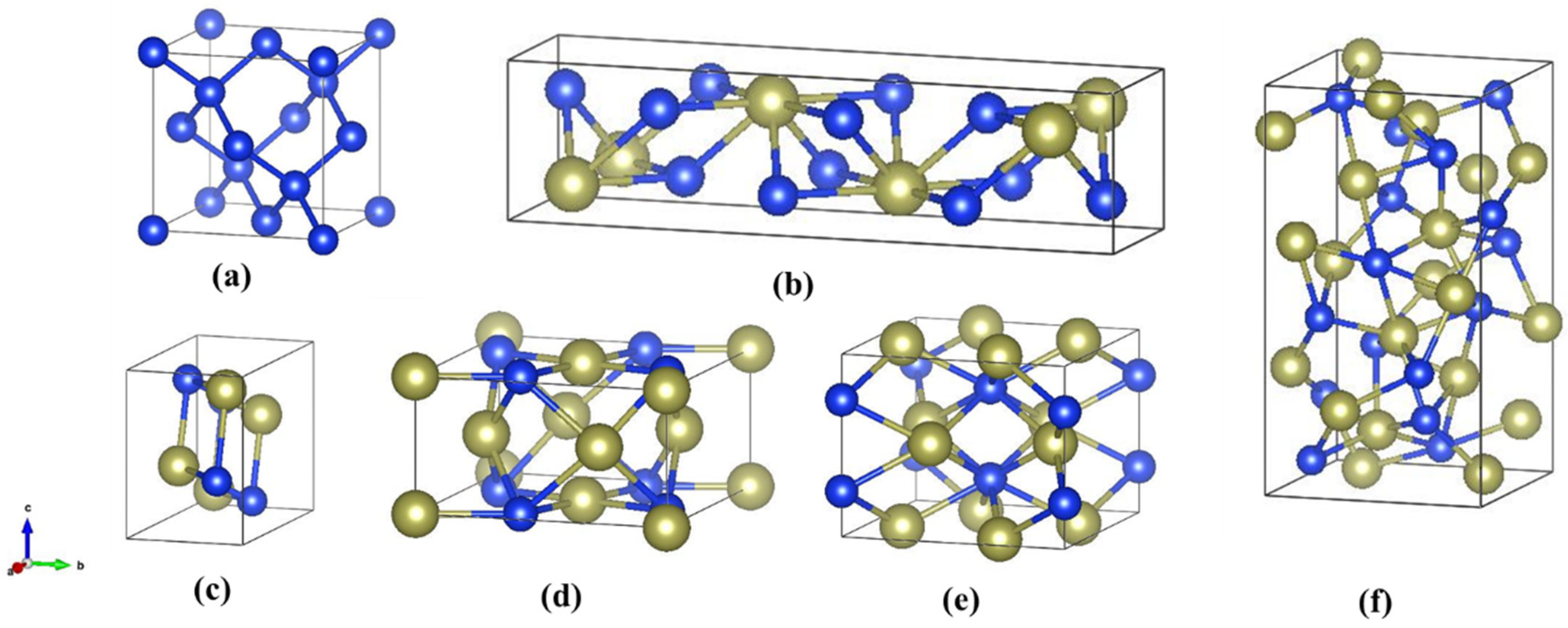



| Materials | a () | b () | c () |
|---|---|---|---|
| Si | 5.450 | 5.450 | 5.450 |
| Si (27-1402) | 5.431 | 5.431 | 5.431 |
| HfSi2 | 3.656 | 14.640 | 3.670 |
| HfSi2 (38-1373) | 3.680 | 14.556 | 3.649 |
| HfSi | 6.896 | 3.788 | 5.249 |
| HfSi (13-0369) | 6.885 | 3.753 | 5.191 |
| Hf5Si4 | 7.067 | 7.067 | 12.877 |
| Hf5Si4 (42-1166) | 7.039 | 7.039 | 12.869 |
| Hf3Si2 | 7.014 | 7.014 | 3.681 |
| Hf3Si2 (14-0427) | 7.000 | 7.000 | 3.671 |
| Hf2Si | 6.579 | 6.579 | 5.180 |
| Hf2Si (12-0467) | 6.480 | 6.480 | 5.210 |
| Materials | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C66 | |
|---|---|---|---|---|---|---|---|---|---|
| Si | 138 | 52 | 69 | ||||||
| HfSi2 | 237 | 57 | 113 | 156 | 97 | 258 | 111 | 92 | 104 |
| HfSi | 238 | 109 | 83 | 250 | 86 | 316 | 139 | 81 | 92 |
| Hf5Si4 | 272 | 91 | 88 | 255 | 99 | 81 | |||
| Hf3Si2 | 294 | 62 | 100 | 185 | 84 | 117 | |||
| Hf2Si | 250 | 86 | 80 | 272 | 83 | 114 |
| Materials | B (GPa) | G (GPa) | E (GPa) | μ | H (HV) | G/B |
|---|---|---|---|---|---|---|
| Si | 80 | 57 | 139 | 0.213 | 11 | 0.722 |
| HfSi2 | 125 | 83 | 204 | 0.229 | 13 | 0.664 |
| HfSi | 150 | 94 | 234 | 0.241 | 13 | 0.627 |
| Hf5Si4 | 148 | 88 | 219 | 0.253 | 12 | 0.595 |
| Hf3Si2 | 142 | 93 | 229 | 0.231 | 14 | 0.655 |
| Hf2Si | 140 | 96 | 235 | 0.221 | 15 | 0.686 |
| Materials | vL (m/s) | vT (m/s) | vm (m/s) | ΘD (K) | kmin (w/(m·k)) |
|---|---|---|---|---|---|
| Si | 4.42 | 2.67 | 2.94 | 488 | 1.26 |
| HfSi2 | 5.42 | 3.21 | 3.56 | 418 | 0.77 |
| HfSi | 5.21 | 3.05 | 3.38 | 391 | 0.71 |
| Hf5Si4 | 5.02 | 2.88 | 3.20 | 366 | 0.65 |
| Hf3Si2 | 4.93 | 2.91 | 3.23 | 361 | 0.65 |
| Hf2Si | 4.83 | 2.89 | 3.20 | 359 | 0.63 |
| Materials | Si | HfSi2 | HfSi | Hf5Si4 | Hf3Si2 | Hf2Si |
|---|---|---|---|---|---|---|
| kp | 1025.82 | 811.96 | 996.11 | 771.05 | 878.01 | 792.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, P.; Han, G.; Liu, H.; Zhang, W.; Peng, K.; Li, J.; Wang, W.; Zhang, J. Mechanical and Thermal Properties of the Hf–Si System: First-Principles Calculations. J. Compos. Sci. 2024, 8, 129. https://doi.org/10.3390/jcs8040129
Huang P, Han G, Liu H, Zhang W, Peng K, Li J, Wang W, Zhang J. Mechanical and Thermal Properties of the Hf–Si System: First-Principles Calculations. Journal of Composites Science. 2024; 8(4):129. https://doi.org/10.3390/jcs8040129
Chicago/Turabian StyleHuang, Panxin, Guifang Han, Huan Liu, Weibin Zhang, Kexue Peng, Jianzhang Li, Weili Wang, and Jingde Zhang. 2024. "Mechanical and Thermal Properties of the Hf–Si System: First-Principles Calculations" Journal of Composites Science 8, no. 4: 129. https://doi.org/10.3390/jcs8040129
APA StyleHuang, P., Han, G., Liu, H., Zhang, W., Peng, K., Li, J., Wang, W., & Zhang, J. (2024). Mechanical and Thermal Properties of the Hf–Si System: First-Principles Calculations. Journal of Composites Science, 8(4), 129. https://doi.org/10.3390/jcs8040129






