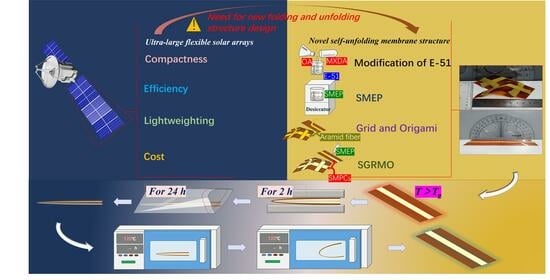
Self-Unfolding Properties of Smart Grid-Reinforced Membrane Origami
Abstract
1. Introduction
2. Materials and Method
2.1. Materials and Ratios
- m—Required hardener content per 100 g of epoxy resin (g);
- A—Mass fraction;
- M—Molecular weight of amine (g/mol);
- nH—Number of active hydrogens in amine curing agents;
- K—Epoxy content.
- mr—The amount of SMP (g);
- mf—The amount of aramid fiber (g).
2.2. Preparation of SGRMO
2.3. Materials Characterization
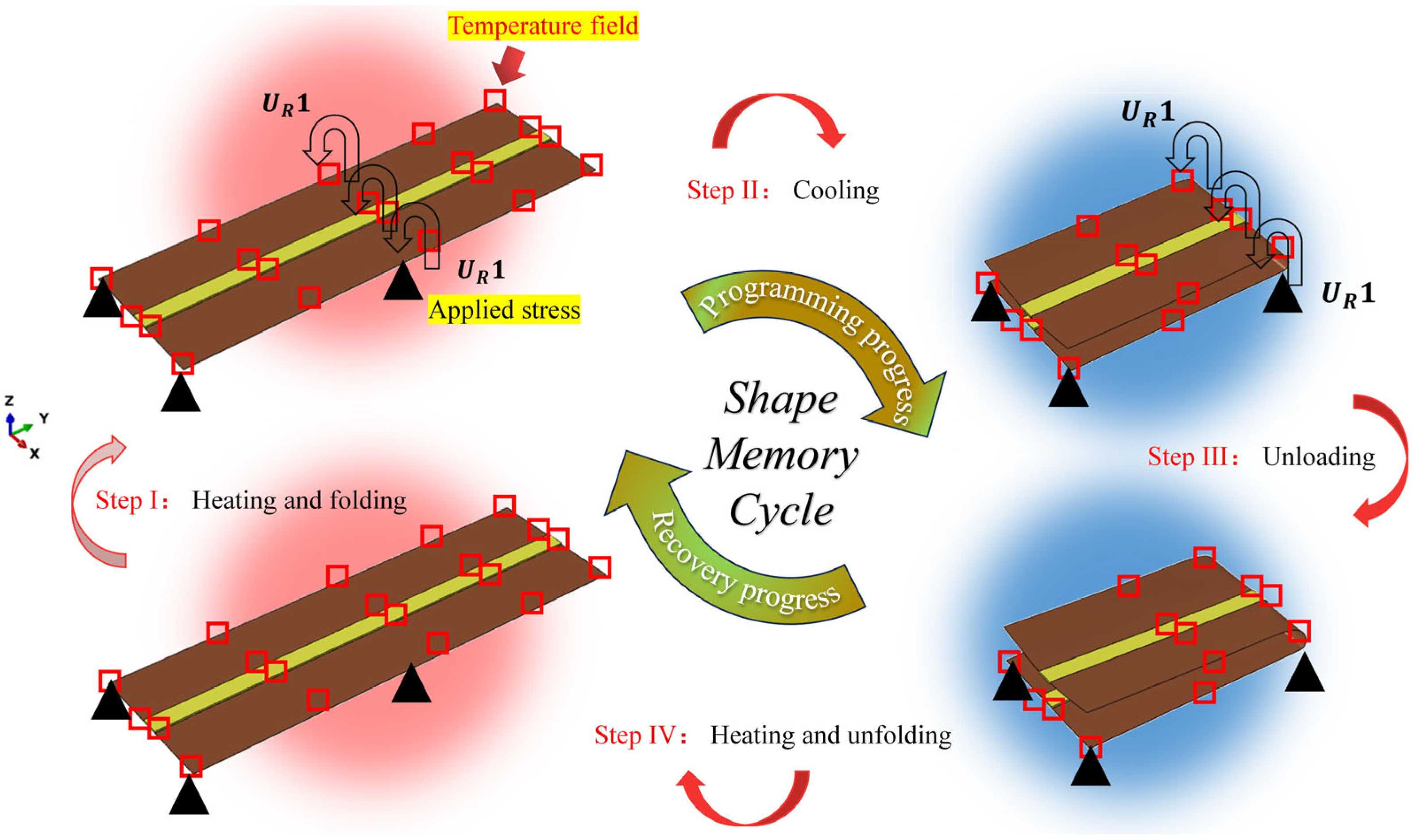
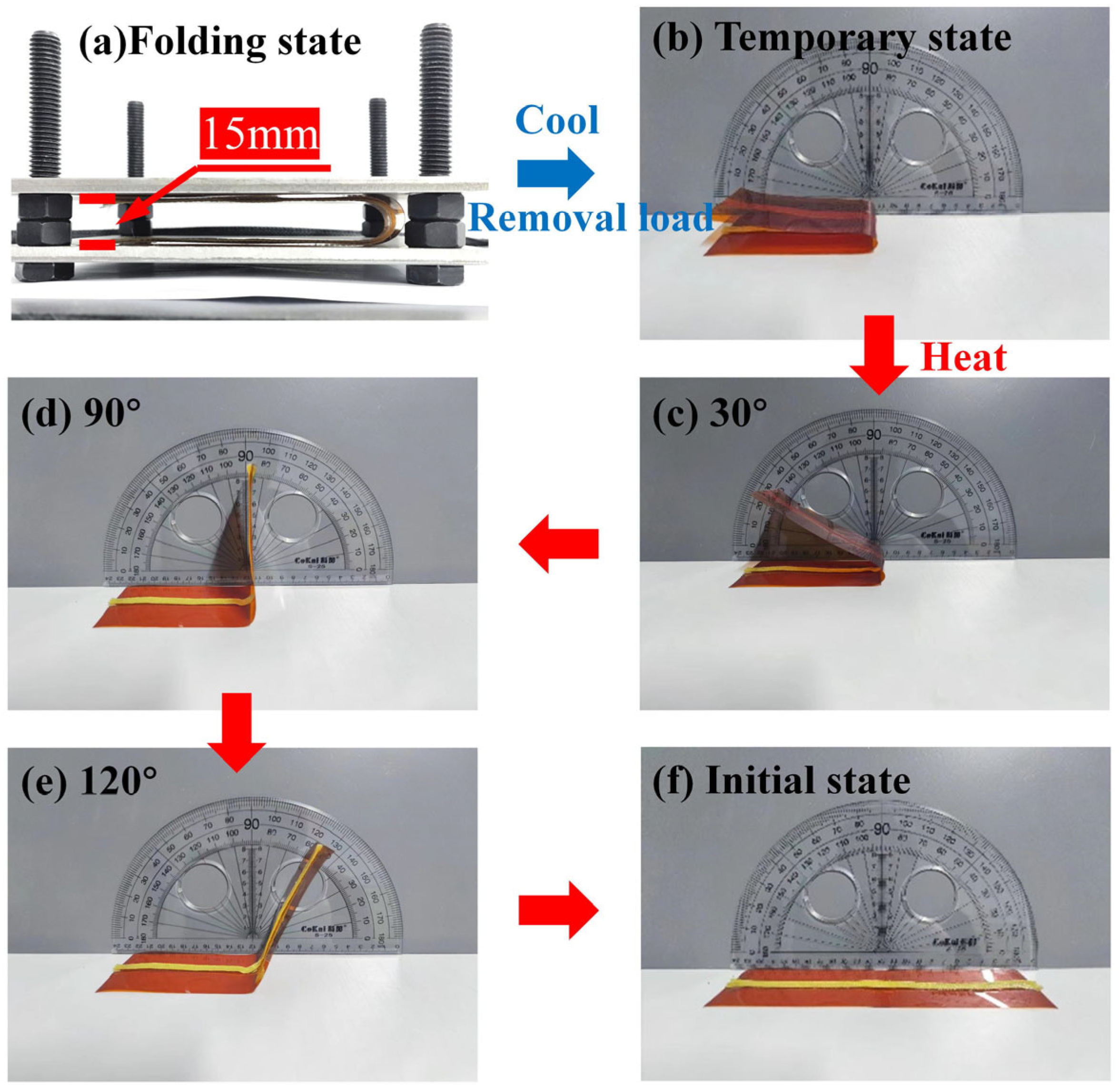
2.4. Shape Memory Performance Test
- (a)
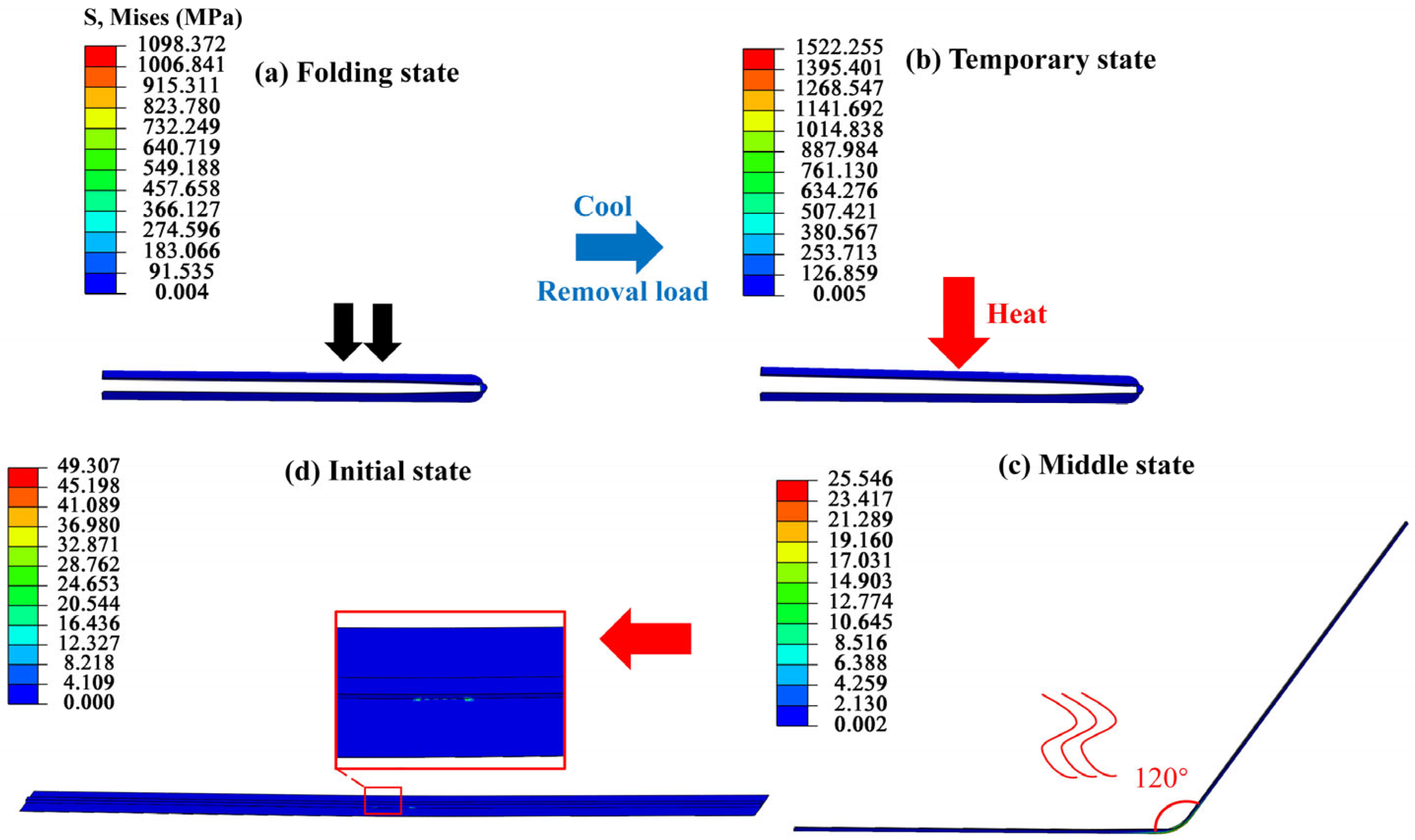
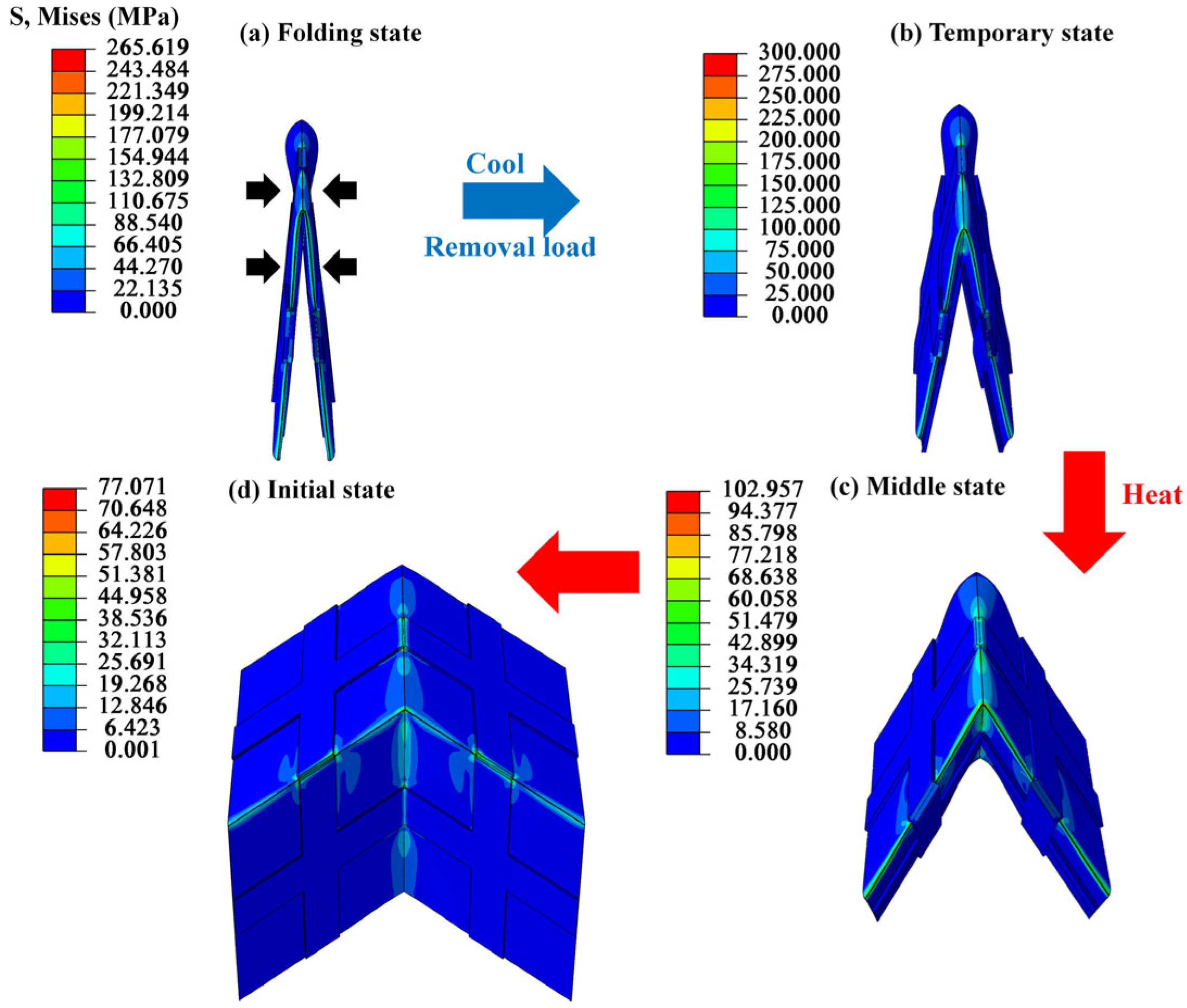
- Initially, the SGRMO was placed in an oven at an elevated temperature (Tg + 50 °C), and after one minute, the structure softened. Further, we folded the SGRMO and placed it between parallel plates with 15 mm apart.
- (b)
- Then, the SGRMO was placed in the room temperature condition (20 °C) with an invariant external load condition. We let it stand for one hour.
- (c)
- We removed the external load in the room temperature condition, and the SGRMO showed a slight rebound. We waited for 24 h to allow the structure to adequately rebound, until the shape remained stable.
- (d)
- Finally, we tested the SGRMO at a specific temperature (Tg + 10 °C), and the structure gradually unfolded into its initial state. After five minutes, the SGRMO was removed from the oven and kept at room temperature for one minute. After one minute, the shape could be fixed and stable.
2.5. Finite Element Simulation
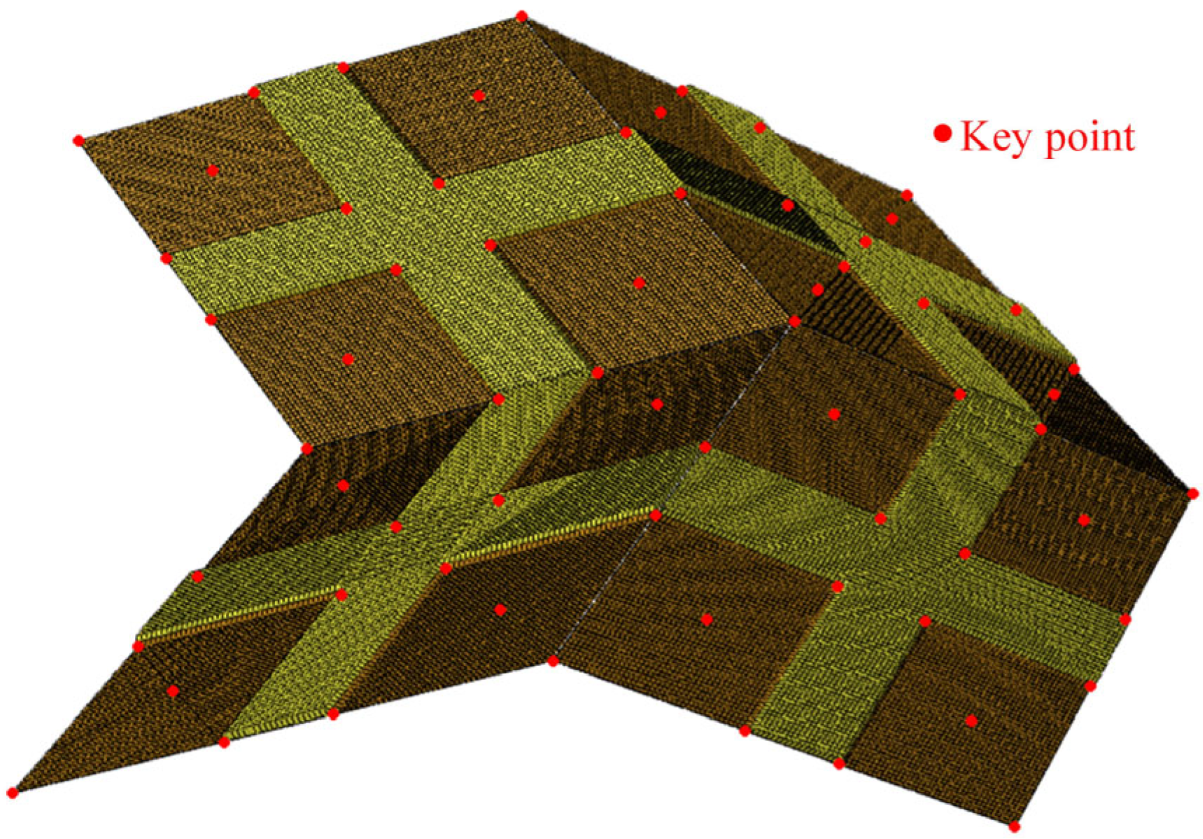
2.5.1. Modeling
2.5.2. Simulation Steps
2.5.3. Viscoelastic Parameterization
- —Young’s modulus relaxation function
- —Long-term modulus
- —Young’s relaxation modulus at time i
- —Relaxation time at moment i ()
2.6. Performance Estimation Method of Miura-SGRMO
3. Results and Discussion
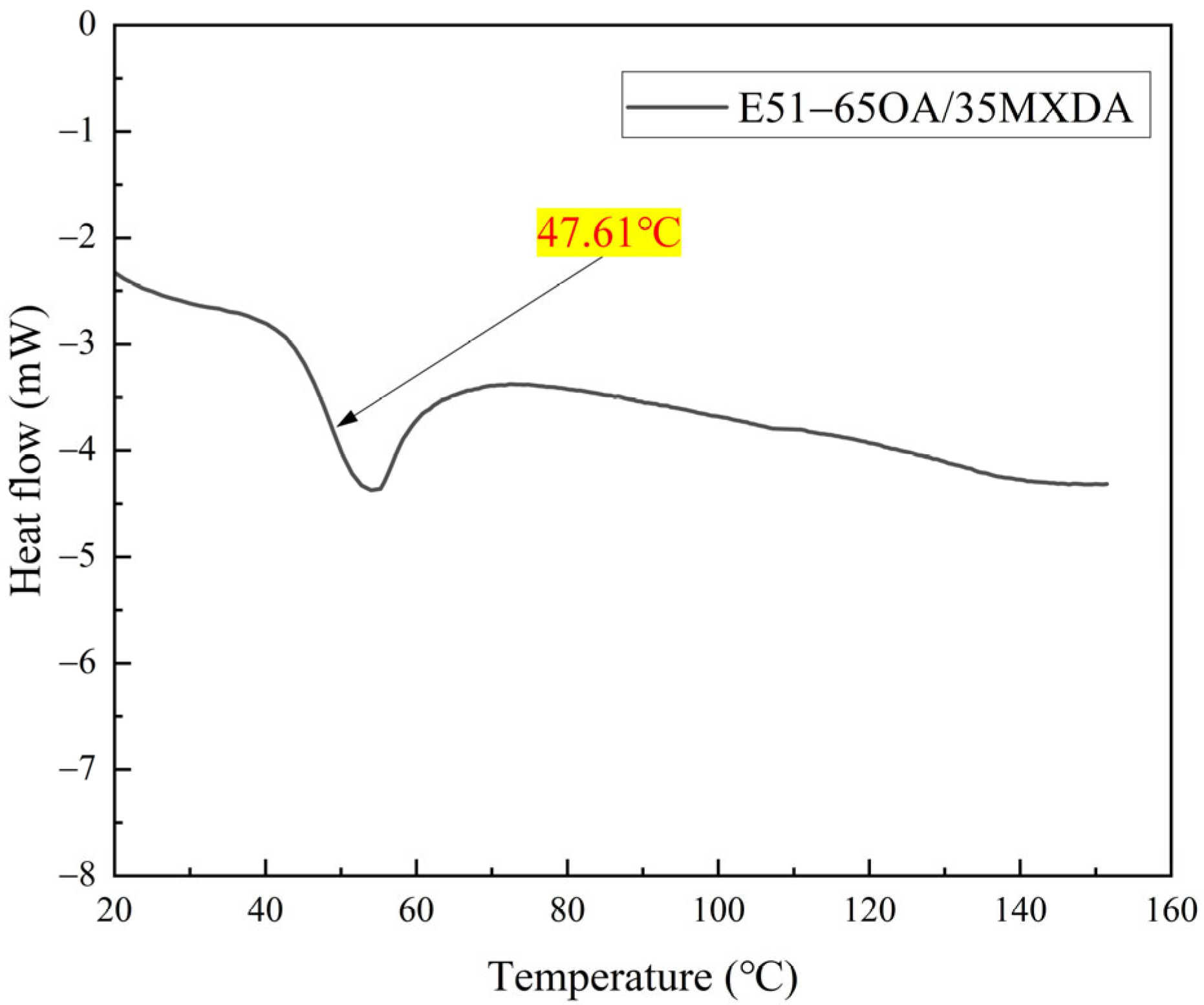
3.1. DSC Analysis of SMP
3.2. Thermomechanical Properties of SMPCs
3.3. Shape Memory Test Results
3.3.1. Shape Memory Performance of SGRMO
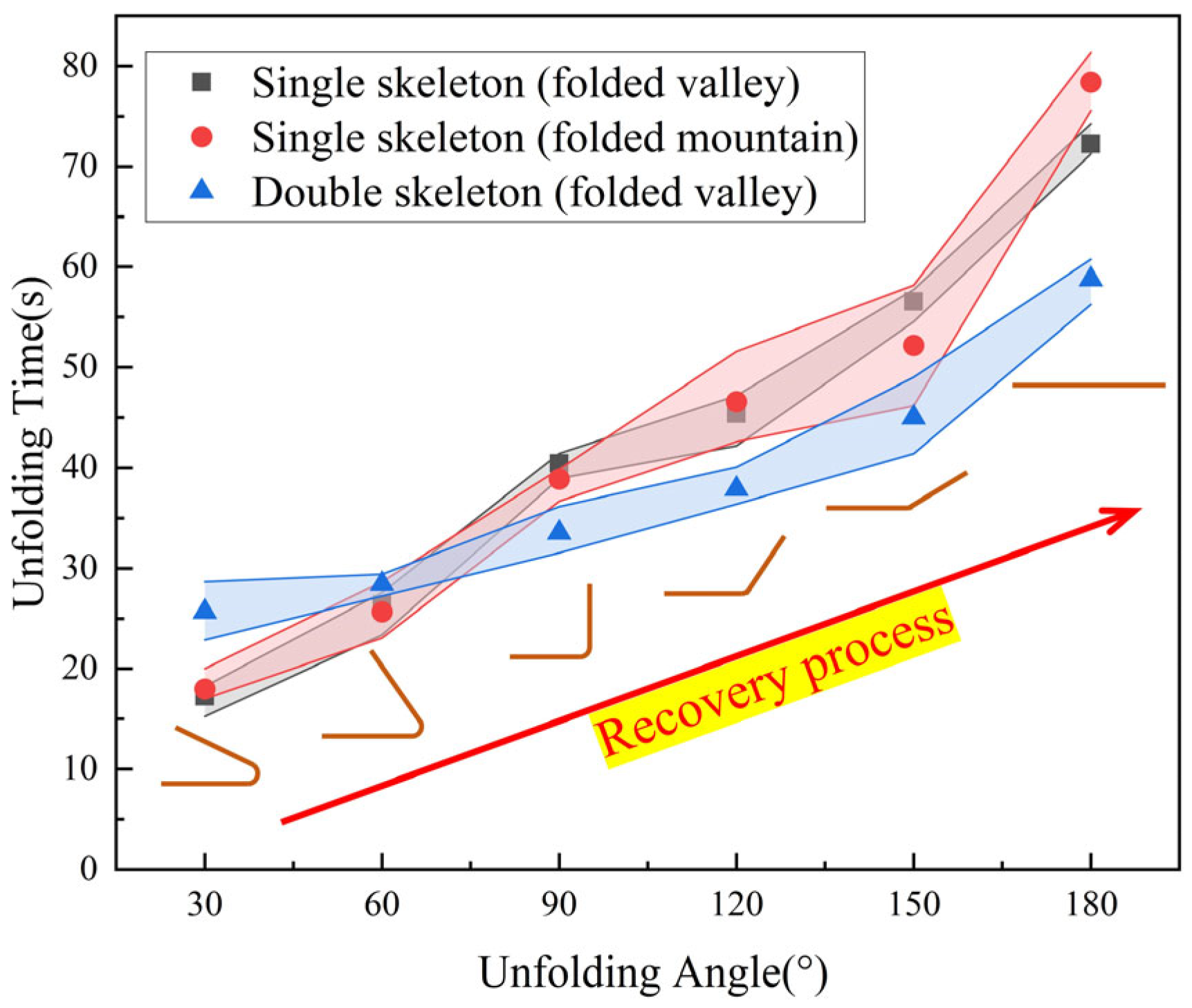
3.3.2. Different Structural Forms
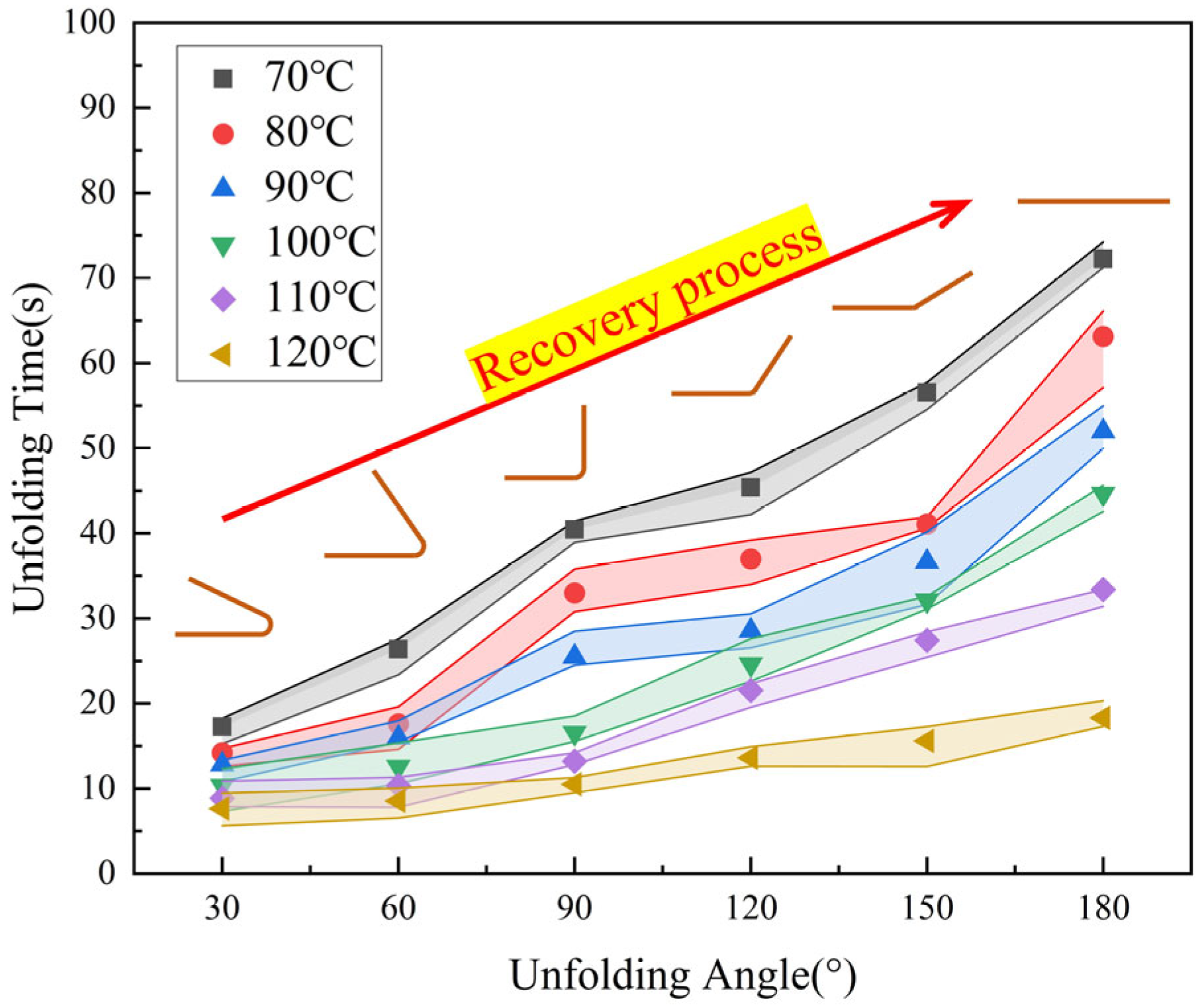
3.3.3. Ambient Temperature
3.3.4. Folding Frequency
3.4. Finite Element Results
3.4.1. Elastic and Viscoelastic Parameters
3.4.2. Shape Memory Recovery Process of SGRMO
3.4.3. Shape Memory Recovery Process of Miura-SGRMO
3.4.4. The Displacement of Miura-SGRMO
3.4.5. The Analysis of Surface Precision
4. Conclusions
- For SGRMO, the shape memory performance was almost the same for forward and backward folding, while increasing the number of smart skeletons improved the shape memory performance. Even after multiple shape memory cycles, SGRMO could guarantee excellent shape memory performance. The Rf of the SGRMO was maintained above 98.5% and Rr above 99% for the first three shape memory cycles.
- The ambient temperature exerted a profound influence on the recovery performance of SGRMO, where heightened temperatures correlated with an accelerated recovery process. Nevertheless, elevated temperatures precipitated earlier instances of debonding.
- The Miura-SGRMO unfolded without large bending deformations in the panel area. The unfolding process of SGRMO could be approximated as a rigid unfolding.
- Our investigation attested to the reliability of utilizing the grid structure for facilitating the unfolding process. The Miura-SGRMO unfolded with a high degree of unfolding distance and surface precision. At angle-ψ values of 15°, 30°, 45°, 60°, and 75°, respectively, our observations revealed that the optimal surface precision was attained at 30°, and the RMSE of this configuration stood at approximately 0.05 mm. However, the result was influenced by a dimensional effect, which must be thoroughly explored in subsequent research efforts.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Turner, N.; Goodwine, B.; Sen, M. A review of origami applications in mechanical engineering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2345–2362. [Google Scholar] [CrossRef]
- Mintchev, S.; Salerno, M.; Cherpillod, A.; Scaduto, S.; Paik, J. A portable three-degrees-of-freedom force feedback origami robot for human–robot interactions. Nat. Mach. Intell. 2019, 1, 584–593. [Google Scholar] [CrossRef]
- Peraza-Hernandez, E.A.; Hartl, D.J.; Malak, R.J., Jr.; Lagoudas, D.C. Origami-inspired active structures: A synthesis and review. Smart Mater. Struct. 2014, 23, 094001. [Google Scholar] [CrossRef]
- Wang, L.C.; Song, W.L.; Zhang, Y.J.; Qu, M.J.; Zhao, Z.; Chen, M.; Yang, Y.; Chen, H.; Fang, D. Active reconfigurable tristable square-twist origami. Adv. Funct. Mater. 2020, 30, 1909087. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, F.; Wang, J.; Liu, F.; Guo, X.; Nan, K.; Lin, Q.; Gao, M.; Xiao, D.; Shi, Y. Controlled mechanical buckling for origami-inspired construction of 3D microstructures in advanced materials. Adv. Funct. Mater. 2016, 26, 2629–2639. [Google Scholar] [CrossRef] [PubMed]
- Velvaluri, P.; Soor, A.; Plucinsky, P.; de Miranda, R.L.; James, R.D.; Quandt, E. Origami-inspired thin-film shape memory alloy devices. Sci. Rep. 2021, 11, 10988. [Google Scholar] [CrossRef] [PubMed]
- Pesaran, S.; Rafatmah, E.; Hemmateenejad, B. An all-in-one solid state thin-layer potentiometric sensor and biosensor based on three-dimensional origami paper microfluidics. Biosensors 2021, 11, 44. [Google Scholar] [CrossRef]
- Cai, J.; Ren, Z.; Ding, Y.; Deng, X.; Xu, Y.; Feng, J. Deployment simulation of foldable origami membrane structures. Aerosp. Sci. Technol. 2017, 67, 343–353. [Google Scholar] [CrossRef]
- Huang, J. The development of inflatable array antennas. IEEE Antennas Propag. Mag. 2001, 43, 44–50. [Google Scholar] [CrossRef]
- Murphy, D.M. Validation of a scalable solar sailcraft system. J. Spacecr. Rocket. 2007, 44, 797–808. [Google Scholar] [CrossRef]
- Harkness, P.; McRobb, M.; Lützkendorf, P.; Milligan, R.; Feeney, A.; Clark, C. Development status of AEOLDOS–A deorbit module for small satellites. Adv. Space Res. 2014, 54, 82–91. [Google Scholar] [CrossRef]
- Huang, H.; Guan, F.-L.; Pan, L.-L.; Xu, Y. Design and deploying study of a new petal-type deployable solid surface antenna. Acta Astronaut. 2018, 148, 99–110. [Google Scholar] [CrossRef]
- Lillie, C.; Dailey, D.; Polidan, R. Large aperture telescopes for launch with the Ares V launch vehicle. Acta Astronaut. 2010, 66, 374–381. [Google Scholar] [CrossRef]
- Häuplik-Meusburger, S.; Sommer, B.; Aguzzi, M. Inflatable technologies: Adaptability from dream to reality. Acta Astronaut. 2009, 65, 841–852. [Google Scholar] [CrossRef]
- Webb, D.; Hirsch, B.; Bach, V.; Sauder, J.F.; Bradford, S.; Thomson, M. Starshade mechanical architecture & technology effort. In Proceedings of the 3rd AIAA Spacecraft Structures Conference, AIAA SciTech, San Diego, CA, USA, 4–8 January 2016; pp. 1–11. [Google Scholar]
- Ze, Q.; Wu, S.; Nishikawa, J.; Dai, J.; Sun, Y.; Leanza, S.; Zemelka, C.; Novelino, L.S.; Paulino, G.H.; Zhao, R.R. Soft robotic origami crawler. Sci. Adv. 2022, 8, 7834. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Wang, J.; Cai, C.; Xin, W.; Wei, L.; Yang, Q.; Peng, B.; Hu, Y.; Li, J.; Wang, X. Construction of Laminated Luminescent Solar Concentrator “Smart” Window Based on Thermoresponsive Polymer and Carbon Quantum Dots. Crystals 2022, 12, 1612. [Google Scholar] [CrossRef]
- Krysiak, Z.J.; Abdolmaleki, H.; Agarwala, S.; Stachewicz, U. Inkjet Printing of Electrodes on Electrospun Micro-and Nanofiber Hydrophobic Membranes for Flexible and Smart Textile Applications. Polymers 2022, 14, 5043. [Google Scholar] [CrossRef] [PubMed]
- Paik, J.K.; Wood, R.J. A bidirectional shape memory alloy folding actuator. Smart Mater. Struct. 2012, 21, 065013. [Google Scholar] [CrossRef]
- Liu, X.; Kang, S.; Zhang, D.; Li, Y.; Zhao, R.; Wu, C.; Cheng, Z.; Tao, Q.; Liu, Y. A liquid metal–based shape memory composite with the multi-responsive regulation of solid/liquid adhesion. Adv. Compos. Hybrid Mater. 2023, 6, 124. [Google Scholar] [CrossRef]
- Yang, Z.; Song, F.; Wang, Q.; Wang, T. Shape memory induced structural evolution of high performance copolyimides. J. Polym. Sci. Part A Polym. Chem. 2016, 54, 3858–3867. [Google Scholar] [CrossRef]
- Zi, Y.; Pei, D.; Wang, J.; Qi, S.; Tian, G.; Wu, D. High-Temperature-Induced Shape Memory Copolyimide. Polymers 2021, 13, 3222. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.D.; Ravikumar, A.; Prasad, E. PVA–Polystyrene-Based Polymer Films with Water-Induced Shape-Memory Effect. Ind. Eng. Chem. Res. 2022, 61, 5797–5806. [Google Scholar] [CrossRef]
- Wang, M.; Dong, L.; Wu, J.; Shi, J.; Gao, Q.; Zhu, C.; Morikawa, H. Leaf-meridian bio-inspired nanofibrous electronics with uniform distributed microgrid and 3D multi-level structure for wearable applications. NPJ Flex. Electron. 2022, 6, 34. [Google Scholar] [CrossRef]
- Chao, Y.; Yi, H.; Cao, F.; Lu, S.; Ma, L. Experimental Analysis of Polycaprolactone High-Resolution Fused Deposition Manufacturing-Based Electric Field-Driven Jet Deposition. Crystals 2022, 12, 1660. [Google Scholar] [CrossRef]
- Wagner, M.; Chen, T.; Shea, K. Large shape transforming 4D auxetic structures. 3D Print. Addit. Manuf. 2017, 4, 133–142. [Google Scholar] [CrossRef]
- Tao, Q.; Wang, C.; Wang, K.; Xie, Z.; Tan, H. Mixed-mode bending of a smart reconfigurable lattice structure with bi-directional corrugated core. Int. J. Mech. Sci. 2020, 185, 105848. [Google Scholar] [CrossRef]
- Zhang, Y.; Tao, Q.; Liu, Y.; Wang, C. Mesh/membrane composite with superior mechanical performance: A deep learning-based design. Compos. Sci. Technol. 2022, 230, 109735. [Google Scholar] [CrossRef]
- Pagitz, M.; Pellegrino, S. Buckling pressure of "pumpkin" balloons. Int. J. Solids Struct. 2007, 44, 6963–6986. [Google Scholar] [CrossRef][Green Version]
- Saito, Y.; Iijima, I.; Matsuzaka, Y.; Matsushima, K.; Tanaka, S.; Kajiwara, K.; Shimadu, S. Development of a super-pressure balloon with a diamond-shaped net. Adv. Space Res. 2014, 54, 1525–1529. [Google Scholar] [CrossRef]
- Chen, T.; Bilal, O.R.; Lang, R.; Daraio, C.; Shea, K. Autonomous deployment of a solar panel using elastic origami and distributed shape-memory-polymer actuators. Phys. Rev. Appl. 2019, 11, 064069. [Google Scholar] [CrossRef]
- Tolley, M.T.; Felton, S.M.; Miyashita, S.; Aukes, D.; Rus, D.; Wood, R.J. Self-folding origami: Shape memory composites activated by uniform heating. Smart Mater. Struct. 2014, 23, 094006. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, K.; Isakov, M.S.; Wu, J.; Dunn, M.L.; Jerry Qi, H. Sequential self-folding structures by 3D printed digital shape memory polymers. Sci. Rep. 2015, 5, 13616. [Google Scholar] [CrossRef]
- Liu, Y.; Shaw, B.; Dickey, M.D.; Genzer, J. Sequential self-folding of polymer sheets. Sci. Adv. 2017, 3, e1602417. [Google Scholar] [CrossRef] [PubMed]
- Madbouly, S.A.; Lendlein, A. Shape-memory polymer composites. Shape-Mem. Polym. 2010, 226, 41–95. [Google Scholar]
- Qi, H.J.; Nguyen, T.D.; Castro, F.; Yakacki, C.M.; Shandas, R. Finite deformation thermo-mechanical behavior of thermally induced shape memory polymers. J. Mech. Phys. Solids 2008, 56, 1730–1751. [Google Scholar] [CrossRef]
- Leng, J.; Lan, X.; Liu, Y.; Du, S. Shape-memory polymers and their composites: Stimulus methods and applications. Prog. Mater. Sci. 2011, 56, 1077–1135. [Google Scholar] [CrossRef]
- Emmanuel, K.; Jeewantha, L.; Herath, H.; Epaarachchi, J.; Aravinthan, T. Shape memory polymer composite circular and square hollow members for deployable structures. Compos. Part A Appl. Sci. Manuf. 2023, 171, 107559. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, Y.; Huang, C.; Zhao, X.; Yan, X.-P.; Huang, Y.; Li, L.; Liu, T. Shape memory polyimide aerogel composites with high programming temperatures and exceptional shape recovery capability. Compos. Part A Appl. Sci. Manuf. 2023, 174, 107717. [Google Scholar] [CrossRef]
- Xia, Y.; He, Y.; Zhang, F.; Liu, Y.; Leng, J. A review of shape memory polymers and composites: Mechanisms, materials, and applications. Adv. Mater. 2021, 33, 2000713. [Google Scholar] [CrossRef]
- Cui, F.; Moon, S.; Rao, I.J. Modeling the viscoelastic behavior of amorphous shape memory polymers at an elevated temperature. Fluids 2016, 1, 15. [Google Scholar] [CrossRef]
- Zheng, X.; Zhou, B.; Xue, S. A viscoelastic-plastic constitutive model of shape memory polymer. J. Mech. 2019, 35, 601–611. [Google Scholar] [CrossRef]
- Duan, H.; Gu, J.; Zeng, H.; Khatibi, A.A.; Sun, H. A thermoviscoelastic finite deformation constitutive model based on dual relaxation mechanisms for amorphous shape memory polymers. Int. J. Smart Nano Mater. 2023, 14, 243–264. [Google Scholar] [CrossRef]
- Shangguan, Y.; Chen, F.; Jia, E.; Lin, Y.; Hu, J.; Zheng, Q. New insight into time-temperature correlation for polymer relaxations ranging from secondary relaxation to terminal flow: Application of a universal and developed WLF equation. Polymers 2017, 9, 567. [Google Scholar] [CrossRef] [PubMed]
- Beex, L.; Peerlings, R. An experimental and computational study of laminated paperboard creasing and folding. Int. J. Solids Struct. 2009, 46, 4192–4207. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, C.; Tan, H. Elastoplastic folding behavior of membrane ribbon based on plane strain beam theory. Int. J. Solids Struct. 2018, 143, 167–174. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, C.; Tan, H.F. Quasi-static unfolding mechanics of a creased membrane based on a finite deformation crease-beam model. Int. J. Solids Struct. 2020, 207, 104–112. [Google Scholar] [CrossRef]
- Jarrah, H.R.; Zolfagharian, A.; Hedayati, R.; Serjouei, A.; Bodaghi, M. Nonlinear finite element modelling of thermo-visco-plastic styrene and polyurethane shape memory polymer foams. Actuators 2021, 10, 46. [Google Scholar] [CrossRef]
- Gu, J.; Sun, H.; Fang, J.; Fang, C.; Xu, Z. A unified modeling approach for amorphous shape memory polymers and shape memory polymer based syntactic foam. Polym. Adv. Technol. 2016, 27, 1237–1245. [Google Scholar] [CrossRef]
- Battini, D.; Avanzini, A.; Pandini, S.; Bignotti, F. Modeling approach and finite element analyses of a shape memory epoxy-based material. In Proceedings of the XXIV AIMETA Conference 2019, Rome, Italy, 15–19 September 2019; pp. 689–704. [Google Scholar]
- Ghobadi, E.; Shutov, A.; Steeb, H. Parameter identification and validation of shape-memory polymers within the framework of finite strain viscoelasticity. Materials 2021, 14, 2049. [Google Scholar] [CrossRef]
- Wang, Q.; Bai, Y.; Chen, Y.; Ju, J.; Zheng, F.; Wang, T. High performance shape memory polyimides based on π–π interactions. J. Mater. Chem. A 2015, 3, 352–359. [Google Scholar] [CrossRef]
- Zarghami Dehaghani, M.; Kaffashi, B.; Haponiuk, J.T.; Piszczyk, L. Shape memory thin films of Polyurethane: Does graphene content affect the recovery behavior of Polyurethane nanocomposites? Polym. Compos. 2020, 41, 3376–3388. [Google Scholar] [CrossRef]
- Tobushi, H.; Hashimoto, T.; Hayashi, S.; Yamada, E. Thermomechanical constitutive modeling in shape memory polymer of polyurethane series. J. Intell. Mater. Syst. Struct. 1997, 8, 711–718. [Google Scholar] [CrossRef]

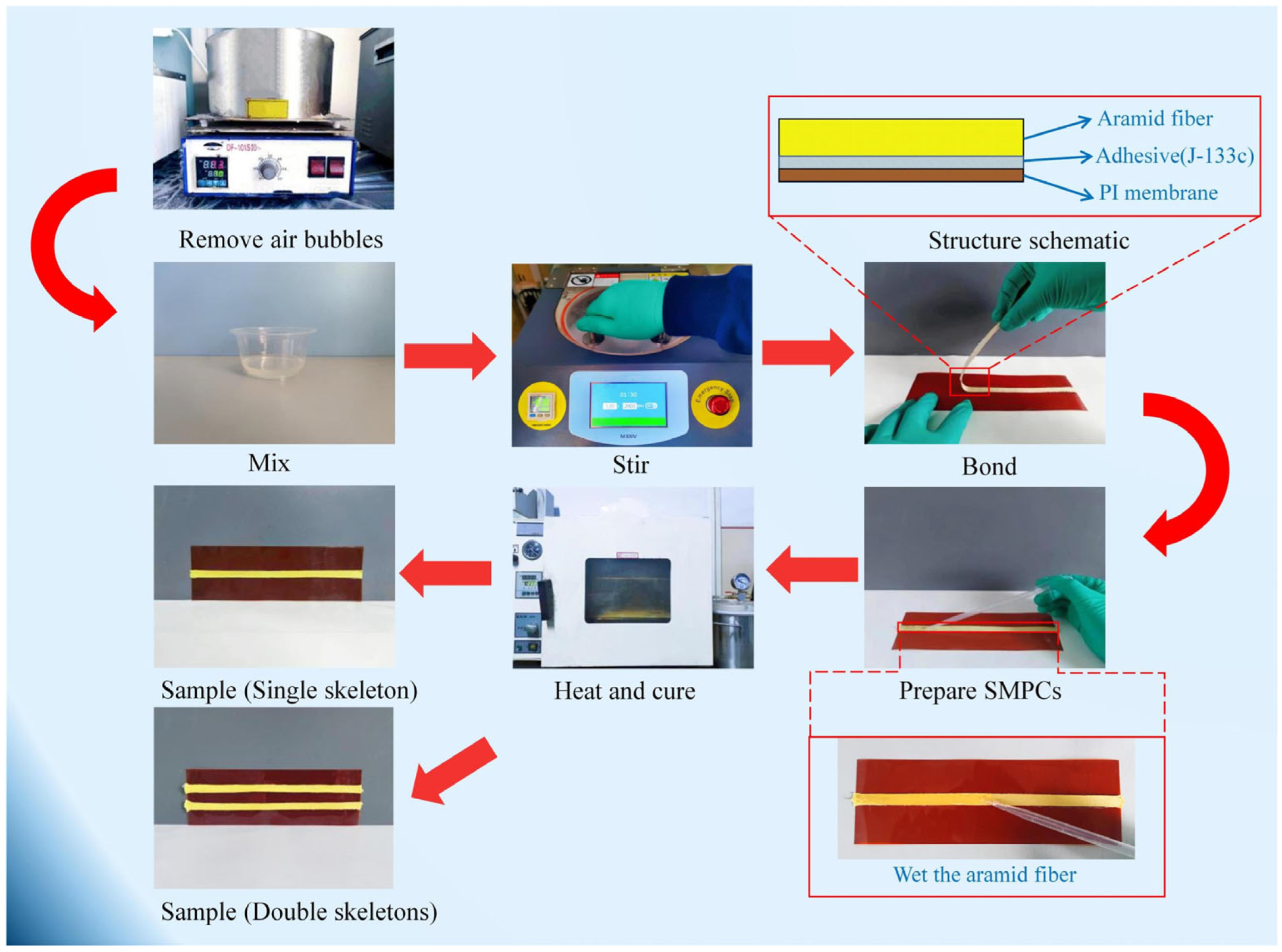












| Product | Manufacturer (of a Product) |
|---|---|
| E-51 epoxy resin | Shandong Yousuo Chemical Co., LTD, Linyi, China |
| OA | Shanghai Aladdin Bio-Chem Technology Co., LTD, Shanghai, China |
| MXDA | Shanghai Aladdin Bio-Chem Technology Co., LTD |
| J-133c-structural adhesive (A/B) | Institute of Petrochemistry, Heilongjiang Academy of Sciences, Harbin, China |
| Acetone | Shanghai Aladdin Bio-Chem Technology Co., LTD |
| Anhydrous ethanol | Shanghai Aladdin Bio-Chem Technology Co., LTD |
| Aramid fiber | Dongguan Shengmao Special Weaving Technology Co., LTD, Dongguan, China |
| Membrane | Guangdong Chenghao Plastic Industry Co., LTD, Dongguan, China |
| Product | Weight (g) |
|---|---|
| E-51 epoxy resin | 1.200 |
| OA | 0.257 |
| MXDA | 0.073 |
| Relative Shear Modulus | Relative Bulk Modulus | Relaxation Time | |
|---|---|---|---|
| 1 | 0.384 | 0 | 0.017 |
| 2 | 0.272 | 0 | 0.09 |
| 3 | 0.105 | 0 | 1 |
| 4 | 0.031 | 0 | 12 |
| 5 | 0.207 | 0 | 56 |
| Total | 0.999 |
| Tg | C1 | C2 |
|---|---|---|
| 64.1 °C | 17.4 | 51.6 |
| Elastic Modulus (mPa) | Poisson | Coefficient of Thermal Expansion (CTE) (1/°C) |
|---|---|---|
| 2060 | 0.4 | 6.47 × 10−5 |
| Elastic Modulus (mPa) | Poisson | Yield Strain | Yield Stress (mPa) |
|---|---|---|---|
| 2240 | 0.34 | 0.03 | 69 |
| Model | L1-L2-L3-L4 (mm) | ψ (°) |
|---|---|---|
| Ori1 | 50-50-50-50 | 15 |
| Ori2 | 50-50-50-50 | 30 |
| Ori3 | 50-50-50-50 | 45 |
| Ori4 | 50-50-50-50 | 60 |
| Ori5 | 50-50-50-50 | 75 |
| Model | X-Displacement | Y-Displacement | ρ |
|---|---|---|---|
| Ori1 | 1.0523 mm | 19.401 mm | 98.93% |
| Ori2 | 7.1401 mm | 47.437 mm | 99.96% |
| Ori3 | 18.350 mm | 69.681 mm | 100.05% |
| Ori4 | 35.347 mm | 85.945 mm | 99.92% |
| Ori5 | 57.701 mm | 95.337 mm | 99.95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Xia, Z.; Tao, Q.; Ye, Z.; Yuan, K.; Song, L. Self-Unfolding Properties of Smart Grid-Reinforced Membrane Origami. J. Compos. Sci. 2024, 8, 64. https://doi.org/10.3390/jcs8020064
Hu H, Xia Z, Tao Q, Ye Z, Yuan K, Song L. Self-Unfolding Properties of Smart Grid-Reinforced Membrane Origami. Journal of Composites Science. 2024; 8(2):64. https://doi.org/10.3390/jcs8020064
Chicago/Turabian StyleHu, Haotian, Zhenmeng Xia, Qiang Tao, Zixin Ye, Kaifeng Yuan, and Leying Song. 2024. "Self-Unfolding Properties of Smart Grid-Reinforced Membrane Origami" Journal of Composites Science 8, no. 2: 64. https://doi.org/10.3390/jcs8020064
APA StyleHu, H., Xia, Z., Tao, Q., Ye, Z., Yuan, K., & Song, L. (2024). Self-Unfolding Properties of Smart Grid-Reinforced Membrane Origami. Journal of Composites Science, 8(2), 64. https://doi.org/10.3390/jcs8020064