Hygroscopicity of Gel-Forming Composite Materials: Thermodynamic Assessment and Technological Significance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Tested Composite Gel-Forming Materials
2.2. Thermo-Desorption Instrumental Method for Laboratory Testing of Composite Gel-Forming Materials
2.3. Additional Methods and Data Processing
3. Results
3.1. Theoretical and Methodological Basis for the Thermodynamic Assessment of Hygroscopicity in Polydisperse Materials
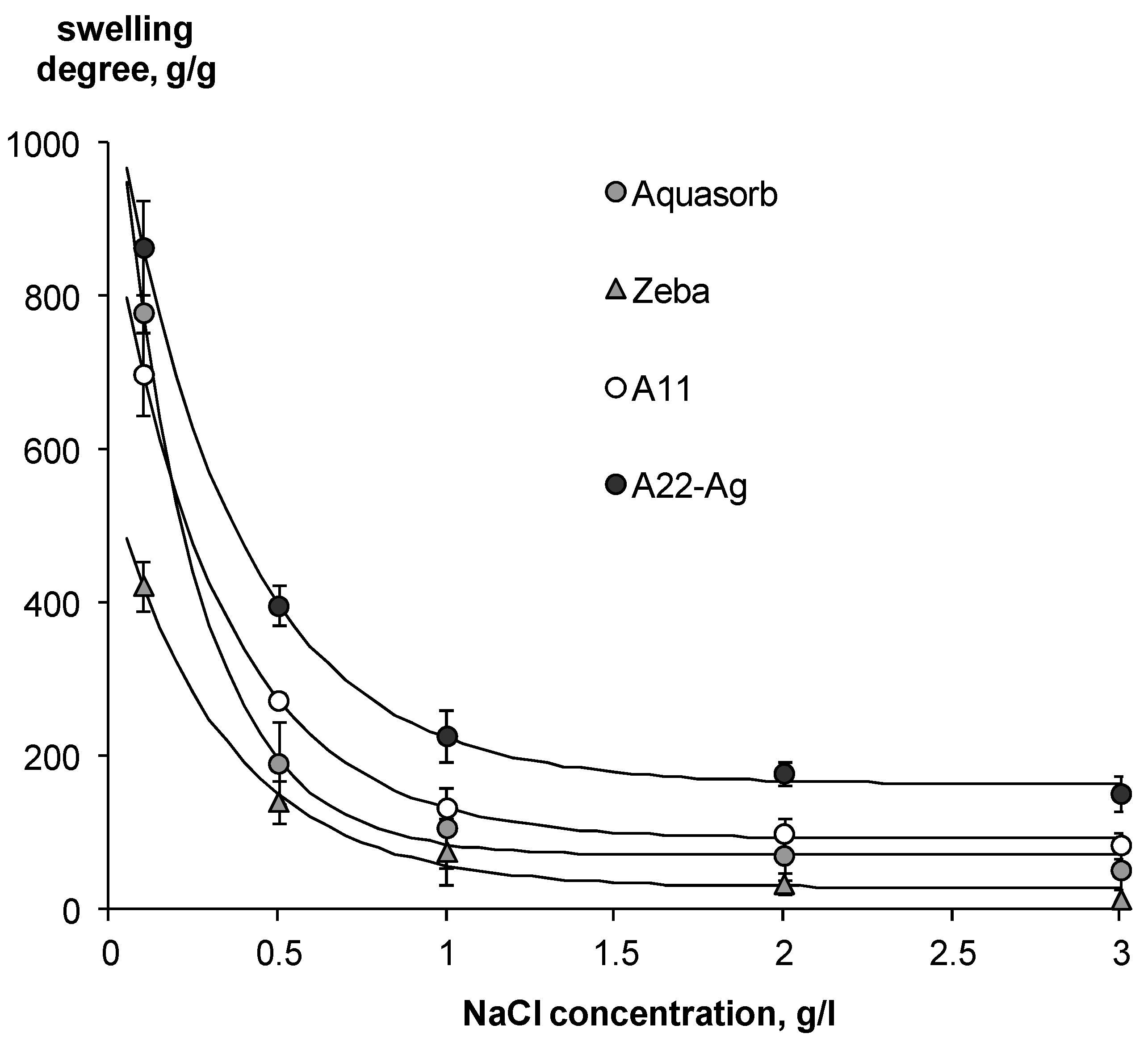
3.2. Experimental Results and Their Modeling
4. Discussion and Practical Use of Results
4.1. Comparison of the Obtained Results with Known Data
4.2. The Debatable Problem of Obtaining Water from the Air by Hygroscopic Materials
4.3. Practical Application of the Results
5. Conclusions
6. Patents
- Patent RU no. 2726561 (https://findpatent.ru/patent/272/2726561.html (accessed on 22 July 2022)).
- Patent RU no. 2639789 (http://www.findpatent.ru/patent/263/2639789.html (accessed on 22 July 2022)).
Author Contributions
Funding
Conflicts of Interest
References
- Certini, G.; Scalenghe, R. Soils: Basic Concepts and Future Challenges; Cambridge University Press: Cambridge, UK, 2006; 310 pp. [Google Scholar] [CrossRef]
- Al-Darby, A.M.; Al-Asfoor, S.I.; El-Shafei, Y.Z. Effect of Soil Gel-Conditioner on the Hydrophysical Properties of Sandy Soil. J. Saudi Soc. Agric. Sci. 2002, 1, 14–40. [Google Scholar]
- Lentz, R.D.; Sojka, R.E. Long-term polyacrylamide formulation effects on soil erosion, water infiltration, and yields of furrow-irrigated crops. Agron. J. 2009, 101, 305–314. [Google Scholar] [CrossRef]
- Shahid, S.A.; Qidwai, A.A.; Anwar, F.; Ullah, I.; Rashid, U. Improvement in the Water Retention Characteristics of Sandy Loam Soil Using a Newly Synthesized Poly(acrylamide-co-acrylic Acid)/AlZnFe2O4 Superabsorbent Hydrogel Nanocomposite Material. Molecules 2012, 17, 9397–9412. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Yang, Y.; Chen, Z. Influence of Super Absorbent Polymer on Soil Water Retention, Seed Germination and Plant Survivals for Rocky Slopes Eco-engineering. Ecol. Eng. 2014, 62, 27–32. [Google Scholar] [CrossRef]
- Banedjschafie, S.; Durner, W. Water Retention Properties of a Sandy Soil with Superabsorbent Polymers as Affected by Aging and Water Quality. J. Plant Nutr. Soil Sci. 2015, 178, 798–806. [Google Scholar] [CrossRef]
- Smagin, A.; Sadovnikova, N.; Smagina, M. Synthetic Gel Structures in Soils for Sustainable Potato Farming. Sci. Rep. 2019, 9, 18588. [Google Scholar] [CrossRef]
- Behera, S.; Mahanwar, P.A. Superabsorbent Polymers in Agriculture and Other Applications: A review. Polym. -Plast. Technol. Mater. 2020, 59, 341–356. [Google Scholar] [CrossRef]
- Ghani, A.A.; Shahzad, A.; Moztahida, M.; Tahir, K.; Jeon, H.; Kim, B.; Lee, D.S. Adsorption and electrochemical regeneration of intercalated Ti3C2Tx MXene for the removal of ciprofloxacin from wastewater. Chem. Eng. J. 2020, 421, 127780. [Google Scholar] [CrossRef]
- Mikula, P.; Mlnaříková, M.; Nadres, E.T.; Takahashi, H.; Babica, P.; Kuroda, K.; Blaha, L.; Sovadinova, I. Synthetic Biomimetic Polymethacrylates: Promising Platform for the Design of Anti-Cyanobacterial and Anti-Algal Agents. Polymers 2021, 13, 1025. [Google Scholar] [CrossRef]
- Xu, X.; Bizmark, N.; Christie, K.S.S.; Datta, S.S.; Ren, Z.J.; Priestley, R.D. Thermoresponsive Polymers for Water Treatment and Collection. Macromolecules 2022, 55, 1894–1909. [Google Scholar] [CrossRef]
- Guo, Y.; Guan, W.; Lei, C.; Lu, H.; Shi, W.; Yu, G. Scalable super hygroscopic polymer films for sustainable moisture harvesting in arid environments. Nat. Commun. 2022, 13, 2761. [Google Scholar] [CrossRef] [PubMed]
- Smagin, A.V. Thermodynamic Concept of Water Retention and Physical Quality of the Soil. Agronomy 2021, 11, 1686. [Google Scholar] [CrossRef]
- SNF Water Science. Available online: https://www.snf.com (accessed on 1 September 2022).
- UPL. Available online: https://www.upl-ltd.com (accessed on 1 September 2022).
- Smagin, A.V. Thermogravimetric Determination of Specific Surface Area for Soil Colloids. Colloid J. 2016, 78, 391–396. [Google Scholar] [CrossRef]
- Arthur, E.; Tuller, M.; Moldrup, P.; de Jonge, L.W. Evaluation of theoretical and empirical water vapor sorption isotherm models for soils. Water Resour. Res. 2016, 52, 190–205. [Google Scholar] [CrossRef]
- Smagin, A.V. About Thermodynamic Theory of Water Retention Capacity and Dispersity of Soils. Eur. Soil Sci. 2018, 51, 782–796. [Google Scholar] [CrossRef]
- Smagin, A.V.; Kol’tsov, I.N.; Pepelov, I.L.; Kirichenko, A.V.; Sadovnikova, N.B. The physical state of finely dispersed soil-like systems with drilling sludge as an example. Eur. Soil Sci. 2011, 44, 163–172. [Google Scholar] [CrossRef]
- Likos, W.J.; Ning, L. Water vapor sorption behavior of smectite-kaolinite mixtures. Clays Clay Miner. 2002, 50, 553–561. [Google Scholar] [CrossRef]
- Smagin, A.V. Physically Based Mathematical Models of the Water Vapor Sorption by Soils. Eur. Soil Sci. 2011, 44, 659–669. [Google Scholar] [CrossRef]
- Ayala, A.A.; Serna-Cock, L.; Giraldo, C.J.G. Moisture adsorption isotherms in yellow pitahaya (Selenicereusmegalanthus). Dyna 2011, 78, 7–14. [Google Scholar]
- Asomaning, J.M.; Sacande, M.; Olympio, N.S. Water sorption isotherm characteristics of seeds of six indigenous forest tree species in Ghana. West Afr. J. Appl. Ecol. 2011, 18, 15–28. [Google Scholar]
- Andrade, R.D.; Lemus, R.; Perez, C.E. Models of sorption isotherms for food: Uses and limitations. Vitae 2011, 18, 325–334. [Google Scholar]
- Baker, M.L.; Baas, J.H.; Malarkey, J.; Jacnito, R.S.; Craig, M.J.; Kane, I.A.; Barker, S. The effect of clay type on the properties of cohesive sediment gravity flows and their deposits. J. Sediment. Res. 2017, 87, 1176–1195. [Google Scholar] [CrossRef]
- Ma, S.; Liu, M.; Chen, Z. Preparation and Properties of a Salt-Resistant Superabsorbent Polymer. J. Appl. Polym. Sci. 2004, 93, 2532–2540. [Google Scholar] [CrossRef]
- Muhammad Rizwan, M.; Gilani, S.R.; Durani, A.I.; Naseem, S. Materials diversity of hydrogel: Synthesis, polymerization process and soil conditioning properties in agricultural field. J. Adv. Res. 2021, 33, 15–40. [Google Scholar] [CrossRef]
- Campos, E.V.R.; de Oliveira, J.L.; Fraceto, L.F.; Singh, B. Polysaccharides as Safer Release Systems for Agrochemicals. Agron. Sustain. Dev. 2015, 35, 47–66. [Google Scholar] [CrossRef]
- Johnson, M.S. Effect of Soluble Salts on Water Absorption by Gel-forming Soil Conditioners. J. Sci. Food Agric. 1984, 35, 1063–1066. [Google Scholar] [CrossRef]
- Sing, C.E.; Zwanikken, J.W.; Cruz, M.O. Effect of Ion–Ion Correlations on Polyelectrolyte Gel Collapse and Reentrant Swelling. Macromolecules 2013, 46, 5053–5065. [Google Scholar] [CrossRef]
- Fomina, E.K.; Krul, L.P.; Grinyuk, E.V.; Yakimenko, O.V. Effect of Cu2+, Zn2+, and Mn2+ ions on the water absorption of polyelectrolyte hydrogels based on polyacrylonitrile fiber hydrolyzate. Russ. J. Appl. Chem. 2014, 87, 1334–1339. [Google Scholar] [CrossRef]
- Vorobieva, E.V. Swelling of polyacrylamide-based hydrogel in aqueous solutions of low-molecular salts. Dokl. Natl. Acad. Sci. Belarus 2020, 64, 293–299. [Google Scholar] [CrossRef]
- Richards, L.A.; Weaver, L.R. Fifteem-Atmosphere-Percentage as Related to the Permanent Wilting Percentage. Soil Sci. 1943, 56, 331–339. [Google Scholar] [CrossRef]



| Materials: | Approximation Parameters | Statistical Parameters | |||
|---|---|---|---|---|---|
| Model (7): |ψ|= a×exp(−bW) | |||||
| a, (J/kg) | b, (kg/kg) | R2 | s, (J/kg) | p Value * | |
| “Zeba” | 998457 ± 12520 | 0.168 ± 0.004 | 0.998 | 15405 | <0.0001 |
| “Aquasorb” | 822805 ± 16769 | 0.060 ± 0.002 | 0.998 | 21859 | <0.0001 |
| A11 | 789655 ± 16308 | 0.063 ± 0.002 | 0.998 | 19673 | <0.0001 |
| A22-Ag | 742452 ± 16768 | 0.043 ± 0.003 | 0.996 | 21857 | <0.0001 |
| Model (5): W = Wm×K×f/{(1 − f)×(1 + (K − 1)×f} | |||||
| Wm, (%) | K | R2 | s, (%) | p value * | |
| “Zeba” | 7.42 ± 0.26 | 54.32 ± 12.11 | 0.983 | 0.68 | 0.0028 |
| “Aquasorb” | 18.71 ± 0.96 | 30.14 ± 9.02 | 0.971 | 2.32 | 0.0124 |
| A11 | 16.86 ± 0.62 | 29.80 ± 6.32 | 0.985 | 1.48 | 0.0022 |
| A22-Ag | 23.83 ± 0.50 | 24.69 ± 2.89 | 0.996 | 1.15 | 0.0010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smagin, A.V.; Sadovnikova, N.B.; Belyaeva, E.A. Hygroscopicity of Gel-Forming Composite Materials: Thermodynamic Assessment and Technological Significance. J. Compos. Sci. 2022, 6, 269. https://doi.org/10.3390/jcs6090269
Smagin AV, Sadovnikova NB, Belyaeva EA. Hygroscopicity of Gel-Forming Composite Materials: Thermodynamic Assessment and Technological Significance. Journal of Composites Science. 2022; 6(9):269. https://doi.org/10.3390/jcs6090269
Chicago/Turabian StyleSmagin, Andrey V., Nadezhda B. Sadovnikova, and Elena A. Belyaeva. 2022. "Hygroscopicity of Gel-Forming Composite Materials: Thermodynamic Assessment and Technological Significance" Journal of Composites Science 6, no. 9: 269. https://doi.org/10.3390/jcs6090269
APA StyleSmagin, A. V., Sadovnikova, N. B., & Belyaeva, E. A. (2022). Hygroscopicity of Gel-Forming Composite Materials: Thermodynamic Assessment and Technological Significance. Journal of Composites Science, 6(9), 269. https://doi.org/10.3390/jcs6090269






