Derivation and Validation of Linear Elastic Orthotropic Material Properties for Short Fibre Reinforced FLM Parts
Abstract
:1. Introduction
1.1. Motivation
1.2. State of the Art and Objectives
1.3. Objectives and Novelty of This Contribution
2. Materials and Methods
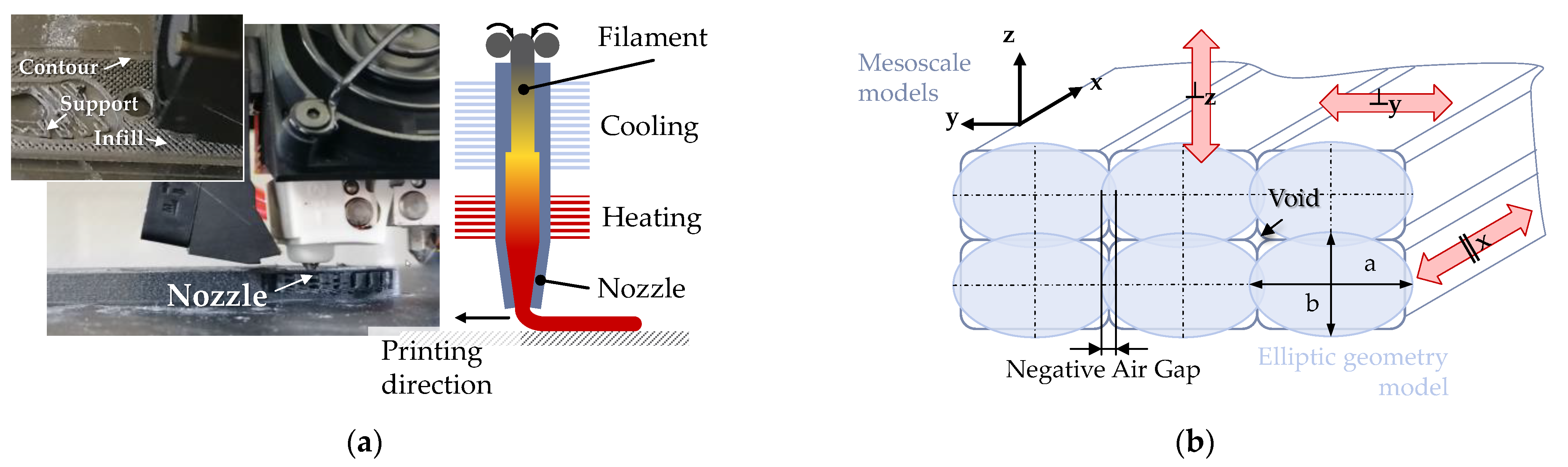
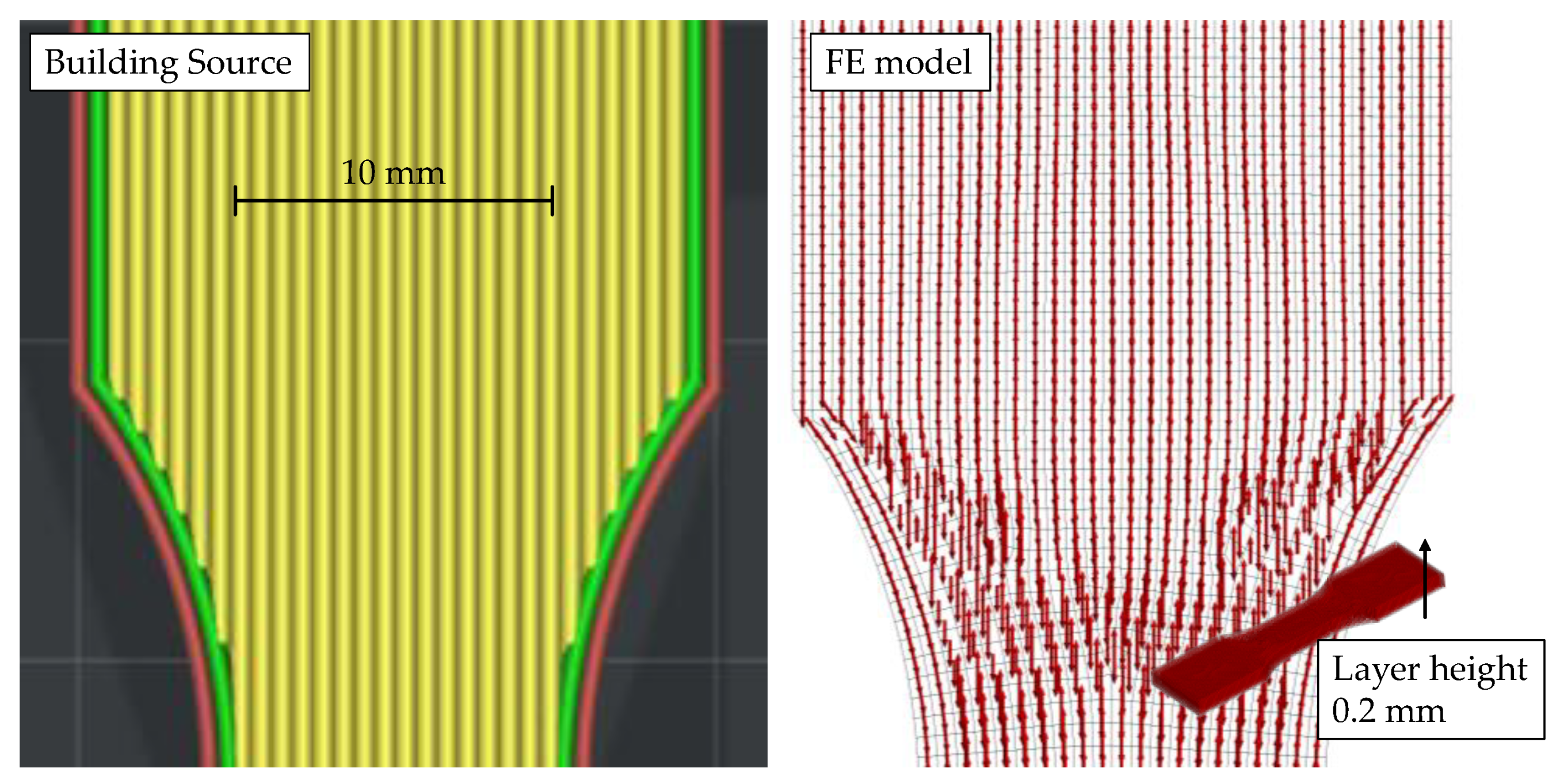
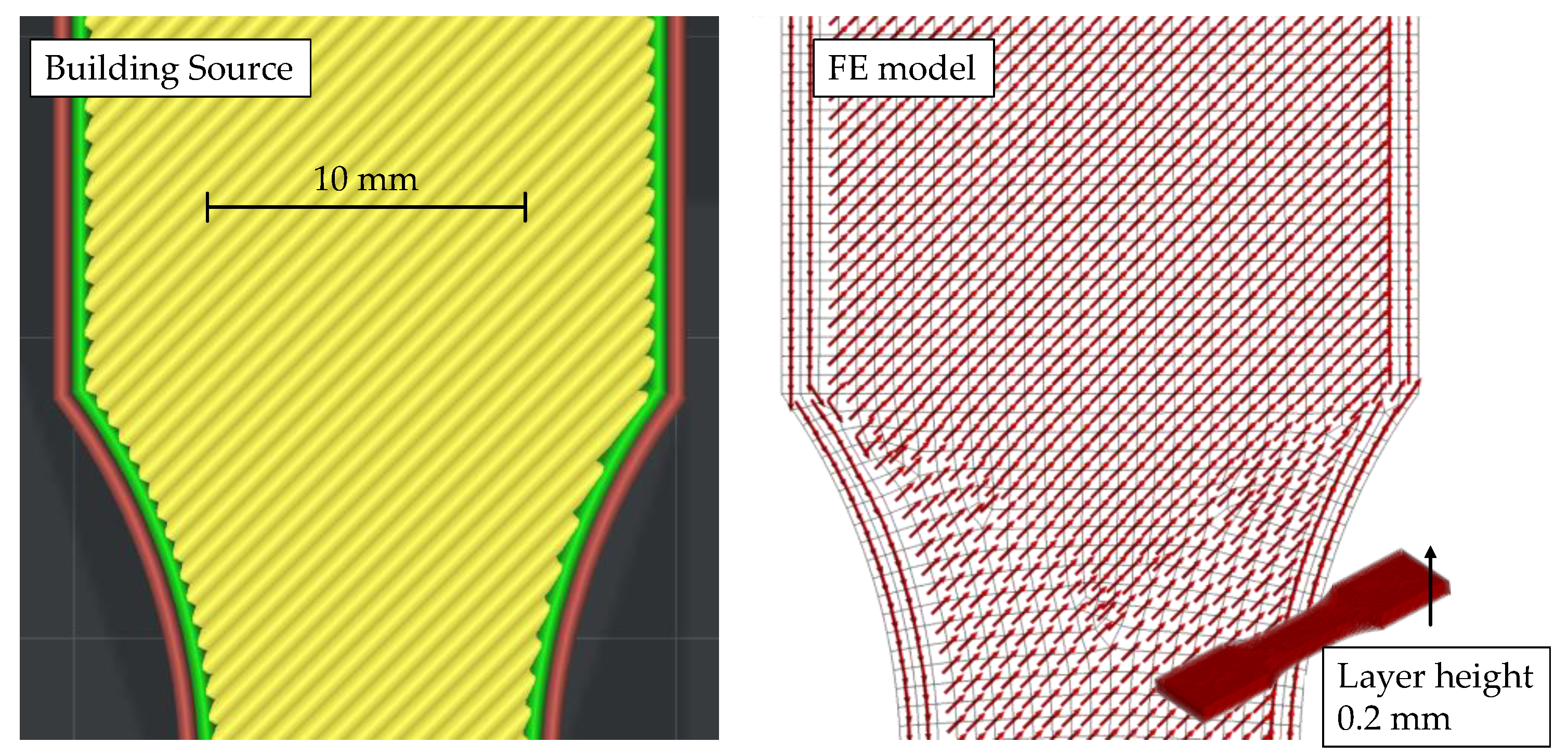
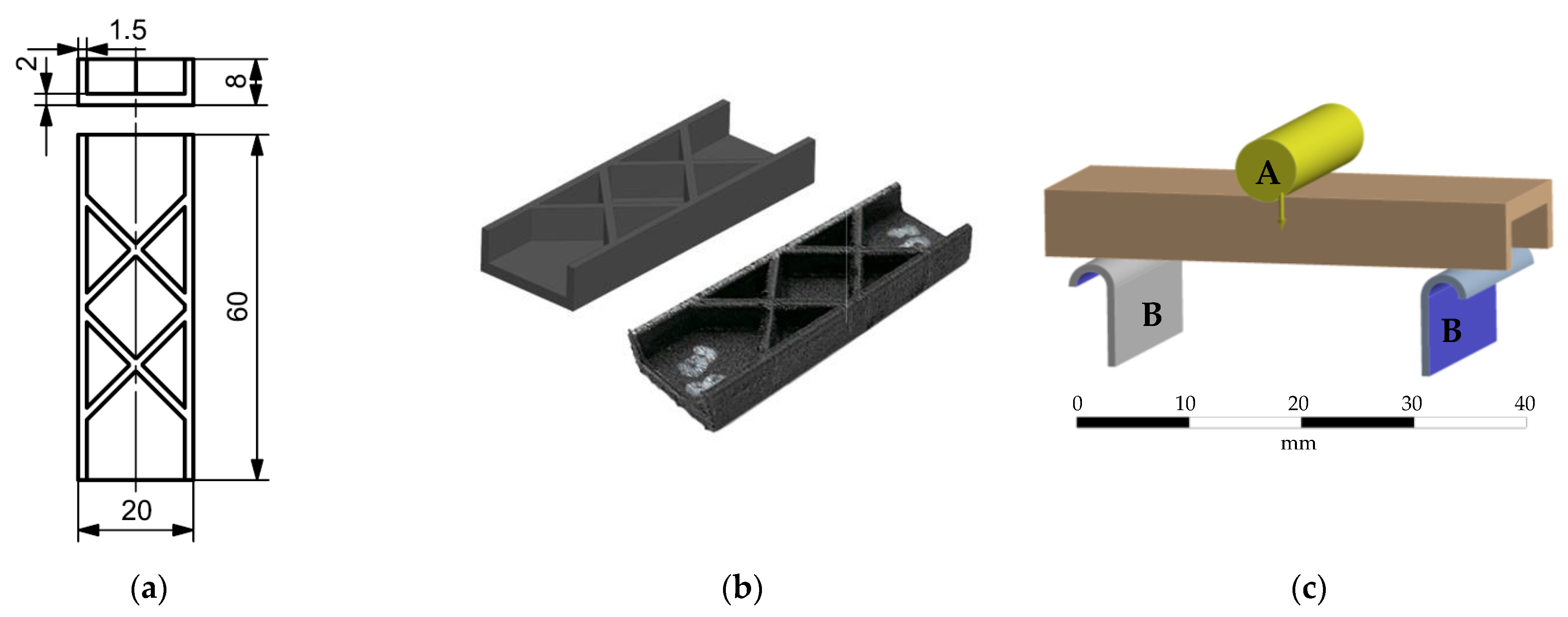
2.1. Specimen Geometry, Slicing and Printing
- The tensile bar is printed flat on the printing platform with longitudinal infill (Flat 0°, F0° in the following), intended to primarily yield Young’s modulus in longitudinal direction ;
- Same orientation, but with perpendicular infill (F90°) for Young’s modulus in perpendicular direction in-plane ;
- Upright position with infill printed in the same direction as F90°, thus called Upright 90° (U90°), intended to explain interlayer modulus ;
- Flat printed position with 45° infill within plane (F45°) for shear modulus ;
- Diagonally printed position (45° to plane) with parallel infill to walls, thus called U45°-90° for shear modulus ;
- And diagonally printed position, yet with perpendicular infill to walls (like F0°), thus called U45°-0° for shear modulus .
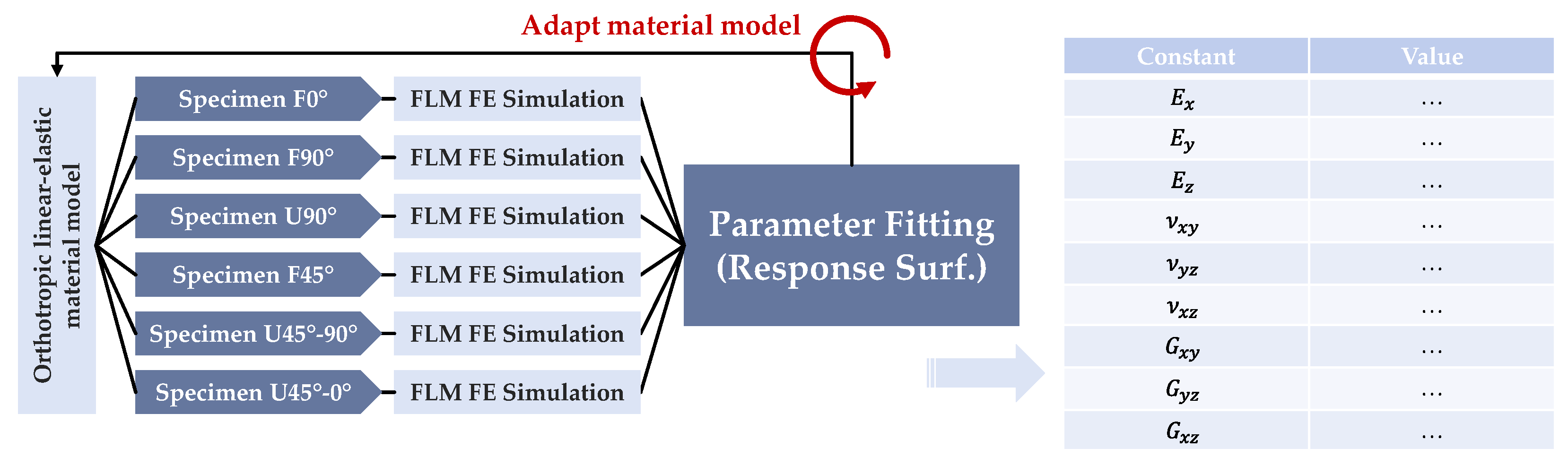
2.2. Simulation and Fitting of Orthotropic Material Parameters
- Average the experiment data to obtain one force-displacement, one longitudinal strain-displacement, and one transverse strain-displacement curve for each of the six samples (18 curves total).
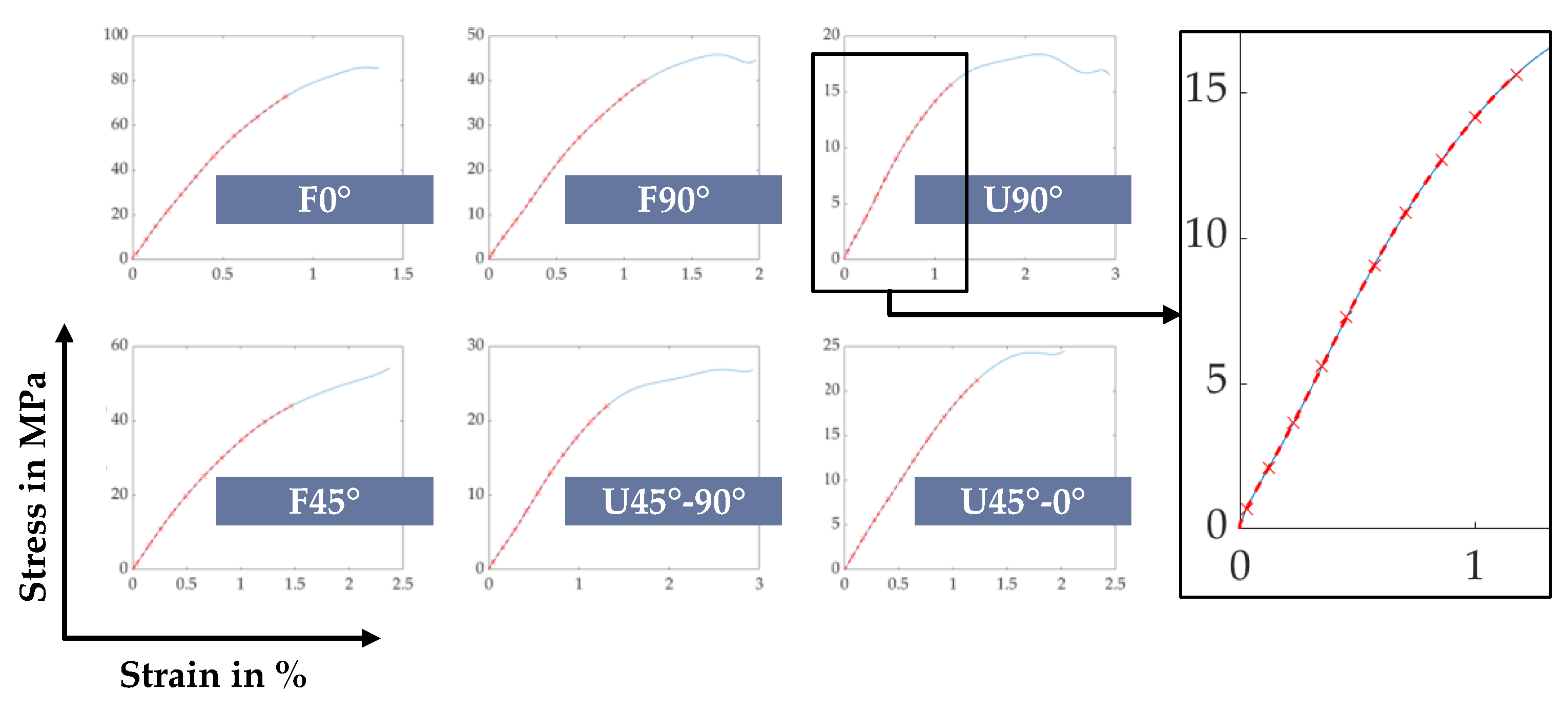
- Find the linear parts of the curves (from displacement = 0 to the end of the linear part), for reference of the experimental data see the results section (Section 3). This is done to allow the linear elastic model to fit to the actual linear section of the curve. To obtain this linear limit, the following steps were taken and are proposed as a solution: (1) Smooth the average curve by a moving average of 10 measurement pairs; (2) Calculate the slope between each curve point and its predecessor ; (3) Calculate the curvature by calculating the “slope’s slope”, in turn; and (4) find the first occurrence where the percentage difference in curvature is smaller than a certain threshold (here, 0.75% were used arbitrarily). The threshold depends on the desired “strictness” of linearity; the smaller, the stricter. To avoid considering the initial, rather noisy data within the first part of the experiment, the linearity detection starts after 10% of the experiment curve data. (4) Finally, 10 equidistant displacement points are selected from the linear span of deformation . Using a mapping function, the closest (minimum-difference) data pairs from the averaged, but still discrete experiment data are selected.
2.3. Validation
2.4. Conduct and Evaluation of Experiments
3. Results
3.1. Calibration
3.1.1. Experiments
3.1.2. Simulation and Parameter Fitting
3.2. Validation
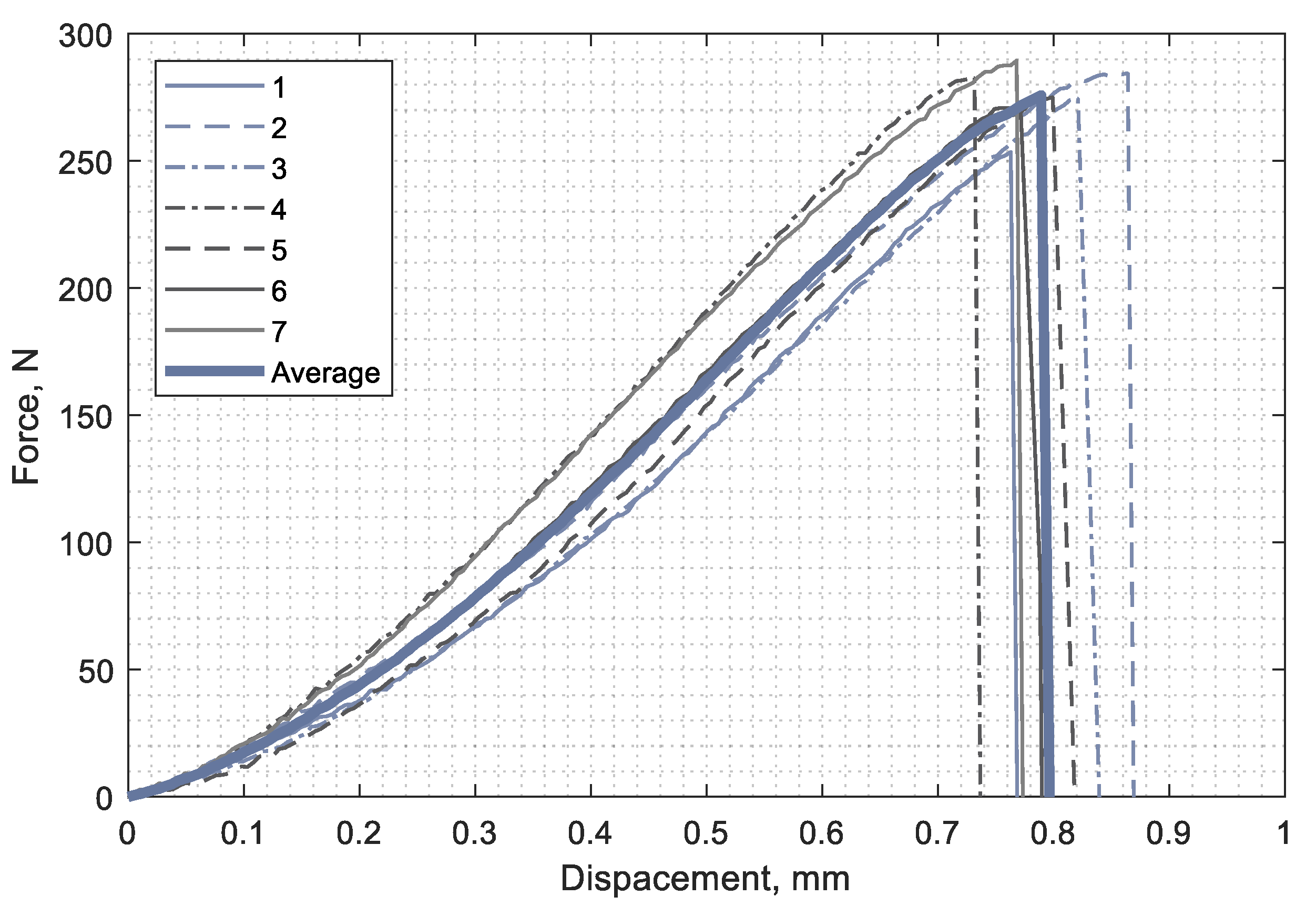
3.2.1. Experiments
3.2.2. Simulation and Material Model Validation
4. Discussion: Advantages, Disadvantages, and Open Research Questions of Simultaneous Parameter Fitting
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lachmayer, R.; Lippert, R.B.; Fahlbusch, T. 3D-Druck Beleuchtet; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for Additive Manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. 2016, 65, 737–760. [Google Scholar] [CrossRef] [Green Version]
- Verein Deutscher Ingenieure. Additive Fertigungsverfahren: Grundlagen, Begriffe, Verfahrensbeschreibungen; 25.020(VDI 3405); Beuth Verlag: Berlin, Germany, 2014. [Google Scholar]
- Vajna, S.; Weber, C.; Zeman, K.; Hehenberger, P.; Gerhard, D.; Wartzack, S. CAx für Ingenieure: Eine Praxisbezogene Einführung, 3rd ed.; Springer Vieweg: Wiesbaden, Germany, 2018. [Google Scholar]
- Tan, P. Numerical simulation of the ballistic protection performance of a laminated armor system with pre-existing debonding/delamination. Compos. Part B Eng. 2014, 59, 50–59. [Google Scholar] [CrossRef]
- Rozylo, P. Failure analysis of thin-walled composite structures using independent advanced damage models. Compos. Struct. 2021, 262, 113598. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Shofner, M.L.; Lozano, K.; Rodríguez-Macías, F.J.; Barrera, E.V. Nanofiber-reinforced polymers prepared by fused deposition modeling. J. Appl. Polym. Sci. 2003, 89, 3081–3090. [Google Scholar] [CrossRef]
- DeNardo, N.M. Additive Manufacturing of Carbon Fiber-Reinforced Thermoplastic Composites. Master’s Thesis, West Purdue University, Lafayette, IN, USA, 2016. [Google Scholar]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive manufacturing of carbon fiber-reinforced plastic composites using fused deposition modeling: Effects of process parameters on tensile properties. J. Compos. Mater. 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.-F.M. A critical review on 3D printed continuous fiber-reinforced composites: History, mechanism, materials and properties. Compos. Struct. 2020, 232, 111476. [Google Scholar] [CrossRef]
- Kolanu, N.R.; Raju, G.; Ramji, M. A unified numerical approach for the simulation of intra and inter laminar damage evolution in stiffened CFRP panels under compression. Compo. Part B Eng. 2020, 190, 107931. [Google Scholar] [CrossRef]
- Thomas, D.S.; Gilbert, S.W. Costs and Cost Effectiveness of Additive Manufacturing, NIST Special Publication 1176; NIST National Institute of Standards and Techology: Gaithersburg, MD, USA, 2014. [Google Scholar]
- Such, M.; Ward, C.; Potter, K. Aligned Discontinuous Fibre Composites: A Short History. JMC 2014, 2, 155–168. [Google Scholar] [CrossRef]
- Armiger, T.E.; Edison, D.H.; Lauterbach, H.G.; Layton, J.R.; Okine, R.K. Composites of Stretch Broken Aligned Fibers of Carbon and Glass Reinforced Resin. European Patent EP0272088A1, 15 December 1987. [Google Scholar]
- Parandoush, P.; Lin, D. A review on additive manufacturing of polymer-fiber composites. Compos. Struct. 2017, 182, 36–53. [Google Scholar] [CrossRef]
- Montero, M.; Roundy, S.; Odell, D.; Ahn, S.; Wright, P. Material Characterization of Fused Deposition Modeling (FDM) ABS by Designed Experiments. In Proceedings of the Rapid Prototyping and Manufacturing Conference, Cincinnati, OH, USA, 15–17 May 2001; pp. 1–21. [Google Scholar]
- Ahn, S.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Geng, P.; Li, G.; Di, Z.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3D-Printed PEEK and a Comparative Mechanical Study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental investigation and empirical modelling of FDM process for compressive strength improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Hernandez, R.; Slaughter, D.; Whaley, D.; Tate, J.; Asiabanpour, B. Analyzing the Tensile, Compressive, and Flexural Properties of 3D Printed ABS P430 Plastic Based on Printing Orientation Using Fused Deposition Modeling. In Solid Freeform Fabrication 2016, Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016; Bourell, D.L., Crawford, R., Seepersad, C., Beaman, J.J., Fish, S., Harris, M., Eds.; University of Texas at Austin: Austin, TX, USA; pp. 939–950.
- Pei, E.; Lanzotti, A.; Grasso, M.; Staiano, G.; Martorelli, M. The impact of process parameters on mechanical properties of parts fabricated in PLA with an open-source 3-D printer. Rapid Prototyp. J. 2015, 21, 604–617. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Sun, Q.; Bellehumeur, C.; Gu, P. Composite Modeling and Analysis for Fabrication of FDM Prototypes with Locally Controlled Properties. J. Manuf. Process. 2002, 4, 129–141. [Google Scholar] [CrossRef]
- Matas, J.F.R. Modeling the Mechanical Behavior of Fused Deposition Acrylonitrile-Butadiene-Styrene Polymer Components. Master’s Thesis, University of Notre Dame, Notre Dame, IN, USA, 1999. [Google Scholar]
- Bellini, A.; Güçeri, S. Mechanical characterization of parts fabricated using fused deposition modeling. Rapid Prototyp. J. 2003, 9, 252–264. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Granada, A.A.G.; Llumà, J.; Borros, S.; Reyes, G. Mechanical property characterization and simulation of fused deposition modeling Polycarbonate parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- Rodríguez, J.F.; Thomas, J.P.; Renaud, J.E. Mechanical behavior of acrylonitrile butadiene styrene fused deposition materials modeling. Rapid Prototyp. J. 2003, 9, 219–230. [Google Scholar] [CrossRef]
- Lee, C.S.; Kim, S.G.; Kim, H.J.; Ahn, S.H. Measurement of anisotropic compressive strength of rapid prototyping parts. J. Mater. Process. Technol. 2007, 187–188, 627–630. [Google Scholar] [CrossRef]
- Cantrell, J.T.; Rohde, S.; Damiani, D.; Gurnani, R.; DiSandro, L.; Anton, J.; Young, A.; Jerez, A.; Steinbach, D.; Kroese, C.; et al. Experimental characterization of the mechanical properties of 3D-printed ABS and polycarbonate parts. Rapid Prototyp. J. 2017, 23, 811–824. [Google Scholar] [CrossRef]
- Somireddy, M.; Czekanski, A. Mechanical Characterization of Additively Manufactured Parts by FE Modeling of Mesostructure. J. Manuf. Mater. Process. 2017, 1, 18. [Google Scholar] [CrossRef] [Green Version]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef] [Green Version]
- Duty, C.E.; Kunc, V.; Compton, B.; Post, B.; Erdman, D.; Smith, R.; Lind, R.; Lloyd, P.; Love, L. Structure and mechanical behavior of Big Area Additive Manufacturing (BAAM) materials. Rapid Prototyp. J. 2017, 23, 181–189. [Google Scholar] [CrossRef]
- Love, L.J.; Kunc, V.; Rios, O.; Duty, C.E.; Elliott, A.M.; Post, B.K.; Smith, R.J.; Blue, C.A. The importance of carbon fiber to polymer additive manufacturing. J. Mater. Res. 2014, 29, 1893–1898. [Google Scholar] [CrossRef] [Green Version]
- Becker, F. Entwicklung Einer Beschreibungsmethodik für das Mechanische Verhalten Unverstärkter Thermoplaste bei Hohen Deformationsgeschwindigkeiten. Ph.D. Thesis, Martin-Luther-Universität Halle-Wittenberg, Halle, Germany, 2009. [Google Scholar]
- Kunkel, F. Zum Deformationsverhalten von Spritzgegossenen Bauteilen aus Talkumgefüllten Thermoplasten unter Dynamischer Beanspruchung. Master’s Thesis, Otto-von-Guericke-Universität Magdeburg, Magdeburg, Germany, 2017. [Google Scholar]
- Witzgall, C.; Wartzack, S. An Investigation of Mechanically Aged Short-Fiber Reinforced Thermoplastics under Highly Dynamic Loads. In Proceedings of the DFX 2016 27th Symposium Design for X, Jesteburg, Germany, 5–6 October 2016; pp. 135–146. [Google Scholar]
- Witzgall, C.; Giolda, J.; Wartzack, S. A novel approach to incorporating previous fatigue damage into a failure model for short-fibre reinforced plastics. Int. J. Impact Eng. 2022, 18, 104155. [Google Scholar] [CrossRef]
- IdeaMaker: 3D Slicer Software; Raise 3D Technologies I; Raise 3D Technologies, Inc.: Irvine, CA, USA, 2020.
- Völkl, H.; Mayer, J.; Wartzack, S. Strukturmechanische Simulation additiv im FFF-Verfahren gefertigter Bauteile. In KfAF 2019 Konstruktion für die Additive Fertigung 2019, 1st ed.; Lachmayer, R., Rettschlag, K., Kaierle, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 143–157. [Google Scholar]
- FormFutura. CarbonFil. Available online: https://www.formfutura.com/shop/product/carbonfil-2788?category=458 (accessed on 26 January 2022).
- ANSYS; ANSYS Help; SAS IP, Inc.: Cheyenne, WY, USA, 2017.
- ISO 527-1:2012-06; Kunststoffe—Bestimmung der Zugeigenschaften—Teil 1: Allgemeine Grundsätze. ISO; Beuth: Berlin, Germany, 2012.
- DIN EN ISO 527-4 1997; Kunststoffe—Bestimmung der Zugeigenschaften—Teil 4: Prüfbedingungen für isotrop und anisotrop faserverstärkte Kunststoffverbundwerkstoffe. ISO; Beuth Verlag: Berlin, Germany, 1997.
- Pierron, F.; Vautrin, A. Accurate comparative determination of the in-plane shear modulus of T300/914 by the iosipescu and 45° off-axis tests. Compos. Sci. Technol. 1994, 52, 61–72. [Google Scholar] [CrossRef]
- Alsoufi, M.; El-Sayed, A. Warping Deformation of Desktop 3D Printed Parts Manufactured by Open Source Fused Deposition Modeling (FDM) System. Int. J. Mech. Mechatron. Eng. 2017, 17, 7–16. [Google Scholar]







| MPa | MPa | MPa | - | - | - | MPa | MPa | MPa |
|---|---|---|---|---|---|---|---|---|
| 8212 | 2615 | 1437 | 0.28 | 0.11 | 0.10 | 883 | 637 | 634 |
| F0° | F90° | U90° | F45° | U45°-90° | U45°-0° | |
|---|---|---|---|---|---|---|
| ) | 14% | 9% | 25% | 13% | 49% | 17% |
| 10% | 8% | 35% | 19% | 6% | 42% | |
| 20% | 21% | 14% | 14% | 21% | 12% |
| MPa | MPa | MPa | - | - | - | MPa | MPa | MPa |
|---|---|---|---|---|---|---|---|---|
| 8153 | 1949 | 1549 | 0.31 | 0.17 | 0.36 | 1096 | 642 | 1120 |
| 8212 | 2615 | 1437 | 0.28 | 0.11 | 0.10 | 883 | 637 | 634 |
| F (reaction forces at boundary) | F0° | 0.99 | 0.40 | 0.32 | 0.23 | 0.23 | 0.38 | 0.43 | −0.08 | 0.15 |
| F90° | 0.52 | 0.98 | 0.40 | 0.66 | 0.50 | 0.39 | 0.44 | 0.27 | 0.31 | |
| U90° | 0.24 | 0.35 | 1.00 | 0.53 | 0.61 | 0.65 | 0.63 | 0.32 | 0.44 | |
| F45° | 0.64 | 0.73 | 0.58 | 0.61 | 0.57 | 0.61 | 0.84 | 0.26 | 0.36 | |
| U45°-90° | 0.10 | 0.46 | 0.77 | 0.58 | 0.66 | 0.67 | 0.62 | 0.81 | 0.69 | |
| U45°-0° | 0.14 | 0.44 | 0.76 | 0.59 | 0.71 | 0.65 | 0.59 | 0.73 | 0.81 | |
(transverse mean strain) | F0° | 0.05 | −0.63 | −0.45 | −0.92 | −0.63 | −0.46 | −0.41 | −0.38 | −0.35 |
| F90° | 0.06 | −0.81 | −0.36 | −0.87 | −0.61 | −0.29 | −0.33 | −0.38 | −0.36 | |
| U90° | 0.05 | −0.09 | −0.82 | −0.47 | −0.64 | −0.80 | −0.56 | −0.42 | −0.50 | |
| F45° | −0.09 | −0.75 | 0.02 | −0.45 | −0.20 | 0.11 | 0.28 | −0.10 | −0.06 | |
| U45°-90° | −0.43 | −0.01 | −0.59 | −0.10 | −0.12 | −0.27 | −0.23 | 0.56 | 0.19 | |
| U45°-0° | −0.39 | −0.08 | −0.60 | −0.15 | −0.15 | −0.27 | −0.23 | 0.52 | 0.30 | |
(longitudinal mean strain) | F0° | −0.56 | 0.25 | 0.30 | 0.50 | 0.49 | 0.35 | 0.36 | 0.79 | 0.51 |
| F90° | −0.39 | 0.23 | 0.19 | 0.45 | 0.43 | 0.27 | 0.23 | 0.44 | 0.36 | |
| U90° | −0.29 | −0.05 | −0.48 | 0.07 | 0.20 | 0.01 | −0.10 | 0.45 | 0.41 | |
| F45° | −0.32 | 0.61 | 0.27 | 0.59 | 0.48 | 0.25 | 0.02 | 0.64 | 0.52 | |
| U45°-90° | 0.55 | −0.08 | 0.05 | −0.11 | −0.12 | 0.01 | 0.08 | −0.85 | −0.40 | |
| U45°-0° | 0.59 | 0.19 | 0.25 | 0.09 | 0.00 | 0.20 | 0.27 | −0.62 | −0.51 |
| MPa | MPa | MPa | - | - | - | MPa | MPa | MPa |
|---|---|---|---|---|---|---|---|---|
| 8153 | 1949 | 1549 | 0.31 | 0.17 | 0.36 | 1096 | 642 | 1120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witzgall, C.; Völkl, H.; Wartzack, S. Derivation and Validation of Linear Elastic Orthotropic Material Properties for Short Fibre Reinforced FLM Parts. J. Compos. Sci. 2022, 6, 101. https://doi.org/10.3390/jcs6040101
Witzgall C, Völkl H, Wartzack S. Derivation and Validation of Linear Elastic Orthotropic Material Properties for Short Fibre Reinforced FLM Parts. Journal of Composites Science. 2022; 6(4):101. https://doi.org/10.3390/jcs6040101
Chicago/Turabian StyleWitzgall, Christian, Harald Völkl, and Sandro Wartzack. 2022. "Derivation and Validation of Linear Elastic Orthotropic Material Properties for Short Fibre Reinforced FLM Parts" Journal of Composites Science 6, no. 4: 101. https://doi.org/10.3390/jcs6040101
APA StyleWitzgall, C., Völkl, H., & Wartzack, S. (2022). Derivation and Validation of Linear Elastic Orthotropic Material Properties for Short Fibre Reinforced FLM Parts. Journal of Composites Science, 6(4), 101. https://doi.org/10.3390/jcs6040101






