Abstract
Here, we discuss a model for the quasi-static magnetoelectric (ME) interaction in three-layer composites consisting of a single piezoelectric (PE) layer and two magnetostrictive (MS) layers with positive and negative magnetostriction. Two types of layer arrangements are considered: Type 1: a sandwich structure with the PE layer between the two MS layers and Type 2: the two MS layers form the adjacent layers. Expressions for the ME response are obtained using the system of equations of elasto- and electrostatics for the PE and MS phases. The contributions from longitudinal and bending vibrations to the net ME response are considered. The theory is applied for trilayers consisting of lead zirconate titanate (PZT), nickel for negative magnetostriction, and Metglas for positive magnetostriction. Estimates of the dependence of the strength of the ME response on the thickness of the three layers are provided. It is shown that the asymmetric three-layer structures of both types lead to an increase in the strength of ME interactions by almost an order of magnitude compared to a two-layer piezoelectric-magnetostrictive structure. The model predicts a much stronger ME response in Type 2 structures than in Type 1. The theory discussed here is of importance for designing composites for applications such as magnetic field sensors, gyrators, and energy harvesters.
1. Introduction
Piezo-magnetostrictive (PE-MS) composites are unique materials for electronics due to the mechanical coupling between the magnetostrictive and piezoelectric phases leading to magnetoelectric (ME) interaction. This interaction manifests as an electric voltage when the composite is subjected to a magnetic field (direct effect), or, conversely, a change in the magnetization of the sample occurs when it is placed in an electric field (inverse or converse ME effect). Due to the ME interaction, there is an interrelation between the electrical and magnetic properties of materials. Due to this relationship, ME composites can be used to fabricate new electronic devices that cannot be created using traditional materials [1,2,3]. Early works investigated various types of composites consisting of a variety of ferromagnetic and ferroelectric phases in the form of bulk composites, as well as thick film or thin film layered structures and nanocomposites in the form of nanopillars in a host matrix, core-shell particles, and core-shell nanofibers [4,5,6,7,8,9,10,11]. In spite of these early efforts, the question of increasing the efficiency of the field conversion in ME materials remains fundamental at present. The efficiency is very important, especially in the low-frequency region, where the strength of the ME coupling is practically independent of frequency. Although the ME effect in the electromechanical resonance region is much stronger than at low frequency, the frequency width of the electromechanical resonance line is rather narrow. Therefore, in applications, such as in energy harvesters, operating at the resonance frequency will not be efficient. In contrast to single-phase multiferroics, where the ME interaction mechanism is a change in the electron spin–orbit interaction upon application of an external electric field [12], the ME response mechanism in PE-MS composites is the mechanical interaction between the piezoelectric and magnetostrictive subsystems [13]. When a magnetic field is applied, mechanical deformations occur due to magnetostriction, which is transferred to the piezoelectric, resulting in a change in polarization. The most common ferromagnetic materials for creating the composites are permendur, nickel, Terfenol-D, and amorphous Metglas alloy. When they are placed in a magnetic field in the plane of the sample, longitudinal deformations of the tension-compression type are transferred to the PE layer, and also bending deformations in the case of asymmetric structures.
In bilayers, the contribution from bending deformation to ME coupling is significant [14,15]. A bimorph asymmetric structure consisting of two layers of PZT with opposite directions of polarization and located between two magnetic layers, which were an amorphous Metglas alloy with positive magnetostriction and a nickel layer with negative magnetostriction, was studied in the work of Ref. [16]. The magnitude of the ME interaction in such a structure turned out to be an order of magnitude higher than in a two-layer Ni-PZT structure with similar parameters and comparable sizes. In the works of Refs. [16,17,18], experimental studies of the ME coupling in the Terfenol-D/PZT/Ni structure at various nickel thicknesses are presented. In these works, it was shown that the efficiency of ME conversion in the region of the flexural vibration mode significantly exceeds the value of ME interaction in two-layer structures. The theory of the ME effect caused by bending deformations in a three-layer structure with two adjacent magnetic layers and a piezoelectric layer was presented in Ref. [19]. In this work, the contribution to the ME interaction only from bending vibrations was considered. However, in a two-layer structure, the contributions to the ME effect from longitudinal and bending vibrations have different signs, and their contributions to the resulting ME effect are dependent on the layer thickness.
In this report, two types of asymmetric three-layer structures are considered: Type 1, in which the piezoelectric (PE) layer is located between two magnetostrictive (MS) layers with positive and negative magnetostriction; and Type 2, in which the PE layer is on top of two adjacent MS layers. The contributions to the ME effect from longitudinal and bending vibrations are taken into account. The purpose of this work was to model the influence of the two MS layers with positive and negative magnetostrictions on the strength of the ME interactions in each type, and to determine the dependence of ME interaction strengths on the thicknesses of the MS layers. A widely used parameter characterizing the value of ME interactions is the ME voltage coefficient (MEVC), which is defined as the ratio of the induced electric field in the PE layer, (Vac/tp) to the applied AC magnetic field hac, i.e., MEVC = Vac/(tp hac). We also considered the dependence of ME sensitivity coefficient, MESC= Vac /hac on the thickness of MS layers for the two types of three-layer structures. The model is applied to the case of composites with PZT and Ni, with negative magnetostriction, Metglas, and Permendur with positive magnetostriction.
2. Model
Figure 1 shows the two types of trilayers consisting of PZT and MS layers with positive and negative magnetostriction considered for modeling.
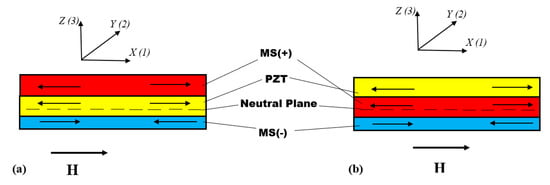
Figure 1.
Schematic drawing of (a) Type 1 and (b) Type 2 asymmetric trilayers, with PZT layer of thickness and magnetostrictive (MS) layers with positive (MS+) and negative (MS−) magnetostriction and thicknesses and , respectively. The dashed line represents the neutral plane.
When a sample is placed in a magnetic field, compressive strains occur in a layer with negative magnetostriction (nickel or nickel ferrite, for example), and tensile strains occur in a layer with positive magnetostriction (Permendur, Terfenol-D, Metglas alloy). By means of a mechanical coupling through the interface, these deformations are transferred to the PZT layer, and as a result, longitudinal tensile or compressive deformations occur in it. In addition, since the mechanical stresses resulting from the deformations are not axial, a bending moment is also present, which leads to bending deformations. As a result, when a sample is placed in a magnetic field, two types of deformations occur simultaneously in a piezoelectric material—longitudinal deformations and bending deformations. Both types of these deformations contribute to the magnitude of the ME interaction.
3. Longitudinal Deformations
When considering the ME interactions, we restrict ourselves to the quasi-static case, i.e., the case when the length and width of the sample are much smaller than the length. In this case, the change in strains and stresses along the length and width of the sample can be neglected and, in this case, elasto- and electrostatic equations have following forms:
where the indices i and j take the values 1 and 2, and i ≠ j. Here , are strain tensor components of piezoelectric, magnetostrictive layers, MS+ and MS−, respectively; , , are their Young’s moduli; , are components of the vector of the electric field and electric induction; , are the stress tensor components of PZT and MS+ and MS−; , are piezoelectric and piezomagnetic coefficients; is the component of the permittivity. In contrast to Ref. [20], we do not assume that the width of the sample is much less than its length, so in this work, we also take into account the contribution to the ME interaction from the stress T2, which is a more accurate modelling.
For the simplicity of calculations, we will assume that the sample’s thickness is much smaller than its length and width. We also suppose that the bond on interface is ideal, and we do not take into account the effects arisen on the interface. In this case, we can assume that longitudinal strains are uniform throughout the layer volume, i.e., the following equality hold:
Under this assumption, the longitudinal deformations for both types of structures, Type 1 and Type 2, will be the same and the contributions to ME interactions for both types of structures will be the same. For the following calculations, we will be using the modified procedure in Ref. [20]. The equilibrium condition of the sample, namely the equality to zero the X and Y projections of the force, gives for this case the following equations:
where the index i takes the values 1, 2. After that, expressing the components of the stress tensor from Equations (1)–(3) and substituting the obtained expressions into Equation (6), we obtain the following equation relating the deformations with the applied magnetic and induced electric fields:
where is the average Young’s modulus, and is the total thickness of the sample. After simple transformations, we get:
Expressing from Equation (1), the components of the stress tensor in terms of the components of the strain tensor, we obtain:
Substituting Equation (8) into Equation (9) and then into Equation (4) and taking into account the open-circuit condition we obtained for the electric field induced in the piezoelectric layer due to longitudinal deformations, we get the following expression:
where denotes the square of the electromechanical coupling coefficient. Using the definition of the MEVC in the form , we obtain the expression for the contribution to MEVC from longitudinal deformations in the form:
Along with the MEVC, which is the main ME parameter to characterize the magnetic field-to-electric field conversion efficiency, we can also use the other parameter to characterize the electric response to the magnetic field. This parameter, namely the ME sensitivity coefficient, is equal to the ratio of the magnitude of the induced electric voltage, , to the magnitude of the alternating magnetic field, i.e., . Using Equation (10), we get the following expression for the ME sensitivity coefficient (MESC):
Equations (10) and (11) make it possible to analyze the dependence of the MEVC and MESC due to longitudinal deformation on the physical parameters of the magnetostrictive and piezoelectric phases and their layer thicknesses.
4. Bending Deformations
When an asymmetric structure is placed in a magnetic field, a bending moment arises, leading to bending along axis and a bending moment , leading to bending of the structure along axis . The deformations and arising in this case are proportional to the bending moments and , respectively, and they are inversely proportional to the stiffness of the structure at bending along length and width .
When considering the bending deformations, we will assume that the bonding between the layers is ideal and, according to the Bernoulli hypothesis [21], the following relation holds for the deformations of the piezoelectric and the two magnetic layers:
where is the neutral line coordinate and is the radius of curvature of the neutral line along the i axe. The bending moment occurs in MS layers by applying magnetic field and is related to the radii of curvature by the relation:
where is the stiffness of the structure. Here, , , and are the moment of inertia of the layered sections about the neutral axis . The position of the neutral line is determined from the condition that the X-projection of the force is equal to zero.
The bending moment, the position of the neutral axis, and, as a result, the moment of inertia of the layers about the neutral axis for Type 1 and Type 2 will be different. It will result in longitudinal deformations opposite in direction, and the contributions to MEVC due to bending deformations from for the two composites will be different.
4.1. Type 1 Structure
For this type of asymmetric composite, the position of the neutral line, the bending moment, and the moments of inertia are given by the following expressions:
where for i =1 and for i =2, is the width of the sample.
As can be seen from Equations (16)–(19), the bending moment and stiffness linear depend on , but their relationship does not depend on W or L. For further calculations, we introduce the following notation, , which is a cylindrical stiffness of the structure and , .
The neutral line position depends on the relation between thicknesses of the PE layer and the first and second MS layers and can lie either in the PE layer or in the MS layers. If the neutral line is in the PE layer, then, in this case, the part of the PE that lies above the neutral line undergoes tension (compression), and the other part undergoes compression (tension). As a result, the resulting electric fields in different parts of the PE layers will have opposite directions, because of which the total electric field will decrease. If the neutral layer is in an MS layer, then the bending moments arising under the action of the magnetic field in the parts located on opposite sides of the neutral line will have opposite directions, and the net bending moment decreases. The maximum ME response will be in the case when the neutral line is located at the interface between the MS layer and the PE layer, i.e., when the neutral line coordinate is or . Using Equation (11), one can calculate the thicknesses of the layers for the maximum MEVC. Under the action of a bending moment, the structure bends, and the resulting deformations induce an electric field, which is induced in the PE layer. Using Equations (13) and (14), as well as the open circuit condition, for the electric field induced by bending deformations, we obtain the following expression:
In contrast to the case of longitudinal deformations in which the induced electric field is uniform over the thickness of the sample, the bending-deformation-induced electric field is nonuniform over the thickness of the piezoelectric. The value of MEVC , associated with the bending, is determined as follows:
where is the average value of the induced electric field strength, which for the given structure is given by:
Substituting Equation (20) into Equation (22) and integrating, we obtain the expression for the average value of the induced electric field strength. Then, using Equation (21) for the contributions to MEVC and MESC by bending deformations for the first type structure, we get the following expressions:
The values of the moments of inertia , , and are proportional to the width of the sample , so the denominators in expressions (23) and (24) do not depend on the width of the sample, and the ME conversion efficiency is determined only by the physical parameters of the three layers and their thicknesses. Equations (22) and (23) can be used to estimate the dependence of the MEVC and the MESC on the physical and geometrical parameters of the Type 1 three-layer structure.
4.2. Type 2 Structure
For the second type of structure, the position of the neutral line and the bending moment are given by the following expressions:
Using these equations and following the same procedure as for the Type 1 composite, we obtain the following expressions for the coefficients characterizing the ME interaction:
5. Results and Discussions
The net MEVC and the MESC are the sums of the contributions from longitudinal and bending deformations and are given by:
Both the longitudinal and bending contributions are proportional to the product of the piezoelectric coefficient , the piezomagnetic coefficients , and the Young’s modulus of the piezoelectric , and are inversely proportional to the permittivity . For the quasi-static case, the contributions do not depend on the width and length of the sample, but will depend on the thickness of the piezoelectric and both magnetic layers.
For longitudinal deformations in a magnetic field, the MS(−) layer experiences compression, and a layer with MS(+) experiences tension. As a result, depending on the thickness ratio of the MS layers, the PE layer can experience either compression or tension; depending on the position of the neutral layer, one part can experience tension and the other part can experience compression. For small thicknesses of the layer with positive magnetostriction, the compression force is greater than the tension force, and as a result, the contribution from longitudinal deformations to the magnitude of the ME effect is positive and decreases with increasing thickness of the second layer until the following equality occurs:
For these thicknesses of MS layers, the contribution to MEVC from longitudinal deformations is zero. With a further increase in the thickness of the second MS layer, the value of MEVClong changes sign and begins to increase, and at thicknesses tends to the limit value equal to
For the Type 1 structure, the contribution to the magnitude of the ME interaction from bending deformations for small thicknesses of the second MS layer has the opposite sign to longitudinal deformation. As the thickness of the second layer increases, its contribution begins to grow and reaches a maximum when the neutral layer lies at the interface between the layers with negative and positive magnetostriction, i.e., when
With a further increase, the value of the ME coefficient begins to decrease, since the neutral layer moves into the piezoelectric, and as a result, a part of the PE experiences tension, and another part compression, which leads to a decrease in the magnitude of the ME interaction. In the case when the neutral layer lies in the middle of the piezoelectric layer, i.e., for a given structure when the relation is satisfied, then, in this case, according to Equation (19), the contribution from bending vibrations to the magnitude of the ME interaction will be equal to zero. With a further increase, the value of MEVC due to bending begins to increase. But the analysis of the contribution with a further increase in the thickness of the second magnetostrictive layer is of no interest, since such structures cannot be used in practice.
Next, we apply the theory to representative three-layer composites with Ni, Permendur (an alloy of Fe, Co, and V), or Metglas for the ferromagnetic layer and PZT for the piezoelectric layer. Nickel has a negative longitudinal magnetostriction, whereas it is positive for Permendur and Metglas. The piezomagnetic coefficients for the ferromagnets and the piezoelectric coefficient for PZT are listed in Table 1.

Table 1.
Parameters of materials of composite structures.
The value of the piezoelectric module d31 was used from [22], and the values of the piezomagnetic modules q = dλ/dH were obtained using the data for magnetostriction curves [23,24,25] at the bias magnetic field near 50 Oe.
Figure 2 and Figure 3 show the MEVC and MESC dependences, respectively, for Type 1 composite for nickel with negative magnetostriction, PZT, and Metglas with positive magnetostriction. In Figure 2, MEVS is shown as a function of Metglas thickness for a fixed PZT and Ni thicknesses of 0.2 mm and = 0.2 mm, respectively. As can be seen from Figure 2, the net MEVC has a broad maximum in the region located beyond the region where (MEVC)long changes sign, and beyond the region where (MEVC)bend has a maximum. For the trilayer composite, the MEVC is a factor of five higher than for the Ni/PZT bilayer. With a further increase in the thickness of the second MS layer, MEVC decreases due to the decrease in the contribution from bending caused by the increase in the stiffness of the structure.
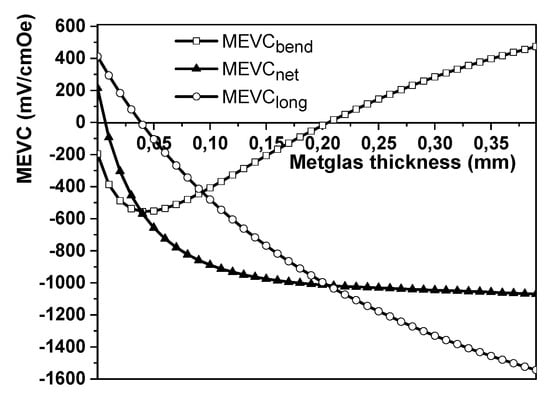
Figure 2.
Estimated dependence of MEVC in a Ni-PZT-Metglas first-type three-layered structure on the Metglas layer thickness. The PZT layer thickness , the Ni thickness
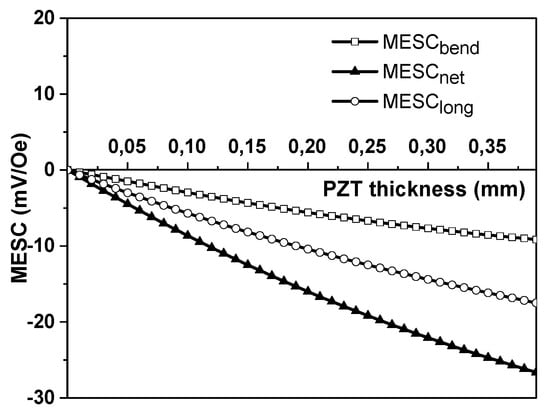
Figure 3.
Estimated dependence of MESC in a Ni-PZT-Metglas first-type three-layered structure on the PZT layer thickness. The Ni layer thickness , the Metglas thickness
Figure 3 shows the estimated variation in MESC with the thickness of the PZT layer. The Ni thickness and Metglas are assumed to be 0.2 mm. These thicknesses were chosen because they correspond to the region where the MEVC has a maximum. The MESC is zero at . The MESC caused by longitudinal deformations increases with the increase of PZT layer thickness and is predicted to attain saturation at . This saturation value of MESC equals:
The MESC due to bending deformations increases with the increase in , then it reaches a maximum value, and then slowly decreases with a further increase in the thickness of the piezoelectric layer. The net MESC first increases with an increase in and then there is a small plateau in its value, but this plateau is observed at large thickness of PZT, which is seldom used in practice.
Theoretical estimates of MEVC and MESC for the Type 2 three-layered structures of Ni-Metglas-PZT are shown in Figure 4 and Figure 5, respectively. As can be seen from Figure 4, MEVC due to longitudinal deformations is the same as for Type 1. This fact is a consequence of the assumption that the longitudinal deformations of the piezoelectric and two magnetostrictive layers are the same. The contribution to MEVC from bending for the Type 2 structure, however, is different from Type 1 structures. The (MEVC)bend value for Type 2 has high rate of increase with the thickness of the Metglas until the position of the neutral line lies into the Metglas layer. With a further increase in Metglas thickness, the rate of change in the (MEVC)bend begins to decrease and reaches a plateau. The (MESC)bend value in Figure 5 increases at first with an increase in PZT thickness, then it has plateau, and then begins to decrease.
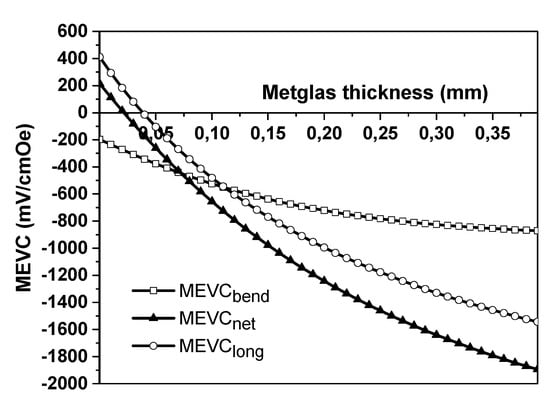
Figure 4.
Estimated dependence of MEVC in a Ni-Metglas-PZT second-type three-layered structure on the Metglas layer thickness. The PZT layer thickness , the Ni thickness
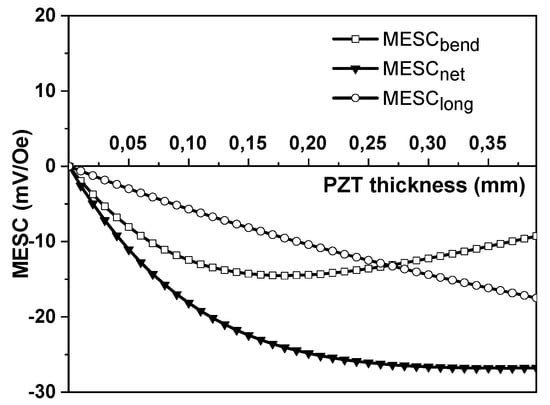
Figure 5.
Estimated dependence of MESC in a Ni-Metglas-PZT second-type three-layered structure on the PZT layer thickness. The Ni layer thickness , the Metglas thickness
Figure 6 shows estimates of MEVC as a function of Metglas thickness for both types of trilayers with Ni and PZT. Both structures are expected to have a higher maximum MEVC than the bilayer of Ni-PZT. The maximum value for the Type 1 structure is a factor higher than the value for the Ni-PZT bilayer, whereas the maximum value for MEVC is an order of magnitude higher than for the Ni-PZT bilayer.
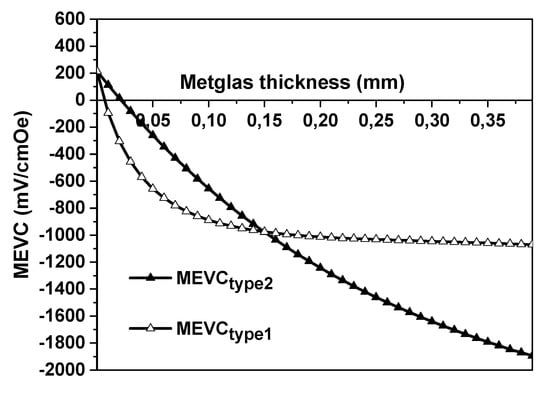
Figure 6.
Estimated dependence of MEVC in Ni-PZT-Metglas (Type 1) and Ni-Metglas-PZT (Type 2) three-layered structures on the Metglas layer thickness. The PZT layer thickness , the Ni thickness
Similar theoretical values of the ME response and sensitivity are shown in Figure 7 and Figure 8 for the Type 1 trilayer with Ni-PZT-Permendur (for positive magnetostriction). The difference between Permendur and Metglas layers is that Pe has a factor of two higher Young’s modulus value than Metglas, but Permendur has a fifteen-times smaller piezomagnetic coefficient value than Metglas. Thus, (MEVC)long~0 for the Permendur layer thickness, which is eight times higher than the Metglas thickness.
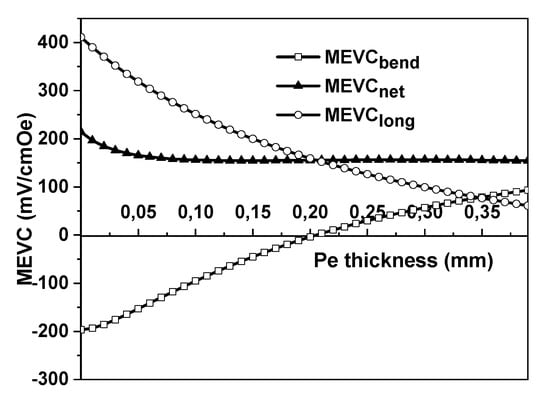
Figure 7.
Estimated dependence of MEVC in a Ni-PZT-Permendur first-type three-layered structure on the Permendur layer thickness. The PZT layer thickness , the Ni thickness
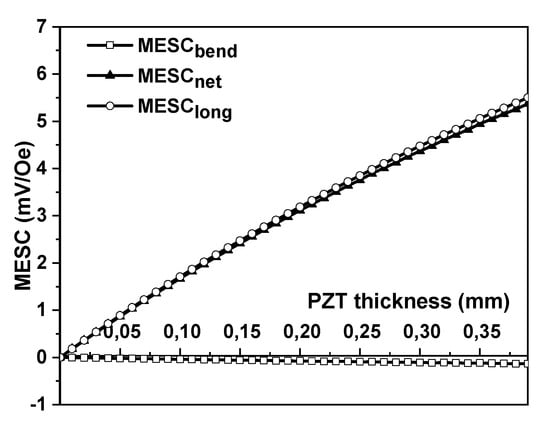
Figure 8.
Estimated dependence of MESC in a Ni-PZT-Permendur first-type three-layered structure on the PZT layer thickness. The Ni layer thickness , the Permendur thickness
Figure 9 and Figure 10 show the theoretical estimates of the dependencies of the MEVC and MESC for Type 2, Ni-Permendur-PZT, trilayer. As can be seen from Figure 7 and Figure 9, the MEVC for three-layered Ni-PZT-Pe structures has the same value as for the bilayer Ni-PZT structures; thus, using the three-layered Ni-PZT-Pe structures is impractical.
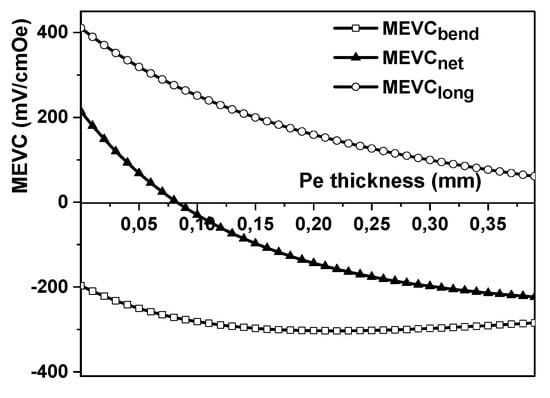
Figure 9.
Estimated dependence of MEVC in a Ni-Permendur-PZT second-type three-layered structure on the Permendur layer thickness. The PZT layer thickness , the Ni thickness
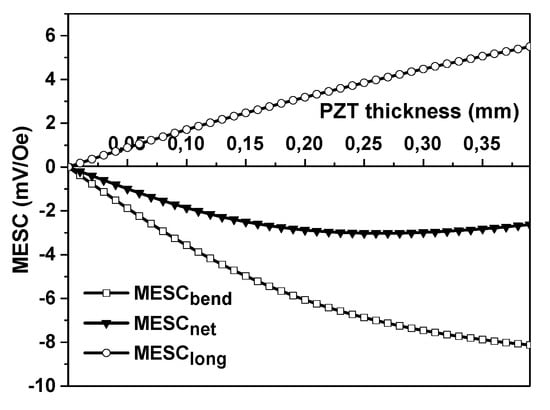
Figure 10.
Estimated dependence of MESC in a Ni-Permendur-PZT second-type three-layered structure on the PZT layer thickness. The Ni layer thickness , the Permendur thickness
Figure 11 shows the dependencies of the net MEVC as a function of Pe thickness for both the first and second types of structures. As can be seen from Figure 11, both Ni-PZT-Pe structures have the same value as for the bilayer Ni-PZT structures; thus, using the three-layered Ni-PZT-Pe structures is impractical.
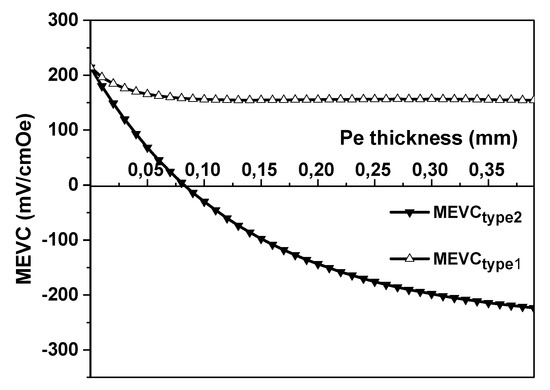
Figure 11.
Estimated dependence of MEVC in Ni-PZT-Pe first-type and Ni-Pe-PZT second-type three-layered structures on the Permendur layer thickness. The PZT layer thickness , the Ni thickness
6. Conclusions
The best ME couplings have the asymmetric three-layered Ni-Metglas-PZT structures. The ME coupling in these structures is several times more than in bilayer Ni-PZT structures. This fact is connected with the fact that both Ni and Metglas have the maximum piezomagnetic coefficient in the region bias magnetic field near 50 Oe. The three-layered Ni-Pe-PZT structures demonstrated the same ME coupling as bilayer Ni-PZT structures at a bias magnetic field near 50 Oe. This is explained by the fact that Pe has a maximum piezomagnetic coefficient at a bias magnetic field near 600 Oe, but at this magnetic field, the Ni piezomagnetic coefficient becomes very decreased; thus, using three-layered Ni-PZT-Pe structures is impractical.
The use of three-layer structures makes it possible to control the ME characteristics over a wide range.
Author Contributions
All the authors contributed to this work. Data curation, D.F., G.S., T.Z. and J.Z.; formal analysis, Y.L., P.Z., B.G. and J.L.; funding acquisition, D.F., G.S., T.Z. and J.Z.; methodology, D.F.; project administration, G.S. and T.Z.; writing—original draft, D.F. and G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded at Novgorod State University by a grant from the Russian Science Foundation Project No. 22-19-00763. Research at Oakland University was funded by the U.S. National Science Foundation (DMR-1808892, ECCS-1923732). Y.L. was supported by a fellowship from the Chinese Scholarship Council. The research at Hubei University was supported by the China Postdoctoral Science foundation (No. 2020M672315) and the Program of Hubei Key Laboratory of Ferro- & Piezoelectric Materials and Devices (No. K202013). The research at the Zhengzhou University of Light Industry was supported by a grant from the National Natural Science Foundation of China (NSFC, Grant No. 61973279).
Data Availability Statement
Data are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tu, C.; Chu, Z.-Q.; Spetzler, B.; Hayes, P.; Dong, C.-Z.; Liang, X.-F.; Chen, H.-H.; He, Y.-F.; Wei, Y.-Y.; Lisenkov, I.; et al. Mechanical-Resonance-Enhanced Thin-Film Magnetoelectric Heterostructures for Magnetometers, Mechanical Antennas, Tunable RF Inductors, and Filters. Materials 2019, 12, 2259. [Google Scholar] [CrossRef] [PubMed]
- Vopson, M.M. Fundamentals of Multiferroic Materials and Their Possible Applications. Crit. Rev. Solid State Mater. Sci. 2015, 40, 223–250. [Google Scholar] [CrossRef]
- Nan, C.W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 31101. [Google Scholar] [CrossRef]
- Zhai, J.; Xing, Z.; Dong, S.; Li, J.; Viehland, D. Magnetoelectric laminate composites: An overview. J. Am. Ceram. Soc. 2008, 91, 351–358. [Google Scholar] [CrossRef]
- Ma, J.; Hu, J.; Li, Z.; Nan, C.W. Recent progress in multiferroic magnetoelectric composites: From bulk to thin films. Adv. Mater. 2011, 23, 1062–1087. [Google Scholar] [CrossRef] [PubMed]
- Geng, D.; Yan, Y.; Priya, S.; Wang, Y. Electric Field Control of Magnetic Permeability in Co-Fired Laminate Magnetoelectric Composites: A Phase-Field Study for Voltage Tunable Inductor Applications. ACS Appl. Mater. Interfaces 2020, 12, 44981–44990. [Google Scholar] [CrossRef] [PubMed]
- Ramesh, R.; Manipatruni, S. Electric field control of magnetism. Proc. R. Soc. A 2021, 477, 20200942. [Google Scholar] [CrossRef]
- Viehland, D.; Li, J.F.; Yang, Y.; Costanzo, T.; Yourdkhani, A.; Caruntu, G.; Zhou, P.; Zhang, T.; Li, T.; Gupta, A.; et al. Tutorial: Product properties in multiferroic nanocomposites. J. Appl. Phys. 2018, 124, 61101. [Google Scholar] [CrossRef]
- Liu, H.J.; Liang, W.I.; Chu, Y.H.; Zheng, H.; Ramesh, R. Self-assembled vertical heteroepitaxial nanostructures: From growth to functionalities. MRS Commun. 2014, 4, 31–44. [Google Scholar] [CrossRef]
- Liang, X.; Chen, H.; Sun., N.X. Magnetoelectric materials and devices. APL Mater. 2021, 9, 41114. [Google Scholar] [CrossRef]
- Sun, X.; MacManus-Driscoll, J.L.; Wang, H. Spontaneous ordering of oxide-oxide epitaxial vertically aligned nanocomposite thin films. Annu. Rev. Mater. Res. 2020, 50, 229–253. [Google Scholar] [CrossRef]
- Rado, G.T. Mechanism of the Magnetoelectric Effect in an Antiferromagnet. Phys. Rev. Lett. 1961, 6, 609–610. [Google Scholar] [CrossRef]
- Avellaneda, M.; Harshe, G. Magnetoelectric effect in piezoelectric/magnetostrictive multilayer (2-2) composites. J. Intell. Mater. Syst. Struc. 1994, 5, 501. [Google Scholar] [CrossRef]
- Petrov, V.M.; Srinivasan, G.; Bichurin, M.I.; Galkina, T.A. Theory of magnetoelectric effect for bending modes in magnetostrictive-piezoelectric bilayers. J. Appl. Phys. 2009, 105, 63911. [Google Scholar] [CrossRef]
- Bichurin, M.; Sokolov, O.; Ivanov, S.; Leontiev, V.; Petrov, D.; Semenov, G.; Lobekin, V. Physics of Composites for Low-Frequency Magnetoelectric Devices. Sensors 2022, 22, 4818. [Google Scholar] [CrossRef]
- Perov, N.S.; Fetisov, L.Y.; Fetisov, Y.K. Resonant magnetoelectric interaction in asymmetric bimorphous ferromagnetic-ferroelectric structure. Tech. Phys. Lett. 2011, 37, 244. [Google Scholar] [CrossRef]
- Bi, K.; Wang, Y.G.; Pan, D.A.; Wu, W. Large magnetoelectric effect in negative magnetostrictive/piezoelectric/positive magnetostrictive laminate composites with two resonance frequencies. Scr. Mater. 2010, 63, 589–592. [Google Scholar] [CrossRef]
- Cheng, J.H.; Wang, Y.G.; Xie, D. Resonance magnetoelectric effect in Ni/Pb(Zr,Ti)O3/Terfenol-D trilayered composites with different mechanical boundary conditions. Appl. Phys. Lett. 2014, 104, 252411. [Google Scholar] [CrossRef]
- Filippov, D.A.; Galichyan, T.A.; Zhang, J.; Liu, Y.; Qi, Y.; Zhang, T.; Srinivasan, G. Magnetoelectric Effect in Three-Layer Asymmetric Structures in the Region of Bending Vibrational Modes. Phys. Solid State 2020, 62, 1338–1345. [Google Scholar] [CrossRef]
- Filippov, D.; Liu, Y.; Zhou, P.; Ge, B.; Liu, J.; Zhang, J.; Zhang, T.; Srinivasan, G. Low-Frequency Magnetoelectric Effects in Magnetostrictive–Piezoelectric Bilayers: Longitudinal and Bending Deformations. J. Compos. Sci. 2021, 5, 287. [Google Scholar] [CrossRef]
- Timoshenko, S. Strength of Materials; D. Van Nostrand Company: New York, NY, USA, 1940. [Google Scholar]
- Sreenivasulu, G.; Mandal, S.K.; Bandekar, S.; Petrov, V.M.; Srinivasan, G. Low-frequency and resonance magnetoelectric effects in piezoelectric and functionally stepped ferromagnetic layered composites. Phys. Rev. B 2011, 84, 144426. [Google Scholar] [CrossRef]
- Chashin, D.V.; Fetisov, Y.K.; Kamentsev, K.E.; Srinivasan, G. Resonance magnetoelectric interactions due to bending modes in a nickel-lead zirconate titanate bilayer. Appl. Phys. Lett. 2008, 92, 102511. [Google Scholar] [CrossRef]
- Hörner, E.; Krykanov, I.M.; Chashin, D.V.; Fetisov, Y.K.; Fetisov, L.Y.; Shamonin, M. Magnetoelectric characteristics of cobalt-iron alloy-lead zirconate titanate bilayer planar structures. Int. J. Mater. Res. 2012, 103, 1345. [Google Scholar] [CrossRef]
- Fetisov, L.Y.; Fetisov, Y.K.; Perov, N.S.; Chashin, D.V. Magnetoelectric effect in amorphous FeNiSiC ferromagnet-piezoelectric planar structures. Tech. Phys. 2011, 56, 485. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).