Abstract
Today, among emerging materials, metal matrix composites, due to their excellent properties, have an increasing demand in the field of aerospace and automotive industries. However, the difficulties associated with the processing of these composites have been a challenge to manufacturing industries due to inhomogeneous mixing of the matrix with the reinforcement, oxidation, and microstructural phase transformation during processing. Hence, in this paper, Ti-6Al-4V reinforced with SiCp has been processed through a specially developed compression molding, followed by vacuum sintering. The main objective of this paper was to determine the favorable vacuum sintering conditions for Ti-6Al-4V reinforced with 15 Wt. % SiCp composites under a different aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C /min) to improve the process output parameters such as the hardness, surface roughness, and to reduce the porosity using Taguchi’s Design of Experiments. Finally, the response surface methodology and random forest regression have been used to predict the optimum process output parameters. From the extensive experimentation and understanding gained from Taguchi’s Design of Experiments, the response surface methodology and random tree regression approach can be successfully used to predict the hardness, porosity, and surface roughness during the processing of Ti-6Al-4V-SiCp composites.
1. Introduction
In recent years, there has been a lot of demand for the replacement of novel materials with conventional metals for their application in aeronautical, automotive, and marine industries. Metal matrix composites (MMCs) are a new class of materials, having metal as a matrix and fibers or particles as a reinforcement, due to its unique properties such as its high strength to weight ratio, ductility, stiffness, and improved corrosion resistance [1,2]. However, there are challenges in the production of a few MMCs such as titanium matrix composites (TMCs) which are prone to high levels of oxidation and embrittlement [3,4,5,6]. Powder metallurgical and near net shape manufacturing routes have always been preferred for the production of TMCs owing to their advantages, such as a homogenous distribution of the reinforcement [7,8,9,10]. Powder metallurgy involves the compaction of composites followed by a sintering just below their melting points [11,12]. Researchers [13] suggested that Titanium undergoes an oxidation above 600 °C and produces brittle Titanium Oxide which decreases the desirable properties of TMCs. Researcher [14], in his research, suggested that the density, hardness, and surface roughness can be improved under a vacuum sintering. Researchers [15,16,17] concluded that under a vacuum sintering, the process input parameters such as the aging time (h), aging temperature, and heating and cooling rates has a considerable effect on the process output characteristics on TMCs. Researchers [18,19,20] suggested that the application of the Design of Experiments is one statistical tool applied in the processing and machining of various metals/alloys and composite materials to obtain the optimum process output parameters. Researchers [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] suggested that Taguchi’s Design of Experiments (TDOE) is one of the most effective methods for obtaining an optimum value with a minimal set of experiments. Researchers [38,39] applied an analysis of variance (ANOVA) to obtain the percentage contribution of each of the input parameters selected. Researchers [40,41] concluded that response surface methodology (RSM) is a mathematical and statistical method which optimizes the response by evaluating the effects of various factors and their interaction on the response variables. Researchers [42,43] suggested that machine learning is a computational model designed to predict the output variables for a given set of input variables. Random forest regression (RFR) is one of the machine learning techniques which uses ensemble learning methods for the regression. Ensemble learning methods combine the predictions from multiple machine learning algorithms and can make a more accurate prediction than a single model [44]. Studies on problem solving by developing machine learning-based prediction models suggested that random forest algorithms performed better than other algorithms in the utilization of machining data [45,46,47,48,49,50,51,52]. This paper focuses on determining the favorable vacuum sintering conditions for Ti-6Al-4V reinforced with 15 Wt. % SiCp composites under a different aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min) to improve the process output parameters such as the hardness and surface roughness, and to reduce the porosity using Taguchi’s Design of Experiments. Finally, response surface methodology and random forest regression have been used to predict the optimum process output parameters.
2. Methodology
A titanium alloy (Ti-6Al-4V) as a matrix reinforced with 15 Wt. % of Silicon Carbide (SiC) and with a particle size of 100 µm has been used in this experimentation. Figure 1 shows the flowchart of the titanium silicon carbide composite processing technique used in this study. The chemical composition, mechanical, and thermal properties of the titanium alloy and silicon carbide are shown in Table 1, Table 2, Table 3 and Table 4. Titanium silicon carbide composites have been processed using specially developed single action split die assembled in a compaction molding machine. The die is made of D3 die steel and is in accordance with ASTM 925-15 [48]. The processed titanium silicon carbide composites are then pre sintered at 5000C in a muffle furnace followed by vacuum sintered using an RHTC 80–710/15 HTV sintering machine under a different aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min). The samples have been mechanically characterized to obtain the optimum hardness value using a Brinell Hardness Testing machine (Model: Analog B 3000 (H)) in accordance with EN ISO 6506-1 standards with an indentation load of 10kgfand allowing a dwell time of 20 s for the indentation using a stainless steel ball of a 10mm diameter. The surface roughness was measured using a ‘Talysurfsurtonic 3+ surface roughness measuring instrument’ and the porosity was measured using a Gas PORG-200 porosimeter. Three sets of measurements for each sample were taken. The average values of the hardness, porosity, and surface roughness of each sample is noted down. Taguchi’s L27 orthogonal array has been used to obtain the optimum process input parameters. Response surface methodology is used to predict the process output parameters this experiment uses as a second order of equation. The microstructure of the samples have been taken from an Olympic System Optical Microscope with a 100 times magnification. The samples have been polished using a bench grinder and etched using Kroll’s Reagent, (i.e., 1–3 mL of hydrofluoric acid with 2–6 mL of nitric acid in 100 mL of water).

Figure 1.
Flowchart of titanium silicon carbide composite processing.

Table 1.
Chemical composition (Wt. %) of titanium alloy (Ti-6Al-4V).

Table 2.
Chemical composition (Wt. %) of silicon carbide (SiC).

Table 3.
Mechanical and thermal properties of titanium alloy (Ti-6Al-4V).

Table 4.
Mechanical and thermal properties of silicon carbide (SiC).
3. Design of Experiments
Taguchi’s Design of Experiments is an effective tool used to study the effect of one or more of the process response variables. Further, it is also an efficient procedure used by various researchers for planning experiments and for the yield of objective conclusions, as well as for the possible interactions between the process parameters selected.
3.1. Taguchi’s Design of Experiments
Taguchi’s Design of Experiments has been used widely in engineering applications to achieve the best levels of a quality characteristic under different conditions. Taguchi’s approach to the design of experiments is easy to adopt and apply for users with a limited knowledge of statistics which resulted in a wide popularity in the area of engineering and the scientific community. In this experimental layout, the S/N ratio characteristic, the smaller the better for the porosity and surface roughness and the larger the better for the hardness, has been adopted as given in Equations (1) and (2).
The smaller the best characteristic:
Larger the better characteristic [26]:
where n is the number of observations and y is the observed data. In this paper, a Taguchi L27 orthogonal array is employed to identify the optimal vacuum sintering process parameters. The levels and factors used for the vacuum sintering (TDOE) are shown in Table 5.

Table 5.
Control factors and levels for vacuum sintering (TDOE).
3.2. Response Surface Methodology
During the processing of metal matrix composites, the hardness, porosity, and surface roughness has been the important process output parameter when subjected to various engineering applications due to the fact that these parameters certainly affect the wear resistance, fatigue resistance, and corrosive resistance. Hence, to understand the quality characteristics in advance, the response surface methodology has become a more popular tool to understand the process output parameters in any experimental domain using a second order model [36].
The β coefficients, used in the above model, can be calculated by the means of using the least square method. The second-order model is normally used when the response function is not known or nonlinear. The central composite design (CCD) of RSM is used for establishing the empirical relationships among the process parameters. The levels and factors used for the vacuum sintering (RSM) are shown in Table 6.

Table 6.
Control factors and levels for vacuum sintering (RSM).
3.3. Random Forest Regression
Random forest regression is a non-parametric method derived from the classification and regression trees. It is a combination of tree predictors where each tree depends on the values of random vectors sampled independently, with the same distribution for all trees in the forest. The experimental results based on L27 TDOE for the hardness, porosity, and surface roughness of Ti-6Al-4V reinforced with 15 Wt. % SiC used as the input parameters were trained on the random forest model. Table 7 shows the algorithm used for random forest model in this paper.

Table 7.
Algorithm for random forest regression.
Steps followed for RFR:
- Step 1: The loading of the data sets.
- Step 2: The selection of the preprocessor.
- Step 3: Classifying the data sets for training and testing.
- Step 4: Training the model using the datasets.
- Step 5: Loading the test data set for a comparison.
- Step 6: Evaluating the prediction performance based on the accuracy and precision.
The performance of the model has been evaluated using the coefficient of determination (R2) as shown in the below equation [33].
where n was the total number of datasets, yref were reference values in the dataset, and Ypred were the predicted values of the models.
4. Results and Discussions
During the processing of Ti-6Al-4V-15 Wt. % SiC, the hardness, porosity, and surface roughness have been the most effective way of understanding the mechanical characteristics. Hence, in this section, the effect of the process input parameters such as the aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min) on the process output parameters such as the hardness (BHN), porosity (%), and surface roughness (µm) using the TDOE, RSM, and RFR has been discussed in this section.
4.1. Hardness
A study on the hardness during the processing of Ti-6Al-4V-SiCp composites is the most effective way of understanding the material characteristics because it certainly affects the wear resistance properties. Figure 2 shows the comparison of the hardness under a different aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min). From Figure 2, it is observed that the hardness value increased at an aging temperature of 1250 °C, compared to a 1050 °C and 1150 °C aging temperature. This is because a 1250 °C aging temperature resulted in microstructural changes, causing an increase in the surface hardness of the composite. A further aging time of 3 h enabled a proper adhesion of Ti-6Al-4V and SiCp to increase the hardness value. The heating rates during the processing of the Ti-6Al-4V-SiCp composites showed no much difference on the hardness. However, as the cooling rates increased, there was a significant increase in the hardness value. This is because faster cooling rates resulted in the formation of brittle carbide with the Ti-6Al-4V alloy followed by work hardening.
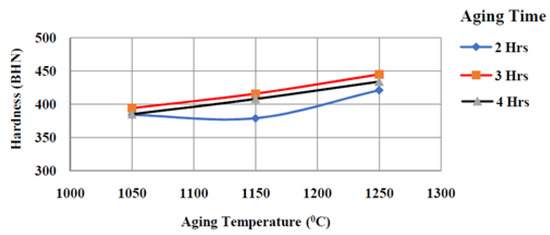
Figure 2.
Age temperature v/s hardness (BHN) at heating rate of 15 °C/min and cooling rate of 5 °C/min (constant).
The main effects plot for the hardness (Figure 3) indicates the selection of the aging temperature (1250 °C), aging time (3 h), heating rate (5 °C/min), and cooling rate (5 °C/min) results in the best combination to get the higher hardness value during the processing of the Ti-6Al-4V-SiCp composites.
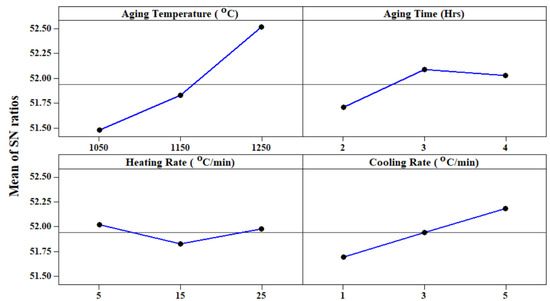
Figure 3.
Mean effect plot for hardness (BHN).
The aging temperature (A), along with cooling rate (D), is a significant factor to be taken into consideration while processing the Ti-6Al-4V-SiCp composites, as shown by the analysis of the percentage of contribution (P percent) of the various factors (Table 5) for the hardness. It can be seen that the interactions of the aging temperature with the cooling rate (A × D) (P = 47.8%), and the interactions of the heating rate with the cooling rate (C × D), (P = 48.54%) have a statistical and physical significance on hardness. The interactions of the aging time with the cooling rate (B × D) “neither provide a statistical significance, nor a percentage of physical significance of contribution” to the hardness.
The result of the ANOVA for the response function of the hardness is presented in Table 8. This analysis is carried out for a “level of significance of 5%, i.e., for a level of confidence of 95%”. From the analysis in Table 9, it is evident that the F-calculated value is greater than the F-table value (F0.05,14,14 = 13.63), and hence the developed second order response function is quite adequate.

Table 8.
Analysis of variance for SN ratios.

Table 9.
Analysis of variance for hardness (BHN).
The second order response of the surface representing the hardness (BHN) can be expressed as a function of the processing parameters, such as the aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min), as shown in Equation (5).
Hardness(BHN) = 404.715 + 22.035A + 0.200B + 1.914C + 7.449D + 2.526A2 − 14.474B2 + 6.531C2 − 0.053D2 + 1.016AB + 4.578AC − 0.633AD + 0.605BC + 2.033BD + 0.580CD
To predict and verify the hardness during the processing of the Ti-6Al-4V-SiCp composites, the verification tests are used. Figure 4 shows the experimental results along with the results of the mathematical model and the random forest regression for the hardness. The comparison of the experimental results with the mathematical model and RFR model results obtained for 27 trials shows that the estimated value is accurate for all tests with an error of 1.106% with the RSM and 8.981% with the RFR estimated values, respectively. Figure 5 represents a scatter plot for the hardness values of the Ti-6Al-4V-SiCp composites.
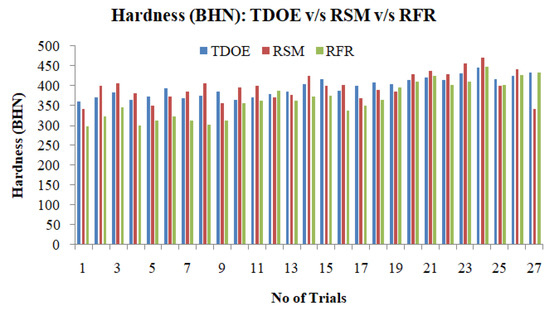
Figure 4.
Verification test results for hardness.
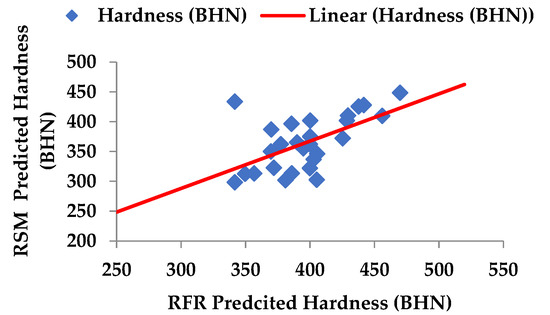
Figure 5.
Scatter plot for hardness (RSM v/s RFR).
4.2. Porosity
A study on the porosity during the processing of the Ti-6Al-4V-SiCp composites is one of the effective ways of understanding the material characteristics. Figure 6 shows the comparison of the porosity under a different aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min). From Figure 6, it is observed that the porosity decreases as the aging temperature is at 1050 °C, compared to 1150 °C and 1250 °C aging temperatures. This is because 15 Wt. % SiC resulted in an increase in the density and a decrease in the porosity. Further, the addition of a PVA binder of 3 Wt. % enabled in the proper adhesion of Ti-6Al-4V and SiCp to increase the hardness value. The compaction pressure during the processing of the Ti-6Al-4V-SiCp composites showed no much difference on the hardness. However, at the compaction pressure of 4 ton/sq.inch, there was a small increase in the hardness value. This is because the compaction pressure resulted in an interlocking of the SiC particles with the Ti-6Al-4V alloy followed by a strain hardening.
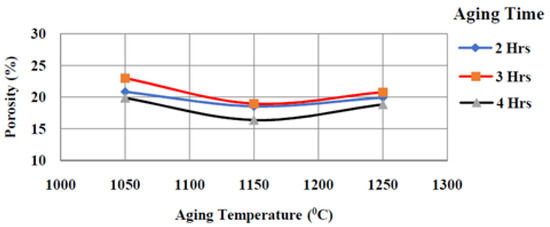
Figure 6.
Age Temperature v/s porosity (%). At heating rate of 25 °C/min and cooling rate of 5 °C/min (constant).
The main effects plot for the porosity (Figure 7), indicates that the selection of the aging temperature (1050 °C), aging time (3 h), heating rate (15 °C/min), and cooling rate (1 °C/min) result in the best combination to get the lower porosity values during the processing of the Ti-6Al-4V-SiCp composites.
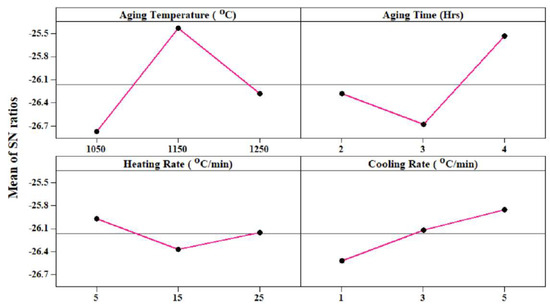
Figure 7.
Mean effect plot for porosity (%).
The aging temperature (A) along with the cooling rate (D) is a significant factor to be taken into consideration while processing the Ti-6Al-4V-SiCp composites, as shown by the analysis of the percentage of contribution (P percent) of the various factors (Table 10) for the porosity. It can be seen that the interactions of the aging temperature with the cooling rate (A × D) (P = 34.72%), interactions of the heating rate with the cooling rate (C × D), (P = 42.1%), along with interactions of the aging time with the cooling rate (B × D), (P = 22.96 have a statistical and physical significance on the porosity.

Table 10.
Analysis of variance for SN ratios.
The second order response surface representing the porosity (%) can be expressed as a function of the processing parameters such as the aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min), as shown in Equation (6).
Porosity (%) = 18.5123 − 0.5611A − 0.8271B + 0.0524C − 0.6652D + 0.5822A2 + 0.0732B2 + 0.8017C2 + 0.1782D2 + 0.1597AB − 0.0465AC − 0.0677AD + 0.2167BC − 0.0118BD + 0.2807CD
The result of the ANOVA for the response function of the hardness is presented in Table 11. This analysis is carried out for a “level of significance of 5%, i.e., for a level of confidence of 95%”. From the analysis in Table 11, it is evident that the F-calculated value is greater than the F-table value (F0.05,14,14 = 10.00), and hence the developed second order response function is quite adequate.

Table 11.
Analysis of variance for Porosity (%).
Figure 8 shows the microstructure of the compacted and vacuum sintered Ti-6Al-4V-SiCp composites under different processing conditions. From the microstructural observation, it was observed that the composites processed under the aging temperature (1050 °C) had a more void formation compared to the composites processed under the aging temperature (1150 °C) and (1250 °C), respectively. Further, aging at 1250 °C resulted in the formation of α-phase, which caused a decrease in the porosity values compared to the aging temperature at 1150 °C. It was also observed that an increase in the SiCp resulted in a crack formation due to a decrease in the bond strength and interlocking between the matrix and reinforcement particle.

Figure 8.
Porosity at different aging temperatures (a) 1050 °C, (b) 1150 °C, (c) and 1250 °C ataging time (4 h), heating rate (25 °C/min), cooling rate (5 °C/min); constant.
To predict and verify the porosity during the processing of the Ti-6Al-4V-SiCp composites, verification tests are used. Figure 9 shows the experimental results along with the results of the mathematical model and random forest regression for the porosity. A comparison of the experimental results with mathematical model and RFR model results obtained for the 27 trials shows that the estimated value is accurate for all tests with an error of 2.76% with an RSM and 1.3% with the RFR estimated values, respectively. Figure 10 represents a scatter plot for the porosity values of the Ti-6Al-4V-SiCp composites.
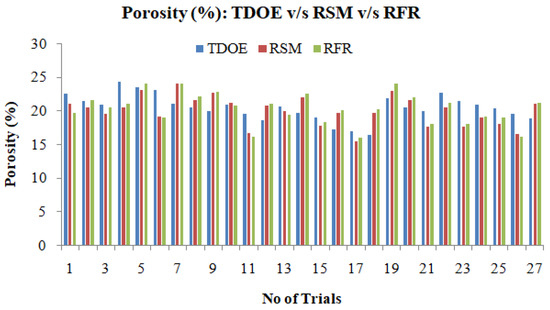
Figure 9.
Verification test results for hardness.
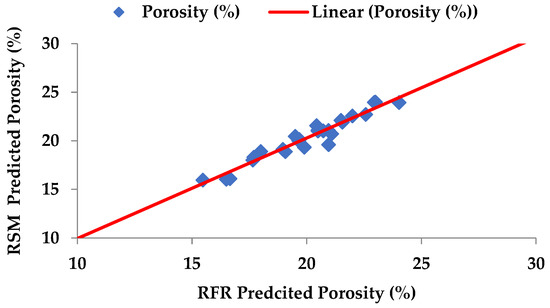
Figure 10.
Scatter plot for porosity (RSM v/s RFR).
4.3. Surface Roughness
A study on the surface roughness during the processing of the Ti-6Al-4V-SiCp composites is one of the effective ways of understanding the material characteristics. Figure 11 shows the comparison of the surface roughness under a different aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min). From Figure 11, it is observed that at an aging temperature of 1150 °C and an aging time of 4 h resulted in an improved surface roughness value (5.78 µm). This is because an aging temperature of 1150 °C and a 4 h aging time resulted in a better bonding and a decrease in the porosity between the Ti-6Al-4V and SiC particles.
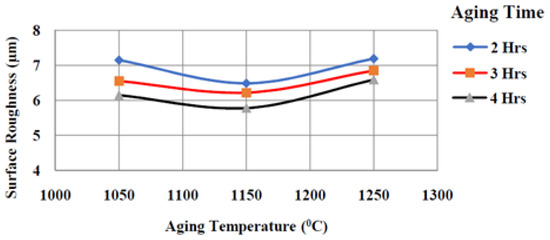
Figure 11.
Age temperature v/s surface roughness (µm). At heating rate of 25 °C/min and cooling rate of 1 °C/min (constant).
The main effects plot for the surface roughness (Figure 12) indicates the selection of the aging temperature (1250 °C), aging time (2 h), heating rate (15 °C/min), and cooling rate (5 °C/min) result in the best combination to get the lower surface roughness values during the processing of the Ti-6Al-4V-SiCp composites.
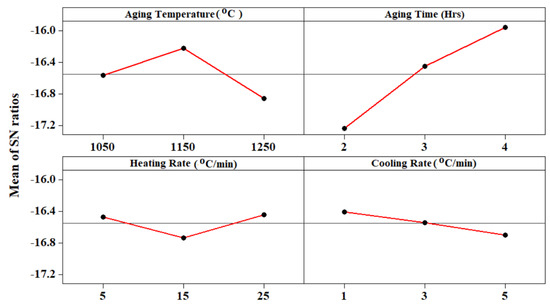
Figure 12.
Mean effect plot for Surface Roughness (µm).
The aging temperature (A), heating rate (C), and cooling rate (D) are significant factors to be taken into consideration while processing the Ti-6Al-4V-SiCp composites, as shown by the analysis of the percentage of contribution (P percent) of the various factors (Table 12) for the surface roughness. It can be seen that the interactions of the aging temperature with the cooling rate (A × D) (P = 29.59%), the interactions f the heating rate with the cooling rate (C × D), (P = 29.65%), along with the interactions of the aging time with the cooling rate (B × D), (P = 29.62 have a statistical and physical significance on the surface roughness.

Table 12.
Analysis of variance for SN ratios.
From the analysis in Table 13, it is evident that the F-calculated value is greater than the F-table value (F0.05,14,14 = 3.53), and hence the developed second order response function is quite adequate. The second order response surface representing the surface roughness (%) can be expressed as a function of the processing parameters such as the aging temperature (°C), aging time (h), heating rate (°C/min), and cooling rate (°C/min), as shown in Equation (7).
Surface Roughness (µm) = 6.12867 + 0.26917A − 0.41122B + 0.12733C − 0.00344D + 0.81829A2 + 0.01679B2 + 0.20799C2 + 0.03279D2 − 0.17588AB − 0.14200AC + 0.14562AD + 0.02013BC − 0.13350BD + 0.09413CD

Table 13.
Analysis of variance for surface roughness (µm).
Figure 13 shows the microstructure of the compacted and vacuum sintered Ti-6Al-4V-SiCp composites under different processing conditions.


Figure 13.
Surface roughness at different aging temperatures: (a) 1050 °C, (b) 1150 °C, (c) 1250 °C; at aging time (4 h), heating rate (25 °C/min), and cooling rate (1 °C/min); constant.
From the microstructural observation, it was observed that the composites processed under the aging temperature (1050 °C) had a more void formation compared to the composites processed under the aging temperature (1150 °C) and (1250 °C), respectively. Further, aging at 1250 °C resulted in the formation of the α-phase, which caused a decrease in the porosity values compared to an aging temperature at 1150 °C. It was also observed that an increase in the SiCp resulted in a crack formation due to a decrease in the bond strength and interlocking between the matrix and reinforcement particle.
To predict and verify the surface roughness during the processing of the Ti-6Al-4V-SiCp composites, verification tests are used. Figure 14 shows the experimental results along with the results of the mathematical model and random forest regression for the surface roughness. A comparison of the experimental results with the mathematical model and RFR model results obtained for the 27 trials shows that the estimated value is accurate for all tests with an error of 1.56% with the RSM and 2.75% with the RFR estimated values, respectively. Figure 15 represents the scatter plot of the surface roughness values of the Ti-6Al-4V-SiCp composites.
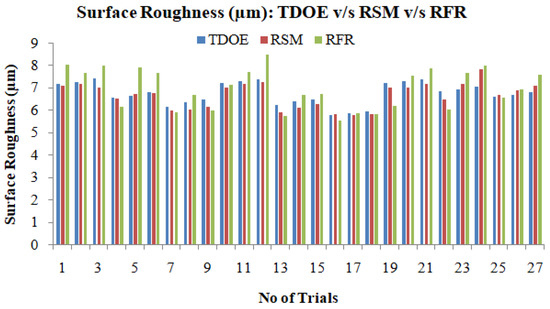
Figure 14.
Verification test results for surface roughness.
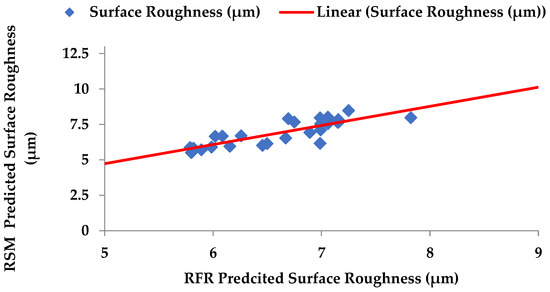
Figure 15.
Scatter plot for surface roughness (RSM v/s RFR).
5. Conclusions
The hardness, porosity, and surface roughness of the Ti-6Al-4V-SiCp composites under different processing using Taguchi’s Design of Experiments, the response surface methodology, and random forest regression have been studied. Based on the results, the following conclusions are drawn:
The aging temperature (1250 °C), aging time (3 h), heating rate (15 °C/min), and cooling rate (5 °C/min) are considered to be the optimum input parameters for achieving higher hardness values during the processing of the Ti-6Al-4V-SiCp composites. For achieving lesser porosity values during the processing of the Ti-6Al-4V-SiCp composites, the aging temperature (1050 °C), aging time (3 h), heating rate (15 °C/min), and cooling rate (1 °C/min) are preferred. Improved surface roughness values can be achieved under an aging temperature of 1250 °C, aging time of 2 h, heating rate of15 °C/min, and cooling rate of 5 °C/min during the processing of the Ti-6Al-4V-SiCp composites.
A second order response surface model generated for the hardness, porosity, and surface roughness can be effectively used during the processing of the Ti-6Al-4V-SiCp composites.
Further, from the microstructural analysis it was observed that an aging temperature at 1250 °C and rapidly cooling at 5 °C/min resulted in α-phase formation, which caused an increase in the hardness values compared to the other set of input process parameters.
From the comparison of the experimental results with the mathematical model and RFR model results for the 27 trials, it was observed that the estimated value is accurate for all tests with an error of 1.106%,2.76%, and 1.3% with the RSM and 8.981%, 1.56%, and 2.75% with the RFR estimated values for the hardness, porosity, and surface roughness, respectively.
Author Contributions
Conceptualization, A.L.H. and R.S.; methodology, A.L.H. and R.S.; software, A.L.H. and R.S.; validation, A.L.H., R.S., N.N., D.S.C. and M.N.; formal analysis, A.L.H. and R.S.; investigation, A.L.H. and R.S.; resources, A.L.H. and R.S.; data curation, A.L.H. and R.S.; writing—original draft preparation, A.L.H. and R.S.; writing—review and editing, A.L.H. and R.S.; visualization, A.L.H. and R.S.; supervision, R.S.; project administration, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon request.
Acknowledgments
Authors would like to acknowledge Central Research Facility, National Institute of Technology, Surathkal, Karnataka, 575025, India for providing the RHTC 80–710/15 vacuum sintering equipment, as mentioned in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Purazrang, K.; Kainer, K.U.; Mordike, B.L. Fracture toughness behavior of a magnesium alloy metal-matrix composite produced by the infiltration technique. Composites 2011, 22, 456–462. [Google Scholar] [CrossRef]
- Tzamtzis, S.; Barekar, N.S.; Hari Babu, N.; Patel, J.; Dhindaw, B.K.; Fan, Z. Processing of advanced Al/SiC particulate metal matrix composites under intensive shearing—A novel rheo-process. Compos. Part A Appl. Sci. Manuf. 2009, 40, 144–151. [Google Scholar] [CrossRef]
- Miracle, D.B. Metal matrix composites—From science to technological significance. Compos. Sci. Technol. 2005, 65, 2526–2540. [Google Scholar] [CrossRef]
- Ragunath, A.S. Review on particulate-reinforced titanium matrix composites. Mater. Sci. 1997, 32, 1–16. [Google Scholar]
- Poletti, C.; Merstallinger, A.; Schubert, T.; Marketz, W.; Degischer, H.p. Wear and Friction Coefficient of Particle Reinforced Ti-Alloys. Mater. Wiss. Werkst. 2009, 35, 741–749. [Google Scholar] [CrossRef]
- Peters, M.; Leyens, C. Titan und Titanlegierungen Weinheim; Wiley VCH: Weinheim, Germany, 2002. [Google Scholar]
- Godfrey, T.; Goodwin, P.s.; Ward, C.M. Titanium’99. In Proceedings of the Ninth World Conference of Titanium, Saint-Petersburg, Russia, 7–11 June 1999; pp. 1868–1877. [Google Scholar]
- Djanarthany, S.; Viala, J.; Bouix, J. Development of SiC/TiAl composites: Processing and interfacial phenomena. Mater. Sci. Eng. A 2001, 300, 211–218. [Google Scholar] [CrossRef]
- Tabrizi, S.G.; Babakhani, A.; Sajjadi, S.A.; Lü, W.-j. Microstructural aspects of in-situ TiB reinforced Ti–6Al–4V composite processed by spark plasma sintering. Trans. Nonferrous Met. Soc. China 2015, 25, 1353–1714. [Google Scholar]
- Kimi, Y.; Choim, J.; Kimy, J.; Lee, Y.Z. Friction and wear behavior of titanium matrix (TiB+TiC) composites. Wear 2011, 271, 1962–1965. [Google Scholar] [CrossRef]
- Oh, J.C.; Yun, E.; Golkovski, M.G.; Lee, S. Improvement of hardness and wear resistance in SiC/Ti–6Al–4V surface composites fabricated by high-energy electron beam irradiation. Mater. Sci. Eng. A 2003, 351, 98–108. [Google Scholar] [CrossRef]
- Abderrazak, H.; Abdellaoui, M. Synthesis and characterization of nano structured silicon carbide. Mater. Lett. 2008, 62, 3839–3841. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Huang, L.J.; Liu, B.X.; Geng, L. Hot deformation behavior of in-situ TiBw/Ti6Al4V composite with novel network reinforcement distribution. Trans. Nonferrous Met. Soc. China 2012, 22, 465–471. [Google Scholar] [CrossRef]
- Recep, C.; Muharrem, P. The effect of reinforcement volume ratio on porosity and thermal conductivity in Al–MgO composites. Mater. Res. 2012, 15, 1057–1063. [Google Scholar]
- Kok, M. Production of Metal Matrix (Al2O3-Reinforced) Composite Materials and Investigation of Their Machinability by Ceramic Tools; Firat University: Elazıg, Turkey, 2000. [Google Scholar]
- Ghosh, P.K.; Ray, S. Influence of process parameters on the porosity content in Mg–alumina cast particulate composite produced by vortex method. Trans. Am. Foundry Soc. 1988, 214, 775–782. [Google Scholar]
- Montealegre, M.; Neubauere, A.; Torralba, J.M. Influence of nano-reinforcements on the mechanical properties and microstructure of titanium matrix composites. Compos. Sci. Technol. 2011, 71, 1154–1162. [Google Scholar] [CrossRef]
- Dinesh, K.K.; Geeta, A.; Rajesh, P. Properties and characterization of Al–Al2O3 composites processed by casting and powder metallurgy routes (Review). Int. J. Latest Trends Eng. Technol. 2013, 2, 486–496. [Google Scholar]
- Oh, J.M.; Heo, K.H.; Kim, W.B.; Choi, G.S.; Lim, J.W. Sintering properties of Ti6Al4V alloys prepared using Ti/TiH2 powders. Mater. Trans. 2013, 54, 119–121. [Google Scholar] [CrossRef]
- Naranje, V.; Sankar, A.R.; Salunke, S.; Bachchhav, B.D. Experimental Evaluation of Mechanical properties of Epoxy based composite material using Taguchi Method. In Advances in Manufacturing Processes; Springer: Singapore, 2021; pp. 381–395. [Google Scholar]
- Chauhan, V.; Karki, T.; Varis, J. Optimization of Compression Molding Process Parameters for NFPC manufacturing using Taguchi’s Design of Experiment and Modlflow Analysis. Processes 2021, 9, 1853. [Google Scholar] [CrossRef]
- Shetty, R.; Hegde, A. Taguchi based fuzzy logic model for optimization and prediction of surface roughness during AWJM of DRCUFP composites. Manuf. Rev. 2022, 9, 2. [Google Scholar]
- Karthik, S.R.; Londe, N.; Shetty, R.; Nayak, R.; Hegde, A. Optimization and prediction of hardness, wear and surface roughness on age hardened Stellite 6 alloys. Manuf. Rev. 2022, 9, 10. [Google Scholar]
- Fuseini, M.; Zaghloul, M.M.Y. Qualtitative and Statstical Approaches of the electrophoretic deposition kinetics of polyaniline copper coating. Prog. Org. Coat. 2020, 171, 107015. [Google Scholar] [CrossRef]
- Zaghloul, M.M.Y.; Mai, M.Y.Z. Experimental and modeling analysis of mechanical-electrical behaviors of polypropylene composites filled with graphite and MWCNT fillers. Mater. Prop. 2007, 63, 467–474. [Google Scholar] [CrossRef]
- Zaghloul, M.M.Y.; Mai, M.Y.Z. Developments in polyester composite materials—An in depth revuew on natural fibers and nano fillers. Compos. Struct. 2021, 278, 114698. [Google Scholar] [CrossRef]
- Zaghloul, M.M.Y.; Yasser, S.M.; El-Gamal, H. Fatigue and tensile behaviors of fiber-reinforced thermosetting composites embedded with nano-particles. J. Compos. Mater. 2018, 53, 709–718. [Google Scholar] [CrossRef]
- Zaghloul, M.M.Y.; Mai, M.Y.Z. Influence of flame retardant magnesium hydroxide on the mechanical properties of high density polyethylene composites. J. Reinf. Plast. Compos. 2017, 36, 1802–1816. [Google Scholar] [CrossRef]
- Zaghloul, M.M.Y. Mechanical Properties of linear low-density polyethylene fire-retarded with melamine polyphosphate. J. Appl. Polym. Sci. 2018, 135, 46770. [Google Scholar] [CrossRef]
- Prathviraj, N.; Udupa, S. Ad-hoc Network Experimental Design with Taguchi Method to Analyze Performance of Routing Protocols. Eng. Sci. 2022, 19, 83–88. [Google Scholar]
- Shahabaz, S.M.; Sharma, S.; Shetty, N.; Shetty, S.D.; Gowrishankar, M.C. Influence of temperature on mechanical properties and machining of fibre reinforced polymer composites: A review. Eng. Sci. 2021, 16, 26–46. [Google Scholar] [CrossRef]
- Kowshik, S.; Sharma, S.; Rao, U.S.; Shettar, M.; Hiremath, P.; Upadhyaya, A. Investigation on the Effects of Uncarbonised, Carbonised and Hybrid Eggshell Filler Addition on the Mechanical Properties of Glass Fibre/Polyester Composites. Eng. Sci. 2022, 18, 121–131. [Google Scholar] [CrossRef]
- Kamath, G.B.; Subramaniam, K.; Devesh, S.; Chavan, V.; Mohan, N.; Bhat, R.; Wijerathne, H.T. Multi-Response Optimization of Milling Process Parameters for Aluminium-Titanium Diboride Metal Matrix Composite Machining Using Taguchi-Data Envelopment Analysis Ranking Approach. Eng. Sci. 2022, 18, 271–277. [Google Scholar] [CrossRef]
- Shetty, R.; Pai, R.B.; Rao, S.S.; Nayak, R. Taguchi’s technique in machining of metal matrix composites. J. Braz. Soc. Mech. Sci. Eng. 2009, 31, 12–20. [Google Scholar] [CrossRef]
- Shetty, R.; Pai, R.; Rao, S.S. Experimental studies on Turning of Discontinuously Reinforced Aluminium Composites under Dry, Oil Water Emulsion and Steam Lubricated Conditions using Taguchi’s Technique. Gazi Univ. J. Sci. 2009, 22, 21–32. [Google Scholar]
- Shetty, R.; Barboza, B.V.A.; Nayak, R. Mechanical and Machinability study on discontinuously reinforced sisal fibre polyester composite laminates. Mater. Res. Express 2019, 6, 105370. [Google Scholar] [CrossRef]
- Shetty, R.; Pai, R.; Barboza, A.B.V.; Gandhi, V.P. Processing, mechanical characterization and its tribological study of discontinuously reinforced Caryota Urens Fibre Polyester composites. ARPN J. Eng. Appl. Sci. 2018, 13, 12. [Google Scholar]
- Elmushyakhi, A. Parametric characterization of nano-hybrid wood polymer composites using ANOVA and regression analysis. Structures 2021, 29, 652–662. [Google Scholar] [CrossRef]
- Bhushan, R.K. Minimising tool wear by optimization (ANOVA) of cutting parameters in machining of 7075Al Alloy SiC particle composite. Aust. J. Mech. Eng. 2021, 1–19. [Google Scholar] [CrossRef]
- Shetty, A.A.; Shetty, R.; Hegde, N.T.; Vaz, A.C.; Srinivasan, C.R. A study on the effect of Radiometric Variations on a Fuzzy Stereo Matching Algorithm: A Statistical Analysis. Eng. Sci. 2021, 16, 269–280. [Google Scholar] [CrossRef]
- Rochardjo, H.S.; Budiyantoro, C. Manufacturing and analysis of overmolded hybrid fiber polyamide 6 composite. Polymers 2021, 13, 3820. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pavlov, Y.L. Random Forests; Taylor & Francis Group: Boca Raton, FL, USA, 2009; pp. 1–122. [Google Scholar] [CrossRef]
- Wu, M.; Liu, L.; Han, Y. Material genetic engineering—Material design, simulation and top-level design of database. Mod. Sci. 2018, 10, 53–58. [Google Scholar]
- Kazi, M.K.; Eljack, F.; Mahdi, E. Optimal filler content for cotton fiber/PP composite based on mechanical properties using artificial neural network. Compos. Struct. 2020, 251, 112654. [Google Scholar] [CrossRef]
- Jiang, H.; Xiao, Y.; Li, J.; Liu, X. Prediction of the melt index based on the relevance vector machine withmodified particle swarm optimization. Chem. Eng. Technol. 2012, 35, 819–826. [Google Scholar] [CrossRef]
- Huang, J.S.; Liew, J.X.; Liew, K.M. Data-driven machine learning approach for exploring and assessing mechanical properties of carbon nanotube-reinforced cement composites. Compos. Struct. 2021, 267, 113917. [Google Scholar] [CrossRef]
- Lu, H.; Behbahani, S.; Ma, X.; Iseley, T. A multi-objective optimizer-based model for predicting composite material properties. Constr. Build. Mater. 2021, 284, 122746. [Google Scholar] [CrossRef]
- Daghigh, V.; Lacy, T.E.; Daghigh, H.; Gud, G.; Baghaeie, K.T.; Horstemeyerf, M.F.; Pittman, C.U., Jr. Heat deflection temperatures of bio-nano-composites using experiments and machine learning predictions. Mater. Today Commun. 2020, 22, 100789. [Google Scholar] [CrossRef]
- Ganesh, C.J.; Vijay, G.S.; Bekinal, S.I. Modelling of Interior Permanent Magnet Motor and Optimization of Its Torque Ripple and Cogging Torque Based on Design of Experiments and Artificial Neural Networks. Eng. Sci. 2022, 18, 193–203. [Google Scholar]
- Wu, Y.; Chen, E.; Weng, X.; He, Z.; Chang, G.; Pan, X.; Liu, J.; Huang, K.; Huang, K.; Lei, M. Conductive polyvinyl alcohol/silver nanoparticles hydrogel sensor with large draw ratio, high sensitivity and high stability for human behavior monitoring. Eng. Sci. 2022, 18, 113–120. [Google Scholar] [CrossRef]
- Sharma, A.K.; Singh, R.; Tiwari, A.K.; Sharma, A.K. Design, fabrication and analysis of compaction die for powder processing. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Chennai, India, 16–17 September 2020; Volume 992, p. 012005. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).