Abstract
The 3D shear deformation and failure behaviour of a glass fibre reinforced polypropylene in a shear strain rate range of is investigated. An Iosipescu testing setup on a servo-hydraulic high speed testing unit is used to experimentally characterise the in-plane and out-of-plane behaviour utilising three specimen configurations (12-, 13- and 31-direction). The experimental procedure as well as the testing results are presented and discussed. The measured shear stress–shear strain relations indicate a highly nonlinear behaviour and a distinct rate dependency. Two methods are investigated to derive according material characteristics: a classical engineering approach based on moduli and strengths and a data driven approach based on the curve progression. In all cases a Johnson–Cook based formulation is used to describe rate dependency. The analysis methodologies as well as the derived model parameters are described and discussed in detail. It is shown that a phenomenologically enhanced regression can be used to obtain material characteristics for a generalising constitutive model based on the data driven approach.
1. Introduction
Fibre reinforced plastics (FRPs) have become a widely used material for a broad range of structural applications. Especially, the high capacity for energy dissipation is exploited in components exposed to crash and impact loading scenarios in the automotive [1,2] and aviation industries [3,4].
The key aspect for a reliable design process is the characterisation and accurate description of the material behaviour considering arbitrary three-dimensional loading cases as well as loading rates. Characterisation of material properties is particularly challenging for the through thickness (TT) shear behaviour of composites [5]. They typically exhibit pronounced nonlinear behaviour, which is strongly influenced and changed by the presence of other stress components [6,7]. The challenges of determining such behaviour arise mainly from two domains: (a) specimen design and experimental evaluation and (b) deduction of TT material characteristics and material modelling. Regarding test design and evaluation, many different approaches have been investigated. Jalai and Taheri developed the varying span method, where three point bending experiments with different span to thickness ratios are used in combination with extensive analytical models to determine the initial TT shear modulus [8]. Yoneyama et al. used a curved beam specimen, also subjected to three point bending, with permanent strain measurement throughout the experiment, enabled by digital image correlation (DIC) [9]. They determined the interlaminar shear modulus, as well as other elastic properties, at predefined load levels by utilising supporting finite element analyses (FEA). Several authors found a V-notched specimen in combination with DIC for strain measurement to be suitable for determining quasi-static shear characteristics [10,11,12].
Regarding the experimental determination of the shear properties of FRP at elevated velocities, only a few investigations have been published. Hsiao et al. used a combination of servo-hydraulic test machine, drop tower and split Hopkinson pressure bar (SHPB) to investigate a wide range of strain rates [13]. Zhao et al. employed a combination of a universal testing machine and an electromagnetic SHPB [14]. A modified Iosipescu-test setup on a servo-hydraulic high speed testing machine [15] was successfully used by Hufenbach et al. to determine rate dependent shear properties in composite materials [16]. The experimental investigations in the present study follow the latter approach.
Especially for FEA with respect to crash and impact applications, the in-depth knowledge of the characteristic 3D-stress–strain and -failure behaviour is of high importance. With respect to delamination failure in laminated textile reinforced composites, interlaminar shear properties are of special relevance for the determination of failure onset. Typical approaches to model the material behaviour are based on phenomenologically driven models, in combination with engineering constants. To capture the nonlinearity of the stress–strain relationship under TT shear, different approaches with varying experimental effort and potential for generalisation have been applied in literature. The approach requiring the least additional effort is to define parameter pairs of loading state and corresponding modulus [9]. It yields a good approximation close to the sampling points but is not well suited for extensive extrapolation. In regions of high nonlinearity, a high density of sampling points is required to capture the curve’s progression. Alternatively, attempts to model the underlying effects leading to the deviation from linear behaviour have been made. Hassan et al. superposed inelastic behaviour, continuum damage and interface failure to analyse the energy dissipation during quasi-static failure of composite joints [17].
However, the impact of the strain rate on the TT shear behaviour of textile reinforced composites and the respective characteristics has not yet been investigated in detail. In order to add strain rate dependency to initially static models, often a Johnson–Cook [18] based approach is used. This enables the model’s application to a wider range of problems. However, it doubles the number of model parameters necessary, significantly increasing the effort for parameter identification. This effect is further amplified by the additional interaction parameters often used to unify different loading scenarios [19,20,21]. Additionally, the simultaneous occurrence of different sources of nonlinearity during the loading of composites poses an enormous challenge to realise experimentally and to extract said parameters from the resulting curves. In the field of FRP, no standardised models or methods for parameter identification exist; it is rather up to the engineer to find a suitable model, familiarise oneself enough to understand the physical meaning of the material parameters, what kind of experimental procedure is necessary to trigger underlying effects and how to extract the necessary parameters from the experimental results.
Therefore, the aim of this paper is to develop the simplest model possible—with as few parameters as possible—still capable of accurately predicting the macroscopic material response. This type of model is chosen to provide a proof of concept for the proposed modelling approach as well as a stepping stone for the usage of more sophisticated data driven (DD) methods in the field of material modelling—in particular, considering that currently established strategies which focus on deriving ’stand alone’ engineering parameter, based on e.g., ASTM or DIN-ISO standards, tend to disregard the majority of the acquired data. This is particularly relevant for highly nonlinear constitutive material behaviour, where conventional characterisation methodologies significantly reduce relevant information on the material behaviour initially observed experimentally, which may be important for subsequent modelling purposes. In addition, more comprehensive data and information are demanded by the rapidly increasing application of (semi-)automatised methods for data processing and analysis. The presented work aims to contribute to a paradigm shift: from material characteristics, which are evaluated at predefined points, towards a characteristic curve based one. To achieve this, here, a purely regression based model is derived from the development of the tangent modulus. The resulting DD model is compared with a classical modulus and strength based (MaS) approach, keeping track of the change in secant stiffness at predefined strain states.
2. Experimental Methodology
2.1. Material Configuration and Specimen Preparation
For all presented experiments, a multi-layered weft knitted fabric (MKF) reinforcement was used, which has previously been developed and manufactured at the TU Dresden [22]. A characteristic feature of the fibre architecture is the non-crimped fibres of the warp and weft threads without any undulations. Knitting loop threads secure the fibre interlock and prevent the delamination within each individual layer (detailed schematic and computed tomographic illustrations are given in [23]).
The MKF consists of commingled hybrid E-glass fibre polypropylene (GF/PP) rovings, with a fibre-fineness of 1400 tex in 1- (warp) and 2-direction (weft) and a loop yarn of 139 tex, representing a layer-wise 3D-reinforcement. The result is an equal mass share of 42% (warp and weft) and 16.5% (loop) and a total fibre volume fraction of 55%.
The base plates have been manufactured using the hot pressing technology. A more detailed description of the manufacturing process is given in [15]. The thickness of a single consolidated textile layer equals 0.5 mm. Specimens have been cut from the plates by water jet cutting.
2.2. Experimental Setup and Testing Program
Three different specimen configurations have been used for the evaluation of the strain rate dependent shear behaviour of the GF/PP. Figure 1a illustrates the alignment of each shear specimen configuration: 12- (in-plane), 13- and 31-configuration (out-of-plane). The notation of the specimen configuration conforms to the orientation of the material axes related to the specimen dimensions whereupon the first index corresponds to the length dimension and the second to the width dimension. The specimen has a length of 78 mm, a width of 20 mm and is 45° V-notched in the middle with a notch tip distance of 13 mm. The thickness is 4 mm for 12- and 13-configuration and 10 mm for the 31-configuration. In case of the 31-configuration, a higher thickness is necessary since the material strength is very low, due to the layers being sheared off of one another.
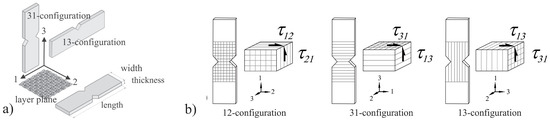
Figure 1.
(a) Specimen configurations with respect to the fibre reinforcement plane and (b) the corresponding stress states during Iosipescu testing [15].
The determination of the shear properties has been performed with the Iosipescu shear testing device shown in Figure 2a. This test arrangement is in accordance with ASTM D 5379 [24], where the specimen, which is notched on both sides, is clamped and, when compressed, a zone of torque-free shear load between the notches is created [15,16]. The load is applied with a servo-hydraulic test system Instron VHS 160/20 with a load cell of 160 , enabling tests at deformation speeds of up to 20 with a load cell accuracy of %. Deformation measurements and subsequent strain analysis were performed using high speed DIC, based on the stochastic grey scale pattern on the specimens’ surface. For that, two high speed cameras with a maximum frame rate of 200,000 images per second in combination with the 3D DIC system Aramis by GOM mbH have been used.
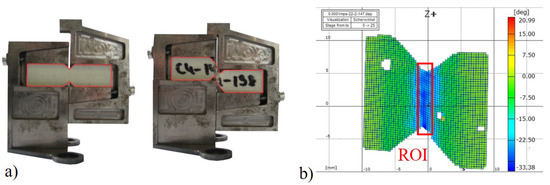
Figure 2.
Iosipescu shear test setup: (a) specimen with undeformed (before) and deformed (after the experiment) specimen; (b) representative strain distribution from DIC with the chosen ROI for further analysis.
The shear strain is calculated by averaging the values within a region of interest (ROI) and determined by the principal strains and :
Anticipatory to the experimental results and as illustrated in Figure 2b, the shear distribution is of inhomogeneous nature in the analysed area. Therefore, a constant ROI of 15 × 3 is chosen for all experiments, in which the shear deformation is analysed and averaged, resulting in one representative value. The chosen ROI covers the area between the V-notches of the specimen with a shear-dominated deformation ratio.
A current associated shear strain rate is determined during the the optical measurements by
within the ROI, where the measurement time step corresponds to the camera acquisition rate. The associated shear stress is calculated with respect to the loading force at the smallest specimen cross sectional area between the notch tips.
Each of the investigated configurations (12, 13 and 31) was tested at four nominal loading velocities: 0.00001, 0.0001, 0.01 and 0.1 . For each of the three lower loading velocities, four repetitions were performed, three for the highest, leading to a total of 45 experiments. The nominal shear strain rate of each experiment is calculated between % and % and is seen as the reference value for the entire experiment, although the value varies slightly throughout the experiment. Subsequently, the shear strain rates determined for the respective experiments are averaged over all samples for each material configuration and loading velocity. An overview over the conducted experiments can be found in Table 1. The slight differences in strain rate at equal loading velocity and geometry are due to differences in the strain localisation behaviour for the different material configurations.

Table 1.
Overview of the conducted tests.
3. Experimental Results
3.1. Stress–Strain Behaviour and Experimental Classification
The experimental stress–strain results for the investigated 12-, 13- and 31-configuration are illustrated in Figure 3.
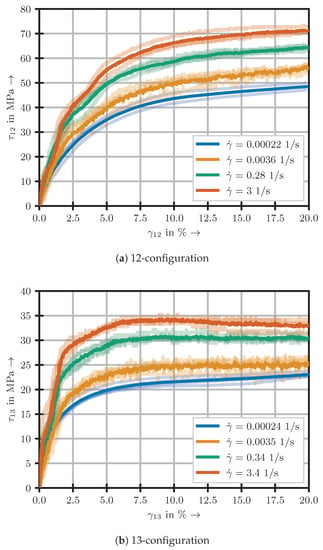
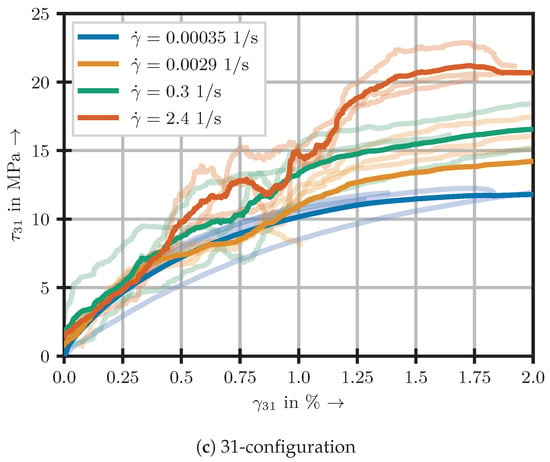
Figure 3.
Stress–strain curves for the investigated material configurations.
The curves of the 12- and 13-configuration all exhibit an almost linear behaviour at very low strain. With increasing strain, the curves become strongly nonlinear until a re-linearisation occurs. In case of the 12–configuration, a slight slope remains, whereas, in the 13–configuration, a plateau of constant stress is reached. The results of both configurations are clipped at a strain of 20%. At higher strains, the curves begin to steepen quickly. This behaviour can be attributed to the fibres aligning with the load application. Thus, its cause can be found in the specimen’s overall structure, not the material behaviour itself. Therefore, the steepening aspect is not considered in subsequent analyses.
A low pass filter was applied to the results from the 31-configuration, since high frequency oscillations dominated the raw measurements. The identifiable behaviour begins similar to the other two configurations, though the linear regime is limited to strains smaller than 0.5%. Again, it is followed by strongly nonlinear behaviour. However, catastrophic failure occurs before re-linearisation can take place.
Due to the highly nonlinear nature of the stress–strain curves, the identification of single representative stiffness or failure parameters analogous to materials of brittle characteristic is not possible. Therefore, two approaches to characterise the behaviour are investigated in Section 4.
3.2. Failure and Fracture Behaviour
An exemplary post-experimental failure pattern for each investigated material configuration is shown in Figure 4. An influence of the strain rate on the observable failure patterns could not be identified. The displayed images are therefore considered to be representative across the investigated strain rate domains.

Figure 4.
Post-experimental images of representative deformation and failure patterns for the investigated material configurations.
For both the 12- and the 13-configuration, nonlinearities dominate the stress–deformation behaviour. In both the 13- and the 31-configuration, the predominant failure mode is of an interlaminar nature. This results in delaminations, which in turn lead to catastrophic failure and specimen separation in the 31-configuration. A more in-depth assessment of the observed phenomena and their origins is given in [15], where a 2/2-twill weave reinforcement is made of commingled hybrid GF/PP yarn and experimentally investigated in a similar manner, without addressing strain rate effects. Their findings are consistent with the ones obtained in this study for MKF reinforcement.
4. Material Modelling and Property Identification
Two approaches to model the experimentally identified material behaviour are pursued:
- modulus and strength based (MaS): An analysis based on ASTM D5379 [24] and DIN EN ISO 14129 [25] with the determination of engineering constants at fixed strain values.
- data driven (DD): A closed formulation describing the entire experimental curves by coherent formulae with the determining parameters being the material’s characteristics.
In both cases, the causes of the nonlinearities are not further investigated for the modelling, since all experiments were carried out with continuously increasing strain, making a differentiation of intrinsic effects impossible.
4.1. Modulus and Strength Based (MaS) Approach
4.1.1. Determination of Engineering Constants
Four slopes, referred to as shear moduli, were determined for each experiment (see Table 1): three secant moduli (between % and %) and a tangent modulus at % determined between %:
The determined parameters are arithmetically averaged over the conducted experiments for each strain rate and material configuration. They are summarised in Table 2, and respective maximum stress values of the experiments are given additionally.

Table 2.
Characteristic strain rate dependent shear modulus and maximum stress.
4.1.2. Strain Rate Dependency and Model Parameters
The effects of the shear strain rate on the material parameters and stress levels for the respective shear directions 12, 13 and 31 within the considered strain rate range are presented in Figure 5. The remaining values at 1 and 2% exhibit similar behaviour.
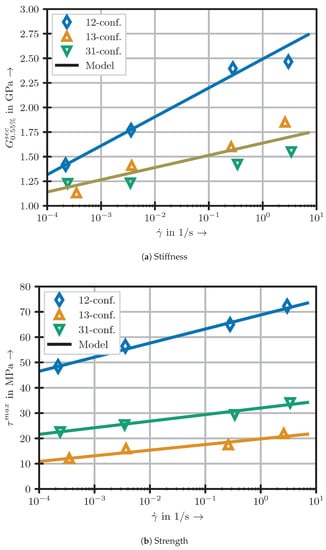
Figure 5.
Strain rate dependency of exemplary shear modulus and for different material configurations.
In order to incorporate the increase of those parameters with the strain rate, a model originally proposed by Johnson and Cook [18], which is widely used in literature to model the strain rate dependency of model parameters, e.g., [26,27,28], is chosen:
The strain rate dependency was found to be accurately described by this model. In (4), and denote model parameters, which control the linear slope (in the log plot) of the model’s predictions over the considered shear strain rates. These parameters are determined by a best fit approach. and are the values at reference shear strain rate . It is worth emphasising that this type of natural logarithm-formulation may result in unreasonable negative values when the model is evaluated far below the reference strain rate. Special attention has to be paid to this in implementations for FEA, since large local jumps in strain rate may occur, leading to negative moduli.
With the identified strain rate material constants and for the corresponding 12, 31 and 13-configurations, the tendency of the rising values of shear modulus and shear stress respectively can be accurately estimated. An overview of the model constants for selected material parameters is given in Table 3.

Table 3.
Final material parameters for strain rate dependency—MaS approach.
In this regard, it is emphasised that the shear moduli and are considered to be identical due to the typical assumption of a symmetric stiffness tensor for these textile reinforced composites. Reference values were taken at the lowest measured shear strain rates to avoid the aforementioned problems at strain rates lower than the reference one. The corresponding model predictions are presented for the initial shear modulus and the maximum shear stress in Figure 5. The resulting trajectories at different strains are presented in Figure 6 for the 12-configuration and strain rates of 2.2 × 10−4 and 3.
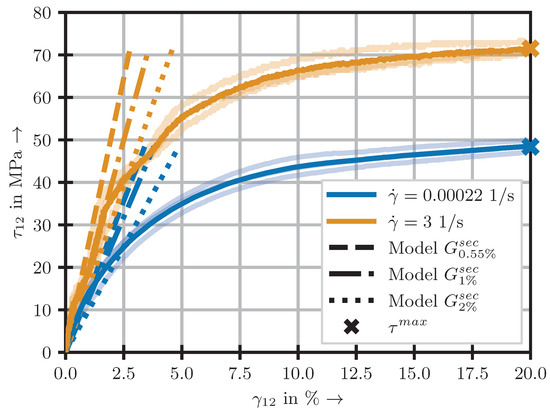
Figure 6.
Mas model predictions for secant moduli and maximum shear stress, exemplary for the 12-configuration at lowest and highest investigated strain rates.
4.2. Data Driven (DD) Approach
4.2.1. Determination of Material Characteristics
Within this subsection, the applied strategy to model the material’s behaviour by continuous formulae is exemplary presented using the 12-configuration. For the other configurations, an identical procedure is used unless stated otherwise. In order to obtain a continuous description of the material’s behaviour, the slopes along the curves—hereafter referred to as tangent modulus —are investigated. Therefore, each experimental curve is considered as subsequent stress–strain points and preprocessed by applying a low-pass filter. The tangent modulus at a given strain point , with , is subsequently calculated by
The results are presented in Figure 7.
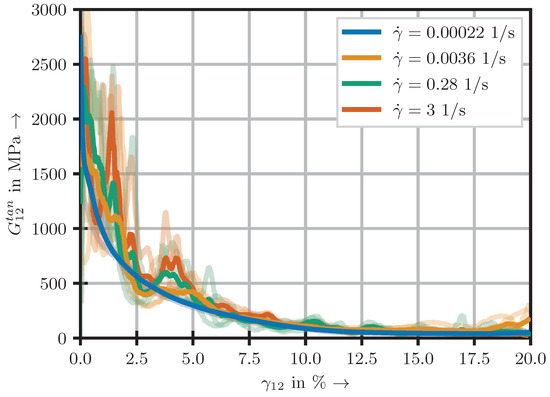
Figure 7.
Experimental tangent modulus for the 12-configuration.
The curves show a finite value at zero strain and a rapid decay with an asymptotic approach to zero. Given these curve characteristics, an exponential law is chosen as model:
with the initial tangent modulus and the decay parameter a. Integration of (6) with the initial condition yields a closed form for the stress–strain relationship:
From this, it becomes clear that the chosen model contains the asymptotic stress , which can be seen for the material configurations 12 and 13 in Figure 3 as
Parameter identification for and a is carried out individually for each test by a standard least square fit. In all cases, both parameters exhibit a distinct dependency on the strain rate. The experimental curves in combination with the corresponding model predictions based on the previously identified parameters and a are presented in Figure 8 (“Model, standard”).
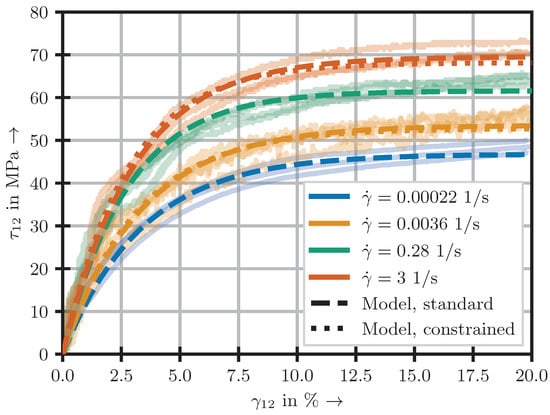
Figure 8.
Juxtaposition of experimental results and corresponding model predictions with parameters based on standard and constrained regression.
The respective dependency of the identified model parameters in (7) on the strain rate can be found in Figure 9 (“Standard fit“). In the case of the decay parameter a (Figure 9b), it becomes apparent that there is no simple dependency of the material parameters on the strain rate. In particular, the simultaneous increase and decrease from to pose a major challenge to deterministic models. However, the usage of such an approach is highly desirable to obtain a more generalised and predictive model. Therefore, a second set of parameters is identified.
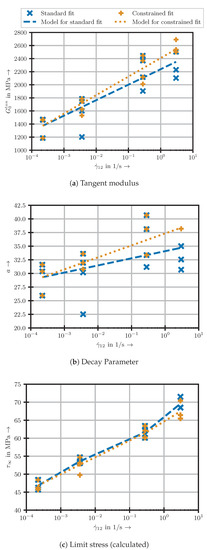
Figure 9.
Dependency of material parameters on the strain rate.
For this second methodology, additional bounds on the fitting parameters are applied: The fits at the lowest tested strain rate are carried out without any restrictions. For all subsequent fits, the lower bounds for the parameters are set to the means of the parameter at the previous strain rate. This ensures that the well-known tendency of stiffness parameters increasing with the strain rate [16,18,19,29,30] is preserved within the resulting parameter set. The model predictions for the stress–strain curves based on the parameters determined by this constrained method are illustrated in Figure 8 (“Model, constrained“) and the respective model parameters in Figure 9 (“Constrained fit“).
4.2.2. Modelling of the Strain Rate Dependency
Given the excellent results of the Johnson–Cook-model for strain rate dependency in Section 4.1.2, the same approach is taken to model the strain rate dependency of the material parameters and a:
with the values and at the reference strain rate and the material constants and . The values and are obtained by a standard least square fit. Given the advantageous generalisation capability of the constrained methodology, the final model with the parameters , and as well as the parameters and (Table 4) are obtained by fitting the constrained model’s parameters. In Figure 10, the resulting curves are plotted alongside the conducted tests.

Table 4.
Final material model parameters including strain rate dependency—DD approach.
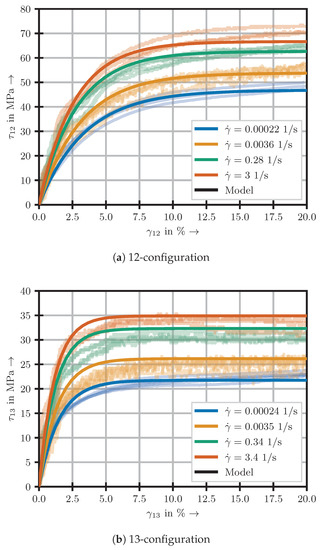
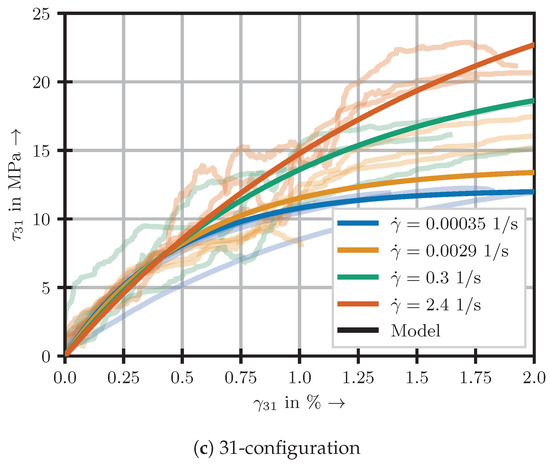
Figure 10.
Comparison of experimental results and presented model.
It can be seen that the model is in excellent agreement with the experimental results for the 12- and 13-configuration. In case of the 31-configurations, sound results are obtained as well, even though failure occurred already at shear strains of approximately 2%. The determined material parameters for the respective material configurations are presented in Table 4.
4.3. Determining the Range of Validity of the Material Modelling Approaches
A criterion to determine the range of validity for the MaS model—exemplary shown for the initial secant shear modulus —is presented. It is intended to provide an indicator under which circumstances the additional effort required for the DD model is expected to yield a significant improvement in the quality of prediction. As a basis, the degree of nonlinearity and the subsequent deviation from a straight line is used for the assessment.
The transition from linear to nonlinear behaviour can be described by a defined percentage based deviation of the experimental curve from a given straight line with the initial modulus as slope. However, significant oscillations in the low strain area in some of the experiments at high strain rates are observed. Due to the low absolute values, small deviations with respect to the standard testing accuracies already lead to high percentage changes, resulting in an erroneous immediate prediction of the onset of nonlinearity. Therefore, the criterion has to be robust against such small absolute deviations. Thus, a criterion based on the coefficient of determination is employed, where a maximum value of 1 indicates perfect conformity.
For each experimental point k, the value is determined for the straight line with the slope approximating the actual experimental curve. In an extension of the definition for an entire data set, e.g., given in [31], this leads to
as the coefficient of determination at every point along the curve. Significant nonlinearity is thereby defined as the strain at which the value reaches the last local maximum since the quality of approximation steadily decreases with proceeding strain. An example for this criterion is presented in Figure 11 up to a strain of 5%.
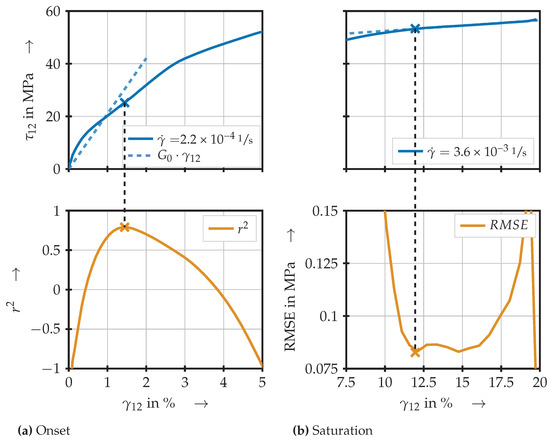
Figure 11.
Comparison of models predicting onset and saturation of significant nonlinearity for the 12-configuration.
This method yields good results for the material configurations 12 and 13 with one exception in the 13 case at . Therefore, the respective specimen is not taken into account for further investigations. Furthermore, it becomes clear that no exact boundaries for the range of validity can be specified. However, from a certain point on, the approximation quality of the linear model constantly decreases. Therefore, this point is chosen as a guideline, even though it must be noted that, in individual cases, the linear approximation might be valid for larger or smaller strains. The determined stresses at which initial nonlinearity becomes significant are presented in Figure 12. A distinct dependency on the shear rate may be observed.
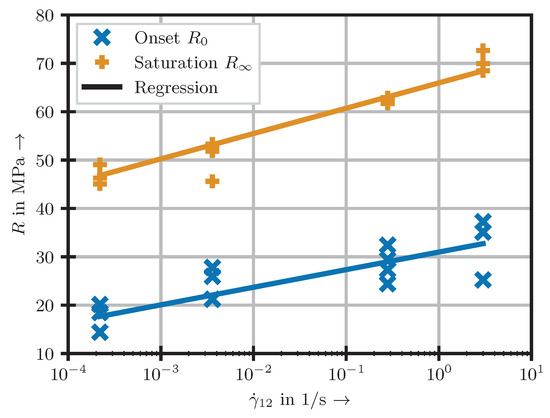
Figure 12.
Summary of the onset and saturation points of significant nonlinearity for the 12-configuration.
Similar to the onset of damage, the stress–strain curves show a distinct point at which the behaviour changes back to an almost linear one with a very small slope. This behaviour is attributed to the saturation of underlying effects. The point of nonlinearity saturation is determined analogously to the onset by linear regression, this time starting at the maximum considered strain of 20% of the specimen and moving on to lower strains. In this case, the first local minimum of the mean squared error, calculated between the linear approximation and the experimental curve, has been found to be a well-suited criterion. The determined stress values are shown in Figure 12. Furthermore, it becomes apparent that the stress at which the re-linearisation occurs increases with the strain rate. The area of the stress–strain curve following yields great potential for use cases in which the energy absorption is crucial.
5. Discussion
5.1. Strain Rate and Configuration Dependent Experimental Characterisation
The investigated GF/PP-MKF shows similar behaviour under the three shear loading conditions 12, 13 and 31 (see Figure 13).
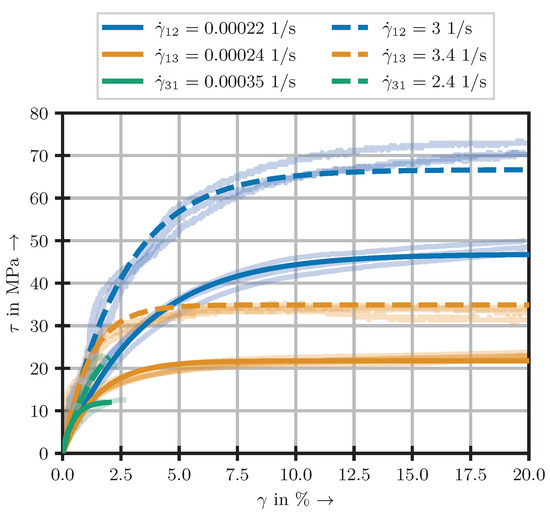
Figure 13.
Comparison of experimental and model results for the three investigated load cases.
In the beginning of the linear regime, the stiffness under 12, 13 and 31 loading is almost identical. This supports the often made assumption of all these kinds of loading being identical for balanced MKF. However, this equality of the curves only holds up to %, at which point nonlinearity appears in the 31 case. At %, the 12 and 13 cases show nonlinear behaviour as well. All specimens of the 31–configuration fail in this nonlinear phase. In the other configurations, a re-linearisation occurs. This phenomenon is much more pronounced and progresses much quicker in the 13 case than in the 12. In the 13 case, an almost constant value is reached at %, whereas the nonlinear regime in the 12 case reaches up to %. In both cases, the behaviour stays linear up to strains of approximately 20%.
The experimental design does not allow for a final assessment of the underlying effects leading to the change in principal material behaviour. This would require unloading of the specimen at intermediate loading states, which currently cannot be implemented with the presented test set-up. However, possible causes are discussed in the context of the developed models and existing literature in more detail in Section 5.3.
Furthermore, the GF/PP’s behaviour shows a distinct dependency on the strain rate. In particular, the initial material stiffness increases strongly with the strain rate, and the overall shape of the curve is only influenced slightly. This unequal impact of strain rate on the different aspects of the material behaviour is also captured by the DD-model: For the 12- and 13-configurations, the ratio of the rate dependency parameters is around 3, indicating a three times stronger rate dependency of the stiffness.
5.2. Presented Modelling Approaches
Two approaches to capture the highly nonlinear material behaviour exhibited by the GF/PP under different shear-loading conditions have been investigated.
5.2.1. Modulus and Strength Based (MaS) Approach
The MaS method is very close to well-known linear elasticity models and can therefore be used almost directly in all FEA-programs. It makes use of established analysis techniques and provides a simple framework. Furthermore, the identification of “material parameters” for constant strain rates is as easy as reading values of experimental data. These aspects greatly facilitate the usage of this approach.
It was shown that the results obtained by the MaS-model can yield good results, as long as the analysis is limited to small strains. Within this range, the model captures the dependency of the material’s behaviour on the strain rate with high accuracy. However, it leads to non-smooth curves, with the deviation between experimental and numerical curve depending highly on the number of evaluation points. This necessitates a multitude of “material parameters” for high fidelity analyses, due to the large nonlinear regime within the stress–strain curve. The determination of how many parameters are necessary is aggravated by the fact that the model contains no information about its own applicability, i.e., up to which strain the error is acceptable. In addition, the generalisation to arbitrary strain rates becomes increasingly difficult with every “material parameter”, since each requires additional parameters to model this dependency.
5.2.2. Data Driven (DD) Approach
On the other hand, the presented DD approach poses a comparatively high initial hurdle. The underlying model is not necessarily implemented in every FEA-program, requiring a potential user to implement the constitutive model via some subroutine. Furthermore, the material parameters cannot be read directly from the stress–strain curve. It is rather necessary to perform a nonlinear regression analysis of the curve.
In this work, two regression techniques were applied and the resulting parameter sets compared. In Figure 8, it can be seen that the model predictions for both parameter identification methodologies are in good agreement with the experimental data and among themselves. Solely at very high strain rates of and high strains of more than 15%, the constrained model predictions differ notably from the approximation without additional assumptions. Additionally, the trend of rising material parameters with increased strain rate can be captured more accurately by the constrained fit (cf. Figure 9). This allows for the model to be more generalising and predictive. Furthermore, the two physically based curve parameters and barely differ between both fitting approaches. Therefore, the parameters identified by the constrained methodology are suggested for future works.
The DD approach tremendously outperforms the MaS method in terms of accuracy—as long as the number of data points for the MaS method remains somewhat capped—extensibility to arbitrary strain rates and therefore overall generalisability. This is mainly due to the fact that, within the presented framework, the strain rates dependency of every single material parameter is modelled individually with an additional parameter, doubling the necessary parameters if rate effects are to be considered. Furthermore, it provides a closed and differentiable form of the stress–strain relationship. This is highly beneficial for the numeric time integration schemes implemented in commercial FEA-programs.
5.3. Interpretability of the Nonlinearities
The respective transitions between the aforementioned material states cannot be distinctly attributed to a material phenomenon, based on the experiments conducted. However, other works on similar materials allow for a preliminary analysis of the underlying effects.
In the case of the first transition, the determined stress value marks the point from which, going forward, the prediction accuracy of linear models significantly decreases. Therefore, such models should only be used in cases where it is previously known that stresses will not significantly exceed . However, given the plateau-like nature of the local maximum, minor overstepping of the boundary could only result in slight discrepancies between the models. On the material side, the fibres’ support in the form of the matrix begins to degrade and behave nonlinearly. It has been shown that GF/PP exhibits strongly nonlinear viscoelastic behaviour [32,33], which in itself can lead to significant deviations from a linear stress–strain behaviour at strains of less than 1% [34]. Another common cause for the nonlinearity in the behaviour of FRP can be found in the occurrence of micro- or macroscopic cracks within the matrix, which lead to a decrease in the material’s stiffness [35,36,37]. Additionally, PP is known to accumulate plastic strain even at very low levels of stress [38]. This in turn weakens the support of the fibres and therefore limits the material’s load bearing capabilities [39]. Recent studies have shown that, in the case of GF/PP, the viscoelastic behaviour is nonlinear from the beginning and that damage and plasticity are triggered at the same time, for the in plane behaviour at shear stresses as little as [19].
The re-linearisation occurring at higher strains suggests that the underlying effects begin saturating. In the case of inter-fibre fracture, this behaviour has been thoroughly investigated in recent years [35,37,40,41]. In that case, the material’s stiffness has been significantly reduced by the formation of a multitude of cracks; however, the initiation of new cracks is energetically not feasible. Therefore, some loads can still be transmitted even though they lead to drastically increasing defamation, with a return to the linear stress–strain relation.
6. Conclusions and Outlook
The TT behaviour of GF/PP with MKF reinforcement at various strain rates has been determined experimentally by using a lightweight Iosipescu test setup in combination with high speed DIC. It was subsequently modelled using a MaS and a DD method.
The MaS model has been shown to be mostly suitable for preliminary analyses, reaching only small strain values. Otherwise, the amount of model parameters necessary quickly becomes unfeasible.
On the other hand, the DD model represents the entire stress–strain curve by only two parameters. Furthermore, it requires only two additional parameters to generalise to arbitrary strain rates, if the phenomenologically enhanced regression method is used. Therefore, the resulting model is applicable to high fidelity analyses with monotonically increasing loading, a high number of model and gradient evaluations (i.e., in the case of a large number of elements or time steps) and varying or previously unknown strain rate and state.
Future research of the following two aspects is expected to offer great potential: firstly, the investigation of the constitutive material behaviour describing the orthotropic shear stress–strain relations. In that respect, models incorporating damage and failure as well as multi scale approaches to directly address the influence of the textile architecture should be studied in detail. In particular, the influence of viscoelasticity and plasticity of the composite constituent materials glass and PP [19,42] are identified to be promising to describe the observable strain rate sensitivity; secondly, the pursuit of DD methods in the field of complex material behaviour. Treating experimental results as pure data with known input and output and thus applying methods from the field of supervised machine learning to them is expected to further facilitate model generation. Additionally, such methods could be employed to completely automatise the parameter identification process and thereby significantly lower the initial hurdle for using new material models.
Author Contributions
Conceptualization, J.G. and A.H.; methodology, J.G. and A.H.; software, J.G.; validation, J.G. and A.H.; formal analysis, J.G.; investigation, A.H.; resources, A.H. and M.G.; data curation, J.G. and A.H.; writing—original draft preparation, J.G. and A.H.; writing—review and editing, J.G., A.H., B.G. and M.G.; visualization, J.G. and A.H.; supervision, M.G.; project administration, A.H. and M.G.; funding acquisition, A.H., B.G. and M.G.. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 418701707—TRR 285—sub-project A03.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The algorithms used for fitting and optimisation are implemented in the open source Python library scipy [43]. Most of the figures presented here were created using the open source Python library matplotlib [44].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DD | data driven |
| DIC | digital image correlation |
| FEA | finite element analysis |
| FRP | fibre reinforced plastic |
| GF/PP | E-glass fibre polypropylene |
| MaS | modulus and strength based |
| MKF | multi-layered weft knitted fabric |
| PP | polypropylene |
| ROI | region of interest |
| SHPB | split Hopkinson pressure bar |
| TT | through thickness |
References
- Sarfraz, M.S.; Hong, H.; Kim, S.S. Recent developments in the manufacturing technologies of composite components and their cost-effectiveness in the automotive industry: A review study. Compos. Struct. 2021, 266, 113864. [Google Scholar] [CrossRef]
- Böhm, R.; Hornig, A.; Weber, T.; Grüber, B.; Gude, M. Experimental and Numerical Impact Analysis of Automotive Bumper Brackets Made of 2D Triaxially Braided CFRP Composites. Materials 2020, 13, 3554. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, N.; Wang, P.H. A review of failure modes and fracture analysis of aircraft composite materials. Eng. Fail. Anal. 2020, 115, 104692. [Google Scholar] [CrossRef]
- Haufe, A.; Cavariani, S.; Liebold, C.; Usta, T.; Kotzakolios, T.; Giannaros, E.; Kostopoulos, V.; Hornig, A.; Gude, M.; Djordjevic, N.; et al. On Composite Model Calibration for Extreme Impact Loading Exemplified on Aerospace Structures. In Proceedings of the 16th LS-Dyna International Users Conference, Aerospace, LSTC-Ansys, Virtual Event, 10–11 June 2020. [Google Scholar]
- Olsson, R. A survey of test methods for multiaxial and out-of-plane strength of composite laminates. Compos. Sci. Technol. 2011, 71, 773–783. [Google Scholar] [CrossRef]
- Gude, M.; Schirner, R.; Weck, D.; Dohmen, E.; Andrich, M. Through-thickness compression testing of fabric reinforced composite materials: Adapted design of novel compression stamps. Polym. Test. 2016, 56, 269–276. [Google Scholar] [CrossRef]
- Kanno, T.; Kurita, H.; Suzuki, M.; Tamura, H.; Narita, F. Numerical and Experimental Investigation of the Through-Thickness Strength Properties of Woven Glass Fiber Reinforced Polymer Composite Laminates under Combined Tensile and Shear Loading. J. Compos. Sci. 2020, 4, 112. [Google Scholar] [CrossRef]
- Jalali, S.J.; Taheri, F. A New Test Method for Measuring the Longitudinal and Shear Moduli of Fiber Reinforced Composites. J. Compos. Mater. 1999, 33, 2134–2160. [Google Scholar] [CrossRef]
- Yoneyama, S.; Ifju, P.G.; Rohde, S.E. Identifying through-thickness material properties of carbon-fiber-reinforced plastics using the virtual fields method combined with moiré interferometry. Adv. Compos. Mater. 2018, 27, 1–17. [Google Scholar] [CrossRef]
- Gude, M.; Hufenbach, W.; Andrich, M.; Mertel, A.; Schirner, R. Modified V-notched rail shear test fixture for shear characterisation of textile-reinforced composite materials. Polym. Test. 2015, 43, 147–153. [Google Scholar] [CrossRef]
- Stojcevski, F.; Hilditch, T.; Henderson, L.C. A modern account of Iosipescu testing. Compos. Part Appl. Sci. Manuf. 2018, 107, 545–554. [Google Scholar] [CrossRef]
- Guseinov, K.; Kudryavtsev, O.; Bezmelnitsyn, A.; Sapozhnikov, S. Determination of Interlaminar Shear Properties of Fibre-Reinforced Composites under Biaxial Loading: A New Experimental Approach. Polymers 2022, 14, 2575. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, H.M.; Daniel, I.M.; Cordes, R.D. Strain Rate Effects on the Transverse Compressive and Shear Behavior of Unidirectional Composites. J. Compos. Mater. 1999, 33, 1620–1642. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, P.; Dang, H.; Nie, H.; Guo, Z.; Zhang, C.; Li, Y. Effects of loading rate and loading direction on the compressive failure behavior of a 2D triaxially braided composite. Int. J. Impact Eng. 2021, 156, 103928. [Google Scholar] [CrossRef]
- Hufenbach, W.; Langkamp, A.; Hornig, A.; Zscheyge, M.; Bochynek, R. Analysing and modelling the 3D shear damage behaviour of hybrid yarn textile-reinforced thermoplastic composites. Compos. Struct. 2011, 94, 121–131. [Google Scholar] [CrossRef]
- Hufenbach, W.; Langkamp, A.; Gude, M.; Ebert, C.; Hornig, A.; Nitschke, S.; Böhm, H. Characterisation of Strain rate Dependent Material Properties of Textile Reinforced Thermoplastics for Crash and Impact Analysis. Procedia Mater. Sci. 2013, 2, 204–211. [Google Scholar] [CrossRef][Green Version]
- Hassan, J.; O’Higgins, R.M.; McCarthy, C.T.; Toso, N.; McCarthy, M.A. Mesoscale modelling of extended bearing failure in tension-absorber joints. Int. J. Mech. Sci. 2020, 182, 105777. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Zscheyge, M.; Böhm, R.; Hornig, A.; Gerritzen, J.; Gude, M. Rate dependent nonlinear mechanical behaviour of continuous fibre-reinforced thermoplastic composites – Experimental characterisation and viscoelastic-plastic damage modelling. Mater. Des. 2020, 193, 108827. [Google Scholar] [CrossRef]
- Böhm, R.; Gude, M.; Hufenbach, W. A phenomenologically based damage model for textile composites with crimped reinforcement. Compos. Sci. Technol. 2010, 70, 81–87. [Google Scholar] [CrossRef]
- Gude, M.; Hufenbach, W.; Ebert, C. The strain-rate-dependent material and failure behaviour of 2D and 3D non-crimp glass-fibre-reinforced composites. Mech. Compos. Mater. 2009, 45, 467–476. [Google Scholar] [CrossRef]
- Diestel, O.; Godau, U.; Offermann, P. Biaxially reinforced multilayer weft knitted fabrics - a new textile structure for composite reinforcement. In Proceedings of the 30th International SAMPE Technical Conference, San Antonio, TX, USA, 21–24 October 1998; pp. 40–47. [Google Scholar]
- Hufenbach, W.; Gude, M.; Ebert, C.; Zscheyge, M.; Hornig, A. Strain rate dependent low velocity impact response of layerwise 3D-reinforced composite structures. Int. J. Impact Eng. 2011, 38, 358–368. [Google Scholar] [CrossRef]
- ASTM D5379/D5379M-19e1; Standard Test Method for Shear Properties of Composite Materials by the V-Notched Beam Method. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- DIN EN ISO 14129:1998-02; Fibre-Reinforced Plastic Composites—Determination of the In-Plane Shear Stress/Shear Strain Response, Including the In-Plane Shear Modulus and Strength, by ±45° Tension Test Method (ISO 14129:1997). Beuth Verlag: Berlin, Germany, 1998. [CrossRef]
- Pantalé, O.; Bacaria, J.L.; Dalverny, O.; Rakotomalala, R.; Caperaa, S. 2D and 3D numerical models of metal cutting with damage effects. Comput. Methods Appl. Mech. Eng. 2004, 193, 4383–4399. [Google Scholar] [CrossRef]
- Krasauskas, P.; Kilikevičius, S.; Česnavičius, R.; Pačenga, D. Experimental analysis and numerical simulation of the stainless AISI 304 steel friction drilling process. Mechanics 2014, 20, 590–595. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.t.; He, Y.t.; Zhang, T.; Fan, X.h.; Zhang, T.y. Damage analysis of typical structures of aircraft under high-velocity fragments impact. Alex. Eng. J. 2023, 62, 431–443. [Google Scholar] [CrossRef]
- Fedulov, B.N.; Fedorenko, A.N.; Kantor, M.M.; Lomakin, E.V. Failure analysis of laminated composites based on degradation parameters. Meccanica 2018, 53, 359–372. [Google Scholar] [CrossRef]
- Martínez-Hergueta, F.; Ares, D.; Ridruejo, A.; Wiegand, J.; Petrinic, N. Modelling the in-plane strain rate dependent behaviour of woven composites with special emphasis on the nonlinear shear response. Compos. Struct. 2019, 210, 840–857. [Google Scholar] [CrossRef]
- Kvålseth, T.O. Cautionary Note about R2. Am. Stat. 1985, 39, 279–285. [Google Scholar] [CrossRef]
- Fritsch, J.; Hiermaier, S.; Strobl, G. Characterizing and modeling the nonlinear viscoelastic tensile deformation of a glass fiber reinforced polypropylene. Compos. Sci. Technol. 2009, 69, 2460–2466. [Google Scholar] [CrossRef]
- Hufenbach, W.; Langkamp, A.; Hornig, A.; Ebert, C. Experimental determination of the strain rate dependent outof-plane shear properties of textile-reinforced composites. In Proceedings of the 17th International Conference on Composite Materials, Edinburgh, UK, 27–32 July 2009. [Google Scholar]
- Kästner, M. Skalenübergreifende Modellierung und Simulation des Mechanischen Verhaltens von Textilverstärktem Polypropylen unter Nutzung der XFEM. Ph.D. Thesis, Technische Universität, Dresden, Germany, 30 June 2009. [Google Scholar]
- Shen, H.; Yao, W.; Qi, W.; Zong, J. Experimental investigation on damage evolution in cross-ply laminates subjected to quasi-static and fatigue loading. Compos. Part B Eng. 2017, 120, 10–26. [Google Scholar] [CrossRef]
- Yarysheva, A.Y.; Bagrov, D.V.; Bakirov, A.V.; Yarysheva, L.M.; Chvalun, S.N.; Volynskii, A.L. Effect of initial polypropylene structure on its deformation via crazing mechanism in a liquid medium. Eur. Polym. J. 2018, 100, 233–240. [Google Scholar] [CrossRef]
- Pakdel, H.; Mohammadi, B. Characteristic damage state of symmetric laminates subject to uniaxial monotonic-fatigue loading. Eng. Fract. Mech. 2018, 199, 86–100. [Google Scholar] [CrossRef]
- Imaddahen, M.A.; Shirinbayan, M.; Ayari, H.; Foucard, M.; Tcharkhtchi, A.; Fitoussi, J. Multi–scale analysis of short glass fiber–reinforced polypropylene under monotonic and fatigue loading. Polym. Compos. 2020, 41, 4649–4662. [Google Scholar] [CrossRef]
- Flatscher, T.; Pettermann, H.E. A constitutive model for fiber-reinforced polymer plies accounting for plasticity and brittle damage including softening – Implementation for implicit FEM. Compos. Struct. 2011, 93, 2241–2249. [Google Scholar] [CrossRef]
- Just, G.; Koch, I.; Brod, M.; Jansen, E.; Gude, M.; Rolfes, R. Influence of Reversed Fatigue Loading on DamageEvolution of Cross-Ply Carbon Fibre Composites. Materials 2019, 12, 1153. [Google Scholar] [CrossRef]
- Just, G.; Koch, I.; Gude, M. Experimental Analysis of Matrix Cracking in Glass Fiber Reinforced Composite Off-Axis Plies under Static and Fatigue Loading. Polymers 2022, 14, 2160. [Google Scholar] [CrossRef] [PubMed]
- Ebert, C.; Hufenbach, W.; Langkamp, A.; Gude, M. Modelling of strain rate dependent deformation behaviour of polypropylene. Polym. Test. 2011, 30, 183–187. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).