A Machine Learning Model to Detect Flow Disturbances during Manufacturing of Composites by Liquid Moulding
Abstract
1. Introduction
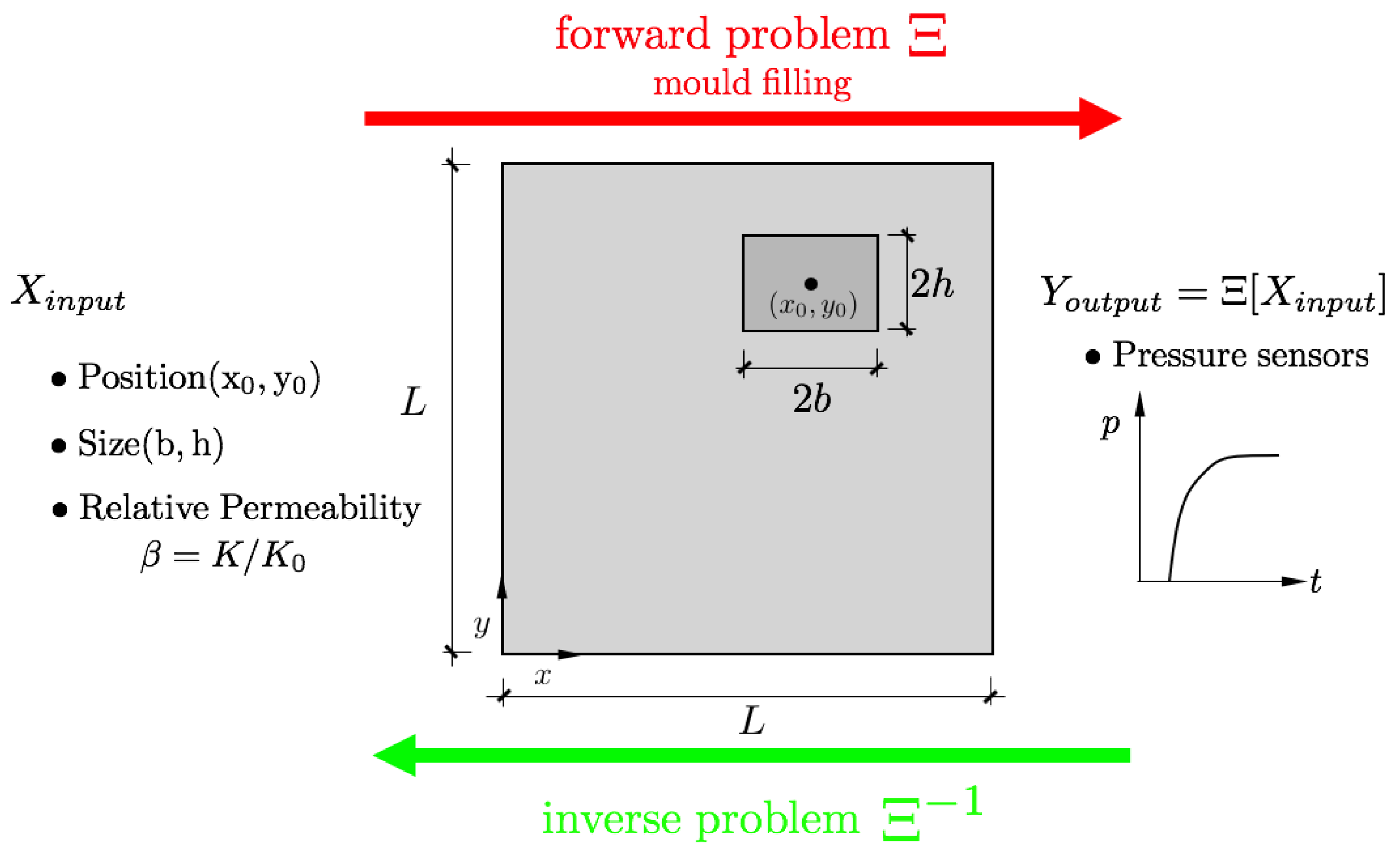
2. Model Description
3. Dataset Synthetic Generation
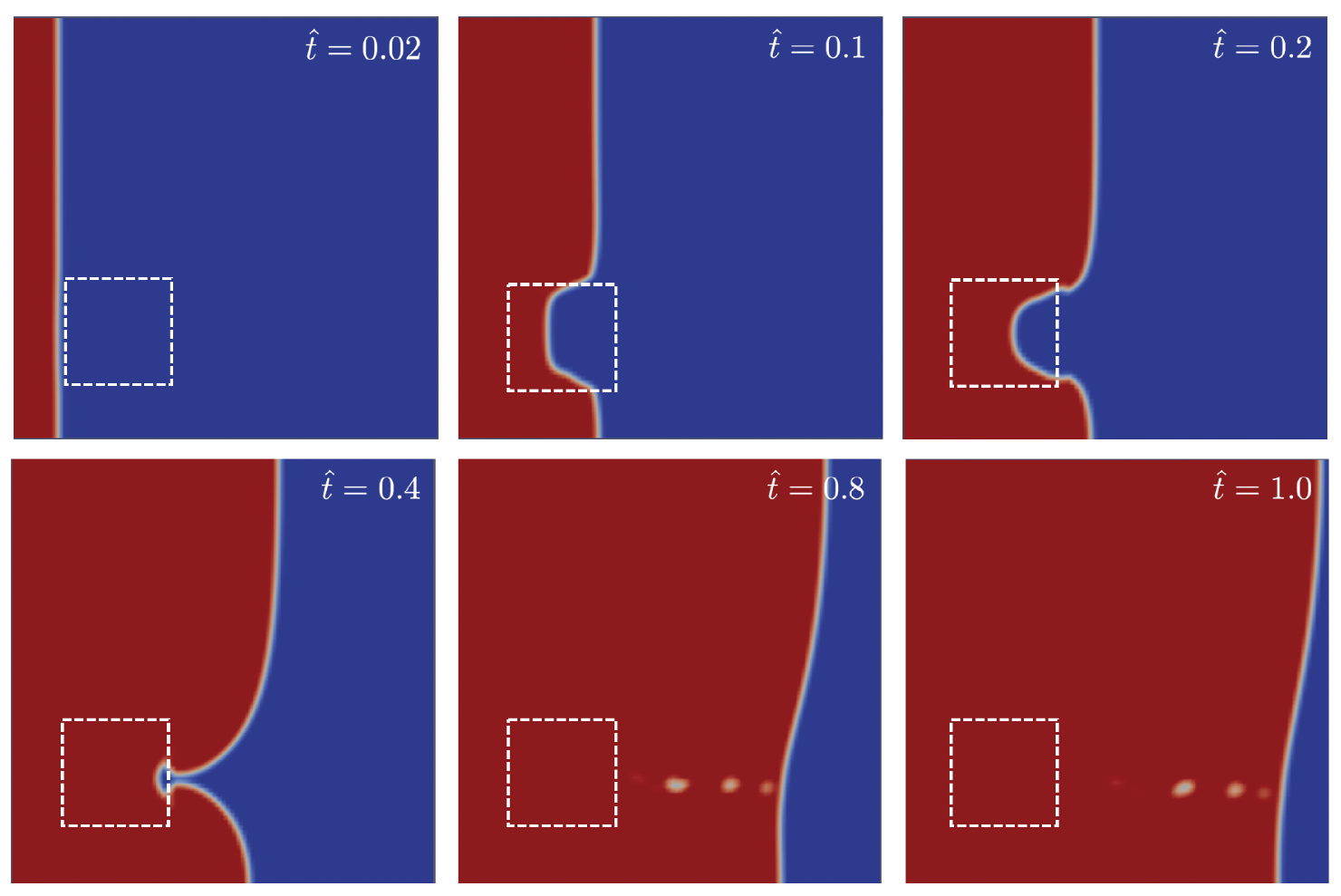
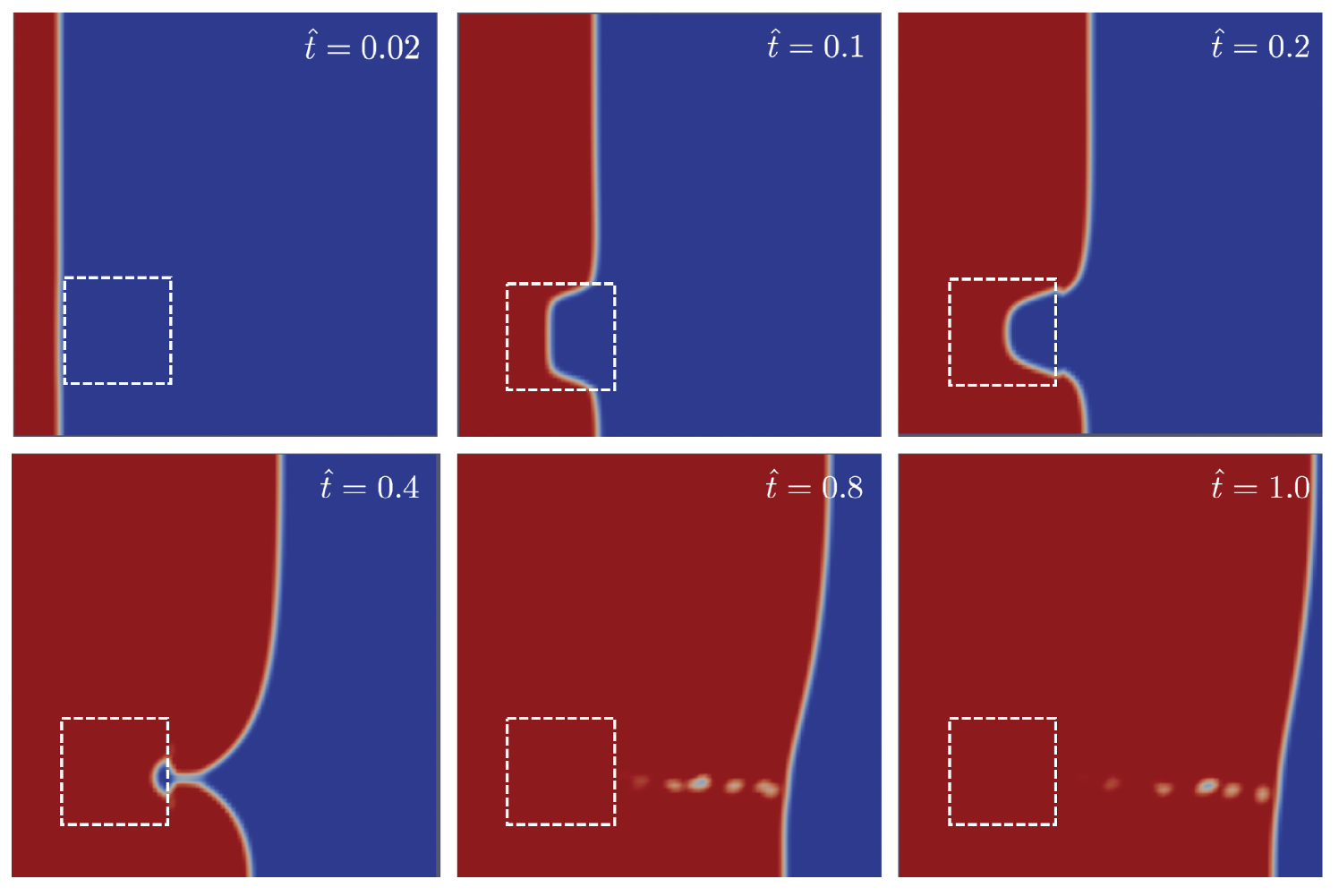
3.1. Mould Filling Model
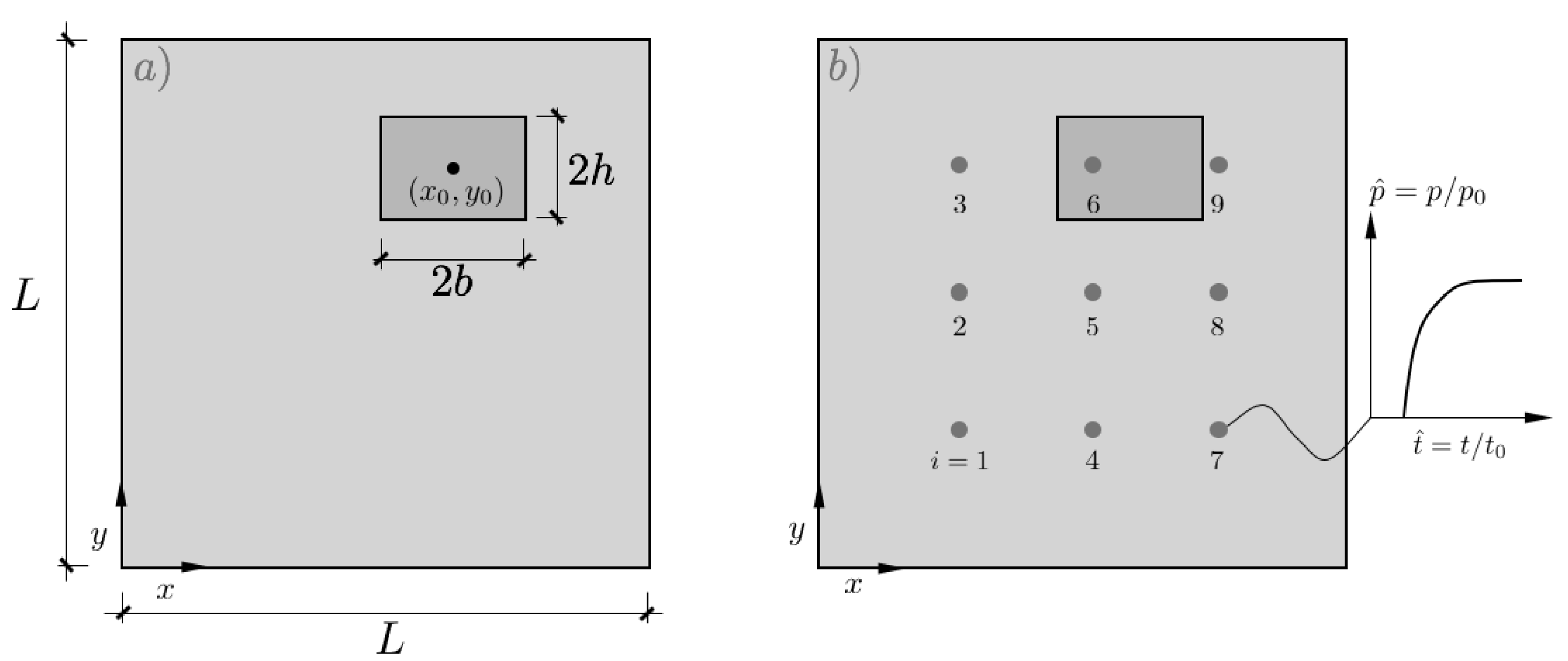
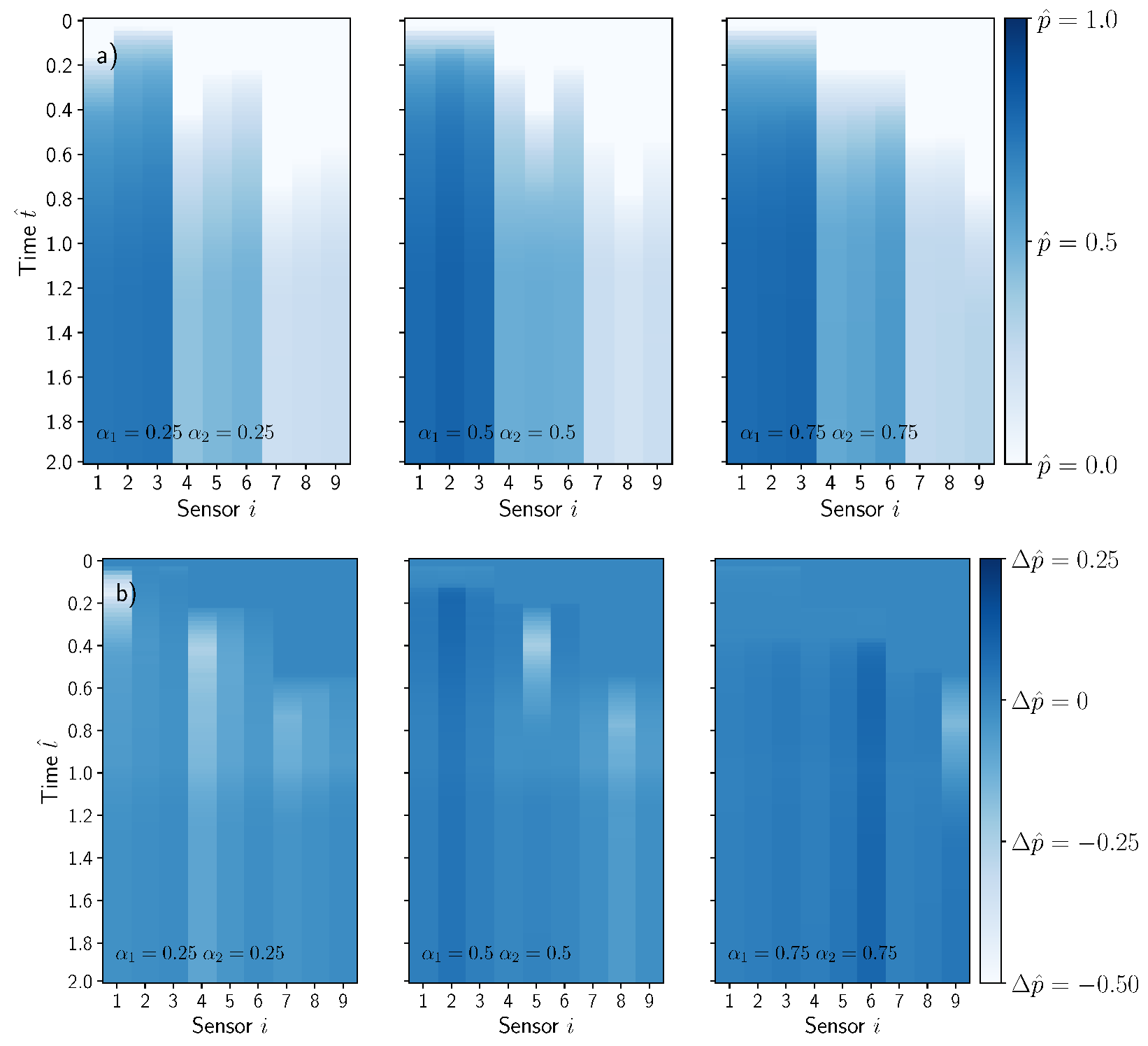
3.2. Mould Filling Simulations Containing Dissimilar Material Regions
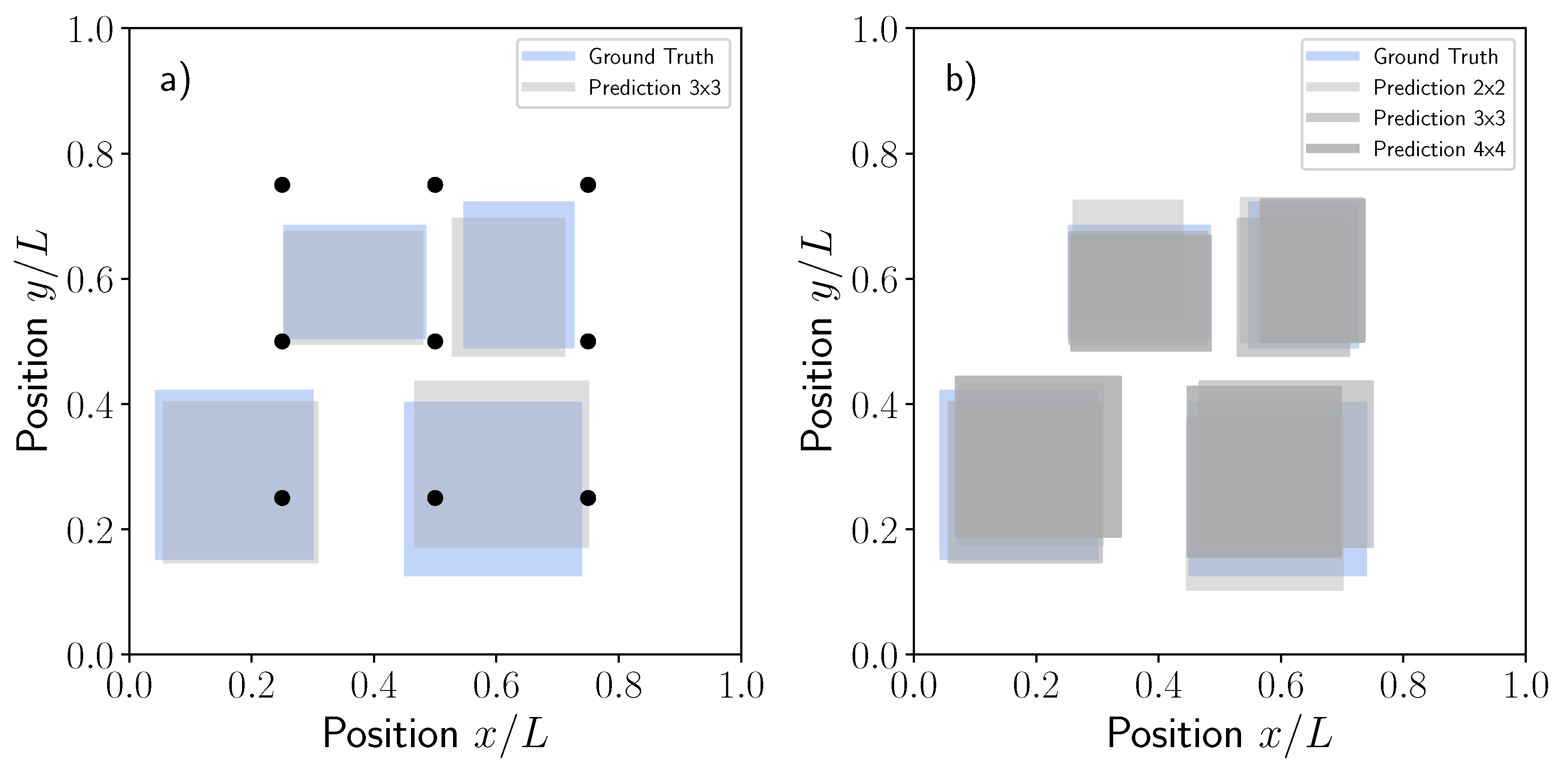
3.3. Dataset Generation
4. Building, Training and Deploying Machine Learning Models
4.1. CNN Machine Learning Networks
- Convolution2D (Conv2D). This corresponds to an image operation based on the application of a given set of filters to enhance specific features of the image. If the input image is A (see Figure 5 with footprint of ) the 2D convolutions of this individual image may be obtained, namely B, by applying the kernel function F, aswhere F stands for the filter applied and ∗ the convolution operator. The operation can be parametrized by using different filter sizes, strides, paddings, activation functions or kernel regularization. Filters of size are intended to highlight specific features in time and space produced by the presence of the dissimilar material region in the mould. Input image dimensions are given by , where for greyscale images, and output image dimensions are calculated by . For instance, the first Conv2D layer in Figure 6 uses a kernel with an input grayscale image object of . This filter operation produces an output image of for this first convolution. Filters normally make use of a certain step, named stride, that move the convolution filter along the x and y axis of the input image. Padding is the parameter which maintains the size of the output images resulting from the convolution B. Keras uses the padding=’same’ technique to avoid image edge trimming. Lastly, when convolution is completed, a ReLu (Rectified Linear Unit ) is used as cut-off function thus avoiding negative outputs that can be generated.
- MaxPooling (MaxPooling2D). This is applied to reduce the dimensions of the convolution filtered images with the purpose of obtaining more efficient and robust characteristics. The model uses a pooling filter, taking the maximum value of the pixels in the neighborhood as the result for a given point. For instance, Figure 6 shows MaxPooling operations used to reduce the image size from to in the first convolution.
- Batch normalization (BatchNormalization). This seeks to alleviate the movements produced in the distributions of internal nodes of the network with the intention of accelerating its training. Those movements are avoided via a normalization step, constraining means and variances of the layer inputs. Furthermore, it reduces the need for dropout, local response normalization and other regularization techniques [23].
- Flatten (Flatten). This operation splits up the characteristics, transforming them and preparing for obtaining a vector-type object [24]. It is used as training input of the subsequent fully-connected neural network (FCNN).
- Dense (Dense). The fully-connected layer is implemented by one or several dense functions. Each layer obtains n inputs from the precedent layer or, in case of the first dense layer, n inputs from the Flatten layer. Then, these inputs are balanced by the neural network weights and bias, and transformed into a set of outputs for the following layer according to their specific activation functions. The final dense layer contains a five-component vector-type to perform the regression on the values of and . Particularly, the neural network used in this work contains three fully connected layers, containing 128, 256 and 512 neurons respectively.
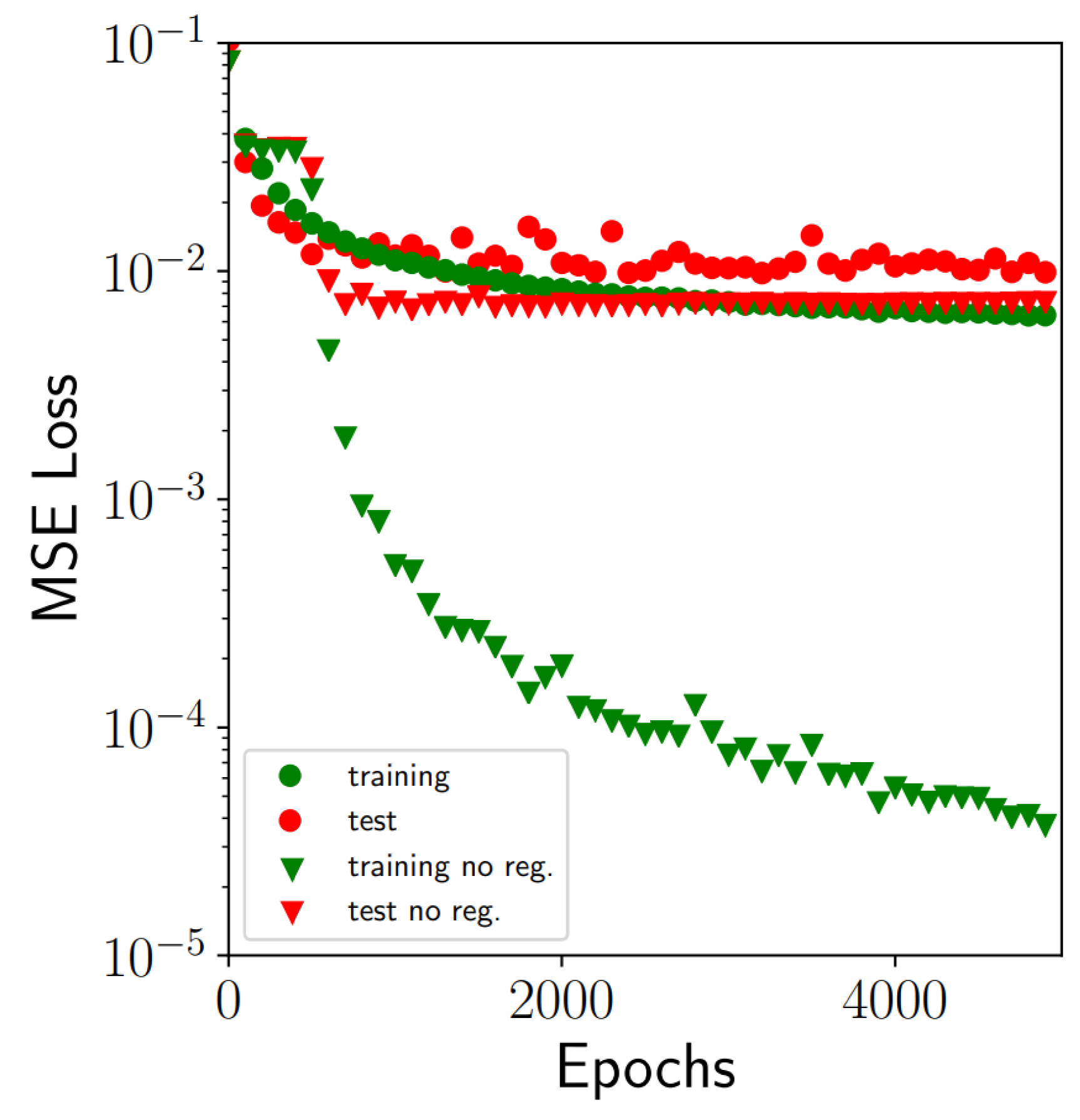
4.2. Training Machine Learning Models
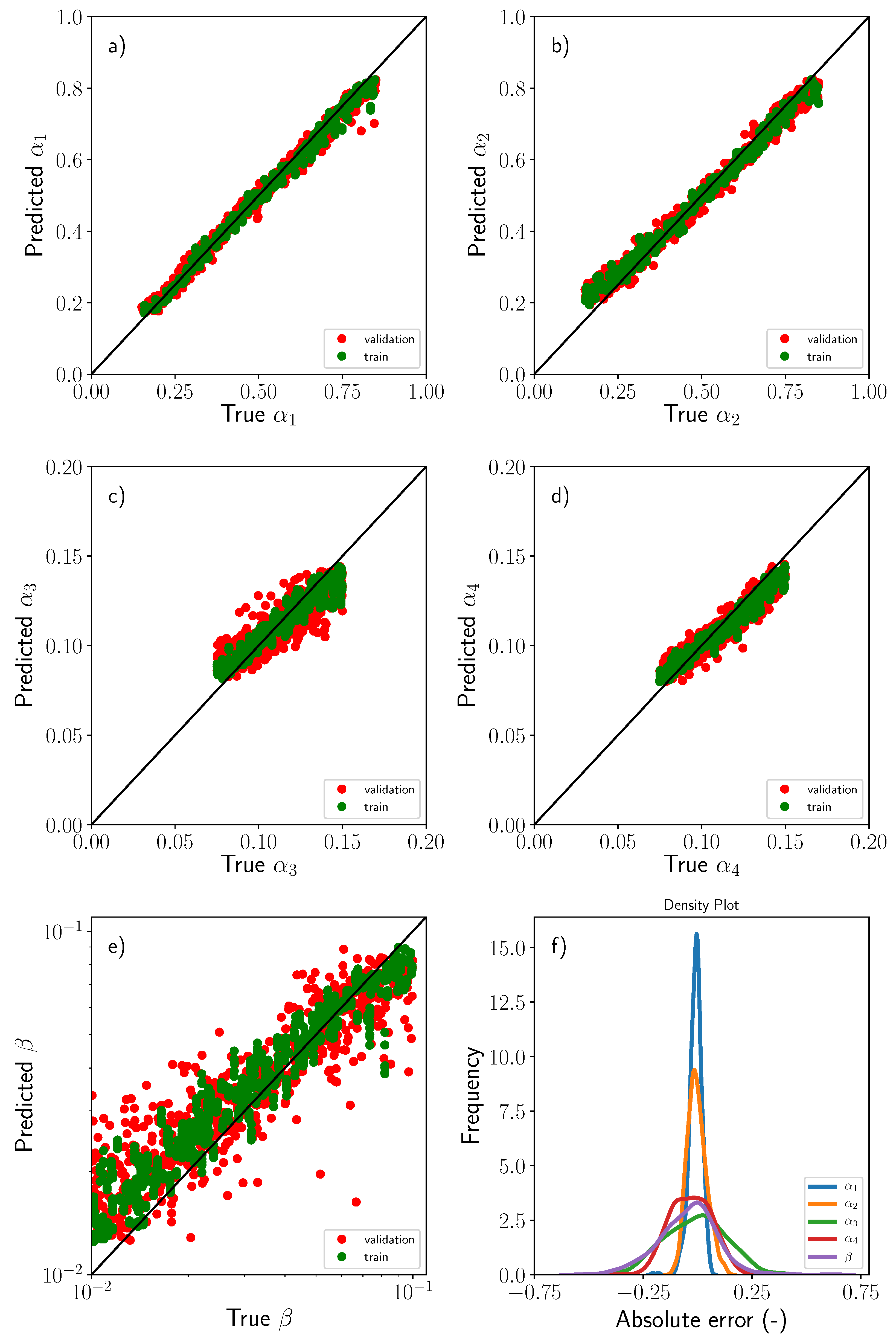
4.3. Deploying Machine Learning Models
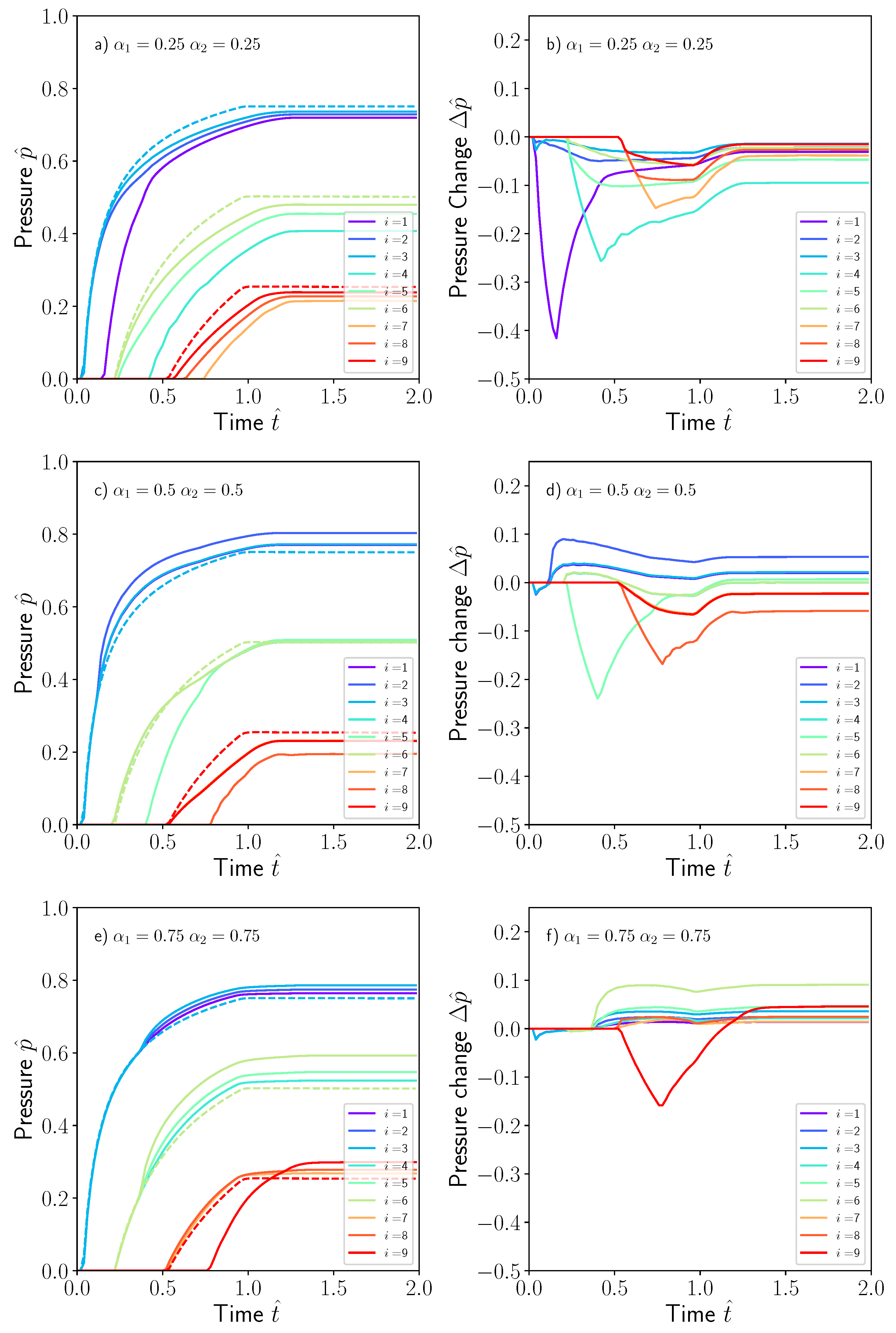
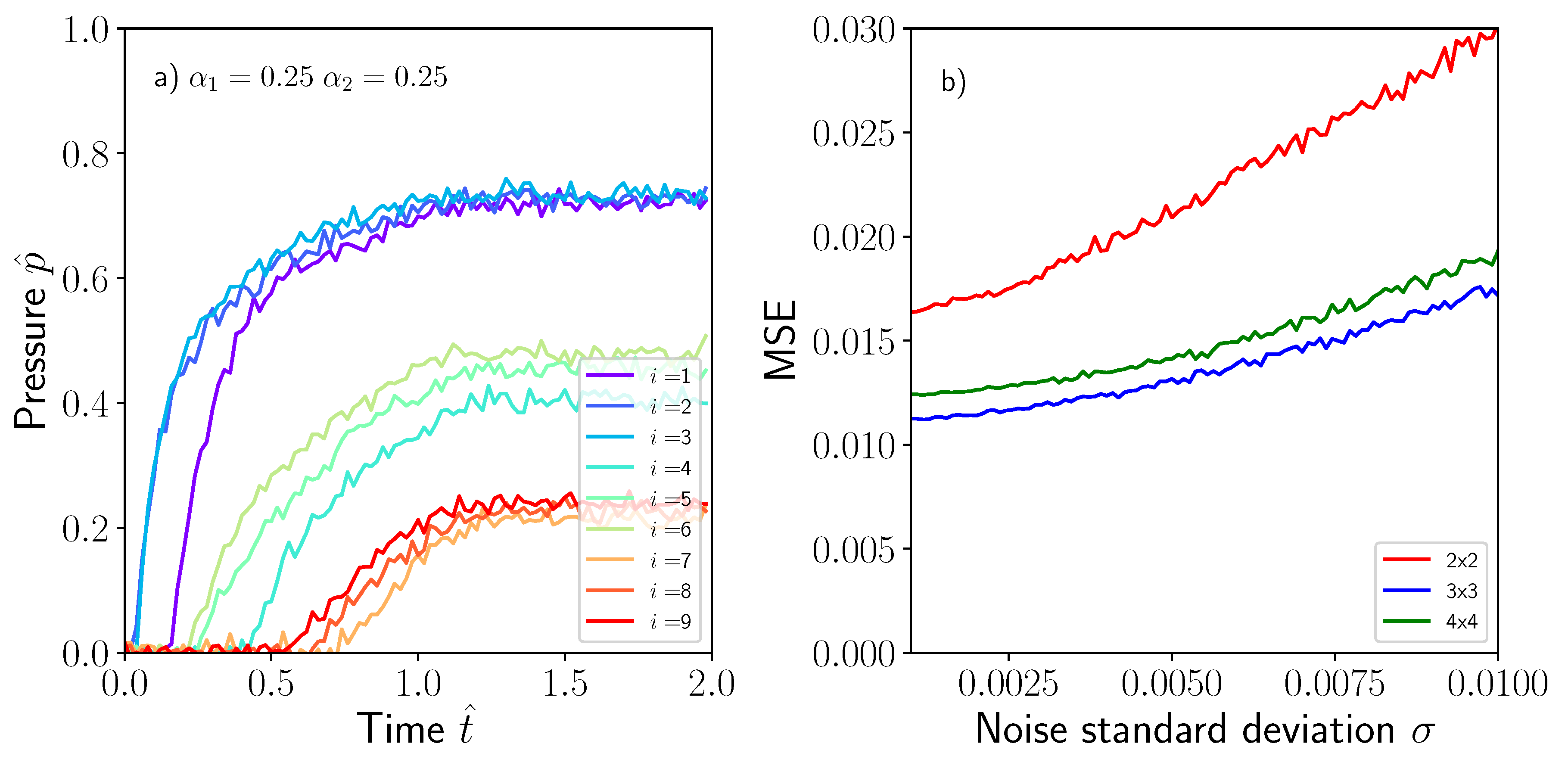
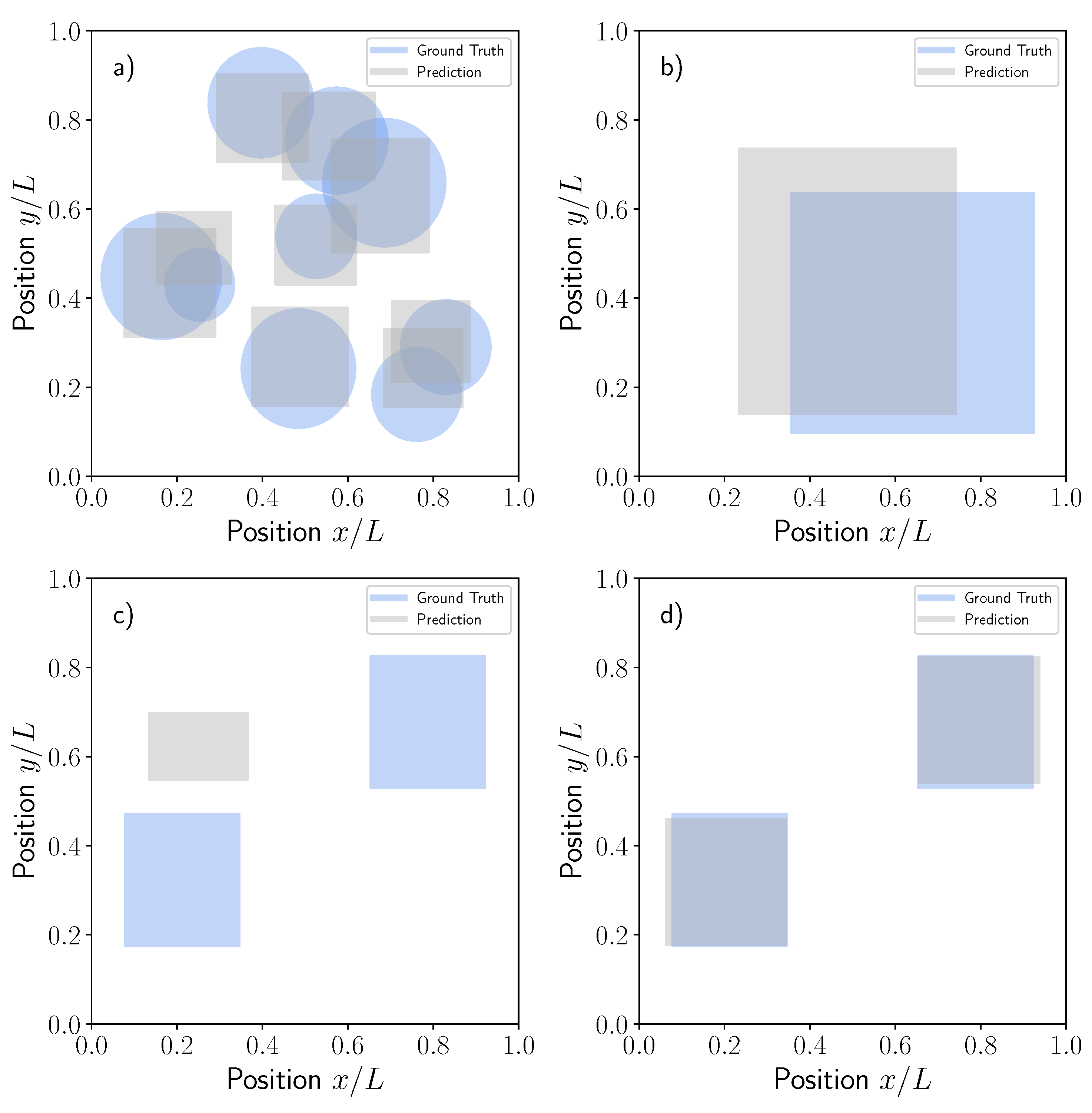
5. Discussion
Model Robustness
6. Conclusions and Final Remarks
- Machine learning and artificial intelligence strategies open revolutionary opportunities in material science and, more specifically, in materials and parts manufacturing. The ability of these technologies to deal and overcome complex physical and engineering problems that relate different datasets, as sensors and dissimilar material regions in this work, is highly aligned with Industry 4.0 concepts. In the future, this will enable the development of efficient cyber-physical systems to detect defects automatically during manufacturing while guaranteeing the implementation of the appropriate corrective actions.
- Some of the major concerns and drawbacks of the application of machine learning methods in manufacturing of structural composites are related with enormous costs and development times associated with the experimental generation of the large datasets required for training. A way of easing the burden on experimental tasks is to involve the cooperative help of simulation results to create augmented datasets. Of course, it could be argued that the accuracy of processing simulation tools to predict the involved variables is dubious, specially if manufacturing disturbances should be taken into account. This paper has presented a fully simulation-based machine learning model, although the purpose in future implementations will be to combine both experimental and model datasets.
- Many modelling techniques involve machine learning algorithms and include different architectures and methods. It should be noted that similar or even better results could be obtained by using other approaches not examined here. The aim of the paper was not to provide the optimum model configuration but to analyze the ability of machine learning to detect automatically flow disturbances occurring during liquid moulding by testing a simple problem. A future objective will entail examining of integration into a complete system able to detect manufacturing disturbances while implementing automatically the required corrective actions to maintain a constant quality of the manufactured part.
Author Contributions
Funding
Conflicts of Interest
References
- González, C.; Vilatela, J.; Molina-Aldareguía, J.; Lopes, C.; LLorca, J. Structural composites for multifunctional applications: Current challenges and future trends. Prog. Mater. Sci. 2017, 89, 194–251. [Google Scholar] [CrossRef]
- Llorca, J.; González, C.; Molina-Aldareguía, J.; Segurado, J.; Seltzer, R.; Sket, F.; Rodríguez, M.; Sádaba, S.; Muñoz, R.; Canal, L. Multiscale modeling of composite materials: A roadmap towards virtual testing. Adv. Mater. 2011, 23. [Google Scholar] [CrossRef] [PubMed]
- Roth, Y.C.; Weinholdt, M.; Winkelmann, L. Liquid Composite Moulding - Enabler for the automated production of CFRP aircfraft components. In Proceedings of the 16th European Conference on Composite Materials, ECCM 2014, Seville, Spain, 22–26 June 2014; pp. 22–26. [Google Scholar]
- Advani, S.; Hsiao, K.T. (Eds.) 1—Introduction to composites and manufacturing processes. In Manufacturing Techniques for Polymer Matrix Composites (PMCs); Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Sawston, UK, 2012; pp. 1–12. [Google Scholar] [CrossRef]
- Rudd, C.D.; Long, A.C.; Kendall, K.N.; Mangin, C.G.E. Liquid Moulding Technologies; Woodhead Publishing: Sawston, UK, 1997. [Google Scholar] [CrossRef]
- Siddig, N.A.; Binetruy, C.; Syerko, E.; Simacek, P.; Advani, S. A new methodology for race-tracking detection and criticality in resin transfer molding process using pressure sensors. J. Compos. Mater. 2018, 52, 4087–4103. [Google Scholar] [CrossRef]
- Zhou, B.; Lapedriza, A.; Xiao, J.; Torralba, A.; Oliva, A. Learning deep features for scene recognition using places database. Adv. Neural Inf. Process. Syst. 2014, 1, 487–495. [Google Scholar]
- Xiao, J.; Hays, J.; Ehinger, K.A.; Oliva, A.; Torralba, A. SUN database: Large-scale scene recognition from abbey to zoo. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3485–3492. [Google Scholar] [CrossRef]
- Mezzasalma, S.A. Chapter Three The General Theory of Brownian Relativity. Interface Sci. Technol. 2008, 15, 137–171. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A review of the application of machine learning and data mining approaches in continuum materials mechanics. Front. Mater. 2019, 6. [Google Scholar] [CrossRef]
- Wu, J.; Yin, X.; Xiao, H. Seeing permeability from images: Fast prediction with convolutional neural networks. Sci. Bull. 2018, 63, 1215–1222. [Google Scholar] [CrossRef]
- Iglesias, M.; Park, M.; Tretyakov, M.V. Bayesian inversion in resin transfer molding. Inverse Probl. 2018, 34, 1–49. [Google Scholar] [CrossRef]
- Lähivaara, T.; Kärkkäinen, L.; Huttunen, J.M.J.; Hesthaven, J.S. Deep convolutional neural networks for estimating porous material parameters with ultrasound tomography. J. Acoust. Soc. Am. 2018, 143, 1148–1158. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zabaras, N. Bayesian deep convolutional encoder–decoder networks for surrogate modeling and uncertainty quantification. J. Comput. Phys. 2018, 366, 415–447. [Google Scholar] [CrossRef]
- Bruschke, M.V.; Advani, S.G. A finite element/control volume approach to mold filling in anisotropic porous media. Polym. Compos. 1990, 11, 398–405. [Google Scholar] [CrossRef]
- Bruschke, M.V.; Advani, S.G. A numerical approach to model non-isothermal viscous flow through fibrous media with free surfaces. Int. J. Numer. Methods Fluids 1994, 19, 575–603. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- PyDOE. The Experimental Design Package for Python. Available online: https://pythonhosted.org/pyDOE/ (accessed on 9 June 2020).
- Chollet, F.; KERAS. Available online: https://github.com/fchollet/keras (accessed on 9 June 2020).
- Cun, Y.L.; Boser, B.; Denker, J.S.; Howard, R.E.; Habbard, W.; Jackel, L.D.; Henderson, D. Handwritten Digit Recognition with a Back-propagation Network. In Advances in Neural Information Processing Systems 2; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1990; pp. 396–404. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Jin, J.; Dundar, A.; Culurciello, E. Flattened convolutional neural networks for feedforward acceleration. arXiv 2014, arXiv:1412.5474. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:abs/1212.5701. [Google Scholar]
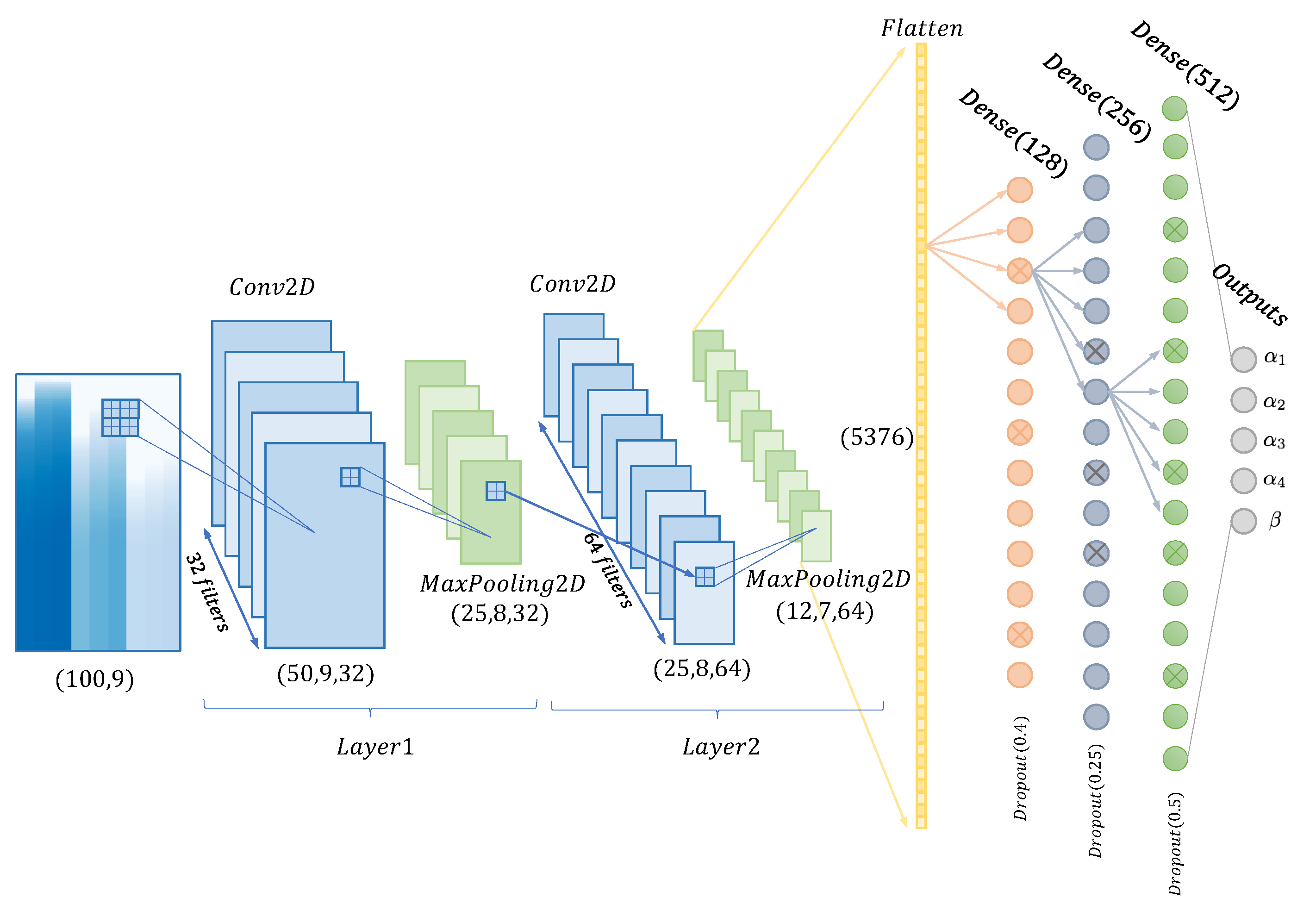
| Layers | Specifications |
|---|---|
| Conv2D | 32 filters with stride and padding same |
| activation ReLu + Regularization | |
| Batch Normalization | - |
| MaxPooling2D | filter with stride |
| Conv2D | 64 filters with stride and padding same |
| activation ReLu + Regularization | |
| Batch Normalization | - |
| MaxPooling2D | filter with stride |
| Flatten | - |
| Fully Connected | 128 (activation ReLu+ Dropout 0.4) |
| Fully Connected | 256 (activation ReLu+ Dropout 0.25) |
| Fully Connected | 512 (activation Softmax+ Dropout 0.5) |
| Fully Connected | 5 (, , , , ) |
| Error | |||||
|---|---|---|---|---|---|
| 0.5% | 3.0% | 49% | 35% | 42% | |
| 0.2% | 0.0% | 16% | 3% | 15% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, C.; Fernández-León, J. A Machine Learning Model to Detect Flow Disturbances during Manufacturing of Composites by Liquid Moulding. J. Compos. Sci. 2020, 4, 71. https://doi.org/10.3390/jcs4020071
González C, Fernández-León J. A Machine Learning Model to Detect Flow Disturbances during Manufacturing of Composites by Liquid Moulding. Journal of Composites Science. 2020; 4(2):71. https://doi.org/10.3390/jcs4020071
Chicago/Turabian StyleGonzález, Carlos, and Joaquín Fernández-León. 2020. "A Machine Learning Model to Detect Flow Disturbances during Manufacturing of Composites by Liquid Moulding" Journal of Composites Science 4, no. 2: 71. https://doi.org/10.3390/jcs4020071
APA StyleGonzález, C., & Fernández-León, J. (2020). A Machine Learning Model to Detect Flow Disturbances during Manufacturing of Composites by Liquid Moulding. Journal of Composites Science, 4(2), 71. https://doi.org/10.3390/jcs4020071





