Fracture Analysis of Particulate Metal Matrix Composite Using X-ray Tomography and Extended Finite Element Method (XFEM)
Abstract
1. Introduction
2. Methodology
2.1. Implicit Geometry Representation
2.2. Formulation of XFEM for Discontinuities
2.3. Implementation of Weibull Strength Distribution Model
| Algorithm 1. Particle fracture approximation |
| Identify all ⸦ as intact particles |
| Assign a random critical probability to each particle |
| for Quasi-static load step i = 1 to n do |
| Calculate stress field with XFEM algorithm |
| if No intact particle left in the domain then |
| Continue to next step i = i + 1 |
| for ⸦ do |
| Compute Weibull fracture probability |
| If max then |
| Break the particle with the max |
| Create a strong discontinuous plane at with normal direction |
| Mark as failed particle, Ȼ |
| Roll back and repeat load step i |
| else |
| Continue to next step i + 1 |
3. Fracture of SiC Particle Reinforced 2080 Aluminum Alloy by XFEM
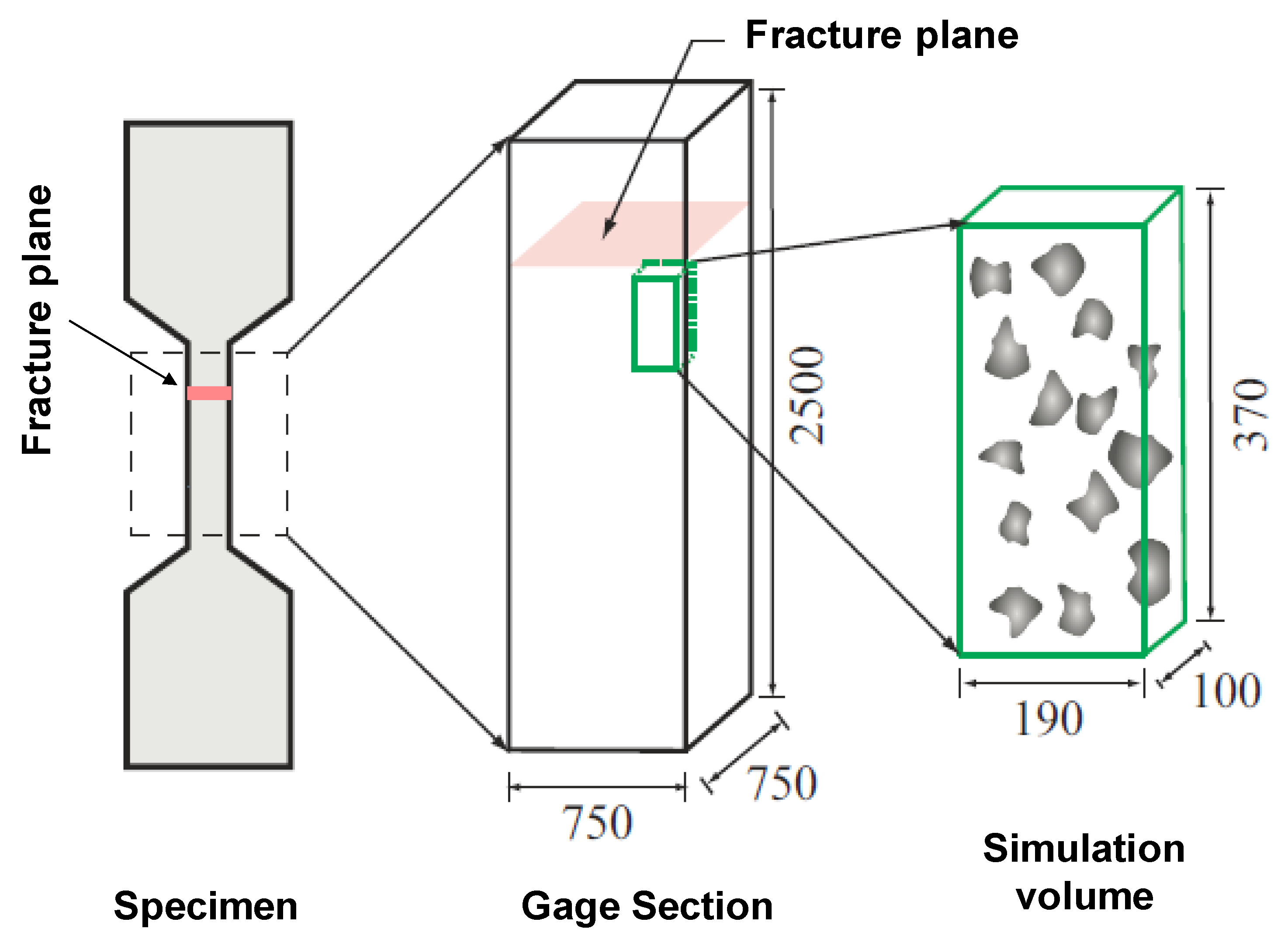
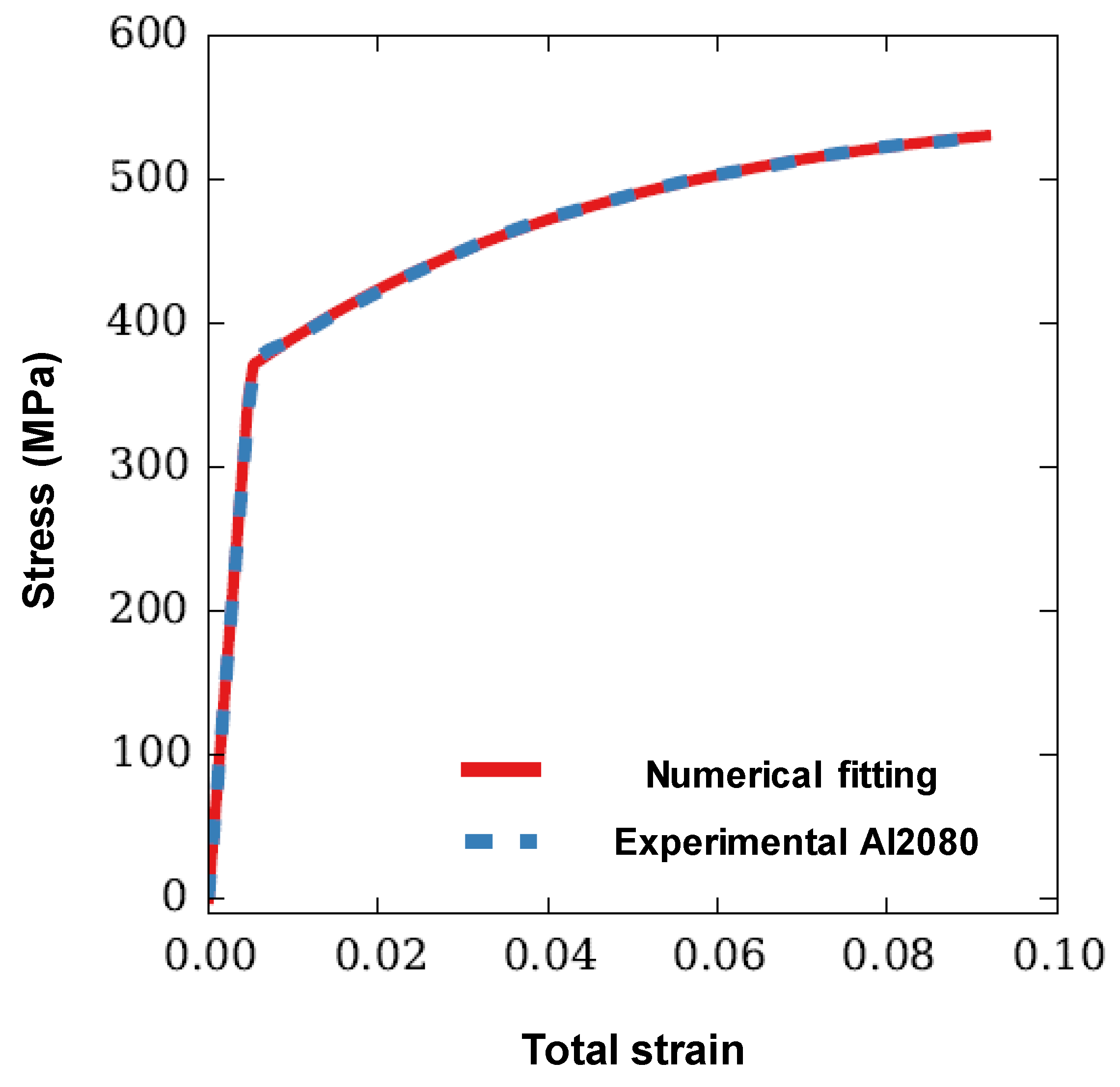
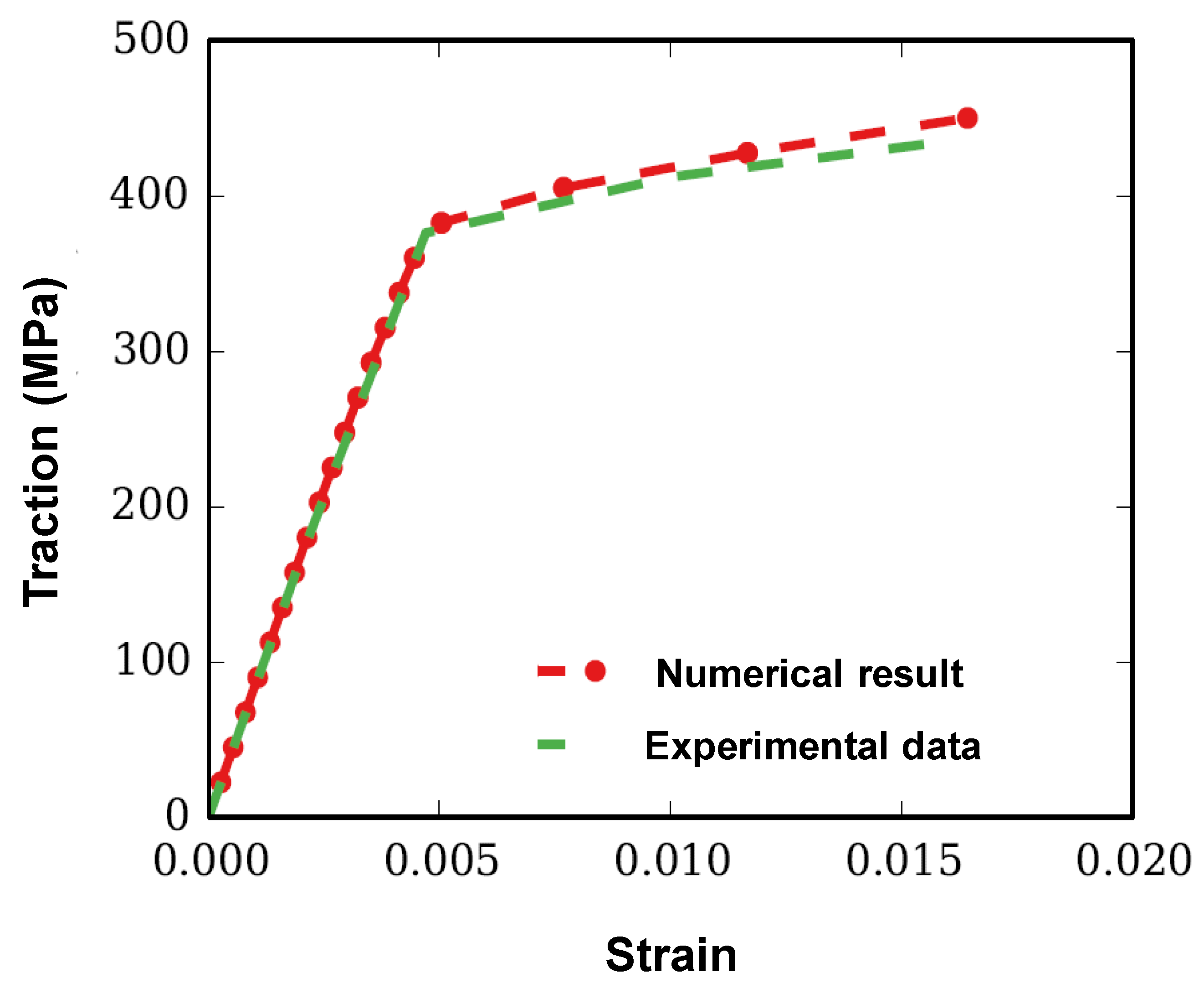
3.1. Numerical Modeling
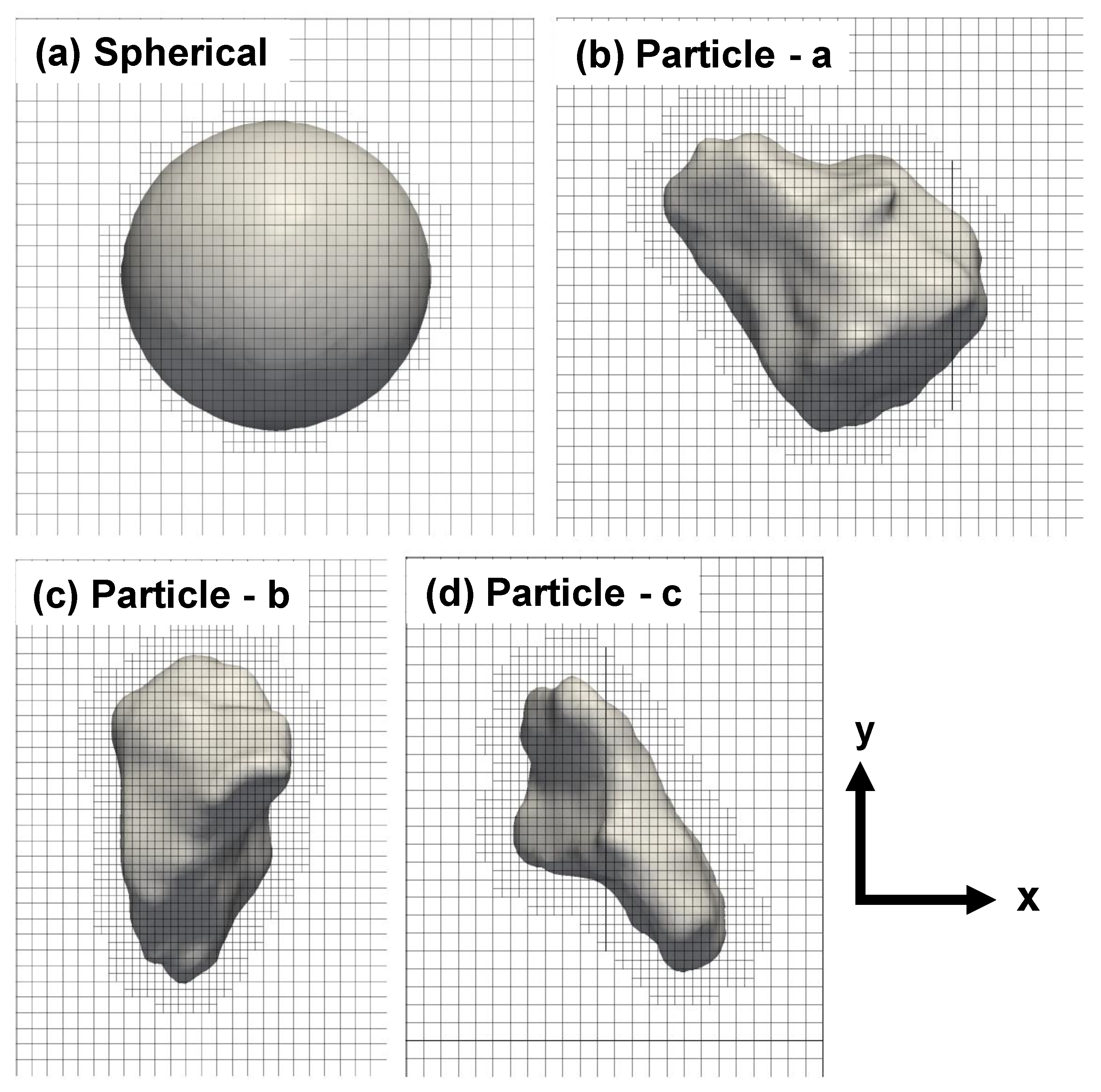
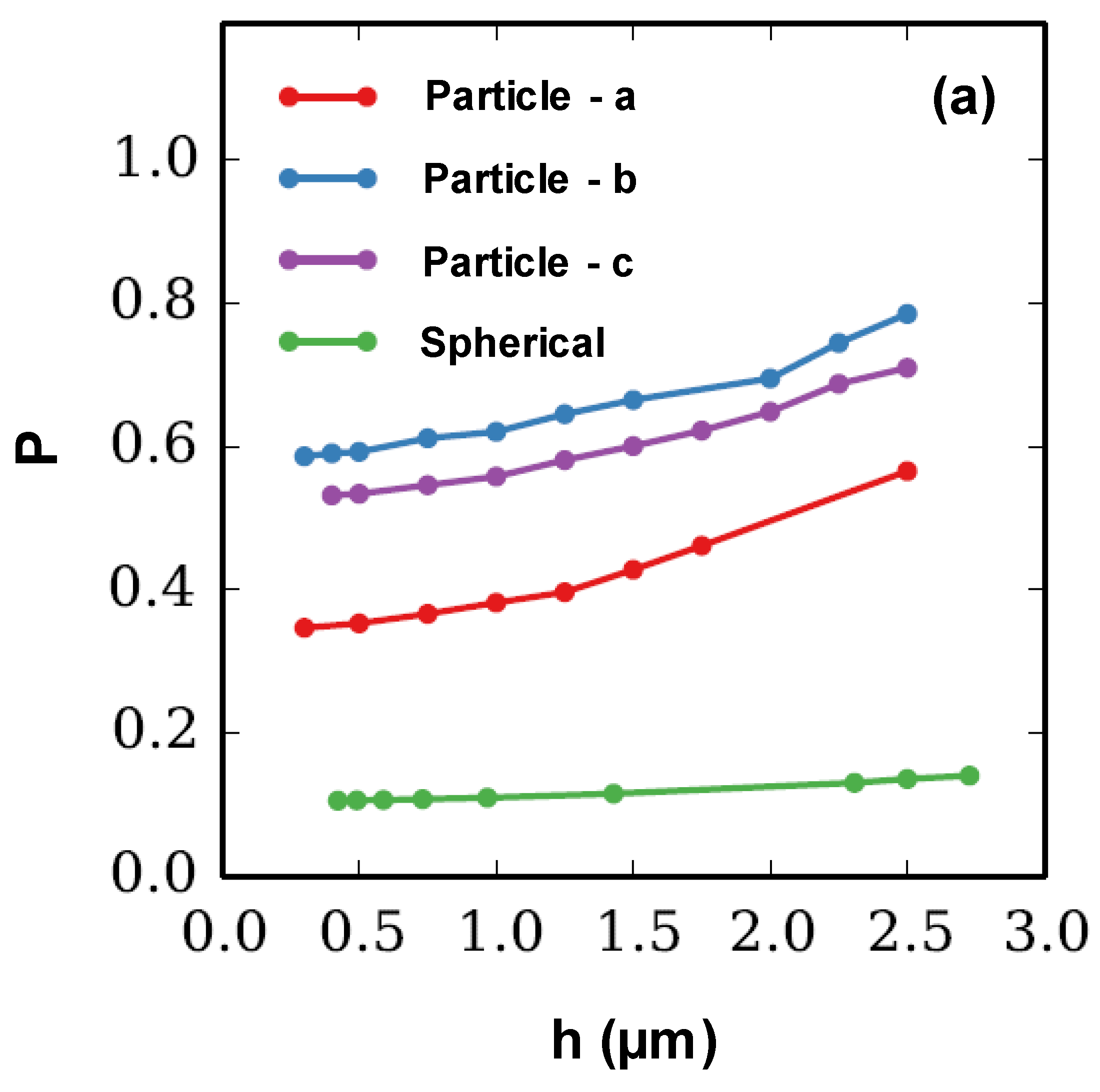
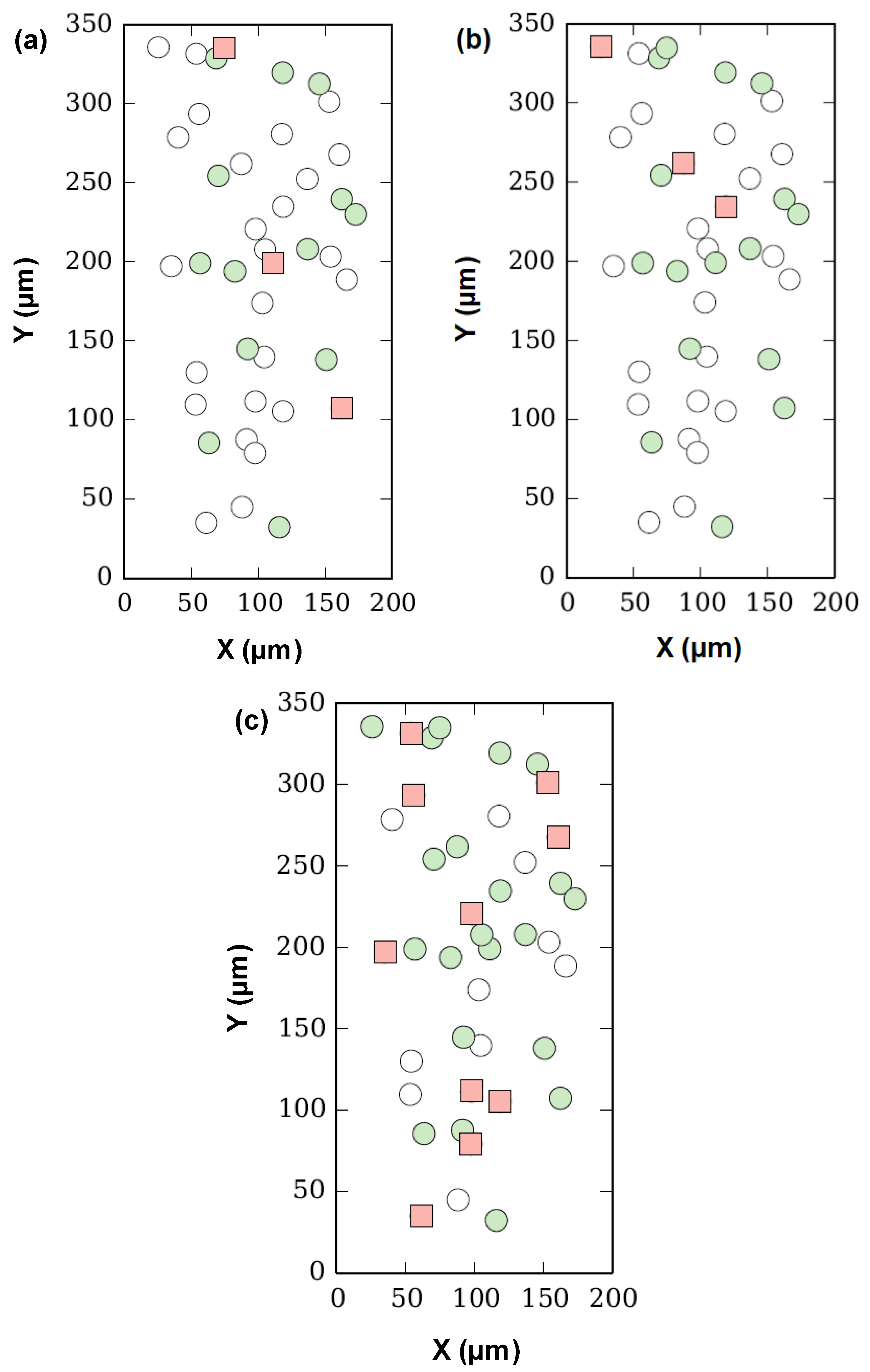
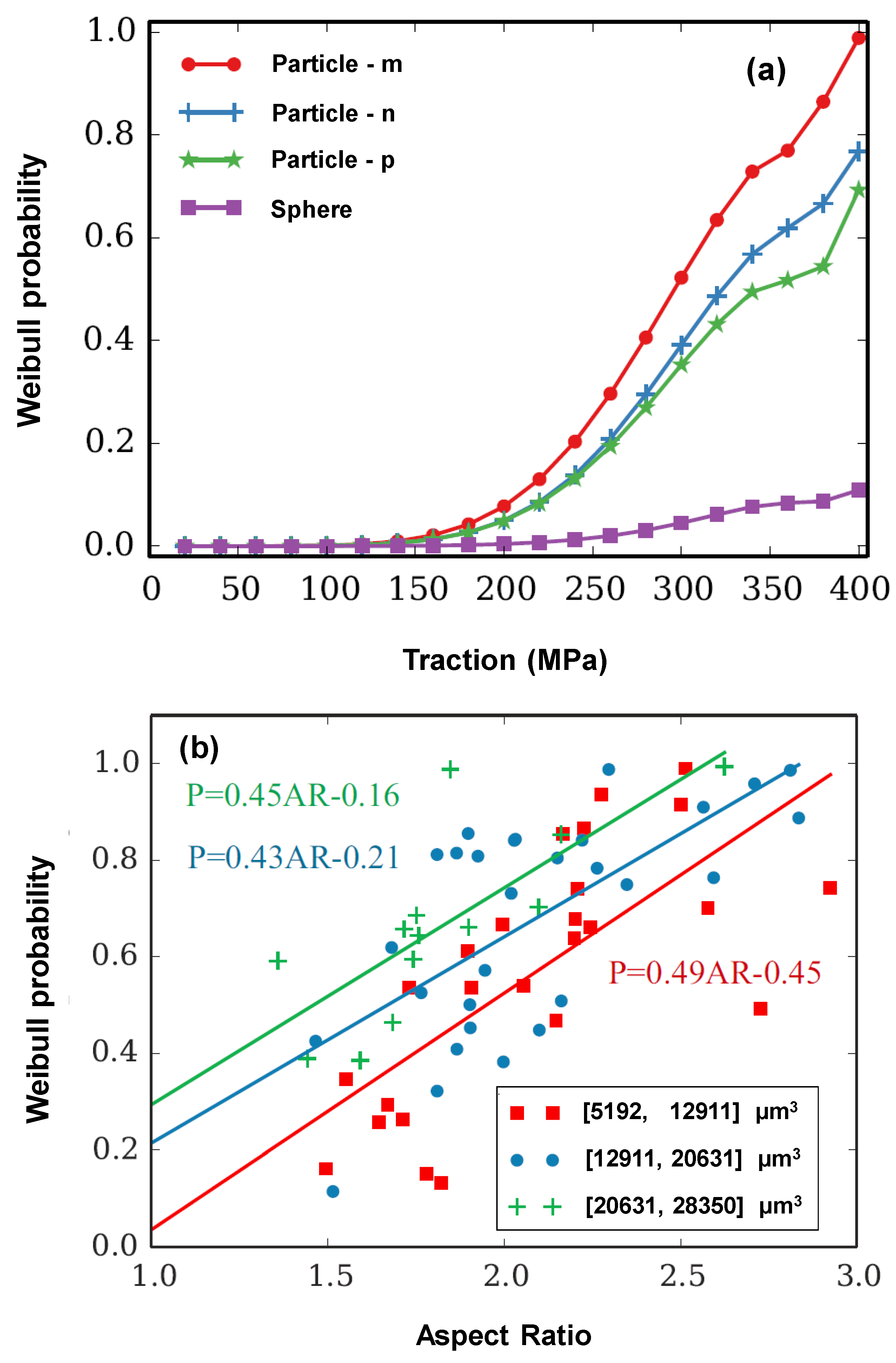
3.2. Convergence study of Weibull Probability
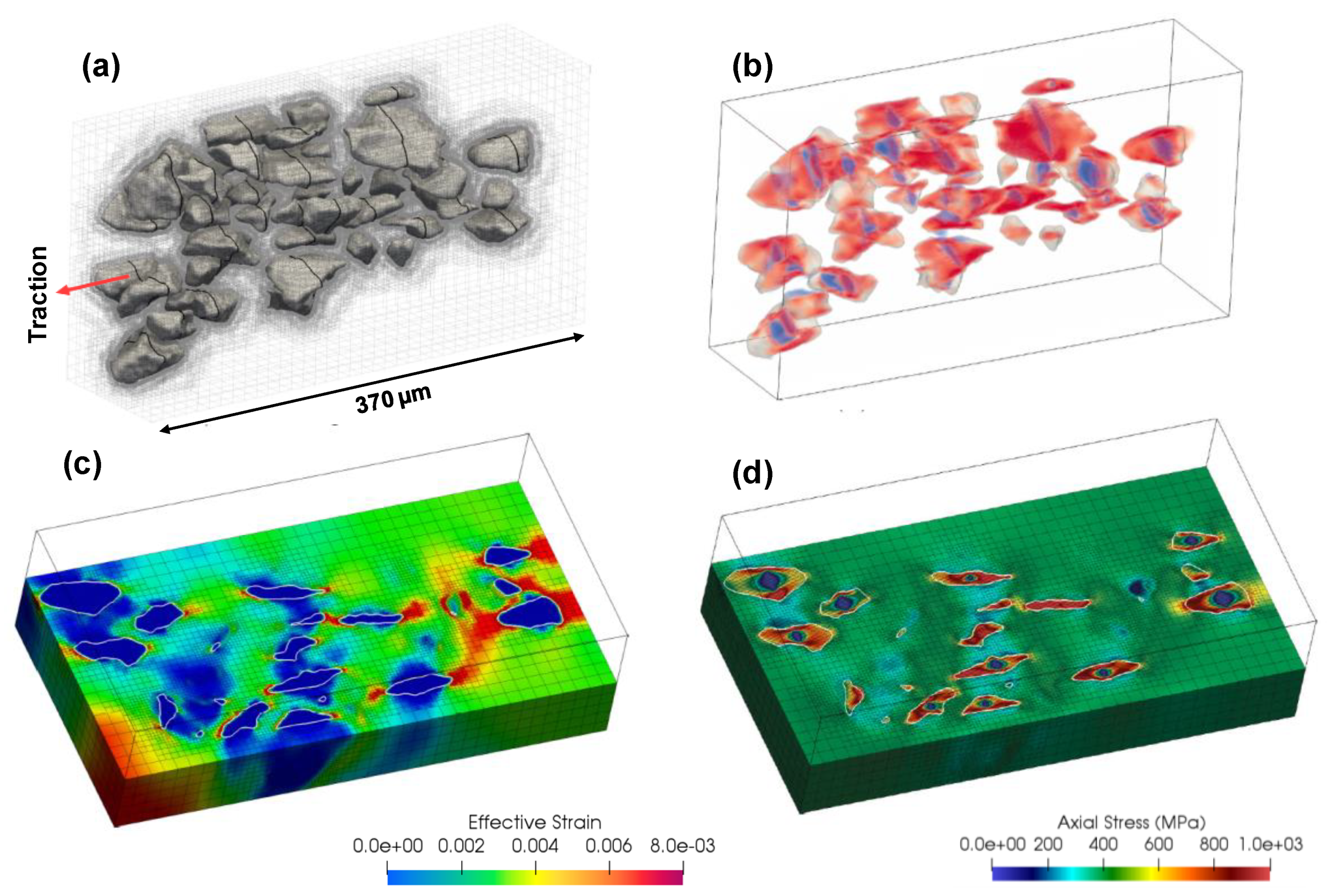
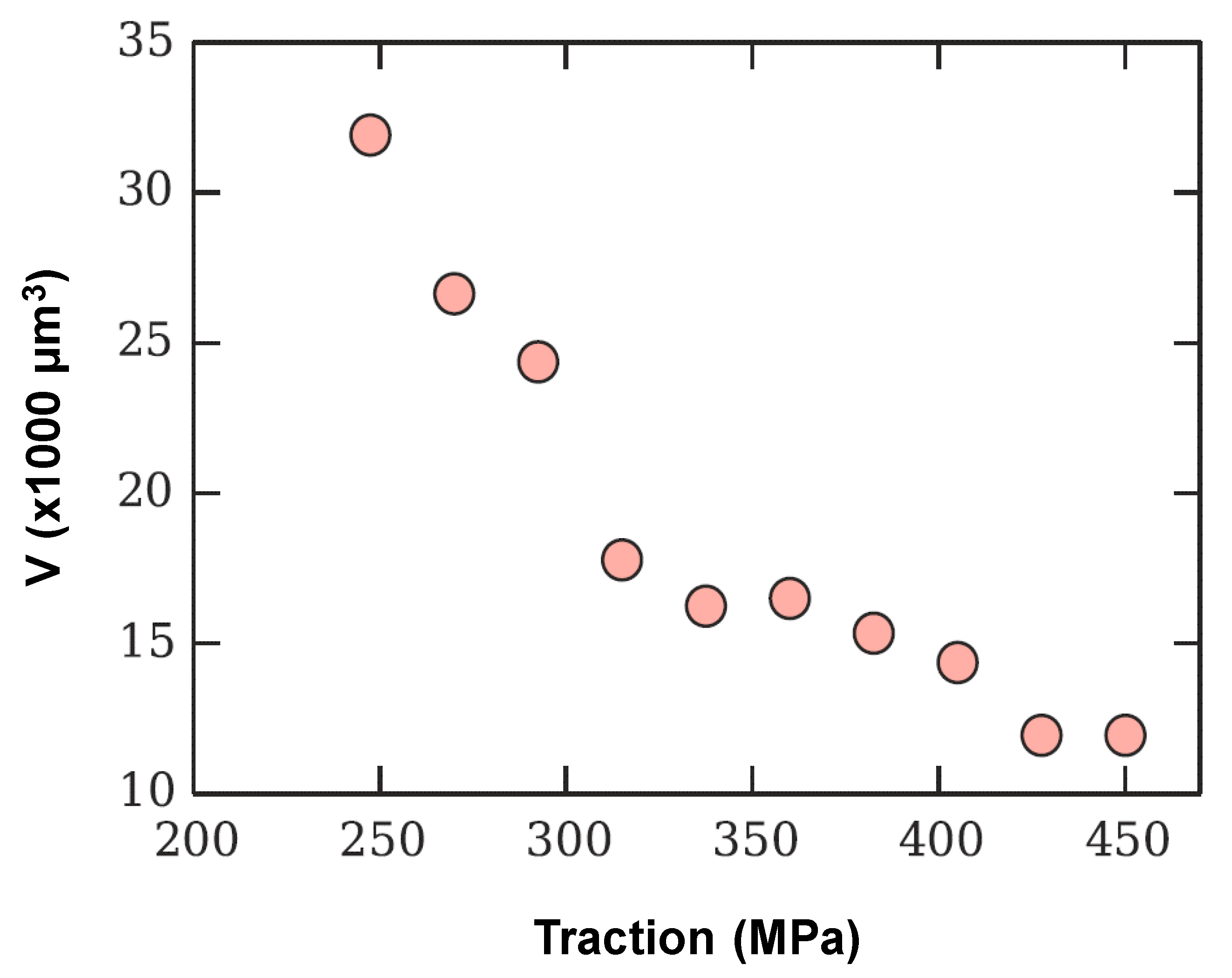
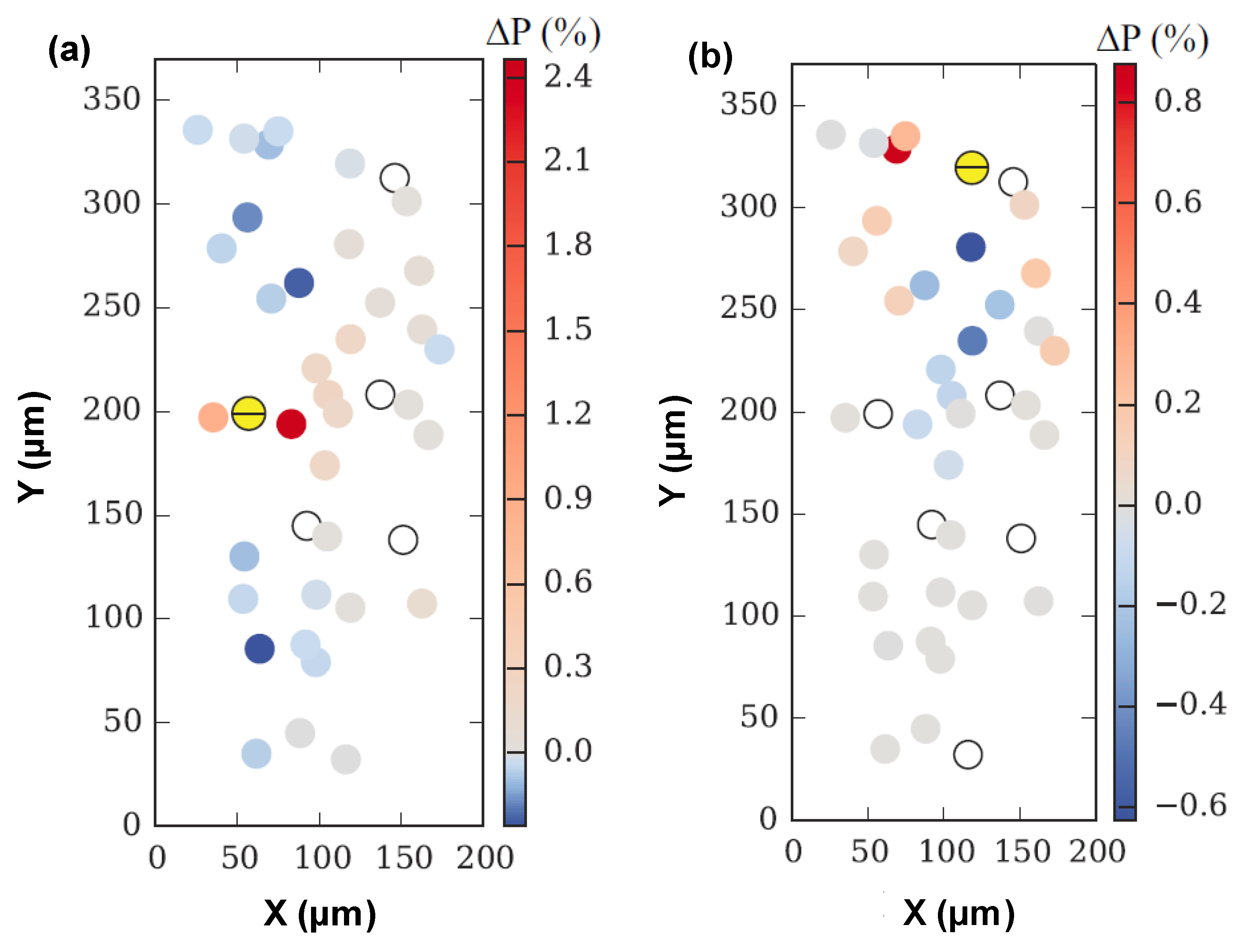
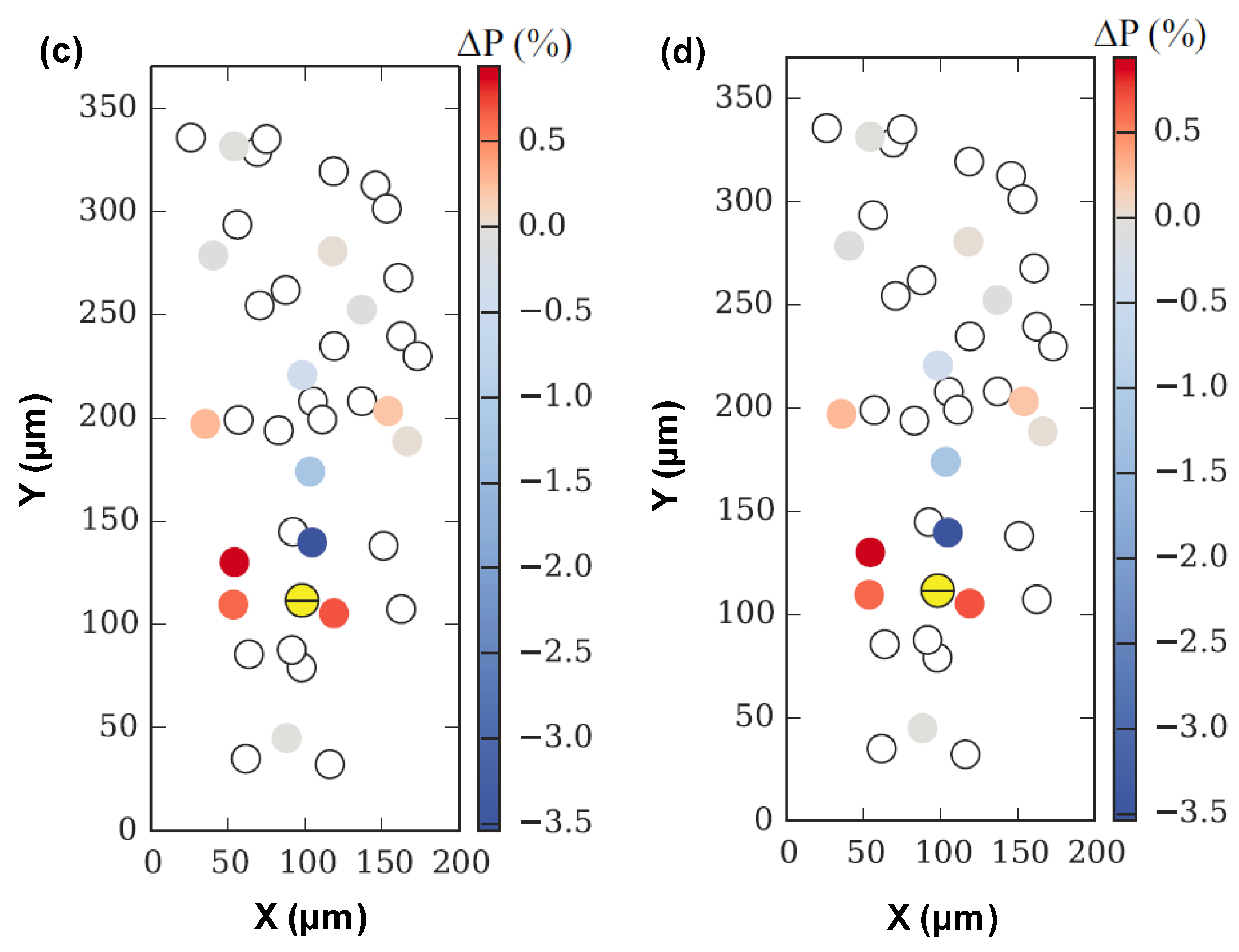
3.3. Fracture Analysis of the Simulation Volume
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chawla, K.K. Metal Matrix Composites; Springer Science & Business Media LLC: New York, NY, USA, 2019; pp. 199–249. [Google Scholar]
- Bazant, Z.P.; Tabbara, M.R.; Kazemi, M.T.; Pijaudier-Cabot, G. Random Particle Model for Fracture of Aggregate or Fiber Composites. J. Eng. Mech. 1990, 116, 1686–1705. [Google Scholar] [CrossRef]
- Ayyar, A.; Crawford, G.; Williams, J.; Chawla, N. Numerical simulation of the effect of particle spatial distribution and strength on tensile behavior of particle reinforced composites. Comput. Mater. Sci. 2008, 44, 496–506. [Google Scholar] [CrossRef]
- Mishnaevsky, L., Jr.; Derrien, K.; Baptiste, D. Effect of microstructure of particle reinforced composites on the damage evolution: Probabilistic and numerical analysis. Compos. Sci. Technol. 2004, 64, 1805–1818. [Google Scholar] [CrossRef]
- Bray, D.J.; Gilmour, S.G.; Guild, F.J.; Taylor, A.C. The effects of particle morphology on the analysis of discrete particle dispersion using Delaunay tessellation. Compos. Part A Appl. Sci. Manuf. 2013, 54, 37–45. [Google Scholar] [CrossRef]
- Singh, S.S.; Chawla, N. 3D/4D X-Ray Microtomography: Probing the Mechanical Behavior of Materials. In Handbook of Mechanics of Materials; Springer Science & Business Media LLC: New York, NY, USA, 2018; pp. 1–21. [Google Scholar]
- Williams, J.; Flom, Z.; Amell, A.; Chawla, N.; Xiao, X.; De Carlo, F. Damage evolution in SiC particle reinforced Al alloy matrix composites by X-ray synchrotron tomography. Acta Mater. 2010, 58, 6194–6205. [Google Scholar] [CrossRef]
- Hruby, P.; Singh, S.S.; Williams, J.J.; Xiao, X.; De Carlo, F.; Chawla, N. Fatigue crack growth in SiC particle reinforced Al alloy matrix composites at high and low R-ratios by in situ X-ray synchrotron tomography. Int. J. Fatigue 2014, 68, 136–143. [Google Scholar] [CrossRef]
- Babout, L.; Maire, E.; Buffiere, J.; Fougères, R. Characterization by X-ray computed tomography of decohesion, porosity growth and coalescence in model metal matrix composites. Acta Mater. 2001, 49, 2055–2063. [Google Scholar] [CrossRef]
- Singh, S.S.; Schwartzstein, C.; Williams, J.J.; Xiao, X.; De Carlo, F.; Chawla, N. 3D microstructural characterization and mechanical properties of constituent particles in Al 7075 alloys using X-ray synchrotron tomography and nanoindentation. J. Alloy. Compd. 2014, 602, 163–174. [Google Scholar] [CrossRef]
- Kastner, J.; Harrer, B.; Degischer, H.P. High resolution cone beam X-ray computed tomography of 3D-microstructures of cast Al-alloys. Mater. Charact. 2011, 62, 99–107. [Google Scholar] [CrossRef]
- Padilla, E.; Jakkali, V.; Jiang, L.; Chawla, N. Quantifying the effect of porosity on the evolution of deformation and damage in Sn-based solder joints by X-ray microtomography and microstructure-based finite element modeling. Acta Mater. 2012, 60, 4017–4026. [Google Scholar] [CrossRef]
- Sarvesha, R.; Alam, W.; Gokhale, A.; Guruprasad, T.; Bhagavath, S.; Karagadde, S.; Jain, J.; Singh, S.S. Quantitative assessment of second phase particles characteristics and its role on the deformation response of a Mg-8Al-0.5Zn alloy. Mater. Sci. Eng. A 2019, 759, 368–379. [Google Scholar] [CrossRef]
- Singh, S.S.; Williams, J.J.; Hruby, P.; Xiao, X.; De Carlo, F.; Chawla, N. In situ experimental techniques to study the mechanical behavior of materials using X-ray synchrotron tomography. Integr. Mater. Manuf. Innov. 2014, 3, 109–122. [Google Scholar] [CrossRef]
- Withers, P.J.; Preuss, M. Fatigue and Damage in Structural Materials Studied by X-Ray Tomography. Annu. Rev. Mater. Res. 2012, 42, 81–103. [Google Scholar] [CrossRef]
- Singh, S.S.; Williams, J.J.; Xiao, X.; De Carlo, F.; Chawla, N. In Situ Three Dimensional (3D) X-Ray Synchrotron Tomography of Corrosion Fatigue in Al7075 Alloy. In Fatigue of Materials II: Advances and Emergences in Understanding, Materials Science and Technology; John Witey & Sons Inc.: Pittsburgh, PA, USA, 2012; pp. 17–25. [Google Scholar]
- Babout, L.; Marrow, T.J.; Engelberg, D.L.; Withers, P.J. X-ray microtomographic observation of intergranular stress corrosion cracking in sensitised austenitic stainless steel. Mater. Sci. Technol. 2006, 22, 1068–1075. [Google Scholar] [CrossRef]
- Robertson, I.; Schuh, C.A.; Vetrano, J.S.; Browning, N.D.; Field, D.; Jensen, D.J.; Miller, M.K.; Baker, I.; Dunand, D.C.; Dunin-Borkowski, R.E.; et al. Towards an integrated materials characterization toolbox. J. Mater. Res. 2011, 26, 1341–1383. [Google Scholar] [CrossRef]
- Chawla, N.; Sidhu, R.; Ganesh, V. Three-dimensional visualization and microstructure-based modeling of deformation in particle-reinforced composites. Acta Mater. 2006, 54, 1541–1548. [Google Scholar] [CrossRef]
- Watson, I.G.; Lee, P.D.; Dashwood, R.J.; Young, P. Simulation of the mechanical properties of an aluminium matrix composite using X-ray microtomography. Metall. Mater. Trans. A 2006, 37, 551–558. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moes, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Melenk, J.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Huynh, D.B.P.; Belytschko, T. The extended finite element method for fracture in composite materials. Int. J. Numer. Methods Eng. 2009, 77, 214–239. [Google Scholar] [CrossRef]
- Ye, C.; Shi, J.; Cheng, G.J. An eXtended Finite Element Method (XFEM) study on the effect of reinforcing particles on the crack propagation behavior in a metal–matrix composite. Int. J. Fatigue 2012, 44, 151–156. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, L.; Wu, L.; Yu, H. Numerical simulation of crack growth in brittle matrix of particle reinforced composites using the xfem technique. Acta Mech. Solida Sin. 2012, 25, 9–21. [Google Scholar] [CrossRef]
- Doremus, R.H. Fracture statistics: A comparison of the normal, Weibull, and Type I extreme value distributions. J. Appl. Phys. 1983, 54, 193. [Google Scholar] [CrossRef]
- Lu, C.; Danzer, R.; Fischer, F.D. Fracture statistics of brittle materials: Weibull or normal distribution. Phys. Rev. E 2002, 65, 067102. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 292–297. [Google Scholar]
- Vlassov, S.; Polyakov, B.; Dorogin, L.M.; Antsov, M.; Mets, M.; Umalas, M.; Saar, R.; Lohmus, R.; Kink, I. Elasticity and yield strength of pentagonal silver nanowires: In situ bending tests. Mater. Chem. Phys. 2014, 143, 1026–1031. [Google Scholar] [CrossRef]
- Van Boekel, M. On the use of the Weibull model to describe thermal inactivation of microbial vegetative cells. Int. J. Food Microbiol. 2002, 74, 139–159. [Google Scholar] [CrossRef]
- Darveaux, R. Effect of Simulation Methodology on Solder Joint Crack Growth Correlation and Fatigue Life Prediction. J. Electron. Packag. 2002, 124, 147–154. [Google Scholar] [CrossRef]
- Mudry, F. A local approach to cleavage fracture. Nucl. Eng. Des. 1987, 105, 65–76. [Google Scholar] [CrossRef]
- Ruggieri, C.; Gao, X.; Dodds, R. Transferability of elastic–plastic fracture toughness using the Weibull stress approach: Significance of parameter calibration. Eng. Fract. Mech. 2000, 67, 101–117. [Google Scholar] [CrossRef]
- Hidalgo, R.C.; Moreno, Y.; Kun, F.; Herrmann, H.J. Fracture model with variable range of interaction. Phys. Rev. E 2002, 65, 046148. [Google Scholar] [CrossRef]
- Xia, L.; Shih, C. Ductile crack growth—III. Transition to cleavage fracture incorporating statistics. J. Mech. Phys. Solids 1996, 44, 603–639. [Google Scholar] [CrossRef]
- Eckschlager, A.; Han, W.; Böhm, H.J. A unit cell model for brittle fracture of particles embedded in a ductile matrix. Comput. Mater. Sci. 2002, 25, 85–91. [Google Scholar] [CrossRef]
- Gao, X.; Ruggieri, C.; Dodds, R.H., Jr. Calibration of Weibull stress parameters using fracture toughness data. Int. J. Fract. 1998, 92, 175–200. [Google Scholar] [CrossRef]
- Gao, X.; Ruggieri, C.; Dodds, R.H., Jr. A Weibull stress model to predict cleavage fracture in plates containing surface cracks. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 481–493. [Google Scholar] [CrossRef]
- Yuan, R.; Singh, S.S.; Chawla, N.; Oswald, J. Geometry segmentation of voxelized representations of heterogeneous microstructures using betweenness centrality. Mater. Charact. 2016, 118, 553–559. [Google Scholar] [CrossRef]
- Belytschko, T.; Parimi, C.; Moes, N.; Sukumar, N.; Usui, S. Structured extended finite element methods for solids defined by implicit surfaces. Int. J. Numer. Methods Eng. 2002, 56, 609–635. [Google Scholar] [CrossRef]
- Sukumar, N.; Chopp, D.; Moes, N.; Belytschko, T. Modeling holes and inclusions by level sets in the extended finite-element method. Comput. Methods Appl. Mech. Eng. 2001, 190, 6183–6200. [Google Scholar] [CrossRef]
- Stolarska, M.; Chopp, D.L.; Moes, N.; Belytschko, T. Modelling crack growth by level sets in the extended finite element method. Int. J. Numer. Methods Eng. 2001, 51, 943–960. [Google Scholar] [CrossRef]
- Gravouil, A.; Moes, N.; Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets-Part II: Level set update. Int. J. Numer. Methods Eng. 2002, 53, 2569–2586. [Google Scholar] [CrossRef]
- Yuan, R.; Singh, S.S.; Chawla, N.; Oswald, J. Efficient methods for implicit geometrical representation of complex material microstructures. Int. J. Numer. Methods Eng. 2014, 98, 79–91. [Google Scholar] [CrossRef]
- Sethian, J.A. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 1996, 93, 1591–1595. [Google Scholar] [CrossRef] [PubMed]
- Chopp, D.L. Some Improvements of the Fast Marching Method. SIAM J. Sci. Comput. 2001, 23, 230–244. [Google Scholar] [CrossRef]
- Belytschko, T.; Gracie, R.; Ventura, G. A review of extended/generalized finite element methods for material modeling. Model. Simul. Mater. Sci. Eng. 2009, 17, 43001. [Google Scholar] [CrossRef]
- Krongauz, Y.; Belytschko, T. EFG approximation with discontinuous derivatives. Int. J. Numer. Methods Eng. 1998, 41, 1215–1233. [Google Scholar] [CrossRef]
- Moes, N.; Cloirec, M.; Cartraud, P.; Remacle, J.-F. A computational approach to handle complex microstructure geometries. Comput. Methods Appl. Mech. Eng. 2003, 192, 3163–3177. [Google Scholar] [CrossRef]
- Mishnaevsky, L.L. Automatic voxel-based generation of 3D microstructural FE models and its application to the damage analysis of composites. Mater. Sci. Eng. A. 2005, 407, 11–23. [Google Scholar] [CrossRef]
- Lewis, C.; Withers, P.J. Weibull modelling of particle cracking in metal matrix composites. Acta Met. Mater. 1995, 43, 3685–3699. [Google Scholar] [CrossRef]
- Li, M.; Ghosh, S.; Richmond, O.; Weiland, H.; Rouns, T. Three dimensional characterization and modeling of particle reinforced metal matrix composites part II: Damage characterization. Mater. Sci. Eng. A 1999, 266, 221–240. [Google Scholar] [CrossRef]
- Antretter, T.; Fischer, F. Particle cleavage and ductile crack growth in a two-phase composite on a microscale. Comput. Mater. Sci. 1998, 13, 1–7. [Google Scholar] [CrossRef]
- Wallin, K.; Saario, T. Fracture of brittle particles in a ductile matrix. Int. J. Fract. 1986, 32, 201–209. [Google Scholar] [CrossRef]
- Williams, J.J.; Chapman, N.C.; Jakkali, V.; Tanna, V.A.; Chawla, N.; Xiao, X.; De Carlo, F. Characterization of Damage Evolution in SiC Particle Reinforced Al Alloy Matrix Composites by In-Situ X-Ray Synchrotron Tomography. Met. Mater. Trans. A 2011, 42, 2999–3005. [Google Scholar] [CrossRef]
- Chawla, N.; Jones, J.W.; Andres, C.; Allison, J.E. Effect of SiC volume fraction and particle size on the fatigue resistance of a 2080 Al/SiC p composite. Met. Mater. Trans. A 1998, 29, 2843–2854. [Google Scholar] [CrossRef]
- Singh, S.S.; Stannard, T.J.; Xiao, X.; Chawla, N. In Situ X-ray Microtomography of Stress Corrosion Cracking and Corrosion Fatigue in Aluminum Alloys. JOM 2017, 69, 1404–1414. [Google Scholar] [CrossRef]
- Patterson, B.; Cordes, N.; Henderson, K.; Williams, J.J.; Stannard, T.; Singh, S.S.; Ovejero, A.R.; Xiao, X.; Robinson, M.W.; Chawla, N. In situ X-ray synchrotron tomographic imaging during the compression of hyper-elastic polymeric materials. J. Mater. Sci. 2015, 51, 171–187. [Google Scholar] [CrossRef]
- De Carlo, F.; Tieman, B. High-Throughput X-Ray Microtomography System at the Advanced Photon Source beamline 2-BM. In Proceedings of the Optical Science and Technology, the SPIE 49th Annual Meeting, Denver, CO, USA, 2–6 August 2004; Volume 5535, pp. 644–651. [Google Scholar] [CrossRef]
- González, C.; Llorca, J. Prediction of the tensile stress-strain curve and ductility in Al/SiC composites. Scr. Mater. 1996, 35, 91–97. [Google Scholar] [CrossRef]
- Chawla, N.; Häbel, U.; Shen, Y.-L.; Andres, C.; Jones, J.W.; Allison, J.E. The effect of matrix microstructure on the tensile and fatigue behavior of SiC particle-reinforced 2080 Al matrix composites. Met. Mater. Trans. A 2000, 31, 531–540. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, R.; Singh, S.S.; Liao, X.; Oswald, J.; Chawla, N. Fracture Analysis of Particulate Metal Matrix Composite Using X-ray Tomography and Extended Finite Element Method (XFEM). J. Compos. Sci. 2020, 4, 62. https://doi.org/10.3390/jcs4020062
Yuan R, Singh SS, Liao X, Oswald J, Chawla N. Fracture Analysis of Particulate Metal Matrix Composite Using X-ray Tomography and Extended Finite Element Method (XFEM). Journal of Composites Science. 2020; 4(2):62. https://doi.org/10.3390/jcs4020062
Chicago/Turabian StyleYuan, Rui, Sudhanshu S. Singh, Xiao Liao, Jay Oswald, and Nikhilesh Chawla. 2020. "Fracture Analysis of Particulate Metal Matrix Composite Using X-ray Tomography and Extended Finite Element Method (XFEM)" Journal of Composites Science 4, no. 2: 62. https://doi.org/10.3390/jcs4020062
APA StyleYuan, R., Singh, S. S., Liao, X., Oswald, J., & Chawla, N. (2020). Fracture Analysis of Particulate Metal Matrix Composite Using X-ray Tomography and Extended Finite Element Method (XFEM). Journal of Composites Science, 4(2), 62. https://doi.org/10.3390/jcs4020062




