Temperature Self-Compensated Strain Sensors based on MWCNT-Graphene Hybrid Nanocomposite
Abstract
1. Introduction
2. Materials and Methods
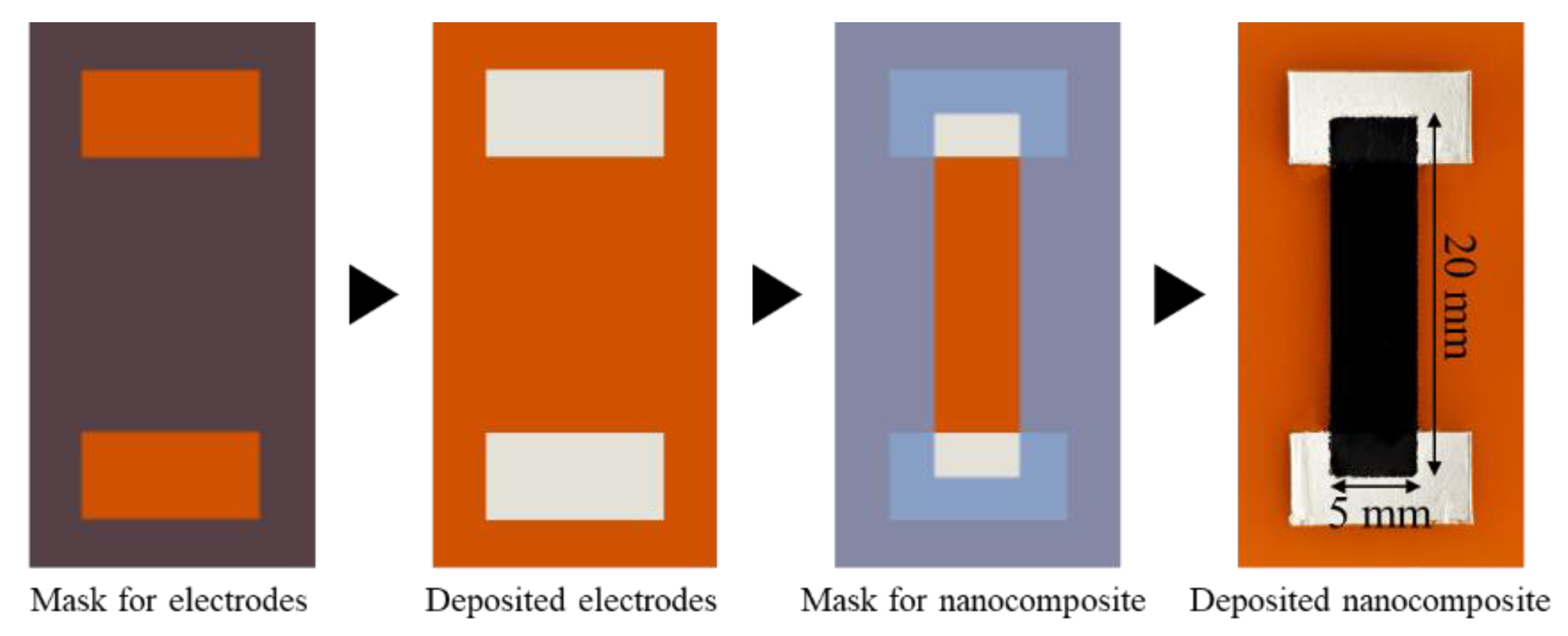
2.1. Synthesis of the Hybrid Nanocomposite Material
- -
- H-55:45, 55% graphene and 45% MWCNT
- -
- H-60:40, 60% graphene and 40% MWCNT
- -
- H-65:35, 65% graphene and 35% MWCNT
- -
- H-70:30, 70% graphene and 30% MWCNT
2.2. Equipment for Material Characterization
2.3. Temperature Measurement Procedure
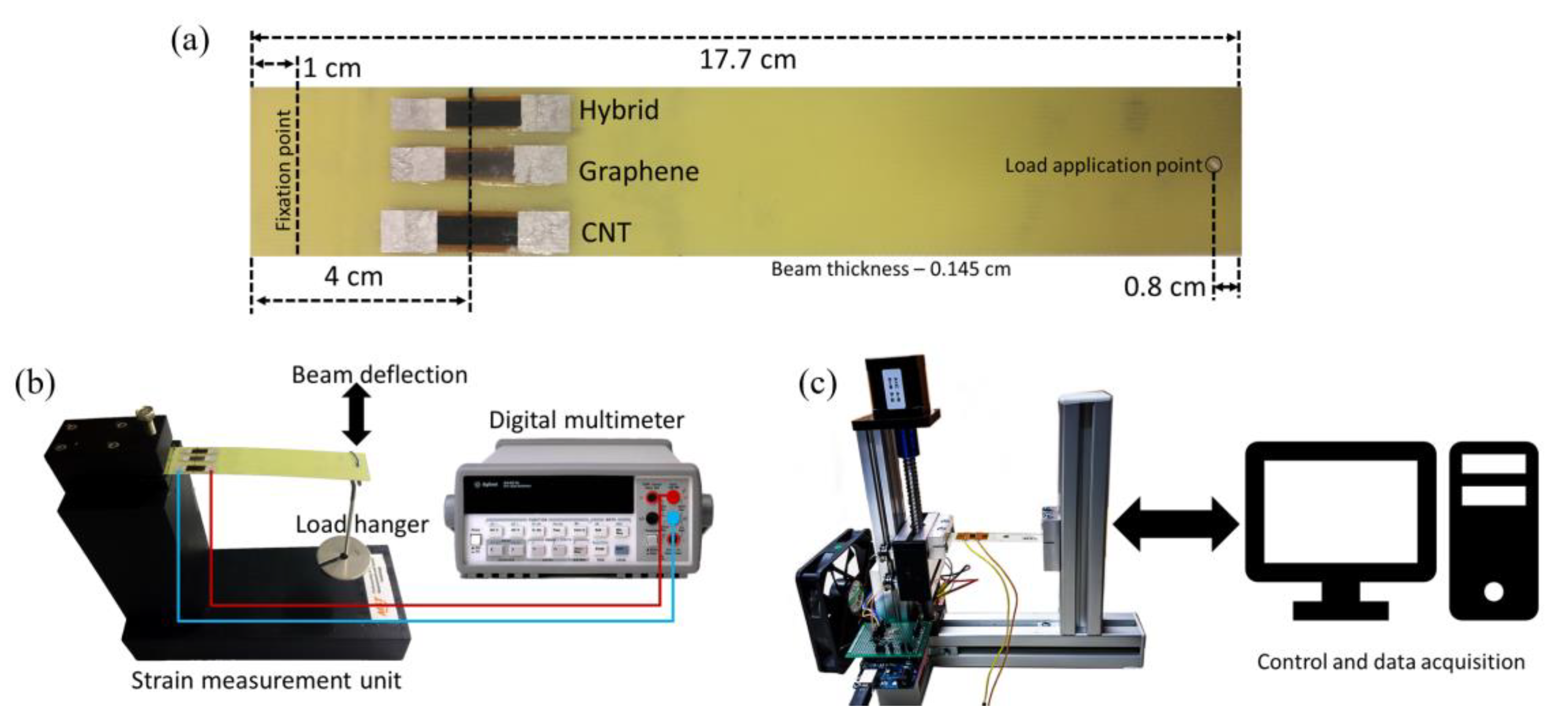
2.4. Strain Measurement Procedure
3. Results and Discussion
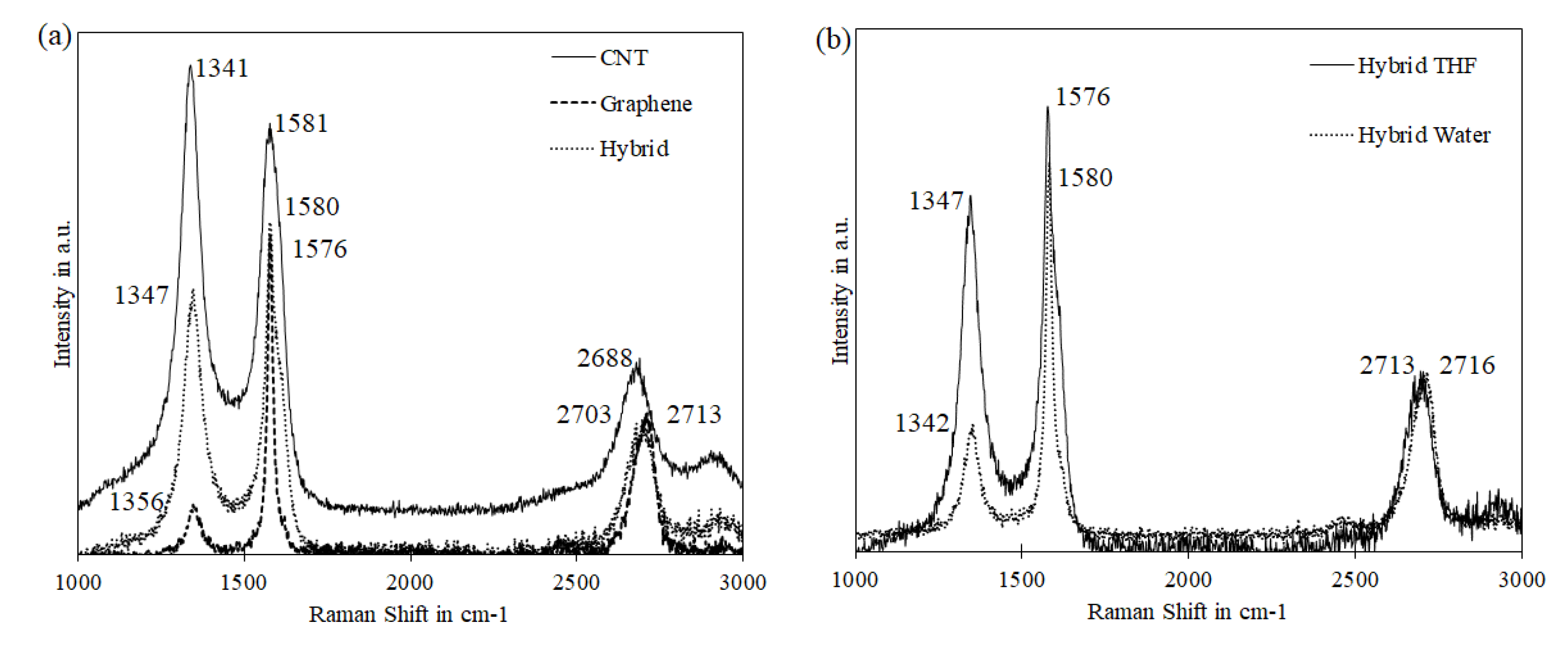
3.1. Material Characterization
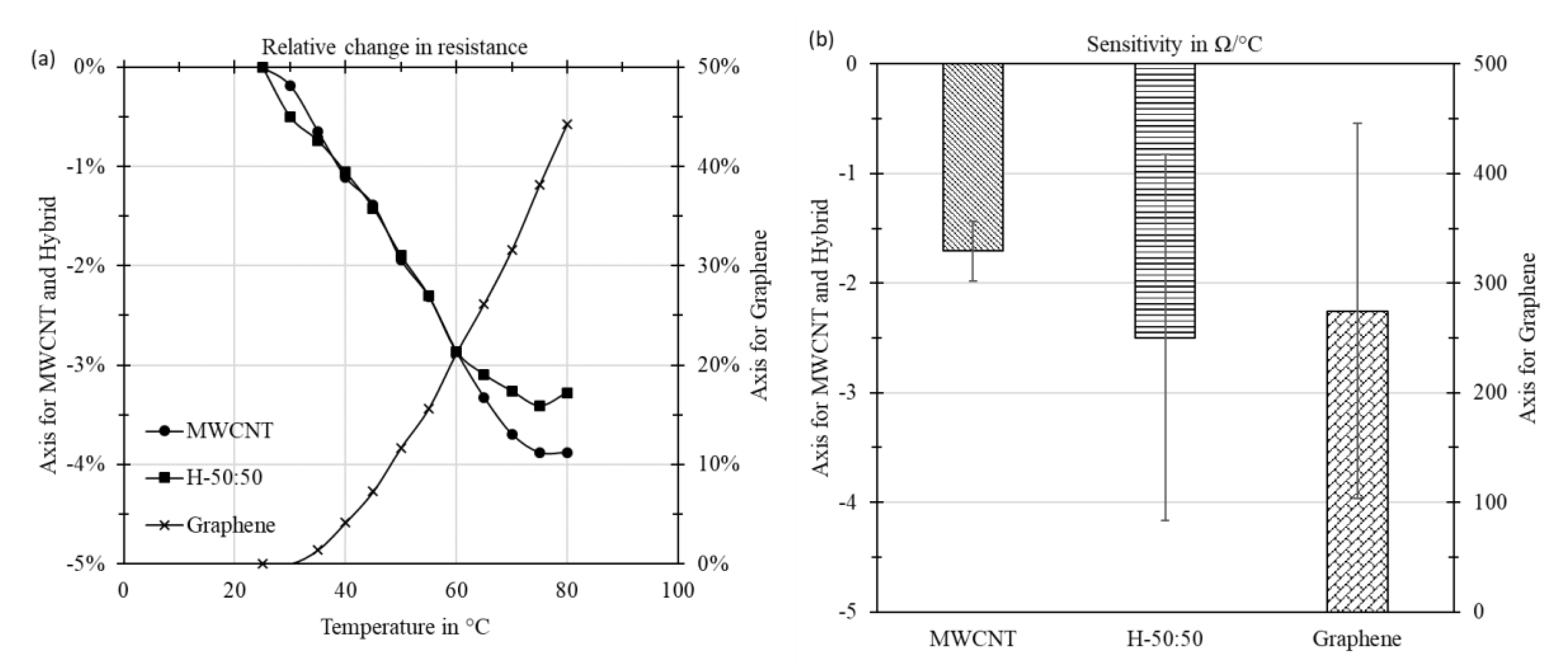
3.2. Temperature Dependency of the Materials
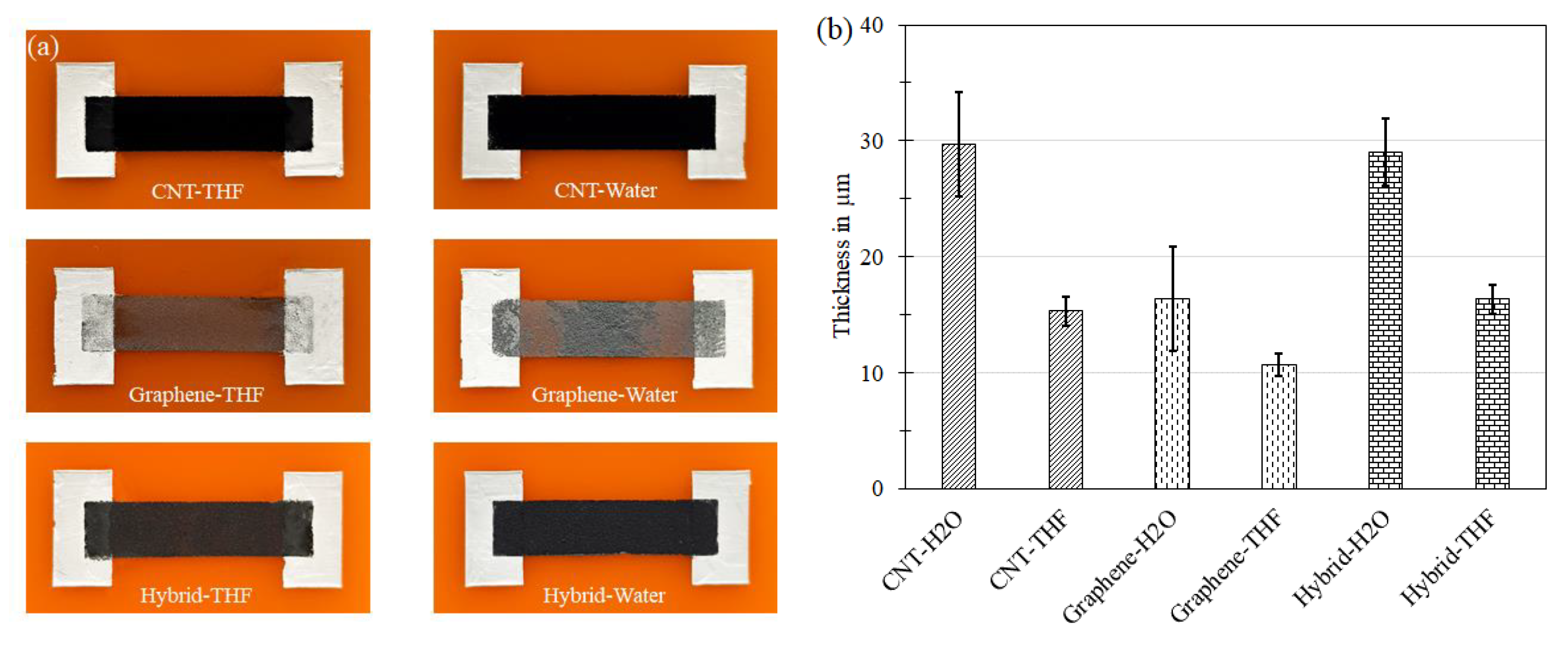
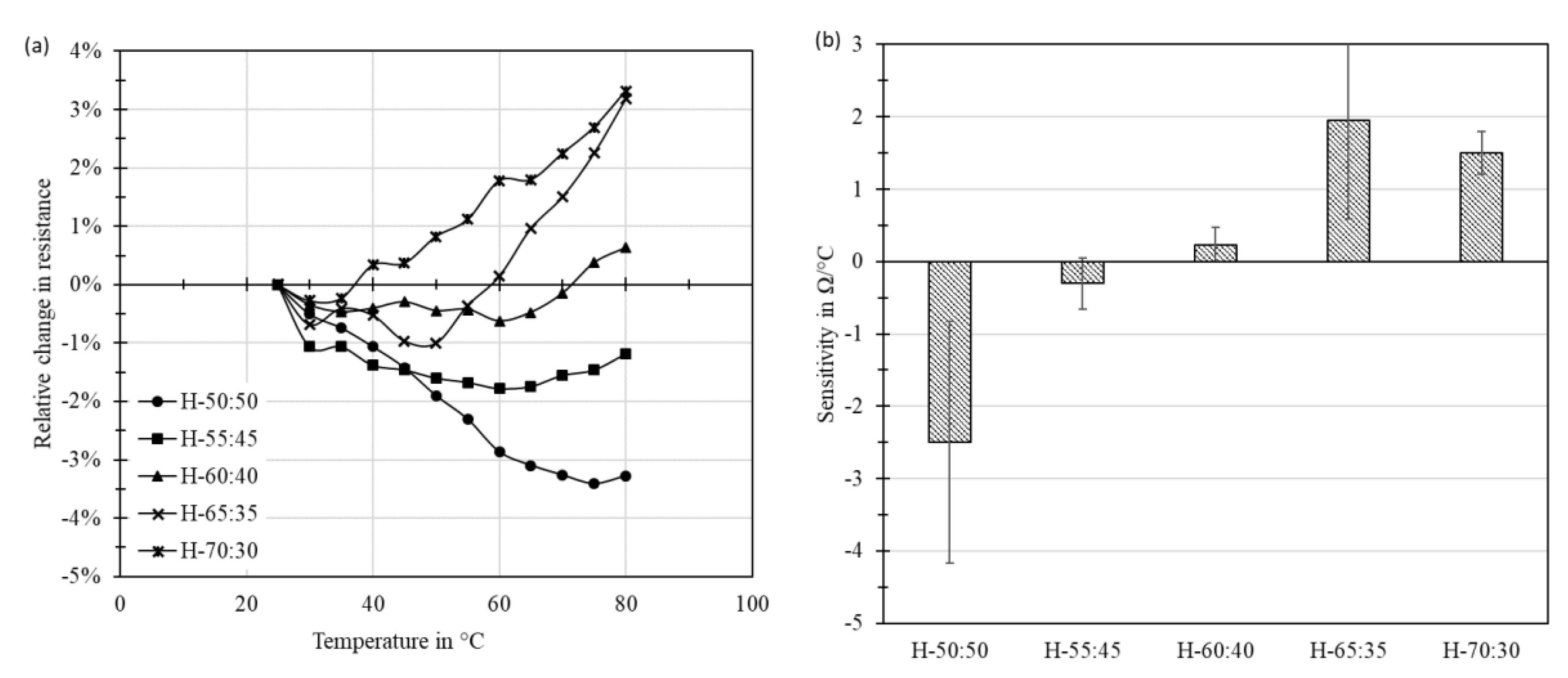
3.3. Evaluation of the Hybrid Materials based on Aqueous Medium
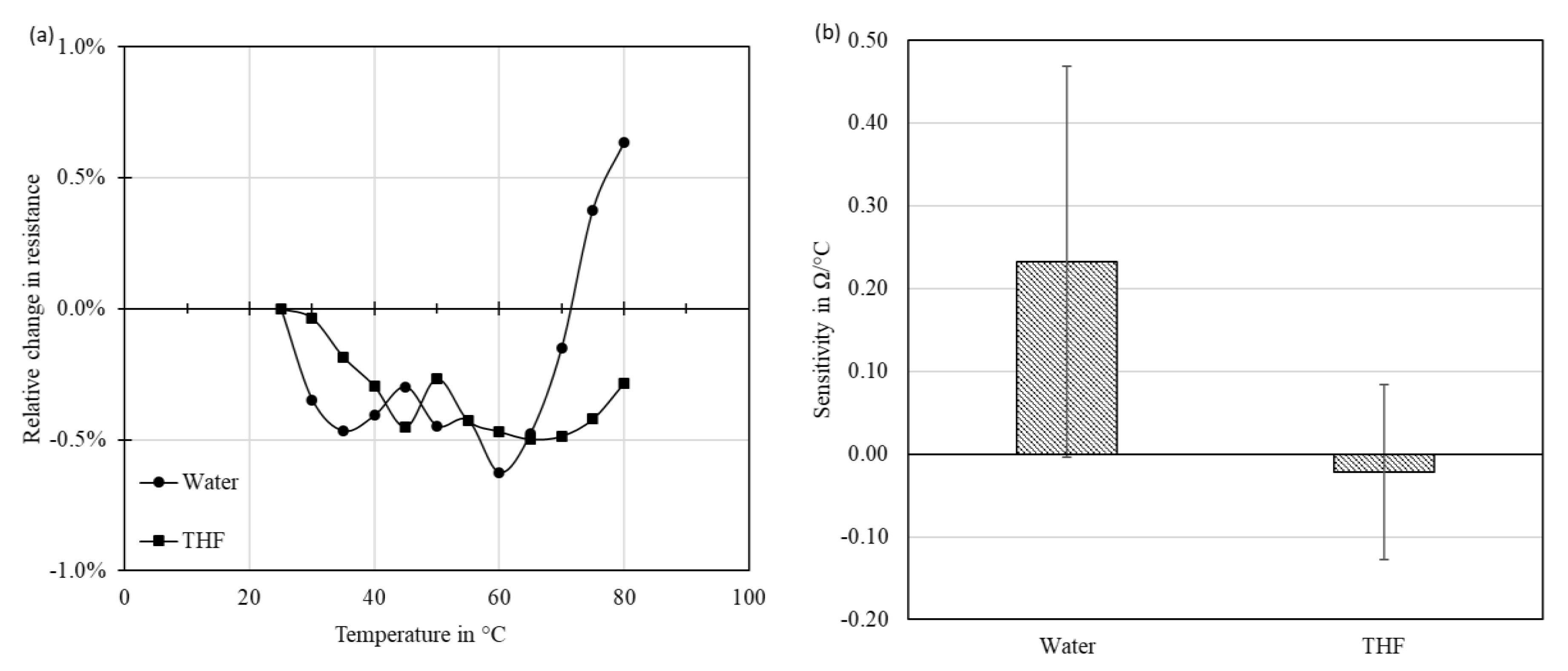
3.4. Dispersion Enhancement using Organic Solvent
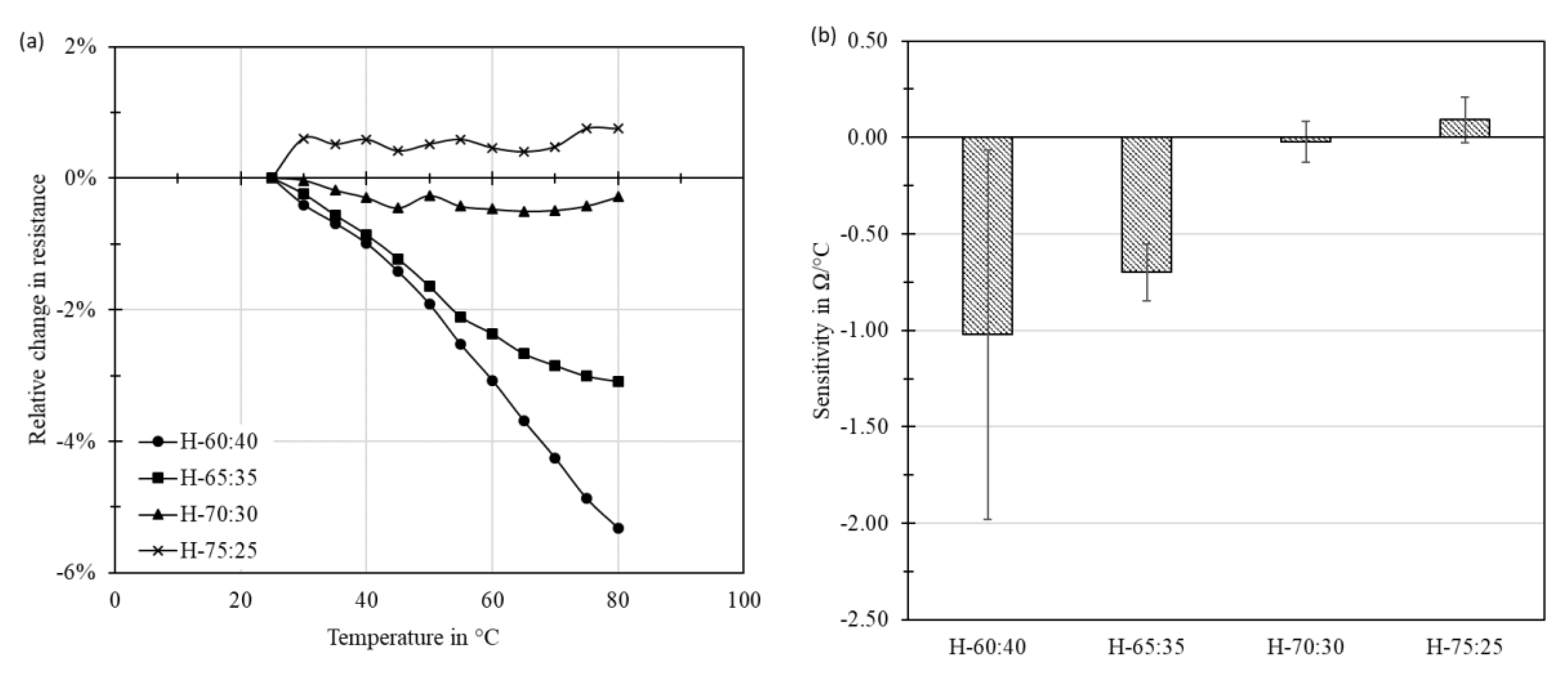
3.5. Evaluation of the Hybrid Materials based on Organic Solvent
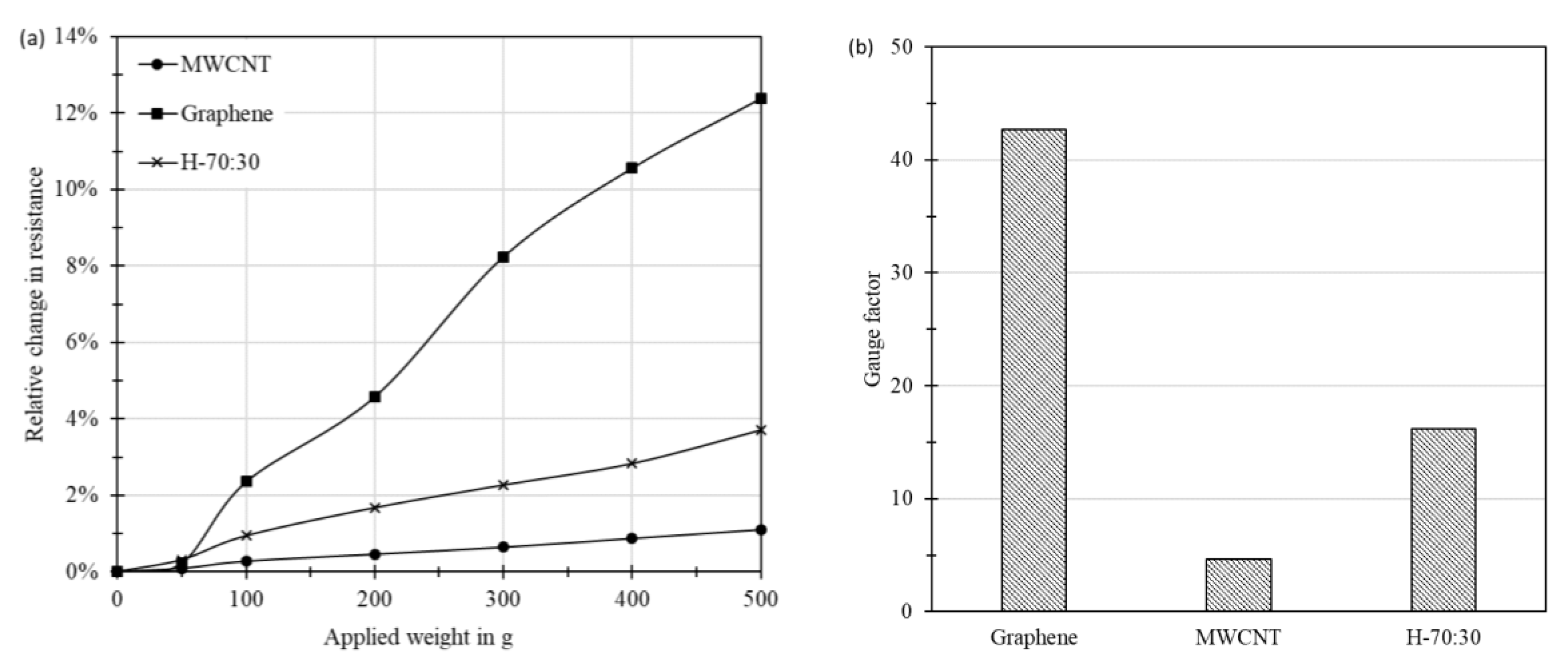
3.6. Evaluation of Strain Response of Thin Film Sensors
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bae, S.-H.; Lee, Y.; Sharma, B.K.; Lee, H.-J.; Kim, J.-H.; Ahn, J.-H. Graphene-based transparent strain sensor. Carbon 2013, 51, 236–242. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Bidmeshkipour, S.; Abdi, Y.; Arzi, E.; Mohajerzadeh, S. Graphene based strain sensors: A comparative study on graphene and its derivatives. Appl. Surf. Sci. 2018, 448, 71–77. [Google Scholar] [CrossRef]
- Tian, H.; Shu, Y.; Cui, Y.; Mi, W.; Yang, Y.; Xie, D.; Ren, T. Scalable fabrication of high-performance and flexible graphene strain sensors. Nanoscale 2013, 6, 699–705. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.; Wu, D.; Li, Y.; Jin, M.; Xiao, T.; Wang, Y.; Xiao, Z.; Zhu, Z.; Li, Z. Temperature-independent piezoresistive sensors based on carbon nanotube/polymer nanocomposite. Carbon 2018, 137, 188–195. [Google Scholar] [CrossRef]
- Bouhamed, A.; Müller, C.; Choura, S.; Kanoun, O. Processing and characterization of MWCNTs/epoxy nanocomposites thin films for strain sensing applications. Sens. Actuators A Phys. 2017, 257, 65–72. [Google Scholar] [CrossRef]
- Zhao, J.; Dai, K.; Liu, C.; Zheng, G.; Wang, B.; Liu, C.; Chen, J.; Shen, C. A comparison between strain sensing behaviors of carbon black/polypropylene and carbon nanotubes/polypropylene electrically conductive composites. Compos. Part A Appl. Sci. Manuf. 2013, 48, 129–136. [Google Scholar] [CrossRef]
- Şanli, A.; Benchirouf, A.; Müller, C.; Kanoun, O. Piezoresistive performance characterization of strain sensitive multi-walled carbon nanotube-epoxy nanocomposites. Sens. Actuators A Phys. 2017, 254, 61–68. [Google Scholar] [CrossRef]
- Sundararaman, V.; Rathod, V.T.; Mahapatra, D.R. Temperature compensation in CNT-composite distributed strain sensors. In Smart Sensor Phenomena, Technology, Networks, and Systems Integration; SPIE 9436; SPIE: Bellingham, WA, USA, 2015; p. 94360M. [Google Scholar]
- Zymelka, D.; Togashi, K.; Ohigashi, R.; Yamashita, T.; Takamatsu, S.; Itoh, T.; Kobayashi, T. Printed strain sensor array for application to structural health monitoring. Smart Mater. Struct. 2017, 26, 105040. [Google Scholar] [CrossRef]
- Bessonov, A.; Kirikova, M.; Haque, S.; Gartseev, I.; Bailey, M.J. Highly reproducible printable graphite strain gauges for flexible devices. Sens. Actuators A Phys. 2014, 206, 75–80. [Google Scholar] [CrossRef]
- De Venuto, D.; Carrara, S.; Cavallini, A.; De Micheli, G. pH sensing with temperature compensation in a Molecular Biosensor for drugs detection. In Proceedings of the 2011 12th International Symposium on Quality Electronic Design, Santa Clara, CA, USA, 14–16 March 2011; pp. 1–6. [Google Scholar]
- Dinh, N.; Kanoun, O. Temperature-Compensated Force/Pressure Sensor Based on Multi-Walled Carbon Nanotube Epoxy Composites. Sensors 2015, 15, 11133–11150. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Liu, T. SWCNT/Graphite Nanoplatelet Hybrid Thin Films for Self-Temperature-Compensated, Highly Sensitive, and Extensible Piezoresistive Sensors. Adv. Mater. 2013, 25, 5650–5657. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Nika, D.L.; Subrina, S.; Pokatilov, E.P.; Lau, C.N.; Balandin, A.A. Dimensional crossover of thermal transport in few-layer graphene materials. Nat. Mater. 2009, 9, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Kihm, K.D.; Ko, S.H. Thermal conductivity reduction of multilayer graphene with fine grain sizes. JMST Adv. 2019, 1, 191–195. [Google Scholar] [CrossRef]
- Osman, M.A.; Srivastava, D. Temperature dependence of the thermal conductivity of single-wall carbon nanotubes. Nanotechnology 2001, 12, 21. [Google Scholar] [CrossRef]
- Kim, P.; Shi, L.; Majumdar, A.; McEuen, P.L. Thermal Transport Measurements of Individual Multiwalled Nanotubes. Phys. Rev. Lett. 2001, 87, 215502. [Google Scholar] [CrossRef] [PubMed]
- Ramalingame, R.; Chandraker, P.; Kanoun, O. Investigation on the Influence of Solvents on MWCNT-PDMS Nanocomposite Pressure Sensitive Films. Proceedings 2017, 1, 384. [Google Scholar] [CrossRef]
- Bokobza, L. Raman spectroscopic characterization of multiwall carbon nanotubes and of composites. Express Polym. Lett. 2012, 6, 601–608. [Google Scholar] [CrossRef]


| Material | Concentration | Temperature Related Parameters | Sensor Parameters | |||
|---|---|---|---|---|---|---|
| Range | Compensation | Influence | Type | GF | ||
| CNT [8] | 8 wt % | 20 to 70 °C | Numerical model | - | Strain | - |
| MWCNT [11] | 1 wt % | 10 to 80 °C | Differential Difference Amplifier | 0.03% | pH | - |
| MWCNT [12] | 2 wt % | −20 to 50 °C | Full-Wheatstone bridge system | 3.1% | Force | - |
| Graphite paste [9] | - | −10 to 95 °C | Full-Wheatstone bridge system | - | Strain | 2.994 |
| Graphite ink [10] | - | 20 to 120 °C | Neutral axis engineering | - | Strain | 19.1 |
| SWCNT/Graphene [13] | Layer 1: 0.016 wt % SWCNT, Layer 2: 0.3 wt % Graphene | 30 to 85 °C | Stacked layers of thin films with an opposite temperature coefficient | <1% | Strain | 5.44 |
| MWCNT/Graphene | 0.1 wt % Hybrid (0.03 wt % MWCNT, 0.07 wt % Graphene) | 25 to 80 °C | Single layer thin film with hybrid nanocomposite material | <0.5% | Strain | 16.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramalingame, R.; Bautista-Quijano, J.R.; Alves, D.d.F.; Kanoun, O. Temperature Self-Compensated Strain Sensors based on MWCNT-Graphene Hybrid Nanocomposite. J. Compos. Sci. 2019, 3, 96. https://doi.org/10.3390/jcs3040096
Ramalingame R, Bautista-Quijano JR, Alves DdF, Kanoun O. Temperature Self-Compensated Strain Sensors based on MWCNT-Graphene Hybrid Nanocomposite. Journal of Composites Science. 2019; 3(4):96. https://doi.org/10.3390/jcs3040096
Chicago/Turabian StyleRamalingame, Rajarajan, Jose Roberto Bautista-Quijano, Danrlei de Farias Alves, and Olfa Kanoun. 2019. "Temperature Self-Compensated Strain Sensors based on MWCNT-Graphene Hybrid Nanocomposite" Journal of Composites Science 3, no. 4: 96. https://doi.org/10.3390/jcs3040096
APA StyleRamalingame, R., Bautista-Quijano, J. R., Alves, D. d. F., & Kanoun, O. (2019). Temperature Self-Compensated Strain Sensors based on MWCNT-Graphene Hybrid Nanocomposite. Journal of Composites Science, 3(4), 96. https://doi.org/10.3390/jcs3040096






