Atomic Structure and Mechanical Properties of Twisted Bilayer Graphene
Abstract
1. Introduction
2. Methods
3. Results and Discussion
3.1. Atomic Corrugation
3.2. Tensile Test Along x Direction
3.3. Compression Test along z Direction
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Westervelt, R.M. Graphene Nanoelectronics. Science 2008, 320, 324–325. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Fal’Ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A Roadmap for Graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Geng, X.; Wang, H.; Wang, P.; Liu, A.; Lan, Y.; Peng, Q. A Review of Current Development of Graphene Mechanics. Crystals 2018, 8, 357. [Google Scholar] [CrossRef]
- Peng, Q.; Dearden, A.K.; Crean, J.; Han, L.; Liu, S.; Wen, X.; De, S. New Materials Graphyne, Graphdiyne, Graphone and Graphane: Review of Properties, Synthesis, and Application in Nanotechnology. Nanotechnol. Sci. Appl. 2014, 7, 1–29. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, Z.; De, S. A Density Functional Theory Study of the Mechanical Properties of Graphane with van Der Waals Corrections. Mech. Adv. Mater. Struct. 2015, 22, 717–721. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. Mechanical Properties of Graphyne Monolayers: A First-Principles Study. Phys. Chem. Chem. Phys. 2012, 64, 135–141. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–389. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Yuan, G.; Zhu, Q.; Wang, J.; Tang, S.; Gao, L. Enhancing the Strength of Graphene by a Denser Grain Boundary. ACS Nano 2018, 12, 4529–4535. [Google Scholar] [CrossRef]
- Peng, Q.; Zamiri, A.R.; Ji, W.; De, S. Elastic Properties of Hybrid Graphene/Boron Nitride Monolayer. Acta Mech. 2012, 223, 2591–2596. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, X.J.; Ji, W.; De, S. Chemically Tuning Mechanics of Graphene by BN. Adv. Eng. Mater. 2013, 15, 718–727. [Google Scholar] [CrossRef]
- Peng, Q.; Liang, C.; Ji, W.; De, S. A First-Principles Study of the Mechanical Properties of g-GeC. Mech. Mater. 2013, 64, 135–141. [Google Scholar] [CrossRef]
- Ng, S.W.; Noor, N.; Zheng, Z. Graphene-Based Two-Dimensional Janus Materials. NPG Asia Mater. 2018, 10, 217–237. [Google Scholar] [CrossRef]
- Muniz, A.R.; Maroudas, D. Opening and Tuning of Band Gap by the Formation of Diamond Superlattices in Twisted Bilayer Graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 86, 075404. [Google Scholar] [CrossRef]
- Machado, A.S.; Maroudas, D.; Muniz, A.R. Tunable Mechanical Properties of Diamond Superlattices Generated by Interlayer Bonding in Twisted Bilayer Graphene. Appl. Phys. Lett. 2013, 103, 013113. [Google Scholar] [CrossRef]
- Muniz, A.R.; Machado, A.S.; Maroudas, D. Mechanical Behavior of Interlayer-Bonded Nanostructures Obtained from Bilayer Graphene. Carbon N. Y. 2015, 81, 663–677. [Google Scholar] [CrossRef]
- Series, C. Bilayer Graphenes with Antidots: Structures, Properties and Applications. J. Phys. Conf. Ser. 2018, 1092, 012018. [Google Scholar] [CrossRef]
- Santos, J.M.B.L.; Peres, N.M.R.; Neto, A.H.C. Graphene Bilayer with a Twist: Electronic Structure. Phys. Rev. Lett. 2007, 99, 19–22. [Google Scholar] [CrossRef]
- Roy, B.; Yang, K. Bilayer Graphene with Parallel Magnetic Field and Twisting: Phases and Phase Transitions in a Highly Tunable Dirac System. Phys. Rev. B 2013, 88, 241107. [Google Scholar] [CrossRef]
- Uchida, K.; Furuya, S.; Iwata, J.; Oshiyama, A. Atomic Corrugation and Electron Localization Due to Moiré Patterns in Twisted Bilayer Graphenes. Phys. Rev. B 2014, 90, 155451. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated Insulator Behaviour at Half-Filling in Magic-Angle Graphene Superlattices. Nature 2018, 556, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional Superconductivity in Magic-Angle Graphene Superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Park, J.; Song, I.; Ok, J.M.; Jo, Y.; Watanabe, K.; Taniquchi, T.; Choi, H.C.; Lee, D.S.; Jung, S.; et al. Broken-Symmetry Quantum Hall States in Twisted Bilayer Graphene. Sci. Rep. 2016, 6, 38068. [Google Scholar] [CrossRef] [PubMed]
- Kvashnin, D.G.; Bellucci, S.; Chernozatonskii, L.A. Sharp Variations in the Electronic Properties of Graphene Deposited on the H-BN Layer. Phys. Chem. Chem. Phys. 2015, 17, 4354–4359. [Google Scholar] [CrossRef] [PubMed]
- Chernozatonskii, L.A.; Demin, V.A. Features of 30° Moiré Graphene Bilayers with Folded Holes. JETP Lett. 2018, 107, 315–319. [Google Scholar] [CrossRef]
- Moon, P.; Koshino, M. Optical Absorption in Twisted Bilayer Graphene. Phys. Rev. B 2013, 87, 205404. [Google Scholar] [CrossRef]
- Tabert, C.J.; Nicol, E.J. Optical Conductivity of Twisted Bilayer Graphene. Phys. Rev. B 2013, 87, 121402. [Google Scholar] [CrossRef]
- Yin, J.; Wang, H.; Peng, H.; Tan, Z.; Liao, L.; Lin, L.; Sun, X.; Koh, A.L.; Chen, Y.; Peng, H.; et al. Selectively Enhanced Photocurrent Generation in Twisted Bilayer Graphene with van Hove Singularity. Nat. Commun. 2016, 7, 10699. [Google Scholar] [CrossRef] [PubMed]
- Razado-Colambo, I.; Avila, J.; Vignaud, D.; Godey, S.; Wallart, X.; Woodruff, D.P.; Asensio, M.C. Structural Determination of Bilayer Graphene on SiC(0001) Using Synchrotron Radiation Photoelectron Diffraction. Sci. Rep. 2018, 8, 10190. [Google Scholar] [CrossRef]
- Ding, Y.; Peng, Q.; Gan, L.; Wu, R.; Ou, X.; Zhang, Q.; Luo, Z. Stacking-Mode-Induced Reactivity Enhancement for Twisted Bilayer Graphene. Chem. Mater. 2016, 28, 1034–1039. [Google Scholar] [CrossRef]
- Cocemasov, A.I.; Nika, D.L.; Balandin, A.A. Phonons in Twisted Bilayer Graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 035428. [Google Scholar] [CrossRef]
- Li, H.; Ying, H.; Chen, X.; Nika, D.L.; Cocemasov, A.I.; Cai, W.; Balandin, A.A.; Chen, S. Thermal Conductivity of Twisted Bilayer Graphene. Nanoscale 2014, 6, 13402–13408. [Google Scholar] [CrossRef]
- Li, C.; Debnath, B.; Tan, X.; Su, S.; Xu, K.; Ge, S.; Neupane, M.R.; Lake, R.K. Commensurate Lattice Constant Dependent Thermal Conductivity of Misoriented Bilayer Graphene. Carbon N. Y. 2018, 138, 451–457. [Google Scholar] [CrossRef]
- Nika, D.; Cocemasov, A.; Balandin, A. Specific Heat of Twisted Bilayer Graphene. Appl. Phys. Lett. 2014, 105, 031904. [Google Scholar] [CrossRef]
- Cocemasov, A.I.; Nika, D.L.; Balandin, A.A. Engineering of the Thermodynamic Properties of Bilayer Graphene by Atomic Plane Rotations: The Role of the out-of-Plane Phonons. Nanoscale 2015, 7, 12851–12859. [Google Scholar] [CrossRef] [PubMed]
- Nika, D.L.; Balandin, A.A. Phonons and Thermal Transport in Graphene and Graphene-Based Materials. Rep. Prog. Phys. 2017, 80, 036502. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Peng, Q. A Molecular Dynamics Study of the Mechanical Properties of Twisted Bilayer Graphene. Micromachines 2018, 9, 440. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A Second-Generation Reactive Empirical Bond Order (REBO) Potential Energy Expression for Hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Crespi, V.H. Registry-Dependent Interlayer Potential for Graphitic Systems. Phys. Rev. B 2005, 71, 235415. [Google Scholar] [CrossRef]
- Dai, S.; Xiang, Y.; Srolovitz, D.J. Twisted Bilayer Graphene: Moire with a Twist. Nano Lett. 2016, 16, 5923–5927. [Google Scholar] [CrossRef]
- Malekpour, H.; Balandin, A.A. Raman-based technique for measuring thermal conductivity of graphene and related materials. J. Raman Spectrosc. 2018, 49, 106–120. [Google Scholar] [CrossRef]
- Gattacceca, J.; Rochette, P.; Folco, L.; Feinberg, J.M.; Muxworthy, A.; Harrison, R.J.; Nakamoto, T.; Doi, M.; Araki, S.; Hubbard, A.; et al. Dynamic Mechanical Behavior of Multilayer Graphene via Supersonic Projectile Penetration. Science 2014, 346, 1092–1097. [Google Scholar] [CrossRef]
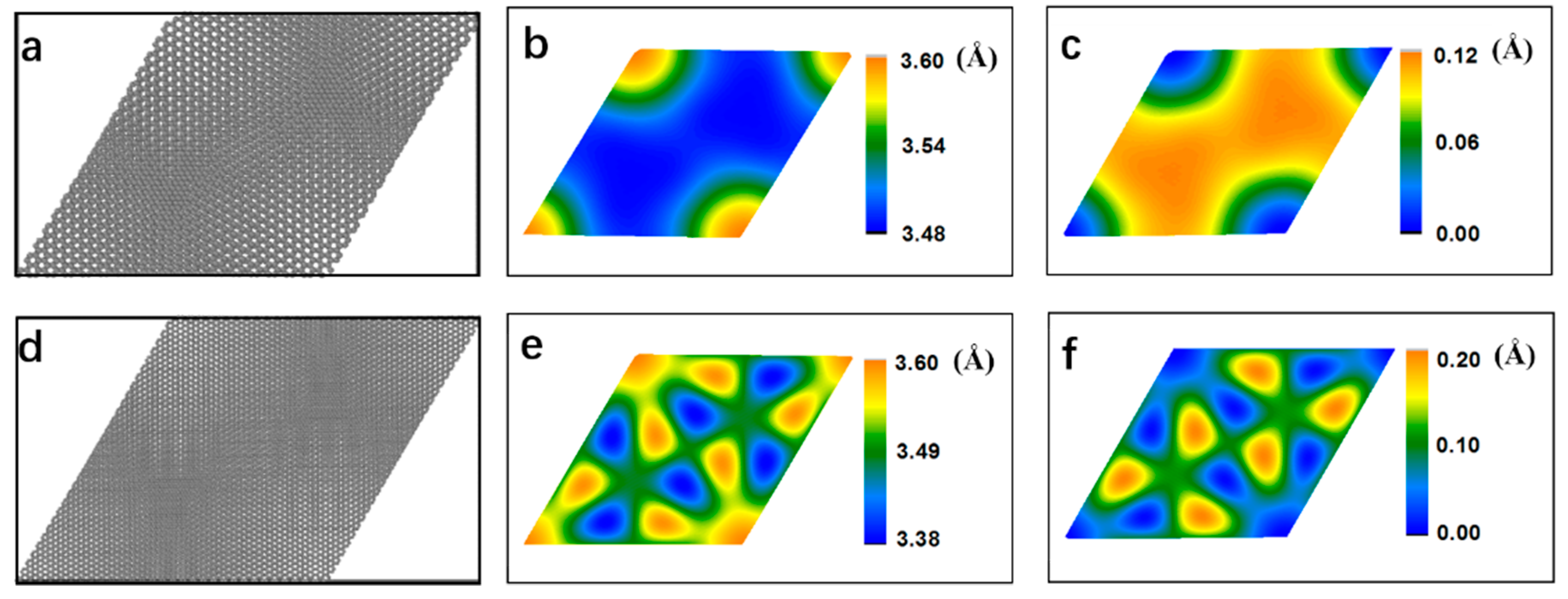
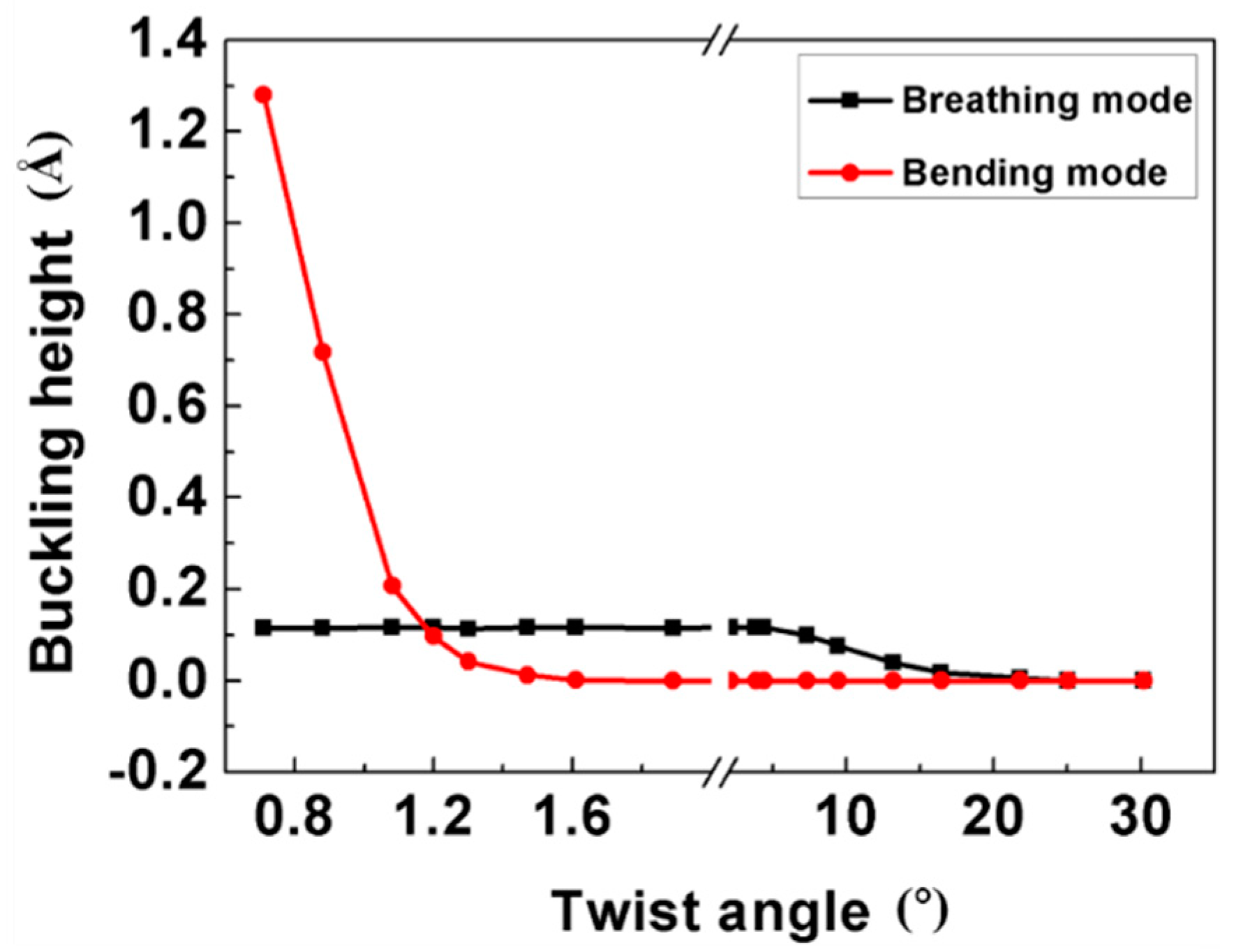
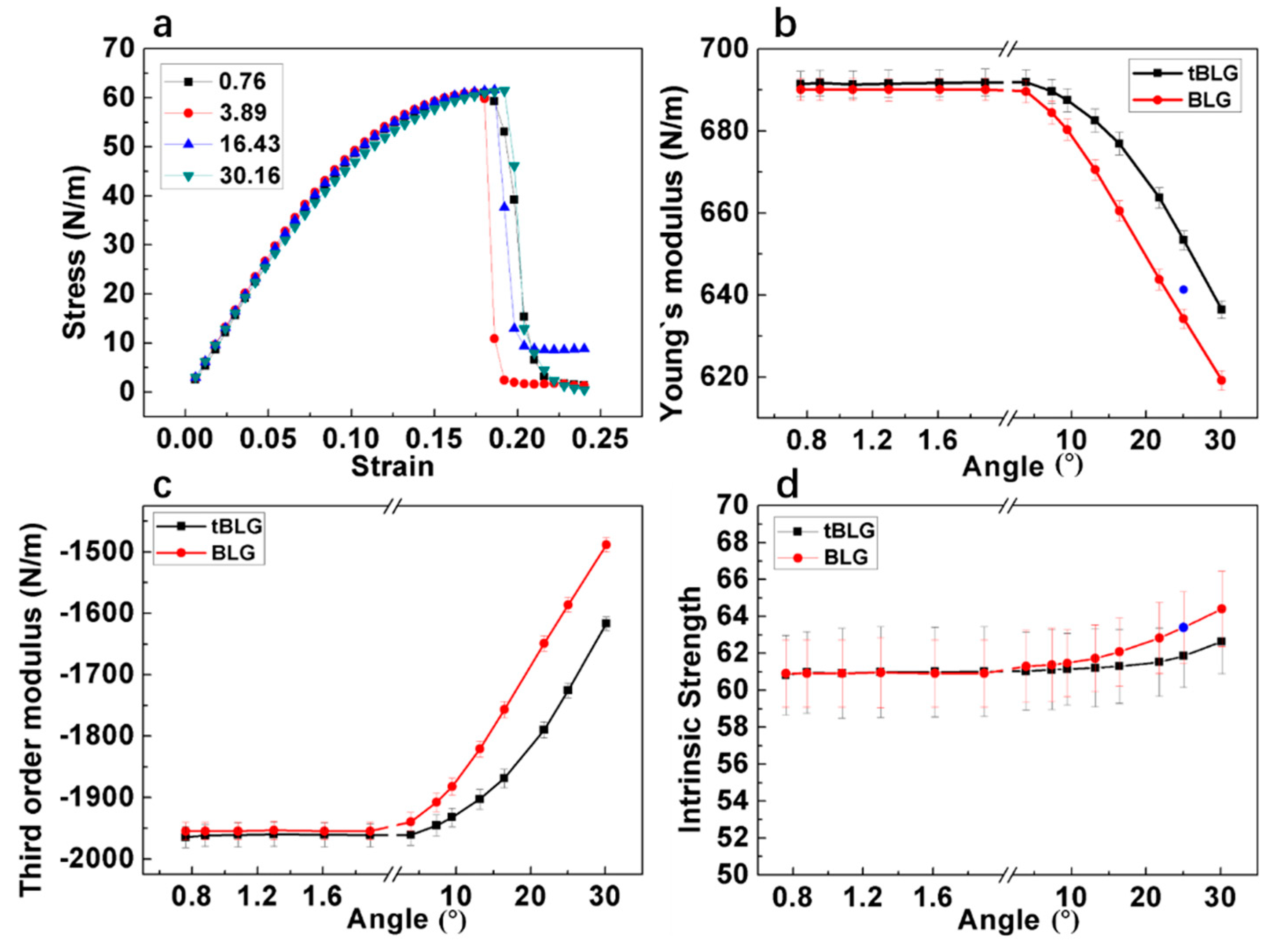
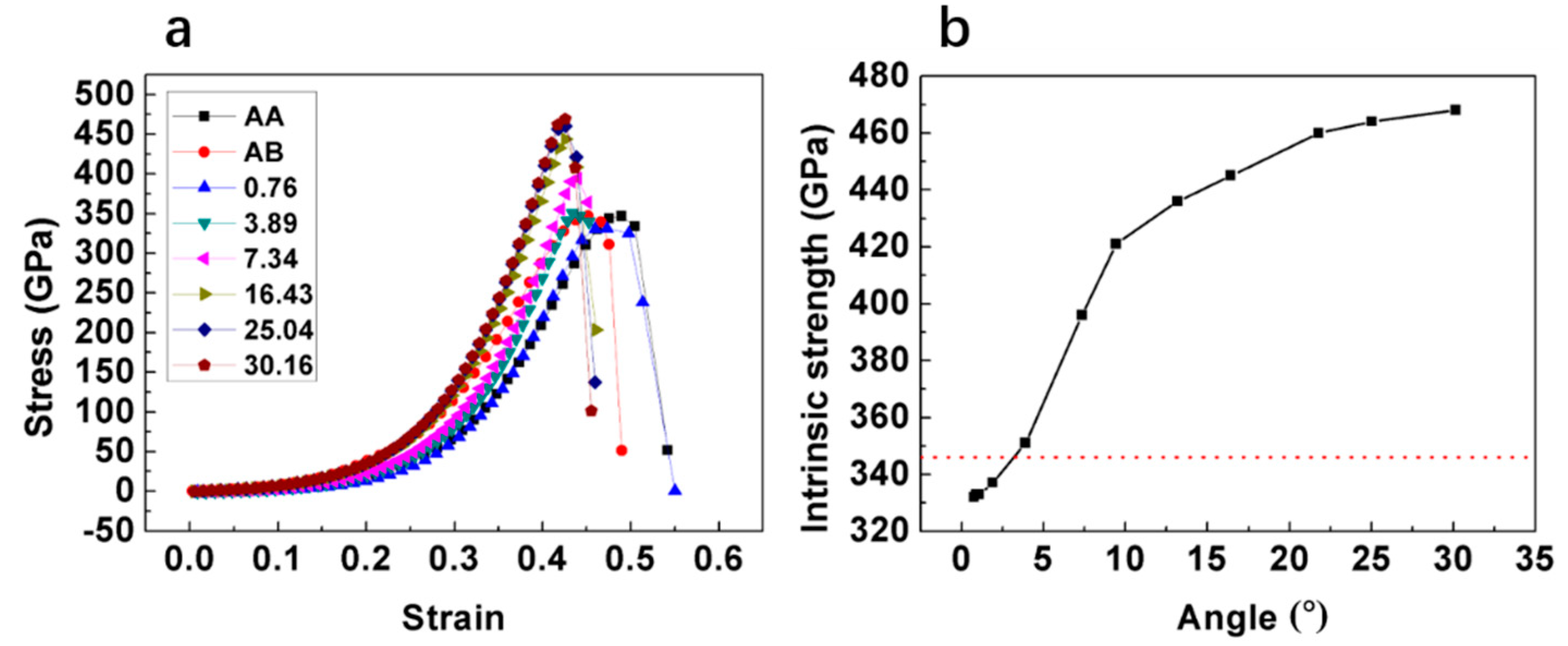
| (m, n) | Twist Angle (°) | L (Cell Length) (Å) | N (Number of Atoms) |
|---|---|---|---|
| (44, 43) | 0.76 | 184.01 | 22,708 |
| (34, 33) | 0.99 | 141.71 | 13,468 |
| (31, 30) | 1.08 | 129.02 | 11,164 |
| (28, 27) | 1.20 | 116.33 | 9076 |
| (26,25) | 1.30 | 108.66 | 7804 |
| (52,50) | 1.30 | 217.32 | 15,608 |
| (23,22) | 1.47 | 95.18 | 6076 |
| (21, 20) | 1.61 | 87.34 | 5044 |
| (9, 8) | 3.89 | 35.98 | 868 |
| (18, 16) | 3.89 | 71.96 | 1736 |
| (8, 7) | 4.41 | 31.75 | 676 |
| (16, 14) | 4.41 | 63.50 | 1352 |
| (10, 8) | 7.34 | 38.14 | 488 |
| (8, 6) | 9.43 | 29.71 | 592 |
| (6, 4) | 13.17 | 21.29 | 304 |
| (10, 6) | 16.43 | 34.2 | 392 |
| (8, 4) | 21.79 | 25.85 | 448 |
| (9, 4) | 25.04 | 28.16 | 532 |
| (11, 4) | 30.16 | 32.86 | 724 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Cao, Q.; Liu, S.; Peng, Q. Atomic Structure and Mechanical Properties of Twisted Bilayer Graphene. J. Compos. Sci. 2019, 3, 2. https://doi.org/10.3390/jcs3010002
Zheng S, Cao Q, Liu S, Peng Q. Atomic Structure and Mechanical Properties of Twisted Bilayer Graphene. Journal of Composites Science. 2019; 3(1):2. https://doi.org/10.3390/jcs3010002
Chicago/Turabian StyleZheng, Shaolong, Qiang Cao, Sheng Liu, and Qing Peng. 2019. "Atomic Structure and Mechanical Properties of Twisted Bilayer Graphene" Journal of Composites Science 3, no. 1: 2. https://doi.org/10.3390/jcs3010002
APA StyleZheng, S., Cao, Q., Liu, S., & Peng, Q. (2019). Atomic Structure and Mechanical Properties of Twisted Bilayer Graphene. Journal of Composites Science, 3(1), 2. https://doi.org/10.3390/jcs3010002






