Manufacturing and Performance Evaluation of Carbon Fiber–Reinforced Honeycombs
Abstract
:1. Introduction
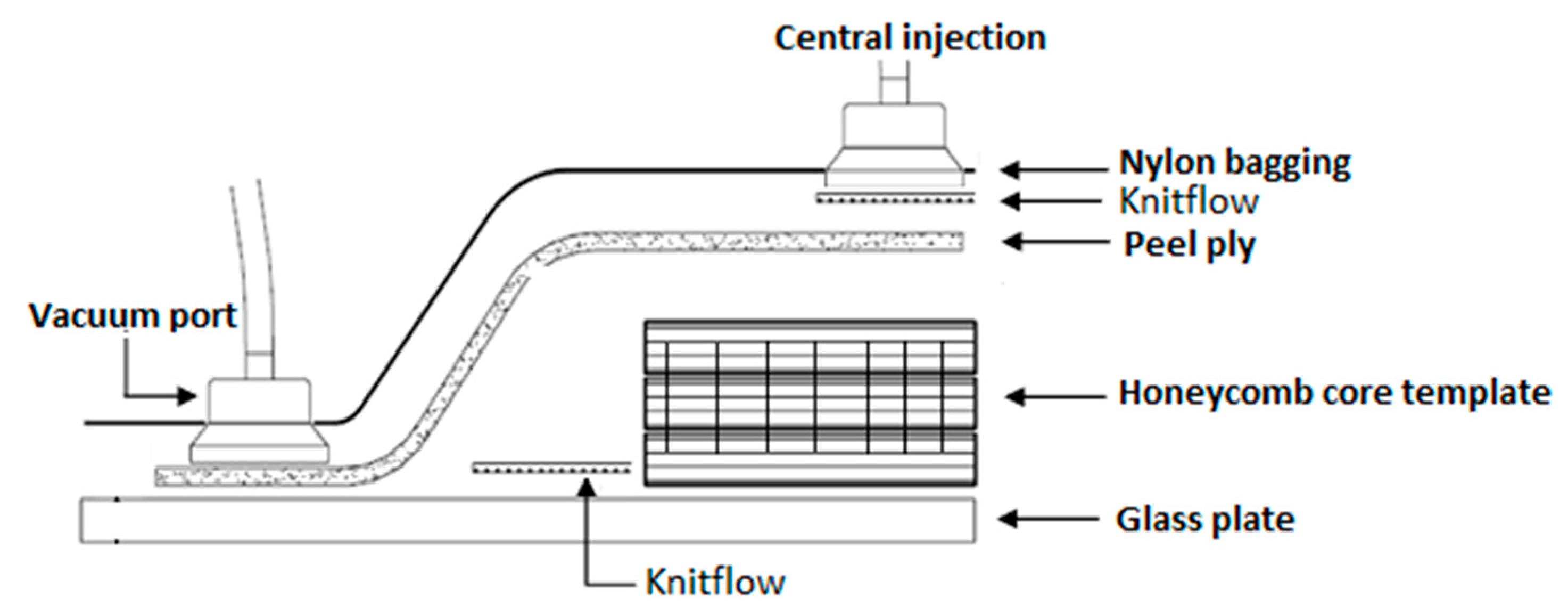
2. Materials and Methods
3. Testing
4. Results
4.1. Fiber Volume Fraction
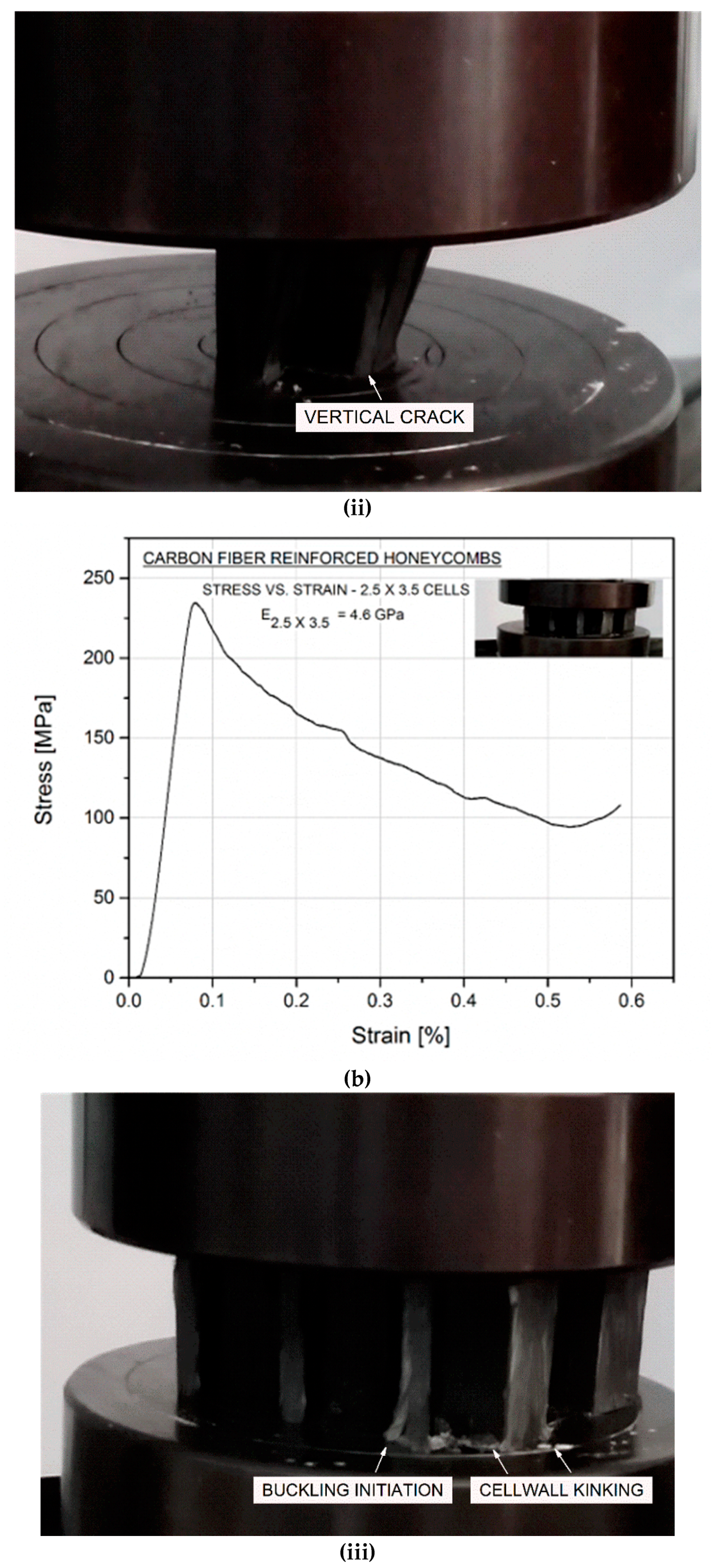
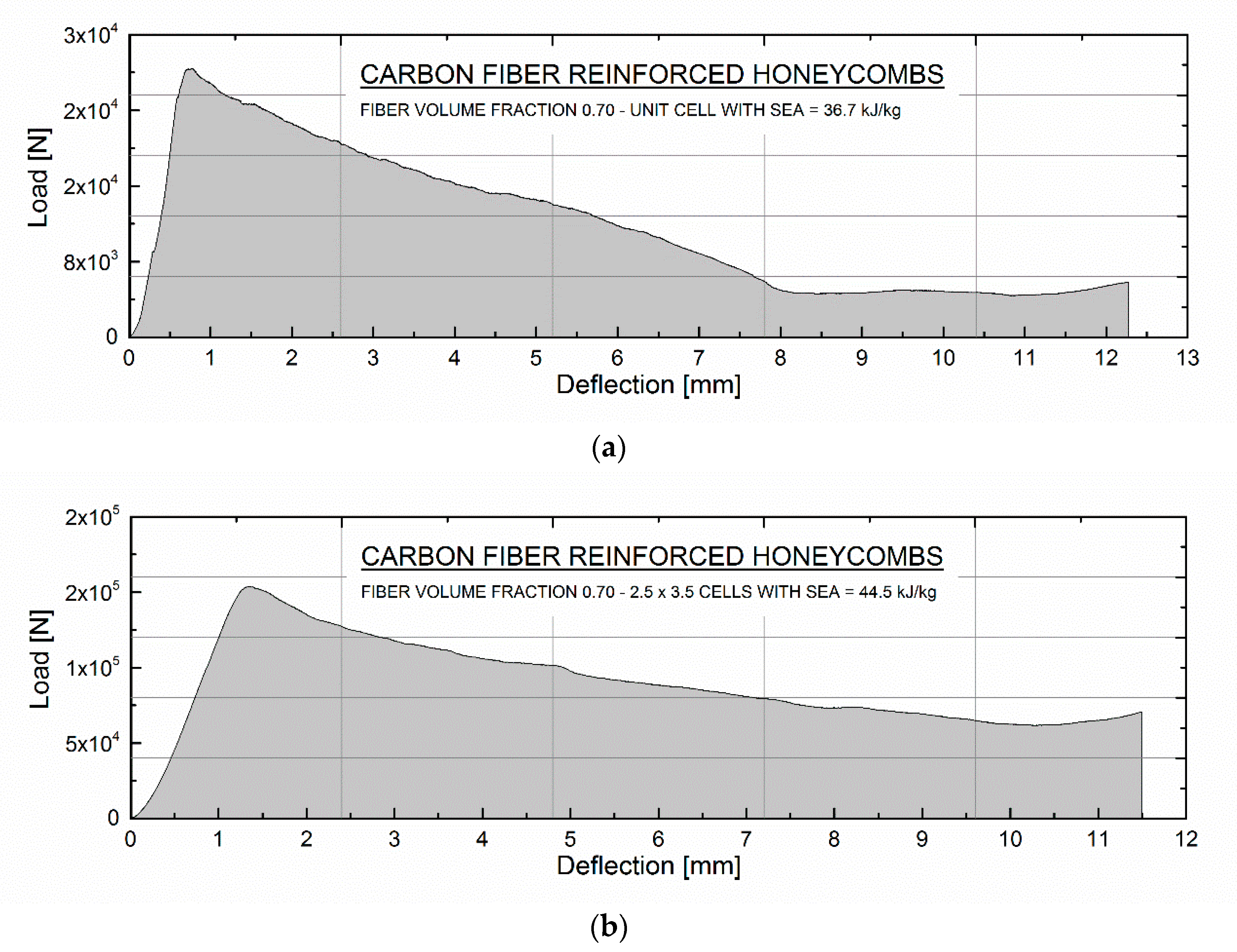
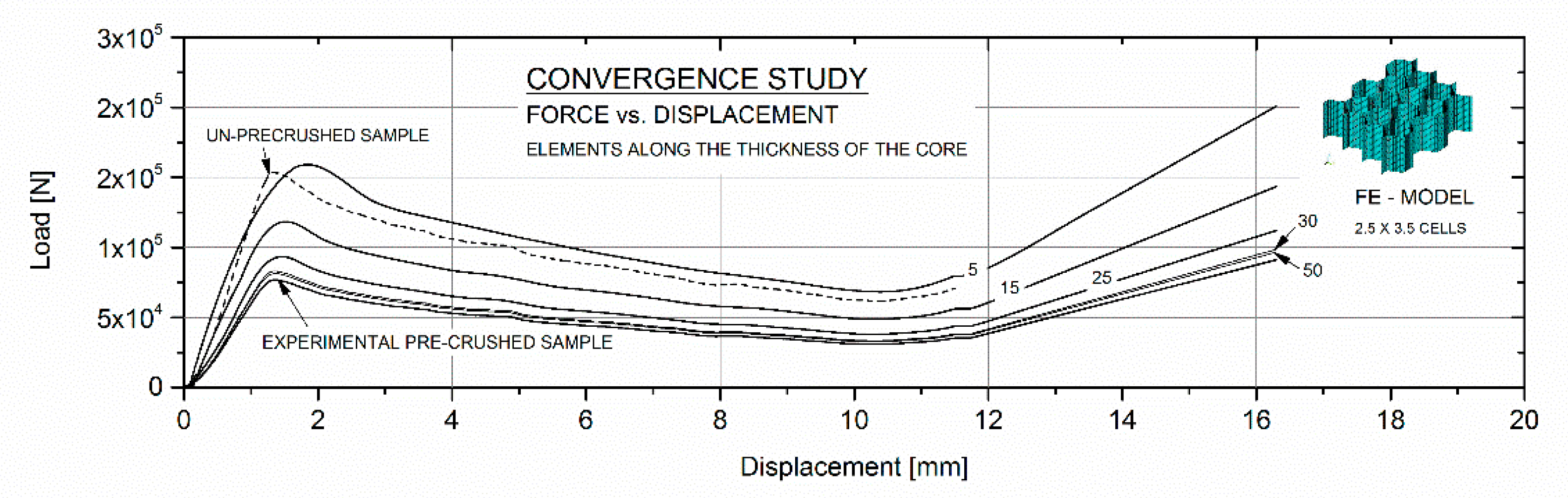
4.2. Compression Tests
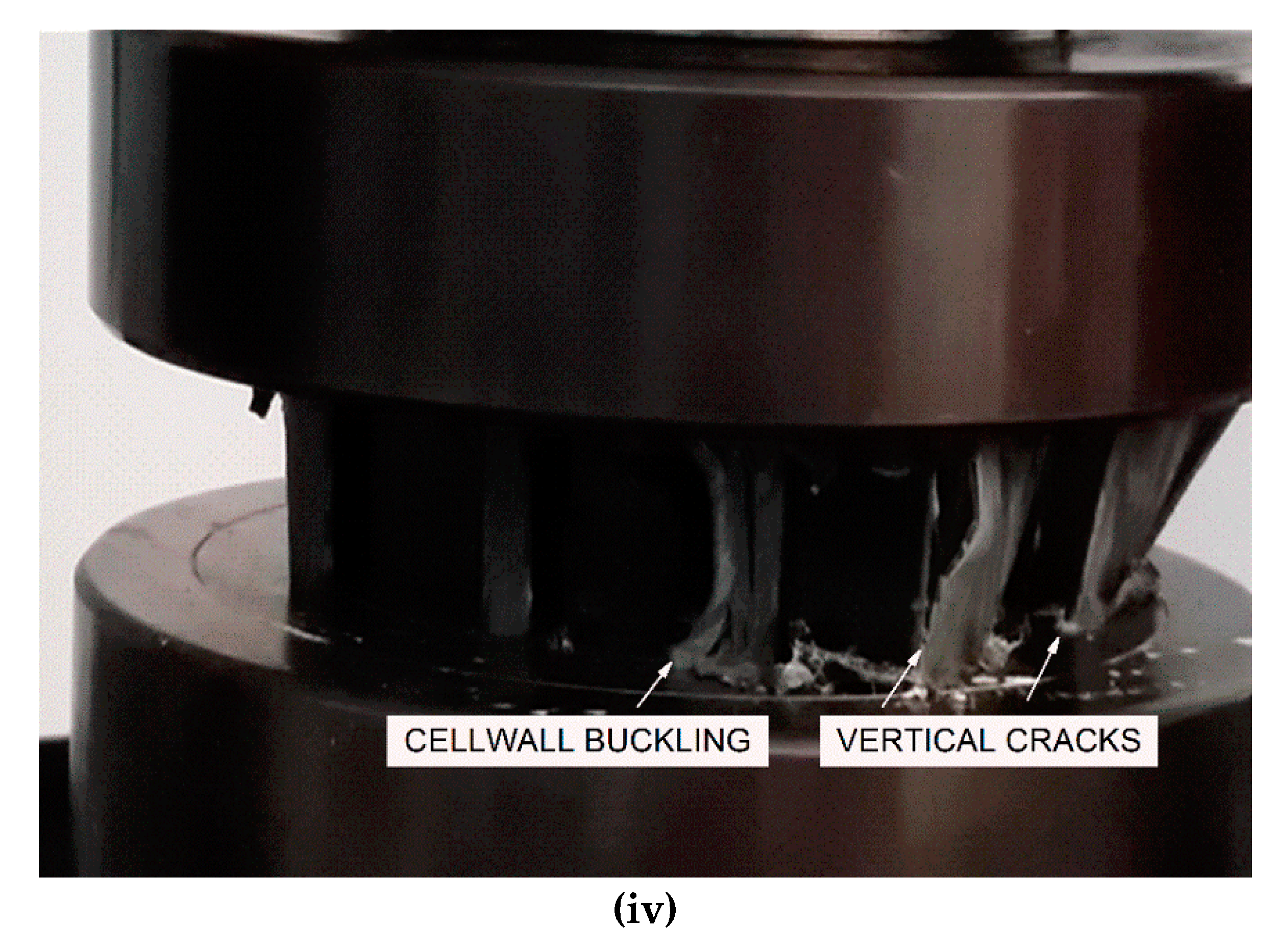
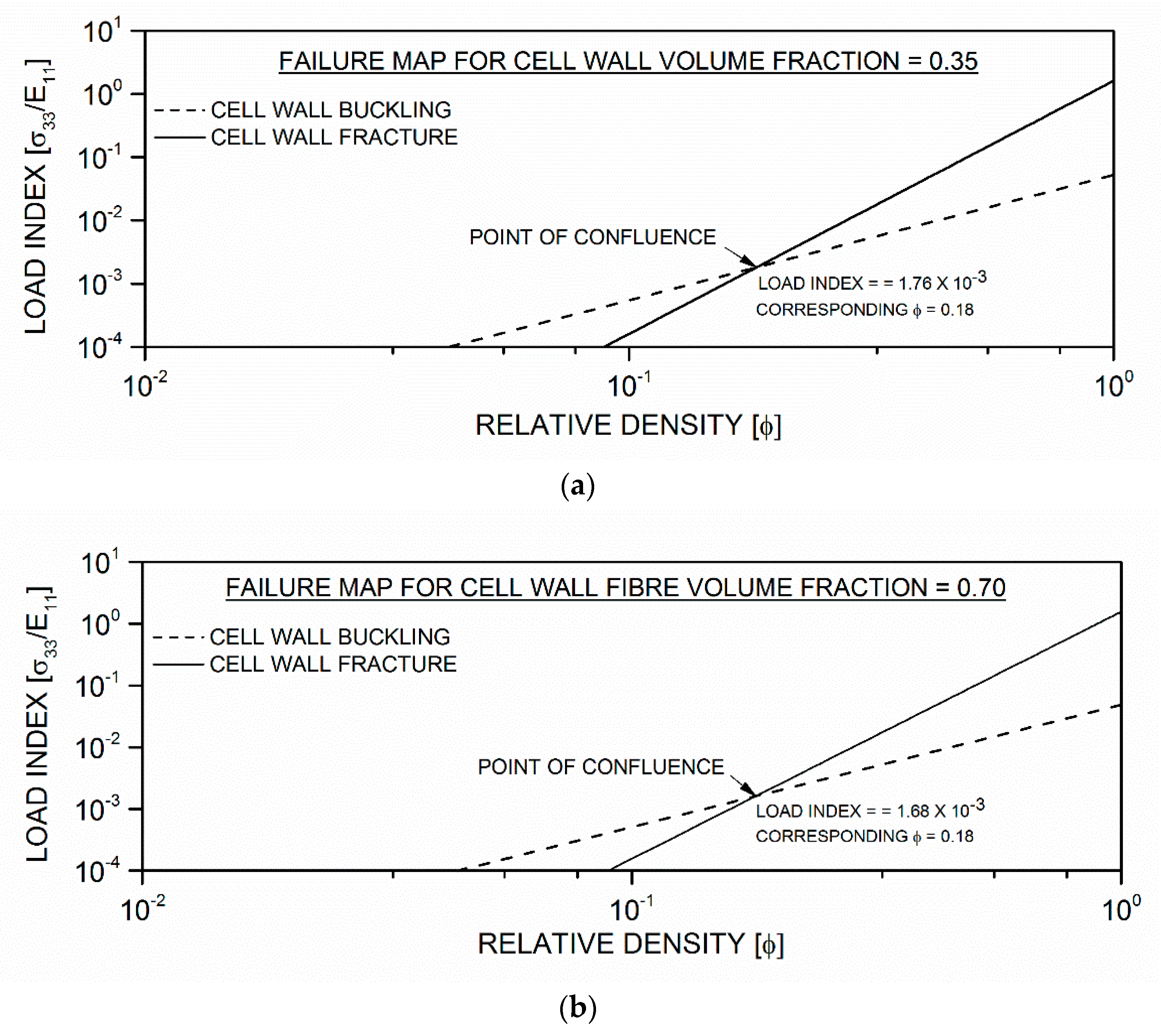
4.3. Failure Maps
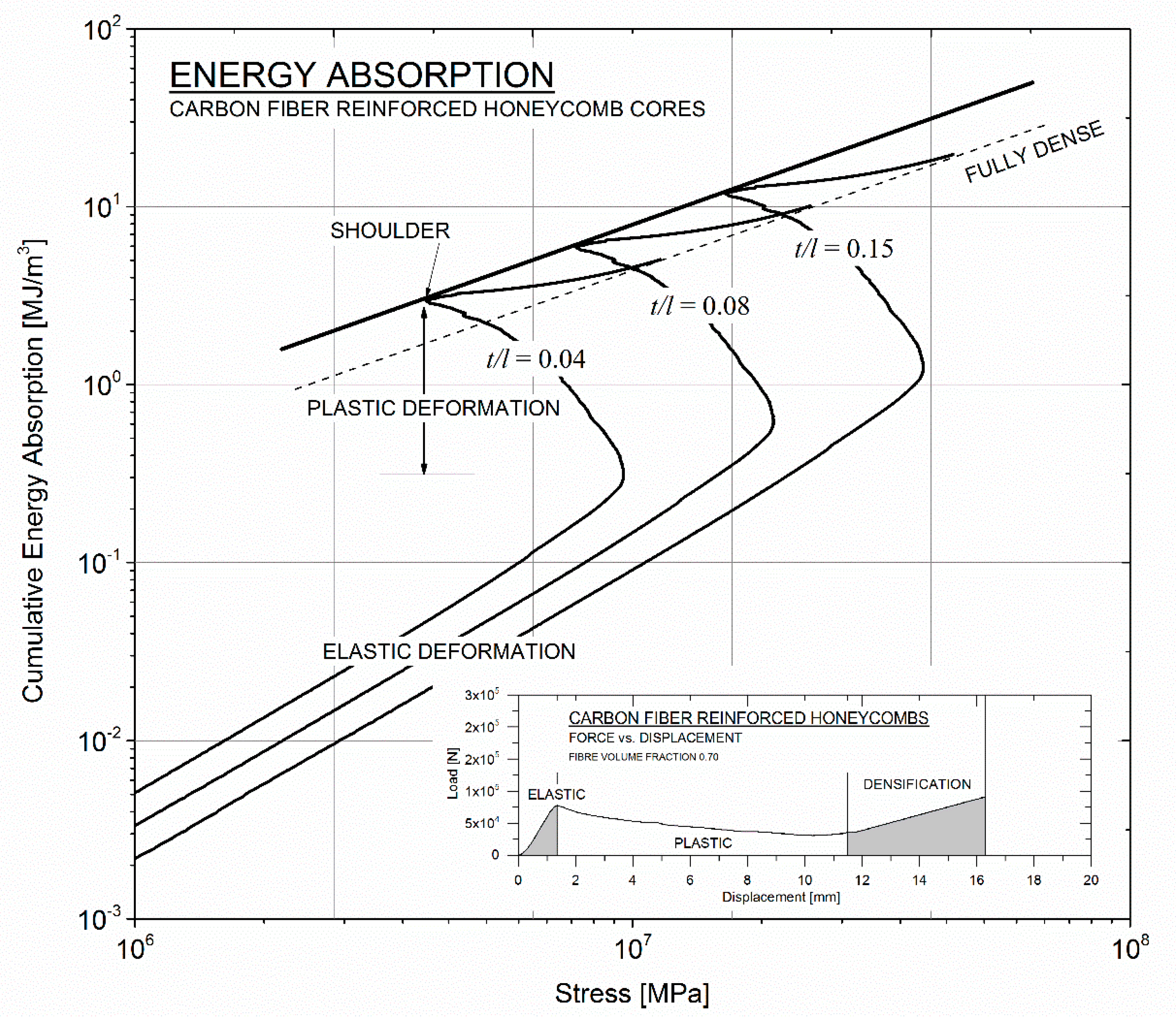
4.4. Energy Absorption
4.5. Energy Absorption Diagram
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bitzer, T. Honeycomb Technology: Materials, Design, Manufacturing, Applications and Testing; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Rao, S.; Jayaraman, K.; Bhattacharyya, D. Short fibre reinforced cores and their sandwich panels: Processing and evaluation. Composites Part A 2011, 42, 1236–1246. [Google Scholar] [CrossRef]
- Rao, S.; Jayaraman, K.; Bhattacharyya, D. Micro and macro analysis of sisal fibre composites hollow core sandwich panels. Composites Part B 2012, 43, 2738–2745. [Google Scholar] [CrossRef]
- Petrone, G.; Rao, S.; De Rosa, S.; Mace, B.R.; Franco, F.; Bhattacharyya, D. Behaviour of fibre-reinforced honeycomb core under low velocity impact loading. Compos. Struct. 2013, 100, 356–362. [Google Scholar] [CrossRef]
- Petrone, G.; Rao, S.; De Rosa, S.; Mace, B.R.; Franco, F.; Bhattacharyya, D. Initial experimental investigations on natural fibre reinforced honeycomb core panels. Composites Part B 2013, 55, 400–406. [Google Scholar] [CrossRef] [Green Version]
- Vivolo, M.; Rao, S.; Vandepitte, D.; Desmet, W.; Mace, B.R.; Bhattacharyya, D. Effects of Core Geometry on the Vibro-Acoustic Behaviour of Fibre Reinforced Corrugated Core Sandwich Panels. In Proceedings of the 15th European Conference on Composite Materials (ECCM15), Venice, Italy, 24–28 June 2012. [Google Scholar]
- Rao, S.; Jayaraman, K.; Bhattacharyya, D. Hollow Core BioPanels: Manufacturing and Analysis; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2011. [Google Scholar]
- Ashby, M.F.; Bréchet, Y.J.M. Designing hybrid materials. Acta Mater. 2003, 51, 5801–5821. [Google Scholar] [CrossRef]
- Finnegan, K.; Kooistra, G.; Wadley, H.N.G.; Deshpande, V.S. The compressive response of carbon fiber composite pyramidal truss sandwich cores. Int. J. Mater. Res. 2007, 98, 1264–1272. [Google Scholar] [CrossRef]
- Fan, H.L.; Meng, F.H.; Yang, W. Sandwich panels with Kagome lattice cores reinforced by carbon fibers. Compos. Struct. 2007, 81, 533–539. [Google Scholar]
- Fan, H.; Fang, D.; Chen, L.; Dai, Z.; Yang, W. Manufacturing and testing of a CFRC sandwich cylinder with Kagome cores. Compos. Sci. Technol. 2009, 69, 2695–2700. [Google Scholar] [CrossRef]
- Heimbs, S.; Cichosz, J.; Klaus, M.; Kilchert, S.; Johnson, A.F. Sandwich structures with textile-reinforced composite foldcores under impact loads. Compos. Struct. 2010, 92, 1485–1497. [Google Scholar] [CrossRef]
- George, T.; Deshpande, V.S.; Sharp, K.; Wadley, H.N.G. Hybrid core carbon fiber composite sandwich panels: Fabrication and mechanical response. Compos. Struct. 2014, 108, 696–710. [Google Scholar] [CrossRef]
- Russell, B.; Deshpande, V.; Wadley, H.N.G. Quasistatic deformation and failure modes of composite square honeycombs. J. Mech. Mater. Struct. 2008, 3, 1315–1340. [Google Scholar] [CrossRef] [Green Version]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Petras, A.; Sutcliffe, M.P.F. Failure mode maps for honeycomb sandwich panels. Compos. Struct. 1999, 44, 237–252. [Google Scholar] [CrossRef]
- Othman, A.R.; Barton, D.C. Failure initiation and propagation characteristics of honeycomb sandwich composites. Compos. Struct. 2008, 85, 126–138. [Google Scholar] [CrossRef]
- Khan, M.K.; Baig, T.; Mirza, S. Experimental investigation of in-plane and out-of-plane crushing of aluminum honeycomb. Mater. Sci. Eng. A 2012, 539, 135–142. [Google Scholar] [CrossRef]
- Ivañez, I.; Fernandez-Cañadas, L.M.; Sanchez-Saez, S. Compressive deformation and energy-absorption capability of aluminium honeycomb core. Compos. Struct. 2017, 174, 123–133. [Google Scholar] [CrossRef]
- Meran, A.P.; Toprak, T.; Muǧan, A. Numerical and experimental study of crashworthiness parameters of honeycomb structures. Thin Walled Struct. 2014, 78, 87–94. [Google Scholar] [CrossRef]
- PRIMETM 20LV Laminating. Available online: http://www.gurit.com/sitecore/content/Old-Product-Pages/Other-Products/Laminating-Infusion-Systems/PRIME-20LV (accessed on 20 July 2018).
- Rodriguez, A. A robust UD dry tape product for automated manufacturing of composites. In Proceedings of the SC Aerospace Conference & Expo (ACE’ 16), South Carolina, SC, USA, 24–25 August 2016. [Google Scholar]

| Samples | Resolution | ||
|---|---|---|---|
| 10× | 20× | ||
| 1 | Region 1 (%) | 70 | 63 |
| Region 2 (%) | 68 | 63 | |
| Region 3 (%) | 60 | 65 | |
| 2 | Region 1 (%) | 70 | 69 |
| Region 2 (%) | 65 | 65 | |
| Region 3 (%) | 68 | 70 | |
| 3 | Region 1 (%) | 65 | 62 |
| Region 2 (%) | 65 | 66 | |
| Region 3 (%) | 60 | 65 | |
| Total | 65 | 65 | |
| Standard deviation | 3.7 | 2.5 | |
| Failure Type | Failure Criterion | |
|---|---|---|
| Cell wall fracture (CF) | where | |
| Core buckling (CB) | ||
| Material | Elastic Modulus—E (Pa) | Shear Modulus—G(Pa) | Poisson’s Ratio—ν |
|---|---|---|---|
| Prime 20 LV | 4.5 × 109 | 1.6 × 109 | 0.4 |
| Cytec Prism TX1100 | 2.3 × 1011 | 5.0 × 1010 | 0.3 |
| Properties | Fiber Volume Fraction | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.35 | 0.4 | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 | 0.7 | |
| E11 (GPa) | 83.34 | 94.7 | 106.0 | 117.0 | 129.0 | 140.0 | 151.0 | 162.0 |
| E22 (GPa) | 6.85 | 7.40 | 8.05 | 8.83 | 9.77 | 10.9 | 12.4 | 14.3 |
| G12 (GPa) | 2.42 | 2.61 | 2.83 | 3.10 | 3.42 | 3.82 | 4.31 | 4.96 |
| ν12 | 0.37 | 0.36 | 0.36 | 0.35 | 0.35 | 0.34 | 0.34 | 0.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, S.; Thomas, J.; Aziz, A.; Cantwell, W. Manufacturing and Performance Evaluation of Carbon Fiber–Reinforced Honeycombs. J. Compos. Sci. 2019, 3, 13. https://doi.org/10.3390/jcs3010013
Rao S, Thomas J, Aziz A, Cantwell W. Manufacturing and Performance Evaluation of Carbon Fiber–Reinforced Honeycombs. Journal of Composites Science. 2019; 3(1):13. https://doi.org/10.3390/jcs3010013
Chicago/Turabian StyleRao, Sanjeev, Jimmy Thomas, Alia Aziz, and Wesley Cantwell. 2019. "Manufacturing and Performance Evaluation of Carbon Fiber–Reinforced Honeycombs" Journal of Composites Science 3, no. 1: 13. https://doi.org/10.3390/jcs3010013
APA StyleRao, S., Thomas, J., Aziz, A., & Cantwell, W. (2019). Manufacturing and Performance Evaluation of Carbon Fiber–Reinforced Honeycombs. Journal of Composites Science, 3(1), 13. https://doi.org/10.3390/jcs3010013




