Prediction of Orthotropic Hygroscopic Swelling of Fiber-Reinforced Composites from Isotropic Swelling of Matrix Polymer
Abstract
1. Introduction
2. Materials and Methods
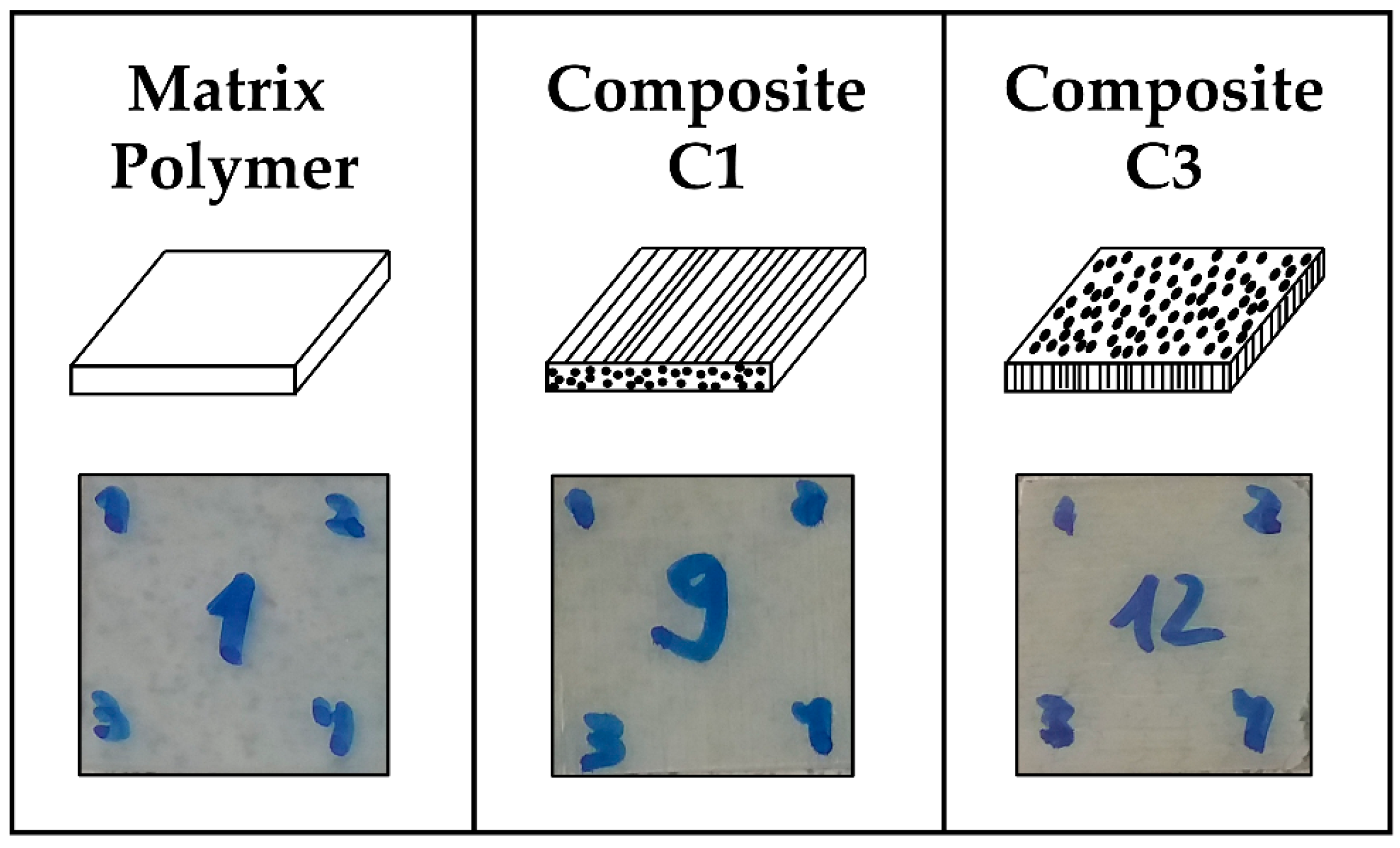
2.1. Materials
2.2. Methods
3. Model
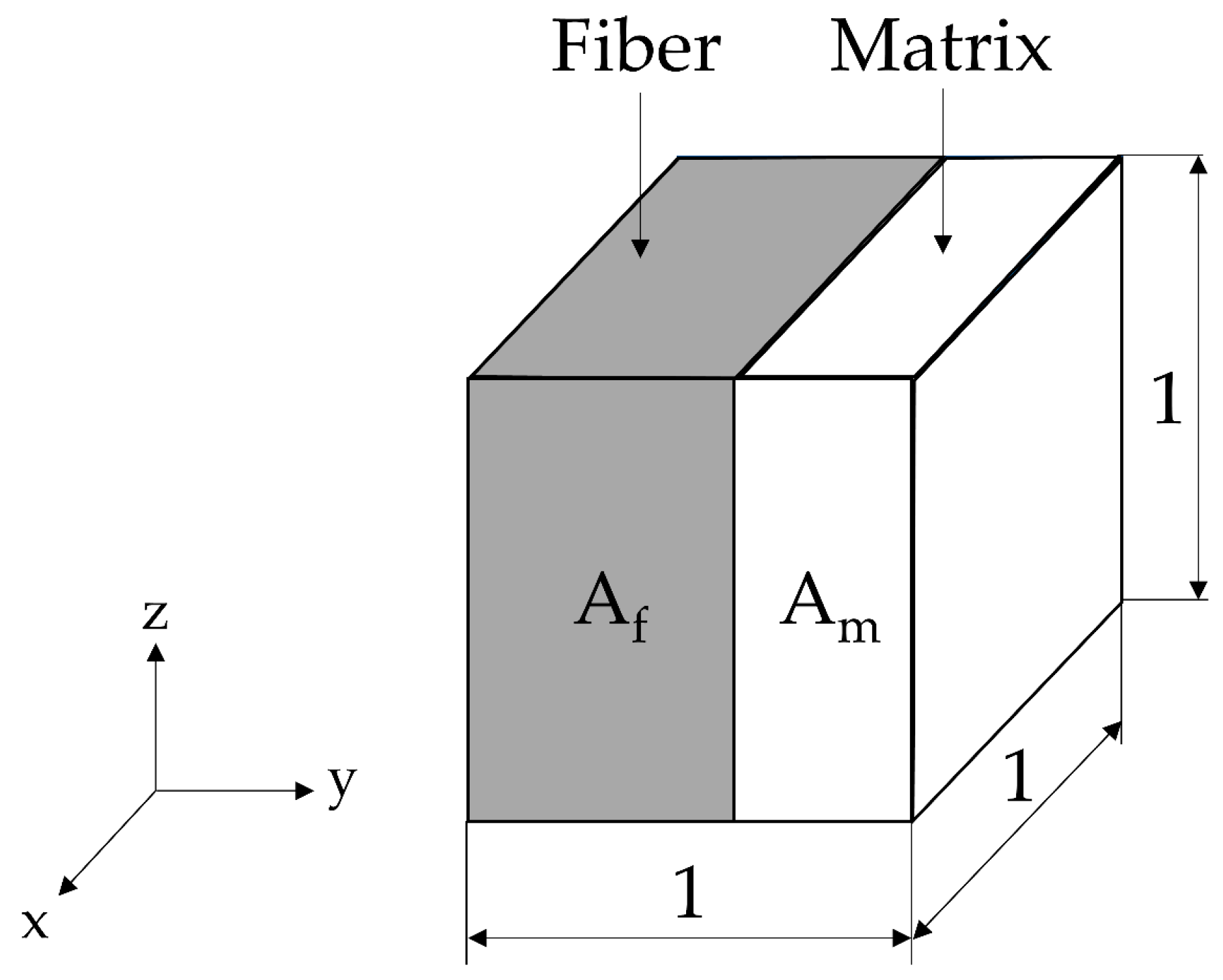
3.1. Swelling Analytical Model
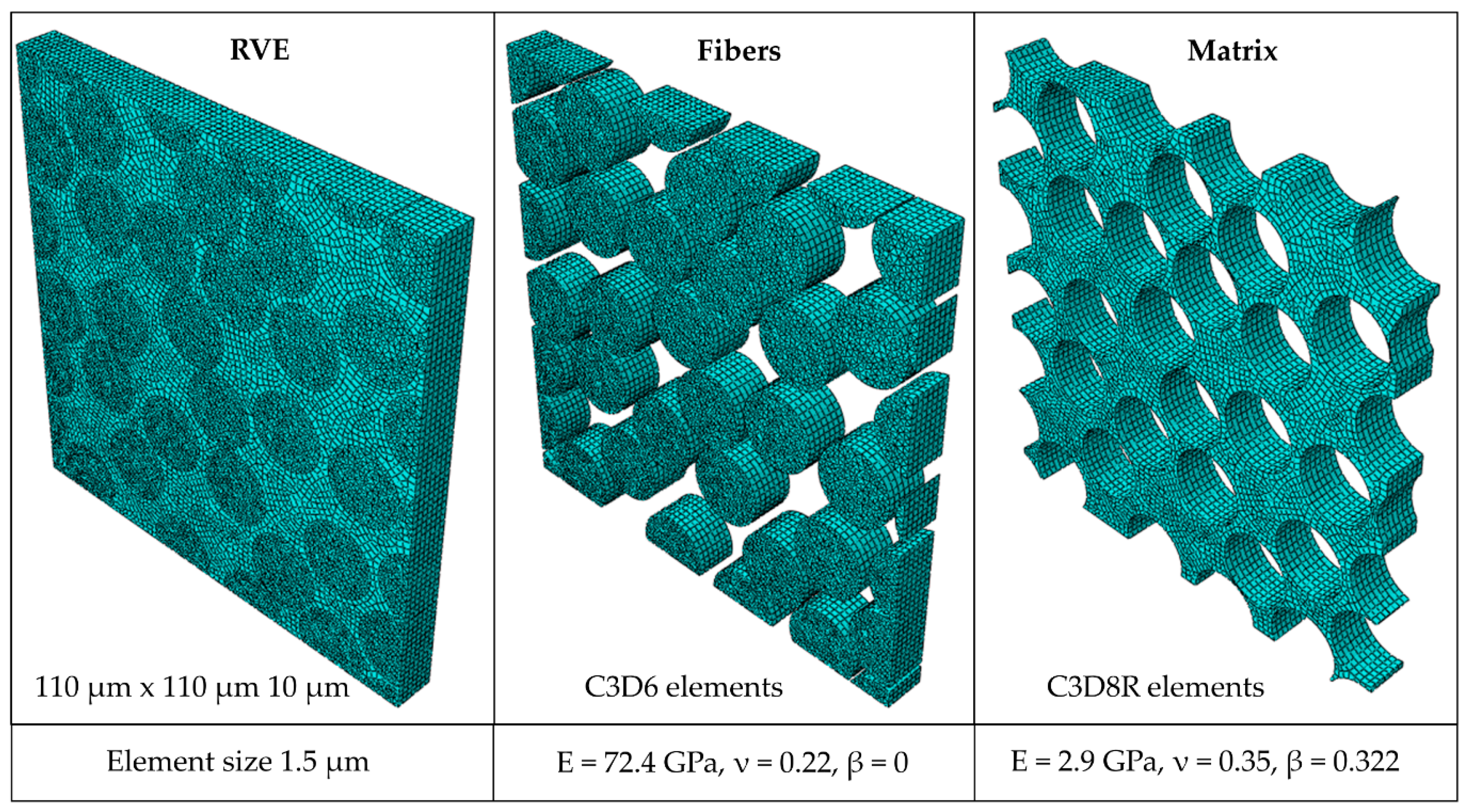
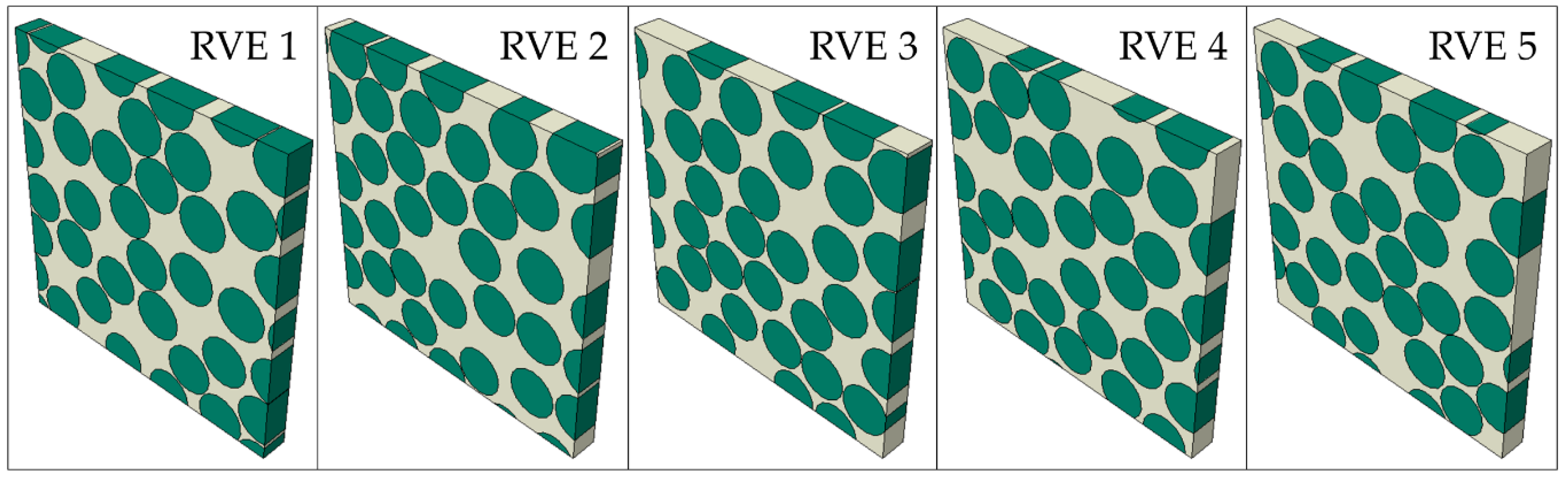
3.2. Finite Element Model
4. Results
4.1. Swelling Measurements
4.2. Analytical and Finite Element Predictions
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krauklis, A.; Echtermeyer, A. Mechanism of yellowing: Carbonyl formation during hygrothermal aging in a common amine epoxy. Polymers 2018, 10, 1017. [Google Scholar] [CrossRef]
- Xiao, G.Z.; Shanahan, M.E.R. Swelling of DGEBA/DDA epoxy resin during hygrothermal ageing. Polymer 1998, 39, 3253–3260. [Google Scholar] [CrossRef]
- Toscano, A.; Pitarresi, G.; Scafidi, M.; Di Filippo, M.; Spadaro, G.; Alessi, S. Water diffusion and swelling stresses in highly crosslinked epoxy matrices. Polym. Degrad. STable 2016, 133, 255–263. [Google Scholar] [CrossRef]
- Grabovac, I.; Whittaker, D. Application of bonded composites in the repair of ships structures—A 15-year service experience. Compos. Part A 2009, 40, 1381–1398. [Google Scholar] [CrossRef]
- McGeorge, D.; Echtermeyer, A.T.; Leong, K.H.; Melve, B.; Robinson, M.; Fischer, K.P. Repair of floating offshore units using bonded fibre composite materials. Compos. Part A 2009, 40, 1364–1380. [Google Scholar] [CrossRef]
- Gustafson, C.G.; Echtermeyer, A. Long-term properties of carbon fibre composite tethers. Int. J. Fatigue. 2006, 28, 1353–1362. [Google Scholar] [CrossRef]
- Salama, M.M.; Stjern, G.; Storhaug, T.; Spencer, B.; Echtermeyer, A. The First Offshore Field Installation for a Composite Riser Joint. OTC-14018-MS. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2002; Offshore Technology Conference: Houston, TX, USA, 2002. [Google Scholar] [CrossRef]
- Echtermeyer, A.T.; Gagani, A.I.; Krauklis, A.E.; Mazan, T. Multiscale Modelling of Environmental Degradation—First Steps. In Durability of Composites in a Marine Environment 2. Solid Mechanics and Its Applications; Davies, P., Rajapakse, Y.D.S., Eds.; Springer: Cham, Switzerland, 2018; Volume 245, pp. 135–149. ISBN 978-3-319-65145-3. [Google Scholar]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Hygrothermal aging of amine epoxy: Reversible static and fatigue properties. Open Eng. 2018, 8, 447–454. [Google Scholar] [CrossRef]
- Ibarra, L.; Chamorro, C. Short fiber–elastomer composites. Effects of matrix and fiber level on swelling and mechanical and dynamic properties. J. Appl. Polym. Sci. 1991, 43, 1805–1819. [Google Scholar] [CrossRef]
- Zhou, J. Transient analysis on hygroscopic swelling characterization using sequentially coupled moisture diffusion and hygroscopic stress modeling method. Microelectron. Reliab. 2008, 48, 805–810. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Near-Infrared spectroscopic method for monitoring water content in epoxy resins and fiber-reinforced composites. Materials 2018, 11, 586. [Google Scholar] [CrossRef]
- Hahn, H.T.; Kim, R.Y. Swelling of Composite Laminates. In Advanced Composite Materials: Environmental Effects; ASTM STP 658; American Society for Testing and Materials: Philadelphia, PA, USA, 1978; pp. 98–120. [Google Scholar]
- Shirangi, M.H.; Michel, B. Mechanism of moisture diffusion, hygroscopic swelling, and adhesion degradation in epoxy molding compounds. In Moisture Sensitivity of Plastic Packages of IC Devices; Fan, X.J., Suhir, E., Eds.; Springer: New York, NY, USA, 2010; pp. 29–69. ISBN 978-1-4419-5719-1. [Google Scholar]
- Tsai, S.W. Composites Design, 4th ed.; Think Composites: Dayton, OH, USA, 1988; ISBN 0-9618090-2-7. [Google Scholar]
- Obeid, H.; Clément, A.; Fréour, S.; Jacquemin, F.; Casari, P. On the identification of the coefficient of moisture expansion of polyamide-6: Accounting differential swelling strains and plasticization. Mech. Mater. 2018, 118, 1–10. [Google Scholar] [CrossRef]
- Cairns, D.S.; Adams, D.F. Moisture and thermal expansion properties of unidirectional composite materials and the epoxy matrix. J. Reinf. Plast. Compos. 1983, 2, 239–255. [Google Scholar] [CrossRef]
- Ashton, J.E.; Halpin, J.C.; Petit, P.H. Primer on Composite Materials Analysis; Technomic Pub. Co.: Stamford, CT, USA, 1969; ISBN 978-0-8776-2754-8. [Google Scholar]
- Halpin, J.C. Effects of Environmental Factors on Composite Materials; Technical report AFML-TR-67–423; Air Force Materials Laboratory: Dayton, OH, USA, 1969. [Google Scholar]
- Schapery, R.A. Thermal expansion coefficients of composite materials based on energy principles. J. Compos. Mater. 1968, 2, 380–404. [Google Scholar] [CrossRef]
- Coran, A.Y.; Boustany, K.; Hamed, P. Unidirectional fiber-polymer composites: Swelling and modulus anisotropy. J. Appl. Polym. Sci. 1971, 15, 2471–2485. [Google Scholar] [CrossRef]
- Daniels, B.K. Orthotropic swelling and simplified elasticity laws with special reference to cord-reinforced rubber. J. Appl. Polym. Sci. 1973, 17, 2847–2853. [Google Scholar] [CrossRef]
- Fan, Y.; Gomez, A.; Ferraro, S.; Pinto, B.; Muliana, A.; La Saponara, V. Diffusion of water in glass fiber reinforced polymer composites at different temperatures. J. Compos. Mater. 2018, 1–14. [Google Scholar] [CrossRef]
- Jacquemin, F.; Fréour, S.; Guillén, R. Analytical modeling of transient hygro-elastic stress concentration—Application to embedded optical fiber in a non-uniform transient strain field. Compos. Sci. Technol. 2006, 66, 397–406. [Google Scholar] [CrossRef]
- Meng, M.; Rizvi, M.J.; Le, H.R.; Grove, S.M. Multi-scale modelling of moisture diffusion coupled with stress distribution in CFRP laminated composites. Compos. Struct. 2016, 138, 295–304. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Pannier, Y.; Gueguen, M.; Tandiang, D.; Gigliotti, M. Computed-tomography based modeling and simulation of moisture diffusion and induced swelling in textile composite materials. Int. J. Solids Struct. 2018, 154, 88–96. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Pannier, Y.; Gueguen, M.; Gigliotti, M. Image-based modeling of moisture-induced swelling nd stress in 2D textile composite materials using a global-local approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1505–1519. [Google Scholar] [CrossRef]
- Weitsman, Y.J. Fluid Effects in Polymers and Polymeric Composites; Springer: New York, NY, USA, 2012; ISBN 978-1-4614-1059-1. [Google Scholar]
- Weitsman, Y.J.; Elahi, M. Effects of fluids on the deformation, strength and durability of polymeric composites—An overview. Mech. Time-Depend. Mater. 2000, 4, 107–126. [Google Scholar] [CrossRef]
- Sar, B.E.; Fréour, S.; Davies, P.; Jacquemin, F. Accounting for differential swelling in the multi-physics modelling of the diffusive behaviour of polymers. J. Appl. Math. Mech. 2014, 94, 452–460. [Google Scholar] [CrossRef]
- Fan, Y.; Gomez, A.; Ferraro, S.; Pinto, B.; Muliana, A.; La Saponara, V. The effects of temperatures and volumetric expansion on the diffusion of fluids through solid polymers. J. Appl. Polym. Sci. 2017, 134, 45151–45165. [Google Scholar] [CrossRef]
- Kappert, E.J.; Raaijmakers, M.J.T.; Tempelman, K.; Cuperus, F.P.; Ogieglo, W.; Benes, N.E. Swelling of 9 polymers commonly employed for solvent-resistant nanofiltration membranes: A comprehensive dataset. J. Membr. Sci. 2019, 569, 177–199. [Google Scholar] [CrossRef]
- Ramirez, F.A.; Carlsson, L.A.; Acha, B.A. Evaluation of water degradation of vinylester and epoxy matrix composites by single fiber and composite tests. J. Mater. Sci. 2008, 43, 5230–5242. [Google Scholar] [CrossRef]
- Shirell, C.D.; Halpin, J. Moisture Absorption in Epoxy Composite Materials. In Proceedings of the Composite Materials: Testing and Design (Fourth Conference), ASTM STP617, Valley Forge, PA, USA, 3–4 May 1977; American Society for Testing and Materials: Philadelphia, PA, USA, 1979; pp. 514–528. [Google Scholar] [CrossRef]
- Agarwal, B.D.; Broutman, L.J. Analysis and Performance of Fiber Composites, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990; ISBN 978-0-4715-1152-6. [Google Scholar]
- González, C.; Llorca, J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: Microscopic mechanisms and modeling. Compos. Sci. Technol. 2007, 67, 2795–2806. [Google Scholar] [CrossRef]
- Yang, L.; Yan, Y.; Ma, J.; Liu, B. Effects of inter-fiber spacing and thermal residual stress on transverse failure of fiber-reinforced polymer–matrix composites. Comput. Mater. Sci. 2013, 68, 255–262. [Google Scholar] [CrossRef]
- Yamabe, K.; Goto, H. Synthesis and surface observation of montmorillonite/polyaniline composites. J. Comp. Sci. 2018, 2, 15. [Google Scholar] [CrossRef]
- Bertolino, V.; Cavallaro, G.; Milioto, S.; Parisi, F.; Lazzara, G. Thermal properties of multilayer nanocomposites based on halloysite nanotubes and biopolymers. J. Comp. Sci. 2018, 2, 41. [Google Scholar] [CrossRef]
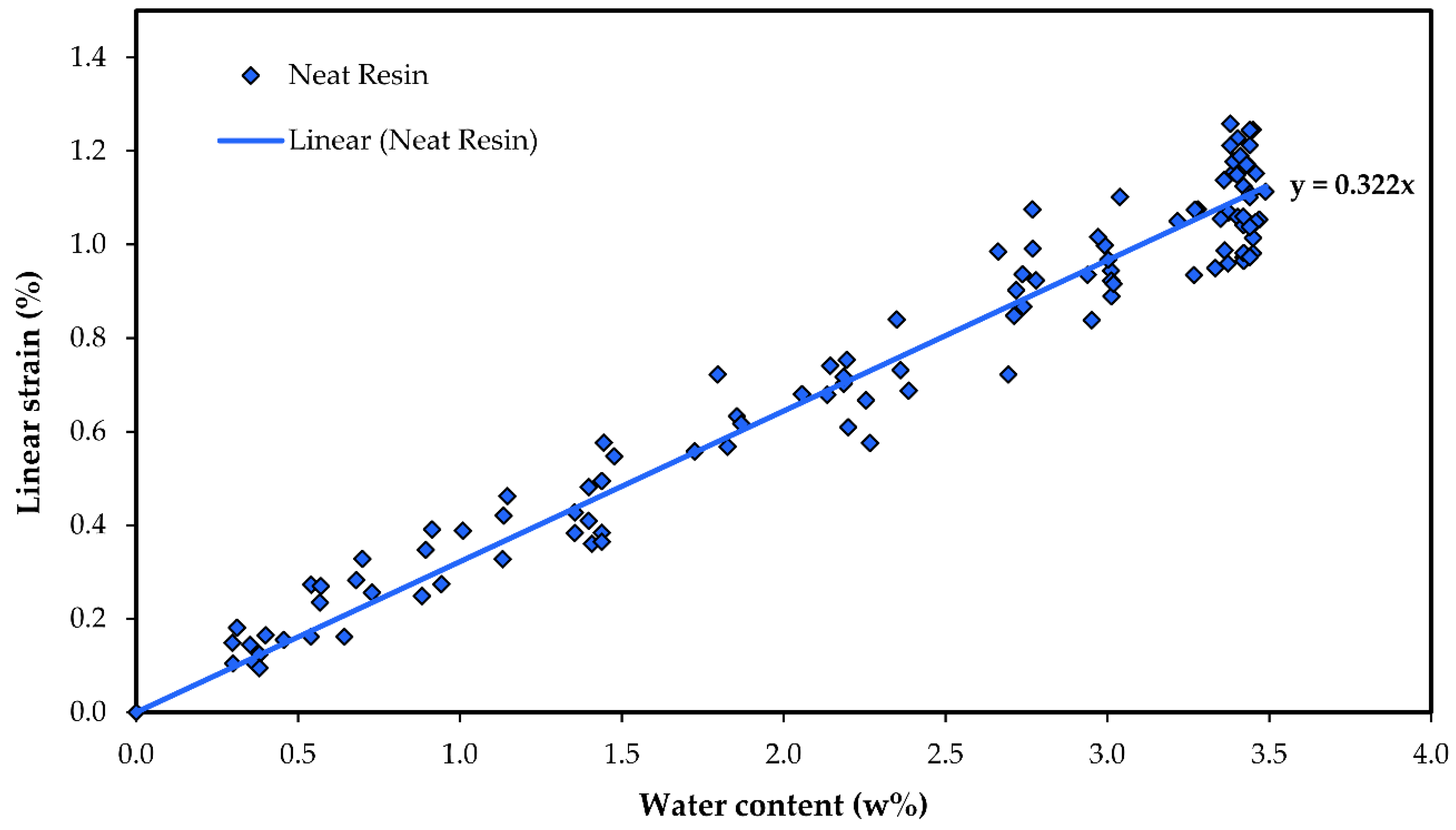
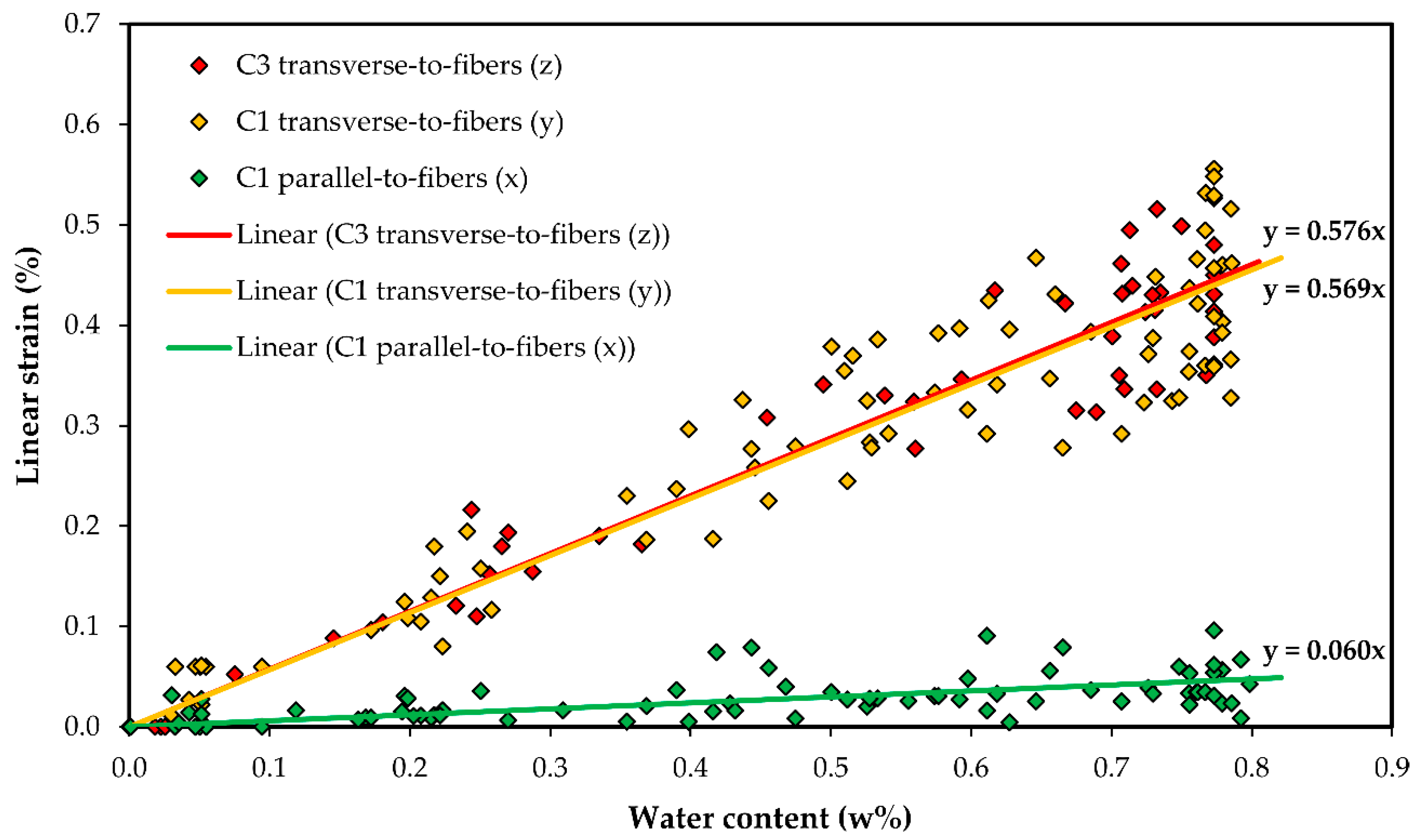
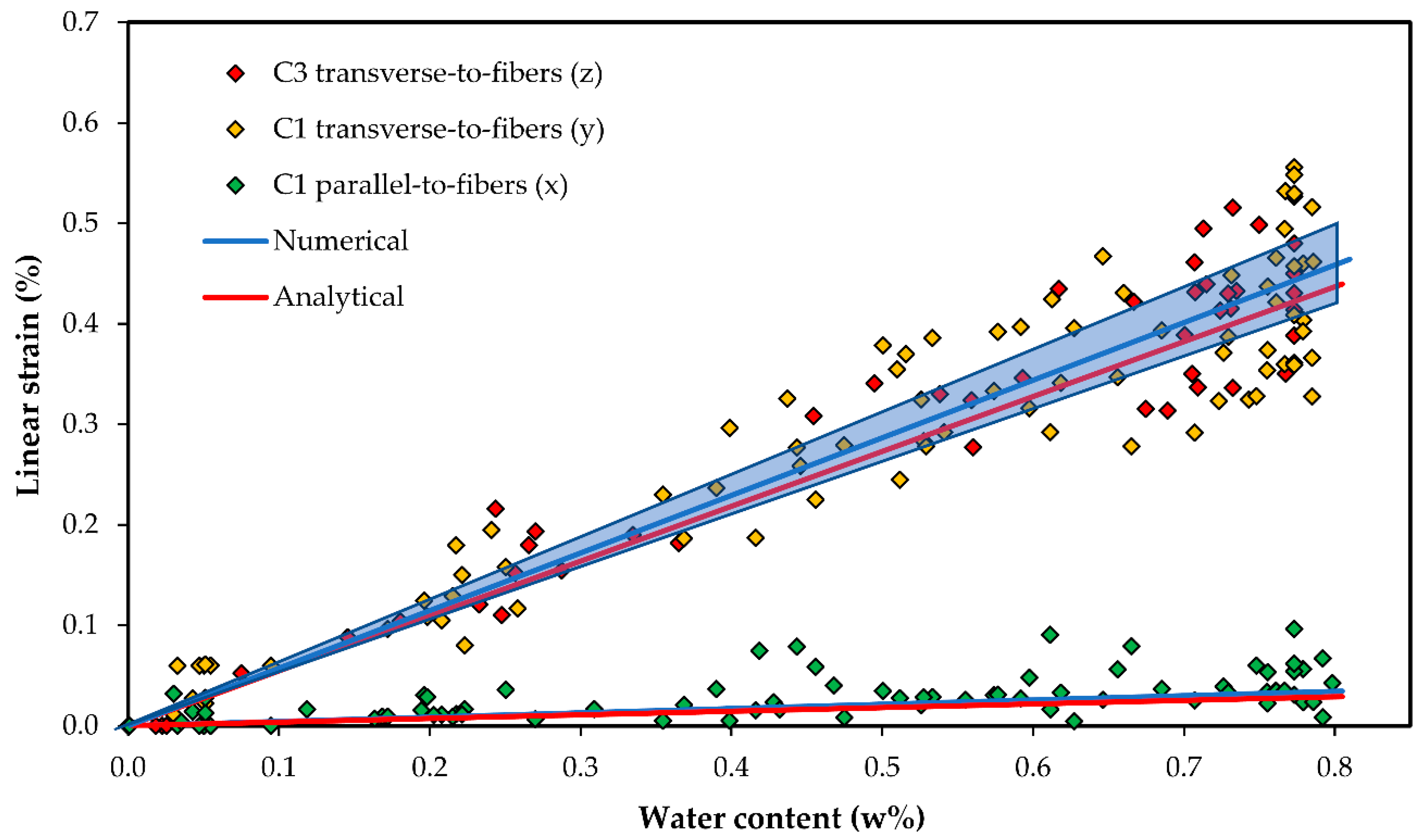
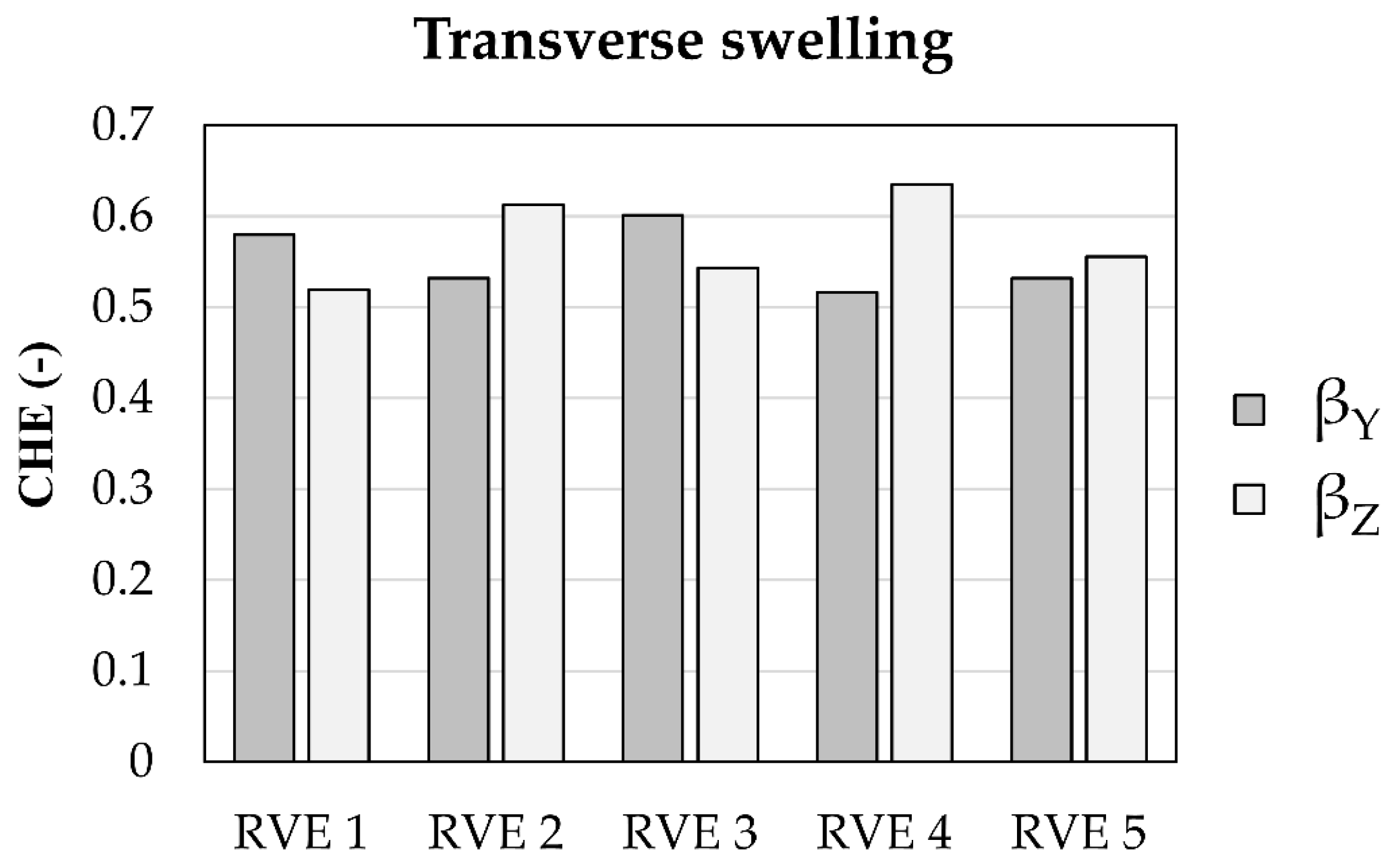
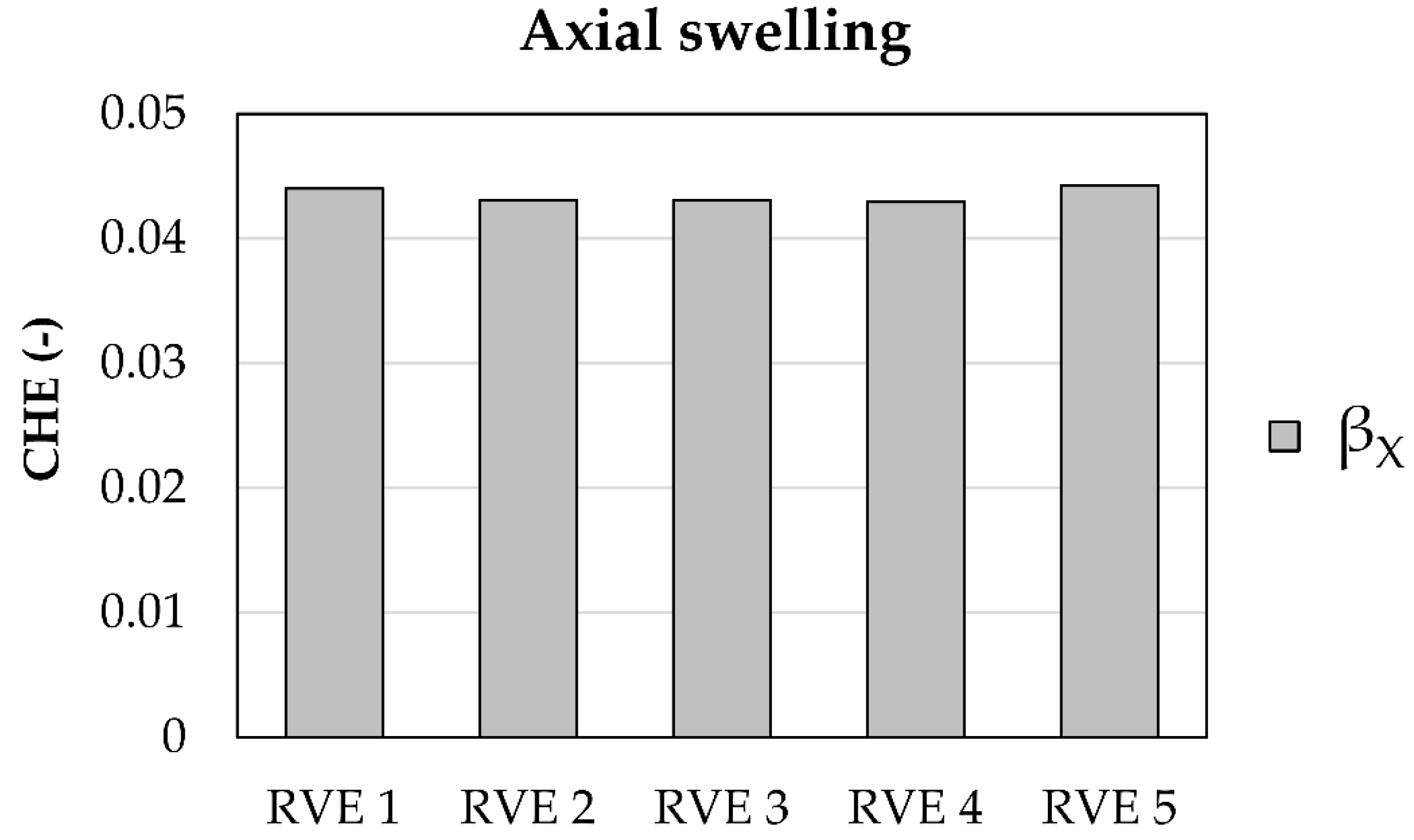
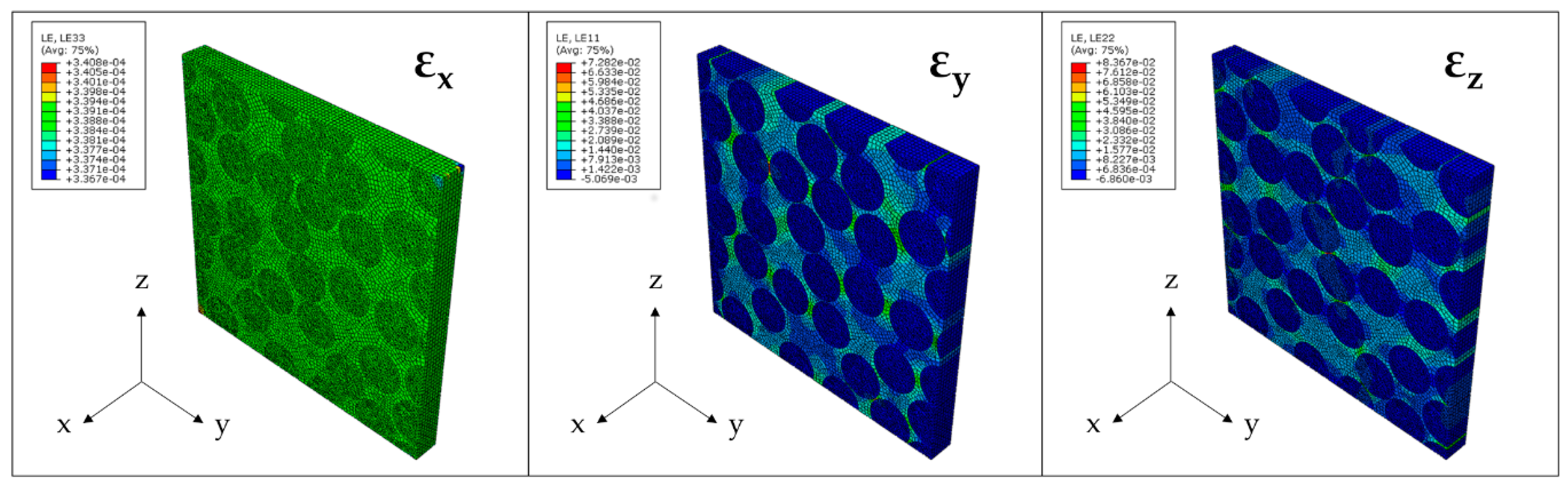
| CHE | Experimental | Analytical | Numerical |
|---|---|---|---|
| βm | 0.332 ± 0.021 | 0.332 * | 0.332 * |
| βX | 0.060 ± 0.018 | 0.036 | 0.044 |
| βY | 0.569 ± 0.066 | 0.546 | 0.552 |
| βZ | 0.576 ± 0.059 | 0.546 | 0.573 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Prediction of Orthotropic Hygroscopic Swelling of Fiber-Reinforced Composites from Isotropic Swelling of Matrix Polymer. J. Compos. Sci. 2019, 3, 10. https://doi.org/10.3390/jcs3010010
Krauklis AE, Gagani AI, Echtermeyer AT. Prediction of Orthotropic Hygroscopic Swelling of Fiber-Reinforced Composites from Isotropic Swelling of Matrix Polymer. Journal of Composites Science. 2019; 3(1):10. https://doi.org/10.3390/jcs3010010
Chicago/Turabian StyleKrauklis, Andrey E., Abedin I. Gagani, and Andreas T. Echtermeyer. 2019. "Prediction of Orthotropic Hygroscopic Swelling of Fiber-Reinforced Composites from Isotropic Swelling of Matrix Polymer" Journal of Composites Science 3, no. 1: 10. https://doi.org/10.3390/jcs3010010
APA StyleKrauklis, A. E., Gagani, A. I., & Echtermeyer, A. T. (2019). Prediction of Orthotropic Hygroscopic Swelling of Fiber-Reinforced Composites from Isotropic Swelling of Matrix Polymer. Journal of Composites Science, 3(1), 10. https://doi.org/10.3390/jcs3010010






