Thermal Buckling Behaviour of Thin and Thick Variable-Stiffness Panels
Abstract
1. Introduction
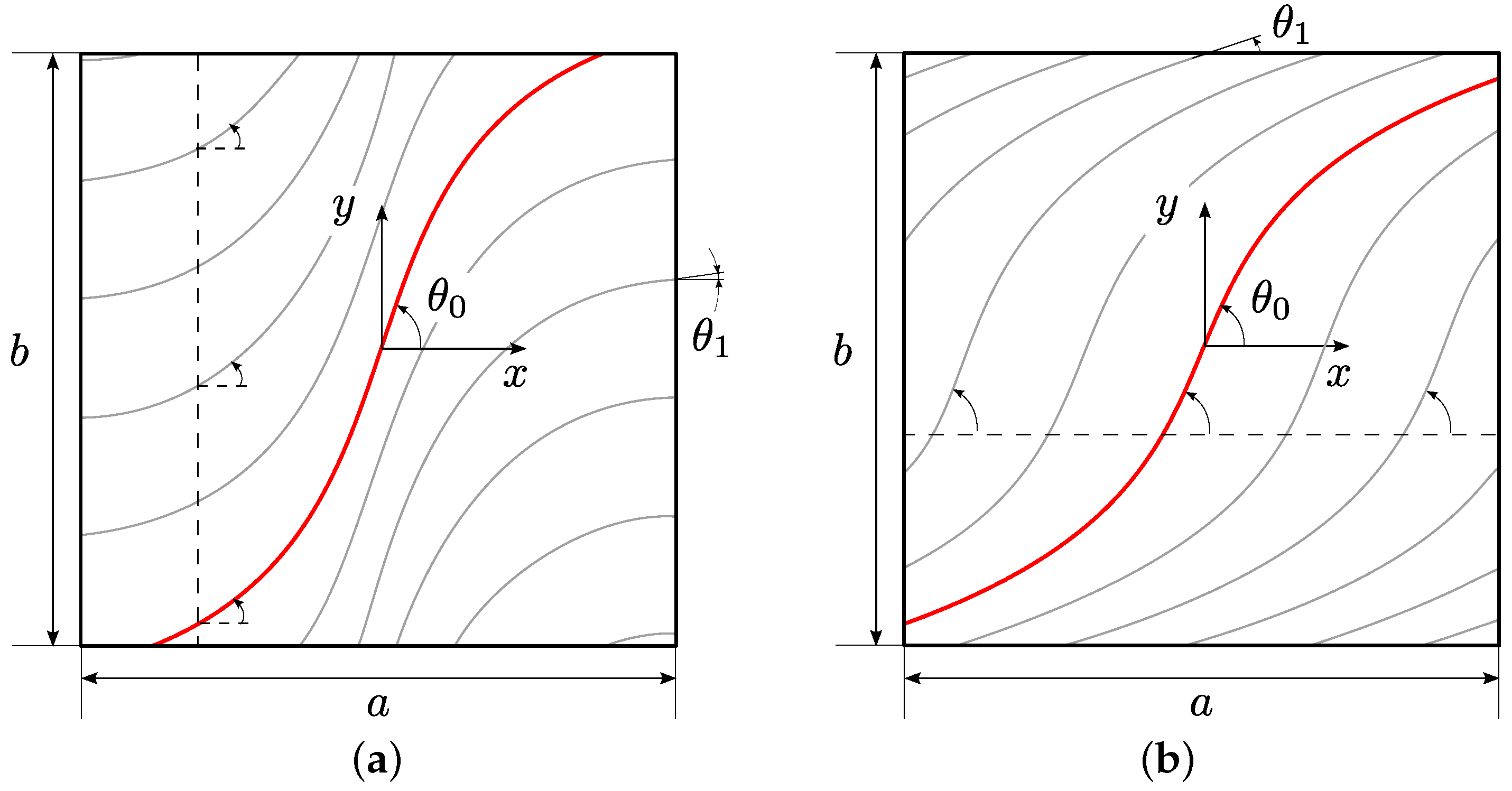
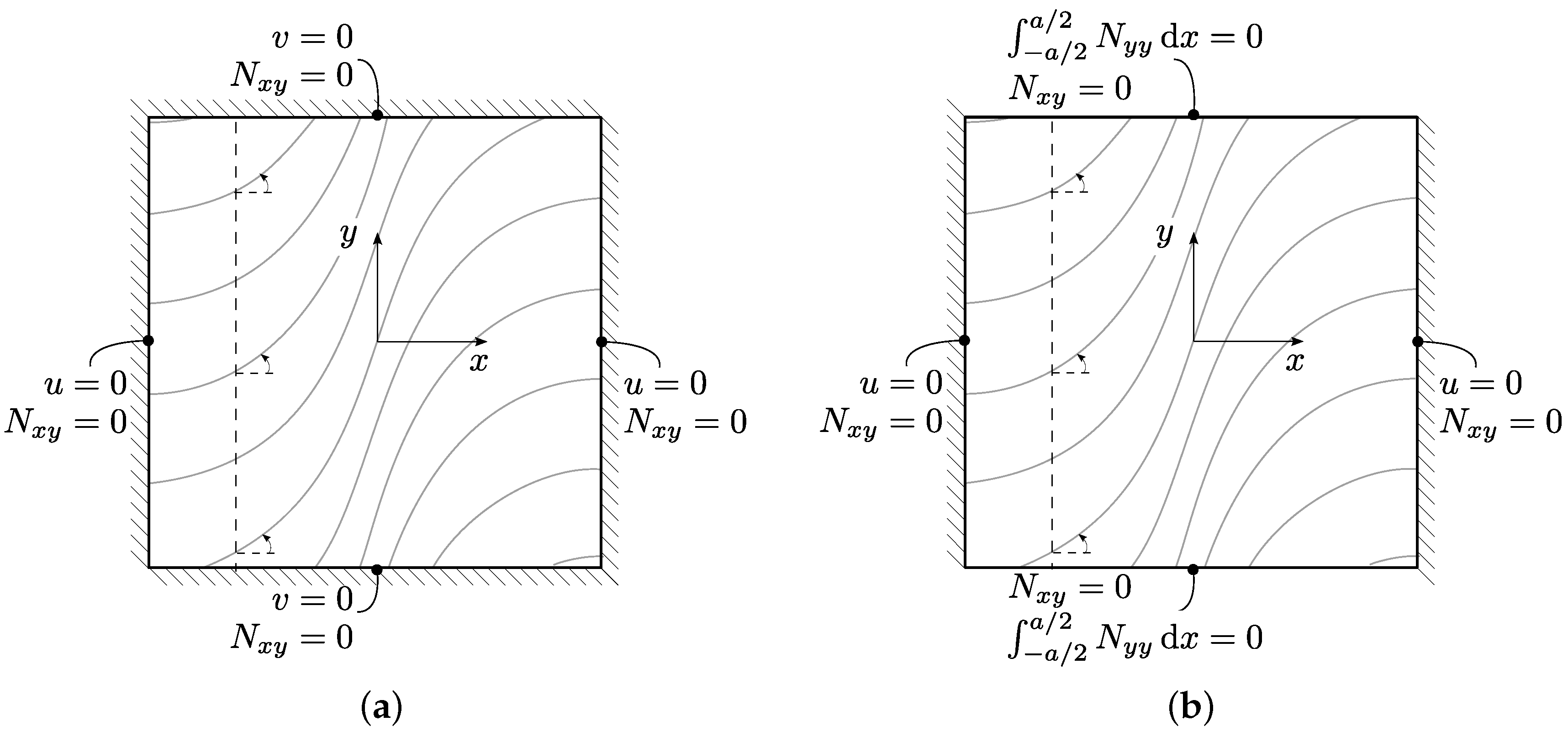
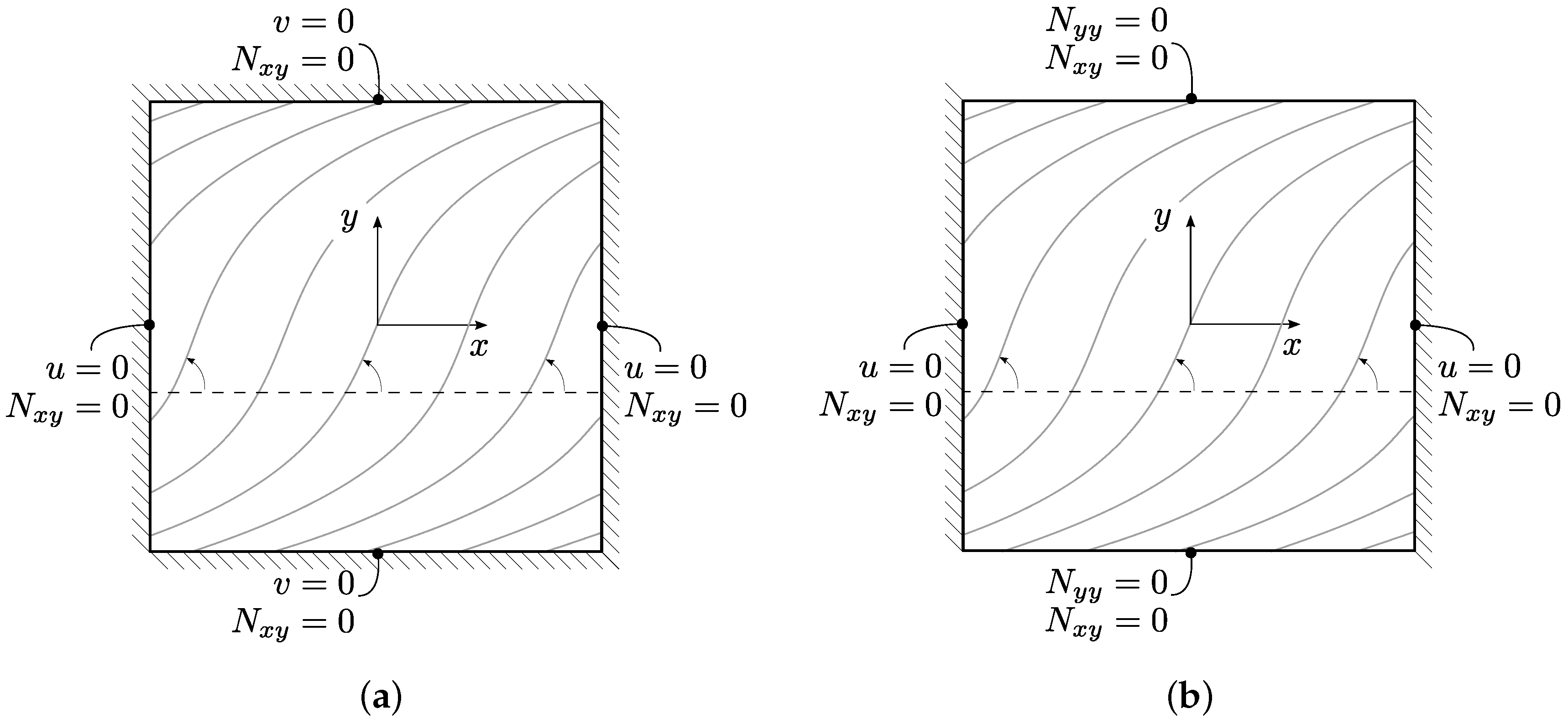
2. Theoretical Framework
2.1. Variational Formulation and Approximate Solution
2.2. Pre-Buckling Solutions
2.2.1. Thermoelastic Strains and Constitutive Relation
2.2.2. Semi-Inverse Approach
2.2.3. Case-Tx1
2.2.4. Case-Tx2
2.2.5. Case-Ty1
2.2.6. Case-Ty2
3. Results
3.1. Comparison with Literature Results
- = 15.0,
- =
- = = 0.5,
- = 0.3356,
- = = 0.3,
- = 0.49,
- = 0.015,
- = 1.0.
- = 40.0,
- =
- = = 0.6,
- = 0.5,
- = = = 0.25,
- = 1 10C,
- = 2.0.
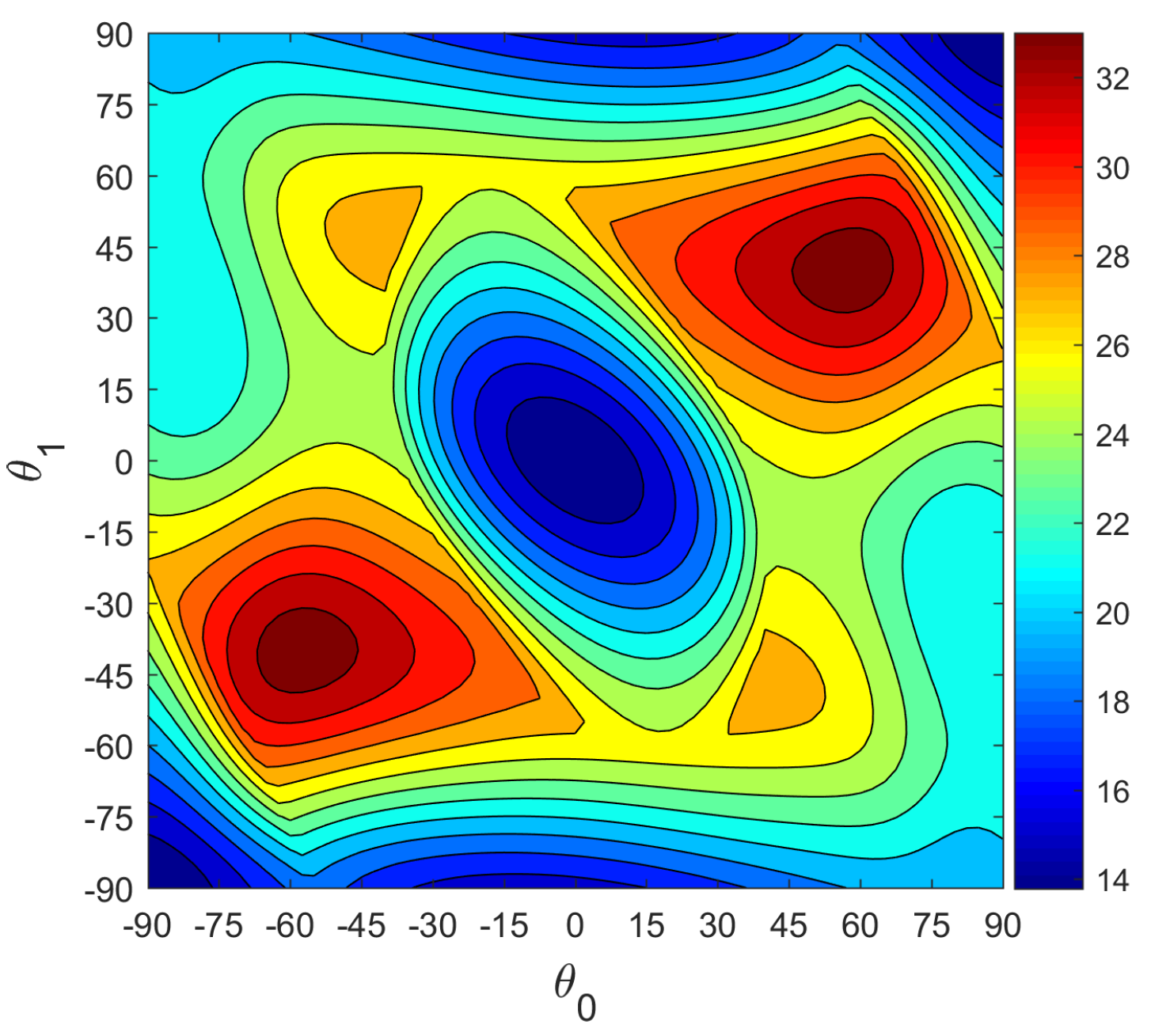
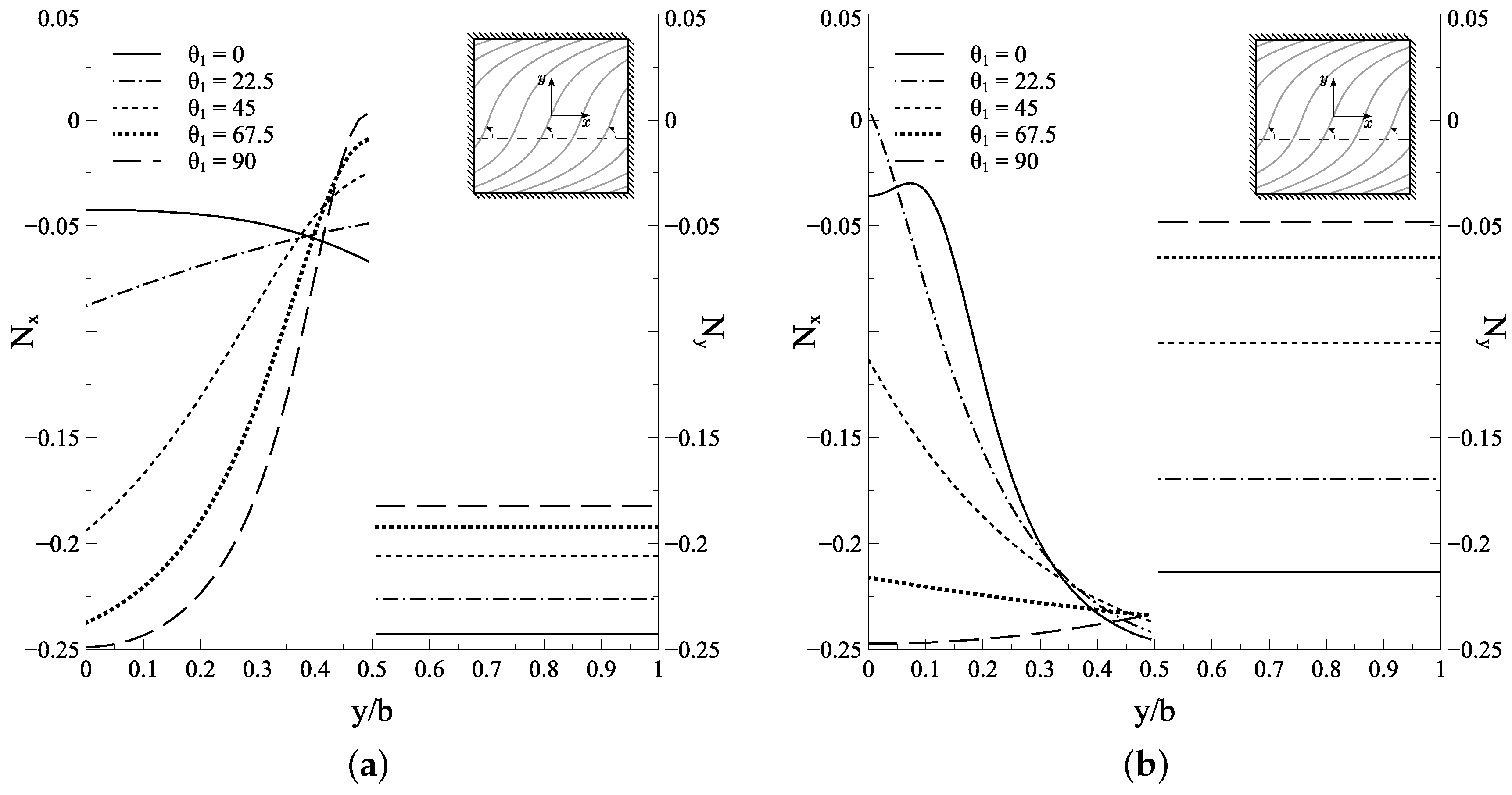
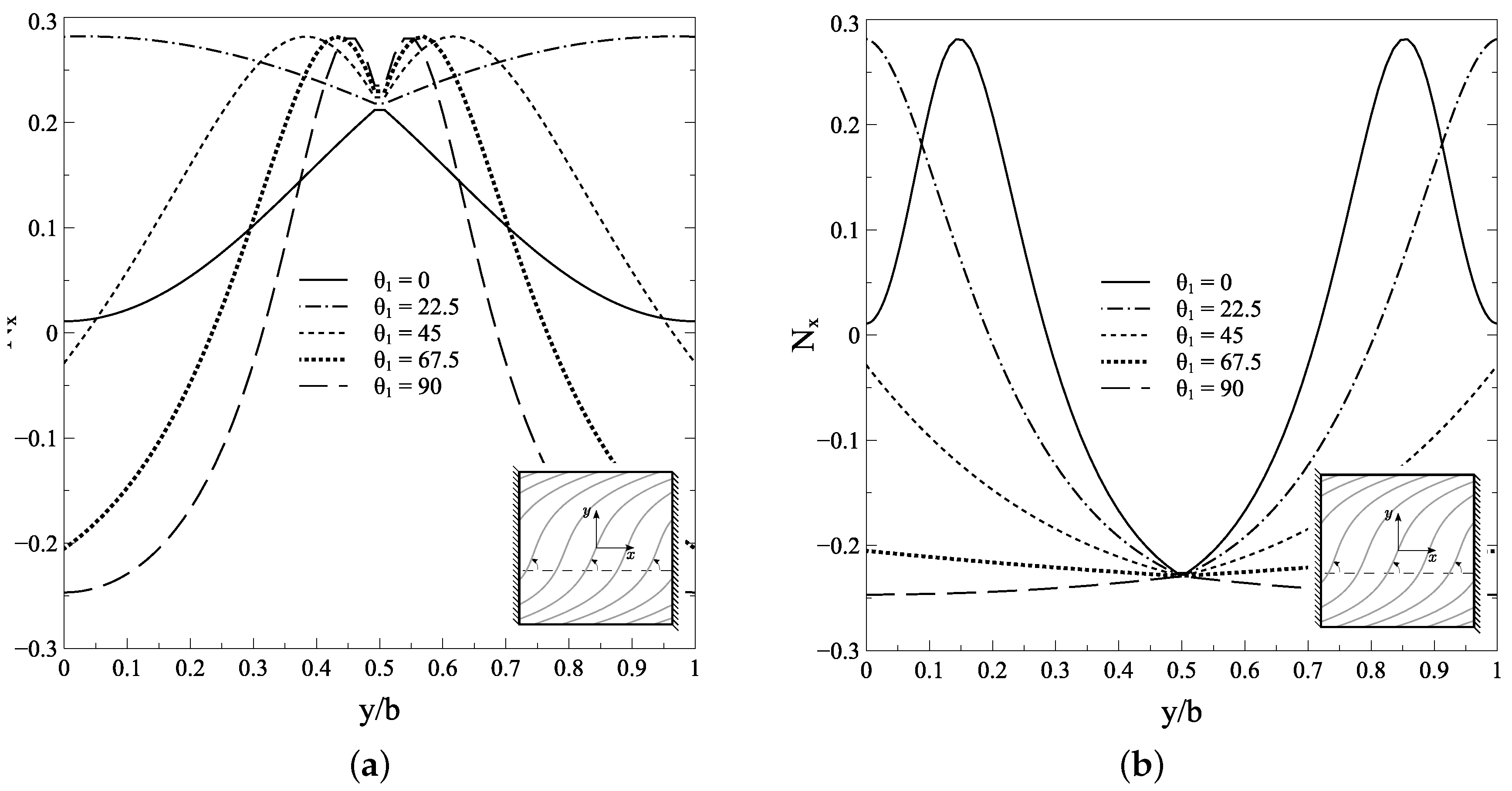
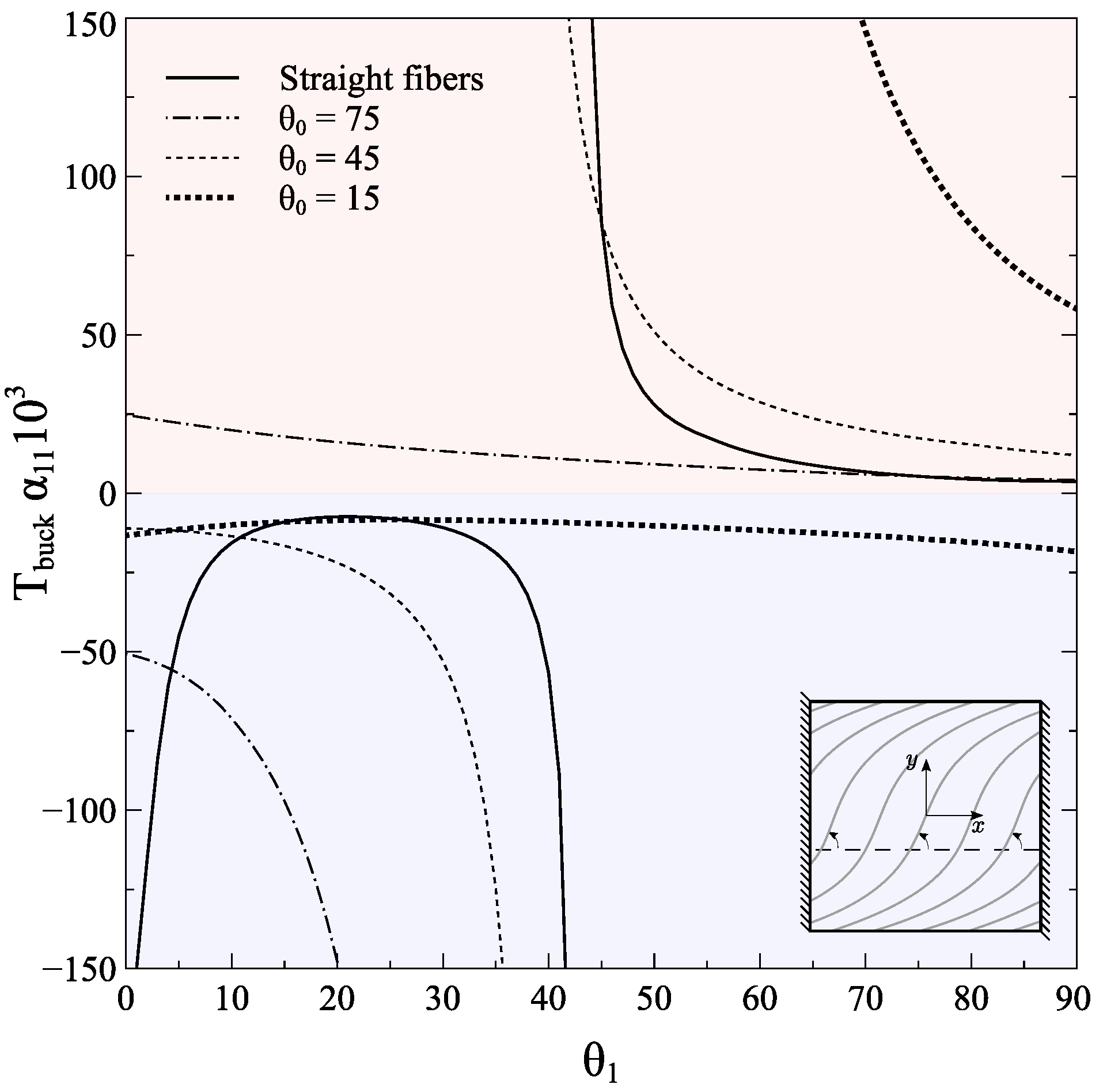
3.2. Pre-Buckling and Buckling Response of Carbon/Epoxy VSP
- = 155,000 MPa,
- = = 8070 MPa,
- = = = 4550 MPa,
- = = = 0.22,
- = 1/C,
- = 2.0.
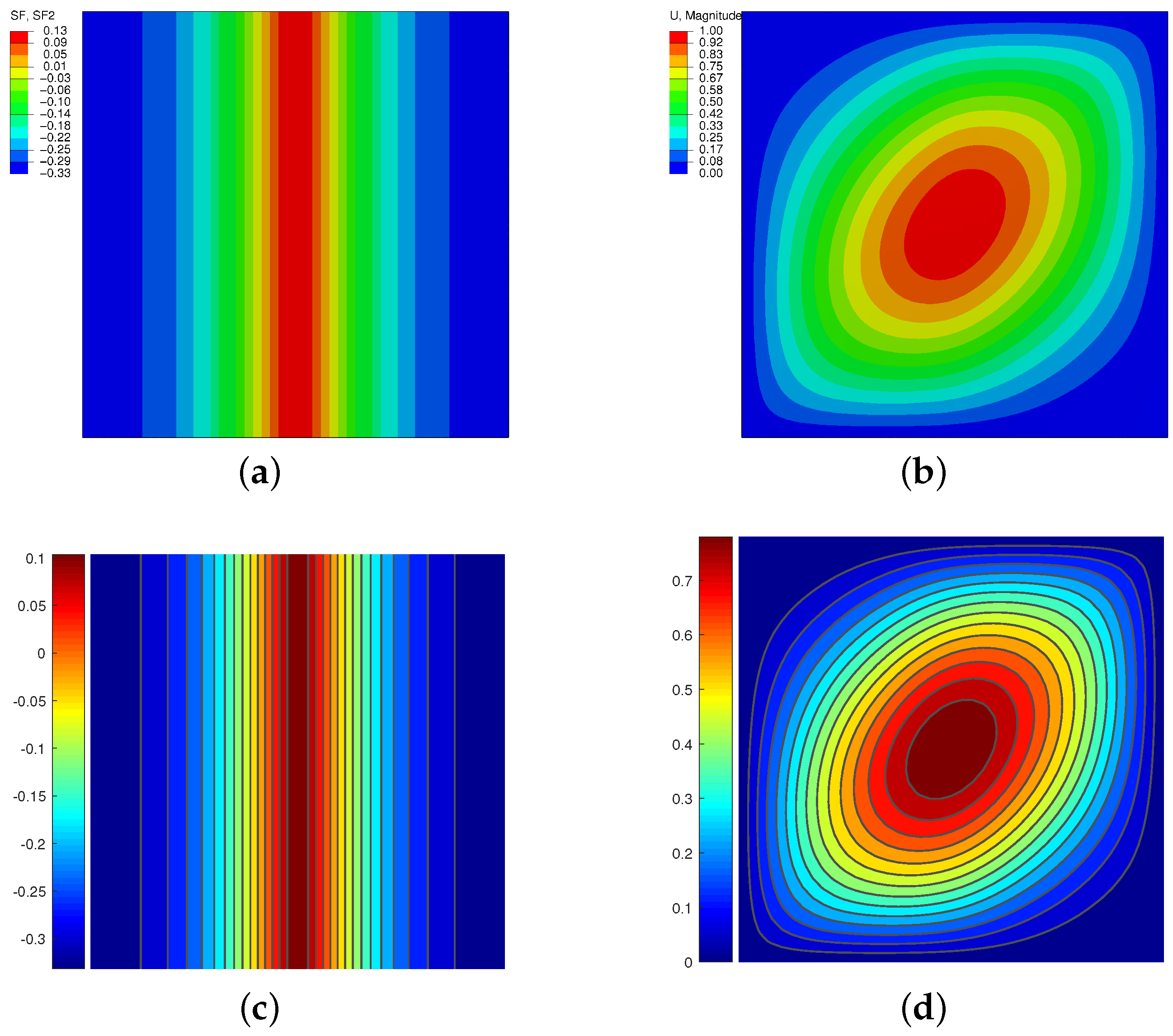
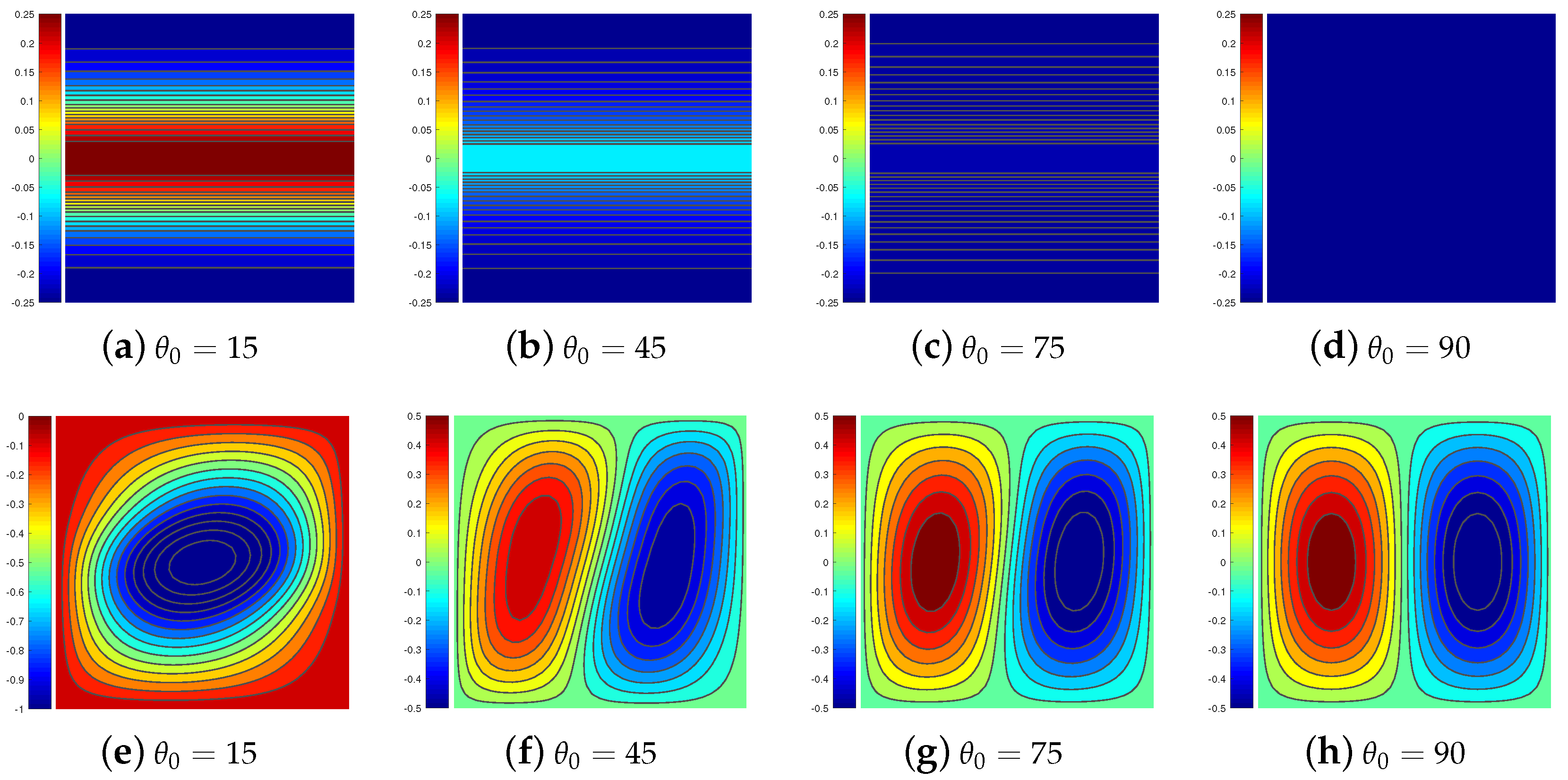
3.2.1. Pre-Buckling Analysis
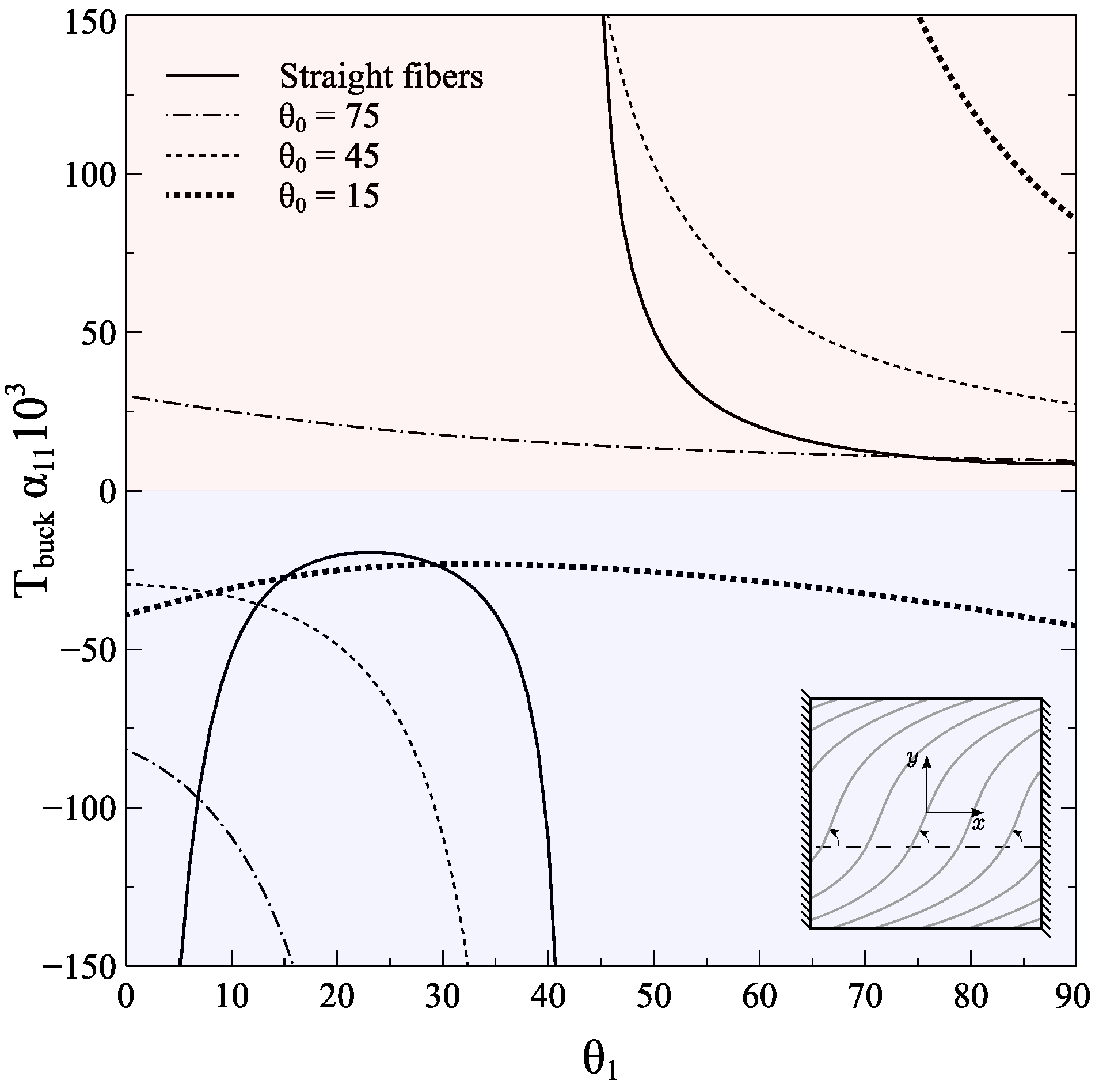
3.2.2. Buckling Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| C | Clamped conditions |
| EDn | Equivalent Single Layer (D denoting a Displacement-based approach) of order n |
| LDn | Layer-wise (D denoting a Displacement-based approach) of order n |
| S | Simply supported conditions |
| VSP | Variable-Stiffness Plate(s) |
References
- Thornton, E. Thermal Structures for Aerospace Applications; AIAA: Reston, Virginia, 1996. [Google Scholar]
- Meyers, C.; Hyer, M. Thermal buckling and postbuckling of symmetrically laminated composite plates. J. Therm. Stresses 1991, 14, 519–540. [Google Scholar] [CrossRef]
- Jones, R. Thermal buckling of uniformly heated unidirectional and symmetric cross-ply laminated fiber-reinforced composite uniaxial in-plane restrained simply supported rectangular plates. Compos. A Appl. Sci. Manuf. 2005, 36, 1355–1367. [Google Scholar] [CrossRef]
- Nemeth, M. Buckling behavior of long anisotropic plates subjected to restrained thermal expansion and mechanical loads. J. Therm. Stresses 2010, 23, 873–916. [Google Scholar] [CrossRef]
- Li, J.; Narita, Y.; Wang, Z. The effects of non-uniform temperature distribution and locally distributed anisotropic properties on thermal buckling of laminated panels. Compos. Struct. 2015, 119, 610–619. [Google Scholar] [CrossRef]
- Li, J.; Tian, X.; Han, Z.; Narita, Y. Stochastic thermal buckling analysis of laminated plates using perturbation technique. Compos. Struct. 2016, 139, 1–12. [Google Scholar] [CrossRef]
- Tauchert, T. Thermal buckling of thick antisymmetric angle-ply laminates. J. Therm. Stresses 1987, 10, 113–124. [Google Scholar] [CrossRef]
- Chang, J.; Shyue, S. Thermal buckling analysis of antisymmetric angle-ply laminates based on a higher-order displacement field. Compos. Sci. Technol. 1991, 41, 109–128. [Google Scholar] [CrossRef]
- Rohwer, K. Letter to the Editor. Compos. Sci. Technol. 1992, 45, 181–182. [Google Scholar] [CrossRef]
- Matsunaga, H. Thermal buckling of cross-ply laminated composite and sandwich plates according to a global higher-order deformation theory. Compos. Struct. 2005, 68, 439–454. [Google Scholar] [CrossRef]
- Matsunaga, H. Thermal buckling of angle-ply laminated composite and sandwich plates according to a global higher-order deformation theory. Compos. Struct. 2006, 72, 177–192. [Google Scholar] [CrossRef]
- Noor, A.; Burton, W. Three-dimensional solutions for thermal buckling of multilayered anisotropic plates. J. Eng. Mech. 1992, 118, 683–701. [Google Scholar] [CrossRef]
- Noor, A.; Burton, W. Three-dimensional solutions for the thermal buckling and sensitivity derivatives of temperature-sensitive multilayered angle-ply plates. J. Appl. Mech. 1992, 59, 848–856. [Google Scholar] [CrossRef]
- Deturk, A.; Diaz, R.; Digiovanni, G.; Hyman, B. Exploratory tests on fiber-reinforced plates with circular holes under tension. AIAA J. 1969, 7, 1820–1821. [Google Scholar] [CrossRef]
- Leissa, A.; Martin, A. Vibration and buckling of rectangular composite plates with variable fiber spacing. Compos. Struct. 1990, 14, 339–357. [Google Scholar] [CrossRef]
- Hyer, M.; Charette, R. Use of curvilinear fiber format in composite structure design. In Proceedings of the 30th Structures, Structural Dynamics and Material Conference, Mobile, AL, USA, 3–5 April 1989. [Google Scholar]
- Hyer, M.; Charette, R. Use of curvilinear fiber format in composite structure design. AIAA J. 1991, 29, 1011–1015. [Google Scholar] [CrossRef]
- Gürdal, Z.; Olmedo, R. Composite laminates with spatially varying fiber orientations: Variable stiffness panel concept. In Proceedings of the 33rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Material Conference, Dallas, TX, USA, 13–15 April 1992. [Google Scholar]
- Raju, G.; Wu, Z.; Kim, B.; Weaver, P. Prebuckling and buckling analysis of variable angle tow plates with general boundary conditions. Compos. Struct. 2012, 94, 2961–2970. [Google Scholar] [CrossRef]
- Wu, Z.; Weaver, P.; Raju, G.; Kim, B. Buckling analysis and optimisation of variable angle tow composite plates. Thin Walled Struct. 2012, 60, 163–172. [Google Scholar] [CrossRef]
- Coburn, B.; Wu, Z.; Weaver, P. Buckling analysis of stiffened variable angle tow panels. Compos. Struct. 2014, 111, 259–270. [Google Scholar] [CrossRef]
- Rahman, T.; Ijsselmuiden, S.; Abdalla, M.; Jansen, E. Postbuckling analysis of variable stiffness composite plates using a finite element-based perturbation method. Int. J. Struct. Stab. Dyn. 2011, 11, 735–753. [Google Scholar] [CrossRef]
- Wu, Z.; Raju, G.; Weaver, P. Postbuckling analysis of variable angle tow composite plates. Int. J. Solids Struct. 2013, 50, 1770–1780. [Google Scholar] [CrossRef]
- Wu, Z.; Raju, G.; Weaver, P. Framework for the buckling optimization of variable-angle tow composite plates. AIAA J. 2015, 53, 3788–3804. [Google Scholar] [CrossRef]
- Coburn, B.; Weaver, P. Buckling analysis, design and optimisation of variable-stiffness sandwich panels. Int. J. Solids Struct. 2016, 96, 217–228. [Google Scholar] [CrossRef]
- Akhavan, H.; Ribeiro, P. Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers. Compos. Struct. 2011, 93, 3040–3047. [Google Scholar] [CrossRef]
- Yazdani, S.; Ribeiro, P. A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Compos. Struct. 2015, 120, 531–542. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L. A variable-kinematic model for variable stiffness plates: Vibration and buckling analysis. Compos. Struct. 2016, 142, 15–26. [Google Scholar] [CrossRef]
- Carrera, E. A class of two-dimensional theories for anisotropic multilayered plates analysis. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Nat. Rend. 1995, 19, 1–39. [Google Scholar]
- Carrera, E. Theories and finite elements for multilayered, anisotropic, composite plates and shells. Arch. Comput. Meth. Eng. 2002, 9, 87–140. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S. A survey with numerical assessment of classical and refined theories for the analysis of sandwich plates. Appl. Mech. Rev. 2009, 62, 010803. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Higher-order theories for the free vibrations of doubly-curved laminated panels with curvilinear reinforcing fibers by means of a local version of the GDQ method. Compos. B Eng. 2015, 81, 196–230. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Higher-order structural theories for the static analysis of doubly-curved laminated composite panels reinforced by curvilinear fibers. Thin Walled Struct. 2016, 102, 222–245. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Foam core composite sandwich plates and shells with variable stiffness: Effect of the curvilinear fiber path on the modal response. J. Sandwich Struct. Mater. 2017, 1–46. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M. Effect of Curvilinear Reinforcing Fibers on the Linear Static Behavior of Soft-Core Sandwich Structures. J. Compos. Sci. 2018, 2, 1–41. [Google Scholar]
- Duran, A.; Fasanella, N.; Sundararaghavan, V.; Waas, A. Thermal buckling of composite plates with spatial varying fiber orientations. Compos. Struct. 2015, 124, 228–235. [Google Scholar] [CrossRef]
- Manickam, G.; Bharath, A.; Das, A.; Chandra, A.; Barua, P. Thermal buckling behaviour of variable stiffness laminated composite plates. Mater. Today Commun. 2018, 16, 142–151. [Google Scholar] [CrossRef]
- Haldar, A.; Reinoso, J.; Jansen, E.; Rolfes, R. Thermally induced multistable configurations of variable stiffness composite plates: Semi-analytical and finite element investigation. Compos. Struct. 2018, 183, 161–175. [Google Scholar] [CrossRef]
- Dano, M.L.; Hyer, M. Thermally-induced deformation behavior of unsymmetric laminates. Int. J. Solids Struct. 1998, 35, 2101–2120. [Google Scholar] [CrossRef]
- Olmedo, R.; Gürdal, Z. Buckling response of laminates with spatially varying fiber orientations. In Proceedings of the 34th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Material Conference, La Jolla, CA, USA, 19 April 1993–22 April 1993. [Google Scholar]
- Waldhart, C.; Gürdal, Z.; Ribbens, C. Analysis of tow placed, parallel fiber, variable stiffness laminates. In Proceedings of the 37th AIAA Structures, Structural Dynamics, and Materials Conference, Salt Lake City, UT, USA, 15–17 April 1996. [Google Scholar] [CrossRef]
- Carrera, E. Theories and finite elements for multilayered plates and shells: A unified compact formulation with numerical assessment and benchmarking. Arch. Comput. Meth. Eng. 2003, 10, 215–296. [Google Scholar] [CrossRef]
- Carrera, E.; Ciuffreda, A. A unified formulation to assess theories of multilayered plates for various bending problems. Compos. Struct. 2005, 69, 271–293. [Google Scholar] [CrossRef]
- D’Ottavio, M.; Dozio, L.; Vescovini, R.; Polit, O. Bending analysis of composite laminated and sandwich structures using sublaminate variable-kinematic Ritz models. Compos. Struct. 2016, 155, 45–62. [Google Scholar] [CrossRef]
- Vescovini, R.; D’Ottavio, M.; Dozio, L.; Polit, O. Thermal buckling response of laminated and sandwich plates using refined 2-D models. Compos. Struct. 2017, 176, 313–328. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L.; D’Ottavio, M.; Polit, O. On the application of the Ritz method to free vibration and buckling analysis of highly anisotropic plates. Compos. Struct. 2018, 192, 460–474. [Google Scholar] [CrossRef]
- Vescovini, R.; D’Ottavio, M.; Dozio, L.; Polit, O. Buckling and wrinkling of anisotropic sandwich plates. Int. J. Eng. Sci. 2018, 130, 136–156. [Google Scholar] [CrossRef]
- D’Ottavio, M.; Dozio, L.; Vescovini, R.; Polit, O. The Ritz–Sublaminate Generalized Unified Formulation approach for piezoelectric composite plates. Int. J. Smart Nano Mater. 2018, 9, 34–55. [Google Scholar] [CrossRef]
- Dozio, L.; Carrera, E. Ritz analysis of vibrating rectangular and skew multilayered plates based on advanced variable-kinematic models. Compos. Struct. 2012, 94, 2118–2128. [Google Scholar] [CrossRef]
- Gürdal, Z.; Olmedo, R. In-plane response of laminates with spatially varying fiber orientations-variable stiffness concept. AIAA J. 1993, 31, 751–758. [Google Scholar] [CrossRef]
- Hyer, M. Stress Analysis of Fiber-Reinforced Composite Materials; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
| [12] | ED2 | ED3 | ED4 | ||
|---|---|---|---|---|---|
| 20/3 | 0 | 0.1029 | 0.1075 | 0.1030 | 0.1029 |
| 15 | 0.1322 | 0.1409 | 0.1325 | 0.1320 | |
| 30 | 0.1859 | 0.2028 | 0.1887 | 0.1877 | |
| 45 | 0.1981 | 0.2187 | 0.2024 | 0.2012 | |
| 10 | 0 | 0.5782 | 0.5939 | 0.5782 | 0.5782 |
| 15 | 0.7904 | 0.8216 | 0.7897 | 0.7879 | |
| 30 | 0.1100 | 0.1159 | 0.1110 | 0.1106 | |
| 45 | 0.1194 | 0.1267 | 0.1209 | 0.1204 | |
| 20 | 0 | 0.1739 | 0.1754 | 0.1739 | 0.1739 |
| 15 | 0.2528 | 0.2557 | 0.2523 | 0.2520 | |
| 30 | 0.3446 | 0.3515 | 0.3467 | 0.3463 | |
| 45 | 0.3810 | 0.3897 | 0.3839 | 0.3833 | |
| 100 | 0 | 0.7463 | 0.7466 | 0.7463 | 0.7463 |
| 15 | 0.1115 | 0.1115 | 0.1114 | 0.1114 | |
| 30 | 0.1502 | 0.1516 | 0.1515 | 0.1515 | |
| 45 | 0.1674 | 0.1692 | 0.1691 | 0.1691 |
| Lay-Up | = 40 | = 20 | = 10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ED2 | ED4 | LD2 | ED2 | ED4 | LD2 | ED2 | ED4 | LD2 | ||||
| 6 | 0.6094 | 0.6056 | 0.6048 | 2.2134 | 2.1633 | 2.1538 | 6.5376 | 6.1240 | 6.0502 | |||
| 10 | 0.6085 | 0.6045 | 0.6029 | 2.2110 | 2.1578 | 2.1417 | 6.5339 | 6.1088 | 6.0087 | |||
| 14 | 0.6084 | 0.6041 | 0.6018 | 2.2107 | 2.1566 | 2.1375 | 6.5335 | 6.1072 | 6.0010 | |||
| [37] | 0.6010 | 2.1605 | 6.2184 | |||||||||
| Abaqus | 0.5970 | 2.1252 | 5.9392 | |||||||||
| 6 | 1.0024 | 0.9942 | 0.9920 | 3.5552 | 3.4550 | 3.4305 | 9.9560 | 9.2104 | 9.0544 | |||
| 10 | 0.9971 | 0.9888 | 0.9843 | 3.5316 | 3.4244 | 3.3777 | 9.9069 | 9.1060 | 8.8573 | |||
| 14 | 0.9950 | 0.9856 | 0.9782 | 3.5275 | 3.4095 | 3.3432 | 9.9016 | 9.0782 | 8.7768 | |||
| [37] | 1.0131 | 3.5521 | 9.5633 | |||||||||
| Abaqus | 0.9769 | 3.4016 | 9.0297 | |||||||||
| 6 | 1.3476 | 1.3383 | 1.3357 | 4.8336 | 4.7177 | 4.6870 | 13.9039 | 13.0001 | 12.8044 | |||
| 10 | 1.3112 | 1.3014 | 1.2958 | 4.6887 | 4.5639 | 4.5089 | 13.4142 | 12.4859 | 12.1912 | |||
| 14 | 1.3097 | 1.2988 | 1.2907 | 4.6843 | 4.5542 | 4.4846 | 13.1196 | 12.4659 | 12.1348 | |||
| [37] | 1.1425 | 4.0844 | 10.6480 | |||||||||
| Abaqus | 1.2882 | 4.5704 | 12.6255 | |||||||||
| Materials | (C) | ||||||
|---|---|---|---|---|---|---|---|
| [36] | Abaqus | ED3 | ED4 | LD2 | |||
| Graphite/Epoxy | 60.70 | 32.19 | 34.26 | 33.084 | 33.0033 | 33.0028 | 32.9562 |
| E-Glass/Epoxy | 6.710 | 58.04 | 5.58 | 5.5558 | 5.5546 | 5.5542 | 5.5532 |
| S-Glass/Epoxy | 16.12 | 54.74 | 5.04 | 5.0368 | 5.0355 | 5.0351 | 5.0339 |
| Kevlar/Epoxy | 66.05 | 11.73 | 22.18 | 16.544 | 16.2724 | 16.2708 | 16.2566 |
| Carbon/Epoxy | 69.00 | −5.705 | 57.79 | 34.715 | 33.6616 | 33.6607 | 33.6509 |
| Carbon/Peek | 63.07 | 29.50 | 38.08 | 35.989 | 35.8670 | 35.8653 | 35.8257 |
| Carbon/Polyimide | 56.30 | 36.68 | 78.28 | 77.640 | 77.6006 | 77.5995 | 77.4214 |
| Boron/Epoxy | −6.57 | 63.28 | 7.50 | 7.5535 | 7.5541 | 7.5541 | 7.5488 |
| Case-Ty1 | Case-Ty2 | |||||||
|---|---|---|---|---|---|---|---|---|
| = 100 | = 50 | = 20 | = 100 | = 50 | = 20 | |||
| 15 | 0 | 0.9956 | 3.9413 | 23.0484 | / | / | / | |
| 22.5 | 1.4483 | 5.7112 | 32.7354 | / | / | / | ||
| 45 | 2.0031 | 7.8947 | 44.3831 | / | / | / | ||
| 67.5 | 1.8844 | 7.4340 | 42.8737 | 49.4171 | 173.7064 | 532.9265 | ||
| 90 | 1.5486 | 6.1172 | 35.4060 | 15.7679 | 58.1094 | 228.6143 | ||
| 45 | 0 | 1.1526 | 4.5691 | 26.9298 | / | / | / | |
| 22.5 | 1.6750 | 6.6240 | 38.6748 | 879.1314 | 2819.5186 | / | ||
| 45 | 2.1300 | 8.4043 | 48.6098 | 21.6560 | 85.4415 | 493.8370 | ||
| 67.5 | 1.9935 | 7.8798 | 45.8766 | 5.4943 | 21.6938 | 125.3990 | ||
| 90 | 1.6876 | 6.6841 | 39.1706 | 3.0478 | 12.0012 | 67.8208 | ||
| 75 | 0 | 1.0292 | 4.0790 | 24.0499 | 6.3514 | 24.7402 | 131.6711 | |
| 22.5 | 1.5674 | 6.1916 | 35.9135 | 3.9223 | 15.3611 | 84.2752 | ||
| 45 | 1.9175 | 7.5626 | 43.5285 | 2.5716 | 10.0869 | 56.0495 | ||
| 67.5 | 1.4448 | 5.6932 | 32.5239 | 1.6004 | 6.3060 | 36.0113 | ||
| 90 | 1.0109 | 4.0036 | 23.4429 | 1.0726 | 4.2482 | 24.8736 | ||
| Case-Ty1 | Case-Ty2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| = 1000 | 50 | 20 | 10 | = 1000 | 50 | 20 | 10 | |||
| 75 | 0 | 12.5529 | 12.3781 | 11.6295 | 9.7402 | 77.9289 | 74.9501 | 63.3306 | 39.9359 | |
| 22.5 | 19.1437 | 18.7351 | 17.2405 | 13.8214 | 48.0354 | 46.5268 | 40.5156 | 28.4722 | ||
| 45 | 23.4373 | 22.8613 | 20.8481 | 15.4961 | 31.4840 | 30.5052 | 26.8569 | 19.5422 | ||
| 67.5 | 17.6631 | 17.2222 | 15.6188 | 12.1018 | 19.5656 | 19.0758 | 17.2935 | 13.3857 | ||
| 75 | 15.2747 | 14.9655 | 13.7574 | 10.9351 | 16.5691 | 16.2332 | 14.9202 | 11.8529 | ||
| 90 | 12.3309 | 12.1678 | 11.3919 | 9.3832 | 13.0840 | 12.9108 | 12.0871 | 9.9547 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vescovini, R.; Dozio, L. Thermal Buckling Behaviour of Thin and Thick Variable-Stiffness Panels. J. Compos. Sci. 2018, 2, 58. https://doi.org/10.3390/jcs2040058
Vescovini R, Dozio L. Thermal Buckling Behaviour of Thin and Thick Variable-Stiffness Panels. Journal of Composites Science. 2018; 2(4):58. https://doi.org/10.3390/jcs2040058
Chicago/Turabian StyleVescovini, Riccardo, and Lorenzo Dozio. 2018. "Thermal Buckling Behaviour of Thin and Thick Variable-Stiffness Panels" Journal of Composites Science 2, no. 4: 58. https://doi.org/10.3390/jcs2040058
APA StyleVescovini, R., & Dozio, L. (2018). Thermal Buckling Behaviour of Thin and Thick Variable-Stiffness Panels. Journal of Composites Science, 2(4), 58. https://doi.org/10.3390/jcs2040058





