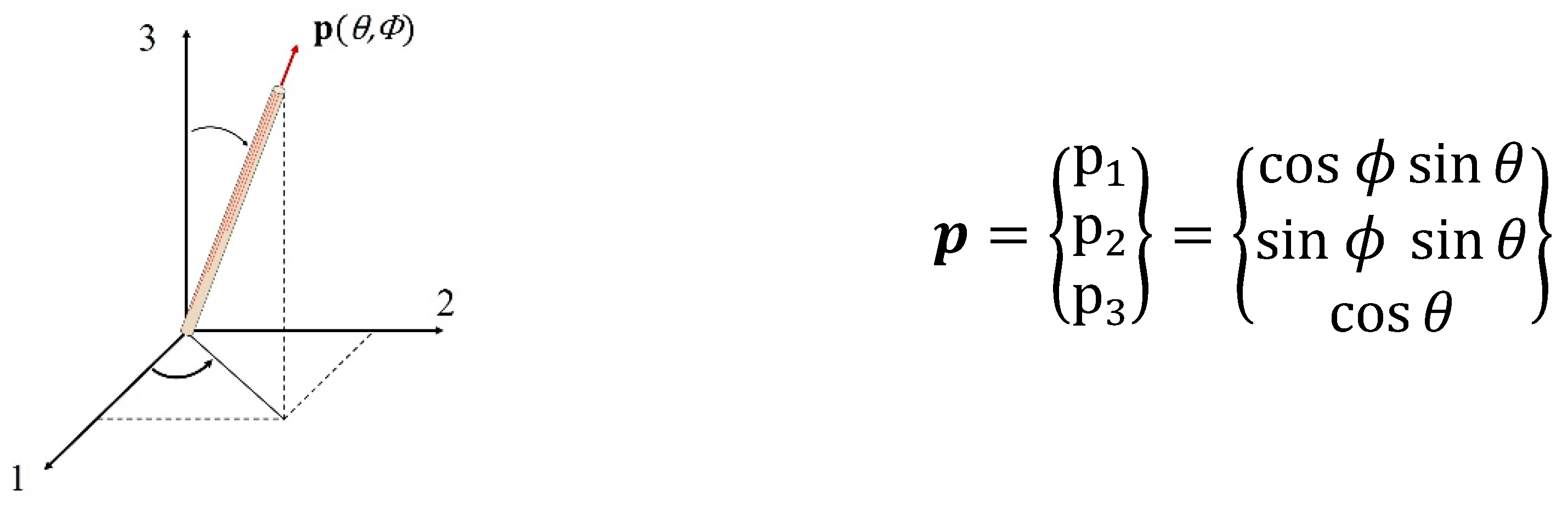1. Introduction
Additive manufacturing (AM) is publicized as a new, exciting technology that is on the cusp of revolutionizing manufacturing everywhere and changing the way we think about the products we buy, whether it be custom designing one’s own clothing or producing spare parts at home (or in space). Of course, there are elements of truth and exaggerations with these ideas. Although there are now many examples of metal AM end-use products in high-cost, high-value industries like aerospace [
1], polymer end-use parts are less prominent. Polymer AM examples are more often related to prototyping or tool-making; however, the correct combination of material, process, and product can lead to more successful applications.
Functionalized polymer materials can increase the scope of available applications for polymer AM parts. Fused filament fabrication (FFF), a material extrusion process that melts and deposits polymer filament through a heated nozzle, is well-suited for AM with composite materials [
2]. FFF filament is produced by extrusion, a mature process that lends itself to the easy incorporation of high loads of fillers [
3]. FFF filaments have been produced with up to 40% vol fillers or higher [
4] to enhance different properties, such as strength, stiffness, electrical conductivity, or thermal conductivity.
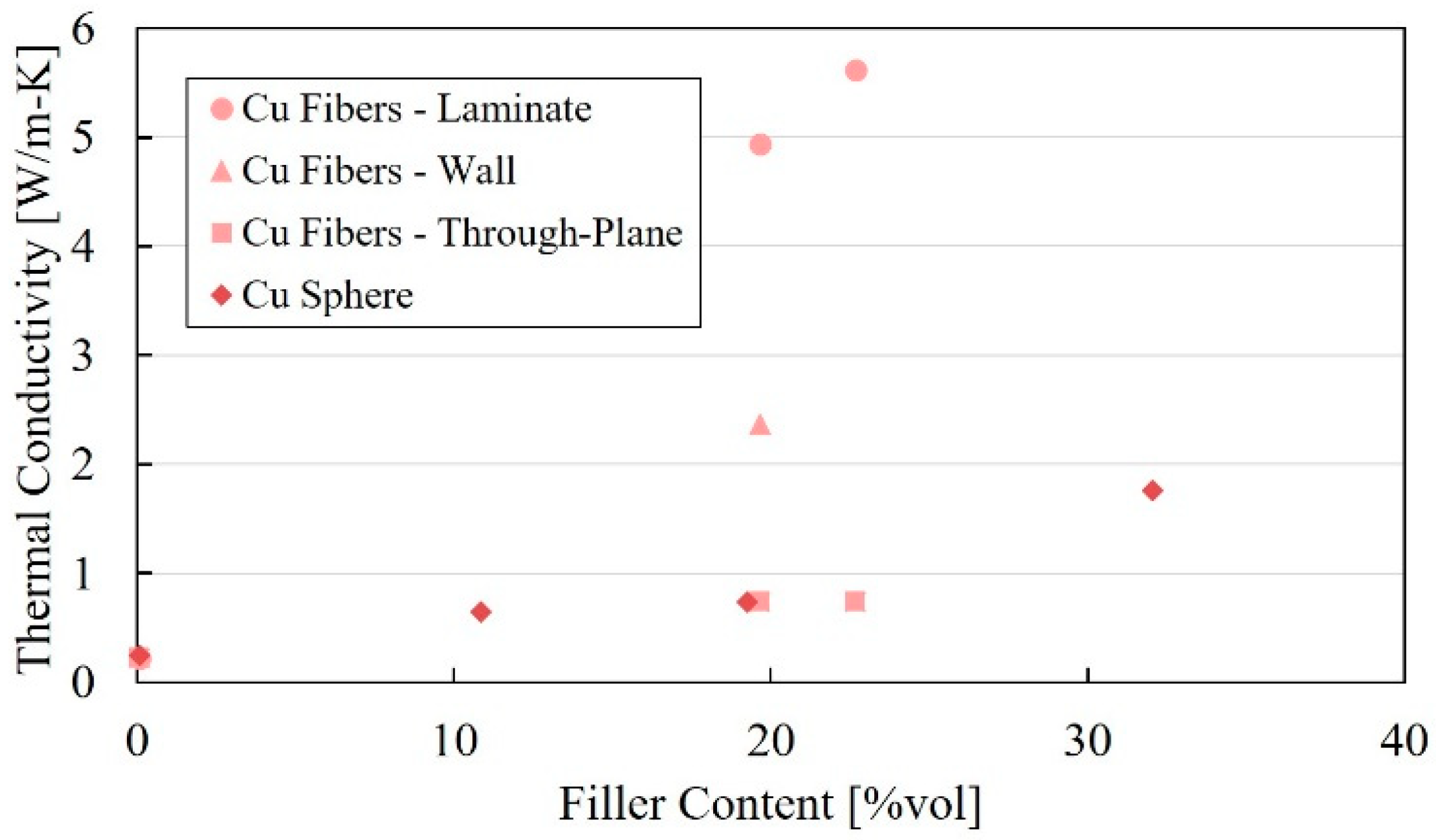
While electrically conductive FFF materials have been available for some time, increased thermal conductivity requires the incorporation of high loads of fillers or generally larger filler sizes. Although some increase in thermal conductivity can be achieved at low filler content [
5], the largest gains are seen as conductive chains are formed along filler particles in contact, leading to increasing gains in the compound thermal conductivity [
6]. These conductive chains are more easily formed by fillers with a higher aspect ratio [
7]. While a sphere has an aspect ratio of 1, a square platelet 15 µm wide and 2 µm thick would have an aspect ratio of 7.5, and a fiber that is 500 µm long and 30 µm in diameter (as is used in this work) has an aspect ratio of 16.7. These high aspect ratio fillers lead to higher thermal conductivity but also exhibit a highly anisotropic thermal conductivity due to the process-induced alignment of the fillers [
7]. This is well-studied in shear flows [
8,
9] and injection molding [
7,
10] but is little understood for FFF processing.
The process-induced fiber alignment in injection molding of discontinuous fiber-reinforced composites has been studied by several groups in the past [
11,
12,
13,
14,
15]. However, little research work has been published on fiber alignment in FFF using discontinuous fiber-reinforced materials. Some simulation work has been done on understanding fiber orientation in a composite material as it passes through a nozzle. Heller found, using the Folgar-Tucker model [
9], that the alignment will increase through the constriction section of the nozzle, and then may decrease again through the land at the nozzle tip, if the land is long enough. The orientation can decrease substantially following the nozzle exit due to die swell, which acts perpendicularly to the shear flow, however this analysis was based on an unrestricted flow through the nozzle into space [
16]. In reality, material exiting the nozzle is immediately deposited on the platform or previously deposited beads, changing the flow direction by 90 degrees from vertical to its final horizontal position. Additionally, different flow lines in the deposited bead undergo different deformations. Therefore, the actual flow in FFF at the nozzle exit is more complex than simple extrusion into space with die swell.
In any case, the thermal conductivity can be seven times higher or more in the flow direction compared to the through-plane direction, as shown in injection molding [
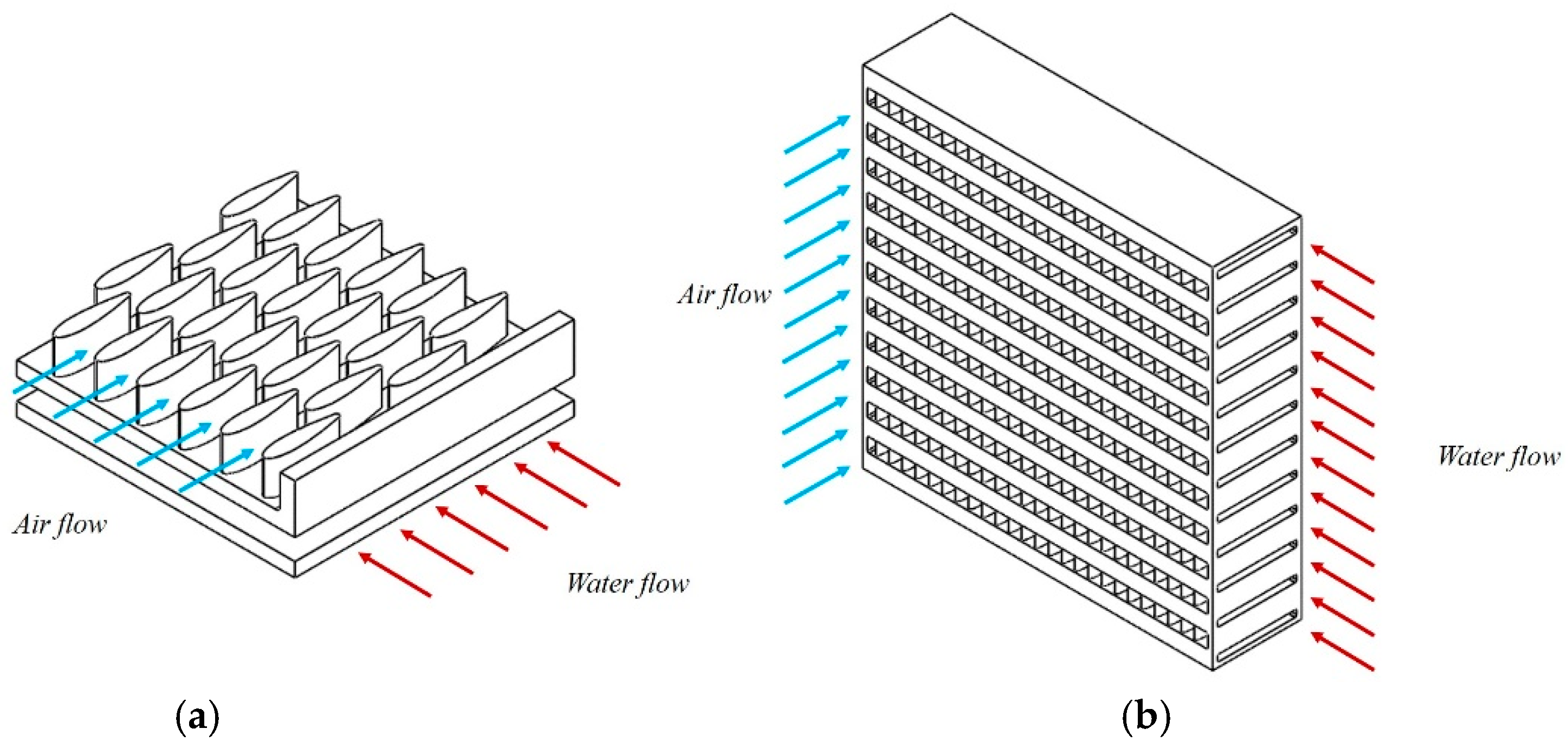
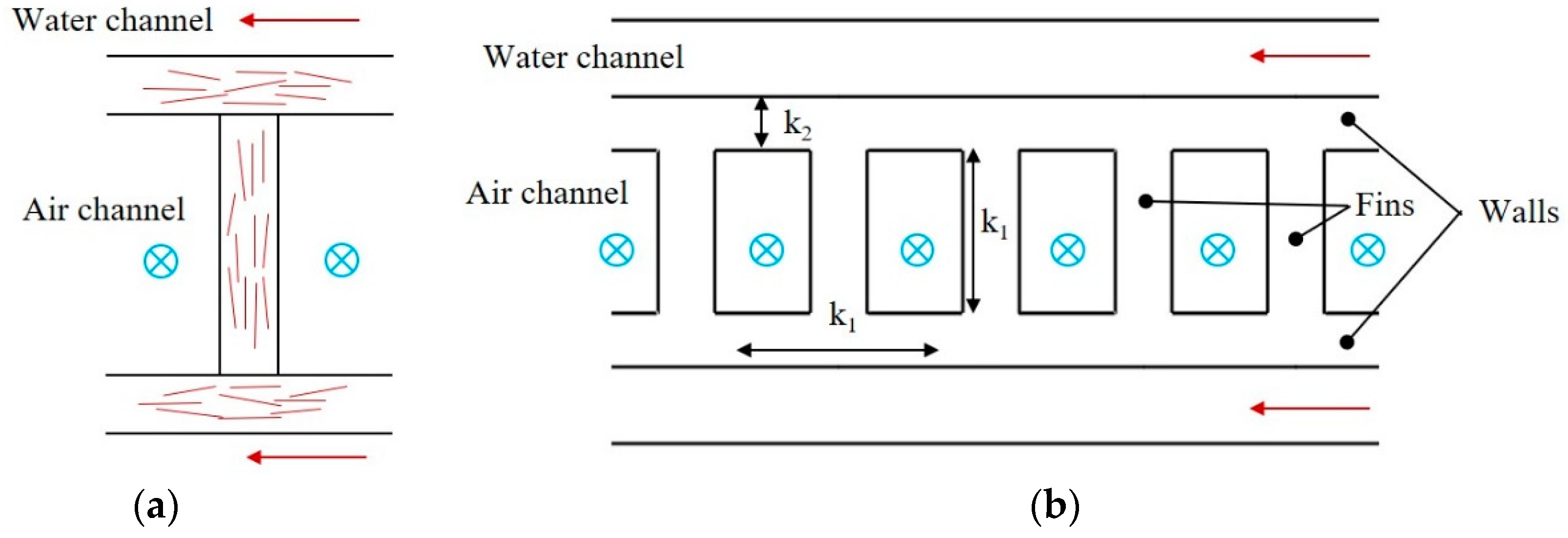
7] and later in this work. This may be advantageous or may present problems in different areas of an FFF part. This work explores FFF filament produced with copper fillers in order to print parts with thermal applications: in this case, a crossflow air-cooled heat exchanger (HX). It will be shown that the flow fields in the production of the filament and the deposition during printing govern the fiber orientation, in turn governing the thermal conductivity, which is one of the main factors in the overall performance of the printed HX. A better understanding of the fiber orientation will help improve the performance of the HX and possibly lead to the prediction of the thermal conductivity in different sections of a printed part.
In addition, measuring the orientation of fibers is essential in the understanding of the physics that govern their movement during processing, but it remains a challenging task [
17]. Characterization methodologies are limited for copper fibers as the measurements by polishing samples and inspecting the cross-sectional footprint of fibers are not feasible due to copper fiber’s irregular shape.
In this article, we show the results of a make-measure-model concept for 3D printing of copper filled polyamide to manufacture air-cooled heat exchangers. This work comprises the compounding and extrusion of the filament, the production and characterization of the samples, and the modeling of the thermal properties that can be achieved.
2. Materials and Methods
2.1. Filament Extrusion
Polyamide 6 (PA6, Ultramid
® B33-01, BASF
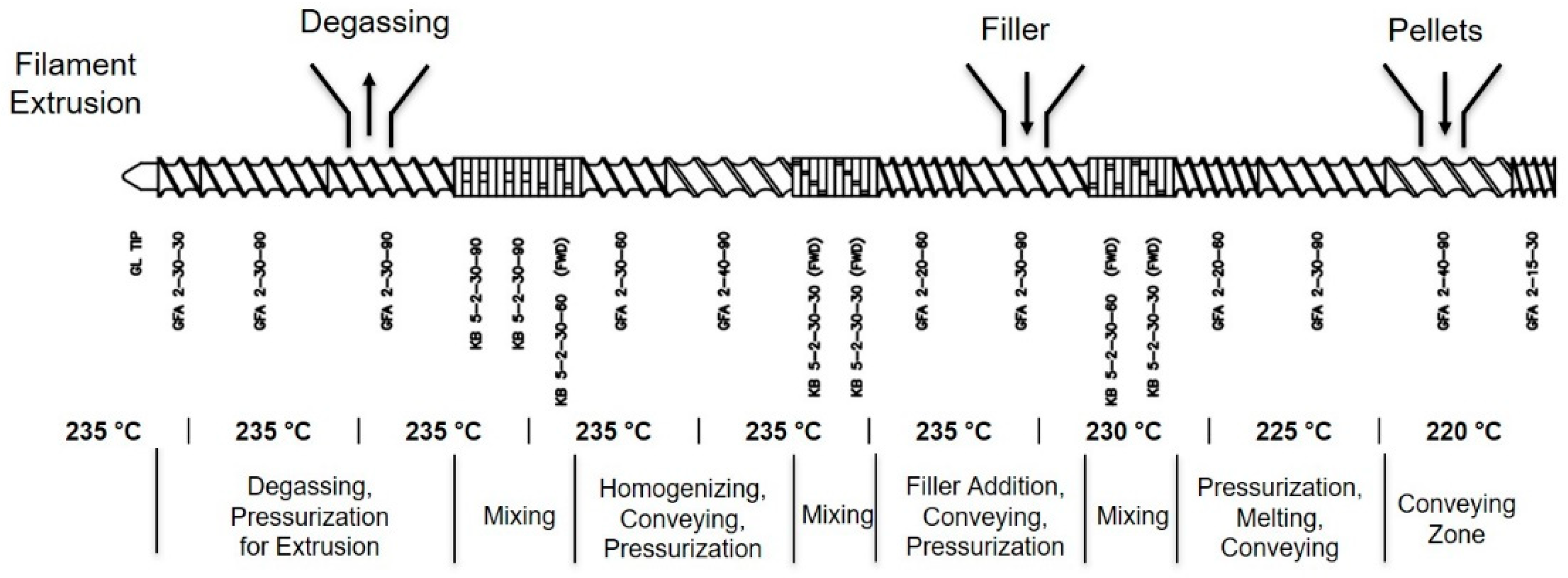
®, Ludwigshafen, Germany) was chosen as the polymer matrix in this work due to its ability to resist the HX service temperature of 70 °C. This was mixed with copper fibers with a 30 µm nominal diameter and 500 µm length (Deutsches Metallfaserwerk, Neidenstein, Germany) or copper spheres with a nominal diameter of 45 µm (Chemical Store, Clifton, NJ, USA). These were compounded on a Leistritz
® (Nürnberg, Germany) ZSE 27 HPe corotating twin screw extruder with a screw diameter of 27 mm and L/D ratio of 36. The screw configuration, shown in
Figure 1 below, was based on previous work by Amesöder [
7] on thermally conductive composites for injection molding. The extruder temperature was controlled in eight zones along the barrel and another for the die, increasing along the length as indicated in
Figure 1.
These temperatures produced a final melt temperature for the compounded PA6 between 248 and 251 °C. Initial trials used higher temperatures for extrusion, but these led to yellowing of the PA6, indicating degradation, so they were lowered to the given temperatures. The screw speed and the side stuffer speed were 100 RPM and 140 RPM, respectively. The resin feed rate was kept at a constant 4 kg/h, and the filler feed rate was varied to achieve the desired fill ratio. For example, 4 kg/h of PA6 with 10.5 kg/h of copper makes a filler mass fraction of 72.4% wt, or a volume fraction of approximately 25% vol. This speed was chosen to run the line slowly while still achieving a steady filler mass flow rate from the gravimetric feeders.
The extruded filament passes from the die into a vacuum cooling tank, a laser micrometer, a belt puller, and finally a winder. A strand die with a 3.5 mm orifice was used to produce the 1.75 mm filament. The strand leaves the die and enters the Conair® (Cranberry Township, PA, USA) MT104-13-3 vacuum cooling tank. This 4 m (13 ft) stainless steel tank is filled with water to a level higher than the top of the product. A light vacuum less than 1.2 kPa (5 inH2O) keeps the water at the entrance flowing inwards, improving the circularity. The strand then passes through a laser micrometer (LaserLincTM Triton331, Fairborn, OH, USA), which measures the diameter in three locations and calculates the ovality of the product. After the laser micrometer, the strand passes through a Conair® 3-20 precision belt puller, which is in a closed feedback loop with the laser micrometer to control the filament diameter. Finally, at the very end of the line is a winder, which winds the filament onto a large spool for easy handling.
Because of the weight of the copper-filled compound, startup of the downstream operations was very difficult; with the low melt viscosity of PA6, the weight would cause the strand to sag before the strand could be passed into the vacuum cooling tank. Therefore, the line had to be started with just PA6 resin. Once the line was in full operation, the side stuffer was started and the filler was added to the extruder. The maximum filler content was limited to 25% vol due to issues such as die drool causing line breakage.
2.2. Fused Filament Fabrication
Fused filament fabrication is an additive manufacturing process that is classified as material extrusion. A solid circular filament of plastic is fed into a heated nozzle, in which it is melted. The molten plastic is extruded through a small diameter nozzle. The material is then deposited onto the part in a layer-by-layer fashion. The molten plastic cools and solidifies in a very short time as it is deposited.
The printer used in this work was the Aon 3DTM (Montreal, QC, Canada), which is equipped with dual hot ends capable of printing at temperatures up to 450 °C. This printer is built in a gantry style, where the extruders move in the x- and y-directions, and the print bed only moves in the z-direction. One interesting feature of the Aon, which should become more common, is its ability to use two nozzles to print a part in two locations on the bed simultaneously. This essentially reduces the machine cost by half in a manufacturing setting.
Filaments selected for printing in this work were PA6 with 20% vol copper fiber (PA6-CuF-20), 25% vol copper fiber (PA6-CuF-25), or neat PA6. Some copper sphere-filled samples were prepared by compression molding at approximately 10, 20, and 30% vol for comparison.
2.3. Laser Flash Analysis
The thermal diffusivity can be measured by laser flash analysis (LFA). The instrument, in this work a Netzsch
® Instruments (Selb, Germany) Nanoflash 447, analyzes the transient heat flow in a material by firing an energy pulse at the bottom side of a sample using a xenon flash lamp. The top side of the sample is monitored with a liquid nitrogen-cooled infrared detector, which measures a signal proportional to temperature rise on the top surface. A thermal diffusivity model can then be fit to the time-dependent temperature rise. The thermal conductivity (
) can be calculated by multiplying the thermal diffusivity (
) with the mass density (
) and specific heat capacity (
), as:
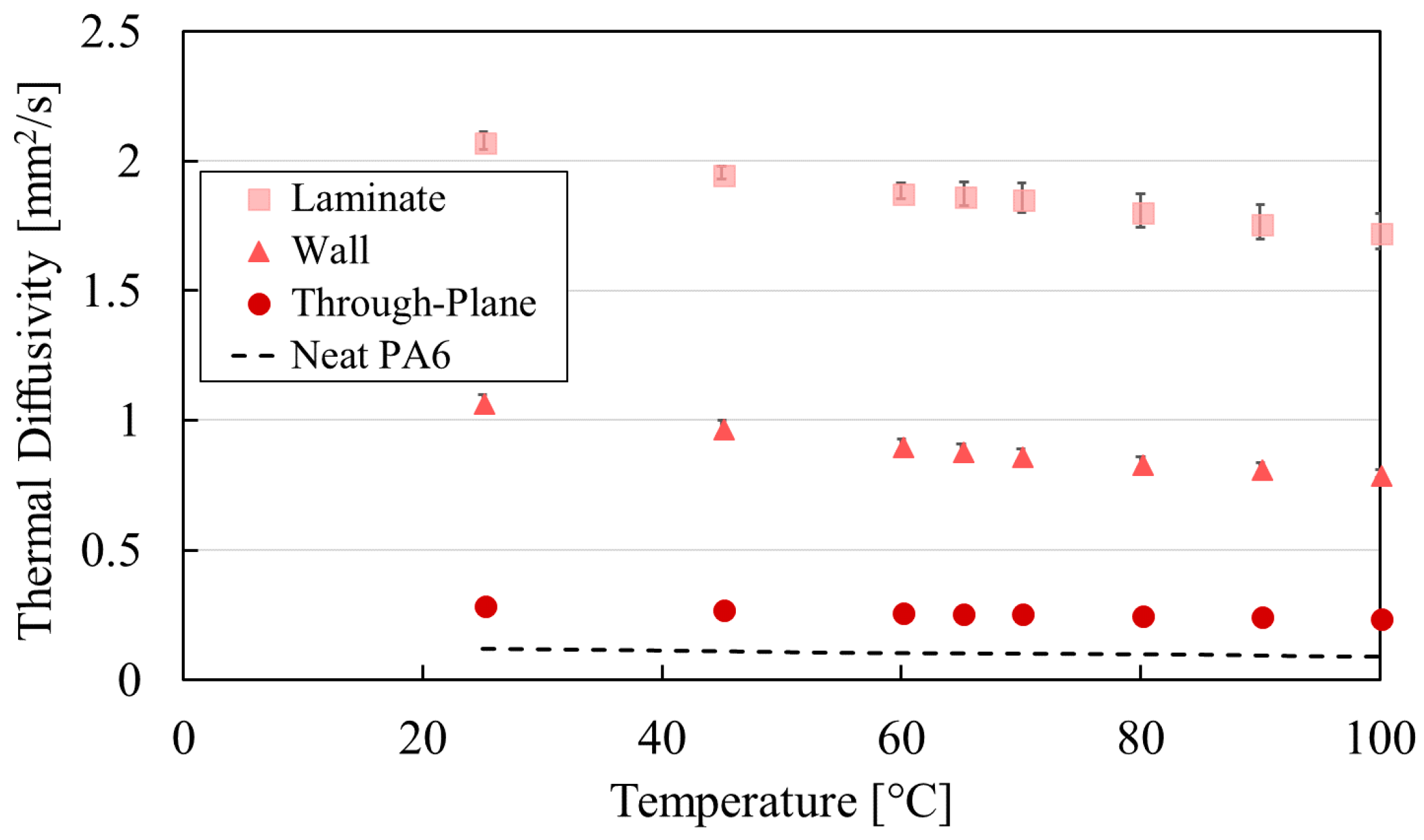
This study analyzed the thermal diffusivity in a range from 25 to 100 °C, as the working temperature for the materials was intended to be 70 °C.
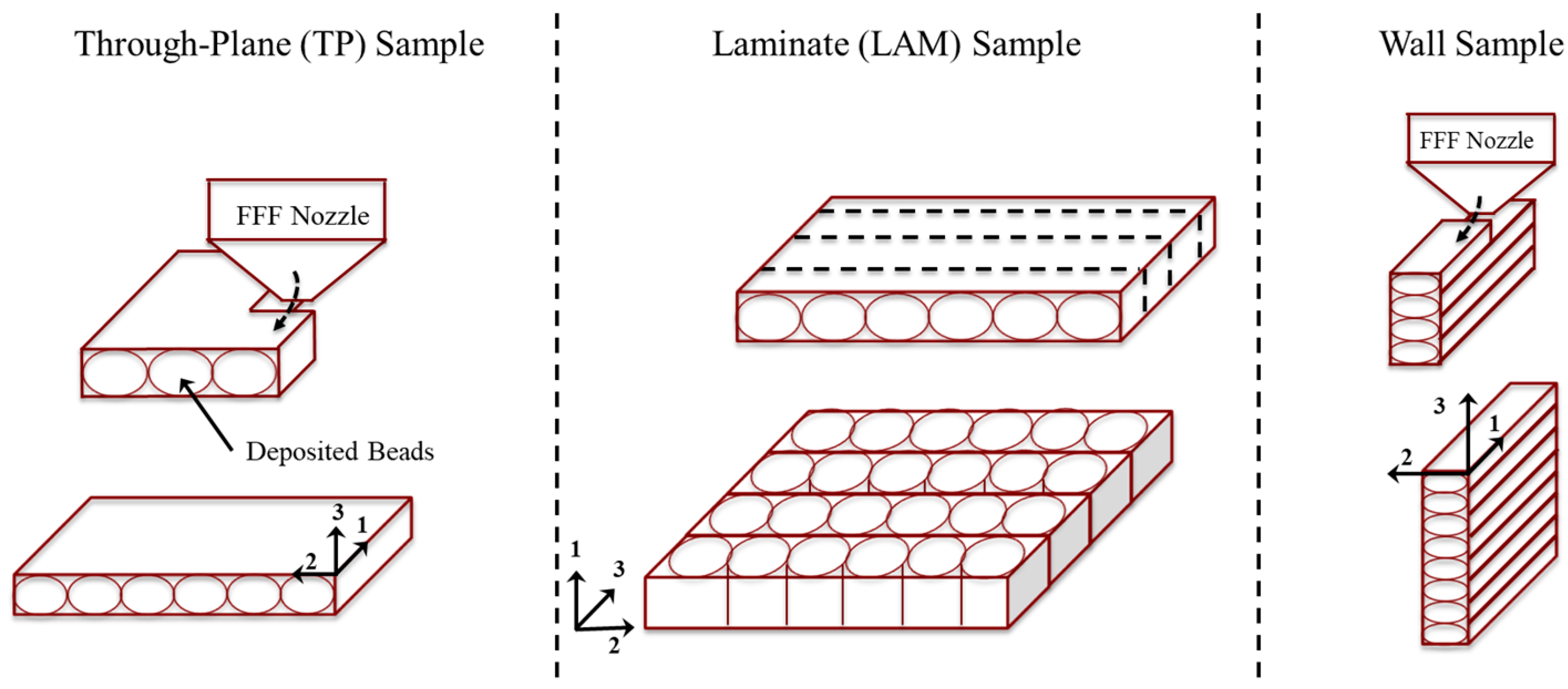
The minimum testable sample size on the Nanoflash 447 LFA is a 6-mm round disc, which is much larger than an FFF filament strand of 1.75 mm or 3 mm diameter. Thus, the filament itself is not easily tested, and the thermal diffusivity must be measured on a prepared sample by printing a test bar that can be used to cut 10 mm × 10 mm × 1 mm square samples. In this case, the test bar is 60 mm × 10 mm × 1 mm. This bar is printed with all tool paths parallel to the long dimension using SciSlice, an open-source slicer developed in-house and available on GitHub [
18]. The ends of the printed bar were cut and discarded, as they contain turns in the toolpath that may disrupt the fiber orientation within each printed bead. The printed bar was polished with 1000 grit sandpaper to produce a flat surface, then cut to the correct sample size. Finally, the sample was spray-coated with graphite to promote absorption of the LFA energy pulse.
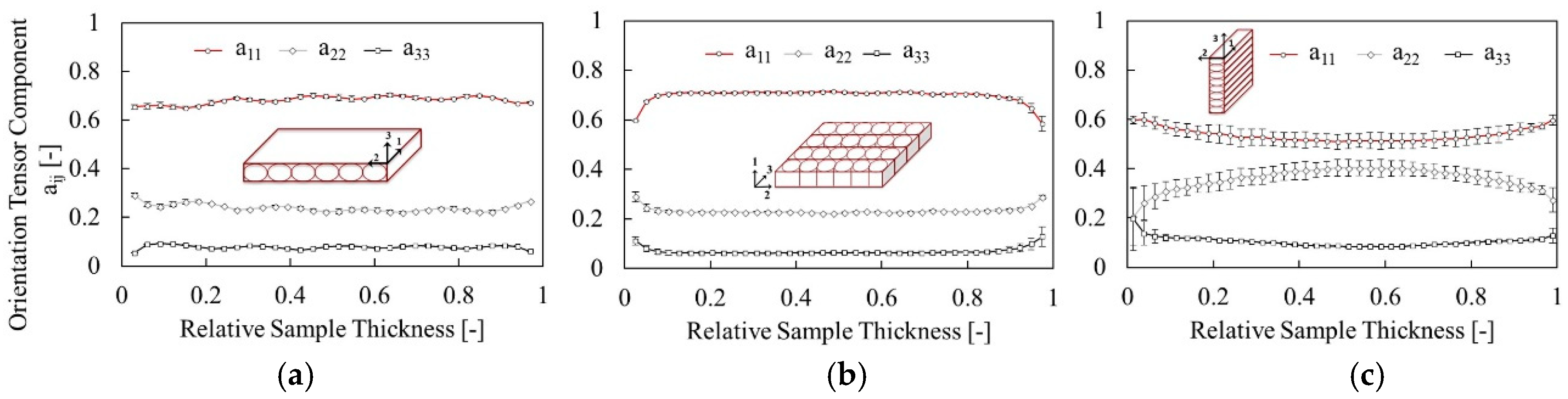
Samples produced in this way measure the thermal diffusivity perpendicular to the printhead direction (in the layer direction), therefore perpendicular to the primary fiber orientation direction. This is referred to as the through-plane (TP) direction, which is the direction through the layers of a print. To study the diffusivity parallel to the fiber orientation direction, which is referred to as the in-plane direction, the samples need to be prepared differently. Using the printed 60 mm × 10 mm × 1 mm bar, strips of dimensions 1 mm × 10 mm × 1 mm are cut with a razor blade. No additional polishing is done. Each strip is rotated 90 degrees, then placed in a sample holder with the printing direction facing the detector. The overall sample thickness was measured with a digital micrometer with the strips already in the sample holder. Now, the energy pulse travels along the length of the printed beads, and therefore along the principal fiber orientation direction. These samples are referred to as laminate (LAM) samples. Sample preparation is illustrated in
Figure 2. The samples were printed with a 1-mm nozzle with an extruder temperature of 270 °C, a bed temperature of 110 °C, a layer height of 0.2 mm, an extrusion ratio of 101%, and a printhead speed of 60 mm/s. Finally, additional samples were printed to measure the crossflow thermal conductivity. Freestanding walls 20 mm long × 1 mm wide × 60 mm tall were printed with a 1-mm nozzle with an extruder temperature of 270 °C, a bed temperature of 110 °C, a layer height of 0.2 mm, an extrusion ratio of 101%, and a printhead speed of 19 mm/s. The 10 mm section of wall closest to the build plate was cut and discarded, since the build plate temperature affects this region. The remaining section was used to cut LFA samples which can be used to measure the thermal diffusivity across the width of a bead. Samples are printed this way, instead of cutting the TP samples as with LAM, because these walls are more representative of the conductivity in a thin-walled part.
2.4. Fiber Orientation Analysis Using Microcomputed Tomography
Microcomputed tomography (µCT) is a nondestructive testing (NDT) method which allows one to obtain the internal material structure of an object and evaluate its micro-structural properties. In general, the system consists of an X-ray source, a rotating platform, and a detector. The basic principle of µCT is to irradiate a sample with penetrating X-rays, which are attenuated and captured downstream of the object with a detector system creating radiographs. At defined energy levels, the X-ray source irradiates the specimen, which is placed on a rotating platform to achieve a full scan of the sample. The detector records the attenuated X-rays as radiographs at each increment of angle during the rotation of the sample. Each captured projection (radiograph) is a two-dimensional intensity distribution of the attenuated X-rays. The intensity distribution is directly related to the material’s atomic density. A phase of high atomic density within the specimen absorbs more energy than low-density materials. The 3D reconstruction of the scanned sample is generated from all captured radiographs using tomographic reconstruction. The µCT data set can be processed using image processing algorithms for both qualitative and quantitative analyses.
The µCT scans in this work were performed with a Metrotom
® 800 µCT system (Carl Zeiss
® AG, Oberkochen, Germany) and the scan settings are summarized in
Table 1. The fiber orientation analysis was performed using VG StudioMAX
® 3.0 (Volume Graphics
® GmbH, Heidelberg, Germany), which computes the fiber orientation based on the structure tensor approach [
19].
In this work, we use tensor representation proposed by Advani and Tucker [
20] to describe the fiber orientation. The orientation of a single rigid fiber in three-dimensional (3D) space is described by the angle pair
, or by the unit vector
directed along the fiber axis as shown in
Figure 3.
For a fiber population in a defined volume, a complete description of the orientation is a probability density function
, which describes the probability of a fiber oriented between the angles
and (
), and between
and (
[
9]. Advani and Tucker [
20] proposed a more concise orientation of the fiber population by using a tensorial description. The Advani orientation tensor
computes the average orientation property of all fibers in a unit volume. The components of the symmetric second-order orientation tensor are defined as:
where
is the dyadic or tensor product of the fiber orientation vector
with itself, and
denotes an integral over all possible fiber orientations. In terms of the orientation distribution and the angle pair
, the tensor components can be calculated as follows [
17]:
| | |
| | |
| | |
where the angle brackets
indicate the average of all fibers in a volume.
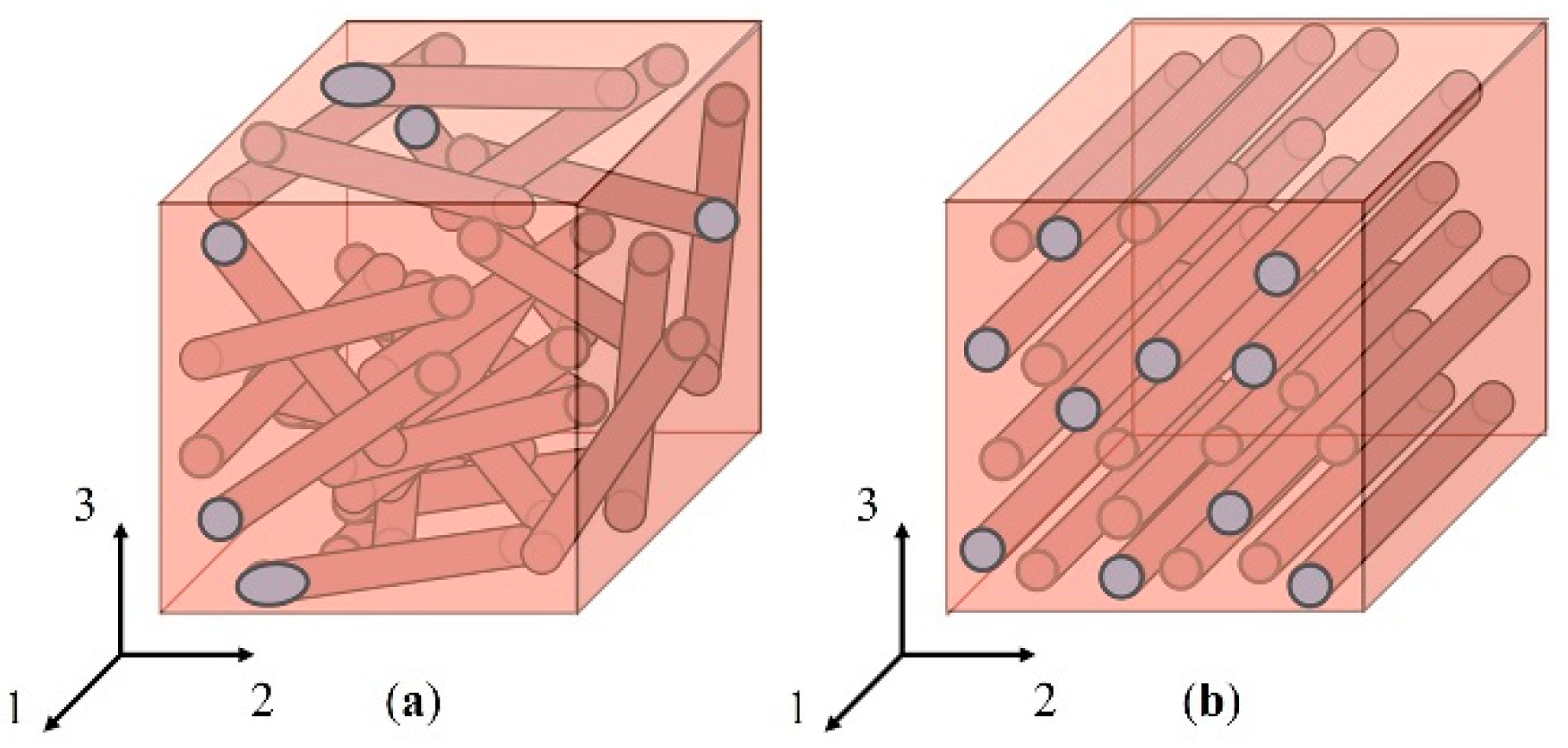
The diagonal components of the second order orientation tensor (
a11,
a22 and
a33) describe the degree of orientation with respect to the defined coordinate system. Conventionally, the reference coordinates are defined so that the 1-direction represents the in-flow direction, the 2-direction is the crossflow direction and the 3-direction is the thickness direction. The off-diagonal components of the orientation tensor show the tilt of the orientation tensor from the coordinate axes. Hence, they are zero only if the coordinate axes align with the principal directions of the orientation tensor [
20]. The physical interpretation of the tensor components focuses mainly on the diagonal components of the tensor, illustrated in
Figure 4.
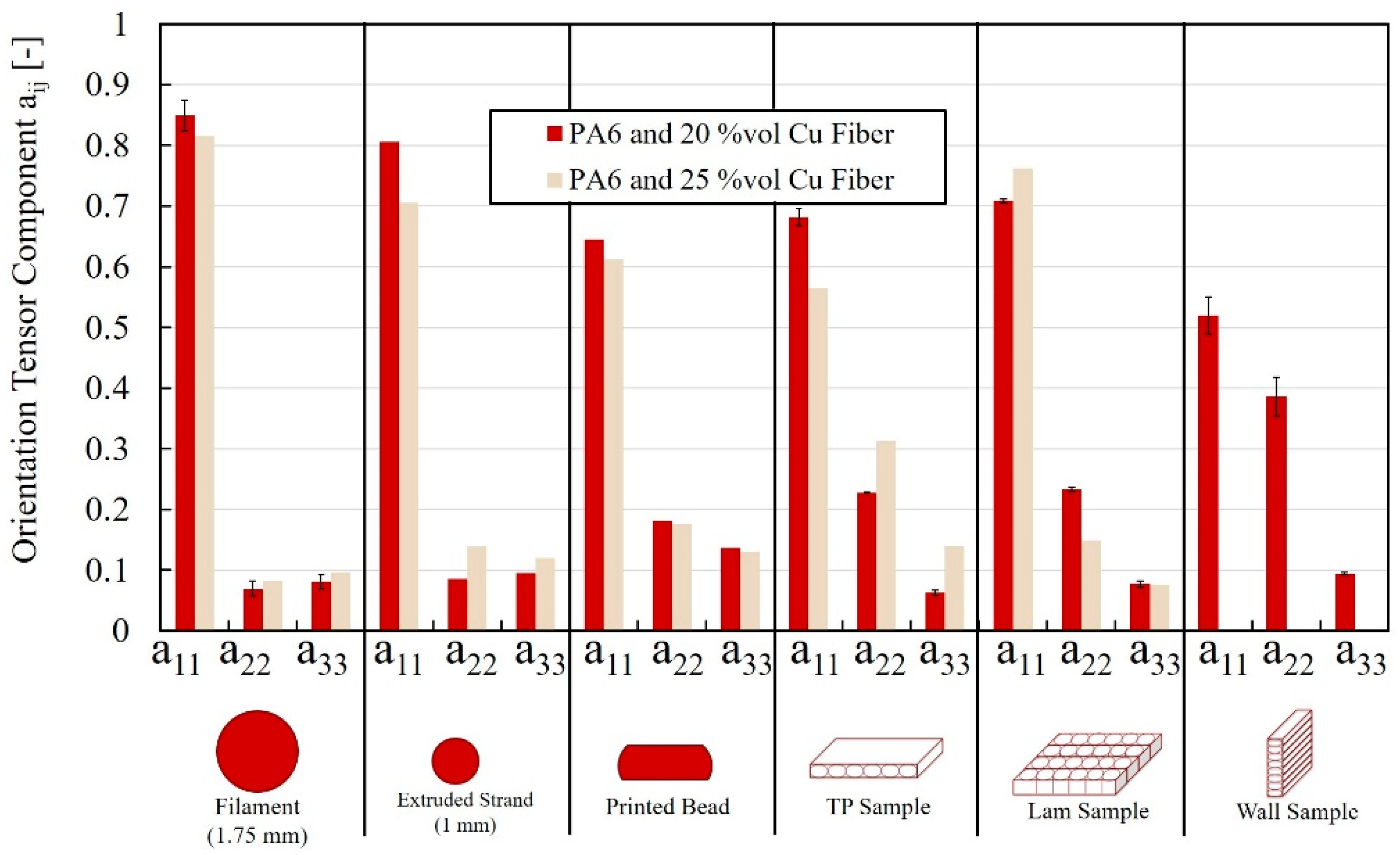
Scans of different samples were made using µCT to capture the change in orientation during processing:
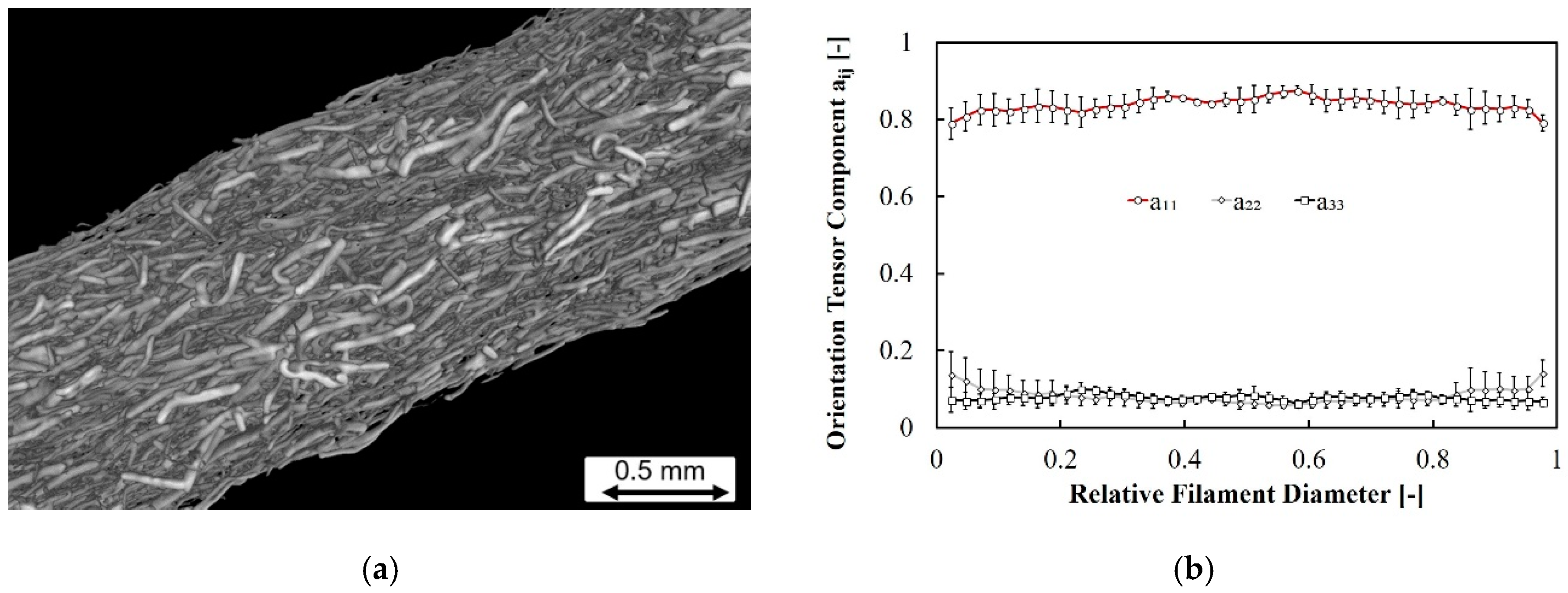
Strands of filament, which defines the initial orientation of the fibers;
Strands extruded from the 1 mm nozzle illustrating the change in fiber orientation due to shear deformations in the nozzle;
Single bead samples deposited on the print bed with a layer height of 0.2 mm;
LFA samples in the through-plane (TP, a33), wall (a22), and laminate (LAM, a11) directions. Wall samples were not tested at 25% vol copper fiber due to issues with producing quality samples at the higher filler content.
Three samples each of filament and through-plane, laminate, and wall samples were scanned for the 20% vol copper fiber material in order to understand the measurement and material variability.
4. Conclusions
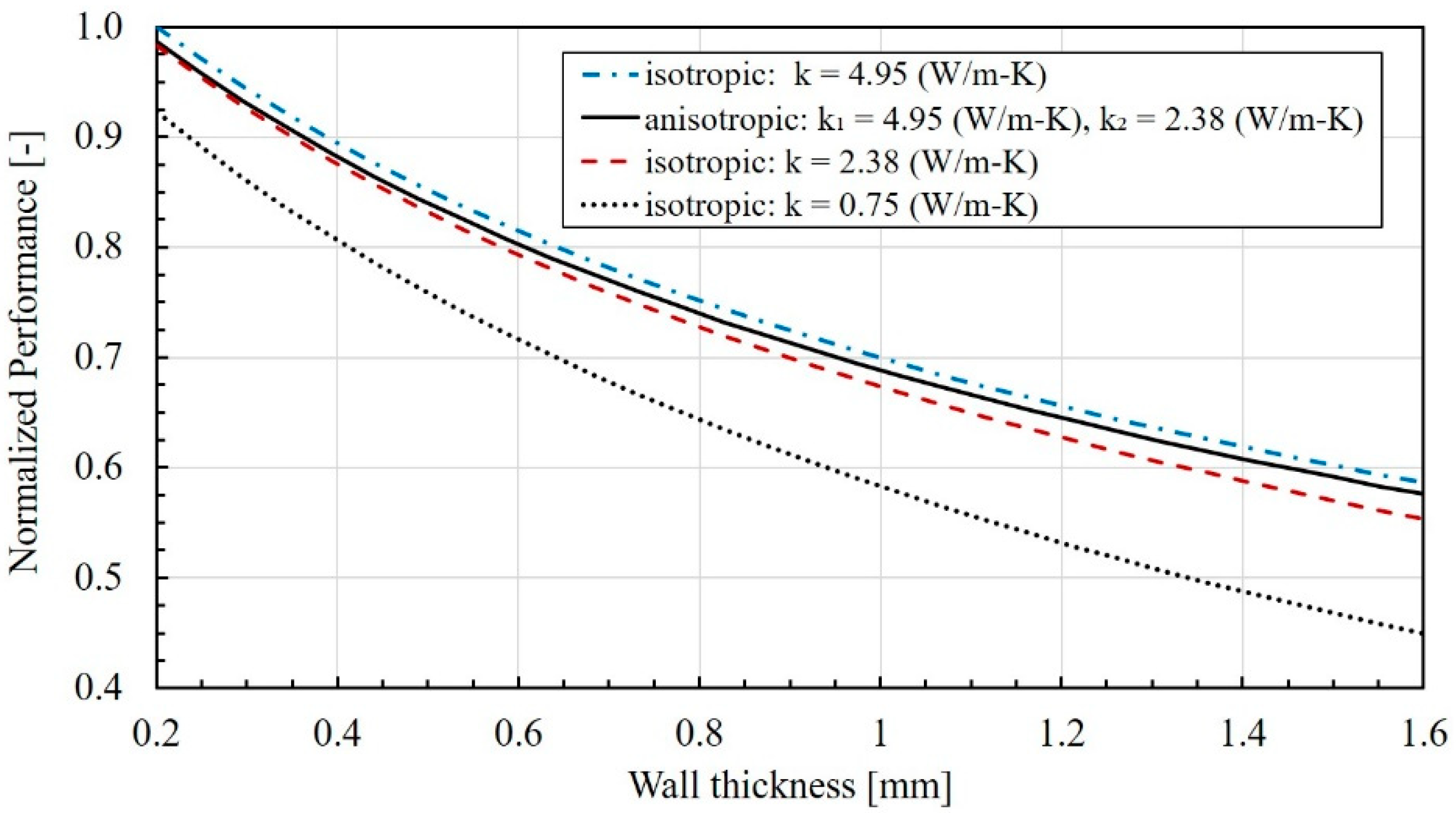
The fiber orientation in FFF filament was shown to be highly preferential in the extrusion direction. This could be analyzed and quantified with µCT analysis, displaying an average orientation as high as 0.8 in filament and 0.7 in printed parts in the principal flow direction. Consequentially, the orientation was lower in the two perpendicular directions. This anisotropy was reflected in the thermal conductivity, where the flow direction conductivity was about seven times larger than the build direction conductivity. Although the addition of fibers can increase the conductivity 19 times higher than the base resin conductivity at only 20% vol, the geometry of the printed part and the toolpath have an equally important role in the final performance, since the toolpath ultimately determines the fiber orientation in the part. While high fiber orientation leads to effective cooling fins in the analyzed air-cooled heat exchanger, the lower orientation in the walls between water and air channels also governs the performance.
The crossflow conductivity can be increased by raising the fiber content; however, a 1-mm FFF nozzle already experienced clogging at 25% vol copper fiber content, implying that higher fiber content is not possible for this filler. The relationships between filler size, shape, and content on FFF nozzle clogging and on the composite thermal conductivity is essential for optimizing the HX performance with the given manufacturing restrictions.
As additive manufacturing slowly starts to become feasible for serial production, continued development and functionalization of materials is essential. Fiber-filled plastics have significant benefits, including thermal and electrical conductivity, so it is essential to advance machine design and manufacturing techniques to take advantage of the materials for new applications.