Capillary Characterization of Fibrous Reinforcement and Optimization of Injection Strategy in Resin Transfer Molding
Abstract
:1. Introduction
2. Capillary Rise Experiments
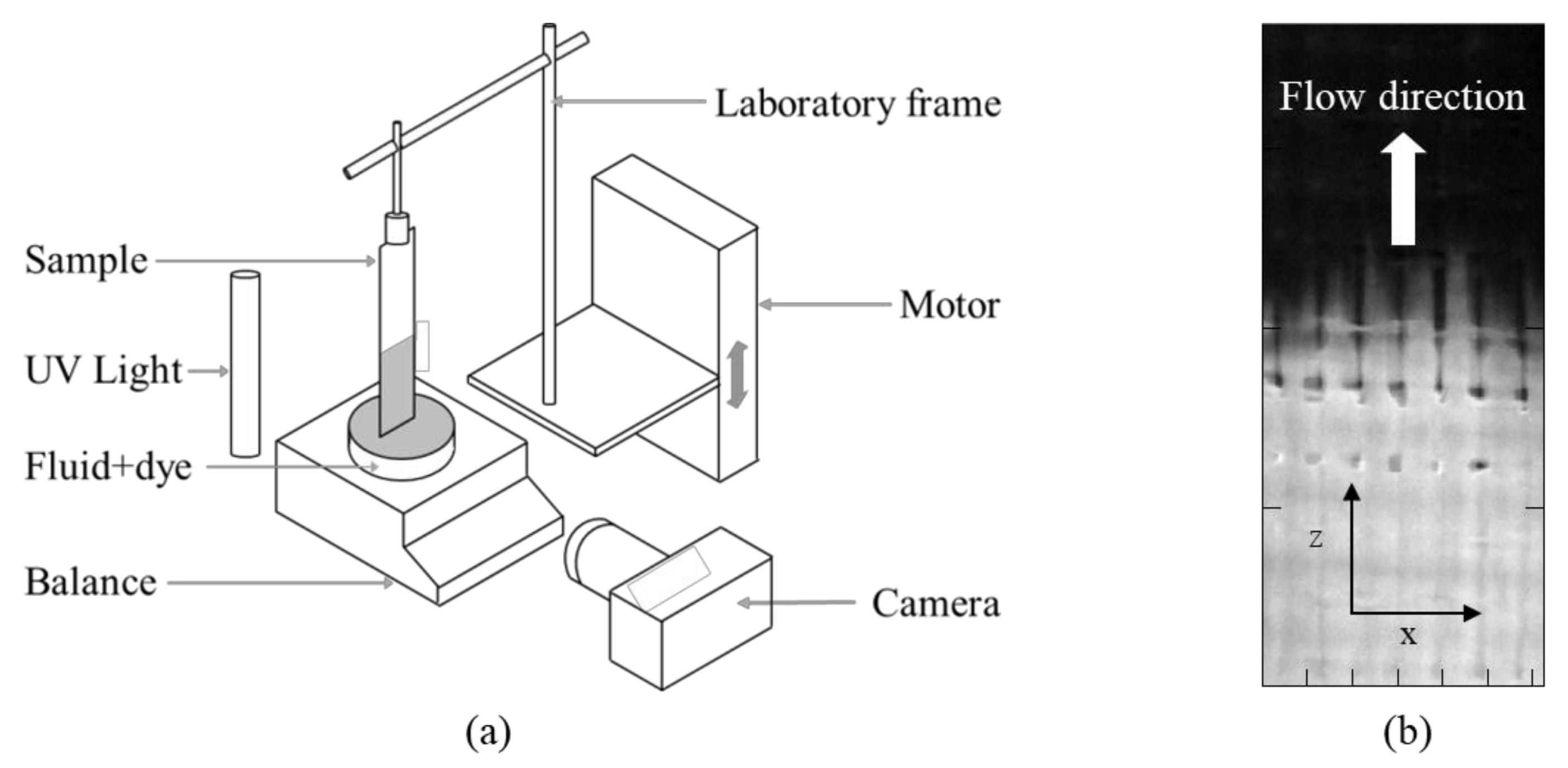
2.1. Materials and Setup
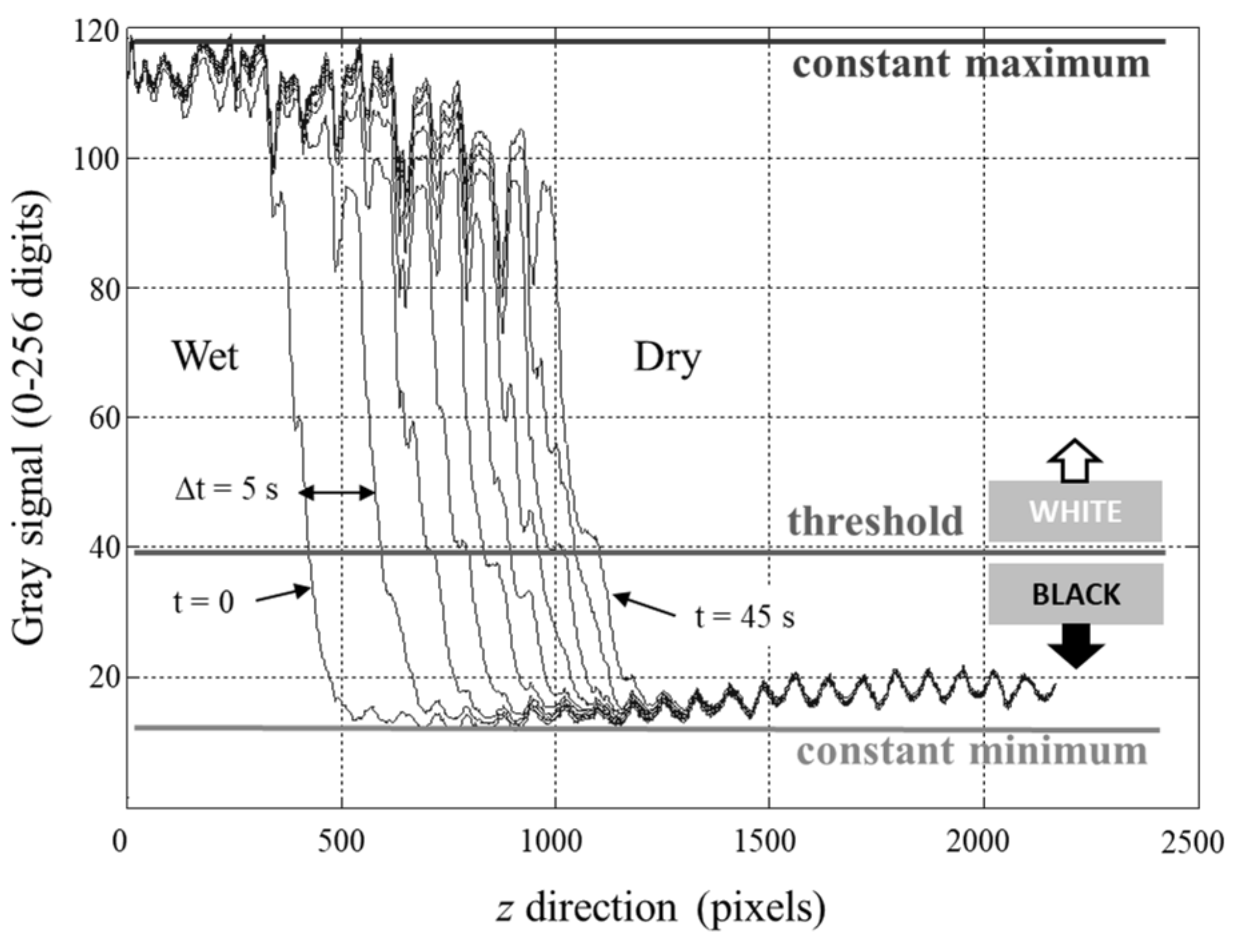
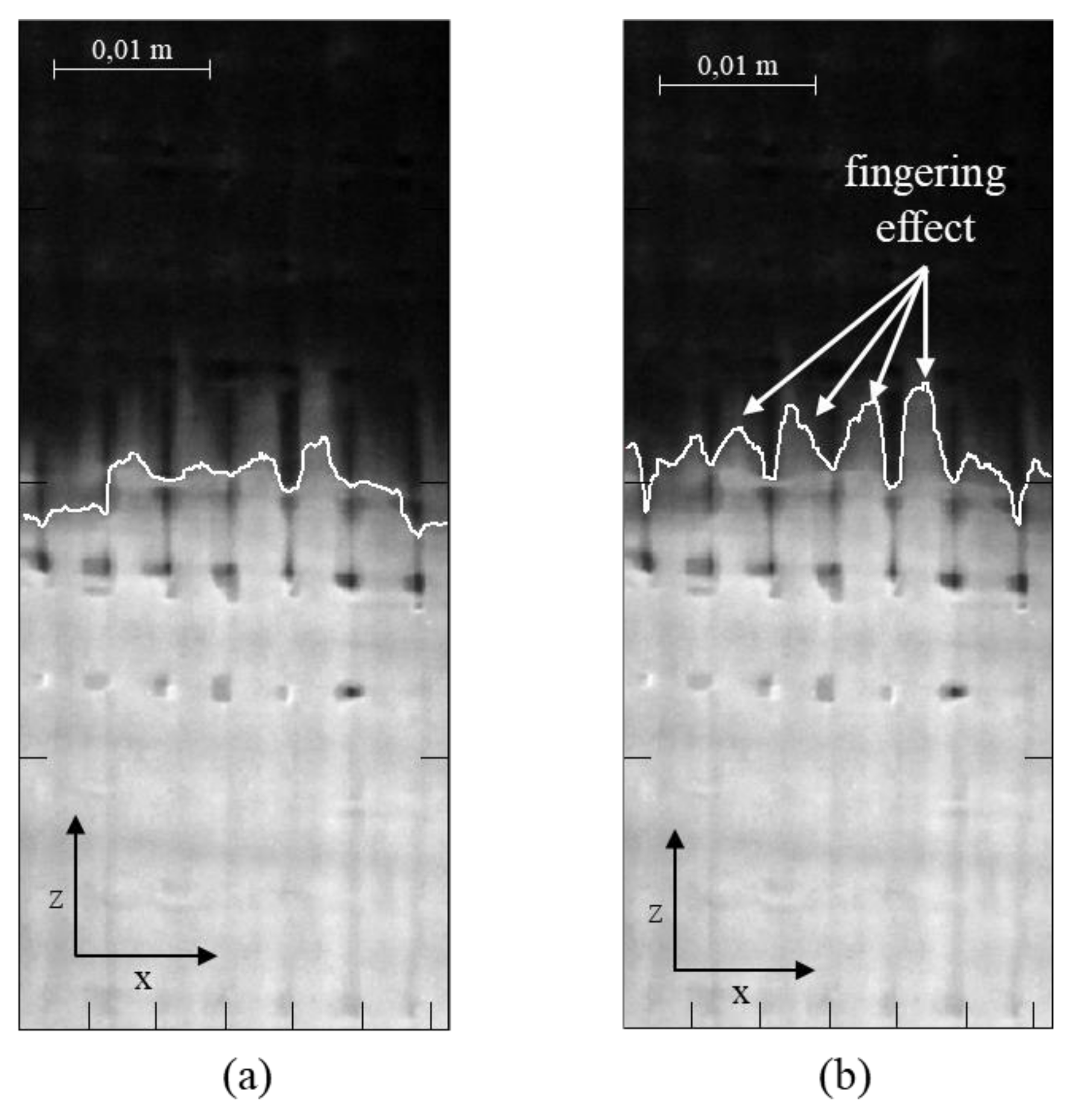
2.2. Image Processing
- -
- conversion of colored pictures into gray levels;
- -
- conversion of gray levels into black and white;
- -
- edge detection to locate the flow front position.
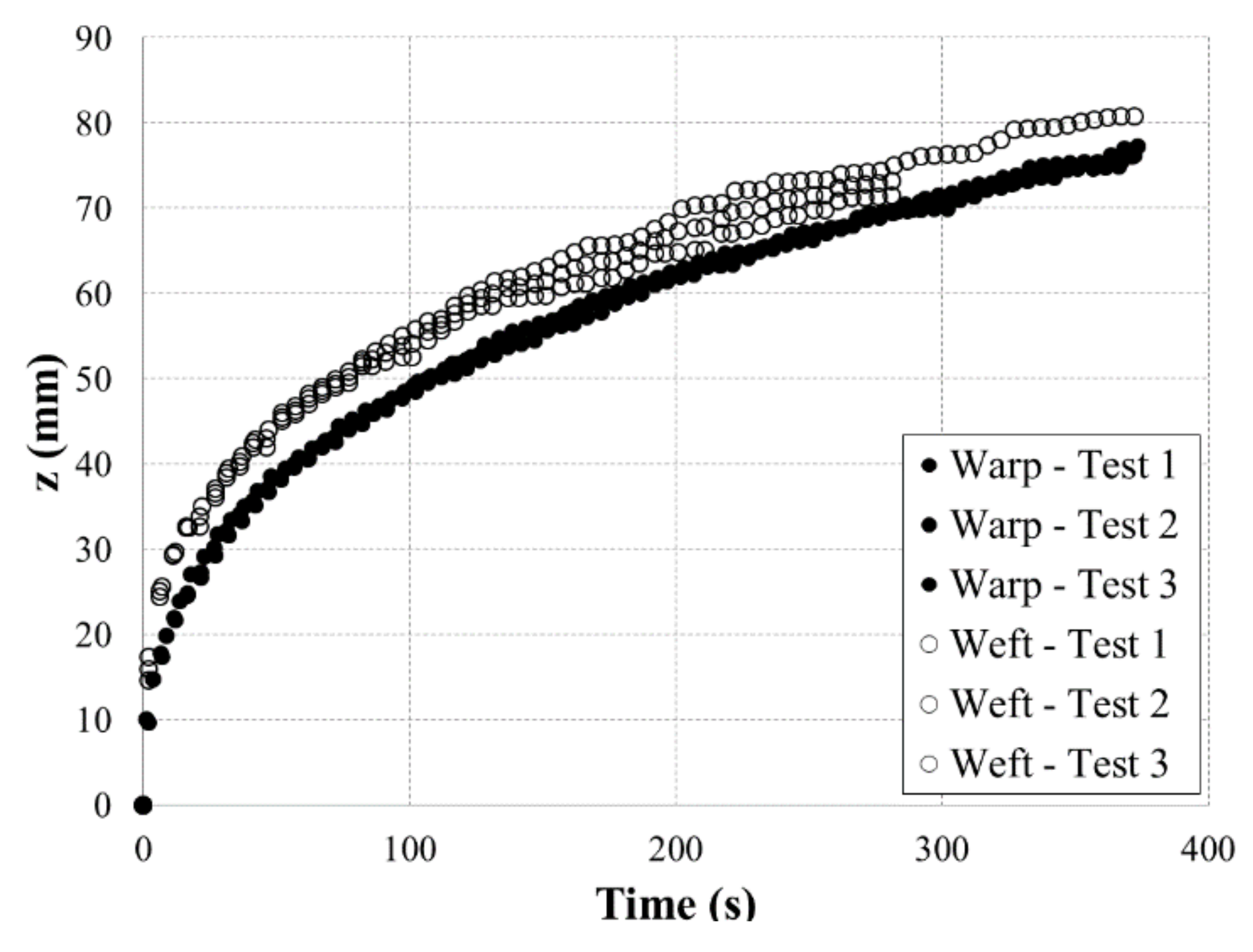
2.3. Modeling of Capillary Rise
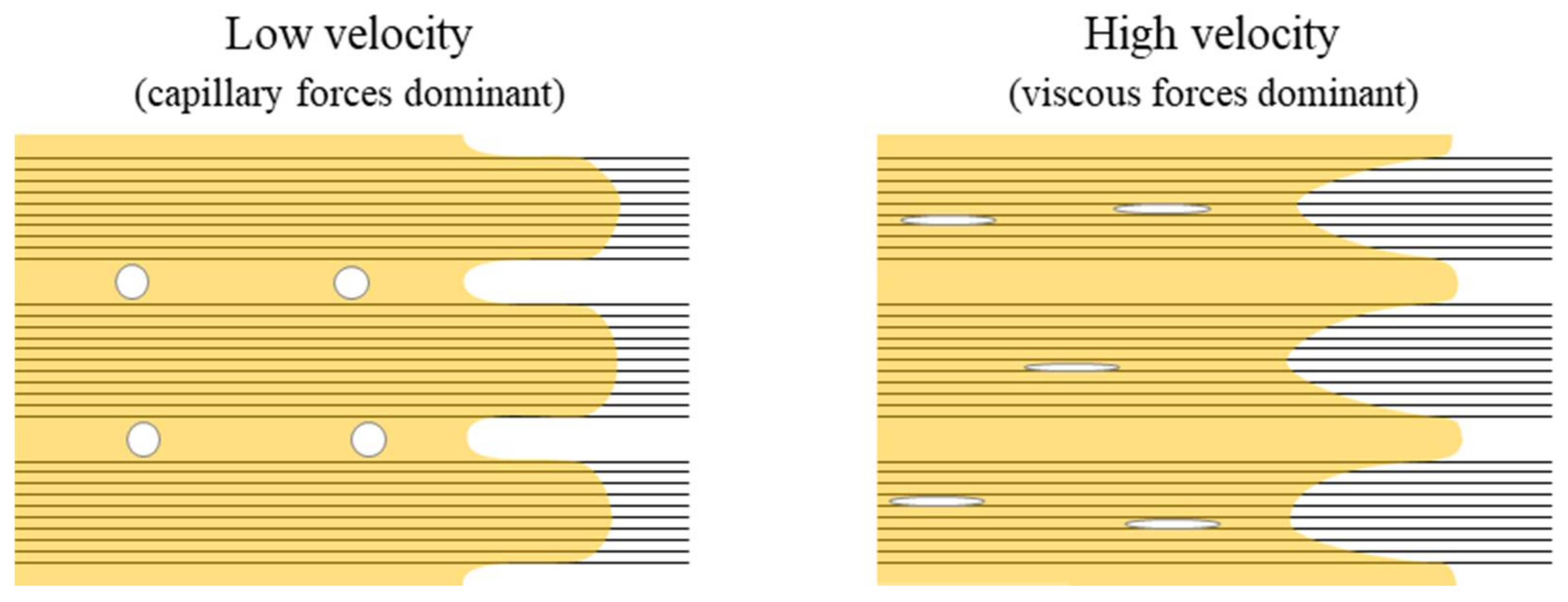
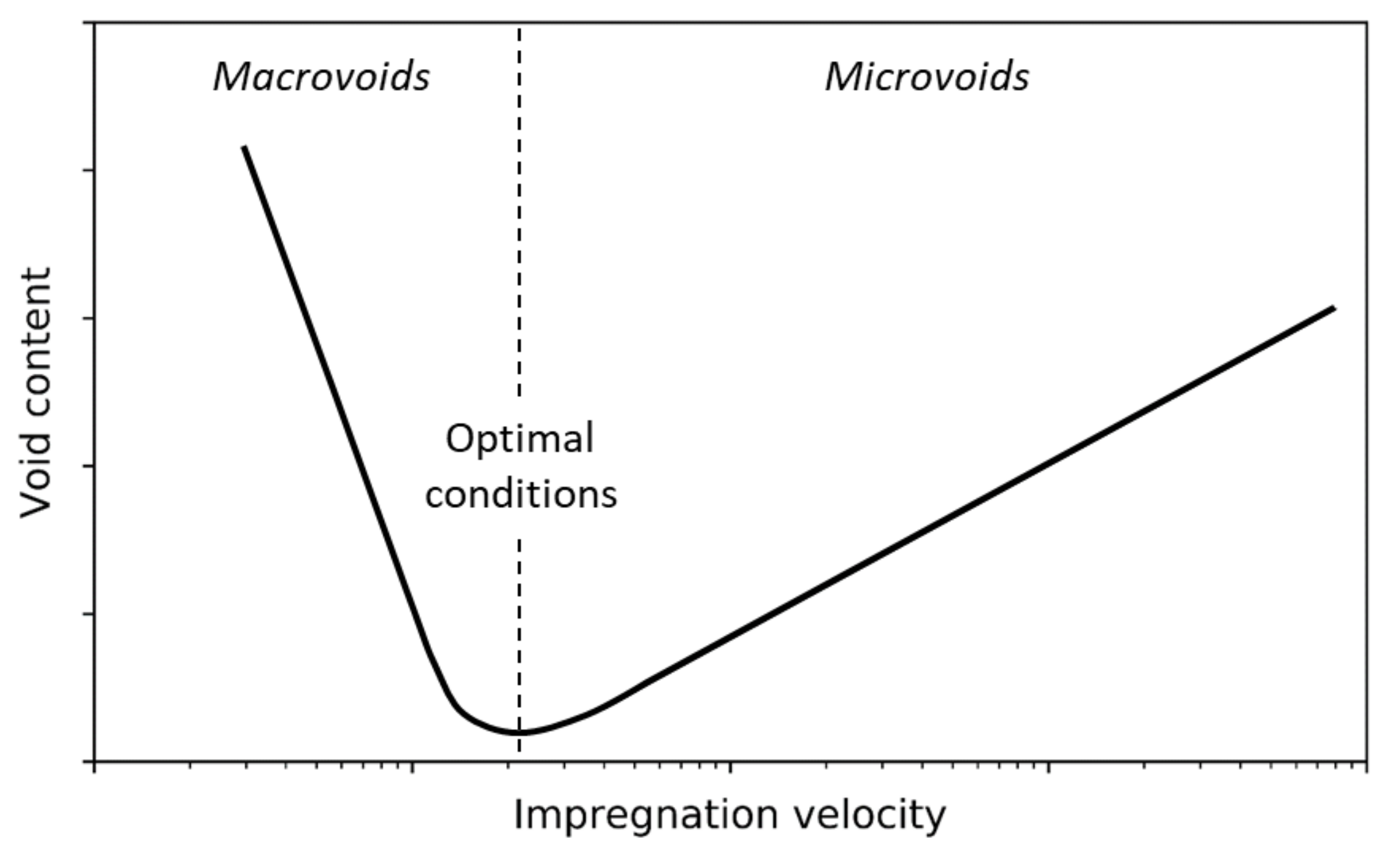
2.4. Optimal Imbibition Velocity
3. Impregnation in RTM Mold of Varying Geometry
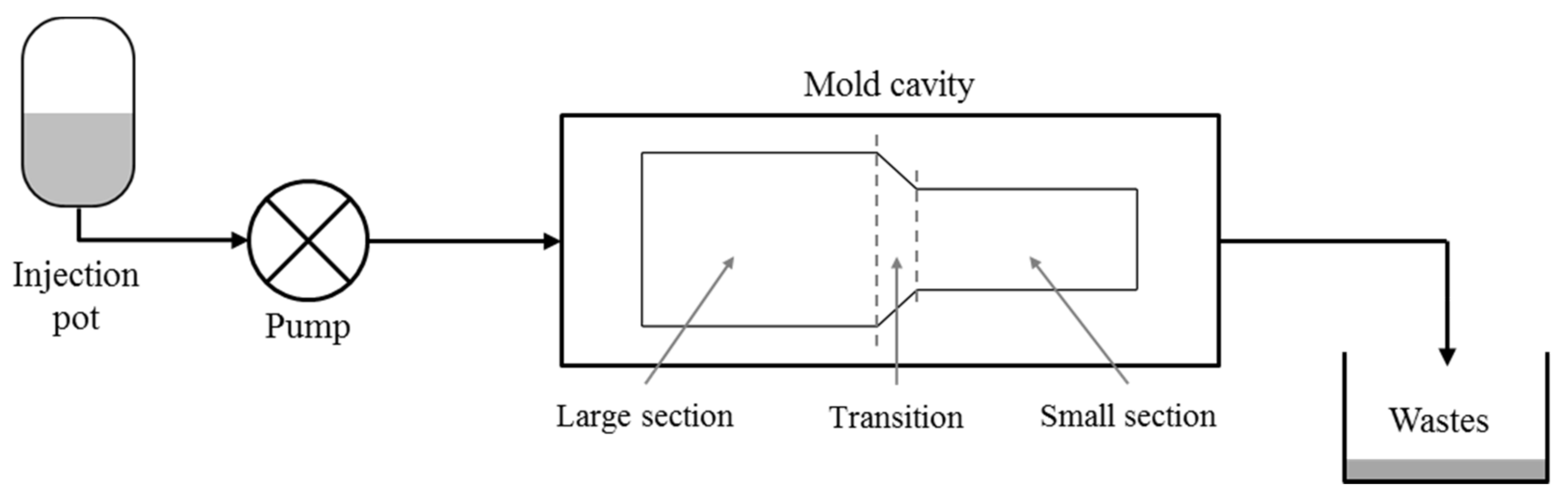
3.1. Manufacturing
- Maintaining the optimal impregnation velocity throughout the plate (CSL and DLS tests).
- Maintaining the optimal impregnation velocity only in the small section (CS and DS tests).
- Maintaining the optimal impregnation velocity only in the large section (CL and DL tests).
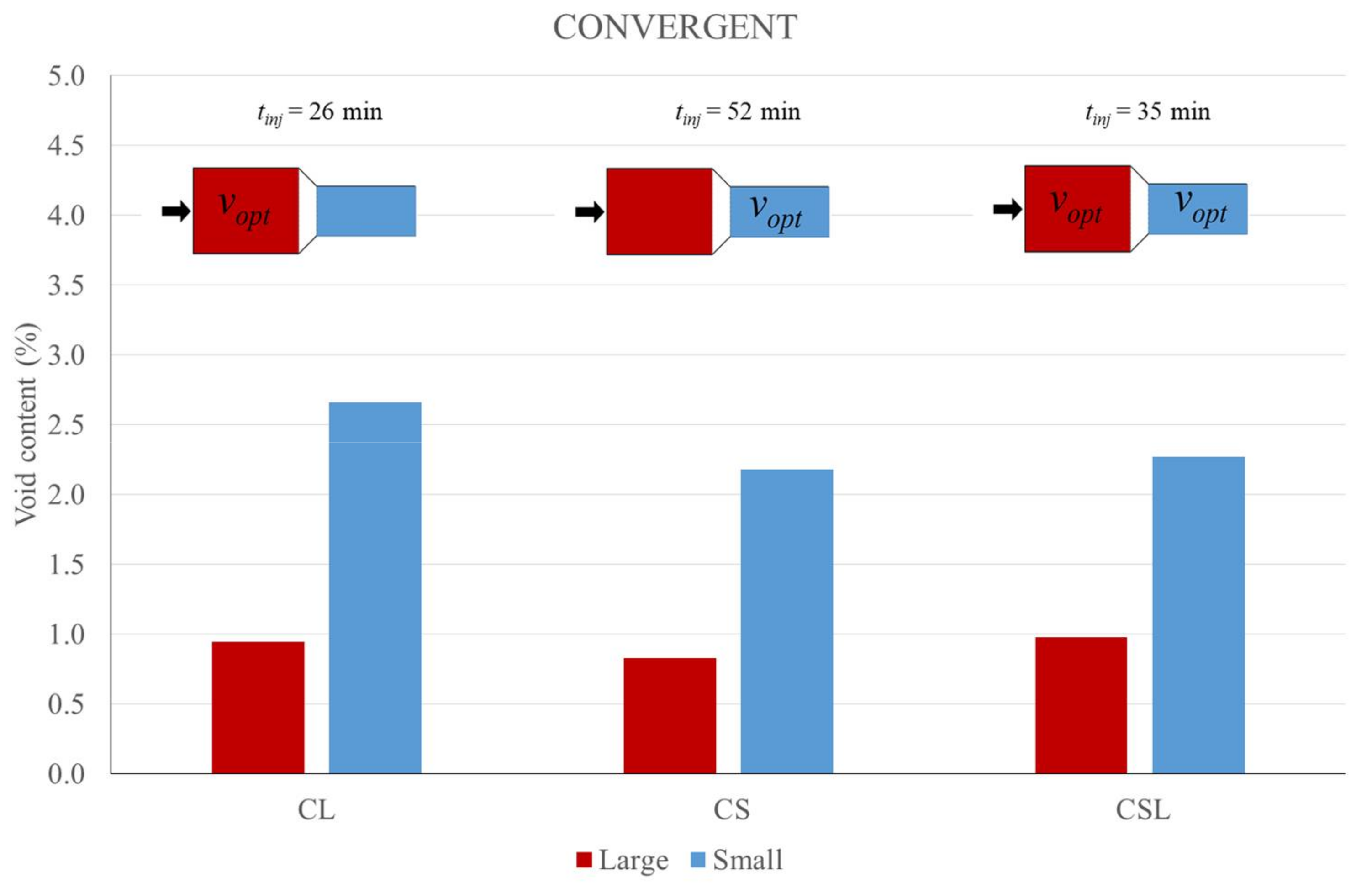
3.2. Void Content Analysis
4. Conclusions
- -
- The capillary rise method gives a good approximation of the optimum velocity for practical manufacturing, which is close to the lower bound of the predicted range.
- -
- The transport of voids during mold filling tends to increase the porosity near the vents. In case of parts of complex geometry, it is recommended to inject in divergent mode in order to minimize the void content near the outlet.
- -
- It is not necessary to inject at the lowest impregnation velocity of the optimal range throughout the whole part. If overall filling time is a critical issue, the injection speed can be increased at the beginning of the filling without compromising the quality of the final part.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gay, D.; Hoa, S.V. Composite Materials: Design and Applications; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Chung, D.D.L. Composite Materials: Science and Applications; Springer: London, UK, 2010. [Google Scholar]
- Parnas, R.S. Liquid Composite Molding; Carl Hanser GmbH: München, Germany, 2000. [Google Scholar]
- Trochu, F.; Ruiz, E.; Achim, V.; Soukane, S. Advanced numerical simulation of liquid composite molding for process analysis and optimization. Compos. Part A Appl. Sci. Manuf. 2006, 37, 890–902. [Google Scholar] [CrossRef]
- Ghiorse, S. Effect of void content on the mechanical properties of carbon/epoxy laminates. SAMPE Q. 1993, 24, 54–59. [Google Scholar]
- Liu, L.; Zhang, B.-M.; Wang, D.-F.; Wu, Z.-J. Effects of cure cycles on void content and mechanical properties of composite laminates. Compos. Struct. 2006, 73, 303–309. [Google Scholar] [CrossRef]
- Varna, J.; Joffe, R.; Berglund, L.A.; Lundström, T.S. Effect of voids on failure mechanisms in RTM laminates. Compos. Sci. Technol. 1995, 53, 241–249. [Google Scholar] [CrossRef]
- Patel, N.; Rohatgi, V.; Lee, L.J. Micro scale flow behavior and void formation mechanism during impregnation through a unidirectional stitched fiberglass mat. Polym. Eng. Sci. 1995, 35, 837–851. [Google Scholar] [CrossRef]
- Patel, N.; Lee, L.J. Effects of fiber mat architecture on void formation and removal in liquid composite molding. Polym. Compos. 1995, 16, 386–399. [Google Scholar] [CrossRef]
- Park, C.H.; Lee, W.I. Modeling void formation and unsaturated flow in liquid composite molding processes: A survey and review. J. Reinf. Plast. Compos. 2011, 30, 957–977. [Google Scholar] [CrossRef]
- Chen, Y.T.; Davis, H.T.; Macosko, C.W. Wetting of fiber mats for composites manufacturing: I. Visualization experiments. AIChE J. 1995, 41, 2261–2273. [Google Scholar] [CrossRef]
- Rohatgi, V.; Patel, N.; Lee, L.J. Experimental Investigation of Flow-Induced Microvoids during Impregnation of Unidirectional Stitched Fiberglass Mat. Polym. Compos. 1996, 17, 161–170. [Google Scholar] [CrossRef]
- Leclerc, J.S.; Ruiz, E. Porosity reduction using optimized flow velocity in Resin Transfer Molding. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1859–1868. [Google Scholar] [CrossRef]
- Park, C.H.; Lebel, A.; Saouab, A.; Bréard, J.; Lee, W.I. Modeling and simulation of voids and saturation in liquid composite molding processes. Compos. Part A Appl. Sci. Manuf. 2011, 42, 658–668. [Google Scholar] [CrossRef]
- DeValve, C.; Pitchumani, R. Simulation of void formation in liquid composite molding processes. Compos. Part A Appl. Sci. Manuf. 2013, 51, 22–32. [Google Scholar] [CrossRef]
- Achim, V.; Ruiz, E. Guiding selection for reduced process development time in RTM. Int. J. Mater. Form. 2009, 3, 1277–1286. [Google Scholar] [CrossRef]
- Ruiz, E.; Achim, V.; Soukane, S.; Trochu, F.; Bréard, J. Optimization of injection flow rate to minimize micro/macro-voids formation in resin transfer molded composites. Compos. Sci. Technol. 2006, 66, 475–486. [Google Scholar] [CrossRef]
- LeBel, F.; Fanaei, A.E.; Ruiz, É.; Trochu, F. Prediction of optimal flow front velocity to minimize void formation in dual scale fibrous reinforcements. Int. J. Mater. Form. 2014, 7, 93–116. [Google Scholar] [CrossRef]
- Amico, S.C.; Lekakou, C. Axial impregnation of a fiber bundle. Part 1: Capillary experiments. Polym. Compos. 2002, 23, 249–263. [Google Scholar] [CrossRef]
- Amico, S.C.; Lekakou, C. Axial impregnation of a fiber bundle. Part 2: Theoretical analysis. Polym. Compos. 2002, 23, 264–273. [Google Scholar] [CrossRef]
- Hsieh, Y.-L.; Yu, B. Liquid Wetting, Transport, and Retention Properties of Fibrous Assemblies: Part I: Water Wetting Properties of Woven Fabrics and Their Constituent Single Fibers. Text. Res. J. 1992, 62, 677–685. [Google Scholar] [CrossRef]
- Bayramli, E.; Powell, R.L. Experimental Investigation of the Axial Impregnation of Oriented Fiber Bundles by Capillary Forces; U.S. Army Laboratory Command: Springfield, VA, USA, 1992. [Google Scholar]
- LeBel, F.; Fanaei, A.E.; Ruiz, É.; Trochu, F. Experimental Characterization by Fluorescence of Capillary Flows in the Fiber Tows of Engineering Fabrics. Open J. Inorg. Non-Met. Mater. 2012, 2, 25–45. [Google Scholar] [CrossRef]
- LeBel, F.; Fanaei, A.E.; Ruiz, E.; Trochu, F. Experimental characterization by fluorescence of capillary flows in dual-scale engineering fabrics. Text. Res. J. 2013, 83, 1634–1659. [Google Scholar] [CrossRef]
- LeBel, F.; Ruiz, É.; Trochu, F. Void content analysis and processing issues to minimize defects in liquid composite molding. Polym. Compos. 2017. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Labat, L.; Bréard, J.; Pillut-Lesavre, S.; Bouquet, G. Void fraction prevision in LCM parts. EPJ Appl. Phys. 2001, 16, 157–164. [Google Scholar] [CrossRef]
- Duan, Y.; Zuo, L.; Zhao, Y.; Zhang, Z.; Liang, Z. Effect of Fabric Structure on Deffects in Composites Manufactured by RTM. In Proceedings of the 16th International Conference on Composite Materials, Kyoto, Japan, 8–13 July 2007. [Google Scholar]
- Pearce, N.; Guild, F.; Summerscales, J. A study of the effects of convergent flow fronts on the properties of fibre reinforced composites produced by RTM. Compos. Part A Appl. Sci. Manuf. 1998, 29, 141–152. [Google Scholar] [CrossRef]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Hamdaoui, M.; Fayala, F.; Nasrallah, S.B. Dynamics of capillary rise in yarns: Influence of fiber and liquid characteristics. J. Appl. Polym. Sci. 2007, 104, 3050–3056. [Google Scholar] [CrossRef]
- Ravey, C.; Ruiz, E.; Trochu, F. Determination of the optimal impregnation velocity in Resin Transfer Molding by capillary rise experiments and infrared thermography. Compos. Sci. Technol. 2014, 99, 96–102. [Google Scholar] [CrossRef]
- Patel, N.; Lee, L.J. Modeling of Void Formation and Removal in Liquid Composite Molding. Part II: Model Development and Implementation. Polym. Compos. 1996, 17, 104–114. [Google Scholar] [CrossRef]

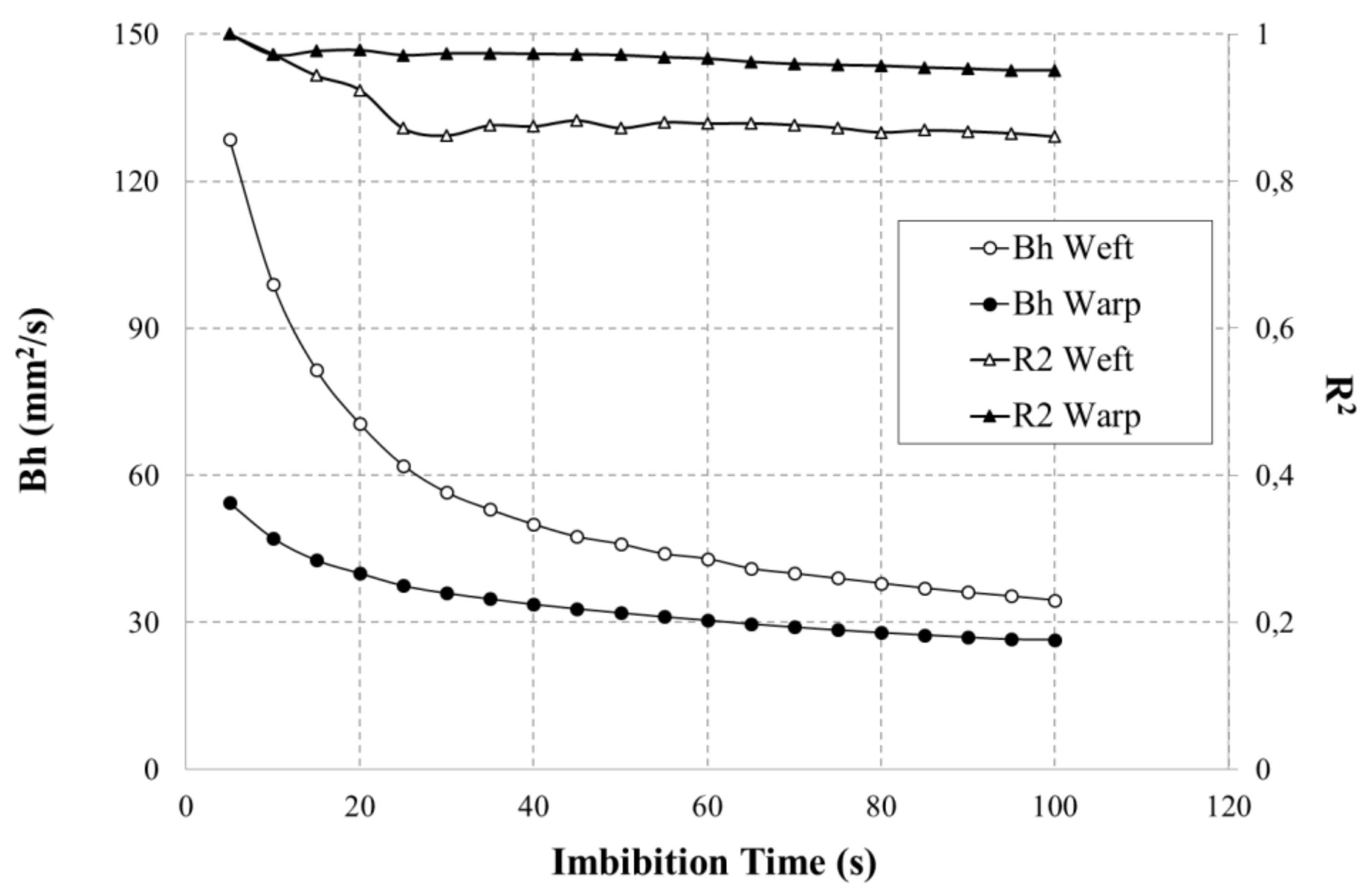




| Bh (mm2·s−1) | Lc (mm) | vopt (mm·s−1) | |
|---|---|---|---|
| Warp | 32–55 | 1.94 | 16.5–28.4 |
| Weft | 45–128 | 3.26 | 13.8–39.3 |
| Hexadecane | Vinyl Ester 411–350 | Epoxy DER 383 | |
|---|---|---|---|
| Viscosity (mPa·s) | 3.51 | 480 | 896 |
| Surface tension (mN/m) | 27.5 | 34.3 | 44.8 |
| Contact angle (°) | 0 | 44 | 32 |
| vopt (mm·s−1) | ||||
|---|---|---|---|---|
| Vinyl Ester Resin | Epoxy Resin | |||
| This Work | Lebel et al. [18] | This Work | Lebel et al. [18] | |
| Warp | 0.109–0.186 | 0.077–0.18 | 0.0912–0.153 | 0.06–0.14 |
| Weft | 0.0909–0.258 | 0.077–0.20 | 0.0763–0.212 | 0.06–0.14 |
CONVERGENT  | DIVERGENT  | |||||
|---|---|---|---|---|---|---|
| Plate Name | Large Section | Small Section | Plate Name | Small Section | Large Section | |
| Case 1 | CL | vopt | 2 vopt | DL | 2 vopt | vopt |
| Case 2 | CS | 0.5 vopt | vopt | DS | vopt | 0.5 vopt |
| Case 3 | CLS | vopt | vopt | DSL | vopt | vopt |
| Distance from Injection Point | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3 cm | 8 cm | 12 cm | 22 cm | 27 cm | 31 cm | |||
| Void content (%) | Divergent | DL | 0.915 | 1.031 | 1.121 | 1.524 | 1.711 | 2.068 |
| DS 1 | 1.499 | 1.300 | 0.990 | 0.956 | 1.053 | 1.437 | ||
| DSL | 1.291 | 1.160 | 1.071 | 1.312 | 1.744 | 2.415 | ||
| Convergent | CL | 0.582 | 0.397 | 1.855 | 1.753 | 2.952 | 3.377 | |
| CS | 0.753 | 0.794 | 0.829 | 1.671 | 2.525 | 2.713 | ||
| CLS | 1.163 | 1.536 | 2.552 | 2.324 | 3.024 | 2.786 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Causse, P.; Ravey, C.; Trochu, F. Capillary Characterization of Fibrous Reinforcement and Optimization of Injection Strategy in Resin Transfer Molding. J. Compos. Sci. 2018, 2, 19. https://doi.org/10.3390/jcs2020019
Causse P, Ravey C, Trochu F. Capillary Characterization of Fibrous Reinforcement and Optimization of Injection Strategy in Resin Transfer Molding. Journal of Composites Science. 2018; 2(2):19. https://doi.org/10.3390/jcs2020019
Chicago/Turabian StyleCausse, Philippe, Christophe Ravey, and François Trochu. 2018. "Capillary Characterization of Fibrous Reinforcement and Optimization of Injection Strategy in Resin Transfer Molding" Journal of Composites Science 2, no. 2: 19. https://doi.org/10.3390/jcs2020019
APA StyleCausse, P., Ravey, C., & Trochu, F. (2018). Capillary Characterization of Fibrous Reinforcement and Optimization of Injection Strategy in Resin Transfer Molding. Journal of Composites Science, 2(2), 19. https://doi.org/10.3390/jcs2020019




