On the Convergence of Laminated Composite Plates of Arbitrary Shape through Finite Element Models
Abstract
1. Introduction
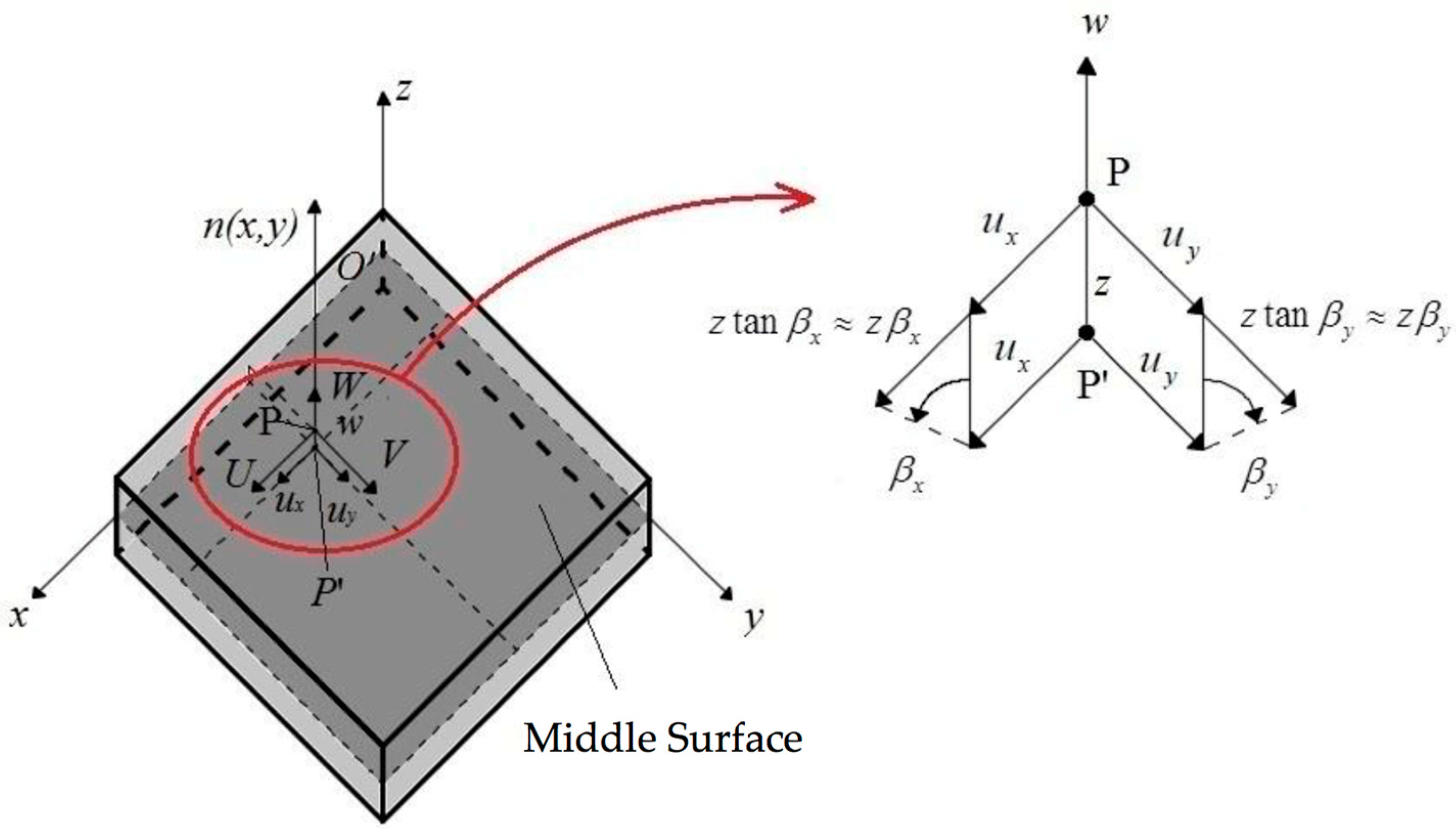
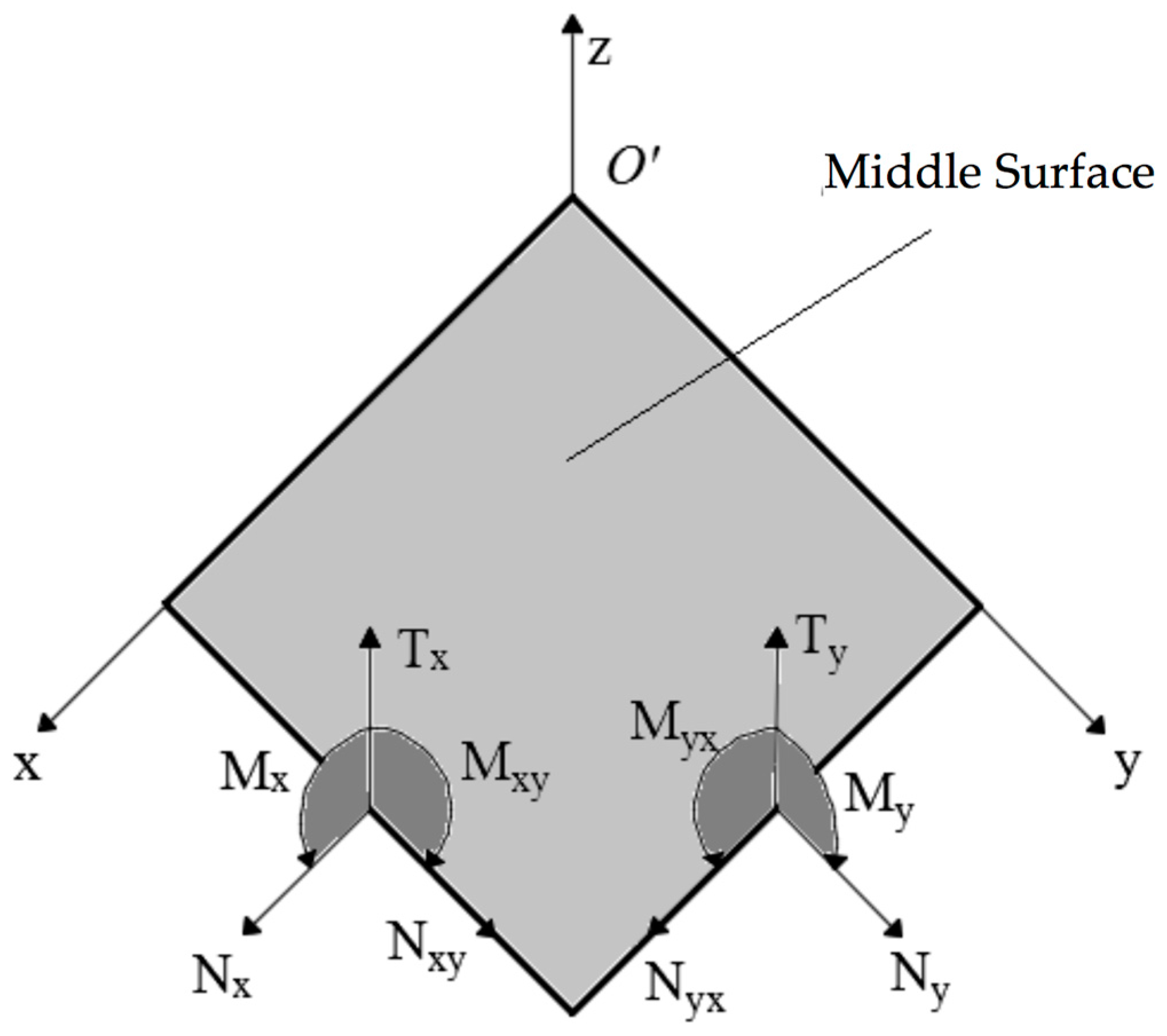
2. First-Order Laminated Plate Theory
3. Numerical Implementation
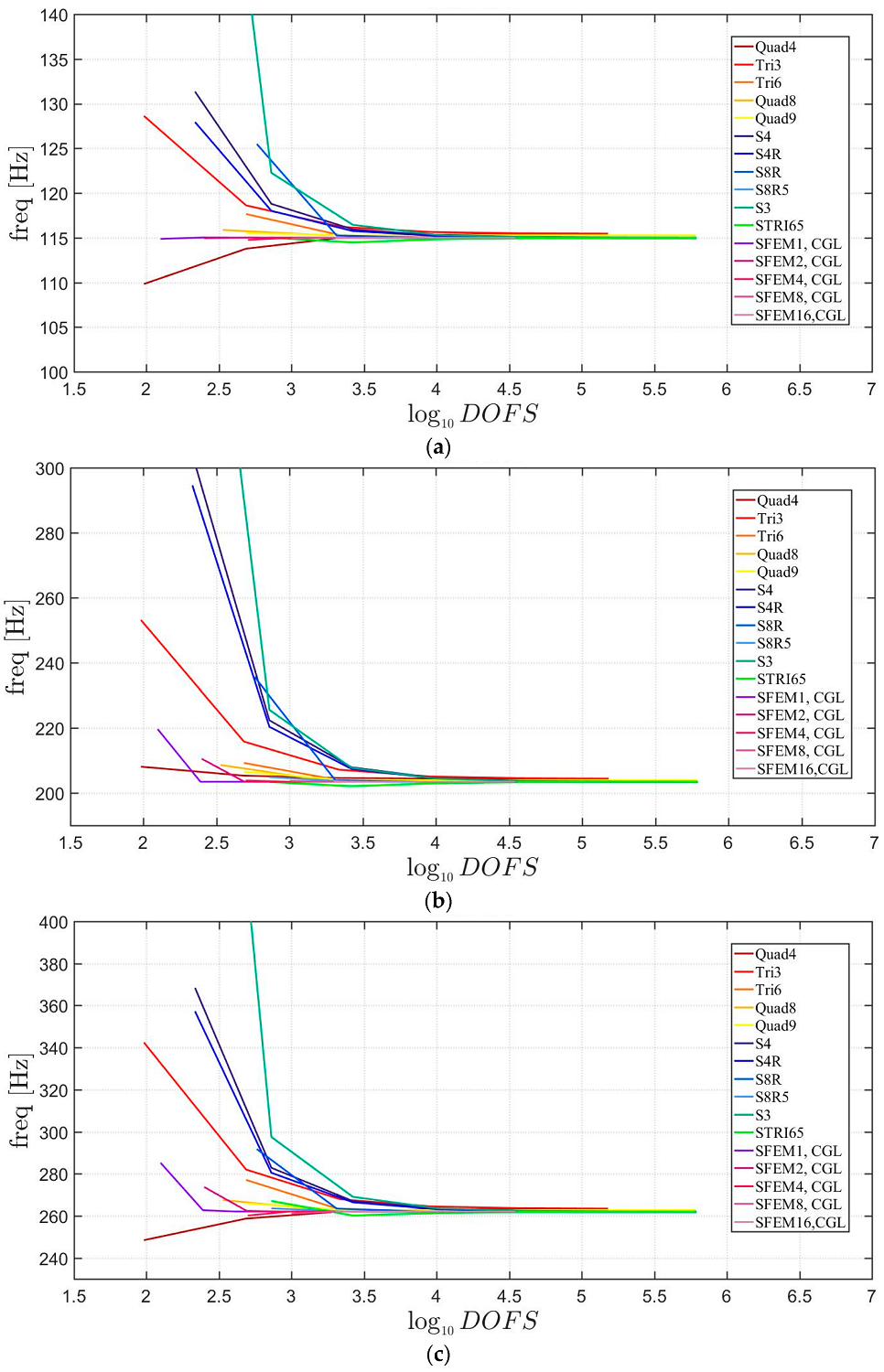
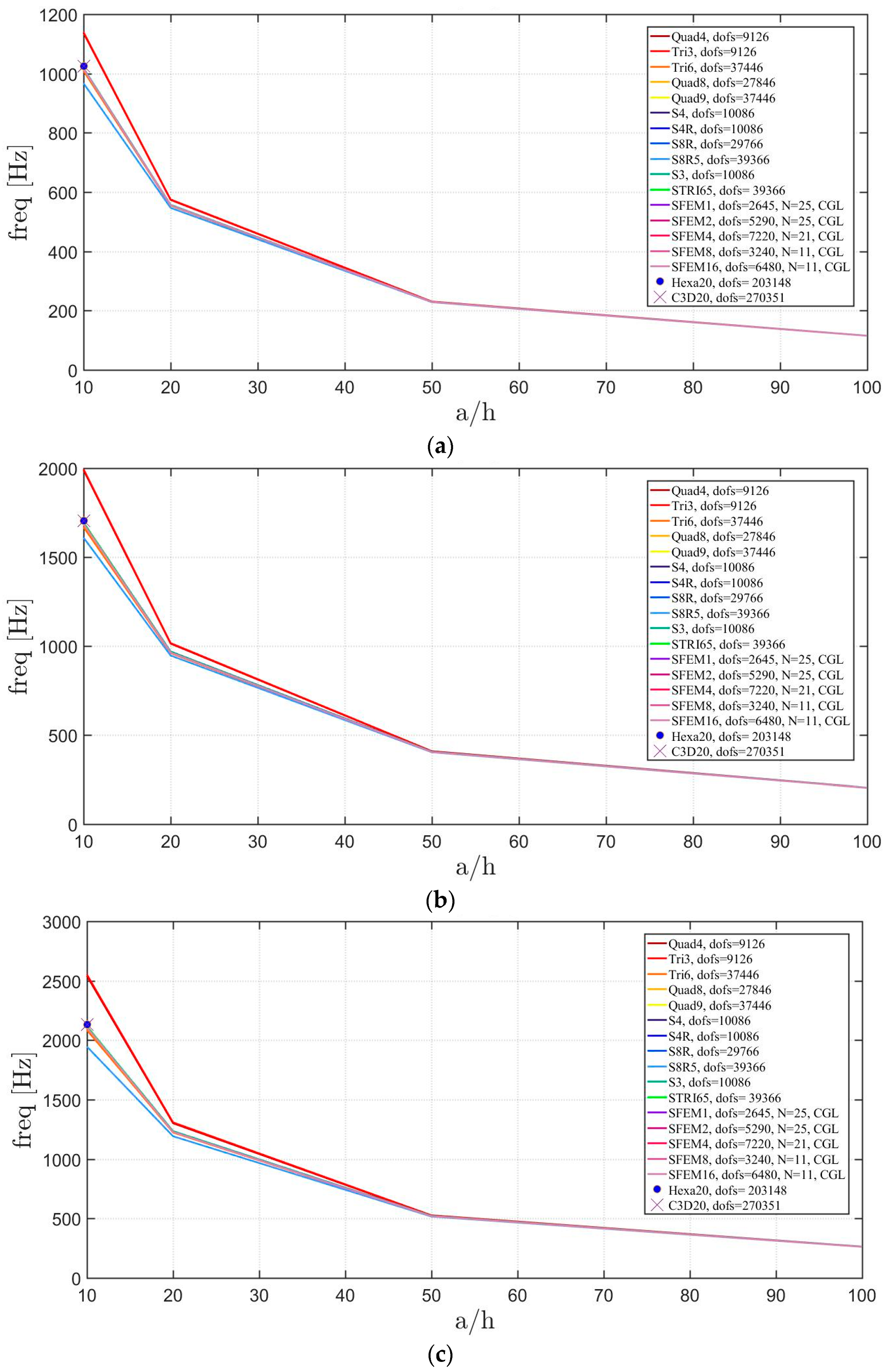
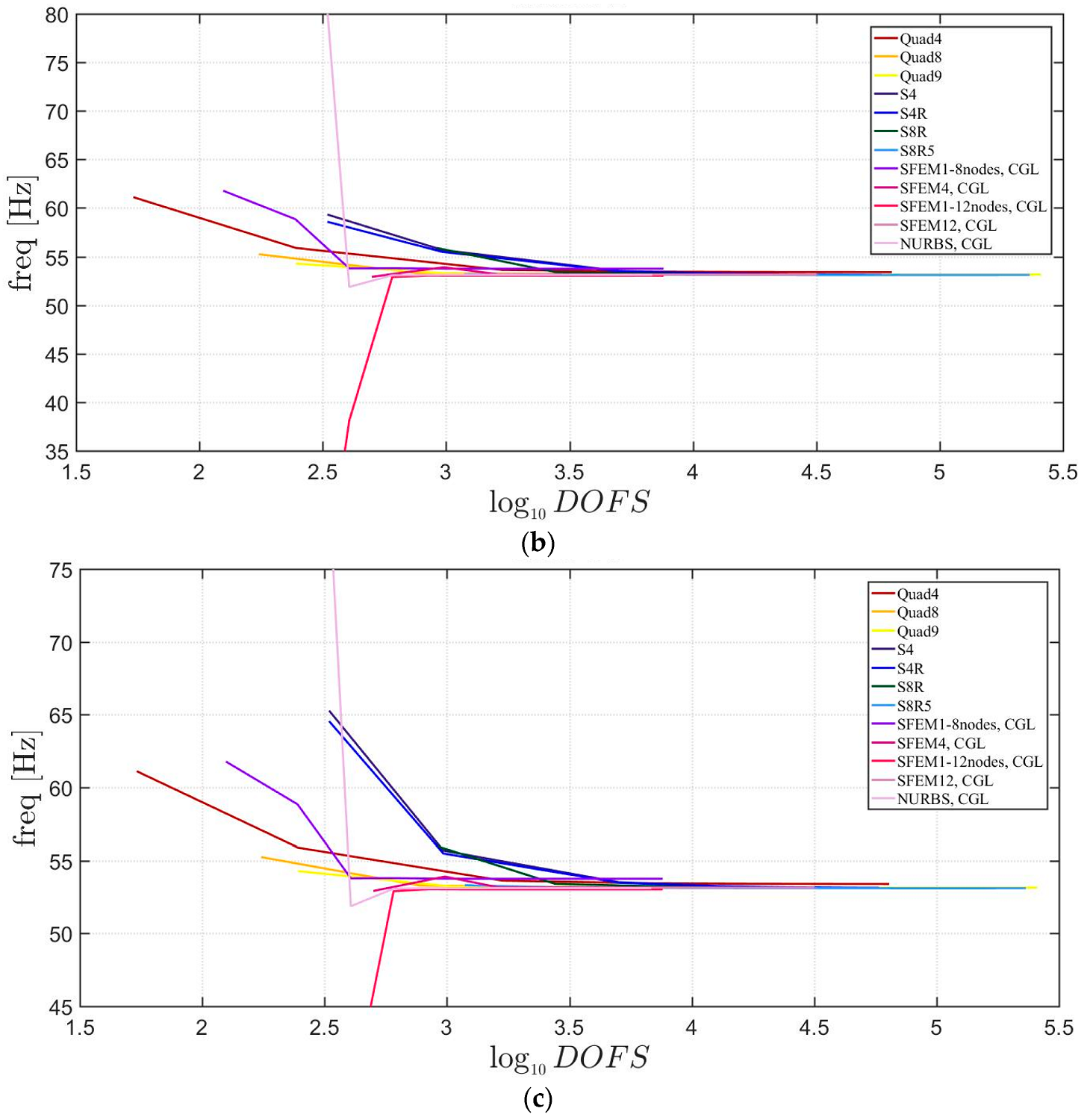
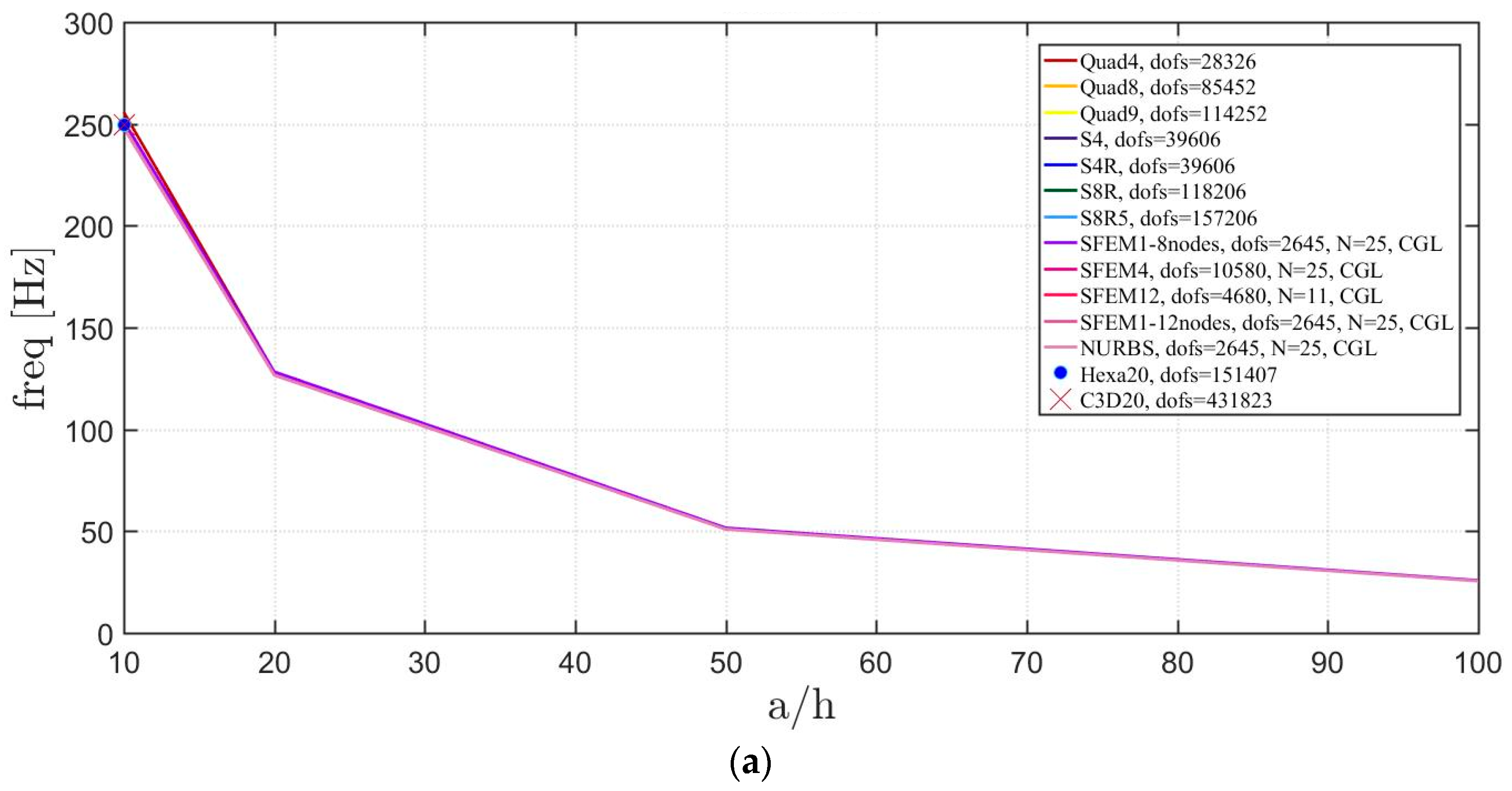
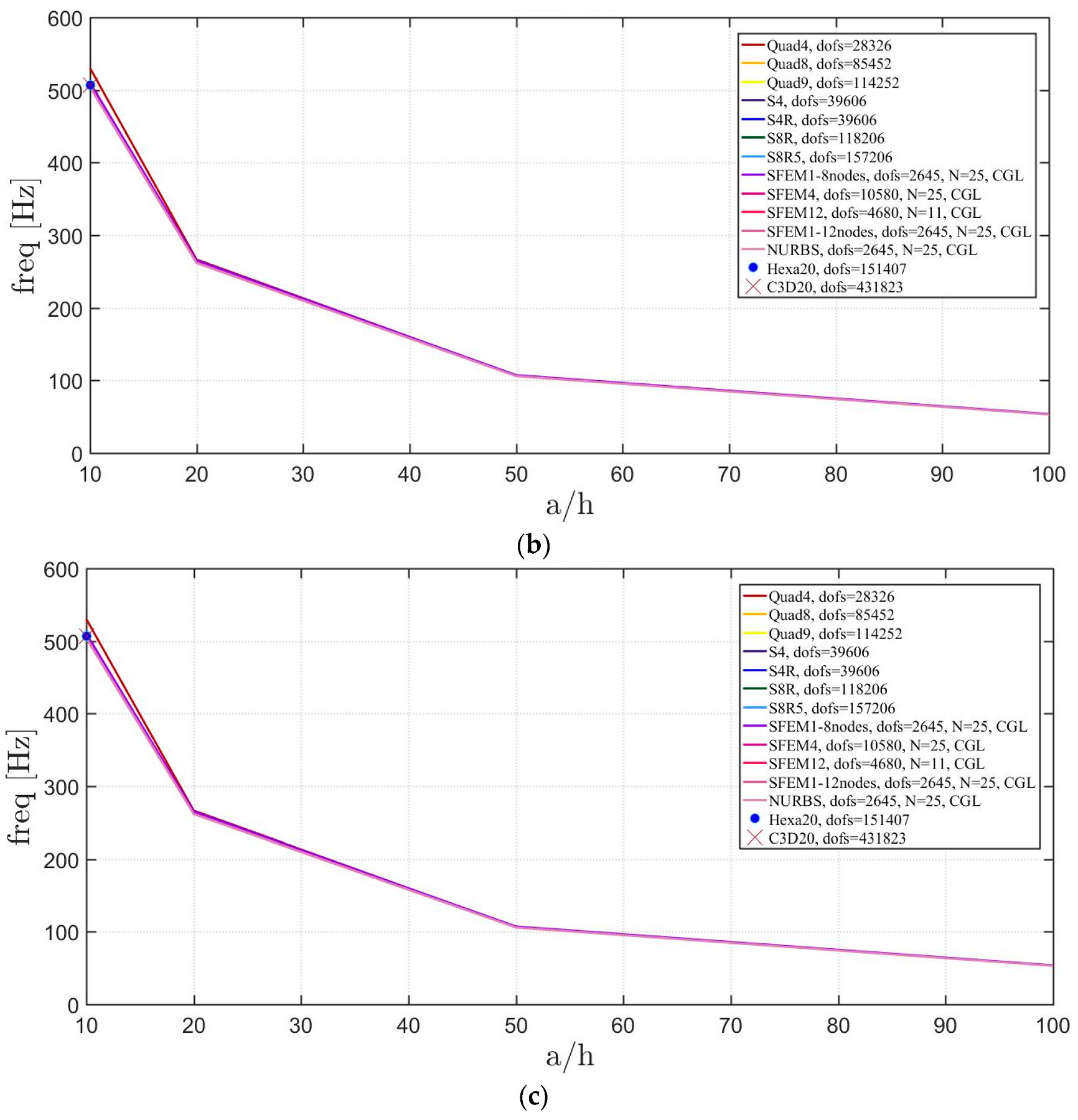
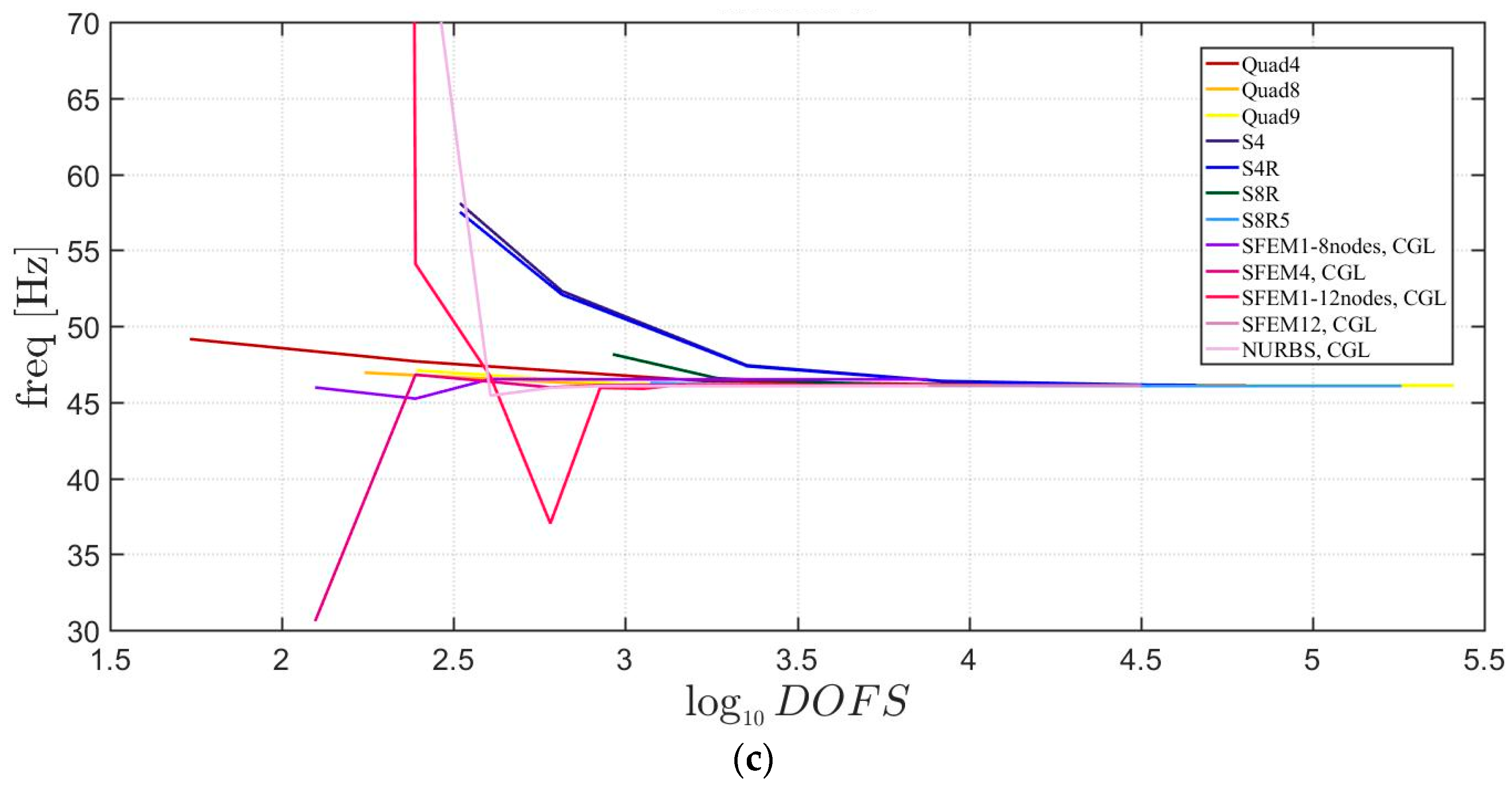
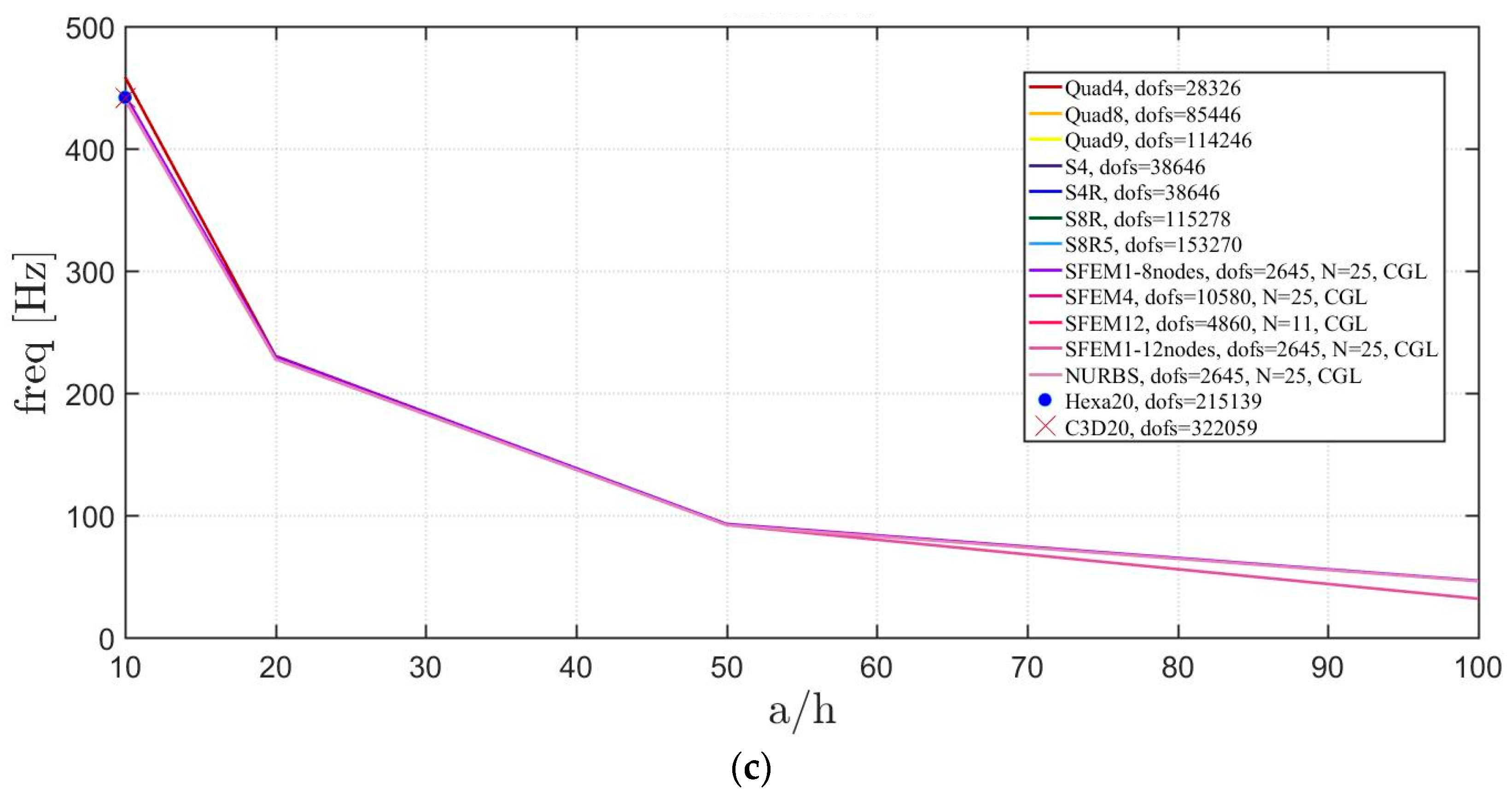
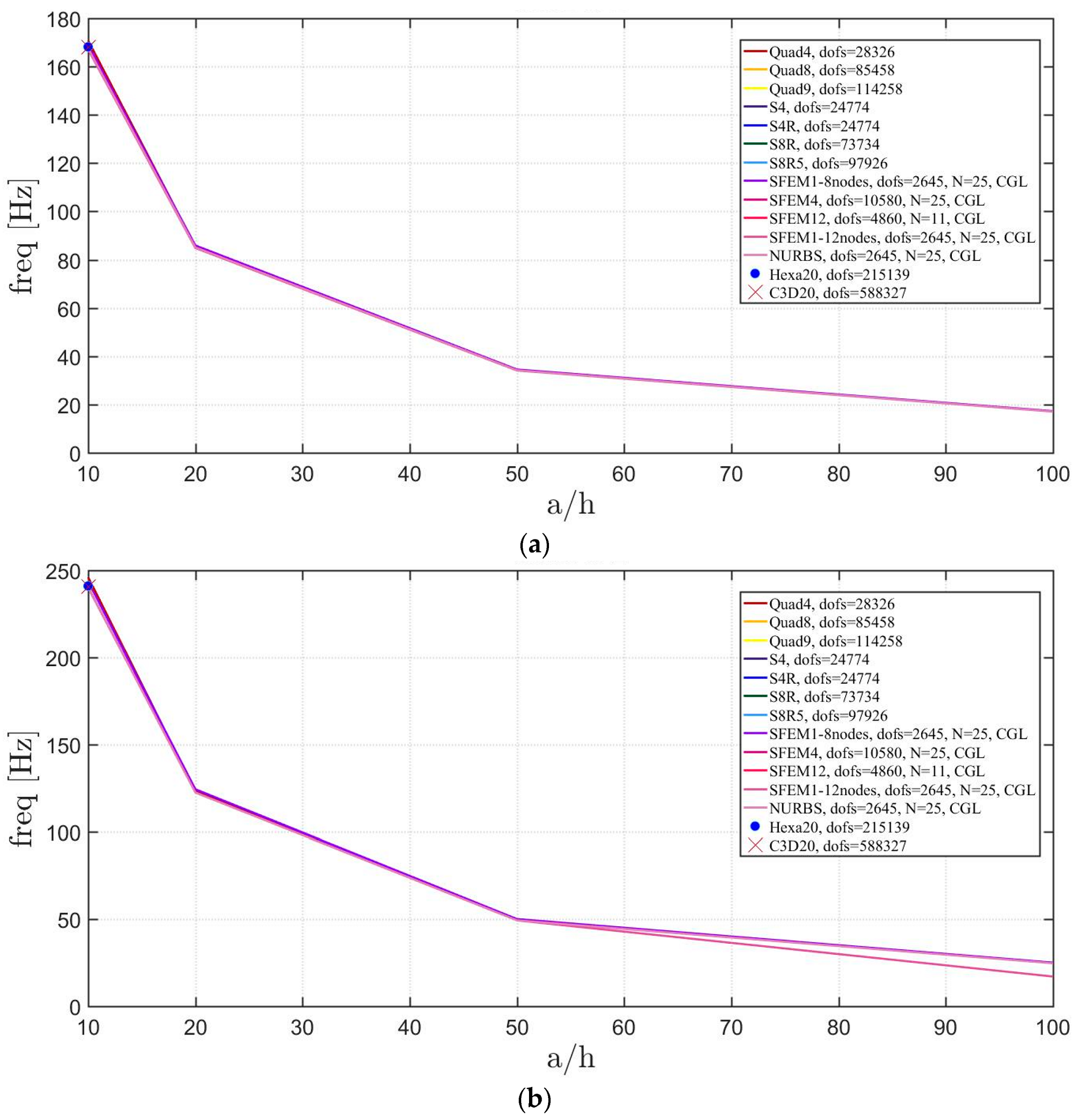
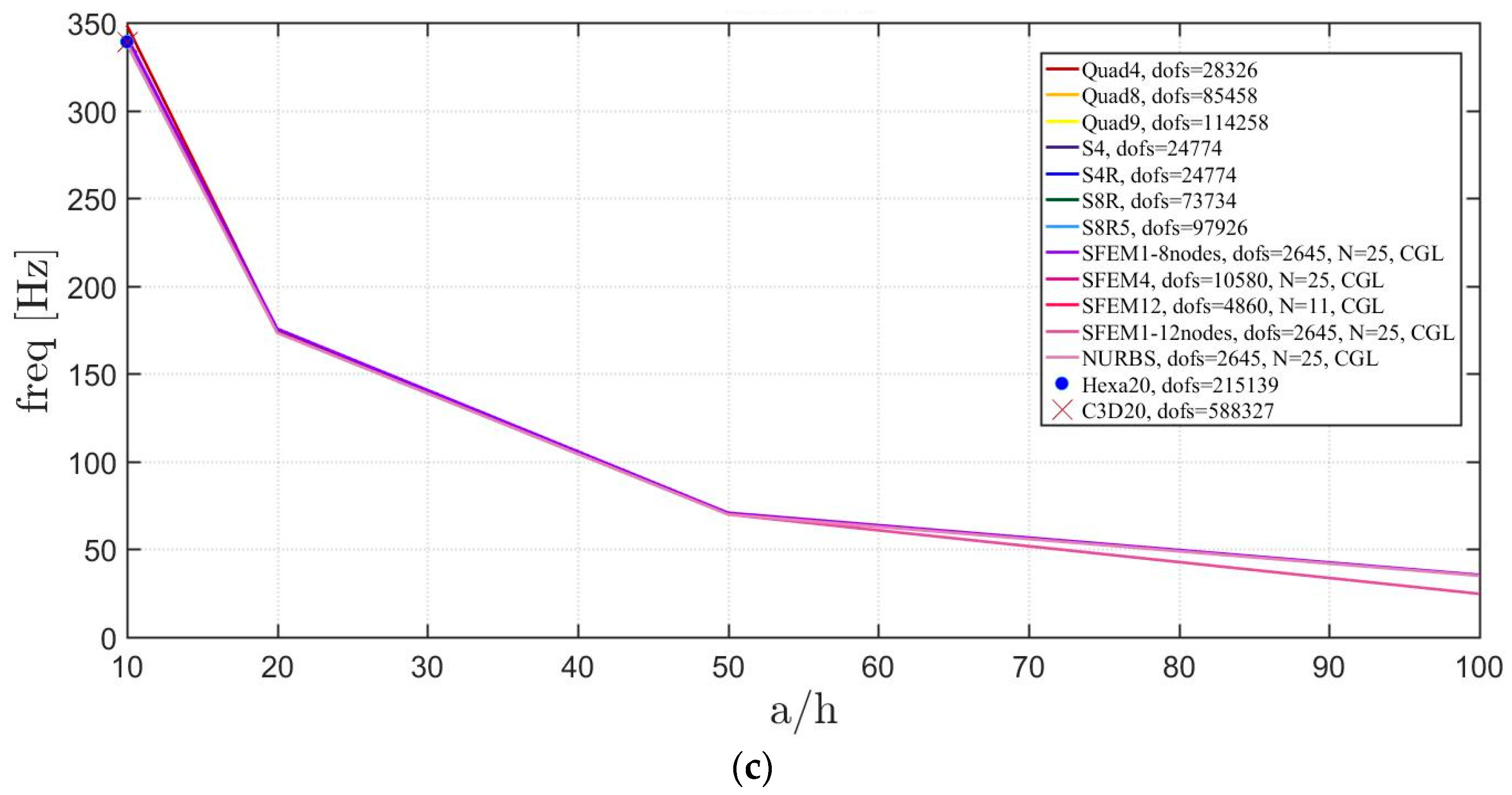
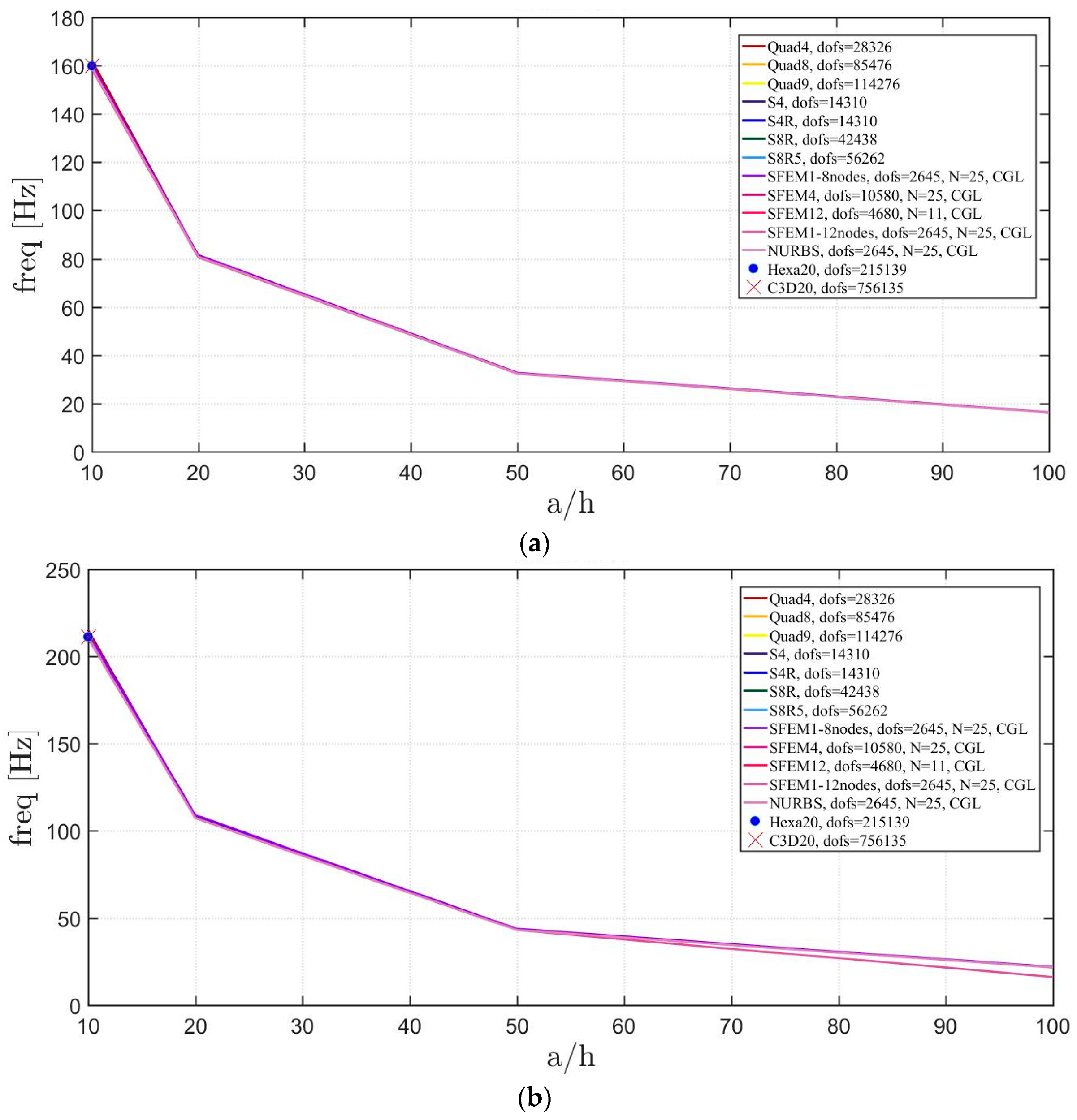
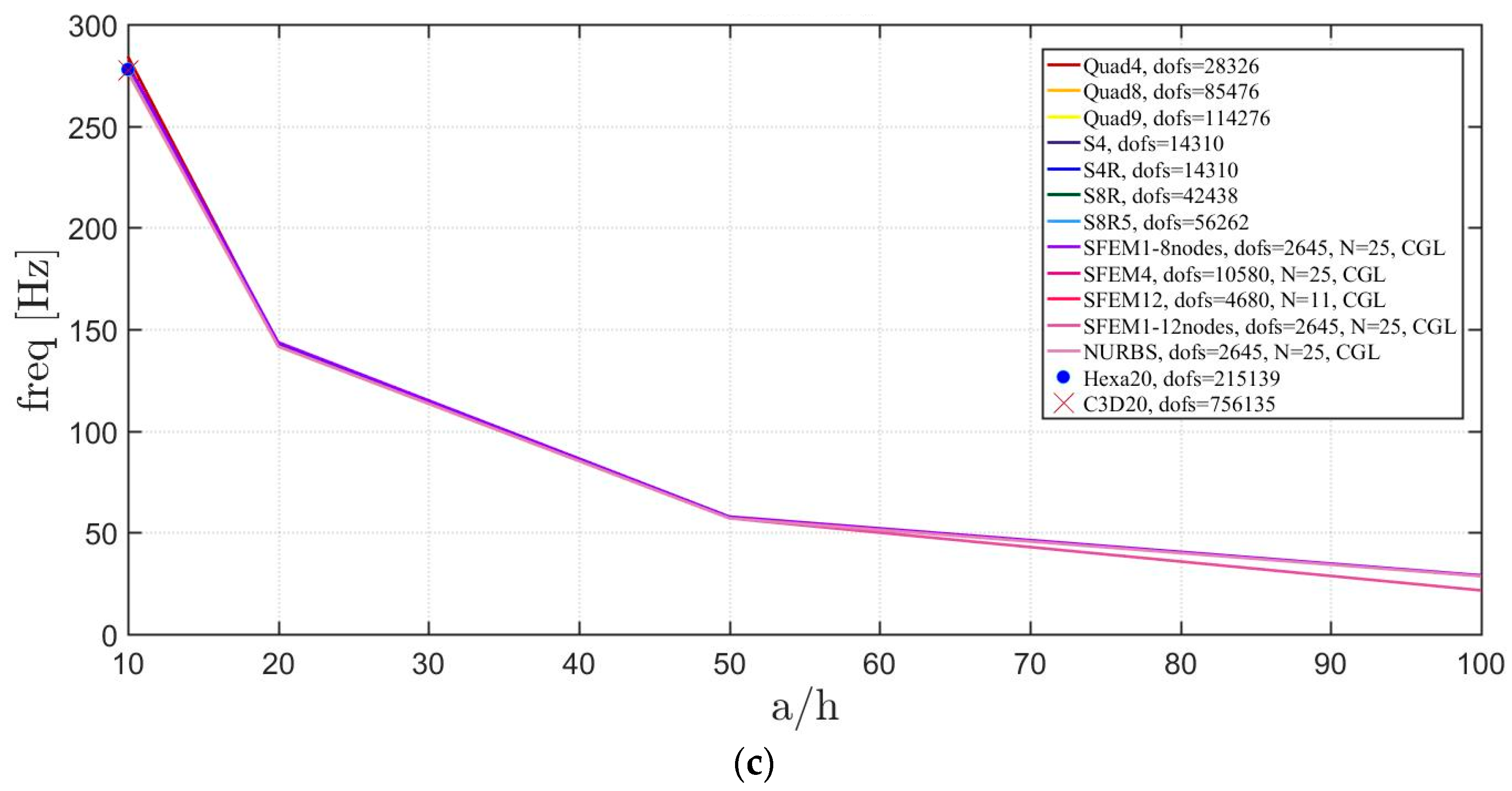
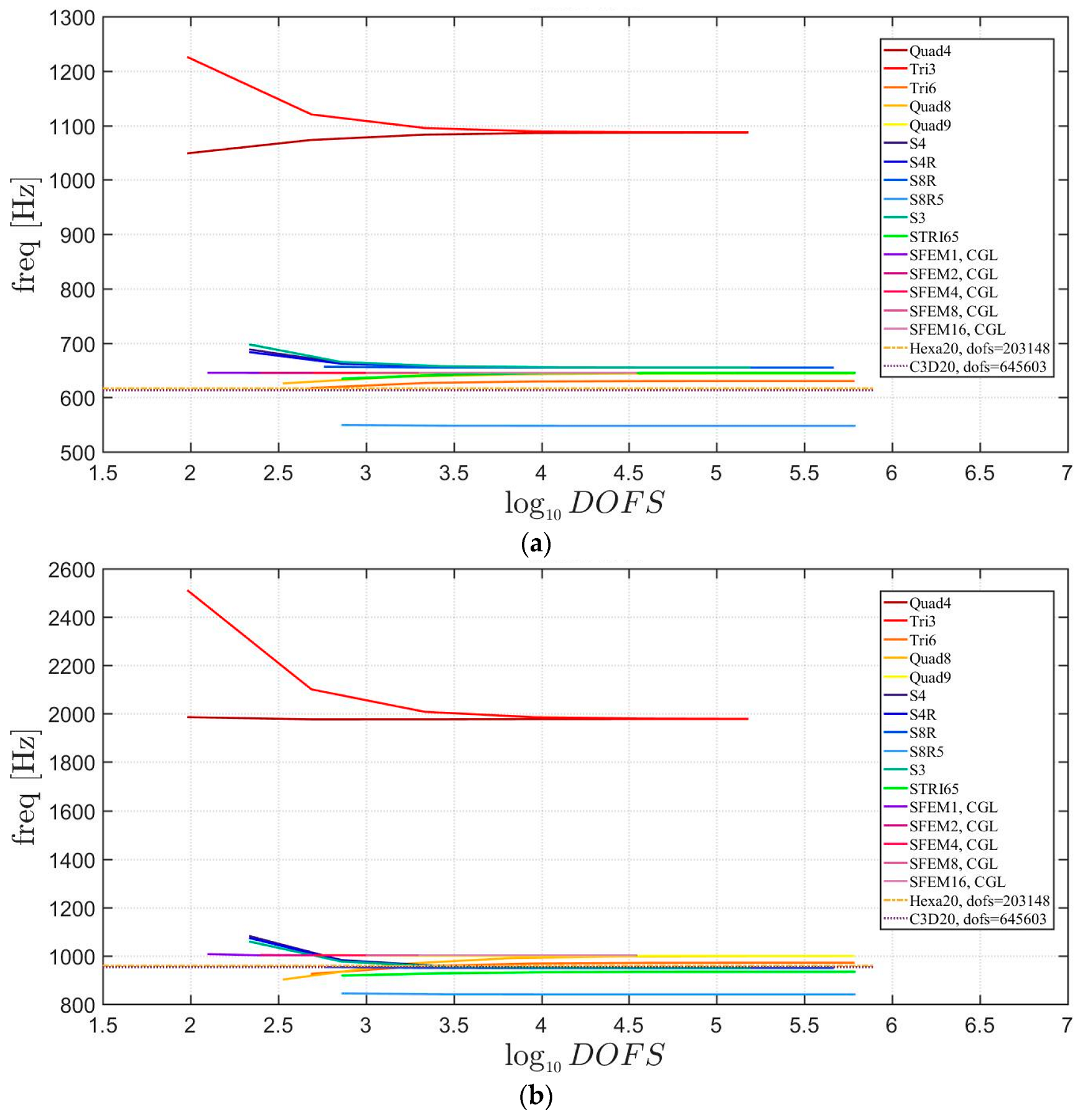
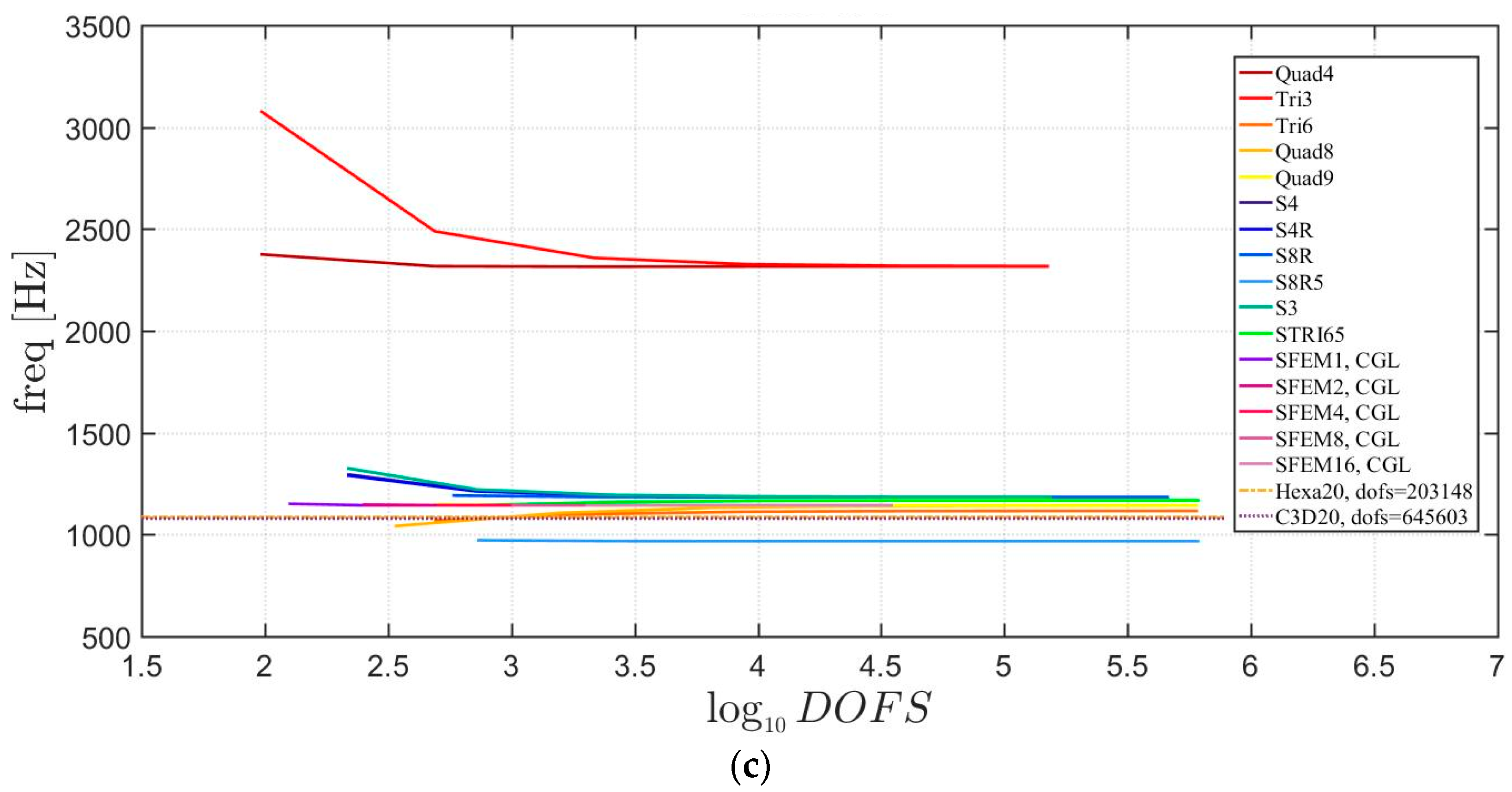
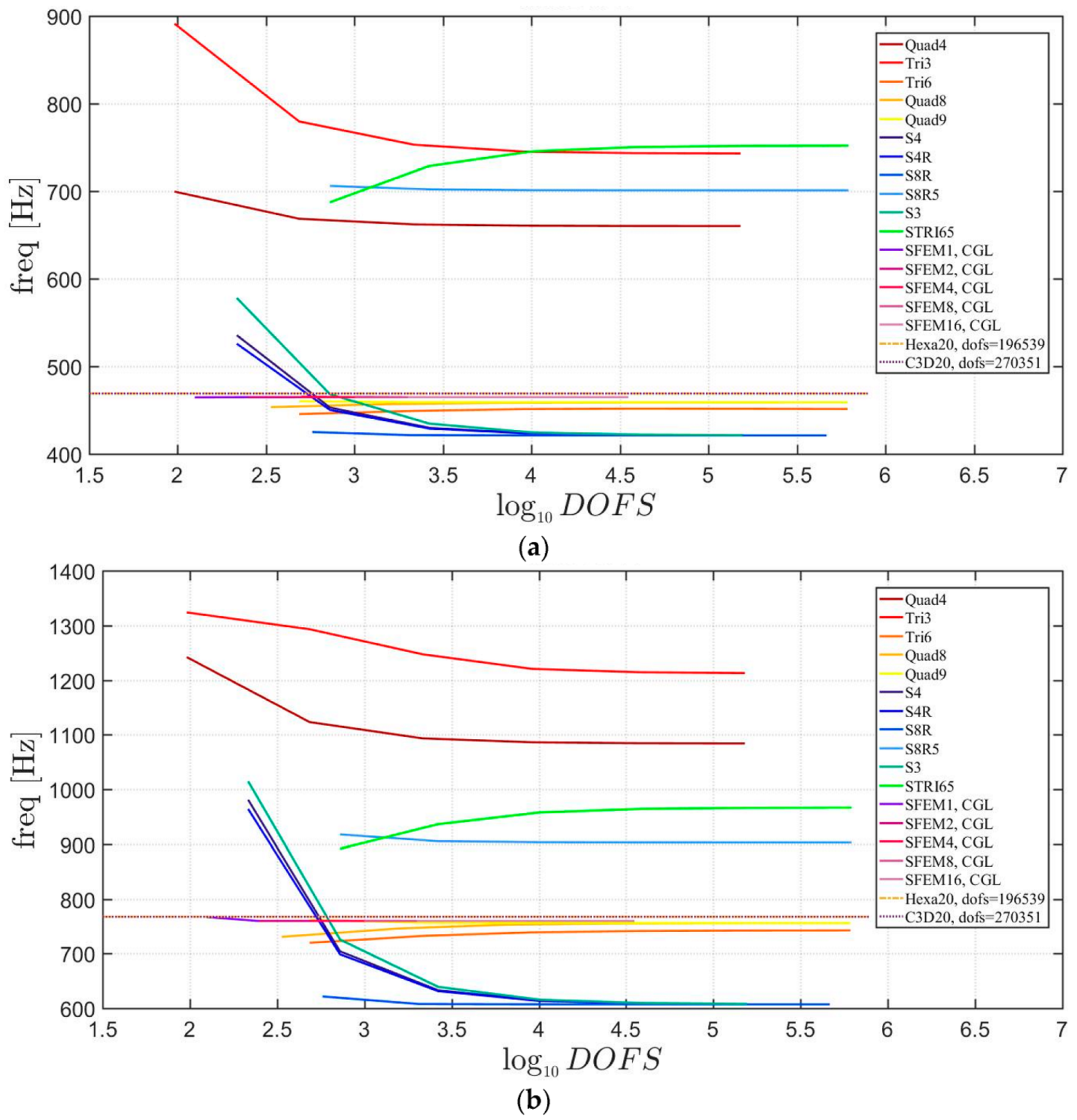
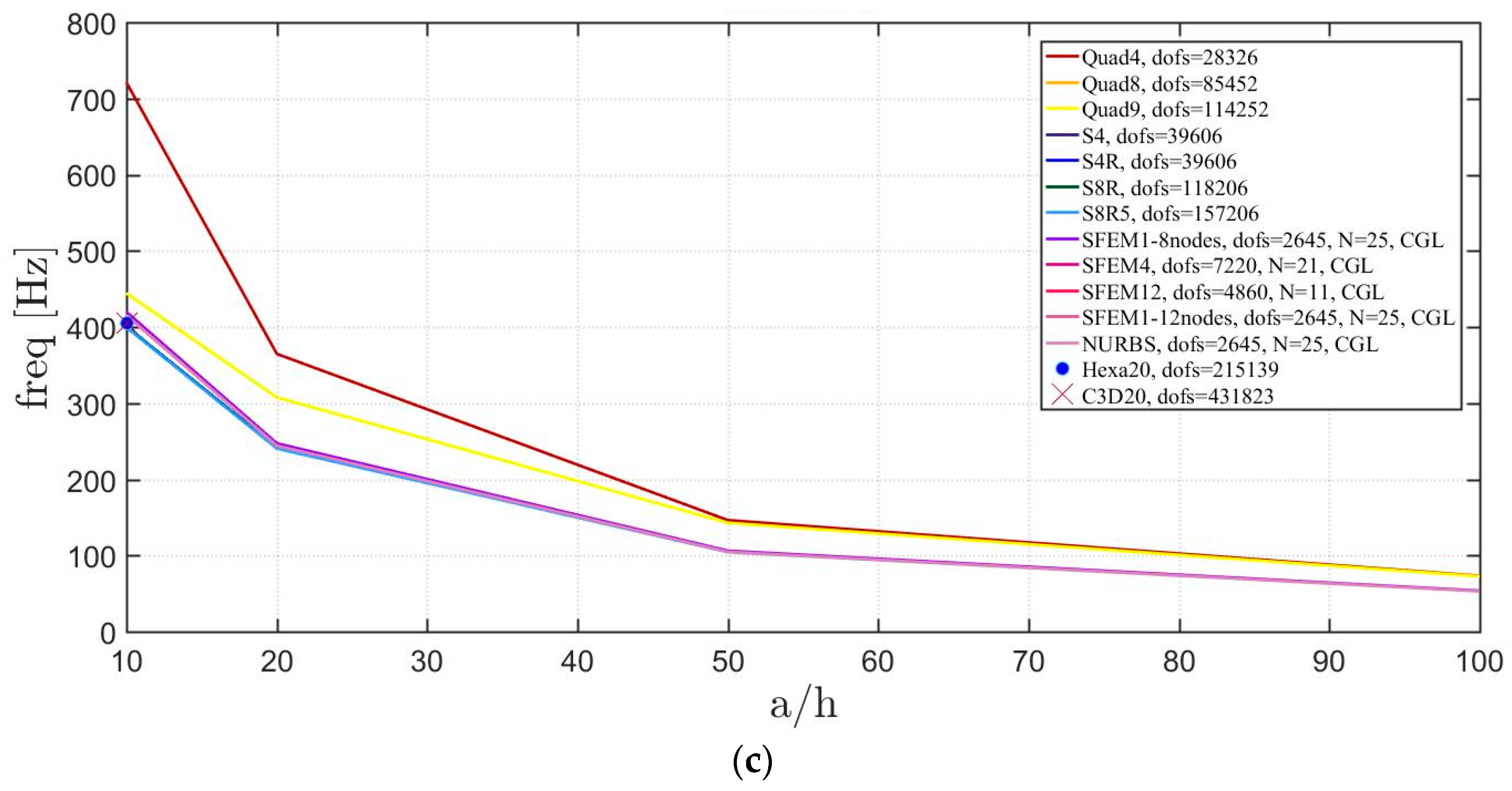
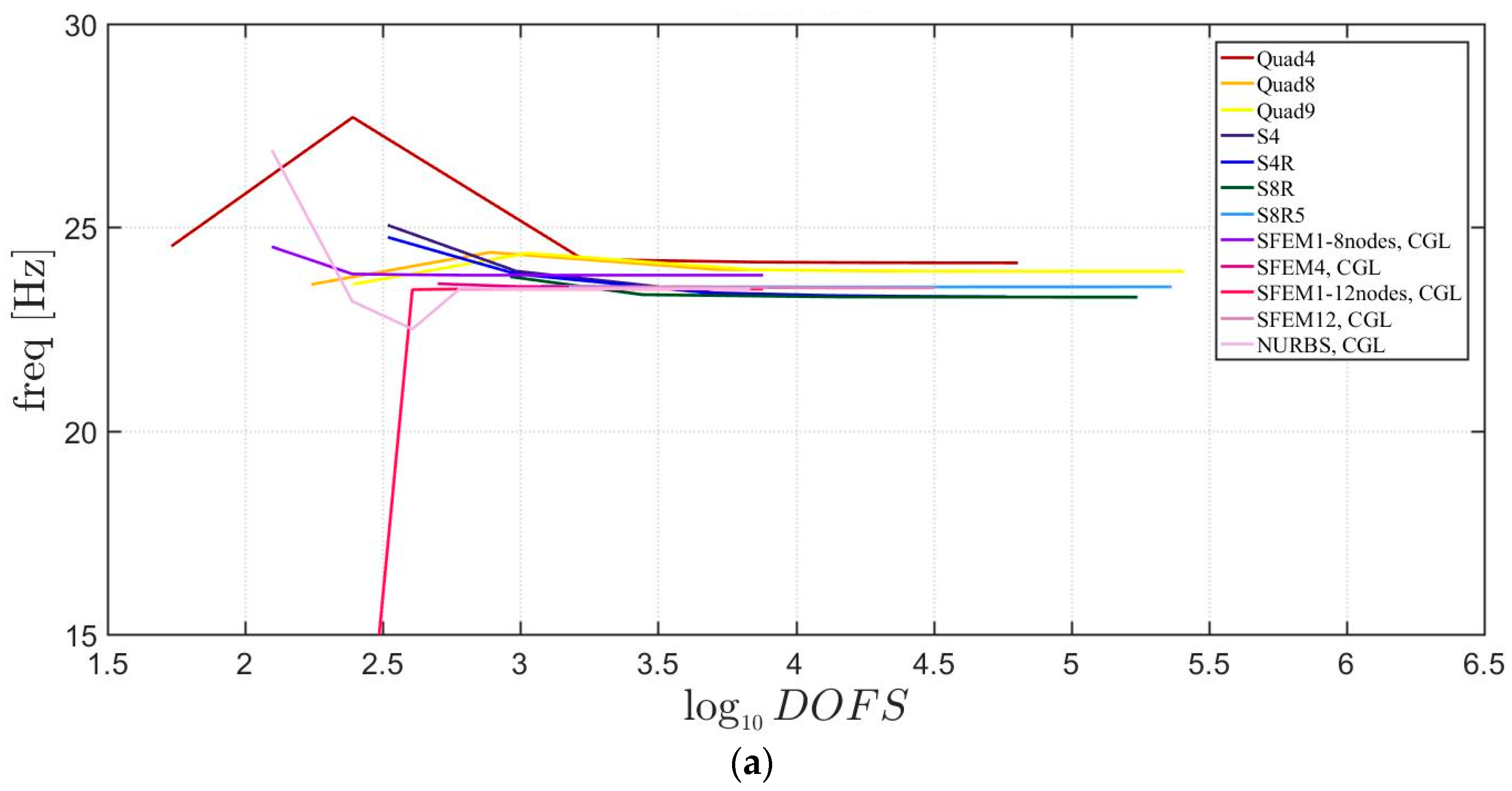
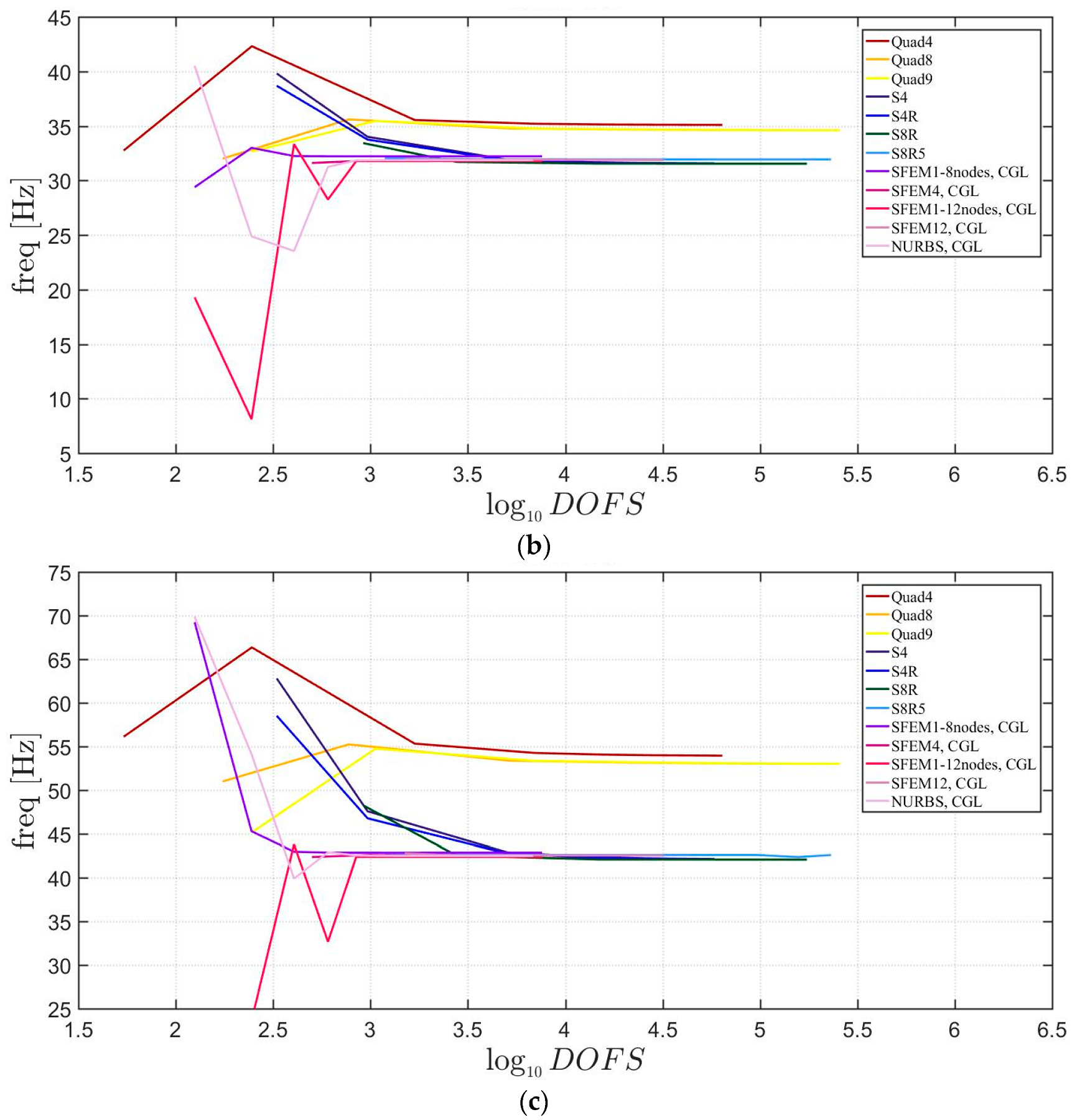
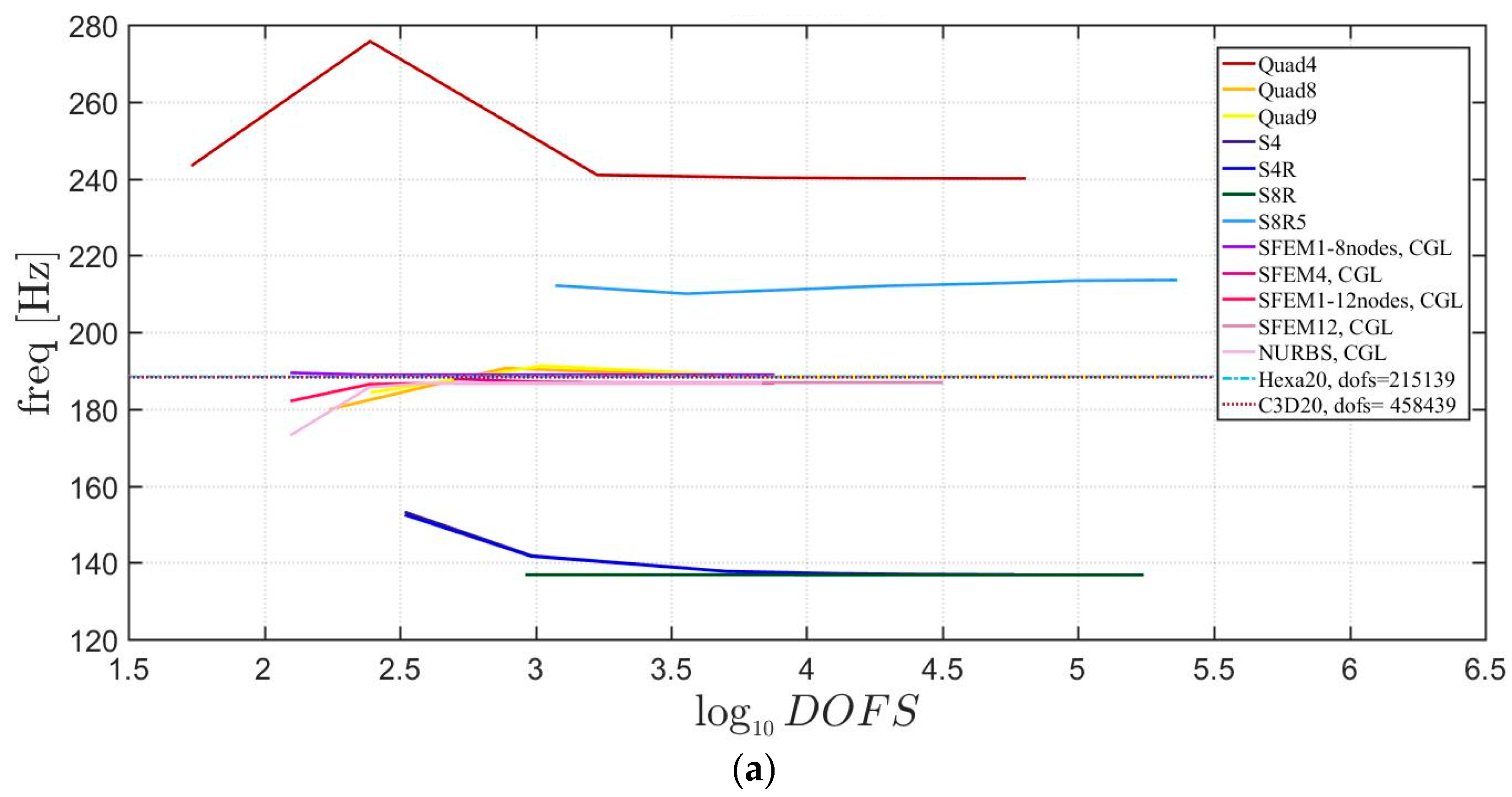
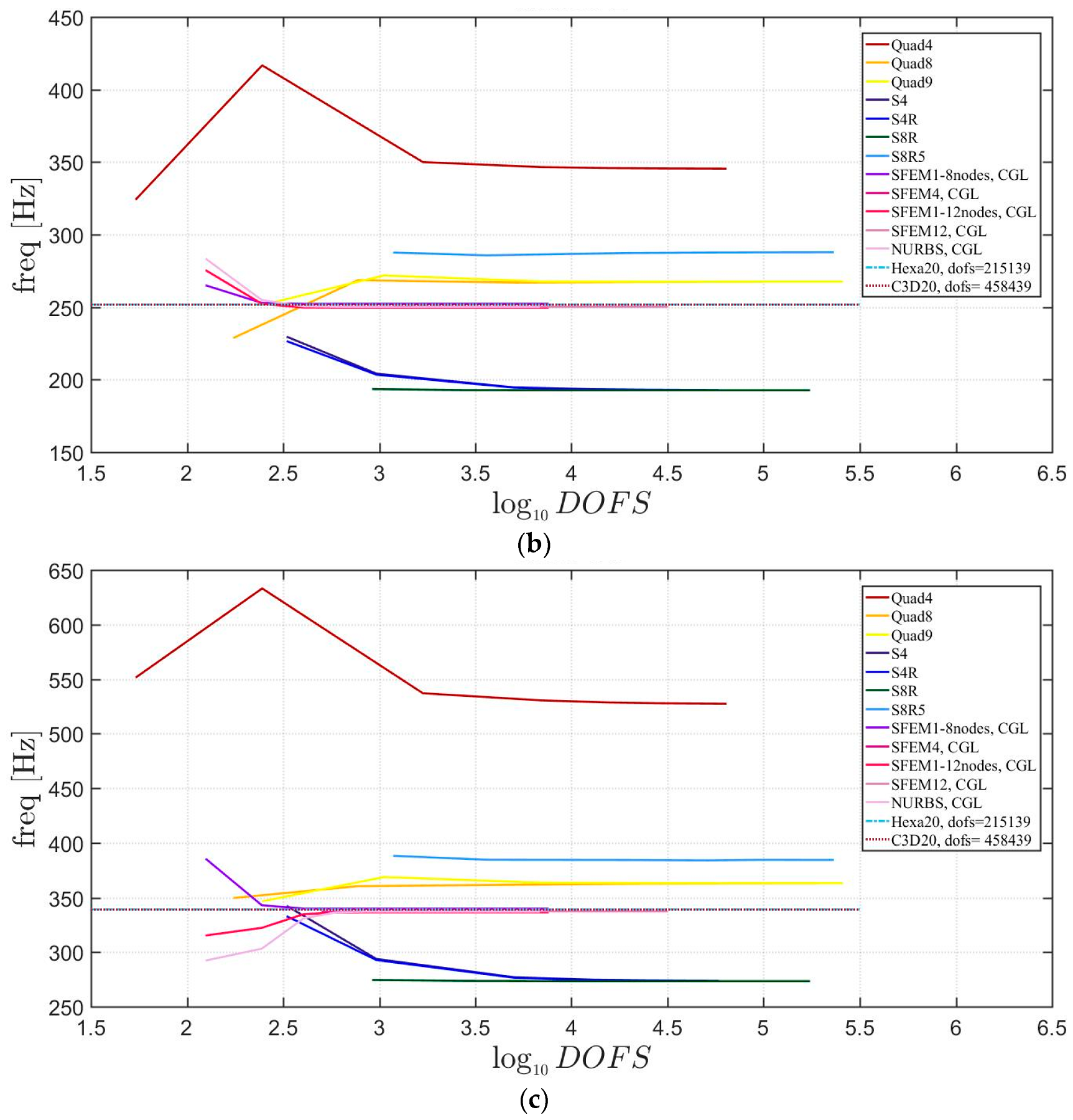
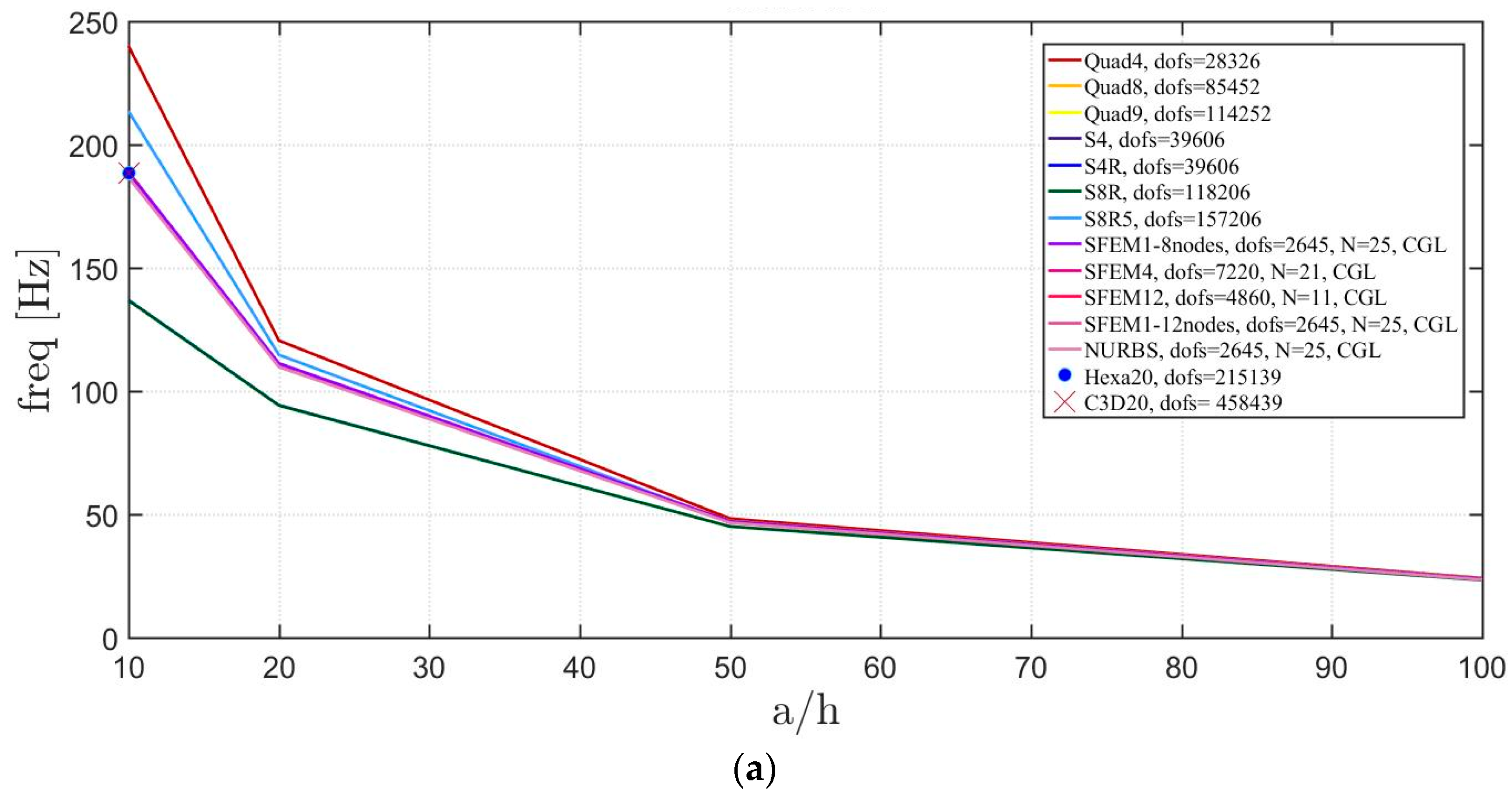
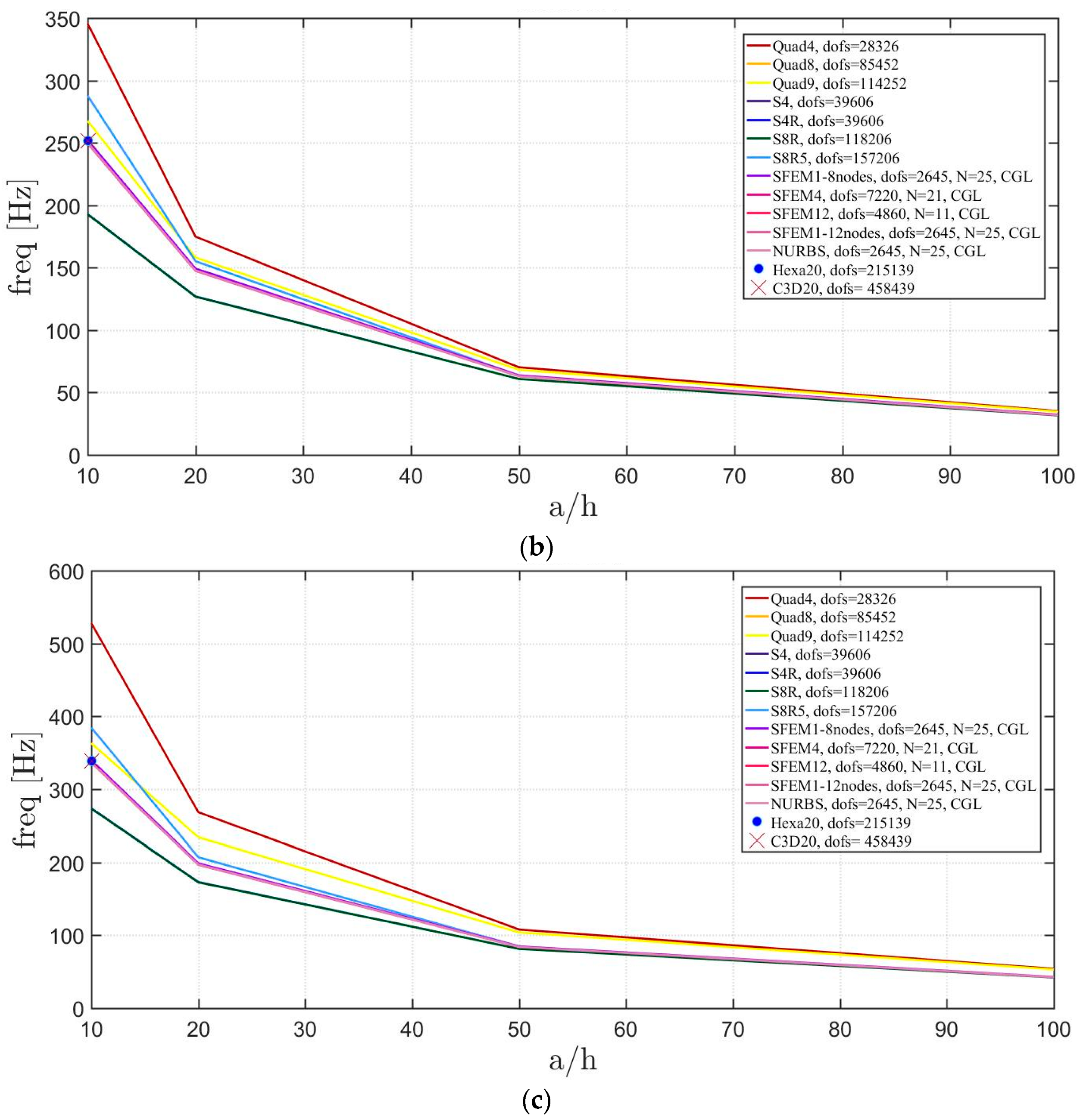
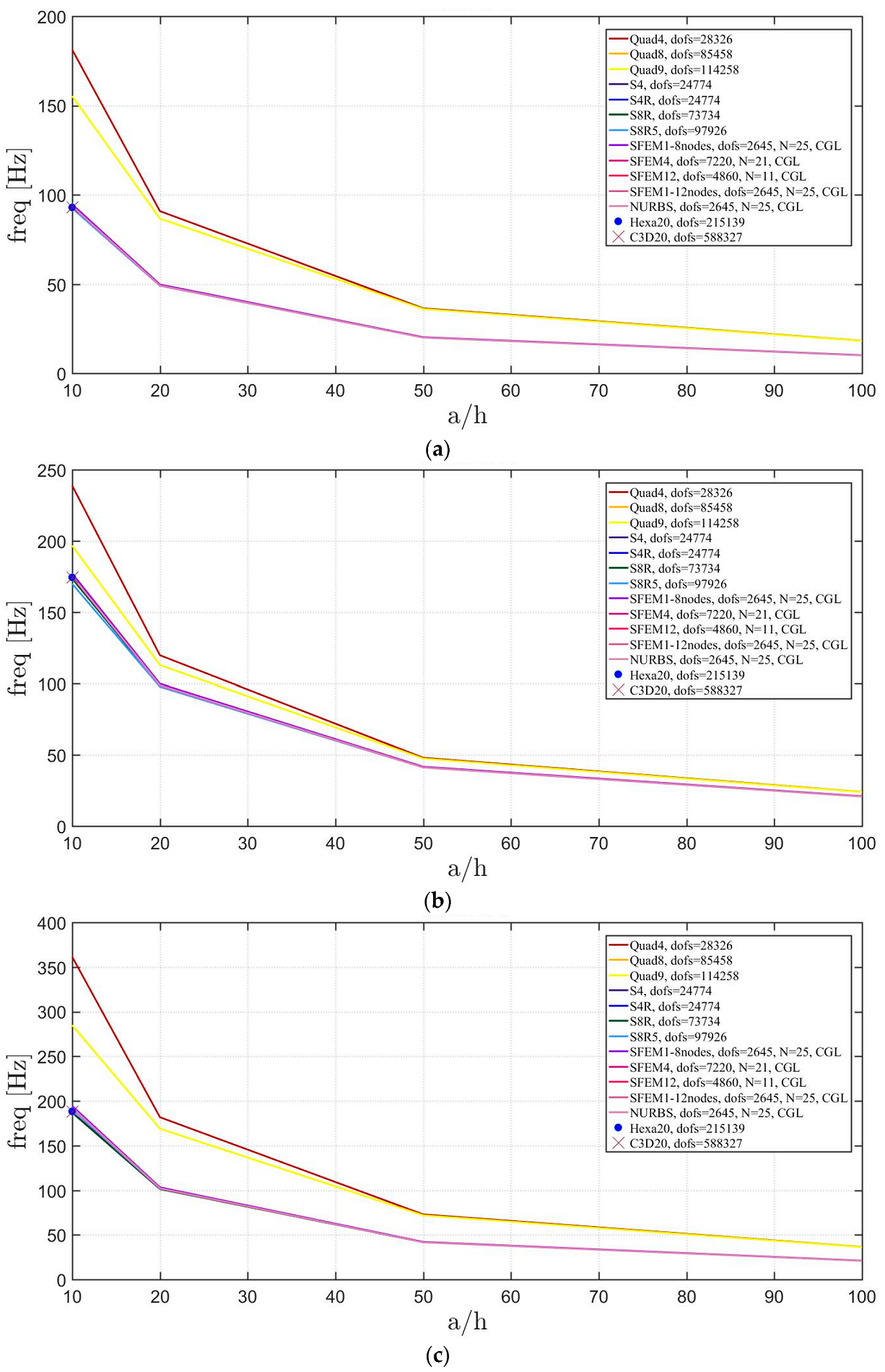
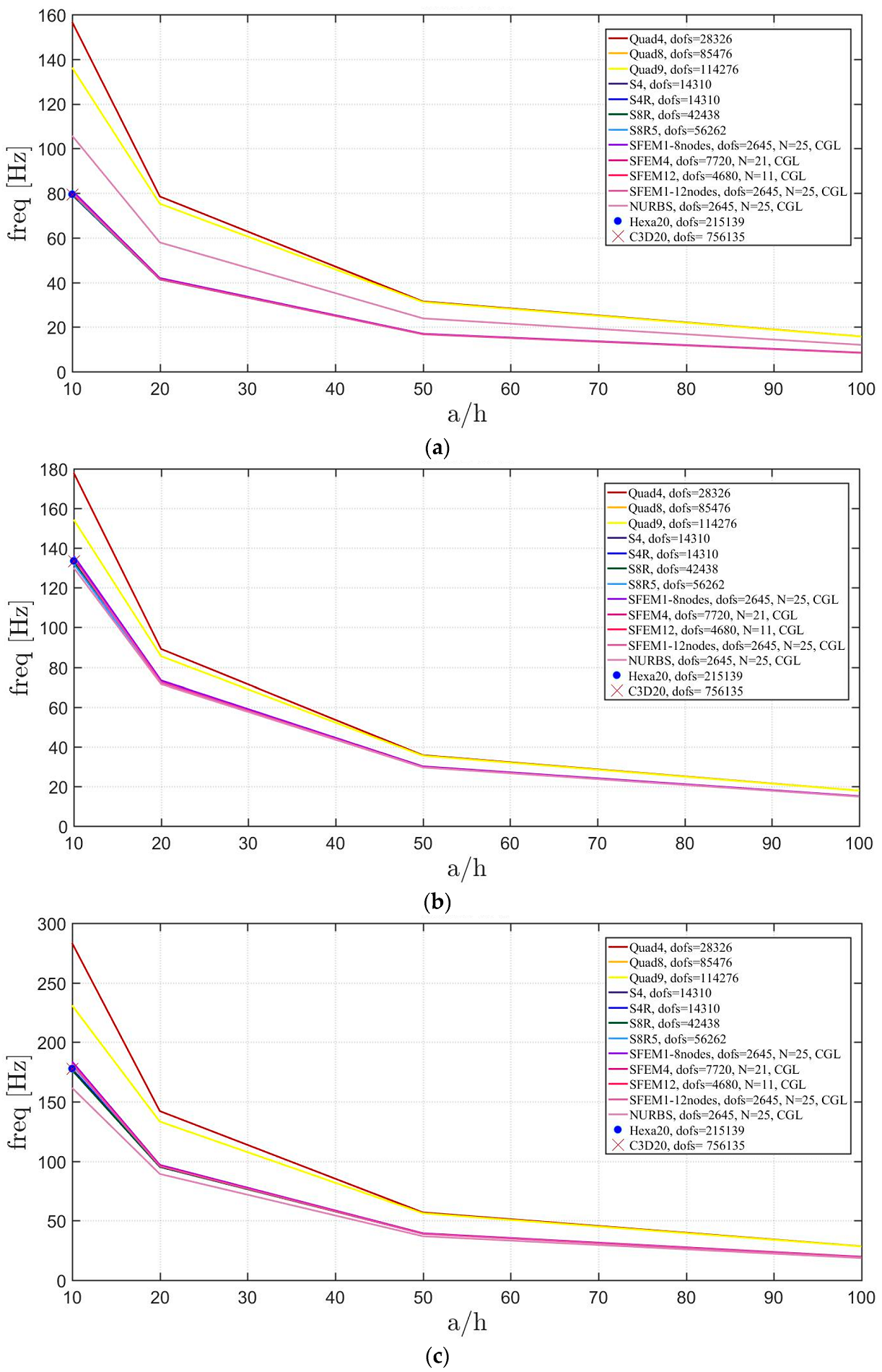
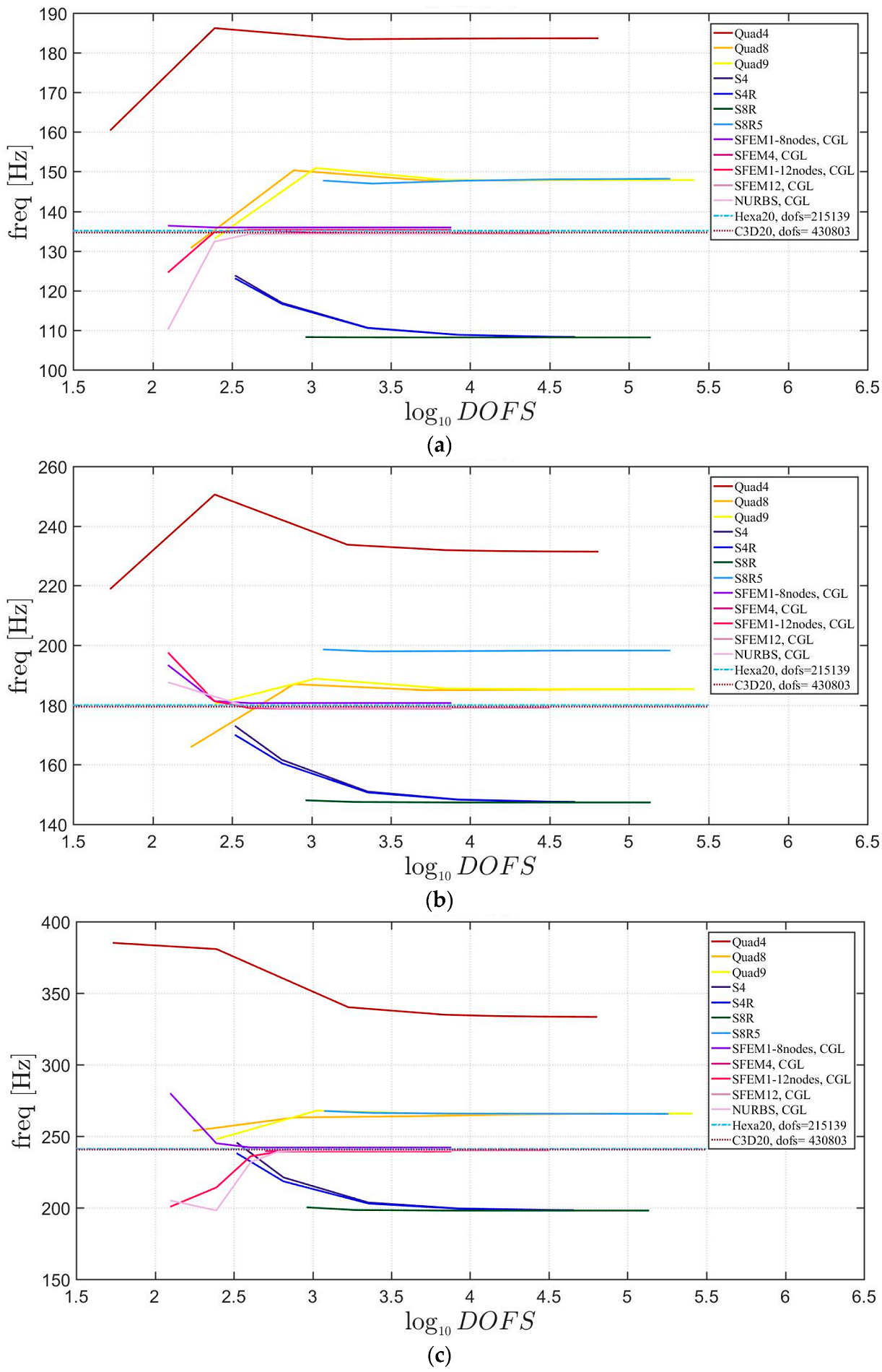
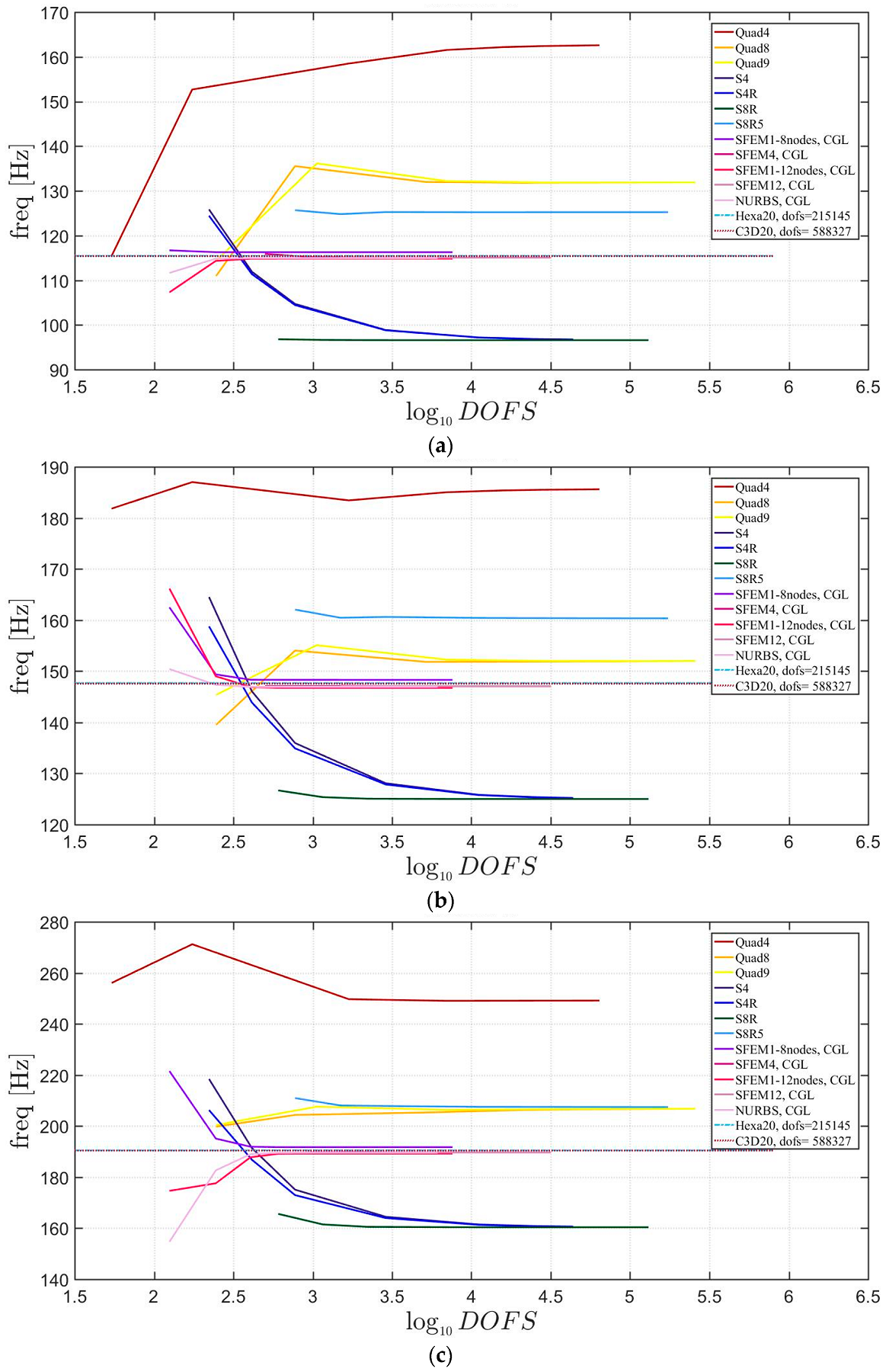
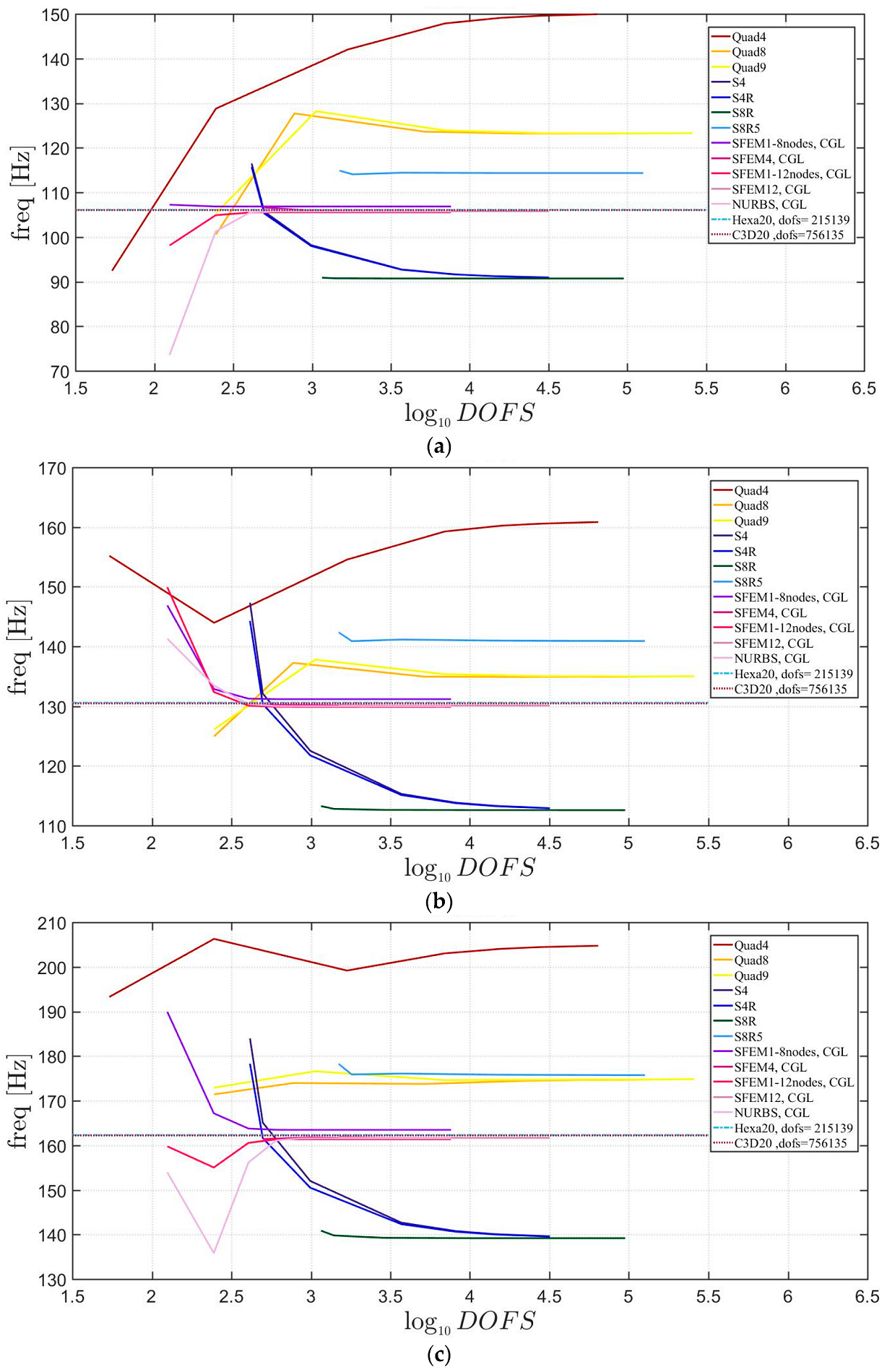
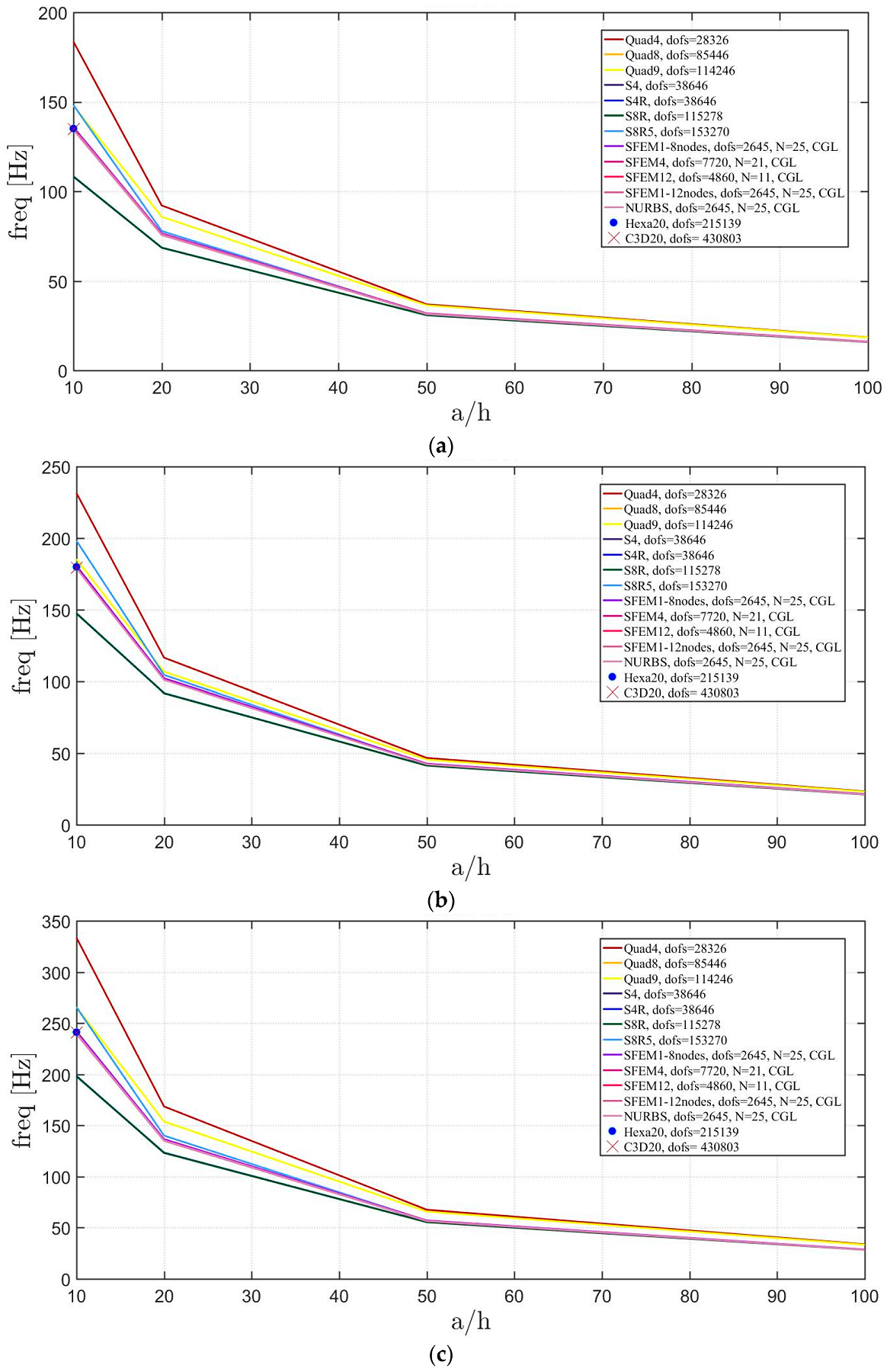
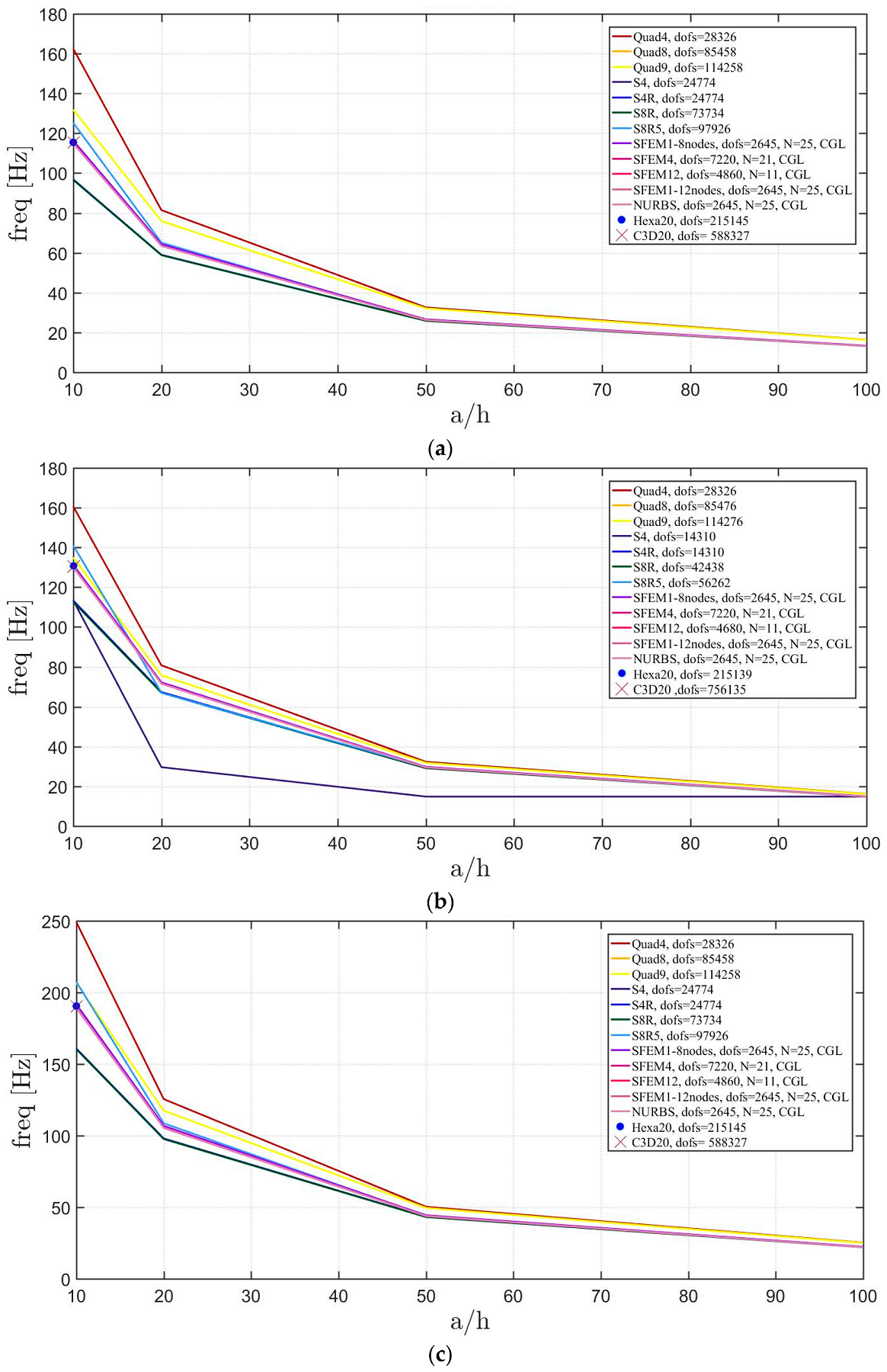
4. Applications
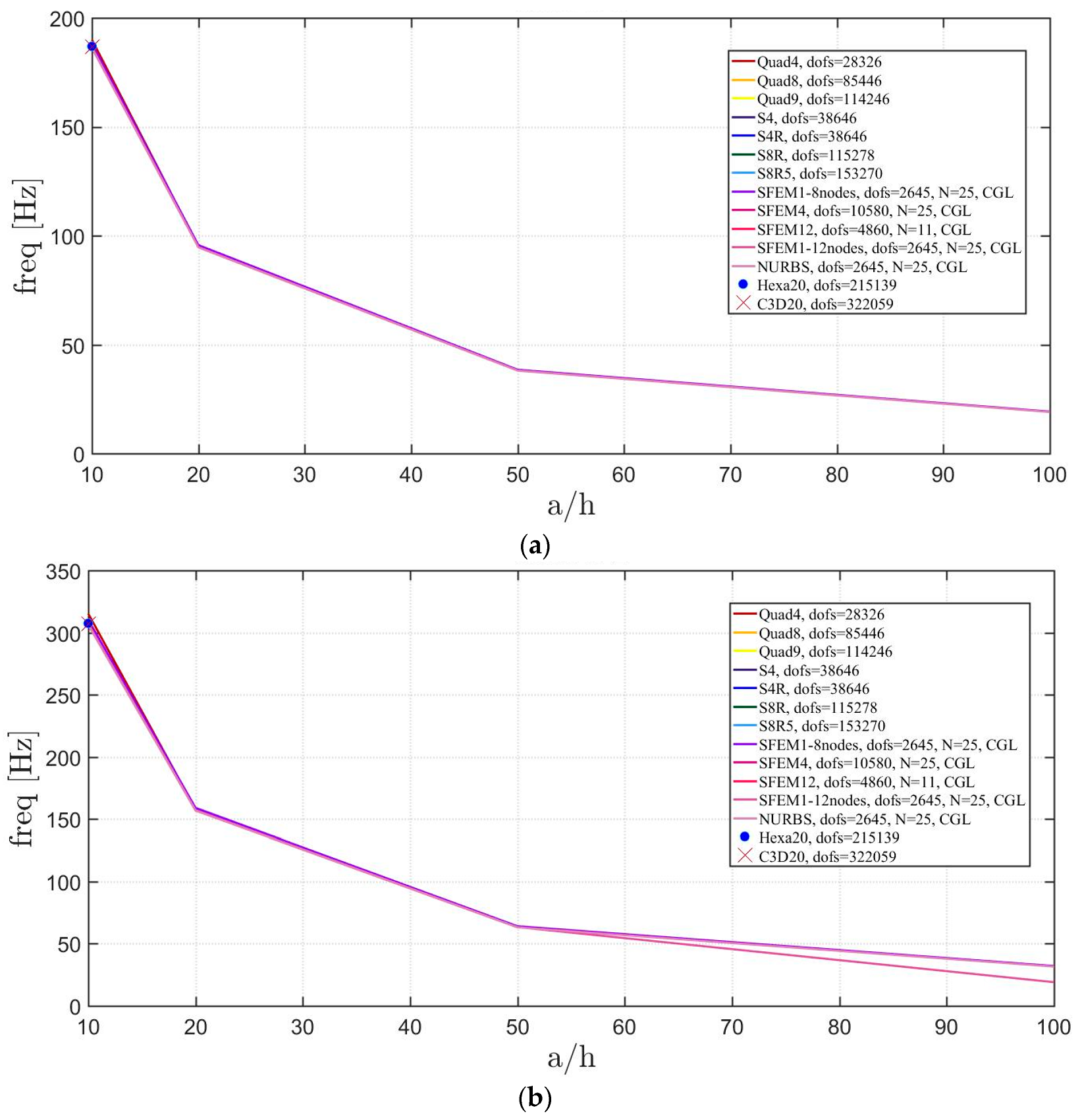
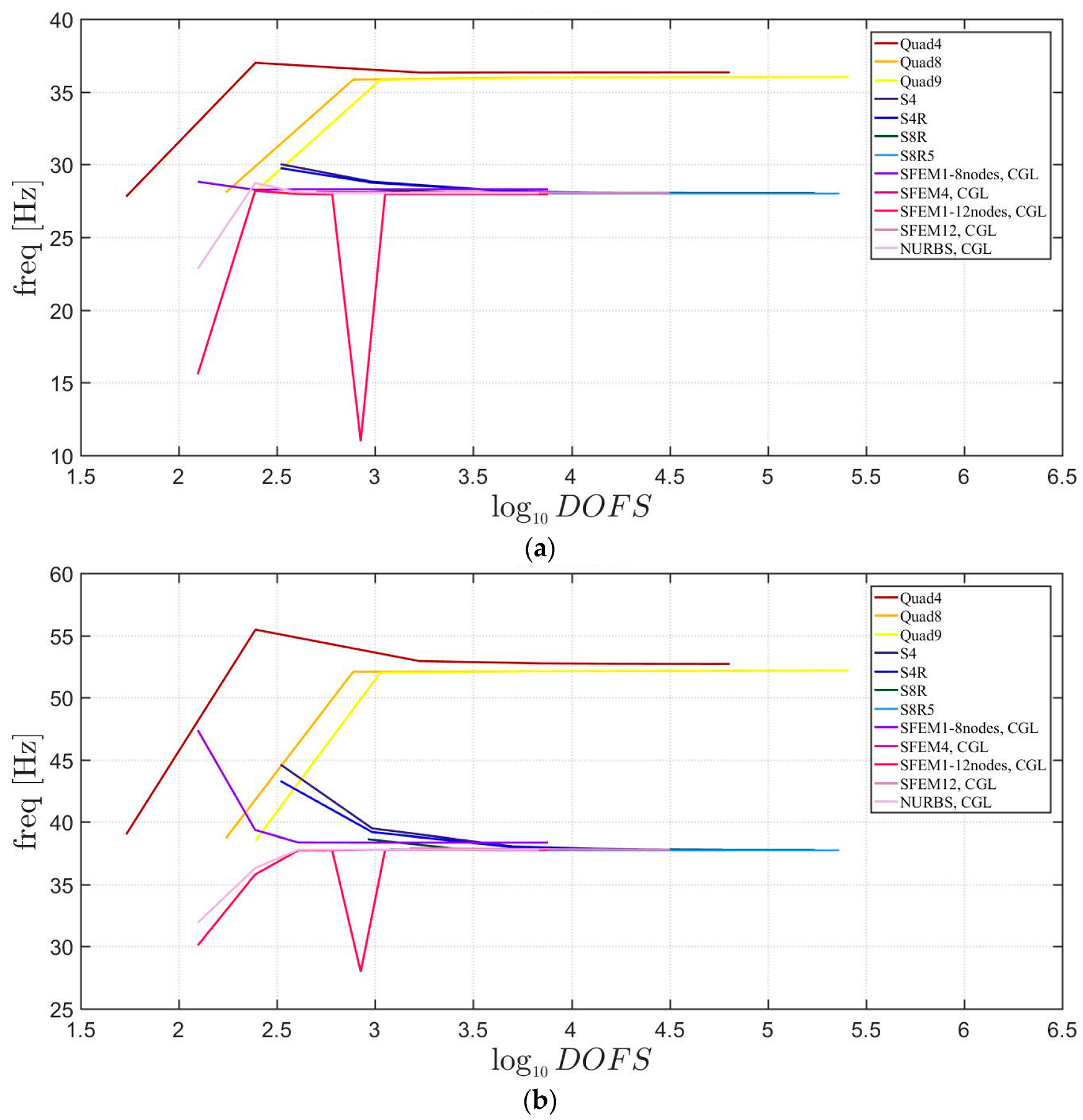
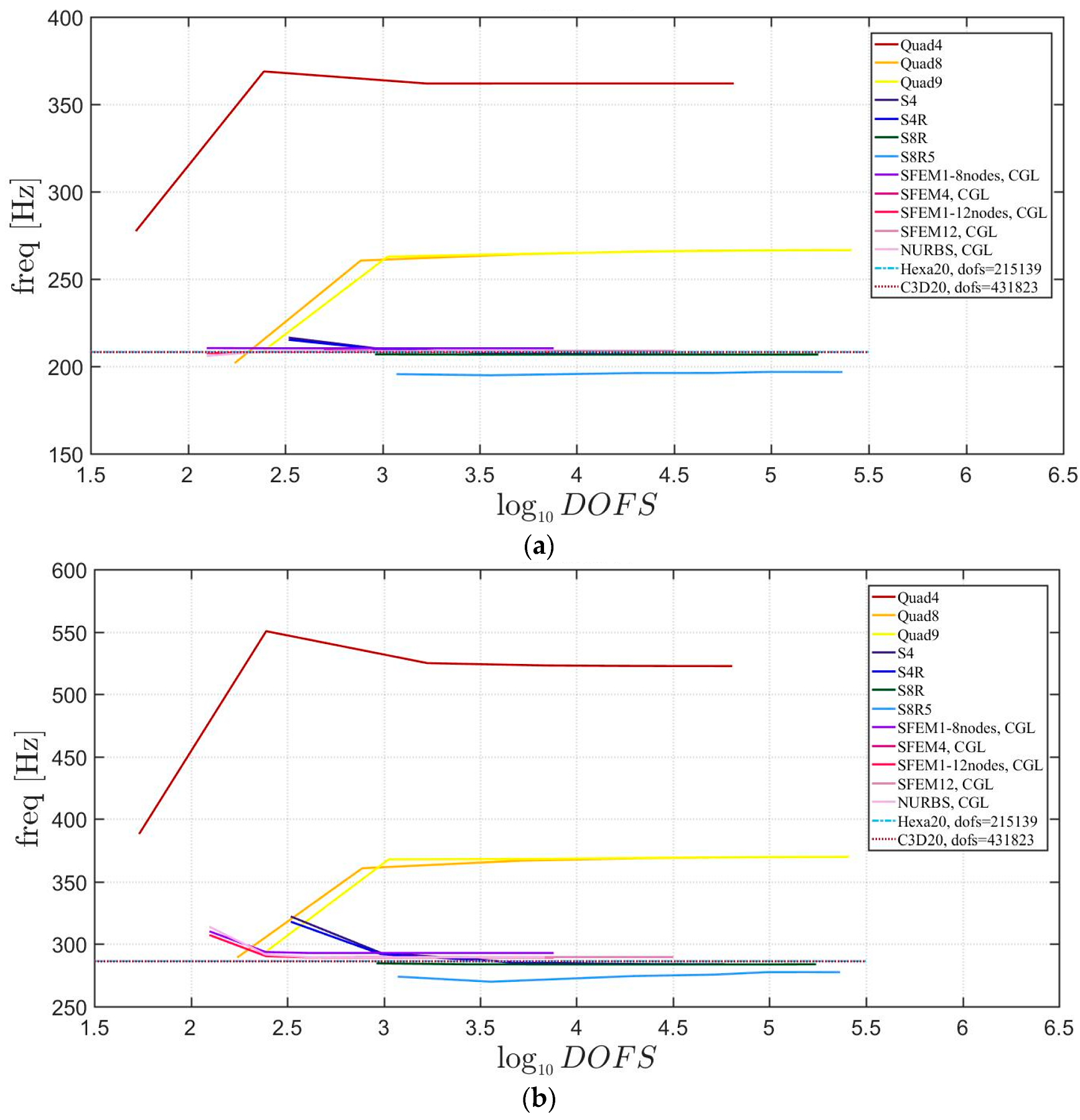
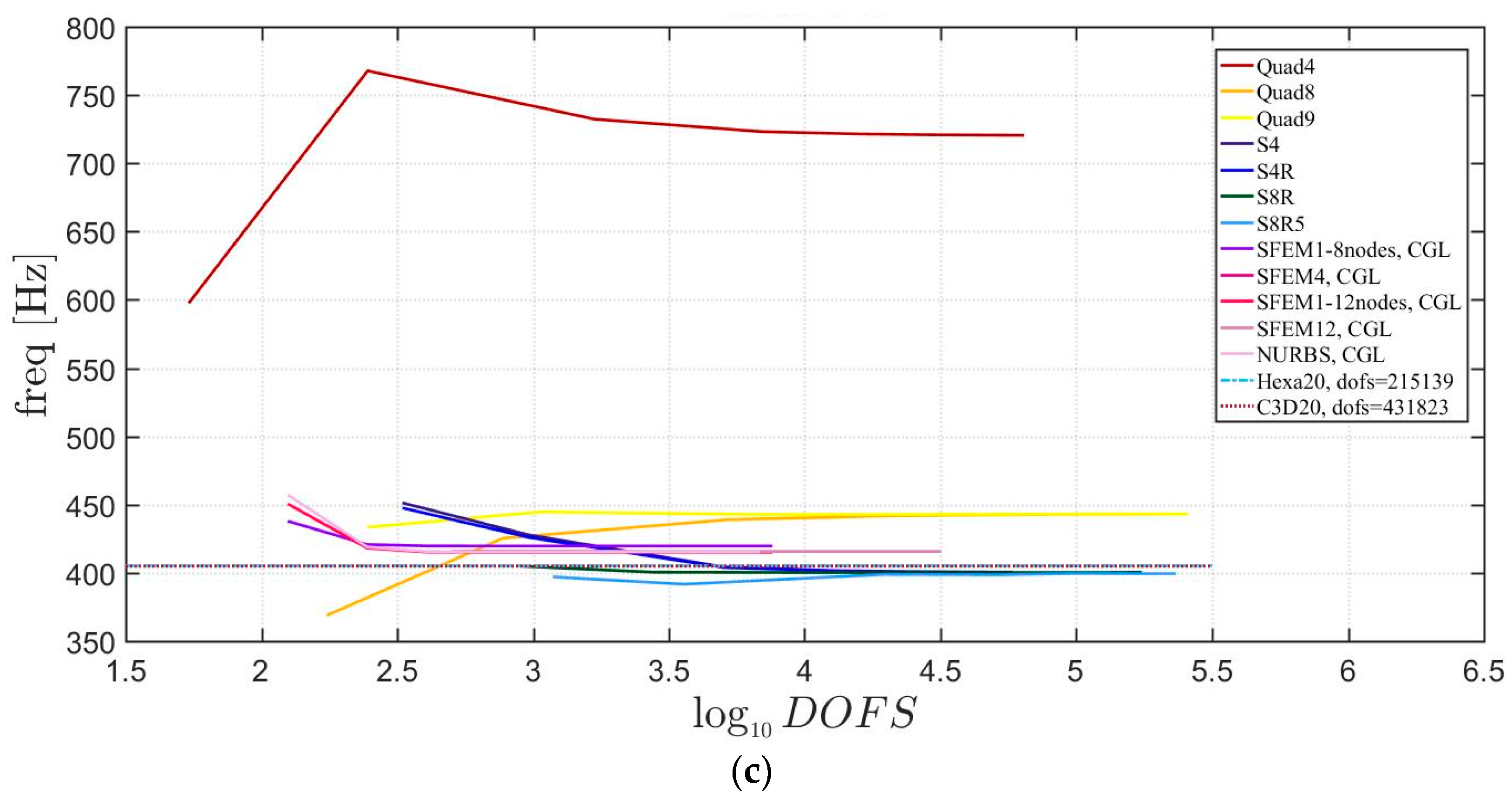
4.1. Isotropic Materials
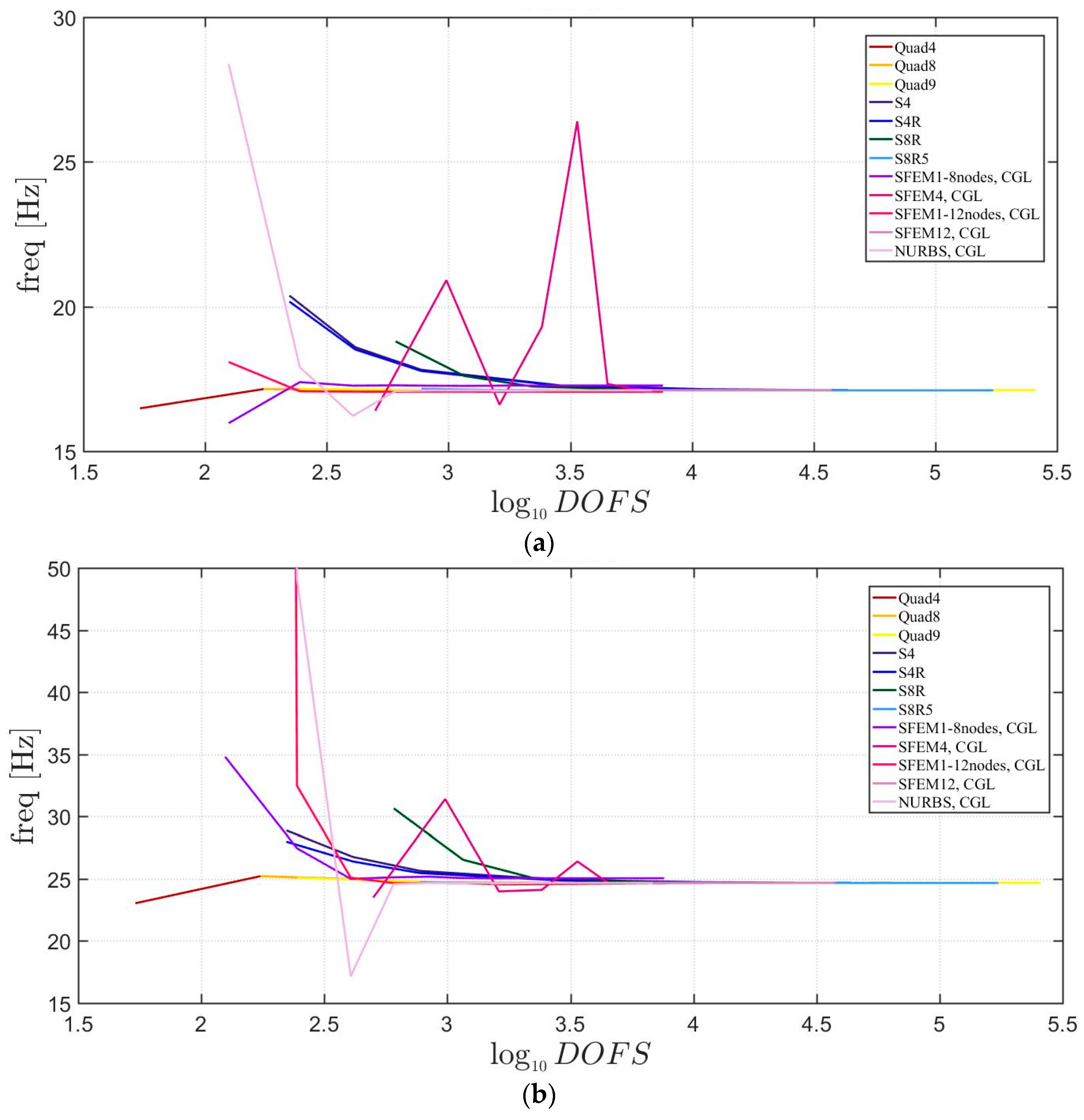
4.1.1. Skew Plates with 30° Skew Angle
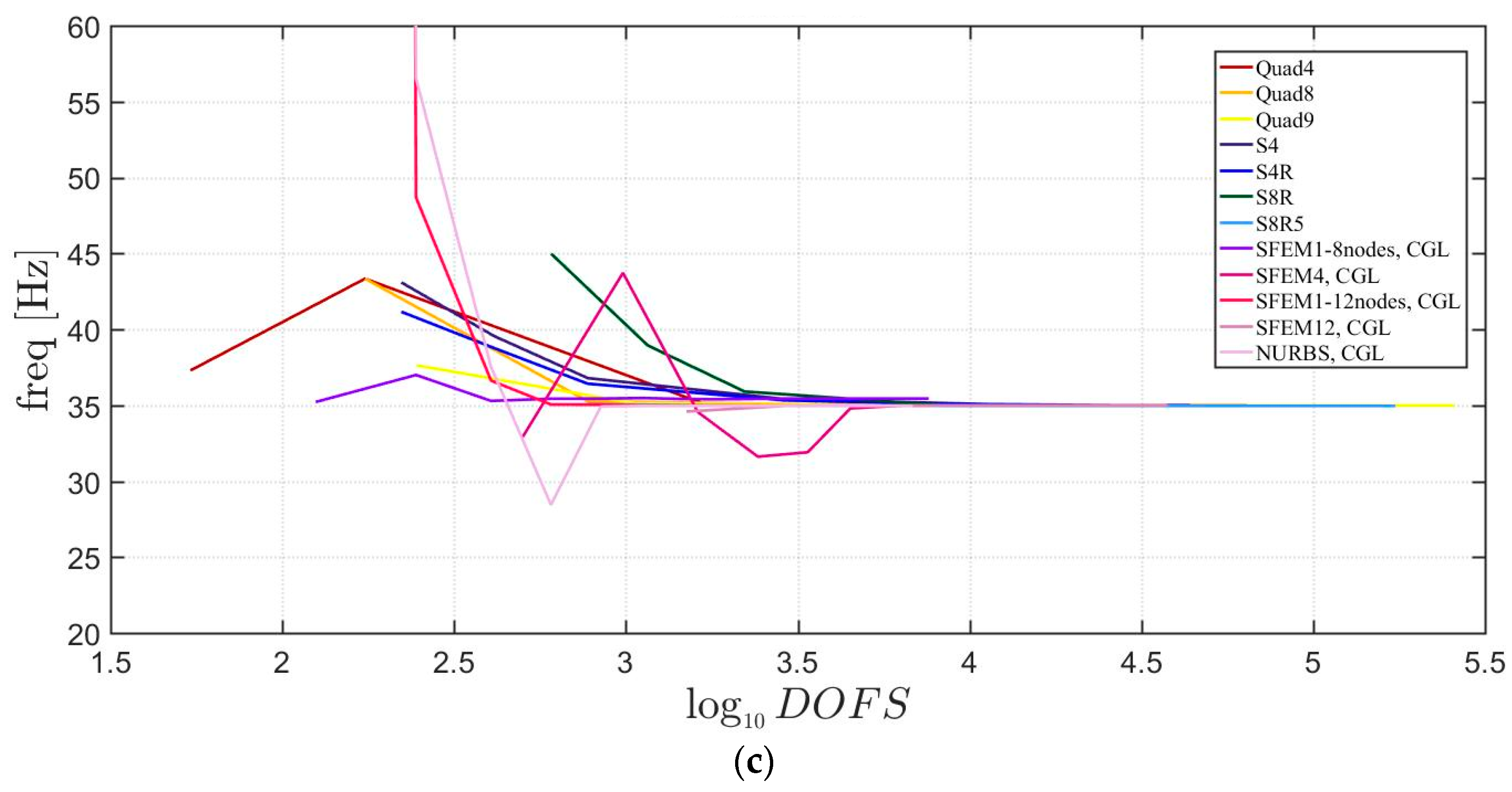
4.1.2. Circular Plates
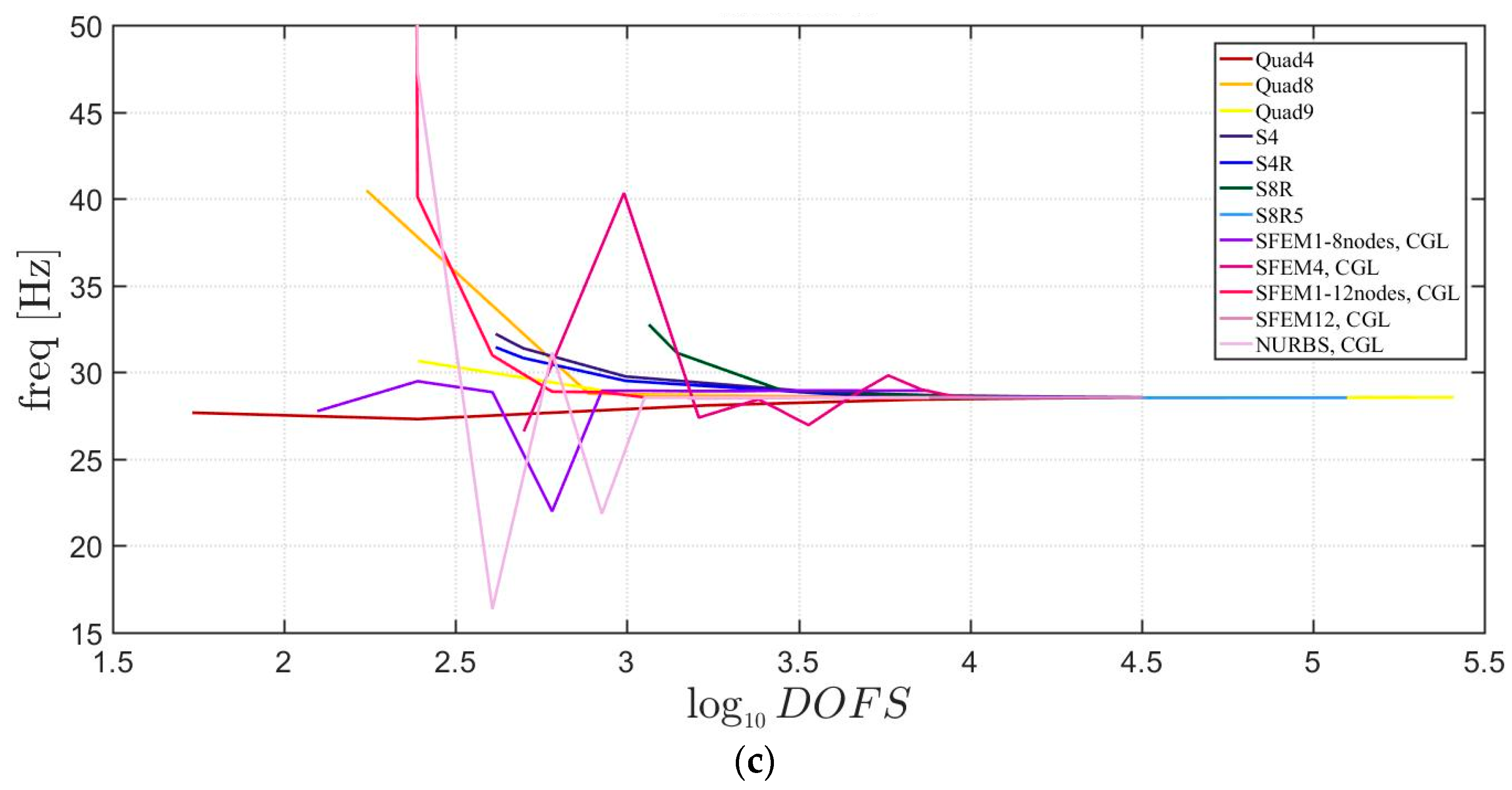
4.1.3. Elliptic Plates
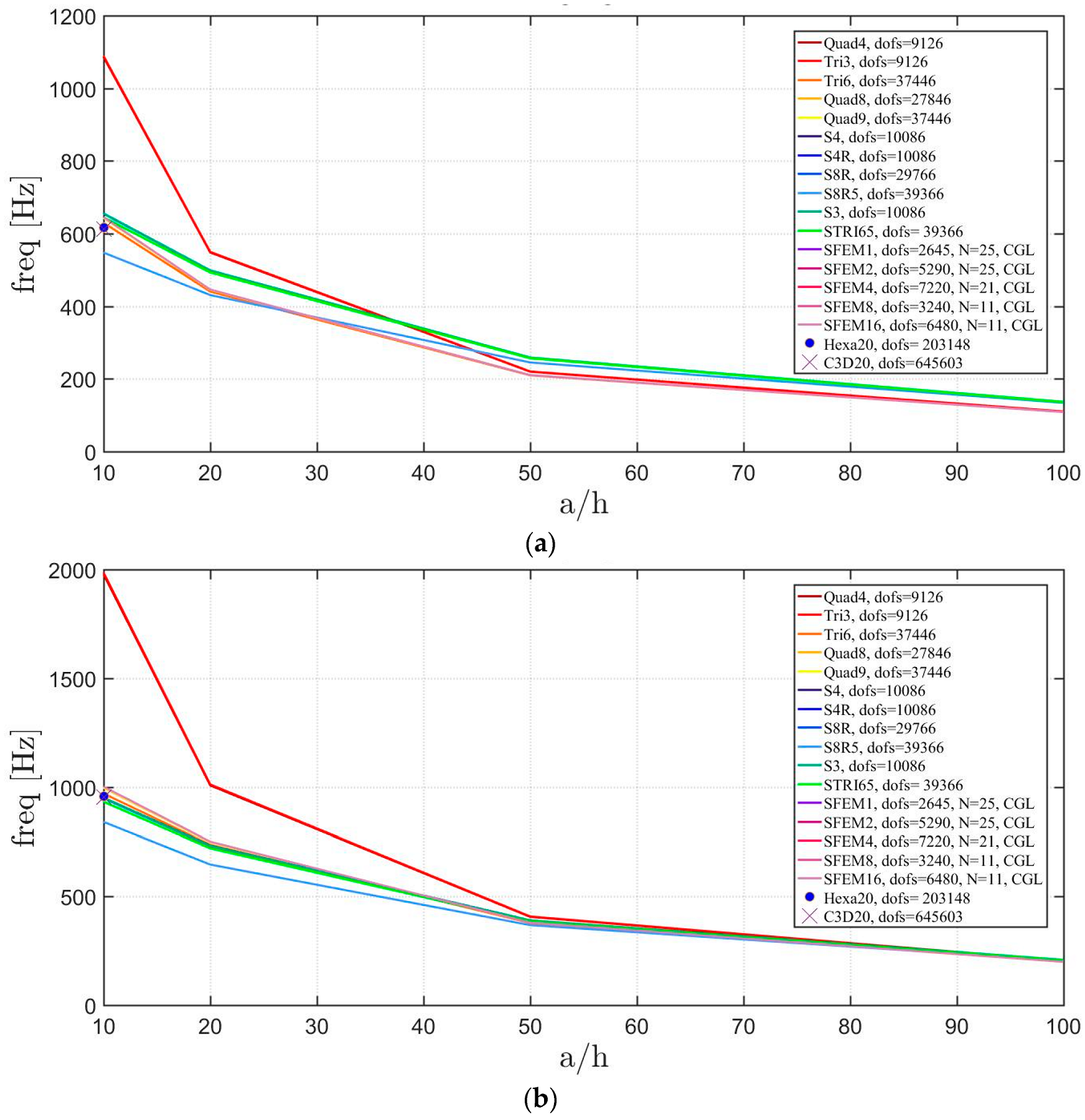
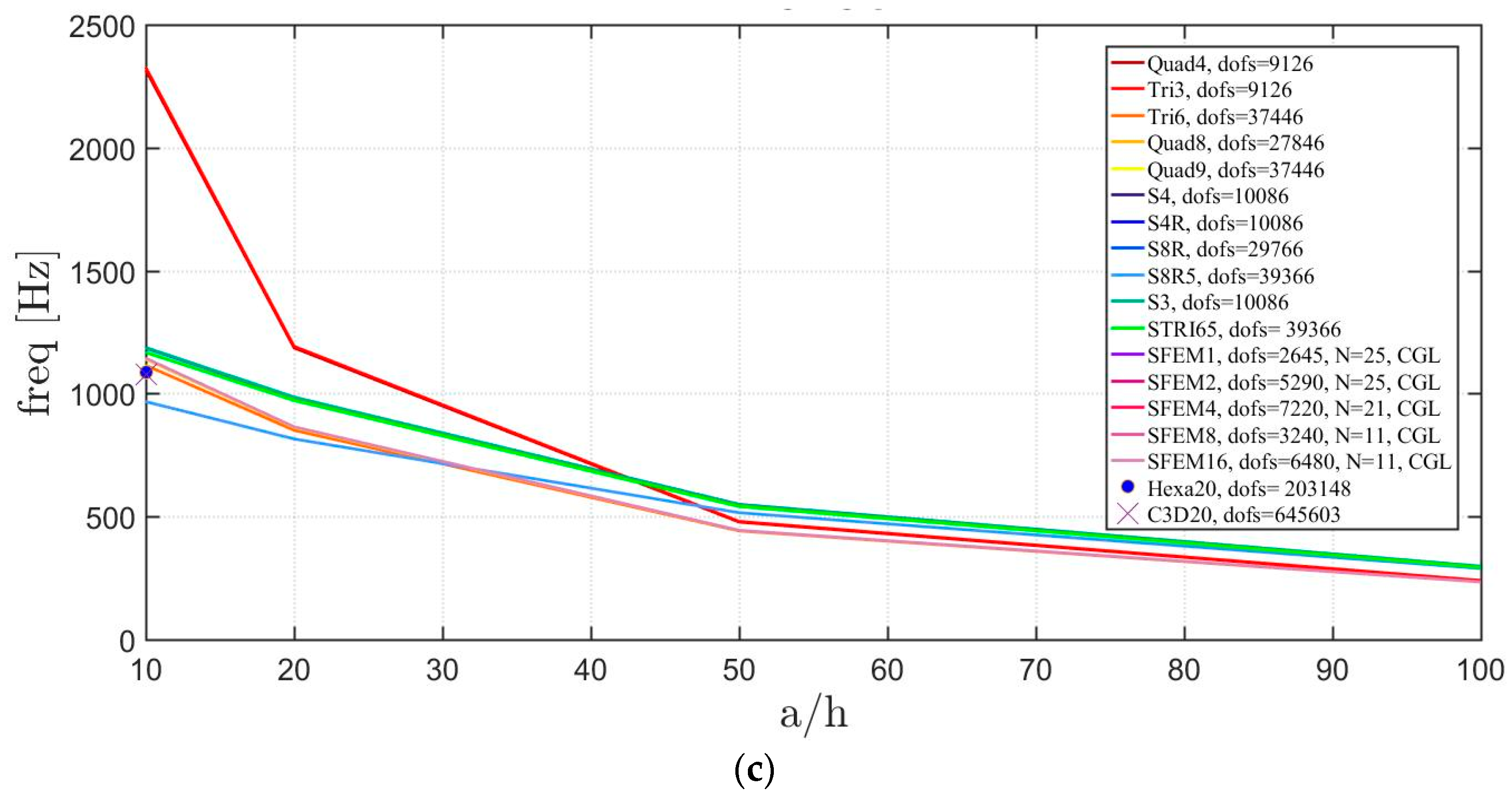
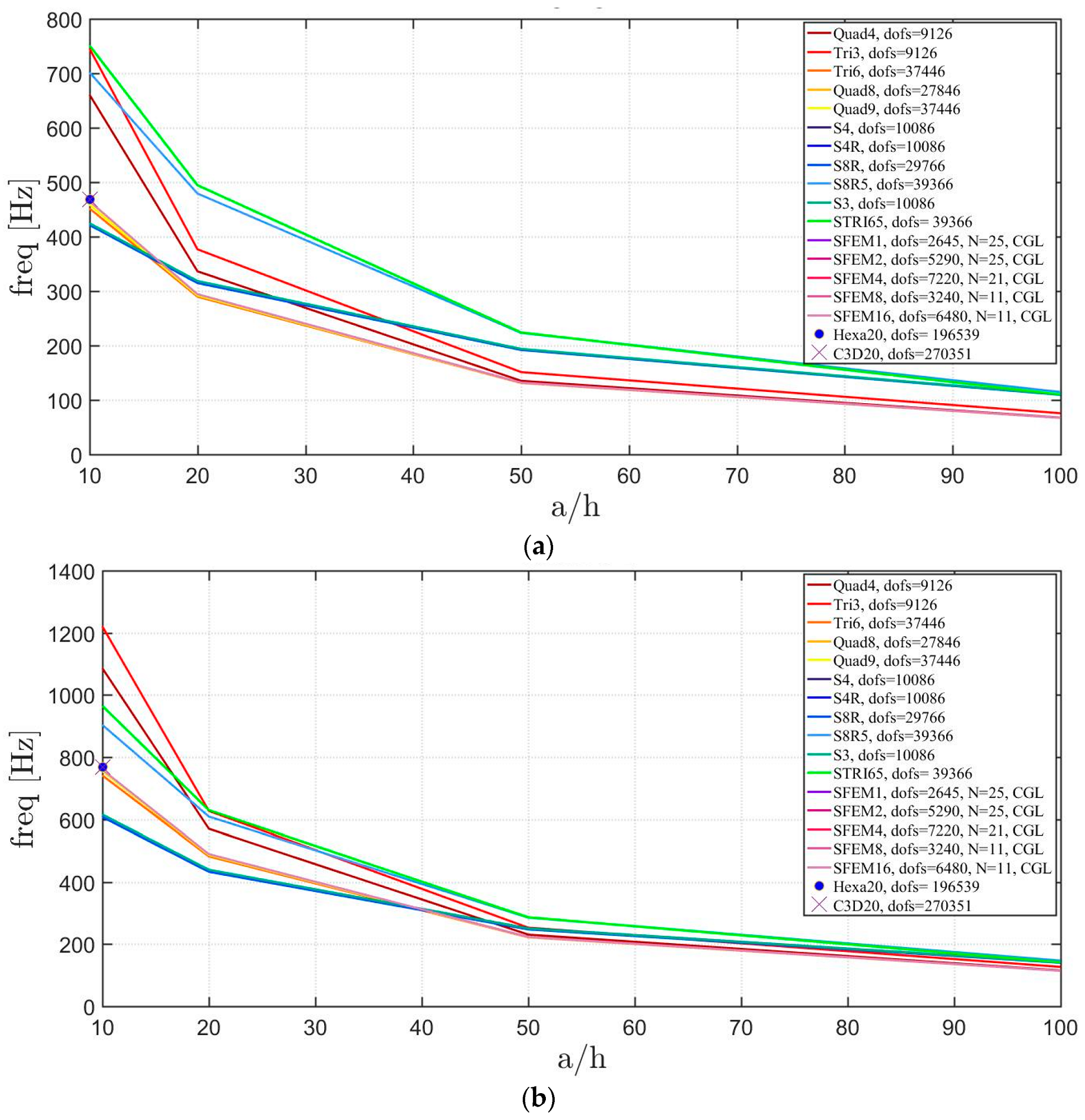
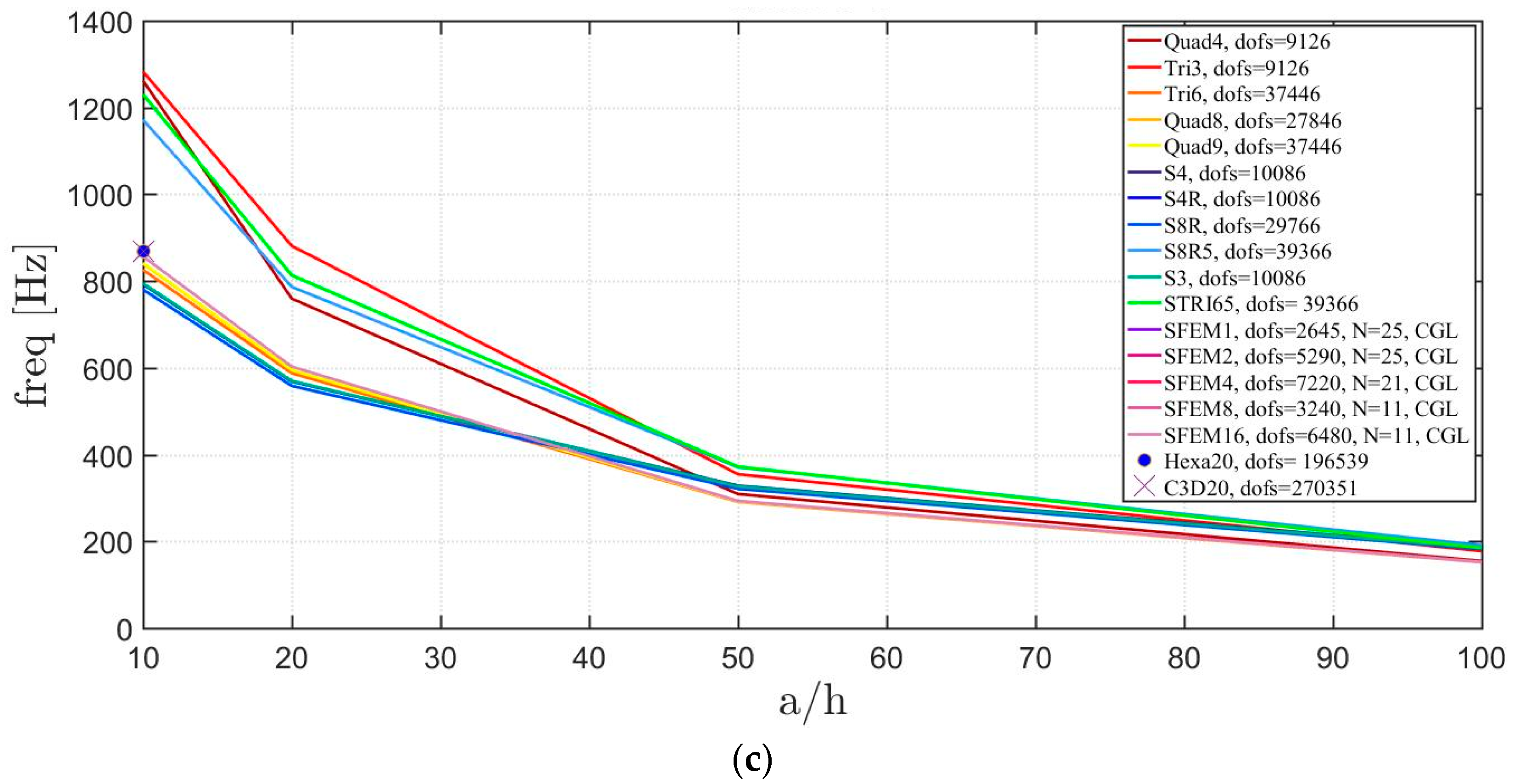
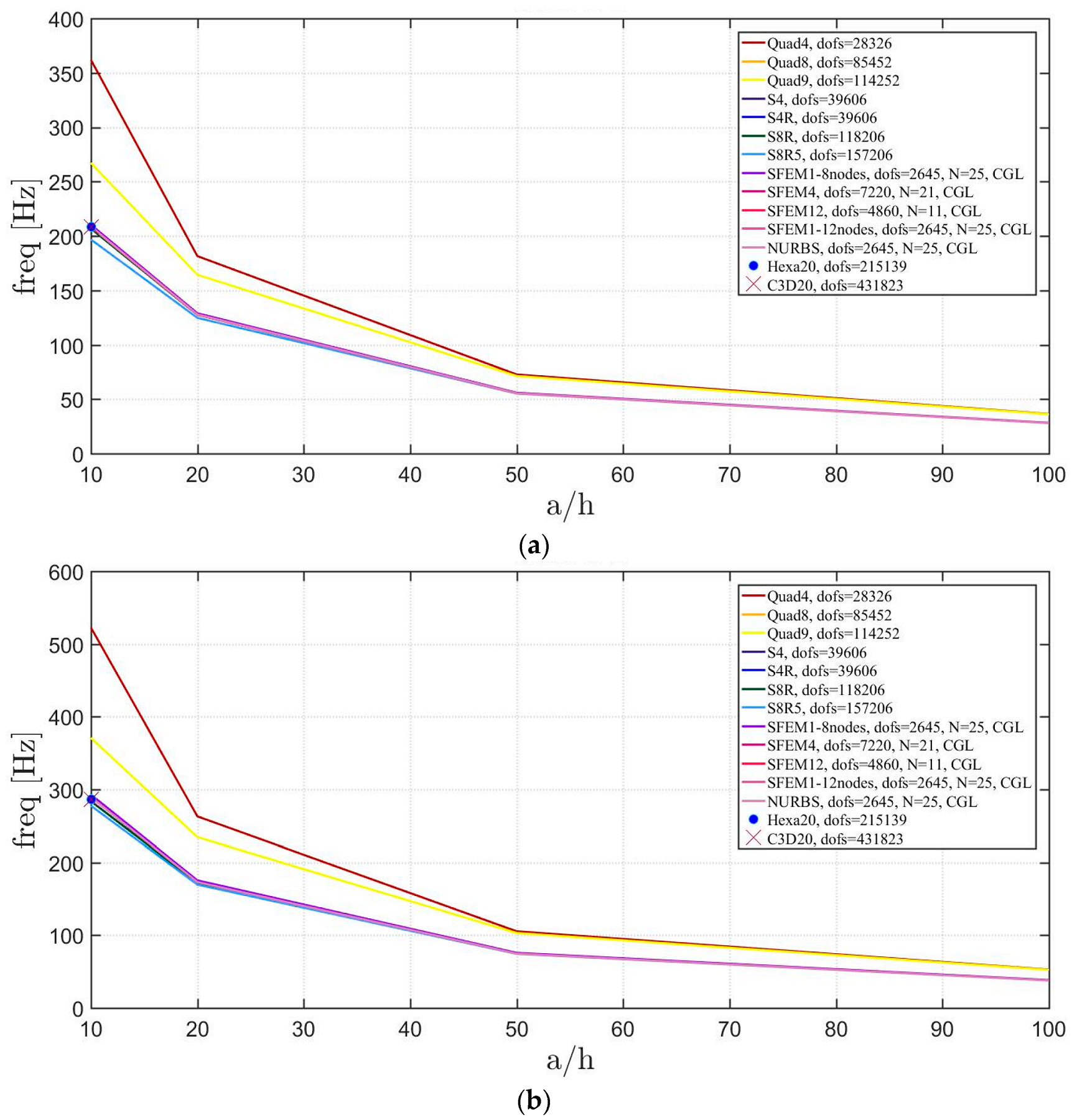
4.2. Laminated Composite Materials
4.2.1. Skew Plates with Skew Angle of 30°
4.2.2. Circular Plate
4.2.3. Elliptic Plate
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mindlin, R.D. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. ASME J. Appl. Mech. 1951, 18, 31–38. [Google Scholar]
- Reissner, E. The effect of transverse shear deformation on the bending of elastic plates. ASME J. Appl. Mech. 1945, 12, 68–77. [Google Scholar]
- Srinivas, S.; Joga Rao, C.V.; Rao, A.K. An exact analysis for vibration of simply supported homogeneous and laminated thick rectangular plates. J. Sound Vib. 1970, 12, 187–199. [Google Scholar] [CrossRef]
- Nelson, H.M. High frequency flexural vibration of thick rectangular bars and plates. J. Sound Vib. 1978, 60, 101–118. [Google Scholar] [CrossRef]
- Ali, R.; Atwal, S.J. Prediction of natural frequencies of vibration of rectangular plates with rectangular cutouts. Comput. Struct. 1980, 12, 819–823. [Google Scholar] [CrossRef]
- Lee, H.P.; Lim, S.P. Free vibration of isotropic and orthotropic square plates with square cutouts subjected to in-plane forces. Comput. Struct. 1992, 43, 431–437. [Google Scholar] [CrossRef]
- Farsa, J.; Kukreti, A.R.; Bert, C.W. Fundamental frequency analysis of laminated rectangular plates by differential quadrature method. Int. J. Numer. Methods Eng. 1993, 36, 2341–2356. [Google Scholar] [CrossRef]
- Farsa, J.; Kukreti, A.R.; Bert, C.W. Fundamental frequency analysis of single specially orthotropic, generally orthotropic and anisotropic rectangular layered plates by the differential quadrature method. Comput. Struct. 1993, 46, 465–477. [Google Scholar] [CrossRef]
- Bardell, N.S.; Dunsdon, J.M.; Langley, R.S. Free vibration analysis of thin coplanar rectangular plate assemblies-Part 1: Theory and initial results for specially orthotropic plates. Compos. Struct. 1996, 34, 129–143. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.L.; Chen, R.B. Static and free vibrational analysis of rectangular plates by the differential quadrature element method. Commun. Numer. Methods Eng. 1998, 14, 1133–1141. [Google Scholar] [CrossRef]
- Huang, M.; Sakiyama, T. Free vibration analysis of rectangular plates with variously shaped holes. J. Sound Vib. 1999, 226, 769–786. [Google Scholar] [CrossRef]
- Karami, G.; Malekzadeh, P. Application of a new differential quadrature methodology for free vibration analysis of plates. Int. J. Numer. Methods Eng. 2003, 56, 847–868. [Google Scholar] [CrossRef]
- Liew, K.M.; Kitipornchai, S.; Leung, A.Y.T.; Lim, C.W. Analysis of the free vibration of rectangular plates with central cut-outs using the discrete Ritz method. Int. J. Mech. Sci. 2003, 45, 941–959. [Google Scholar] [CrossRef]
- Liew, K.M.; Wang, Y.Q.; Reddy, J.N. Vibration analysis of symmetrically laminated plates based on FSDT using the moving least square differential quadrature method. Comput. Methods Appl. Mech. Eng. 2003, 192, 2203–2222. [Google Scholar] [CrossRef]
- Huang, Y.Q.; Li, Q.S. Bending and buckling analysis of antisymmetric laminates using the moving least square differential quadrature method. Comput. Methods Appl. Mech. Eng. 2004, 193, 3471–3492. [Google Scholar] [CrossRef]
- Seok, J.; Tiersten, H.F.; Scarton, H.A. Free vibrations of rectangular cantilever plates. Part 1: Out-of-plane motion, J. Sound Vib. 2004, 271, 131–146. [Google Scholar]
- Singh, A.V.; Tanveer, M. Eingenvalue analysis of doubly connected plates with different configurations. J. Sound Vib. 2006, 295, 76–93. [Google Scholar] [CrossRef]
- Shu, C.; Wu, W.X.; Ding, H.; Wang, C.M. Free vibration analysis of plates using least-square-based finite difference method. Comput. Methods Appl. Mech. Eng. 2007, 196, 1330–1343. [Google Scholar] [CrossRef]
- Houmat, A. In-plane vibration of plates with curvilinear plan-forms by a trigonometrically enriched curved triangular p-element. Thin-Walled Struct. 2008, 46, 103–111. [Google Scholar] [CrossRef]
- Secgin, A.; Sarigul, A.S. Free vibration analysis of symmetrically laminated thin composite plates by using Discrete Singular Convolution (DSC) approach: Algorithm and verification. J. Sound Vib. 2008, 315, 197–211. [Google Scholar] [CrossRef]
- Bui, T.Q.; Nguyen, M.N.; Zhang, C. An efficient meshfree method for vibration analysis of laminated composite plates. Comput. Mech. 2011, 48, 175–193. [Google Scholar] [CrossRef]
- Dozio, L.; Carrera, E. A variable kinematic Ritz formulation for vibration study of quadrilateral plates with arbitrary thickness. J. Sound Vib. 2011, 330, 4611–4632. [Google Scholar] [CrossRef]
- Dozio, L.; Carrera, E. Ritz analysis of vibrating rectangular and skew multilayered plates based on advanced variable-kinematic models. Compos. Struct. 2012, 94, 2118–2128. [Google Scholar] [CrossRef]
- Eftekhari, S.A.; Jafari, A.A. Modified mixed Ritz-DQ formulation for free vibration of thick rectangular and skew plates with general boundary conditions. Appl. Math. Model. 2013, 37, 7398–7426. [Google Scholar] [CrossRef]
- Nassar, M.; Matbuly, M.S.; Ragb, O. Vibration analysis of structural elements using differential quadrature method. J. Adv. Res. 2013, 4, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Kurtaran, H. Shape effect on free vibration of functionally graded plates. Int. J. Eng. Appl. Sci. 2014, 6, 52–67. [Google Scholar] [CrossRef][Green Version]
- Fantuzzi, N.; Brischetto, S.; Tornabene, F.; Viola, E. 2D and 3D Shell Models for the Free Vibration Investigation of Functionally Graded Cylindrical and Spherical Panels. Compos. Struct. 2016, 154, 573–590. [Google Scholar] [CrossRef]
- Brischetto, S.; Tornabene, F.; Fantuzzi, N.; Viola, E. 3D Exact and 2D Generalized Differential Quadrature Models for Free Vibration Analysis of Functionally Graded Plates and Cylinders. Meccanica 2016, 51, 2059–2098. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J.N. A general third-order theory of functionally graded plates with modified couple stress effect and the von Kármán nonlinearity: Theory and finite element analysis. Acta Mech. 2015, 226, 2973–2998. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of Agglomeration on the Natural Frequencies of Functionally Graded Carbon Nanotube-Reinforced Laminated Composite Doubly-Curved Shells. Compos. Part B-Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear Static Response of Nanocomposite Plates and Shells Reinforced by Agglomerated Carbon Nanotubes. Compos. Part B-Eng. 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Reissner’s Mixed Variational Theorem and variable kinematics in the modelling of laminated composite and FGM doubly-curved shells. Compos. Part B-Eng. 2016, 89, 408–423. [Google Scholar] [CrossRef]
- Fazzolari, F.A. Quasi-3D beam models for the computation of eigenfrequencies of functionally graded beams with arbitrary boundary conditions. Compos. Struct. 2016, 154, 239–255. [Google Scholar] [CrossRef]
- Tornabene, F.; Reddy, J.N. FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: A GDQ solution for static analysis with a posteriori stress and strain recovery. J. Indian Inst. Sci. 2013, 93, 635–688. [Google Scholar]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free Vibration Analysis of Arbitrarily Shaped Functionally Graded Carbon Nanotube-Reinforced Plates. Compos. Part B-Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Kumar, D.D.; Shivaprasad, G.; Hari, S.; Reddy, V.K. An experimental and numerical approach to free vibration analysis of glass/epoxy laminated composite plates. Int. J. Eng. Res. Technol. 2015, 4, 559–563. [Google Scholar]
- Claassen, R.W. Vibration of skew cantilever plates. AIAA J. 1963, 1, 1222. [Google Scholar] [CrossRef]
- Nair, P.S.; Durvasula, S. Vibration of skew plates. J. Sound Vib. 1973, 26, 1–19. [Google Scholar] [CrossRef]
- Mizusawa, T.; Kajita, T.; Naruoka, M. Vibration of skew plates by using B-spline functions. J. Sound Vib. 1979, 62, 301–308. [Google Scholar] [CrossRef]
- Raju, K.K.; Hinton, E. Natural frequencies and modes of rhombic Mindlin plates. Earthq. Eng. Struct. Dyn. 1980, 8, 55–62. [Google Scholar] [CrossRef]
- Gorman, D.J. Accurate free vibration analysis of rhombic plates with simply-supported and fully clamped edge conditions. J. Sound Vib. 1988, 125, 281–290. [Google Scholar] [CrossRef]
- Bardell, N.S. The free vibration of skew plates using the hierarchical finite element method. Comput. Struct. 1992, 45, 841–874. [Google Scholar] [CrossRef]
- Liew, K.M.; Wang, C.M. Vibration studies on skew plates: Treatment of internal line supports. Comput. Struct. 1993, 49, 941–951. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. The differential quadrature method for irregular domains and application to plate vibration. Int. J. Mech. Sci. 1996, 38, 589–606. [Google Scholar] [CrossRef]
- Hosokawa, K.; Terada, Y.; Sakata, T. Free vibrations of clamped symmetrically laminated skew plates. J. Sound Vib. 1996, 189, 525–533. [Google Scholar] [CrossRef]
- Han, W.; Dickinson, S. Free vibration of symmetrically laminated skew plates. J. Sound Vib. 1997, 208, 367–390. [Google Scholar] [CrossRef]
- Wang, S. Free vibration analysis of skew fiber-reinforced composite laminates based on first-order shear deformation plate theory. Comput. Struct. 1997, 63, 525–538. [Google Scholar] [CrossRef]
- Wang, S. Vibration of thin skew fiber-reinforced composite laminates. J. Sound Vib. 1997, 201, 335–352. [Google Scholar] [CrossRef]
- Skeikh, A.H.; Haldar, S.; Sengupta, D. Vibration of plates in different situations using a high-precision shear deformable element. J. Sound Vib. 2002, 253, 329–345. [Google Scholar] [CrossRef]
- Karami, G.; Malekzadeh, P. An efficient differential quadrature methodology for free vibration analysis of arbitrary straight-sided quadrilateral thin plates. J. Sound Vib. 2003, 263, 415–442. [Google Scholar] [CrossRef]
- Karami, G.; Malekzadeh, P.; Ali Shahpari, S. DQM analysis of skewed and trapezoidal laminated plates. Compos. Struct. 2003, 59, 393–402. [Google Scholar] [CrossRef]
- Liew, K.M.; Wang, J.; Ng, T.Y.; Tan, M.J. Free vibration and buckling analysis of shear-deformable plates based on FSDT meshfree method. J. Sound Vib. 2004, 276, 997–1017. [Google Scholar] [CrossRef]
- Garg, A.K.; Khare, R.K.; Kant, T. Free vibration of skew fiber-reinforced composite and sandwich laminates using a shear deformable finite element model. J. Sandw. Struct. Mater. 2006, 8, 33–53. [Google Scholar] [CrossRef]
- Civalek, O. Discrete singular convolution methodology for free vibration and stability analyses of arbitrary straight-sided quadrilateral plates. Commun. Numer. Methods Eng. 2008, 24, 1475–1495. [Google Scholar] [CrossRef]
- Das, D.; Sahoo, P.; Saha, K. Large-amplitude dynamic analysis of simply supported skew plates by a variational method. J. Sound Vib. 2008, 313, 246–267. [Google Scholar] [CrossRef]
- Nallim, L.G.; Oller, S. An analytical-numerical approach to simulate the dynamic behavior of arbitrarily laminated composite plates. Compos. Struct. 2008, 85, 311–325. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, W.X. Vibration of skew plates by the MLS-Ritz method. Int. J. Mech. Sci. 2008, 50, 1133–1141. [Google Scholar] [CrossRef]
- Ashour, A.S. The free vibration of symmetrically angle-ply laminated fully clamped skew plates. J. Sound Vib. 2009, 323, 444–450. [Google Scholar] [CrossRef]
- Gurses, M.; Civalek, O.; Korkmaz, A.K.; Ersoy, H. Free vibration analysis of symmetric laminated skew plates by discrete singular convolution technique based on first-order shear deformation theory. Int. J. Numer. Methods Eng. 2009, 79, 290–313. [Google Scholar] [CrossRef]
- Rao, K.D.; Babu, K.S. Modal analysis of thin FRP skew symmetric angle-ply laminate with circular cut-out. Int. J. Eng. Res. Technol. 2012, 1, 1–5. [Google Scholar]
- Srinivasa, C.V.; Suresh, Y.J.; Prema Kumar, W.P. Free flexural vibration studies on laminated composite skew plates. Int. J. Eng. Sci. Technol. 2012, 4, 13–24. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Z. Differential quadrature analysis of free vibration of rhombic plates with free edges. Appl. Math. Comput. 2013, 225, 171–183. [Google Scholar] [CrossRef]
- Zhang, L.W.; Xiao, L.N. Mechanical behavior of laminated CNT-reinforced composite skew plates subjected to dynamic loading. Compos. Part B-Eng. 2017, 122, 219–230. [Google Scholar] [CrossRef]
- Zhang, L.W. On the study of the effect of in-plane forces on the frequency parameters of CNT-reinforced composite skew plates. Compos. Struct. 2017, 160, 824–837. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Yuan, Z. Accurate vibration analysis of skew plates by the new version of the differential quadrature method. Appl. Math. Model. 2014, 38, 926–937. [Google Scholar] [CrossRef]
- Mohazzab, A.H.; Dozio, L. A spectral collocation solution for in-plane eigenvalue analysis of skew plates. Int. J. Mech. Sci. 2015, 94–95, 199–210. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Kunukasseril, V.X. Free vibration of stiffened circular bridge decks. J. Sound Vib. 1976, 44, 209–221. [Google Scholar] [CrossRef]
- Irie, T.; Yamada, G.; Ito, F. Free vibration of polar-orthotropic sector plates. J. Sound Vib. 1979, 67, 89–100. [Google Scholar] [CrossRef]
- Irie, T.; Yamada, G.; Ito, F. Flexural vibrations of polar-orthotropic sector plates with simply-supported straight edges. J. Sound Vib. 1980, 70, 589–596. [Google Scholar]
- Maruyama, K.; Ichinomiya, O. Experimental investigation of free vibrations of clamped sector plates. J. Sound Vib. 1981, 74, 565–573. [Google Scholar] [CrossRef]
- Srinivasan, R.S.; Thiruvenkatachari, V. Free vibration of annular sector plates by an integral equation technique. J. Sound Vib. 1983, 89, 425–432. [Google Scholar] [CrossRef]
- Srinivasan, R.S.; Thiruvenkatachari, V. Free vibration of transverse isotropic annular sector Mindlin plates. J. Sound Vib. 1985, 101, 193–201. [Google Scholar] [CrossRef]
- Harik, I.E.; Molaghasemi, H.R. Analytical solution to free vibration of sector plates. J. Eng. Mech. 1989, 115, 2709–2722. [Google Scholar] [CrossRef]
- Mizusawa, T.; Kajita, T. Vibration of annular sector plates using spline strip method. Commun. Appl. Numer. Methods 1992, 8, 537–546. [Google Scholar] [CrossRef]
- Mizusawa, T.; Takami, K. Vibration of tapered thickness annular sector plates by spline element method. J. Sound Vib. 1992, 154, 147–160. [Google Scholar] [CrossRef]
- Liew, K.M.; Lam, K.Y. On the use of 2D orthogonal polynomials in the Rayleigh-Ritz method for flexural vibration of annular sector plates of arbitrary shape. Int. J. Mech. Sci. 1993, 35, 129–139. [Google Scholar] [CrossRef]
- Xiang, Y.; Liew, K.M.; Kitipornchai, S. Transverse vibration of thick annular sector plates. J. Eng. Mech. 1993, 1579–1599. [Google Scholar] [CrossRef]
- McGee, O.G.; Huang, C.S.; Leissa, A.W. Comprehensive exact solutions for free vibrations of thick annular sectorial plates with simply supported radial edges. Int. J. Mech. Sci. 1995, 37, 537–566. [Google Scholar] [CrossRef]
- McGee, O.G.; Huang, C.S.; Leissa, A.W.; Kim, J.W. Vibrations of circular plates with clamped V-notches or rigidly constrained radial cracks. J. Sound Vib. 1995, 181, 185–201. [Google Scholar] [CrossRef]
- Liew, K.M.; Han, J.B.; Xiao, Z.M. Vibration analysis of circular Mindlin plates using the differential quadrature method. J. Sound Vib. 1997, 205, 617–630. [Google Scholar] [CrossRef]
- Liu, F.L.; Liew, K.M. Free vibration analysis of Mindlin sector plate: Numerical solutions by differential quadrature method. Comput. Methods Appl. Mech. Eng. 1999, 177, 77–92. [Google Scholar] [CrossRef]
- Liu, F.L.; Liew, K.M. Differential quadrature element method: A new approach for free vibration analysis of polar Mindlin plates having discontinuities. Comput. Methods Appl. Mech. Eng. 1999, 179, 407–423. [Google Scholar] [CrossRef]
- Liu, F.L.; Liew, K.M. Differential quadrature element method for static analysis of Reissner-Mindlin polar plates. Int. J. Solids Struct. 1999, 36, 5101–5123. [Google Scholar] [CrossRef]
- Liu, F.L.; Liew, K.M. Differential quadrature method for vibration analysis of shear deformable annular sector plates. J. Sound Vib. 2000, 230, 335–356. [Google Scholar]
- Zhong, H. Application of triangular differential quadrature to problems with curved boundaries. Commun. Numer. Methods Eng. 2002, 18, 633–643. [Google Scholar] [CrossRef]
- Civalek, O.; Catal, H.H. Linear static and vibration analysis of circular and annular plates by the Harmonic Differential Quadrature (HDQ) method. Eng. Arch. Fac. Osmangazi Univ. 2003, 17, 44–71. [Google Scholar]
- Liew, K.M.; Huang, Y.Q.; Reddy, J.N. Analysis of general shaped thin plates by the moving least-squares differential quadrature method. Finite Elem. Anal. Des. 2004, 40, 1453–1474. [Google Scholar] [CrossRef]
- Sharma, A.; Sharda, H.B.; Nath, Y. Stability and vibration of Mindlin sector plates: An analytical approach. AIAA J. 2005, 43, 1109–1116. [Google Scholar] [CrossRef]
- Nie, G.J.; Zhong, Z. Semi-analytical solution for three-dimensional vibration of functionally graded circular plates. Comput. Methods Appl. Mech. Eng. 2007, 196, 4901–4910. [Google Scholar] [CrossRef]
- Dong, C.Y. Three-Dimensional free vibration analysis of functionally graded annular plates using the Chebyshev-Ritz method. Mater. Des. 2008, 29, 1518–1525. [Google Scholar] [CrossRef]
- Civalek, O. Use of eight-node curvilinear domains in discrete singular convolution method for free vibration analysis of annular sector plates with simply supported radial edges. J. Vib. Control 2009, 16, 303–320. [Google Scholar] [CrossRef]
- Civalek, O. Numerical solutions to the free vibration problem of Mindlin sector plates using the discrete singular convolution method. Int. J. Struct. Stab. Dyn. 2009, 9, 267–284. [Google Scholar] [CrossRef]
- Xing, Y.; Liu, B. High-accuracy differential quadrature finite element method and its application to free vibration of thin plate with curvilinear domain. Int. J. Numer. Methods Eng. 2009, 80, 1718–1742. [Google Scholar] [CrossRef]
- Zhou, D.; Lo, S.H.; Cheung, Y.K. 3-D vibration analysis of plates with curvilinear quadrilateral domains by discrete singular convolution method. J. Sound Vib. 2009, 320, 421–437. [Google Scholar] [CrossRef]
- Civalek, O.; Ozturk, B. Vibration analysis of plates with curvilinear quadrilateral domains by discrete singular convolution method. Struct. Eng. Mech. 2010, 36, 279–299. [Google Scholar] [CrossRef]
- Lam, K.Y.; Liew, K.M.; Chow, S.T. Free vibration analysis of isotropic and orthotropic triangular plates. Int. J. Mech. Sci. 1990, 32, 455–464. [Google Scholar] [CrossRef]
- Dubliner, M. Spectral methods on triangles and other domains. J. Sci. Comput. 1991, 6, 345–390. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Liew, K.M.; Xiang, Y.; Wang, C.M. Free vibration of isosceles triangular Mindlin plates. Int. J. Mech. Sci. 1993, 35, 89–102. [Google Scholar] [CrossRef]
- Mirza, S.; Alizadeh, Y. Free vibration of partially supported triangular plates. Comput. Struct. 1994, 51, 143–150. [Google Scholar] [CrossRef]
- Qatu, M.S. Natural frequencies for cantilevered laminated composite right triangular and trapezoidal plates. Compos. Sci. Technol. 1994, 51, 441–449. [Google Scholar] [CrossRef]
- Abrate, S. Vibration of point supported triangular plates. Comput. Struct. 1996, 58, 327–336. [Google Scholar] [CrossRef]
- Karunasena, W.; Kitipornchai, S.; Al-Bermani, F.G.A. Free vibration of cantilevered arbitrary triangular Mindlin plates. Int. J. Mech. Sci. 1996, 38, 431–442. [Google Scholar] [CrossRef]
- Singh, B.; Saxena, V. Transverse vibration of triangular plates with variable thickness. J. Sound Vib. 1996, 194, 471–496. [Google Scholar] [CrossRef]
- Karunasena, W.; Kitipornchai, S. Free vibration of shear-deformable general triangular plates. J. Sound Vib. 1997, 199, 595–613. [Google Scholar] [CrossRef]
- Singh, B.; Hassan, S.M. Transverse vibration of triangular plates with arbitrary thickness variation and various boundary conditions. J. Sound Vib. 1998, 214, 29–55. [Google Scholar] [CrossRef]
- Sakiyama, T.; Huang, M. Free vibration analysis of right triangular plates with variable thickness. J. Sound Vib. 2000, 234, 841–858. [Google Scholar] [CrossRef]
- Zhong, H.Z. Free vibration analysis of isosceles triangular Mindlin plates by the triangular differential quadrature method. J. Sound Vib. 2000, 237, 697–708. [Google Scholar] [CrossRef]
- Sheikh, A.H.; Haldar, S.; Sengupta, D. A high precision shear deformable element for the analysis of laminated composite plates of different shapes. Compos. Struct. 2002, 55, 329–336. [Google Scholar] [CrossRef]
- Civalek, O.; Gurses, M. Frequency analysis of trapezoidal plates and membrane using discrete singular convolution. Asian J. Civ. Eng. 2009, 9, 593–605. [Google Scholar]
- El-Sayad, M.A.; Ghazy, S.S.A. Rayleigh-Ritz method for free vibration of Mindlin trapezoidal plates. Can. J. Sci. Eng. Math. 2012, 3, 271–278. [Google Scholar]
- Quintana, M.V.; Nallim, L.G. A general Ritz formulation for the vibration analysis of thick trapezoidal and triangular laminated plates resting on elastic supports. Int. J. Mech. Sci. 2013, 69, 1–9. [Google Scholar] [CrossRef]
- Rango, R.F.; Nallim, L.G.; Oller, S. Static and dynamic analysis of thick laminated plates using enriched macroelements. Compos. Struct. 2013, 101, 94–103. [Google Scholar] [CrossRef]
- Rango, R.F.; Nallim, L.G.; Oller, S. Formulation of enriched macro elements using trigonometric shear deformation theory for free vibration analysis of symmetric laminated composite plate assemblies. Compos. Struct. 2015, 119, 38–49. [Google Scholar] [CrossRef]
- Singh, B.; Chakraverty, S. On the use of orthogonal polynomials in the Rayleigh-Ritz method for the study of transverse vibration of elliptic plates. Comput. Struct. 1992, 43, 439–443. [Google Scholar] [CrossRef]
- Chakraverty, S.; Jindal, R.; Agarwal, V.K. Flexural vibrations of non-homogeneous elliptic plates. Indian J. Eng. Mater. Sci. 2005, 12, 521–528. [Google Scholar]
- Ghazy, S.S.A.; Barki, F.A.; Safwat, H.M. Free vibration analysis of penta, hepta-gonal shaped plates. Comput. Struct. 1997, 62, 395–407. [Google Scholar] [CrossRef]
- Lim, C.W.; Liew, K.M. Vibrations of perforated plates with rounded corners. J. Eng. Mech. 1995, 121, 203–213. [Google Scholar] [CrossRef]
- Liu, G.R.; Zhao, X.; Dai, K.Y.; Zhong, Z.H.; Li, G.Y.; Han, X. Static and free vibration analysis of laminated composite plates using the conforming radial point interpolation method. Compos. Sci. Technol. 2008, 68, 354–366. [Google Scholar] [CrossRef]
- Lam, K.Y.; Liew, K.M.; Chow, S.T. Use of two-dimensional orthogonal polynomials for vibration analysis of circular and elliptical plates. J. Sound Vib. 1992, 154, 261–269. [Google Scholar] [CrossRef]
- Leissa, A.W. Vibration of Plates; NASA Sp–160; US Government Printing Office: Washington, DC, USA, 1969.
- Ferreira, A.J.M.; Roque Jorge, R.M.N. Free vibration analysis of symmetric laminated composite plates by FSDT and radial basis functions. Comput. Methods Appl. Mech. Eng. 2005, 194, 4265–4278. [Google Scholar] [CrossRef]
- Anlas, G.; Göker, G. Vibration analysis of skew fibre-reinforced composite laminated plates. J. Sound Vib. 2001, 242, 265–276. [Google Scholar] [CrossRef]
- Murthy, M.V.V. An Improved Transverse Shear Deformation Theory for Laminated Anisotropic Plates; NASA Technical Paper; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1981.
- Green, A.E.; Naghdi, P.M. A theory of composite laminated plates. IMA J. Appl. Math. 1982, 29, 1–23. [Google Scholar] [CrossRef]
- Bert, C.W. A Critical Evaluation of New Plate Theories Applied to Laminated Composites. Compos. Struct. 1984, 2, 329–347. [Google Scholar] [CrossRef]
- Reddy, J.N. A Simple Higher-Order Theory for Laminated Composite Plates. J. Appl. Mech. ASME 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Shirakawa, K. Bending of plates based on improved theory. Mech. Res. Commun. 1985, 10, 205–211. [Google Scholar] [CrossRef]
- Reddy, J.N. A Generalization of the Two-Dimensional Theories of Laminated Composite Plates. Commun. Appl. Numer. Methods 1987, 3, 173–180. [Google Scholar] [CrossRef]
- Reddy, J.N. On Refined Theories of Composite Laminates. Meccanica 1990, 25, 230–238. [Google Scholar] [CrossRef]
- Robbins, D.H.; Reddy, J.N. Modeling of Thick Composites Using a Layer-Wise Laminate Theory. Int. J. Numer. Methods Eng. 1993, 36, 655–677. [Google Scholar] [CrossRef]
- Alibeiglooa, A.; Shakeri, M.; Kari, M.R. Free vibration analysis of antisymmetric laminated rectangular plates with distributed patch mass using third-order shear deformation theory. Ocean Eng. 2008, 35, 183–190. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, K.-M. Free vibration analysis of symmetric laminated composite plates by trigonometric shear deformation theory and inverse multiquadric RBF. Thin Walled Struct. 2009, 47, 304–310. [Google Scholar] [CrossRef]
- Groh, R.M.J.; Weaver, P.M. A computationally efficient 2D model for inherently equilibrated 3D stress predictions in heterogeneous laminated plates. Part I: Model formulation. Compos. Struct. 2016, 156, 171–185. [Google Scholar] [CrossRef]
- Groh, R.M.J.; Weaver, P.M. A computationally efficient 2D model for inherently equilibrated 3D stress predictions in heterogeneous laminated plates. Part II: Model validation. Compos. Struct. 2016, 156, 186–217. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, G.; Wang, X. Displacement and stress analysis of laminated composite plates using an eight-node quasi-conforming solid-shell element. Curved Layer. Struct. 2017, 8–20. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M. Free vibrations and buckling analysis of laminated plates by oscillatory radial basis functions. Curved Layer. Struct. 2016, 3, 17–21. [Google Scholar] [CrossRef]
- Wang, Q.; She, D.; Pang, F.; Liang, Q. Vibrations of Composite Laminated Circular Panels and Shells of Revolution with General Elastic Boundary Conditions via Fourier-Ritz Method. Curved Layer. Struct. 2016, 3, 105–136. [Google Scholar] [CrossRef]
- Piskunov, V.G.; Verijenko, V.E.; Adali, S.; Summers, E.B. A Higher-order Theory for the Analysis of Laminated Plates and Shells with Shear and Normal Deformation. Int. J. Eng. Sci. 1993, 31, 967–988. [Google Scholar] [CrossRef]
- Brischetto, S. An exact 3D solution for free vibrations of multilayered cross-ply composite and sandwich plates and shells. Int. J. Appl. Mech. 2014, 6, 1450076. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. Exact 3D solutions and finite element 2D models for free vibration analysis of plates and cylinders. Curved Layer. Struct. 2014, 1, 59–92. [Google Scholar] [CrossRef]
- Whitney, J.M.; Pagano, N.J. Shear Deformation in Heterogeneous Anisotropic Plates. J. Appl. Mech. ASME 1970, 37, 1031–1036. [Google Scholar] [CrossRef]
- Whitney, J.M.; Sun, C.T. A Higher Order Theory for Extensional Motion of Laminated Composites. J. Sound Vib. 1973, 30, 85–97. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. Free vibration of laminated composite plates using two variable refined plate theory. Int. J. Mech. Sci. 2010, 52, 626–633. [Google Scholar] [CrossRef]
- Sahoo, R.; Singh, B.N. A new trigonometric zigzag theory for buckling and free vibration analysis of laminated composite and sandwich plates. Compos. Struct. 2014, 117, 316–332. [Google Scholar] [CrossRef]
- Vidal, P.; Polit, O.; D’Ottavio, M.; Valot, E. Assessment of the refined sinus plate finite element: Free edge effect and Meyer-Piening sandwich test. Finite Elem. Anal. Des. 2014, 92, 60–71. [Google Scholar] [CrossRef]
- Wang, X.; Shi, G. A refined laminated plate theory accounting for the third-order shear deformation and interlaminar transverse stress continuity. Appl. Math. Model. 2015, 39, 5659–5680. [Google Scholar] [CrossRef]
- Zuo, H.; Yang, Z.; Chen, X.; Xie, Y.; Miao, H. Analysis of laminated composite plates using wavelet finite element method and higher-order plate theory. Compos. Struct. 2015, 131, 248–258. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Afsari, A.; Zahedinejad, P.; Bahadori, R. Three-dimensional layerwise-finite element free vibration analysis of thick laminated annular plates on elastic foundation. Appl. Math. Model. 2010, 34, 776–790. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Guedes Soares, C. A new trigonometric layerwise shear deformation theory for the finite element analysis of laminated composite and sandwich plates. Comput. Struct. 2012, 94–95, 45–53. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Carrera, E.; Nguyen-Xuan, H. Isogeometric analysis of laminated composite and sandwich plates using a layerwise deformation theory. Compos. Struct. 2013, 104, 196–214. [Google Scholar] [CrossRef]
- Mantari, J.L.; Soares, C.G. Generalized layerwise HSDT and finite element formulation for symmetric laminated and sandwich composite plates. Compos. Struct. 2013, 105, 319–331. [Google Scholar] [CrossRef]
- Guo, Y.; Nagy, A.P.; Gürdal, Z. A layerwise theory for laminated composites in the framework of isogeometric analysis. Compos. Struct. 2014, 107, 447–457. [Google Scholar] [CrossRef]
- Boscolo, M.; Banerjee, J.R. Layer-wise dynamic stiffness solution for free vibration analysis of laminated composite plates. J. Sound Vib. 2014, 333, 200–227. [Google Scholar] [CrossRef]
- Yazdani, S.; Ribeiro, P. A layerwise p-version finite element formulation for free vibration analysis of thick composite laminates with curvilinear fibres. Compos. Struct. 2015, 120, 531–542. [Google Scholar] [CrossRef]
- Band, U.N.; Desai, Y.M. Coupled higher order and mixed layerwise finite element based static and free vibration analyses of laminated plates. Compos. Struct. 2015, 128, 406–414. [Google Scholar] [CrossRef]
- Biscani, F.; Giunta, G.; Belouettar, S.; Hu, H.; Carrera, E. Mixed-dimensional modeling by means of solid and higher-order multi-layered plate finite elements. Mech. Adv. Mater. Struct. 2016, 23, 960–970. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The GDQ Method for the Free Vibration Analysis of Arbitrarily Shaped Laminated Composite Shells Using a NURBS-Based Isogeometric Approach. Compos. Struct. 2016, 154, 190–218. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Eisenberger, M.; Fantuzzi, N.; Tornabene, F.; Viola, E. Vibration Analysis of Variable Thickness Plates and Shells by the Generalized Differential Quadrature Method. Compos. Struct. 2016, 156, 218–237. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L. A variable-kinematic model for variable stiffness plates: Vibration and buckling analysis. Compos. Struct. 2016, 142, 15–26. [Google Scholar] [CrossRef]
- Wenzel, C.; D’Ottavio, M.; Polit, O.; Vidal, P. Assessment of free-edge singularities in composite laminates using higher-order plate elements. Mech. Adv. Mater. Struct. 2016, 23, 948–959. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Accurate Inter-Laminar Recovery for Plates and Doubly-Curved Shells with Variable Radii of Curvature Using Layer-Wise Theories. Compos. Struct. 2015, 124, 368–393. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Higher-Order Structural Theories for the Static Analysis of Doubly-Curved Laminated Composite Panels Reinforced by Curvilinear Fibers. Thin-Walled Struct. 2016, 102, 222–245. [Google Scholar] [CrossRef]
- Tornabene, F. General Higher Order Layer-Wise Theory for Free Vibrations of Doubly-Curved Laminated Composite Shells and Panels. Mech. Adv. Mater. Struct. 2016, 23, 1046–1067. [Google Scholar] [CrossRef]
- Demasi, L. ∞3 Hierarchy plate theories for thick and thin composite plates: The generalized unified formulation. Compos. Struct. 2008, 84, 256–270. [Google Scholar] [CrossRef]
- D’Ottavio, M. A Sublaminate Generalized Unified Formulation for the analysis of composite structures. Compos. Struct. 2016, 142, 187–199. [Google Scholar] [CrossRef]
- Carpinteri, A. Static-kinematic duality in beams, plates, shells and its central role in the finite element method. Curved Layer. Struct. 2017, 4, 38–51. [Google Scholar] [CrossRef][Green Version]
- Chavan, S.G.; Lal, A. Bending analysis of laminated SWCNT Reinforced functionally graded plate using FEM. Curved Layer. Struct. 2017, 4, 134–145. [Google Scholar] [CrossRef]
- Demir, Ç.; Ersoy, H.; Mercan, K.; Civalek, Ö. Free vibration analysis of annular sector plates via conical shell equations. Curved Layer. Struct. 2017, 4, 146–157. [Google Scholar] [CrossRef]
- Pang, F.; Li, H.; Miao, X.; Wang, X. A modified Fourier solution for vibration analysis of moderately thick laminated annular sector plates with general boundary conditions, internal radial line and circumferential arc supports. Curved Layer. Struct. 2017, 189–220. [Google Scholar] [CrossRef]
- Thai, C.H.; Xuan, N.H.; Thanh, N.N.; Le, T.-H.; Thoi, N.T.; Rabczuk, T. Static, free vibration, and buckling analysis of laminated composite Reissner-Mindlin plates using NURBS-based isogeometric approach. Int. J. Numer. Methods Eng. 2012, 91, 571–603. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Hung, N.-X. High-order B-splines based finite elements for delamination analysis of laminated composites. Compos. Struct. 2013, 102, 261–275. [Google Scholar] [CrossRef]
- Wang, Y.; Waisman, H. Progressive delamination analysis of composite materials using XFEM and a discrete damage zone model. Comput. Mech. 2015, 55, 1–26. [Google Scholar] [CrossRef]
- Li, D.H. Extended layerwise method of laminated composite shells. Compos. Struct. 2016, 136, 313–344. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential Geometry Higher-Order Structural Theories, 1st ed.; Società Editrice Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Laminated Composite Doubly-Curved Shell Structures. Differential and Integral Quadrature. Strong Formulation Finite Element Method, 1st ed; Società Editrice Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong formulation finite element method based on differential quadrature: A survey. Appl. Mech. Rev. 2015, 67, 020801. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Viola, E.; Tornabene, F.; Fantuzzi, N.; Zenkour, A.M. Analysis of Thick Isotropic and Cross-Ply Laminated Plates by Generalized Differential Quadrature Method and a Unified Formulation. Compos. Part B-Eng. 2014, 58, 544–552. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The Strong Formulation Finite Element Method: Stability and Accuracy. Fract. Struct. Integr. 2014, 29, 251–265. [Google Scholar]
- Fantuzzi, N.; Bacciocchi, M.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. Radial Basis Functions Based on Differential Quadrature Method for the Free Vibration of Laminated Composite Arbitrary Shaped Plates. Compos. Part B-Eng. 2015, 78, 65–78. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong Formulation Isogeometric Analysis (SFIGA) for Laminated Composite Arbitrarily Shaped Plates. Compos. Part B-Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Neves, A.M.A.; Ferreira, A.J.M. MLSDQ Based on RBFs for the Free Vibrations of Laminated Composite Doubly-Curved Shells. Compos. Part B-Eng. 2016, 99, 30–47. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Dimitri, R.; Tornabene, F. A SFEM-Based Evaluation of Mode-I Stress Intensity Factor in Composite Structures. Compos. Struct. 2016, 145, 162–185. [Google Scholar] [CrossRef]
- Dimitri, R.; Fantuzzi, N.; Tornabene, F.; Zavarise, G. Innovative Numerical Methods Based on SFEM and IGA for Computing Stress Concentrations in Isotropic Plates with Discontinuities. Int. J. Mech. Sci. 2016, 118, 166–187. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. DiQuMASPAB: Differential Quadrature for Mechanics of Anisotropic Shells, Plates, Arches and Beams. User Manual, 1st ed.; Società Editrice Esculapio: Bologna, Italy, 2018; Available online: https://diqumaspab.editrice-esculapio.com (accessed on 2 February 2018).










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Ferreira, A.J.M. On the Convergence of Laminated Composite Plates of Arbitrary Shape through Finite Element Models. J. Compos. Sci. 2018, 2, 16. https://doi.org/10.3390/jcs2010016
Fantuzzi N, Tornabene F, Bacciocchi M, Ferreira AJM. On the Convergence of Laminated Composite Plates of Arbitrary Shape through Finite Element Models. Journal of Composites Science. 2018; 2(1):16. https://doi.org/10.3390/jcs2010016
Chicago/Turabian StyleFantuzzi, Nicholas, Francesco Tornabene, Michele Bacciocchi, and Antonio J.M. Ferreira. 2018. "On the Convergence of Laminated Composite Plates of Arbitrary Shape through Finite Element Models" Journal of Composites Science 2, no. 1: 16. https://doi.org/10.3390/jcs2010016
APA StyleFantuzzi, N., Tornabene, F., Bacciocchi, M., & Ferreira, A. J. M. (2018). On the Convergence of Laminated Composite Plates of Arbitrary Shape through Finite Element Models. Journal of Composites Science, 2(1), 16. https://doi.org/10.3390/jcs2010016







