Figure 1.
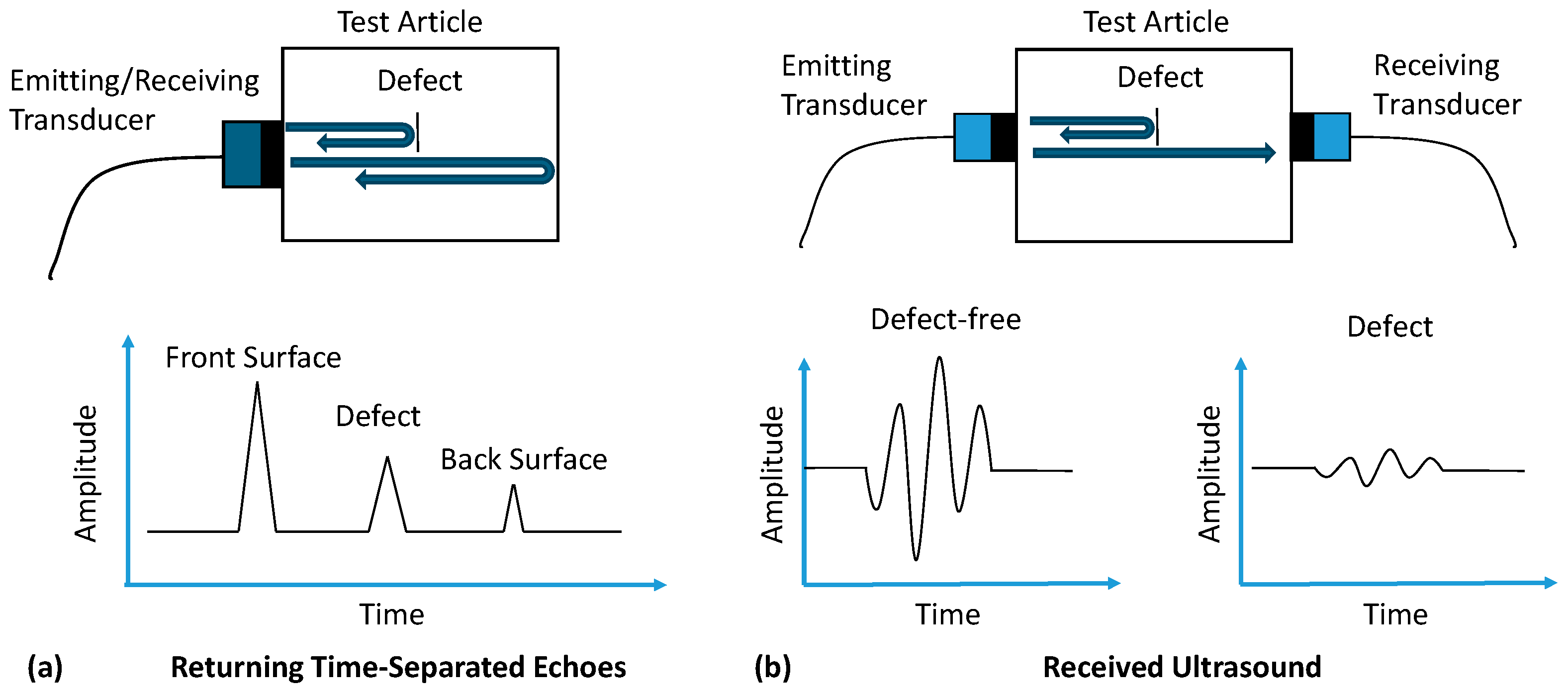
Schematic comparison of (a) echo-mode and (b) through-transmission (TTU) ultrasonic evaluation methods. In the echo-mode, a pulse is reflected off the internal interfaces and surfaces based on acoustic impedance differences, returning time-separated echoes. In the TTU mode, a pulse travels through the material, with defects causing attenuation or absence of the signal on the opposite side, as received echoes, owing to the impedance mismatch.
Figure 1.
Schematic comparison of (a) echo-mode and (b) through-transmission (TTU) ultrasonic evaluation methods. In the echo-mode, a pulse is reflected off the internal interfaces and surfaces based on acoustic impedance differences, returning time-separated echoes. In the TTU mode, a pulse travels through the material, with defects causing attenuation or absence of the signal on the opposite side, as received echoes, owing to the impedance mismatch.
Figure 2.
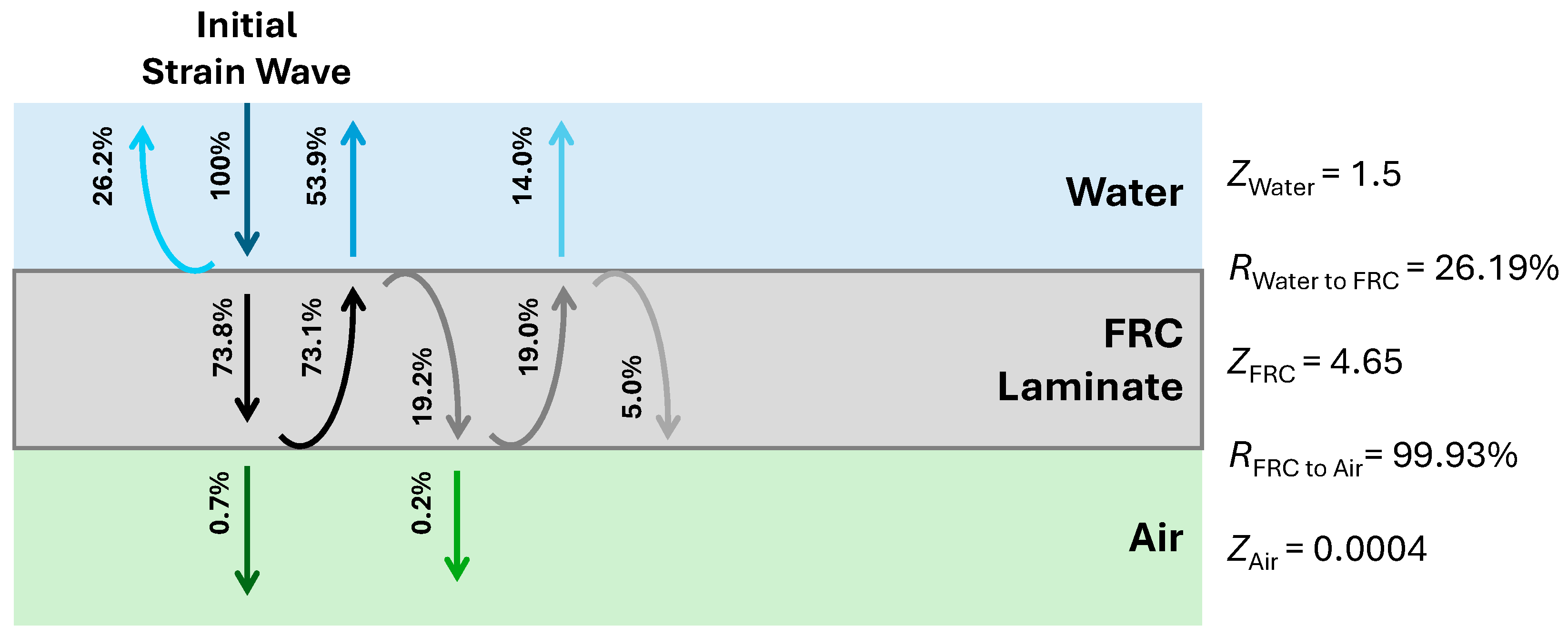
Reflection and transmission coefficients for ultrasonic waves interacting with water, FRC laminate, and air. The reflection coefficient at the water–FRC laminate interface was 26.19%, whereas complete reflection (99.93%) occurred at the FRC–air interface owing to the significant impedance mismatch [
1].
Figure 2.
Reflection and transmission coefficients for ultrasonic waves interacting with water, FRC laminate, and air. The reflection coefficient at the water–FRC laminate interface was 26.19%, whereas complete reflection (99.93%) occurred at the FRC–air interface owing to the significant impedance mismatch [
1].
Figure 3.
Representative standard drawing illustrating the 18 baselines (B) and defects (D), with 36 total waveforms of 49 pixels, equaling 1764 points [
1]. Defects are highlighted in purple.
Figure 3.
Representative standard drawing illustrating the 18 baselines (B) and defects (D), with 36 total waveforms of 49 pixels, equaling 1764 points [
1]. Defects are highlighted in purple.
Figure 4.
This figure illustrates the generation of a pixel-level dataset using the TTU scanning process. (
a) shows the TTU signal amplitude (V
MSA) at a position in volts and peak acquisition gate, (
b) corresponding voltage-to-color mapping illustrating that the peak signal amplitude (V
high) was set to white, amplitudes between the threshold (V
threshold) and the lowest signal amplitude (V
low) were set to red, and signal amplitudes above the threshold (V
threshold) were mapped to a color pallet using 256 shades of grey gradient, and (
c) shows the resulting two-dimensional position array, where each 7 × 7 matrix array of 49 pixels was extracted as an individual sample from either the baseline or defect regions, resulting in a total of 1764 pixel-level waveforms across the dataset [
1].
Figure 4.
This figure illustrates the generation of a pixel-level dataset using the TTU scanning process. (
a) shows the TTU signal amplitude (V
MSA) at a position in volts and peak acquisition gate, (
b) corresponding voltage-to-color mapping illustrating that the peak signal amplitude (V
high) was set to white, amplitudes between the threshold (V
threshold) and the lowest signal amplitude (V
low) were set to red, and signal amplitudes above the threshold (V
threshold) were mapped to a color pallet using 256 shades of grey gradient, and (
c) shows the resulting two-dimensional position array, where each 7 × 7 matrix array of 49 pixels was extracted as an individual sample from either the baseline or defect regions, resulting in a total of 1764 pixel-level waveforms across the dataset [
1].
Figure 5.
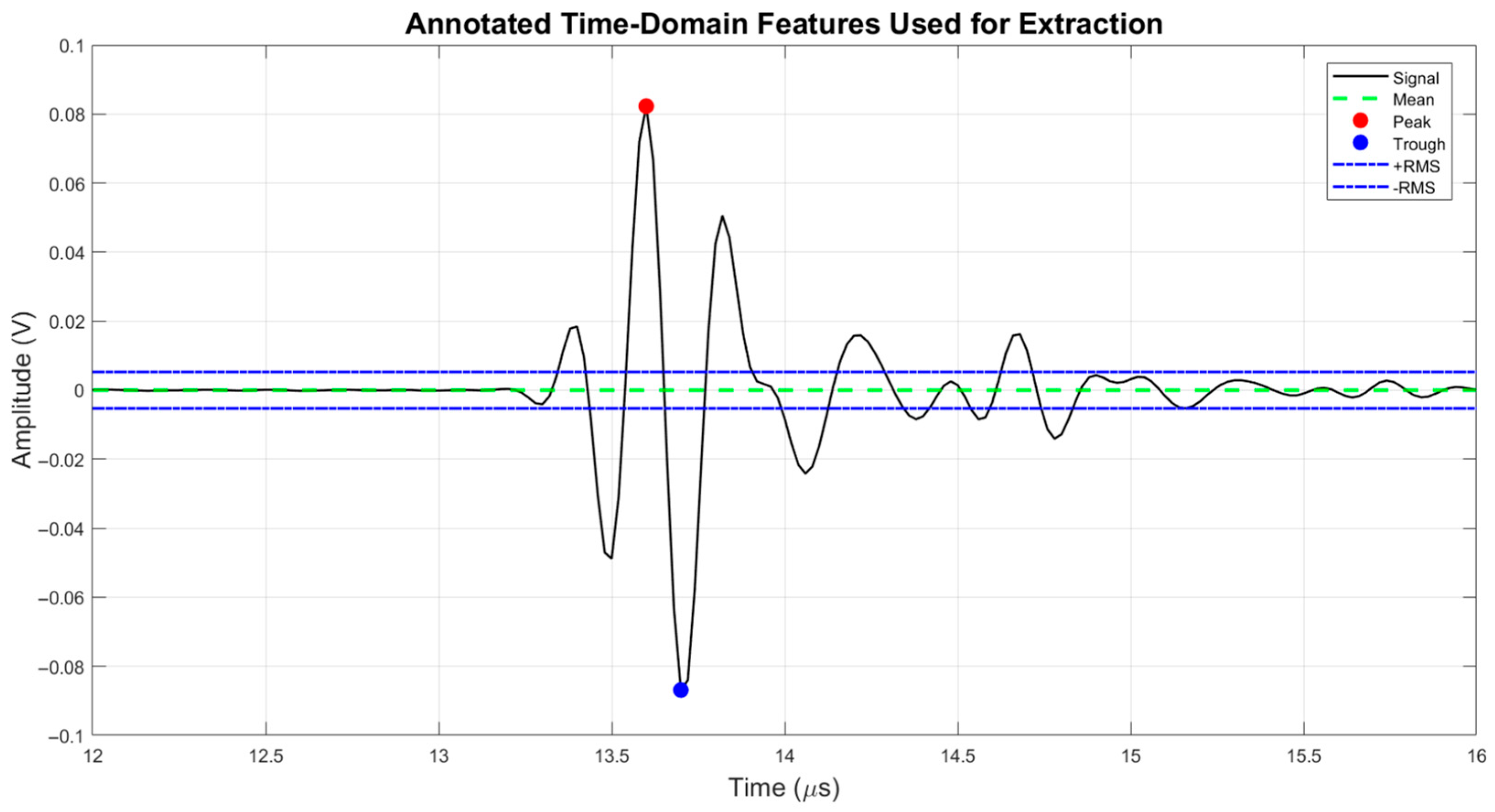
The annotated time-domain features were extracted from a representative ultrasonic waveform, highlighting the mean amplitude, peak-to-peak values (peak and trough), and RMS amplitude boundaries. The variance, skewness, and kurtosis were computed based on the overall signal shape and dispersion.
Figure 5.
The annotated time-domain features were extracted from a representative ultrasonic waveform, highlighting the mean amplitude, peak-to-peak values (peak and trough), and RMS amplitude boundaries. The variance, skewness, and kurtosis were computed based on the overall signal shape and dispersion.
Figure 6.
Annotated frequency-domain features were extracted from a representative ultrasonic waveform, highlighting the spectral centroid, dominant frequency, and spectral roll-off (85% cumulative energy). The spectral spread, skewness, and kurtosis were computed based on the overall spectral distribution.
Figure 6.
Annotated frequency-domain features were extracted from a representative ultrasonic waveform, highlighting the spectral centroid, dominant frequency, and spectral roll-off (85% cumulative energy). The spectral spread, skewness, and kurtosis were computed based on the overall spectral distribution.
Figure 7.
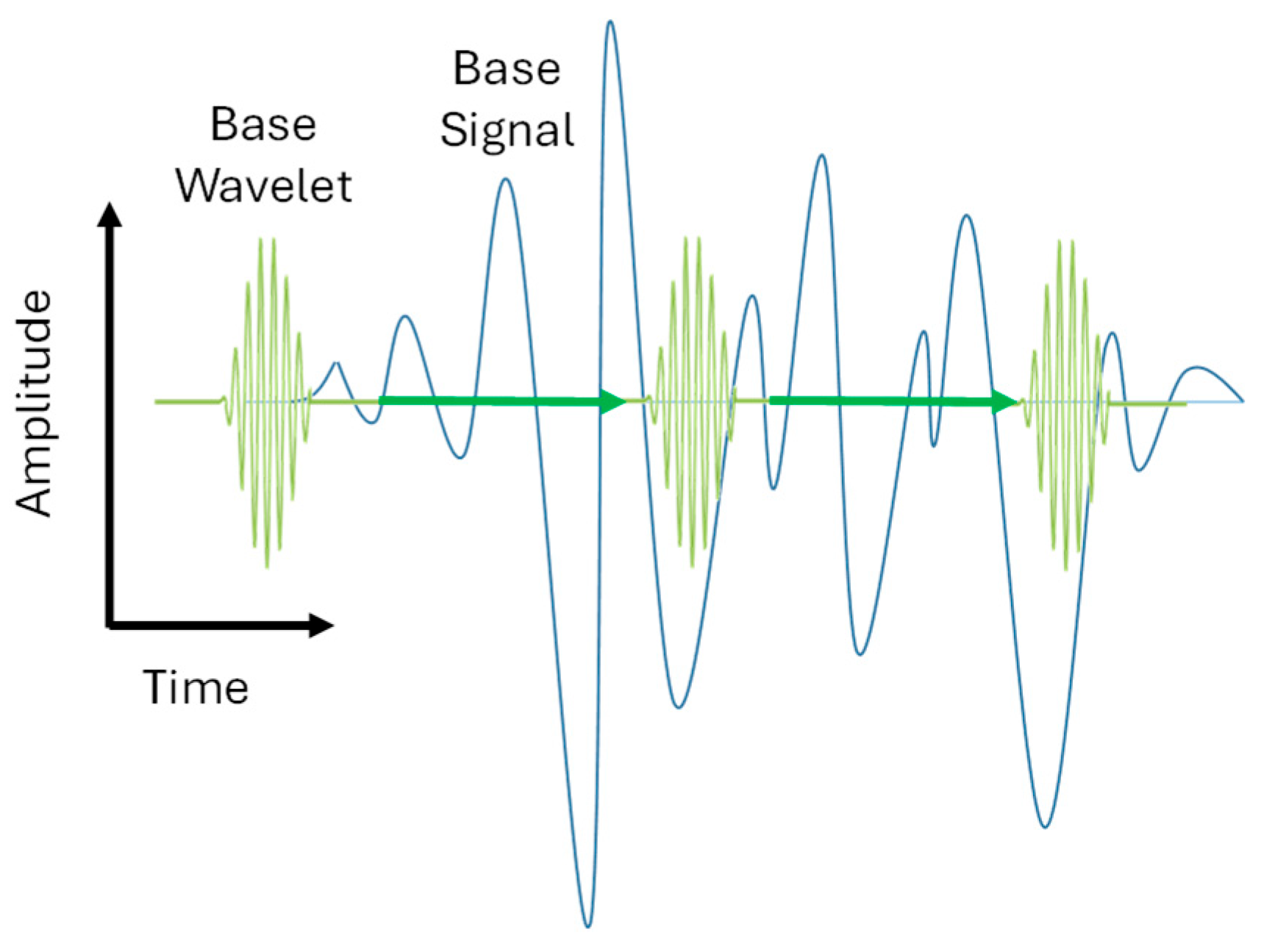
Schematic representation of the wavelet transform process. A compact base wavelet with the green color is convolved with an ultrasonic base signal with the blue color to produce localized coefficients reflecting the time-frequency signal dynamics. The convolution operation is indicated by the green arrows.
Figure 7.
Schematic representation of the wavelet transform process. A compact base wavelet with the green color is convolved with an ultrasonic base signal with the blue color to produce localized coefficients reflecting the time-frequency signal dynamics. The convolution operation is indicated by the green arrows.
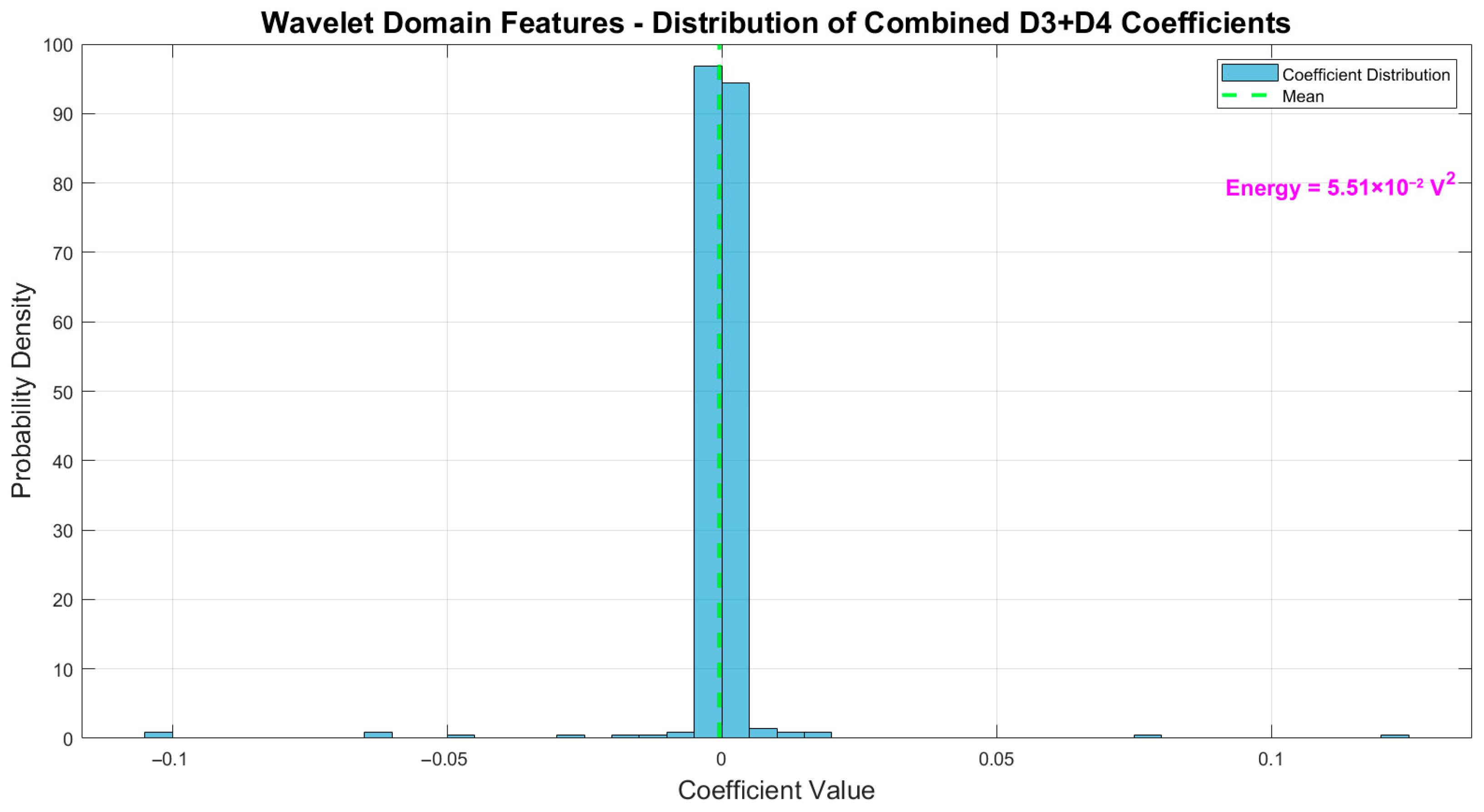
Figure 8.
DWT wavelet decomposition histogram of the combined D3 + D4 coefficients of the db4 wavelet coefficient distribution. The mean is indicated by the dashed green line, and the total energy of the detailed coefficients is annotated, highlighting the concentration of the signal energy in the mid-frequency bands.
Figure 8.
DWT wavelet decomposition histogram of the combined D3 + D4 coefficients of the db4 wavelet coefficient distribution. The mean is indicated by the dashed green line, and the total energy of the detailed coefficients is annotated, highlighting the concentration of the signal energy in the mid-frequency bands.
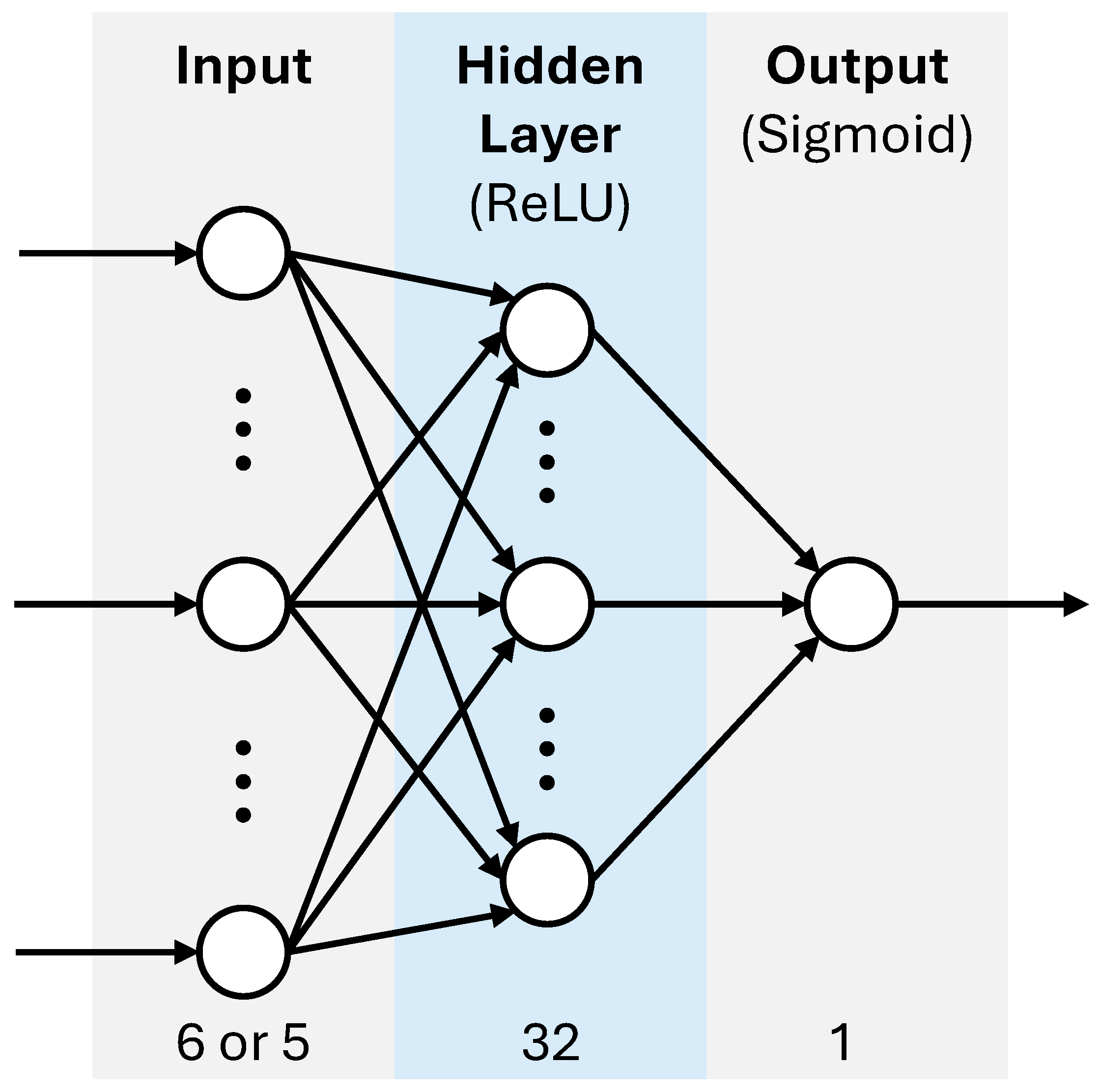
Figure 9.
This NN architecture is used for the binary classification of ultrasonic signal waveform features. The model included a 6-or-5-neuron input layer corresponding to the domain-specific input features, a fully connected hidden layer with 32 neurons using ReLU activation, and a final output layer with sigmoid activation for binary classification. The input layer of the time-domain NN has 6 neurons, but the input layer of the frequency- or wavelet domain NN has 5 neurons. The arrows are feedforward signal transmission. A multitude of neurons is represented by an ellipsis in each NN layer.
Figure 9.
This NN architecture is used for the binary classification of ultrasonic signal waveform features. The model included a 6-or-5-neuron input layer corresponding to the domain-specific input features, a fully connected hidden layer with 32 neurons using ReLU activation, and a final output layer with sigmoid activation for binary classification. The input layer of the time-domain NN has 6 neurons, but the input layer of the frequency- or wavelet domain NN has 5 neurons. The arrows are feedforward signal transmission. A multitude of neurons is represented by an ellipsis in each NN layer.
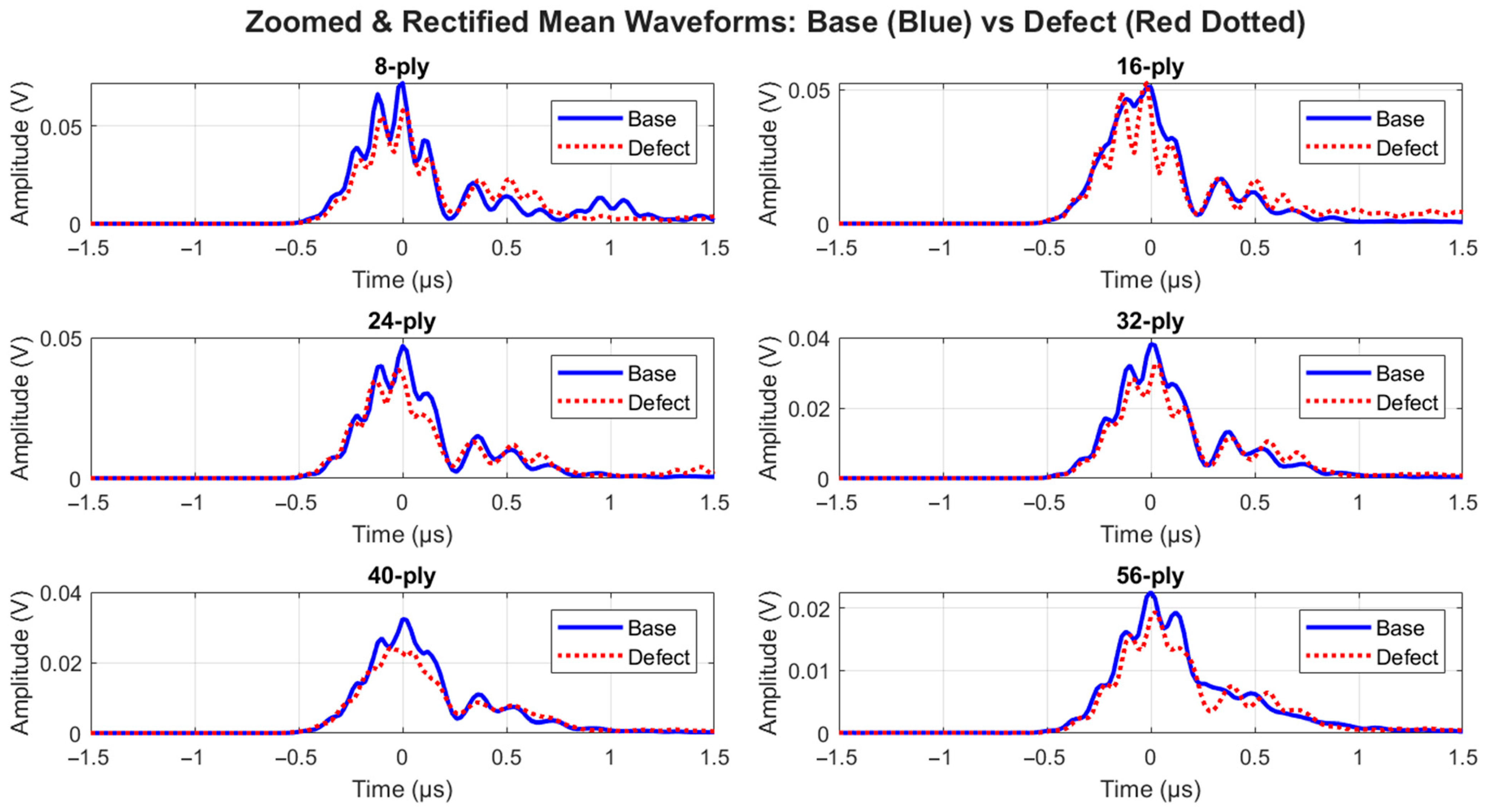
Figure 10.
Mosaic of the mean waveforms in the time-domain comparing baseline (solid blue) and defect (dashed red) across six different ply counts.
Figure 10.
Mosaic of the mean waveforms in the time-domain comparing baseline (solid blue) and defect (dashed red) across six different ply counts.
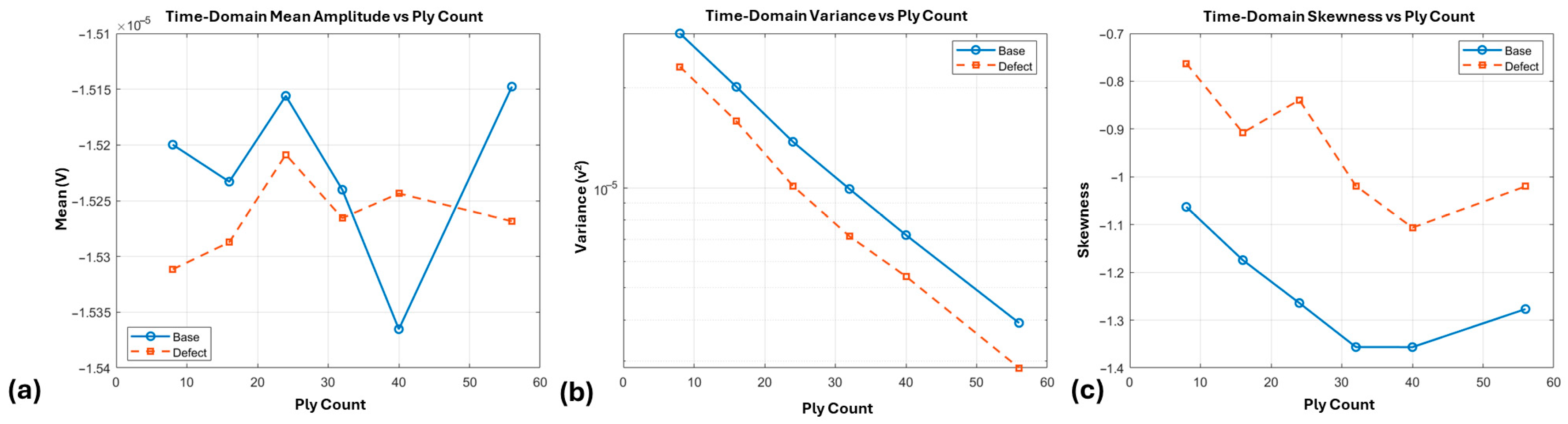
Figure 11.
Time-domain features: (a) mean amplitude vs. ply count, (b) variance vs. ply count, and (c) skewness vs. ply count for baseline and defect conditions.
Figure 11.
Time-domain features: (a) mean amplitude vs. ply count, (b) variance vs. ply count, and (c) skewness vs. ply count for baseline and defect conditions.
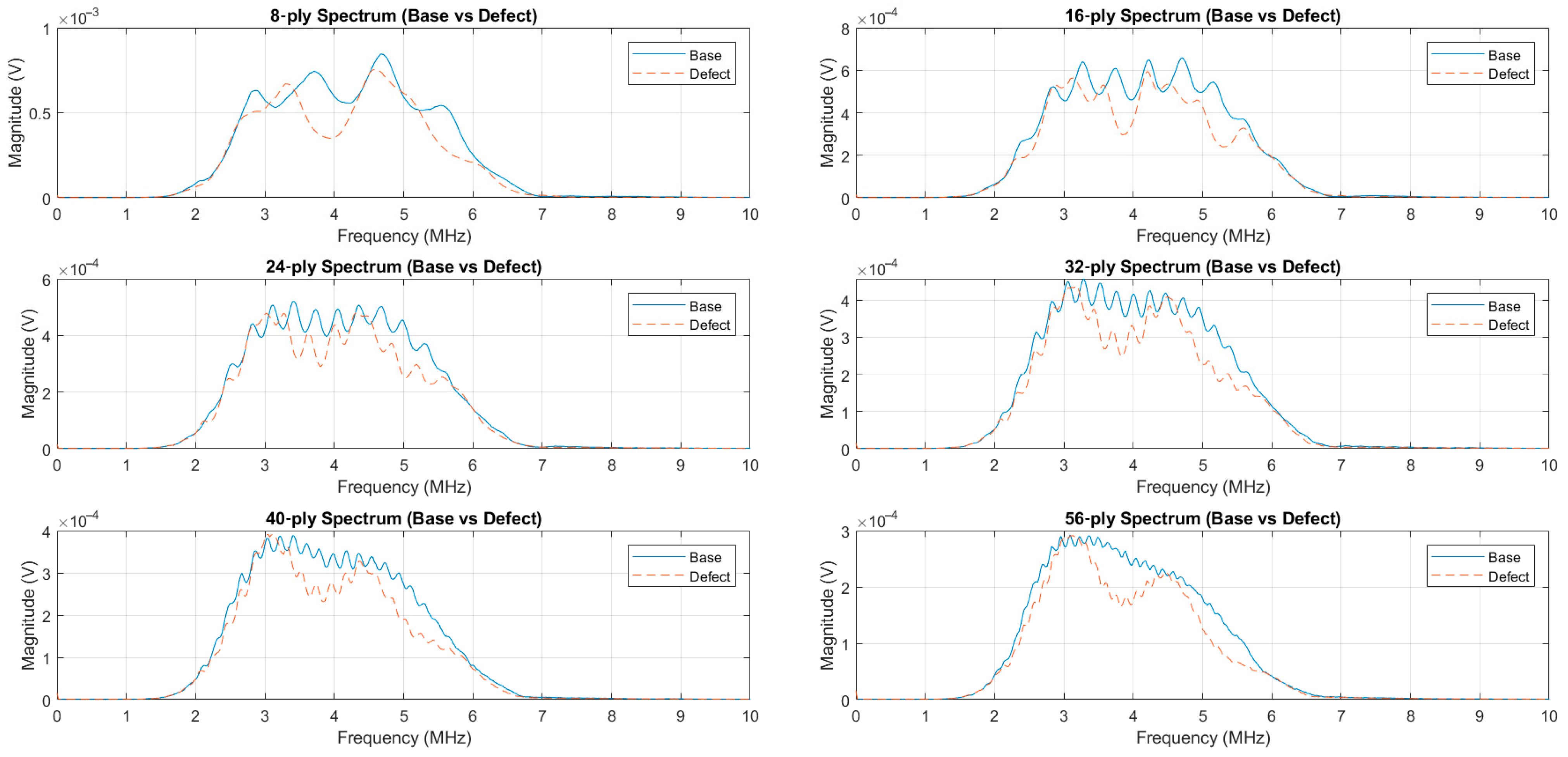
Figure 12.
Mosaic frequency spectrum comparing baseline (solid blue) and defect (dashed red) across six ply counts.
Figure 12.
Mosaic frequency spectrum comparing baseline (solid blue) and defect (dashed red) across six ply counts.
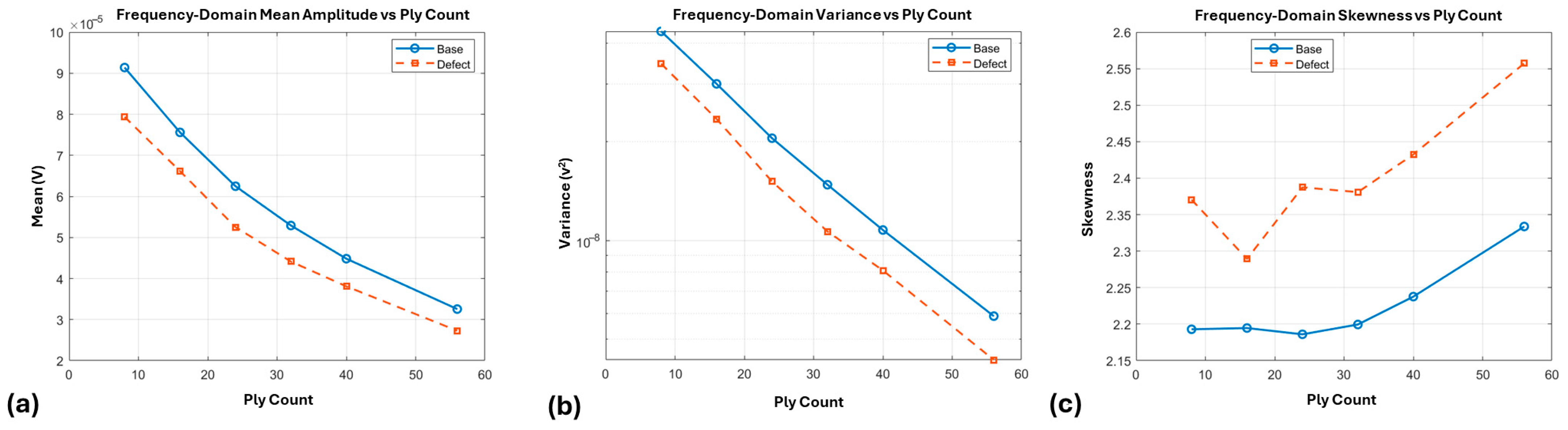
Figure 13.
Frequency-domain features: (a) mean amplitude versus ply count, (b) variance versus ply count, and (c) skewness versus ply count for baseline and defect conditions.
Figure 13.
Frequency-domain features: (a) mean amplitude versus ply count, (b) variance versus ply count, and (c) skewness versus ply count for baseline and defect conditions.
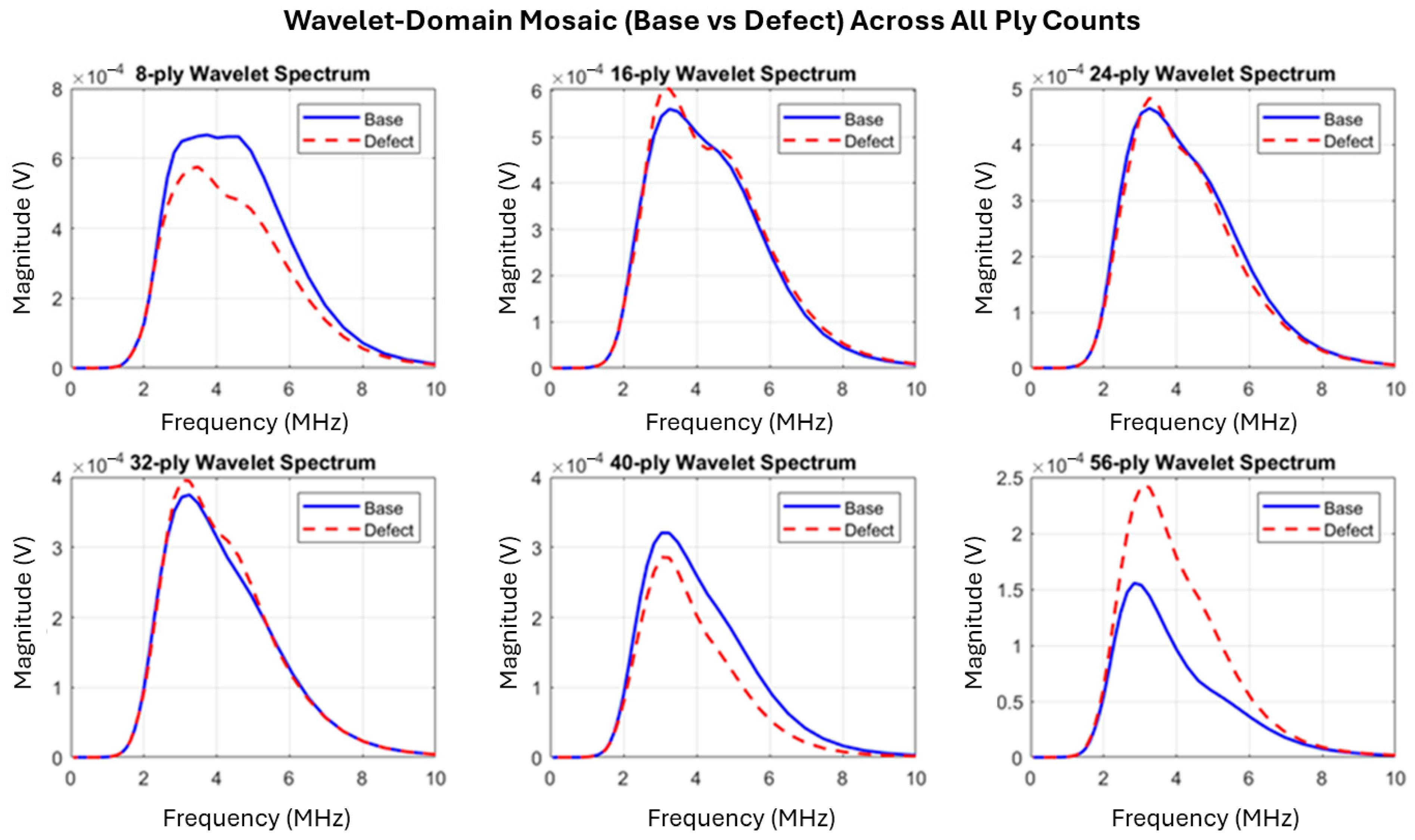
Figure 14.
Mosaic wavelet-domain comparing baseline (solid blue) and defect (dashed red) across six ply counts using db4 decomposition.
Figure 14.
Mosaic wavelet-domain comparing baseline (solid blue) and defect (dashed red) across six ply counts using db4 decomposition.
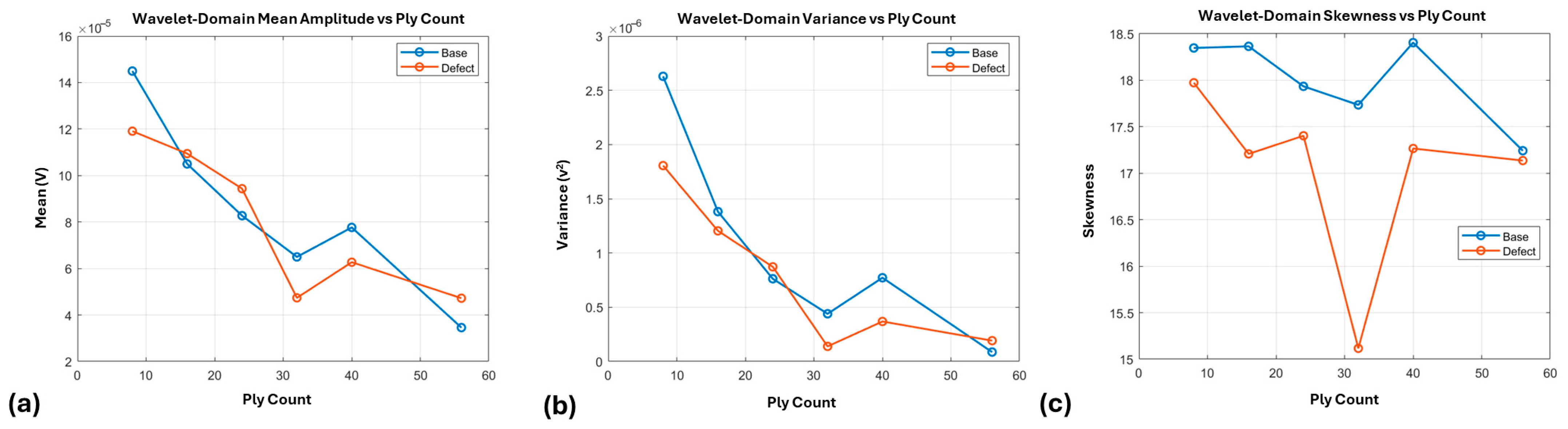
Figure 15.
Wavelet-domain features: (a) mean amplitude versus ply count, (b) variance versus ply count, and (c) skewness versus ply count for the baseline and defect conditions.
Figure 15.
Wavelet-domain features: (a) mean amplitude versus ply count, (b) variance versus ply count, and (c) skewness versus ply count for the baseline and defect conditions.
Figure 16.
Training and validation loss curves for each domain-specific NN classifier. Subplots (a), (b), and (c) correspond to the time, frequency, and wavelet domains, respectively. The NN models converged rapidly with minimal divergence between training and validation performance, indicating strong generalization and effective learning.
Figure 16.
Training and validation loss curves for each domain-specific NN classifier. Subplots (a), (b), and (c) correspond to the time, frequency, and wavelet domains, respectively. The NN models converged rapidly with minimal divergence between training and validation performance, indicating strong generalization and effective learning.
Figure 17.
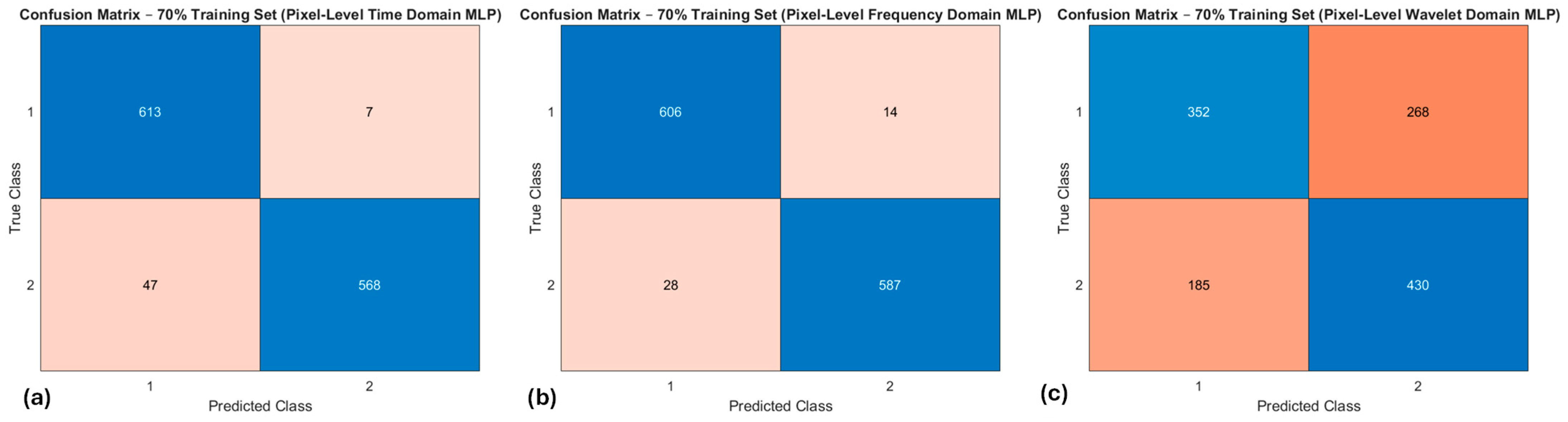
Confusion matrices showing the training set performance of pixel-level NN classifiers performed on the training set: (a) time-domain, (b) frequency-domain, and (c) wavelet-domain features. True class labels are shown along the y-axis and predicted classes along the x-axis. The levels of true positive (TP) and true negative (TN) are mapped to a blue color palette, where a lighter blue color is associated with a lower level. Likewise, the levels of false positive (FP) and false negative (FN) are mapped to a red color palette, where a lighter red color is associated with a lower level.
Figure 17.
Confusion matrices showing the training set performance of pixel-level NN classifiers performed on the training set: (a) time-domain, (b) frequency-domain, and (c) wavelet-domain features. True class labels are shown along the y-axis and predicted classes along the x-axis. The levels of true positive (TP) and true negative (TN) are mapped to a blue color palette, where a lighter blue color is associated with a lower level. Likewise, the levels of false positive (FP) and false negative (FN) are mapped to a red color palette, where a lighter red color is associated with a lower level.
Figure 18.
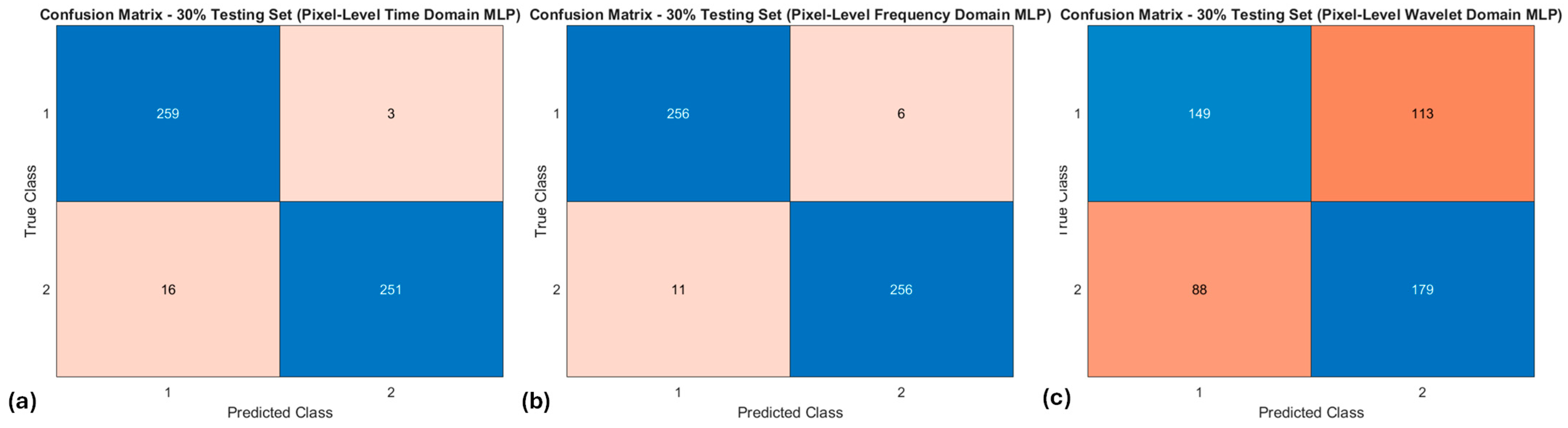
Confusion matrices showing the testing set performance of pixel-level NN classifiers performed on the testing set: (a) time-domain, (b) frequency-domain, and (c) wavelet-domain features. True class labels are shown along the y-axis and predicted classes along the x-axis. The levels of true positive (TP) and true negative (TN) are mapped to a blue color palette, where a lighter blue color is associated with a lower level. Likewise, the levels of false positive (FP) and false negative (FN) are mapped to a red color palette, where a lighter red color is associated with a lower level.
Figure 18.
Confusion matrices showing the testing set performance of pixel-level NN classifiers performed on the testing set: (a) time-domain, (b) frequency-domain, and (c) wavelet-domain features. True class labels are shown along the y-axis and predicted classes along the x-axis. The levels of true positive (TP) and true negative (TN) are mapped to a blue color palette, where a lighter blue color is associated with a lower level. Likewise, the levels of false positive (FP) and false negative (FN) are mapped to a red color palette, where a lighter red color is associated with a lower level.
Figure 19.
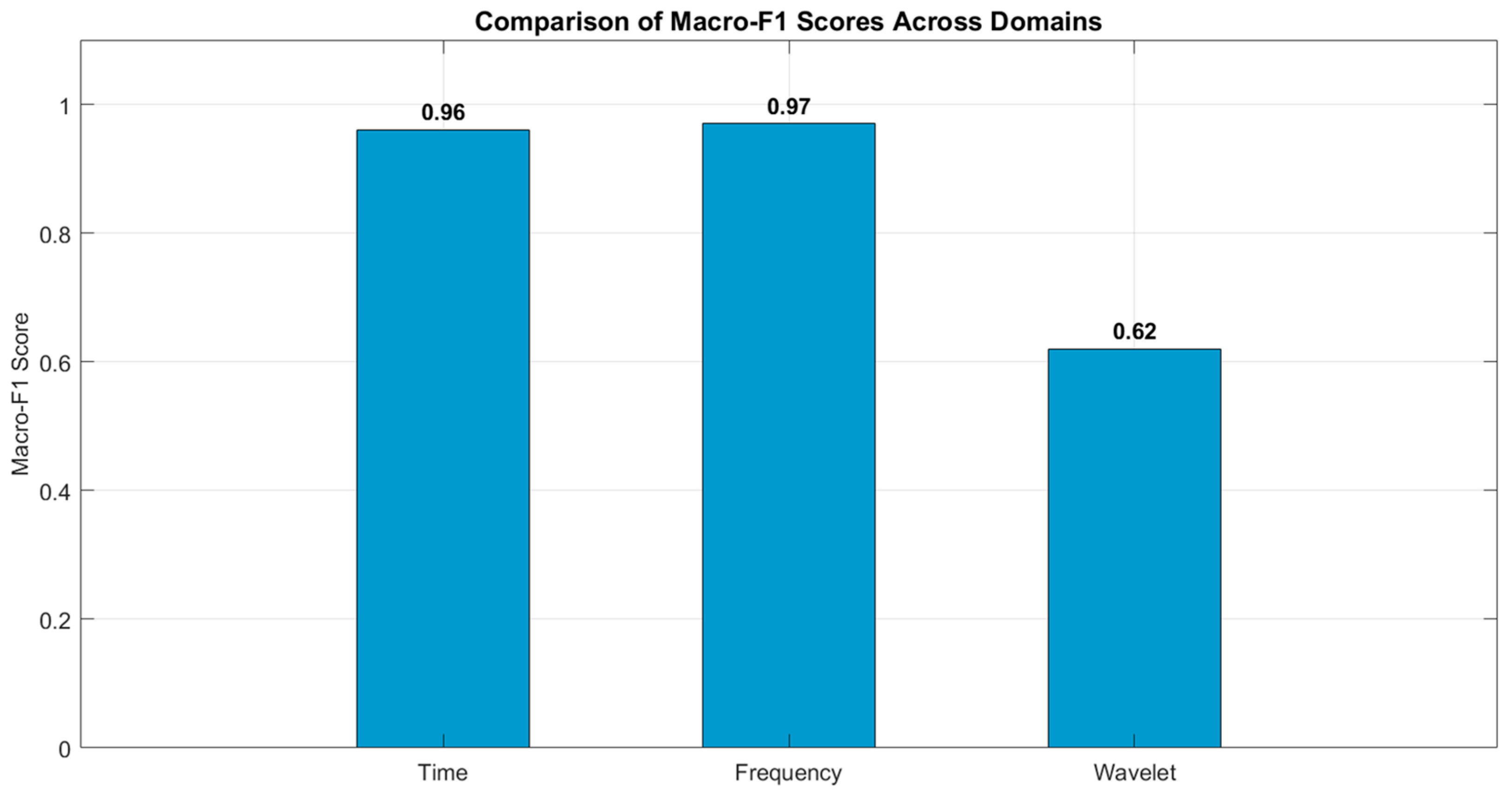
Testing macro-F1 bar chart comparing scores across the time, frequency, and wavelet domains.
Figure 19.
Testing macro-F1 bar chart comparing scores across the time, frequency, and wavelet domains.
Table 1.
TTU Method Setup for Pixel-Level TTU of FRC Laminates.
Table 1.
TTU Method Setup for Pixel-Level TTU of FRC Laminates.
| Dataset Component | Details |
|---|
| Setup Type | TTU (Through-Transmission Ultrasound) |
| Transducer Frequency | 5 MHz |
| Incident Angle | 0° |
| Water Column Standoff | 4.00" |
| Representative Reference Standard | FRC laminate |
| Known Regions (Baseline) | No defects |
| Known Regions (Defects) | Release Fabric Inserts |
| Total Waveforms | 1764 pixel-levels |
| Waveforms-Baseline (No Defects) | 18 |
| Waveforms-Release Fabric Defect | 18 |
| Ply Count | (8, 16, 24, 32, 40, 56) |
Table 2.
Summary of extracted feature descriptions and units categorized by domain.
Table 2.
Summary of extracted feature descriptions and units categorized by domain.
| Domain | Feature Description | Units |
|---|
| Time Domain | Mean | Volts (V) |
| Variance | Volts2 (V2) |
| Skewness | Dimensionless |
| Kurtosis | Dimensionless |
| Peak-to-Peak Amplitude | Volts (V) |
| RMS Amplitude | Volts (V) |
| Frequency Domain | Spectral Centroid | Hertz (Hz) |
| Spectral Spread (Standard Deviation) | Hertz (Hz) |
| Spectral Skewness | Dimensionless |
| Spectral Kurtosis | Dimensionless |
| Spectral Roll-Off (85% Energy) | Hertz (Hz) |
| Wavelet Domain | Mean of Wavelet Coefficients (D3 + D4) | Volts (V) |
| Variance of Wavelet Coefficients | Volts2 (V2) |
| Skewness of Wavelet Coefficients | Dimensionless |
| Kurtosis of Wavelet Coefficients | Dimensionless |
| Energy of Wavelet Coefficients | Volts2 (V2) |
Table 3.
NN architectures for defect classification.
Table 3.
NN architectures for defect classification.
| Layer | Number of Neurons | Activation Function |
|---|
| Input Layer | 6 for time domain features or
5 for frequency or wavelet domain features | - |
| Hidden Layer | 32 | ReLU |
| Output Layer | 1 | Sigmoid |
Table 4.
Summary of key experimental parameters and training configurations used for NNs.
Table 4.
Summary of key experimental parameters and training configurations used for NNs.
| Item | Description |
|---|
| Number of Input Features | 6 time-domain features, 5 frequency-domain features, 5 wavelet-domain features |
| Class Labels | 1 = Baseline, 2 = Defect |
| Output Activation | Sigmoid function |
| Decision Threshold | 0.5 (probability > 0.5 = Defect, ≤0.5 = Baseline) |
| Train/Test Split | 70% Training, 30% Testing |
| Internal Training Split | 80% of training set for weight updates, 20% for internal validation |
| External Testing | 30% reserved testing set (not used during training) |
| Hidden Layer Size | 32 neurons (fully connected) |
| Hidden Layer Activation | Rectified Linear Unit (ReLU) |
| Training Algorithm | Levenberg–Marquardt backpropagation (trainlm) |
| Loss Function | Binary Cross-Entropy |
| Regularization | 0.25 (to prevent overfitting) |
| Early Stopping Criterion | Maximum 6 consecutive validation failures |
| Epochs | 100 |
| Batch Size | 32 samples per batch |
Table 5.
Domain specific p-values based on t-test.
Table 5.
Domain specific p-values based on t-test.
| Ply Count | Time-Domain p-Value | Frequency-Domain p-Value | Wavelet-Domain p-Value |
|---|
| 8-ply | 1.49 × 10−1 | 1.49 × 10−1 | 1.12 × 10−7 |
| 16-ply | 1.71 × 10−1 | 1.71 × 10−1 | 2.32 × 10−1 |
| 24-ply | 7.72 × 10−2 | 7.72 × 10−2 | 8.66 × 10−5 |
| 32-ply | 6.51 × 10−2 | 6.51 × 10−2 | 1.58 × 10−23 |
| 40-ply | 9.98 × 10−2 | 9.98 × 10−2 | 1.40 × 10−9 |
| 56-ply | 8.00 × 10−2 | 8.00 × 10−2 | 4.16 × 10−25 |
Table 6.
NN classification performance across time, frequency, and wavelet domains, based on the training set.
Table 6.
NN classification performance across time, frequency, and wavelet domains, based on the training set.
| Domain | Macro-F1 Score | Accuracy (%) | True Positive (TP) | True Negative (TN) | False Positive (FP) | False Negative (FN) |
|---|
| Time | 0.95 | 95.63 | 568 | 613 | 7 | 47 |
| Frequency | 0.97 | 96.60 | 587 | 606 | 14 | 28 |
| Wavelet | 0.65 | 63.32 | 430 | 352 | 268 | 185 |
Table 7.
NN classification performance across time, frequency, and wavelet domains, based on the testing set.
Table 7.
NN classification performance across time, frequency, and wavelet domains, based on the testing set.
| Domain | Macro-F1 Score | Accuracy (%) | True Positive (TP) | True Negative (TN) | False Positive (FP) | False Negative (FN) |
|---|
| Time | 0.96 | 96.31 | 251 | 259 | 3 | 16 |
| Frequency | 0.97 | 96.78 | 256 | 256 | 6 | 11 |
| Wavelet | 0.62 | 61.91 | 179 | 149 | 113 | 88 |