Investigating the Influence of Mechanical Loads on Built-Up Edge Formation Across Different Length Scales at Diamond–Transition Metal Interfaces
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
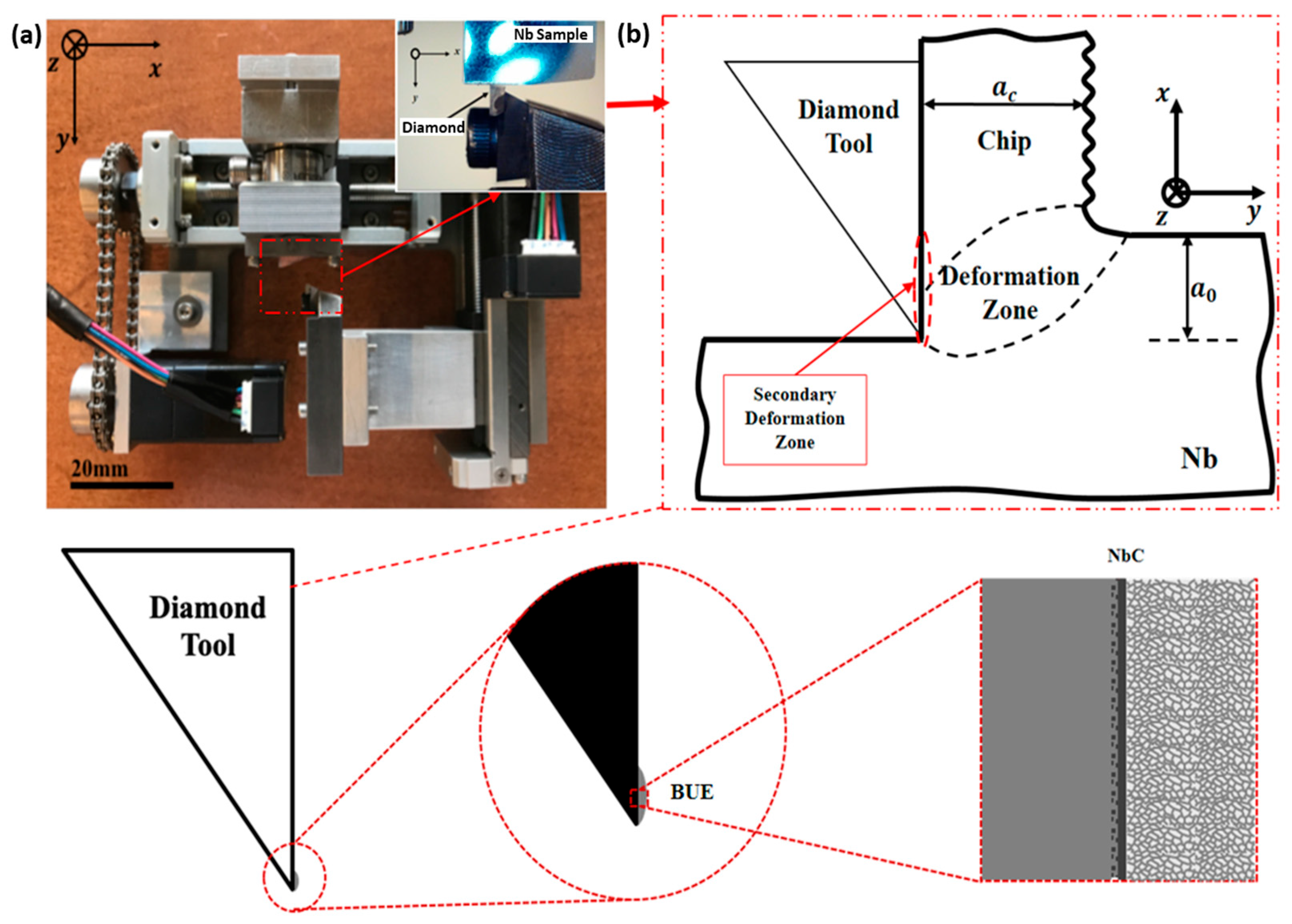
3.1. Deformation Configuration
3.2. Surface Integrity
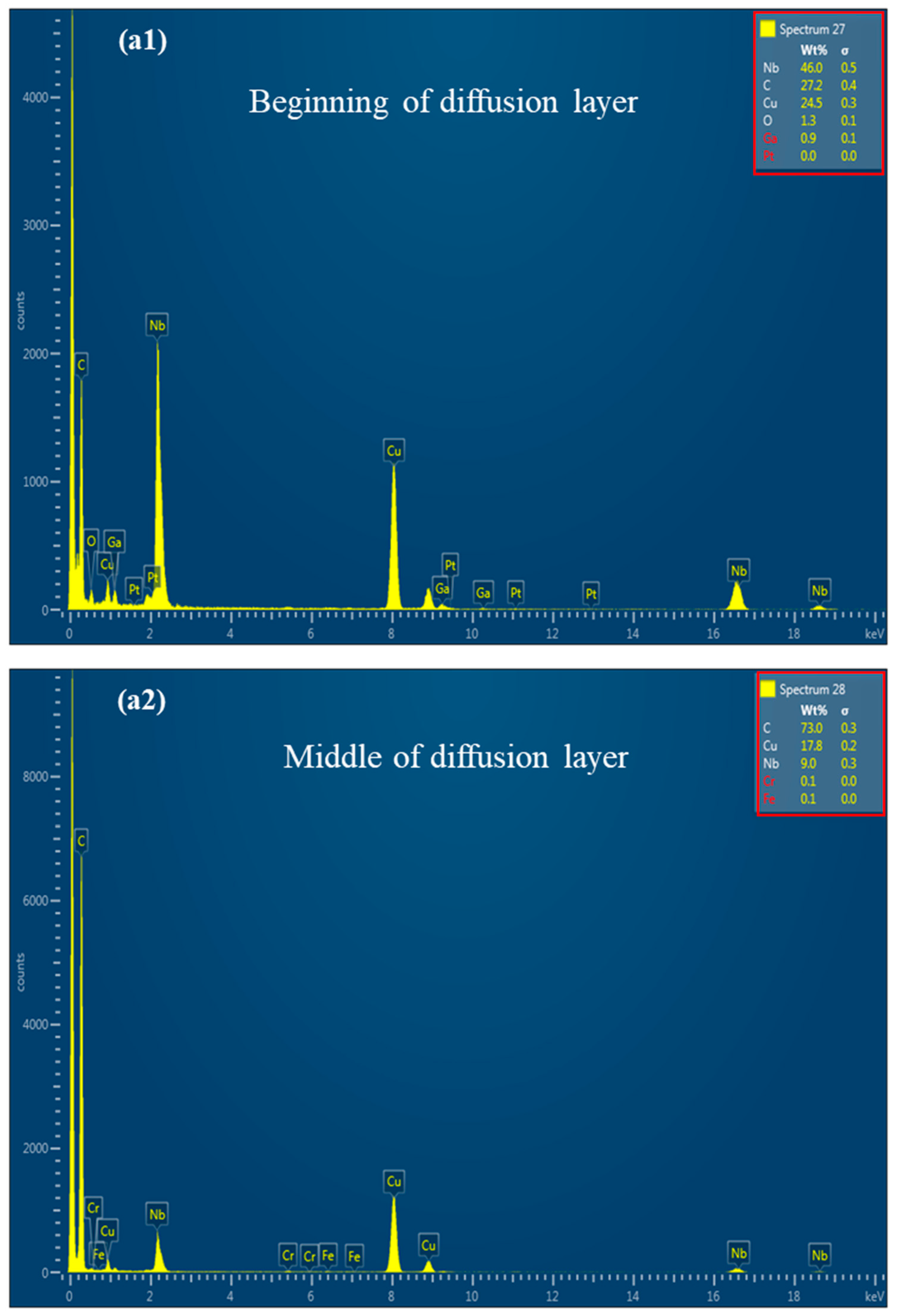
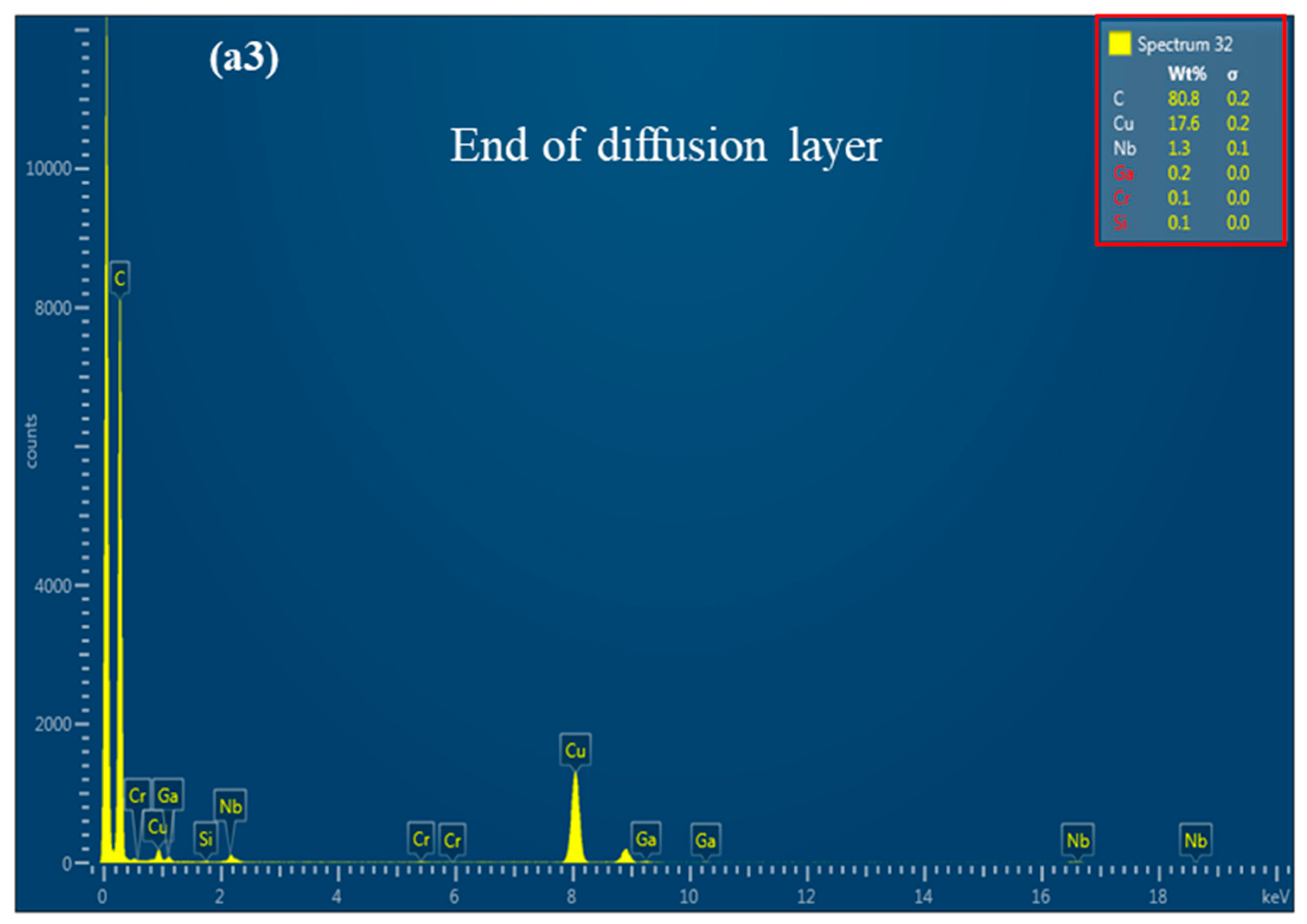
3.3. Characterization of the Underlying Deformation and the Element Concentration Profiles Across the Interface
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| depth of cut | |
| D | diffusion coeffiecient |
| activation energy | |
| J | diffusion flux |
| thermal diffusivity | |
| R | gas constant |
| T | temperature |
| V | machining velocity |
| Vc | chip velocity |
| w | workpeice thickness |
| ε | shear strain |
| γo | rack angle |
| shear angle |
References
- Schey, J.A. Introduction to Manufacturing Processes; McGraw-Hill: New York, NY, USA, 1987; Volume 2. [Google Scholar]
- Schulz, H.; Moriwaki, T. High-speed Machining. CIRP Ann. 1992, 41, 637–643. [Google Scholar] [CrossRef]
- Artini, C.; Muolo, M.L.; Passerone, A. Diamond–metal interfaces in cutting tools: A review. J. Mater. Sci. 2012, 47, 3252–3264. [Google Scholar] [CrossRef]
- Zou, L.; Yin, J.; Huang, Y.; Zhou, M. Essential causes for tool wear of single crystal diamond in ultra-precision cutting of ferrous metals. Diam. Relat. Mater. 2018, 86, 29–40. [Google Scholar] [CrossRef]
- Abolghasem, S.; Basu, S.; Shekhar, S.; Cai, J.; Shankar, M.R. Mapping subgrain sizes resulting from severe simple shear deformation. Acta Mater. 2012, 60, 376–386. [Google Scholar] [CrossRef]
- Tomac, N.; Tønnessen, K.; Rasch, F.O.; Mikac, T. A study of factors that affect the build-up material formation. In AMST’05 Advanced Manufacturing Systems and Technology: Proceedings of the Seventh International Conference; Springer: Vienna, Austria, 2005; pp. 183–192. [Google Scholar]
- Paul, E.; Evans, C.J.; Mangamelli, A.; McGlauflin, M.L.; Polvani, R.S. Chemical aspects of tool wear in single point diamond turning. Precis. Eng. 1996, 18, 4–19. [Google Scholar] [CrossRef]
- Qu, J.; Blau, P.J.; Watkins, T.R.; Cavin, O.B.; Kulkarni, N.S. Friction and wear of titanium alloys sliding against metal, polymer, and ceramic counterfaces. Wear 2005, 258, 1348–1356. [Google Scholar] [CrossRef]
- Kumar, B.; Kumar, D.; Chaudhry, V. Tribological behavior of zirconium alloy against stainless steel under different conditions. Tribol. Int. 2023, 189, 108995. [Google Scholar] [CrossRef]
- Murakami, T.; Mano, H.; Kaneda, K.; Hata, M.; Sasaki, S.; Sugimura, J. Friction and wear properties of zirconium and niobium in a hydrogen environment. Wear 2010, 268, 721–729. [Google Scholar] [CrossRef]
- Bayer, R.G. Mechanical Wear Prediction and Prevention; Marcel Dekker: New York, NY, USA, 1994; p. 280. [Google Scholar]
- Kozasu, I.; Ouchi, C.; Sampei, T.; Okita, T. Hot rolling as a high-temperature thermo-mechanical process. In Proceedings of the Conference on Microalloying 75; Union Carbide Corp.: New York, NY, USA, 1977; pp. 120–135. [Google Scholar]
- Burwell, J.T. Survey of possible wear mechanisms. Wear 1957, 1, 119–141. [Google Scholar] [CrossRef]
- Zhang, S.; To, S.; Zhang, G. Diamond tool wear in ultra-precision machining. Int. J. Adv. Manuf. Technol. 2017, 88, 613–641. [Google Scholar] [CrossRef]
- Cheng, P.; Jiang, N.; Wu, Z. Effect of nickel element diffusion on the tribological properties of cemented carbide materials under high temperature condition. J. Mater. Eng. Perform. 2025, 34, 2788–2799. [Google Scholar] [CrossRef]
- Krishnaraj, N.; Roy, M. Tribology of Diffusion-Treated Surfaces. In Surface Engineering for Enhanced Performance Against Wear; Springer: Vienna, Austria, 2013; pp. 111–147. [Google Scholar]
- Gekonde, H.O.; Subramanian, S.V. Tribology of tool–chip interface and tool wear mechanisms. Surf. Coat. Technol. 2002, 149, 151–160. [Google Scholar] [CrossRef]
- Mehrer, H. Continuum theory of diffusion. In Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes; Springer: Berlin/Heidelberg, Germany, 2007; pp. 27–36. [Google Scholar]
- Goswami, T.K.; Mangaraj, S. 8—Advances in polymeric materials for modifie atmosphere packaging (MAP). In Multifunctional and Nanoreinforced Polymers for Food Packaging; Lagarón, J.-M., Ed.; Woodhead Publishing: Sawston, UK, 2011; pp. 163–242. [Google Scholar]
- Moghadam, M.M.; Rickman, J.M.; Harmer, M.P.; Chan, H.M. The role of boundary variability in polycrystalline grain-boundary diffusion. J. Appl. Phys. 2015, 117, 045311. [Google Scholar] [CrossRef]
- Cahn, R.W.; Haasen, P. (Eds.) Physical Metallurgy; Elsevier: Amsterdam, The Netherlands, 1996; Volume 1. [Google Scholar]
- Shang, S.-L.; Zhou, B.-C.; Wang, W.Y.; Ross, A.J.; Liu, X.L.; Hu, Y.-J.; Fang, H.-Z.; Wang, Y.; Liu, Z.-K. A comprehensive first-principles study of pure elements: Vacancy formation and migration energies and self-diffusion coefficients. Acta Mater. 2016, 109, 128–141. [Google Scholar] [CrossRef]
- Bilbao, L.; Ortueta, M.; Mijangos, F. Effect of concentration and temperature on mass transfer in metal ion exchange. Ind. Eng. Chem. Res. 2016, 55, 7287–7295. [Google Scholar] [CrossRef]
- Gong, S.; Ravi Shankar, M. Effect of microstructural anisotropy on severe plastic deformation during material removal at micrometer length-scales. Mater. Des. 2020, 194, 108874. [Google Scholar] [CrossRef]
- Basu, S.; Shankar, M.R. Microstructure evolution during severe shea deformation at small length-scales. Scr. Mater. 2014, 72, 51–54. [Google Scholar] [CrossRef]
- Basu, S.; Shankar, M.R. Spatial connement-induced switchover in microstructure evolution during severe plastic deformation at micrometer length scales. Acta Mater. 2014, 79, 146–158. [Google Scholar] [CrossRef]
- Shaw, M.C.; Sanghani, S.R. Cutting characteristics with variable undeformed chip thickness. CIRP Ann. 1963, 10, 240. [Google Scholar]
- Shaw, M.C.; Cookson, J.O. Metal Cutting Principles; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Zhong, L.; Wei, J.; Bai, H.; Zhu, J.; Xu, Y. Effects of soaking time on the microstructure and mechanical properties of Nb-NbC/Fe core–shell rod-reinforced cast-iron-matrix composite fabricated through two-step in situ solid-phase diffusion. J. Mater. Res. Technol. 2020, 9, 12308–12317. [Google Scholar] [CrossRef]
- Almeida, A.; Eugénio, S.; Livramento, V.; Marques, M.T.; Correia, J.B.; Vilar, R. Laser cladding of Cu-NbC nanocomposite coatings. In International Congress on Applications of Lasers & Electro-Optics; Laser Institute of America: Orlando, FL, USA, 2006; Volume 2006. [Google Scholar]
- Tengstrand, O.; Nedfors, N.; Andersson, M.; Lu, J.; Jansson, U.; Flink, A.; Eklund, P.; Hultman, L. Model for electron-beam-induced crystallization of amorphous Me–Si–C (Me= Nb or Zr) thin films. J. Mater. Res. 2014, 29, 2854–2862. [Google Scholar] [CrossRef][Green Version]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, M.S.; Alamoudi, M.T.; Almatani, R.A.; Shankar, M.R. Investigating the Influence of Mechanical Loads on Built-Up Edge Formation Across Different Length Scales at Diamond–Transition Metal Interfaces. J. Manuf. Mater. Process. 2025, 9, 176. https://doi.org/10.3390/jmmp9060176
Alghamdi MS, Alamoudi MT, Almatani RA, Shankar MR. Investigating the Influence of Mechanical Loads on Built-Up Edge Formation Across Different Length Scales at Diamond–Transition Metal Interfaces. Journal of Manufacturing and Materials Processing. 2025; 9(6):176. https://doi.org/10.3390/jmmp9060176
Chicago/Turabian StyleAlghamdi, Mazen S., Mohammed T. Alamoudi, Rami A. Almatani, and Meenakshisundaram Ravi Shankar. 2025. "Investigating the Influence of Mechanical Loads on Built-Up Edge Formation Across Different Length Scales at Diamond–Transition Metal Interfaces" Journal of Manufacturing and Materials Processing 9, no. 6: 176. https://doi.org/10.3390/jmmp9060176
APA StyleAlghamdi, M. S., Alamoudi, M. T., Almatani, R. A., & Shankar, M. R. (2025). Investigating the Influence of Mechanical Loads on Built-Up Edge Formation Across Different Length Scales at Diamond–Transition Metal Interfaces. Journal of Manufacturing and Materials Processing, 9(6), 176. https://doi.org/10.3390/jmmp9060176





