Predictive Control and Manufacturing of Rotation Accuracy of Angular Contact Ball Bearings (ACBBs)

Abstract

High-precision angular contact ball bearings (ACBBs) are critical components in advanced manufacturing equipment, where rotation accuracy directly determines system performance and stability. Considering error superposition and equipment processing capability comprehensively, this study establishes an error analysis and control model of the ACBBs, studies the error transmission law, and puts forward a rotation accuracy control strategy for batch manufacturing of precision ACBBs. The ACBBs 7020C/P4, 7020AC/P4, 7020A/P4, and 7020B/P4 (four conventional contact angles of 15°, 25°, 30°, 40°) were taken as examples to verify the experiment. The error of the calculation compared with actual test results was not more than 7.5%, which had good accuracy and practicability. The research shows that the roundness error of bearing raceway, the thickness difference in bearing ring wall, and the parallelism error of raceway to end face were the main influencing factors of bearing rotation accuracy Kia, Sia, Kea, and Sea. The influence coefficient of raceway roundness error on the axial runout of bearing (Sia, Sea) decreased rapidly with the increase in contact angle, while the influence coefficient on radial runout (Kia, Kea) remained constant. The rotation accuracy error of the outer ring was always greater than that of the inner ring, and this law was not affected by the contact angle. Moreover, with the increase in contact angle, the radial runout of the inner and outer rings of the bearing increased. During actual machining, bearings with larger contact angle place lower demands on the equipment process capability index (Cp), particularly on the parameter Cer. This reduction in required capability is equivalent to an effective Cp improvement of about 30%.

1. Introduction

As the core components of mechanical equipment, the accuracy of bearing directly determines the machining accuracy of precision equipment [1,2]. Accuracy is one of the properties of bearings and an important parameter in the bearing manufacturing process, which directly determines the performance, life, and reliability of bearings [3]. The accuracy grade of bearings is divided into five grades: P0, P6, P5, P4, and P2. According to the different dimensional accuracy and rotational accuracy, choosing the appropriate accuracy grade is crucial to ensure the precision operation and efficient performance of the equipment. In particular, rotation accuracy is the degree of accuracy that a bearing can achieve during operation, which reflects the stability and accuracy of the bearing under load and rotation [4].

Taking rolling bearings as objects, scholars have analyzed the influence of geometric error of bearing elements on bearing rotation accuracy. Noguchi et al. [5,6] discussed the concept of non-repetitive accuracy, explored the correlation between the accuracy of key bearing components and non-repetitive accuracy, analyzed the relationship between the accuracy of rolling elements and non-repetitive accuracy, and carried out relevant experimental verification. Yuan et al. [7] applied rolling bearing geometry, elastic mechanics, and raceway control theory, and gave the numerical calculation formula of NRRO caused by the number of steel balls in the geometric error of the parts of high-speed ACBBs. Liu et al. [8] established a multi-degree-of-freedom pseudo-static model of ACBBs and explained the correlation mechanism between the surface topography accuracy of key components and the non-repetitive accuracy of ball bearings. Hu et al. [9,10,11] made a detailed analysis of the internal failure and surface properties of the bearing raceway. The precise control technology of roundness and performance of bearing raceway during machining is studied. According to the geometry and kinematic relationship of cylindrical roller bearings, Yu et al. [12,13,14] discussed the influencing factors of the overall accuracy of cylindrical roller bearings, obtained an analytical method for rotational accuracy, and verified the correctness of the influence law through experiments. Zhou et al. [15] deduced the geometric coordination equation of cylindrical roller bearing according to the geometric relationship among the parts of cylindrical roller bearing, iteratively solved the geometric coordination equation and the load balance equation simultaneously, explained the correlation between the shape-position and topography accuracy of bearings and their overall accuracy. Chen et al. [16] proposed a numerical calculation method of bearing rotation accuracy considering the roundness error of bearing inner ring channel and outer ring channel based on the rotation accuracy of four-point contact ball bearing. Ji et al. [17] studied the correlation characteristics between the dimensional accuracy, shape-position accuracy of components and rotational accuracy, and obtained the influence rules of the dimensional accuracy and shape-position accuracy of components on the rotational accuracy of bearings.

From the current research results, it can be seen that there is little in-depth research on the maximum rotation accuracy error and its control method in the measurement state and the variation law of accuracy error and its control method in the working state of ACBBs. Furthermore, the method of improving the machining accuracy of the bearing component and thus improving the accuracy of the bearing by investing a large amount of money is not applicable to mass production. Therefore, it is very useful to study the relationship between various factors of bearings and bearing slewing accuracy, and to then guide production and assembly to improve the slewing accuracy of bearings. In this paper, the maximum rotation accuracy error in the measurement state and the variation law of accuracy error in working state are studied, the error transmission mechanism and mapping law are analyzed, the method of accurately controlling the overall rotation accuracy of bearing by controlling the topography accuracy of parts is given, and the accuracy of this method is verified by testing.

2. Rotation Accuracy and Measurement Method

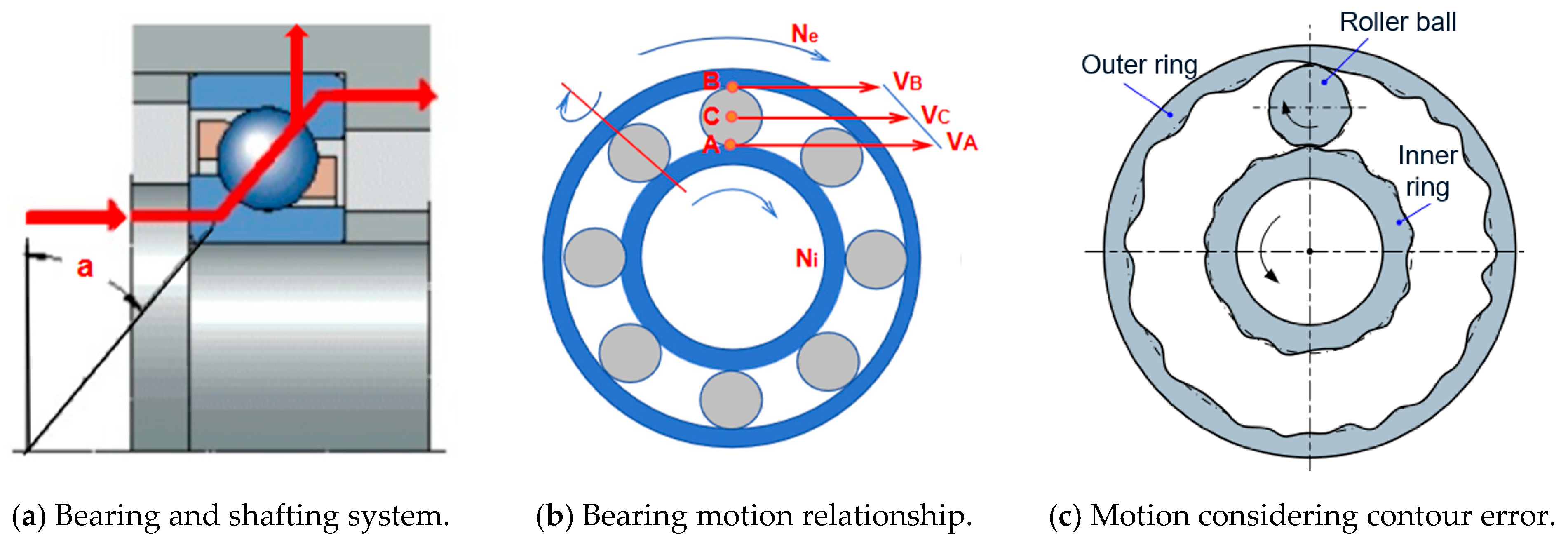
The ACBBs play axial and radial support roles on high-speed rotating spindle [18,19]. As shown in Figure 1a, their radial runout and axial runout have a great influence on the accuracy of the spindle. Usually, the outer ring is fixed in the seat, and the inner ring rotates with the rotation axis as a moving coil, so the rotation accuracy of the inner ring has a more significant influence on the whole axial direction. The relative motion between the inner and outer rings, rolling elements, and cage of ACBBs plays an important role in the performance and life analysis of bearings. The relationship between the parts of the highspeed ACBBs is shown in Figure 1b. The motion of rolling elements is the most complex, with both revolution, rotation, and spin. In the process of movement, the size and contour error of bearing parts leads to the large runout of bearing in radial and axial directions, which is the main reason for the unstable accuracy of bearing and shafting system in the working process, as shown in Figure 1c.

Figure 1. Kinematic relationship of ACBBs and their shafting system.

Rotation accuracy is the amount of swing when the bearing is rotating, that is, the stability and smoothness when the bearing is rotating [20]. The rotational accuracy of rolling bearings includes the radial runout (Kia, Kea) of the inner and outer rings of the bearing and the axial runout (Sia, Sea) of the inner and outer rings of the bearing. The radial runout Kia of the inner ring refers to the difference between the maximum and minimum radial distances between different angular positions of the inner hole surface of the inner ring and a fixed point of the outer ring; the axial runout Sia of the inner ring refers to the difference between the maximum and minimum axial distances between the reference end face of the inner ring, at different angular positions of the inner ring, and a fixed point on the outer ring at a radial distance from the axis of the inner ring equal to half of the contact diameter of the inner ring raceway. Similarly, the radial runout Kea and the axial runout Sea of the bearing outer ring can be understood.

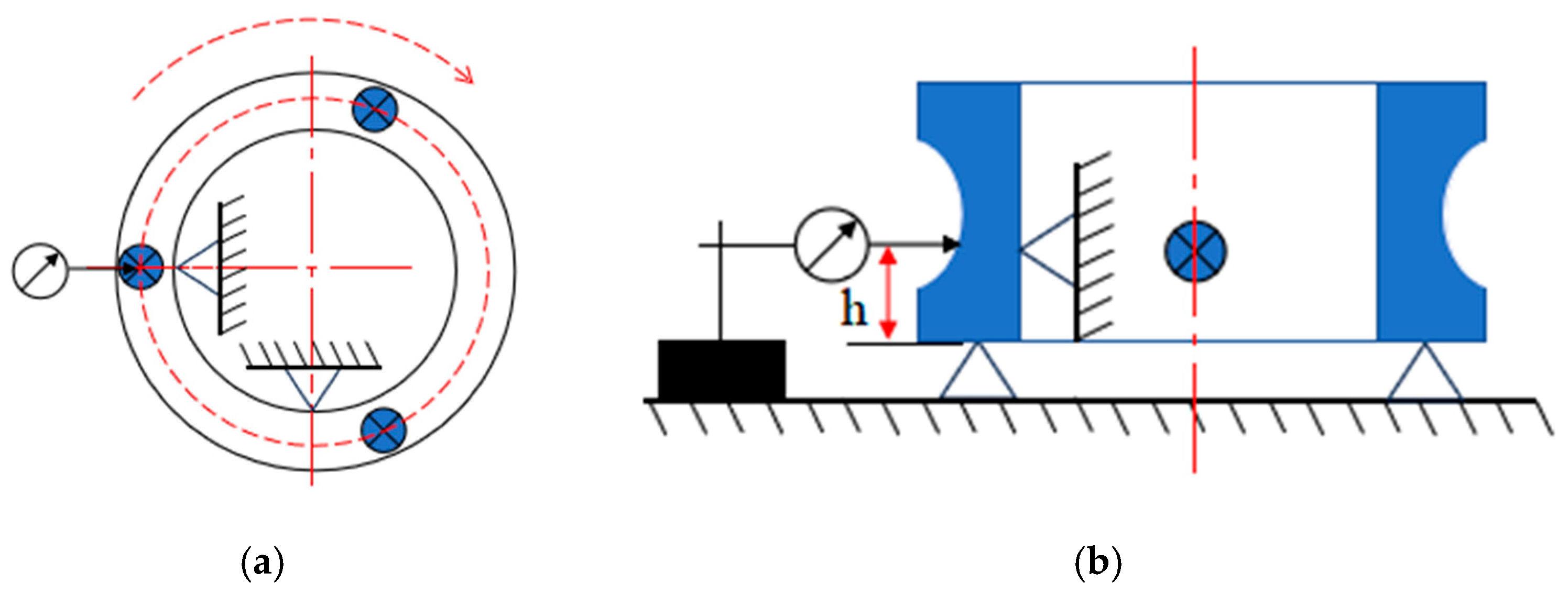
The principle of measuring the rotation accuracy of ACBBs is shown in Figure 2. Figure 2a is the measurement of the radial runout of the bearing inner ring, and Figure 1b is the measurement of the axial runout of the bearing inner ring. The probe of the measuring instrument is in contact with the inner circular surface of the inner ring and should be placed in the middle of the inner circular surface of the inner ring as much as possible. Then let the inner ring rotate steadily once, and the reading of the measuring instrument can be obtained. The difference between the maximum reading and the minimum reading read by the instrument is the measured radial runout of the inner ring. The measurement method of axial runout is similar, except that the measuring instrument is placed on the end face of the inner ring of the bearing.

Figure 2. Measurement of rotation accuracy of ACBBs.

The inner ring of the bearing is supported horizontally; a stable axial load is applied to the outer ring of the bearing on the reference end face of the outer ring along the axial direction, and the outer ring rotates steadily for one turn, so that the radial runout Kea and axial runout Sea of the outer ring of the bearing can be obtained through the reading of the measuring instrument.

3. Prediction and Optimization Model of Rotation Accuracy

3.1. Analysis of Influencing Factors

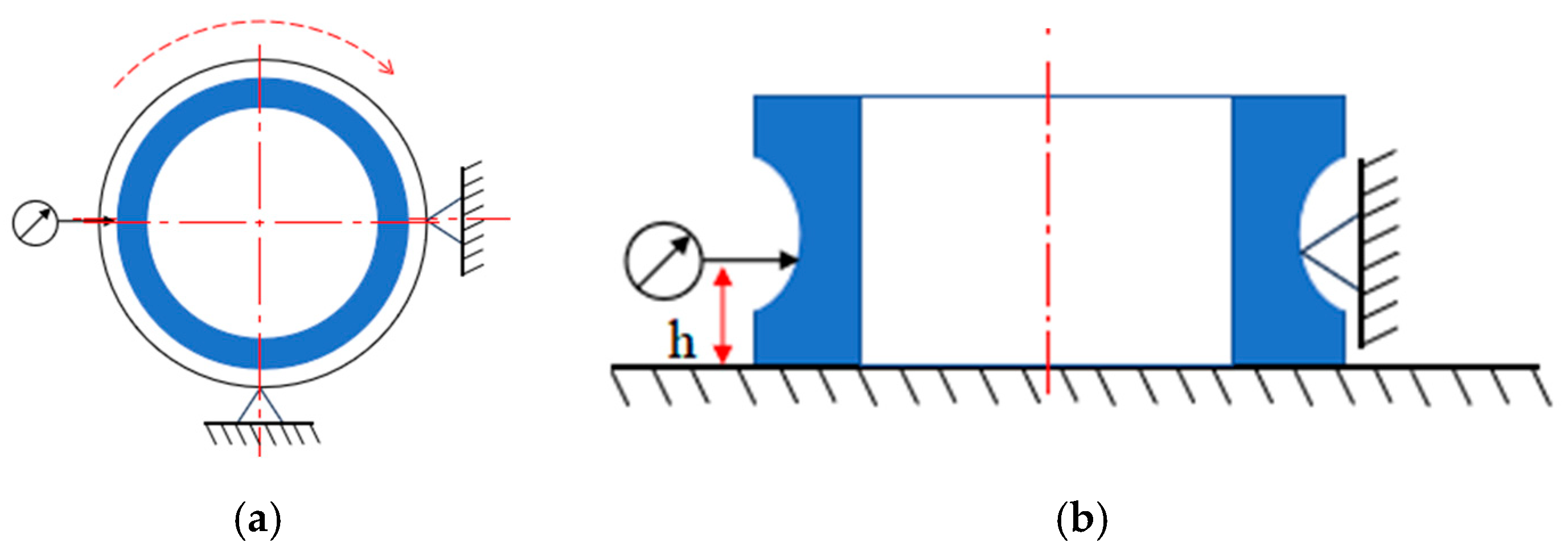
Taking the rotation accuracy of the inner ring and outer ring of the bearing as an example, the error components and influencing factors are analyzed, as shown in Figure 3.

Figure 3. Mathematical model of bearing inner ring rotation accuracy.

For Figure 3a,b, the radial runout Kia and Kea of the bearing and the axial runout Sia and Sea are the superposition of the radial and axial errors of the broken line O₁-O₂-O₃-O₄ and O₅-O₂-O₃-O₆, respectively, which are composed of the shape and position error of the bearing ring itself, the roundness error of the channel, and the shape error of the ball. According to the measurement principle, when measuring the rotation accuracy of the bearing inner ring, the outer ring is fixed (Figure 3), and the inner ring rotates; the measurement error is the superposition of the roundness error of the outer ring channel, the roundness error of the inner ring channel, and the shape and position error of the inner ring. On the contrary, when measuring the rotation accuracy of the outer ring of the bearing, the inner ring is fixed and the outer ring is rotated; the measurement error is the superposition of the roundness error of the inner ring channel, the roundness error of the outer ring channel, and the shape and position error of the outer ring. Let Ke, Ki, Se, and Si be the radial and axial form and position errors of the outer ring and the inner ring, respectively. ΔC_re and ΔC_ri are the roundness errors of the outer ring and the inner ring at points O₂ and O₃, respectively. ΔD_w is the surface topography error of the ball. Then, the components and influencing factors of the bearing rotation accuracy can be expressed as Equations (1)–(4).

$$K_{ia}∍(\Delta C_{re},\Delta D_w,\Delta C_{ri},K_i)$$

(1)

$$S_{ia}∍(\Delta C_{re},\Delta D_w,\Delta C_{ri},S_i)$$

(2)

$$K_{ea}∍(K_e,\Delta C_{re},\Delta D_w,\Delta C_{ri})$$

(3)

$$S_{ea}∍(S_e,\Delta C_{re},\Delta D_w,\Delta C_{ri})$$

(4)

The roundness error here refers to the deviation between the circumferential roundness of the bearing raceway and the ball contact area and the ideal roundness, which is generally measured by a precision roundness instrument. The roundness error and measurement method of the bearing inner ring are shown in Figure 4.

Figure 4. Roundness error and measurement method of bearing inner ring. (a) Diagram of roundness error of bearing inner ring. (b) Roundness meter and measurement method of bearing inner ring.

The shape and position errors inside and outside the bearing include the wall thickness error of the inner ring channel and the parallelism error of the inner ring channel to the end face. In this paper, the wall thickness error of the inner ring refers to the error of the distance from the contact point of the bearing groove and the ball to the cylindrical surface of the inner hole of the inner ring in the circumferential direction, which is measured by a precision groove wall thickness error measuring instrument. The measurement method is shown in Figure 5.

Figure 5. Measurement diagram of wall thickness error of bearing inner ring. (a) Overview of wall thickness error measurement of bearing inner ring. (b) Front view of wall thickness error measurement of bearing inner ring.

The parallelism error of the inner ring channel to the end face, the measurement principle, and method are shown in Figure 6.

Figure 6. Schematic diagram of parallelism error of bearing inner ring groove to end face. (a) Top view of the measurement of the parallelism error of the channel to the end face. (b) Front view of the measurement of the parallelism error of the channel to the end face.

3.2. Calculation of Influence Coefficient

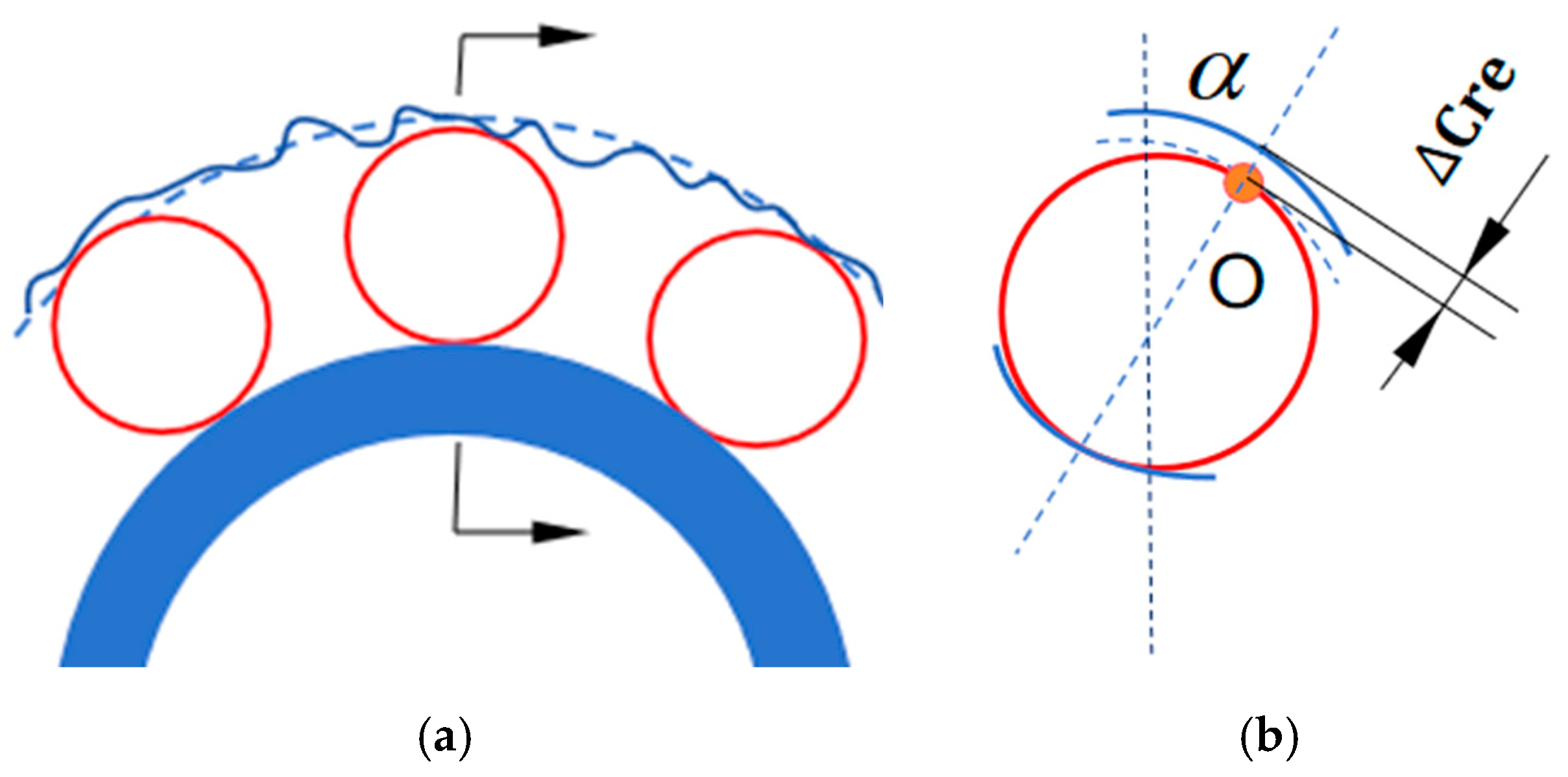
Because the roundness error of the inner and outer rings is very small, it can be approximately considered that the influence of the small change in the size of the inner and outer rings’ channel at the contact point on the rotation accuracy of the bearing can be approximated. For the contact point O in Figure 7, there is a roundness deviation ΔC_re, which can be regarded as a transient runout of radial play S_r and axial play S_a caused by small changes in channel size.

Figure 7. Schematic diagram of the instantaneous fluctuation of each clearance caused by the slight change in the raceway size. (a) Schematic diagram of minor changes in the outer ring. (b) Schematic diagram of instantaneous fluctuation of each clearance.

According to the geometric relationship of the bearing, it can be obtained.

$$S_r=D_e-d_t-2D_w$$

(5)

$$S_a=2\sqrt{\left(D_e-d_t-2D_w\right)\left(R_i+R_e-D_w\right)}$$

(6)

Since the channel roundness error only affects the radial and axial directions of the bearing, assuming that R_i, R_e, and D_w remain unchanged, Equations (5) and (6) are deflected to obtain the bearing outer ring channel diameter D_e, the transient value of the inner ring channel diameter di (channel roundness error) on the radial clearance, and the axial clearance influence coefficient, as shown in Equations (7)–(10).

$${\displaystyle \frac{\partial S_r}{\partial D_e}}=1$$

(7)

$${\displaystyle \frac{\partial S_r}{\partial d_i}}=-1$$

(8)

$${\displaystyle \frac{\partial S_a}{\partial D_e}}={\displaystyle \frac{R_i+R_e-D_w}{\sqrt{(D_e-d_i-2D_w)(R_i+R_e-D_w)}}}$$

(9)

$${\displaystyle \frac{\partial S_a}{\partial d_i}}=-{\displaystyle \frac{R_i+R_e-D_w}{\sqrt{(D_e-d_i-2D_w)(R_i+R_e-D_w)}}}$$

(10)

Therefore, it can be obtained from Equations (7) and (8) that the influence coefficient of the channel roundness error on radial runout is 1, that is, Equation (11).

$$\Delta S_r=1$$

(11)

It should be emphasized that due to the existence of the measurement pressure, the influence of the roundness error ΔC_re and ΔC_ri on the radial direction is two-way, but the influence on the axial direction is one-way. Therefore, the calculation formula of the influence coefficient of the roundness error on the axial runout is Equation (12).

$$\Delta S_a={\displaystyle \frac{1}{2}}{\displaystyle \frac{R_i+R_e-D_w}{\sqrt{(D_e-d_i-2D_w)(R_i+R_e-D_w)}}}$$

(12)

The bearing contact angle Equation (13) can be obtained from the bearing geometric relationship.

$$\alpha =\arccos \left[1-{\displaystyle \frac{D_e-d_i-2D_w}{2(R_i+R_e-D_w)}}\right]$$

(13)

It can be obtained from Equation (13) that when R_i, R_e, and D_w remain unchanged, the contact angle of the bearing increases when the difference (D_e − d_i) between the outer ring channel diameter D_e and the inner ring channel diameter di increases. It can be seen from Equation (12) that the influence coefficient ΔS_a decreases, so the influence coefficient ΔS_a decreases with the increase in contact angle.

3.3. Prediction and Optimization Models

According to the previous study, the numerical calculation formulas of rotation accuracy of bearing inner ring are Equations (14) and (15).

$$K_{ia}=\Delta C_{re}+\Delta C_{ri}+K_i$$

(14)

$$S_{ia}=\Delta S_a\left(\Delta C_{re}+\Delta C_{ri}\right)+S_i$$

(15)

In the same way, the numerical calculation Equations (16) and (17) for the rotation accuracy of the bearing outer ring can be obtained.

$$K_{ea}=\Delta C_{re}+\Delta C_{ri}+K_e$$

(16)

$$S_{ea}=\Delta S_a\left(\Delta C_{re}+\Delta C_{ri}\right)+S_e$$

(17)

If the bearing design parameters D_e, d_i, R_i, R_e, D_w, and the roundness errors ΔC_re, ΔC_ri, and shape and position errors of the inner and outer rings are known, the rotation accuracy of the finished bearing can be accurately predicted by Equations (14)–(17). If the required indexes of rotation accuracy Kia0, Sia0, Kea0, and Sea0 of finished bearings are known, the optimal matching of each error can be carried out according to the model to meet the index requirements. The capability of bearing processing equipment is expressed by the process capacity index C_p and the index evaluation and grading table (Table 1).

Table 1. Process capability index evaluation grading table.

No.	${\mathit{C}}_{\mathit{p}}$	Grade	Determine	Tolerance Range on Both Sides T	Remark
1	≥1.67	Special grade	Excessive capacity	10σ~	Simplifies inspection, compression tolerances
2	1.33~1.67	Grade 1	Sufficient capacity	8σ~10σ	Simplifies detection
3	1.0~1.33	Grade 2	Ability is acceptable	6σ~8σ	Strictly control
4	0.67~1.0	Grade 3	Inadequate capacity	4σ~6σ	Strict control or sorting
5	≤0.67	Grade 4	Serious lack of capacity	~4σ	Replace equipment

The machine tool processing capability index is defined as $C_P=T/\left(6\sigma \right)$, where T is the tolerance range, and σ is the process standard deviation. The parameters $\Delta C_{re}$ and $\Delta C_{ri}$ represent the machine’s ability to control the roundness of the outer and inner raceways, respectively. Their values are obtained by repeatedly measuring the raceway error distribution and normalizing it according to the design tolerance. These parameters directly affect the effective $C_P$ value during the optimization process.

Therefore, the core of the bearing rotation accuracy optimization method is to obtain the highest accuracy range under the highest C_p, so that the control of the rotation accuracy of ACBBs can be realized economically and efficiently. The formula of the optimization model is Equation (18).

$$\left\{\begin{array}{l}\Delta C_{re}+\Delta C_{ri}+K_i\le K_{ia0}\\ \Delta S_a\left(\Delta C_{re}+\Delta C_{ri}\right)+S_i\le S_{ia0}\\ \Delta C_{re}+\Delta C_{ri}+K_e\le K_{ea0}\\ \Delta S_a\left(\Delta C_{re}+\Delta C_{ri}\right)+S_e\le S_{ea0}\\ C_p\ge 1\end{array}\right.$$

(18)

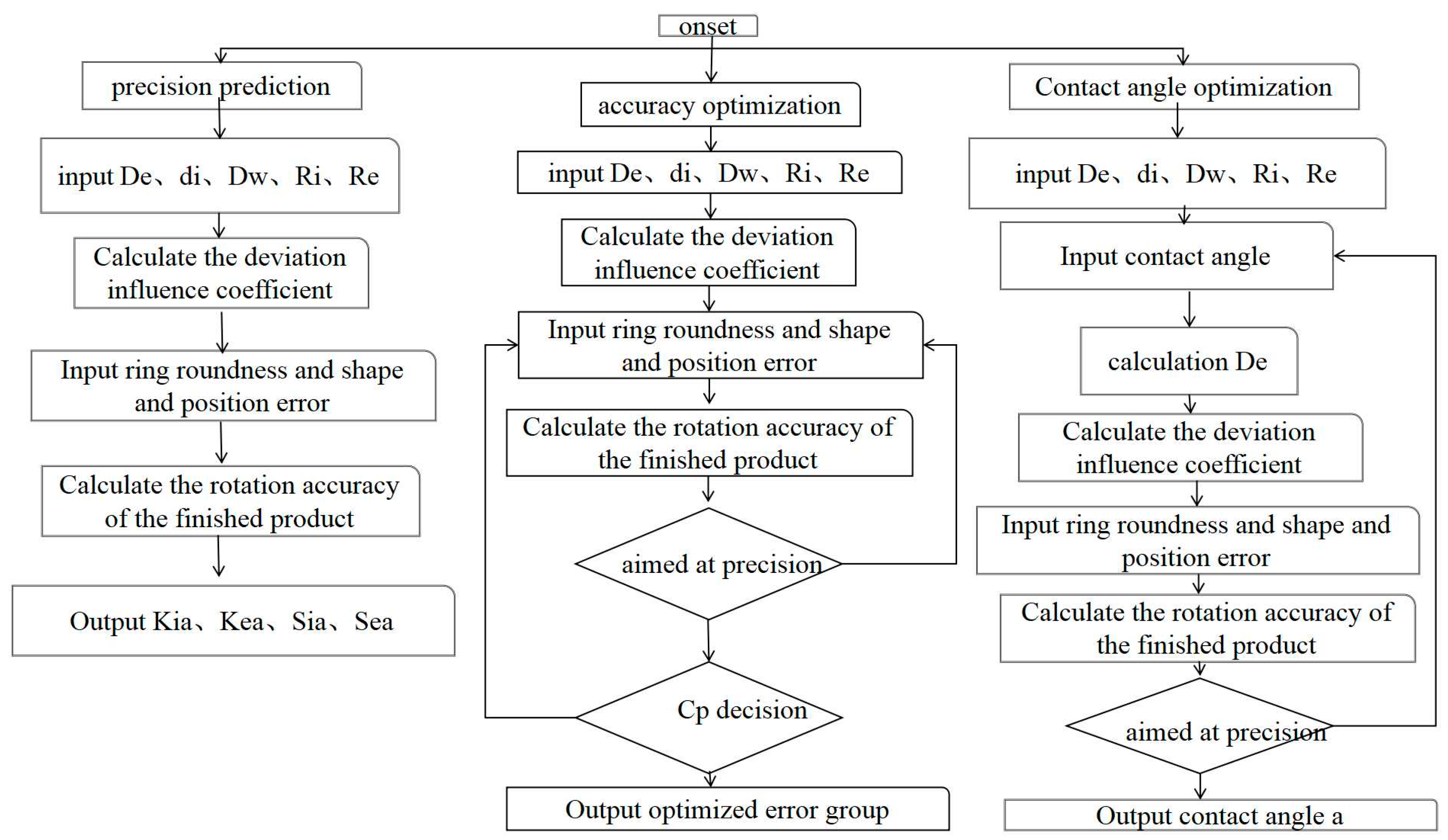
The appropriate contact angle can also be determined according to the rotation accuracy index requirements of the host equipment for the matching bearings. This rotation accuracy prediction and optimization model can economically and efficiently meet the actual production demand, and its process is shown in Figure 8.

Figure 8. The rotation accuracy prediction and optimization process.

4. Model Analysis and Validation

Taking ACBBs 7020C/P4, 7020AC/P4, 7020A/P4, and 7020B/P4 (four conventional contact angles of 15°, 25°, 30°, and 40°), as examples, the model calculation results are analyzed and tested. The relevant structural parameters of the bearings are shown in Table 2.

Table 2. Typical model parameters.

Parameter	7020C/P4	7020AC/P4	7020A/P4	7020B/P4	Units
Outer diameter D	150	150	150	150	mm
Inner diameter d	100	100	100	100	mm
Outer ring channel diameter De	137.736	137.888	137.990	138.244	mm
Inner ring channel diameter di	112.25	112.25	112.25	112.25	mm
Radius of curvature of outer ring groove Re	6.86	6.86	6.86	6.86	mm
Radius of curvature of inner ring groove Ri	7.11	7.11	7.11	7.11	mm
Ball diameter Dw	12.7	12.7	12.7	12.7	mm
Contact angle a	15	25	30	40	°

To evaluate whether the bearing contact angle has a statistically significant effect on the main output metrics (Kia, Sia, Kea, Sea), a one-way analysis of variance (ANOVA) was conducted. The independent variable was contact angle (15°, 25°, 30°, 40°), and the dependent variables were the measured radial and axial runouts. A significance level of α = 0.05 was adopted.

4.1. Influence of Channel Roundness Error

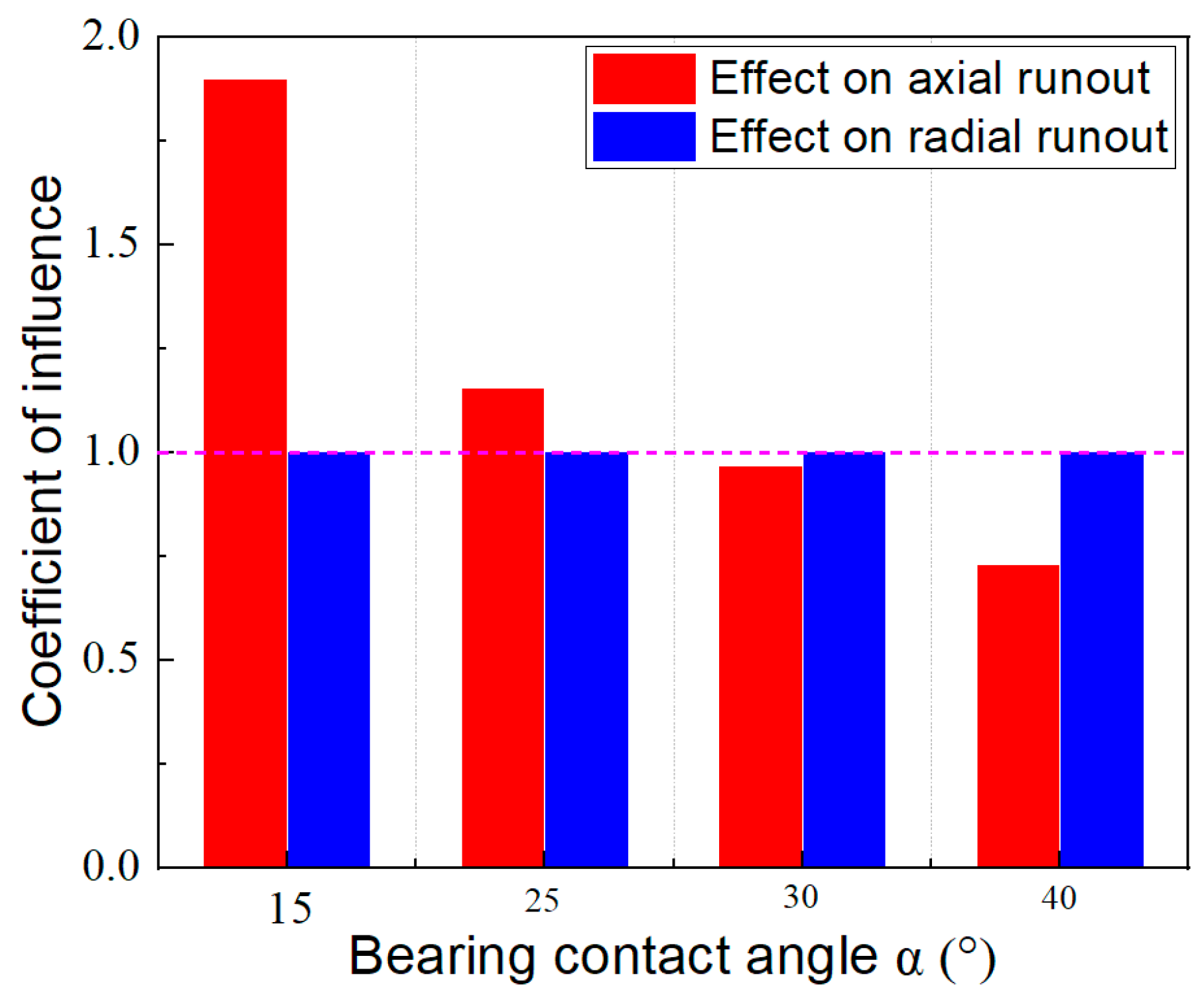
From the above, the influence of the roundness bearing ring channel on overall accuracy of bearing can be calculated. The ACBBs 7020C/P4, 7020AC/P4, 7020A/P4, and 7020B/P4 are calculated, respectively. The influence degree of channel roundness error on axial runout is 1.9, 1.155, 0.966, and 0.731 in turn, and the influence degree decreases in turn, while the influence coefficient on radial runout remains unchanged at 1, as shown in Figure 9.

Figure 9. Effect of channel roundness error on axial runout and radial runout.

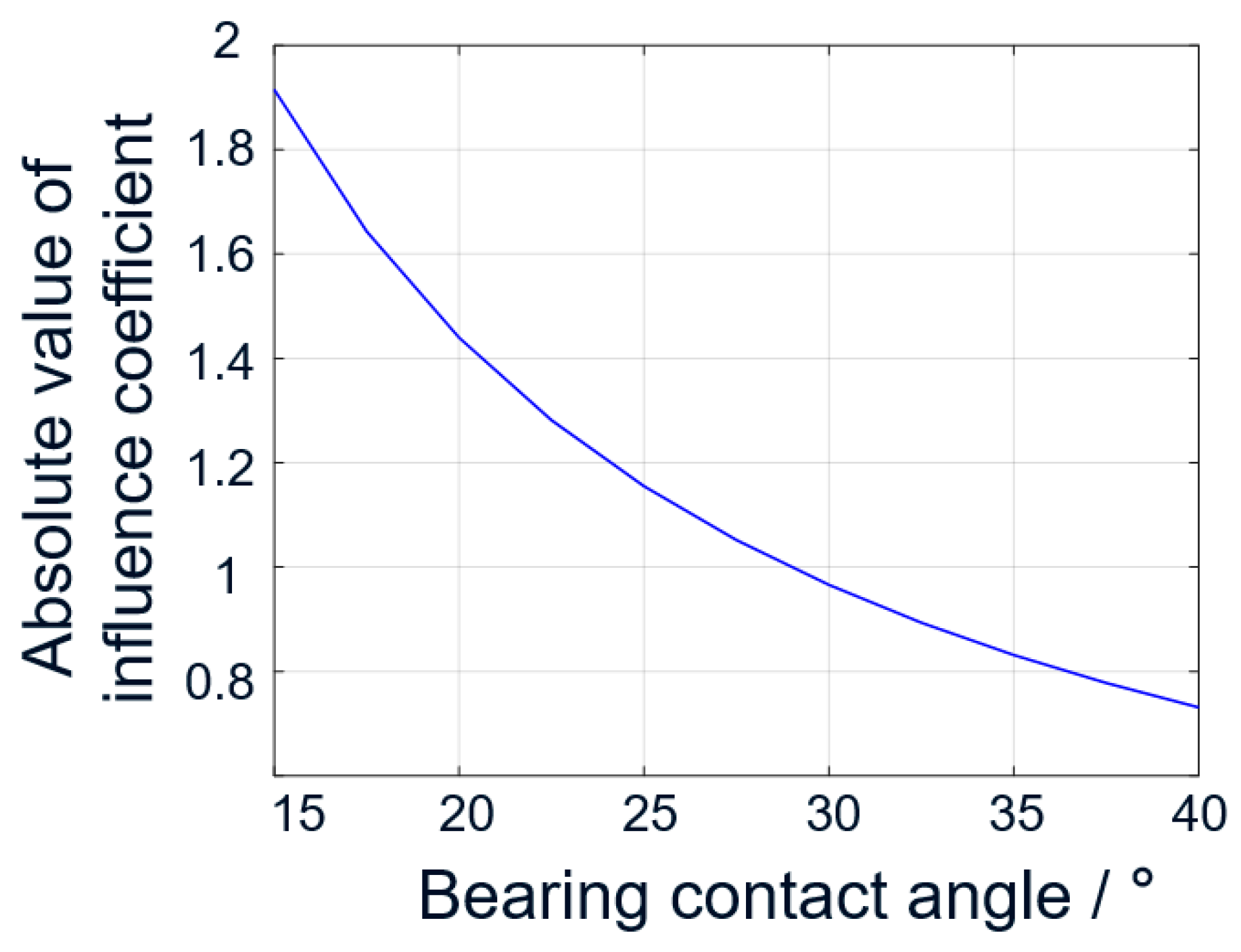
Therefore, we can obtain the model calculation results that with the increase in contact angle, the influence of channel roundness error on the axial runout of bearings is significantly reduced, and the axial runout of ball bearings with small contact angle is difficult to control. Therefore, it is more appropriate to use ball bearings with a large contact angle in application scenarios that generally require higher axial accuracy. The curve of the influence of channel roundness error on axial runout with contact angle is shown in Figure 10.

Figure 10. Effect of channel roundness error on axial runout with contact angle.

4.2. Prediction Analysis and Verification of Rotation Accuracy

Taking 7020C/P4 as the object, 20 sets of finished outer ring and inner ring of this type of bearing are selected, respectively. The corresponding serial numbers are compiled, and the channel roundness error, channel wall thickness difference, and parallelism error of channel to end face at the contact between the inner and outer rings are measured by high-precision measuring instruments, as shown in Figure 11, and the recording results are shown in Table 3.

Figure 11. Measurement of bearing roundness.

Table 3. Related test record sheet of bearing 7020C/P4.

No.	Test Items (μm)
	Ki	Si	Ke	Se	Cir	Cer
1	1.5	2	2.5	3	0.653	0.978
2	2	2.5	2.5	2.5	0.659	0.865
3	1.5	2.5	3.5	3.5	0.562	0.834
4	3	2.5	2.5	2.5	0.432	0.863
5	1.5	1.5	3.0	3	0.612	0.976
6	2	2.5	2.5	2.5	0.659	0.865
7	2.5	2	2.5	2.5	0.653	0.978
8	2	1.5	2.5	2.5	0.337	0.830
9	1.5	1.5	2.5	2.5	0.452	0.778
10	2	2.5	2.5	2.5	0.459	0.765
11	1.5	2.5	3.5	3.5	0.712	0.975
12	3	2.5	2.5	2.5	0.411	0.975
13	1.5	2.5	3.5	3.5	0.653	0.902
14	1.5	2.5	2.5	2.5	0.559	0.865
15	1.5	2	2	3	0.653	0.878
16	2.5	1.5	2.5	2.5	0.501	0.865
17	1.5	2	3.5	3.5	0.603	0.698
18	1.0	2.5	2.5	2.5	0.502	0.865
19	1.5	1.5	2.5	3.5	0.653	0.728
20	2	2.5	3.5	2.5	0.659	0.895
Average	1.85	2.15	2.75	2.825	0.5692	0.8689

All measured values are compared based on the tolerance limits of rolling bearings specified in ISO 492 and ISO 1132 [21]. As long as the deviation between the model prediction and the actual measurement results does not exceed ±10%, it is considered to meet the engineering requirements.

Measurements were carried out using a Taylor Hobson 565 roundness tester, a Mitutoyo LSM-902 wall thickness gauge, and a custom-made parallelism test fixture. For each bearing type, 20 samples were tested, and each sample was measured three times repeatedly.

According to Table 3, the radial and axial runout model results of the rings of bearing 7020C can be obtained from Equations (9)–(12), and Table 4 shows the calculation results and test results.

Table 4. Calculation results and test results of bearing 7020C/P4 rotation accuracy model.

No.	Calculation Results (μm)				Test Results (μm)
	Kia	Sia	Kea	Sea	Kia	Sia	Kea	Sea
1	3.131	5.0989	4.131	6.0989	3.5	5	4.5	5
2	3.524	5.3956	4.024	5.3956	3	4.5	4	5.5
3	2.896	5.1524	4.896	6.1524	3.5	5	4.5	6
4	4.295	4.9605	3.795	4.9605	3.5	4.5	4	5.5
5	3.088	4.5172	4.588	6.0172	3.5	5	4.5	5
6	3.524	5.3956	4.024	5.3956	3	4	5	5.5
7	4.131	5.0989	4.131	5.5989	3.5	4.5	4	5
8	3.167	3.7173	3.667	4.7173	2.5	4	4	5.5
9	2.73	3.837	3.73	4.837	3.5	5	4.5	5
10	3.224	4.8256	3.724	4.8256	2.5	4	5	5.5
11	3.187	5.7053	5.187	6.7053	3.5	4.5	4.5	6
12	4.386	5.1334	3.886	5.1334	4	4	4	5.5
13	3.055	5.4545	5.055	6.4545	3.5	4.5	4.5	4.5
14	2.924	5.2056	3.924	5.2056	3.5	5	5	5.5
15	3.031	4.9089	3.531	5.9089	3.5	4.5	4.5	5
16	3.866	4.0954	3.866	5.0954	3.5	4	5	5.5
17	2.801	4.4719	4.801	5.9719	3.5	5	4.5	6.5
18	2.367	5.0973	3.867	5.0973	3.5	4.5	3.5	5.5
19	2.881	4.1239	3.881	6.1239	3.0	4.5	4.5	5.5
20	3.554	5.4526	5.054	5.4526	3.5	5	3.5	5.5
Average	3.2881	4.88239	4.1881	5.55739	3.35	4.55	4.375	5.425

The comparison figure between the calculation results of the radial and axial jump models of the inner and outer rings of bearing 7020C/P4 and the actual test results is shown in Figure 12.

Figure 12. Comparison of calculation results and detection results.

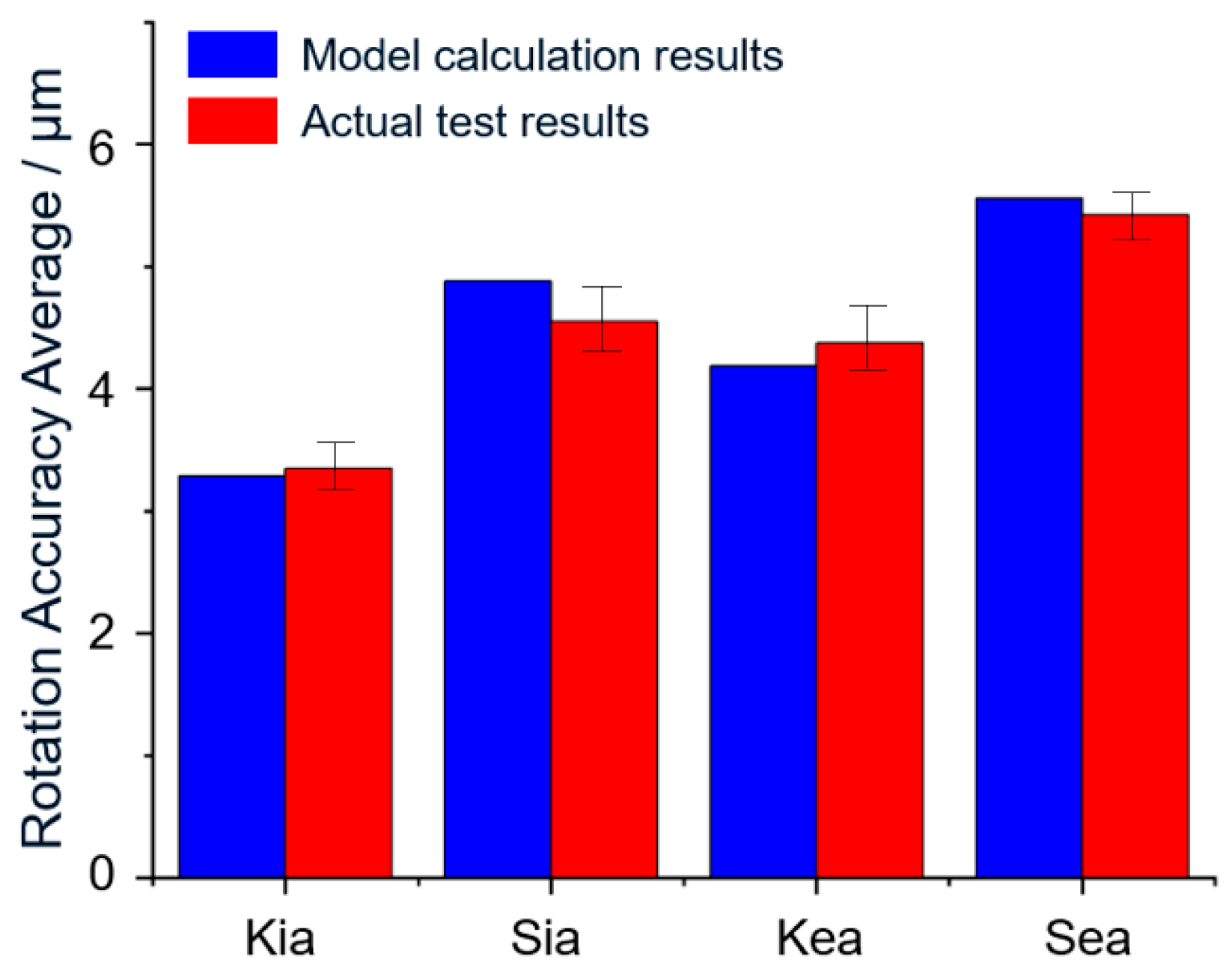
In Figure 12, the errors between the model calculation results and the measured results are 1.8%, 7.2%, 4.0%, and 2.4%, respectively, and the errors are all less than 10%. It can be considered that the model calculation results are in good agreement with the measured results, and the model calculation is accurate and effective. Figure 9 shows that the axial runout is slightly greater than the radial runout, and the rotation accuracy error of the outer ring is greater than the rotation accuracy error of the inner ring, which also explains from the side why high-precision rotating equipment generally prefers shaft rotation over shell rotation.

The rotation accuracy of bearings with different contact angles is verified by the same method, and the model calculation and actual measurement verification of bearings 7020AC/P4, 7020A/P4, and 7020B/P4 are carried out. The average value of model calculation results, the average value of measured results, and error analysis are shown in Table 5.

Table 5. Calculation results and actual test results of rotation accuracy model of bearings with different contact angles.

Bearing Model	Average of Model Calculation Results (μm)				Average of Actual Test Results (μm)				Error (%)
	Kia	Sia	Kea	Sea	Kia	Sia	Kea	Sea	Kia	Sia	Kea	Sea
7020C/P4	3.28	4.88	4.19	5.06	3.35	4.85	4.375	5.425	2.1	0.6	4.2	6.7
7020AC/P4	3.33	3.47	4.21	4.54	3.4	3.45	4.215	4.8	2.1	0.6	0.1	5.4
7020A/P4	3.42	3.51	4.38	4.32	3.55	3.55	4.25	4.45	3.7	1.1	3.1	2.9
7020B/P4	3.55	4.04	4.89	4.96	3.82	4.05	4.55	4.75	7.1	0.2	7.5	4.4

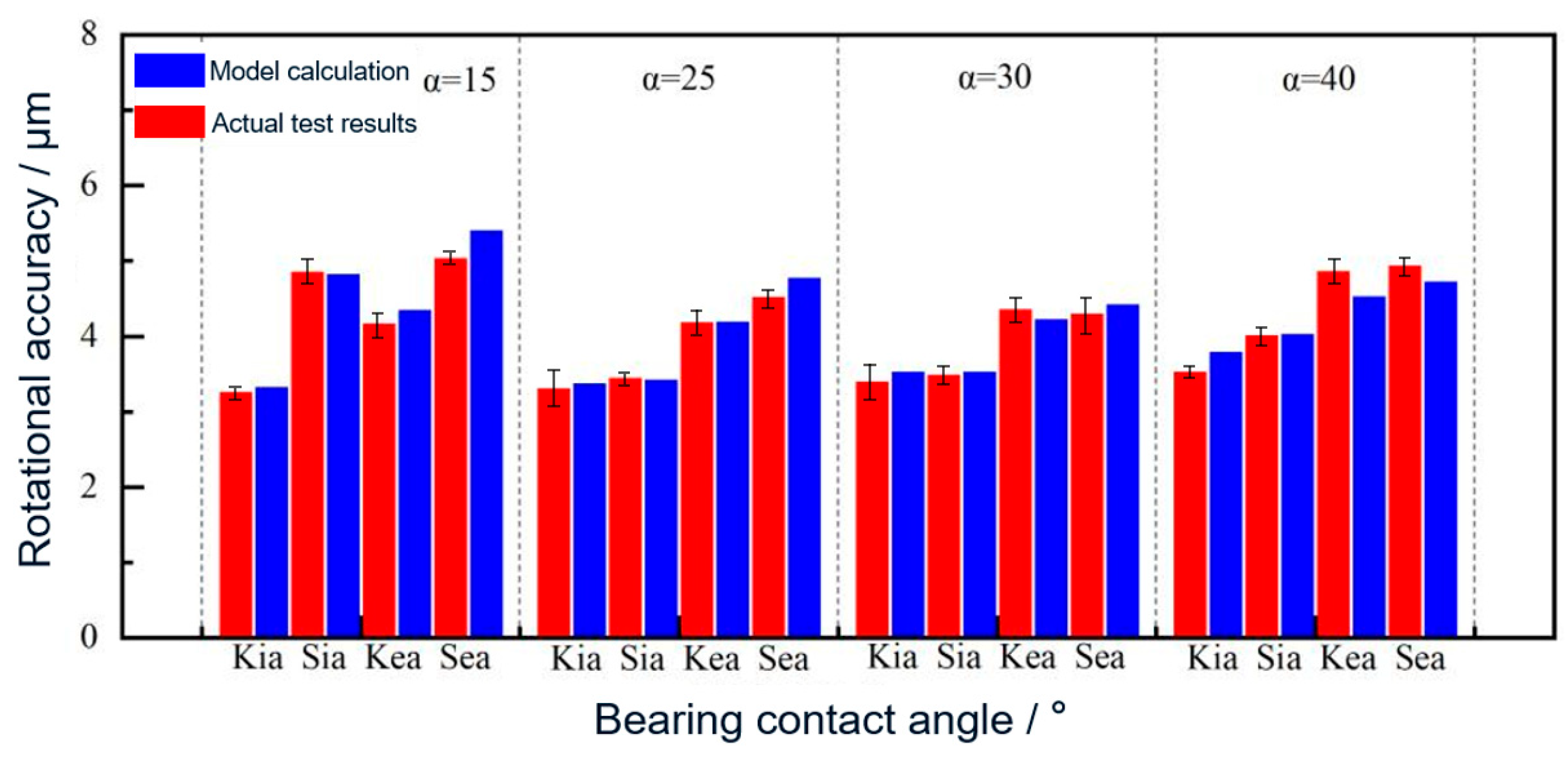
The comparison figure between the calculation results and the actual test results of the radial and axial jump models of the inner and outer rings of the bearings with different contact angles is shown in Figure 13.

Figure 13. Comparison of calculation results and test results of rotation accuracy models of bearings with different contact angles.

From Figure 13, the error between the model calculation results and the measured results is less than 7.5%. The model calculation results are in good agreement with the measured results, and the model calculation is accurate and effective. The figure shows that the axial runout of bearings 7020C/P4 and 7020AC/P is slightly larger than the radial runout, while the axial runout of bearings 7020A/P4 is basically equal to the radial runout, and the axial runout of bearings 7020B/P4 is smaller than the radial runout. This result proves the correctness of the law that the influence of channel roundness error on axial runout decreases with the increase in contact angle analyzed by the model. In addition, it can also be seen from the figure that with the increase in contact angle, the radial runout of the bearing also increases, and the rotation accuracy error of the outer ring is always greater than that of the inner ring, which is not affected by the contact angle.

ANOVA results showed that contact angle had a statistically significant effect on axial runout Sia and Sea (p < 0.05), while its effect on radial runout Kia and Kea was not significant (p > 0.05). This indicates that increasing the contact angle significantly reduces axial runout but does not notably influence radial runout.

4.3. Optimization Analysis and Verification of Rotation Accuracy

Assuming that the rotation accuracy requirement indexes Kia0, Sia0, Kea0, and Sea0 of the bearing are 3.5 μm, 4 μm, 4.5 μm, and 5 μm, respectively, Ke, Ki, Se, Si, ΔC_re, and ΔC_ri are primarily selected according to Equation (18), and the matching is iteratively optimized repeatedly under the premise of considering the processing capacity of the equipment (satisfying C_p ≥ 1), and the optimal group is actually selected for production. In this study, bearing 7020C/P4 (contact angle 15°) is taken as the object to compare the improvement of rotation accuracy before and after optimization, and bearing 7020B/P4 (contact angle 40°) is taken as the reference to analyze the influence of contact angle change on rotation accuracy optimization. The deviation range (maximum value of the model) and optimal deviation group (actual selected value) selected after model optimization are shown in Table 6.

Table 6. Optimization results of rotation accuracy model Before and after comparison of rotational accuracy models.

Bearing Model	Items	Deviation Optimization Combination (μm)
		Ki	Si	Ke	Se	Cir	Cer
7020C/P4	Model Max	2.47	2.04	3.47	3.04	0.48	0.55
	Actual selection value	2.00	2.00	3.00	2.50	0.50	0.60
	Actual Cp value	1.06	1.00	1.33	1.10	0.92	0.92
7020B/P4	Model Max	2.00	2.90	3.00	3.90	0.60	0.90
	Actual selection value	2.00	2.50	3.00	3.50	0.60	0.90
	Actual Cp value	1.06	1.20	1.33	1.33	1.10	1.20

According to Table 6, the qualified rate statistics of bearing rotation accuracy after optimization control are shown in Table 7. From Table 7, it can be seen that before optimization control, the selection of bearing deviation group is very unreasonable, and the qualified rate is very low, especially the qualified rate of axial rotation accuracy is only 25%. After optimization, the bearing accuracy is obviously improved, but based on the limited processing capacity of equipment (C_p < 1), it still cannot fully meet the target accuracy requirements (Sea qualified rate is 96%). When the large contact angle structure is adopted, the accuracy fully meets the requirements (all qualified rates are 100%), and its C_p values are above 1.

Table 7. Optimization results of rotation accuracy model.

Pass Rate Before Optimization	Kia	Sia	Kea	Sea
7020C/P4 of before optimization	80.00	25.00	80.00	25.00
7020C/P4 of after optimization	100.00	98.00	100.00	96.00
7020B/P4 of after optimization	100.00	100.00	100.00	100.00

Table 8 shows in detail the obvious differences in the requirements of equipment process capability index between the two structural bearings in the actual processing process, especially the parameter Cer, which increases the equipment capacity by 30%. Therefore, the larger contact angle can better meet the processing requirements, significantly improve the equipment processing capacity index, and improve the production efficiency.

Table 8. Effect of different contact angles on process capability index.

Processing Capacity Improvement	Different Contact Angle Cp Value
	Kia	Sia	Kea	Sea	Cir	Cer
7020C	1.00	1.00	1.30	1.10	0.92	0.92
7020B	1.00	1.20	1.30	1.30	1.1	1.2
Cp uplift (%)	0	20	0	20	19.5	30

5. Conclusions

In this study, the influencing factors and control measurement of rotation accuracy of ACBBs are deeply studied, and the error influence mechanism and transmission law are obtained. The rotation accuracy control strategy of batch manufacturing precision ACBBs is put forward. One-way ANOVA confirmed that contact angle exerts a significant influence on axial runout (p < 0.05), validating the model’s prediction that larger contact angles reduce axial runout. The main research conclusions are as follows:

(1) Based on the principle of error superposition, this paper establishes a prediction and optimization model of ACBBs rotation accuracy error considering the machining capacity of equipment. The research shows that the roundness error of the bearing channel, the thickness difference in the bearing ring wall, and the parallelism error of the channel to the end face are the main influencing factors of the bearing rotation accuracy Kia, Sia, Kea, and Sea. The influence coefficient of channel roundness error on axial runout (Sia, Sea) decreases rapidly with the increase in contact angle, while the influence coefficient on radial runout (Kia, Kea) remains constant; the rotation accuracy error of the outer ring is always greater than that of the inner ring, which is not affected by the contact angle, and the radial runout of the bearing increases with the increase in the contact angle.

(2) This study takes ACBBs 7020C/P4, 7020AC/P4, 7020A/P4, and 7020B/P4 (four conventional contact angles 15°, 25°, 30°, and 40°) as examples to verify the experiment. The error between the model calculation results and the actual detection results is less than 7.5%. The actual machining proves that the structure with larger contact angle requires lower equipment process capability index C_p, especially the corresponding parameter C_er, and the equipment capability index C_p is equivalent to an increase of 30%.

(3) ACBBs is one of the most classic structures of high-speed rolling bearing, and its rotation accuracy directly determines the machining accuracy of the main machine. In actual production, the precise control of bearing rotation accuracy is one of the technical problems in the batch manufacturing of ACBBs. The research results in this paper will surely further promote the improvement of production manufacturing technology. This model has broad application prospects.

This approach offers practical advantages for industrial mass production of ACBBs in aerospace, high-speed machining, and medical devices. However, the model has been validated only for 7020 series ACBBs. Future research will extend the method to other bearing types and investigate the effects of lubrication and thermal deformation.