Novel Pneumatic Soft Gripper Integrated with Mechanical Metamaterials for Enhanced Shape Matching Performance
Abstract
1. Introduction
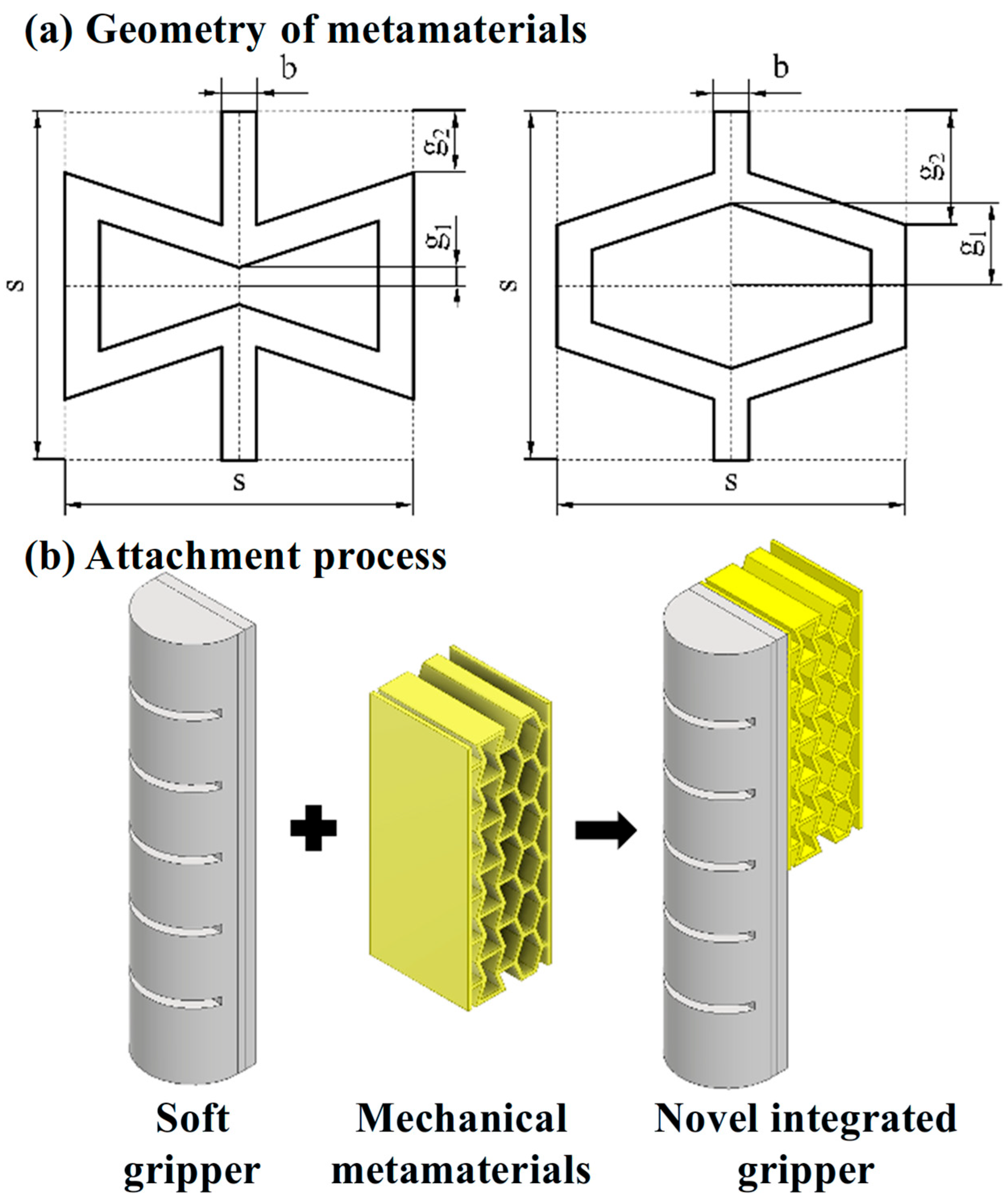
2. Gripper Enhanced by Mechanical Metamaterial
2.1. Pneumatic Soft Actuator
2.2. Attached Mechanical Metamaterial for Higher Shape Match Performance
3. Finite Element Analysis (FEA) of Traditional and Novel Assembled Gripper
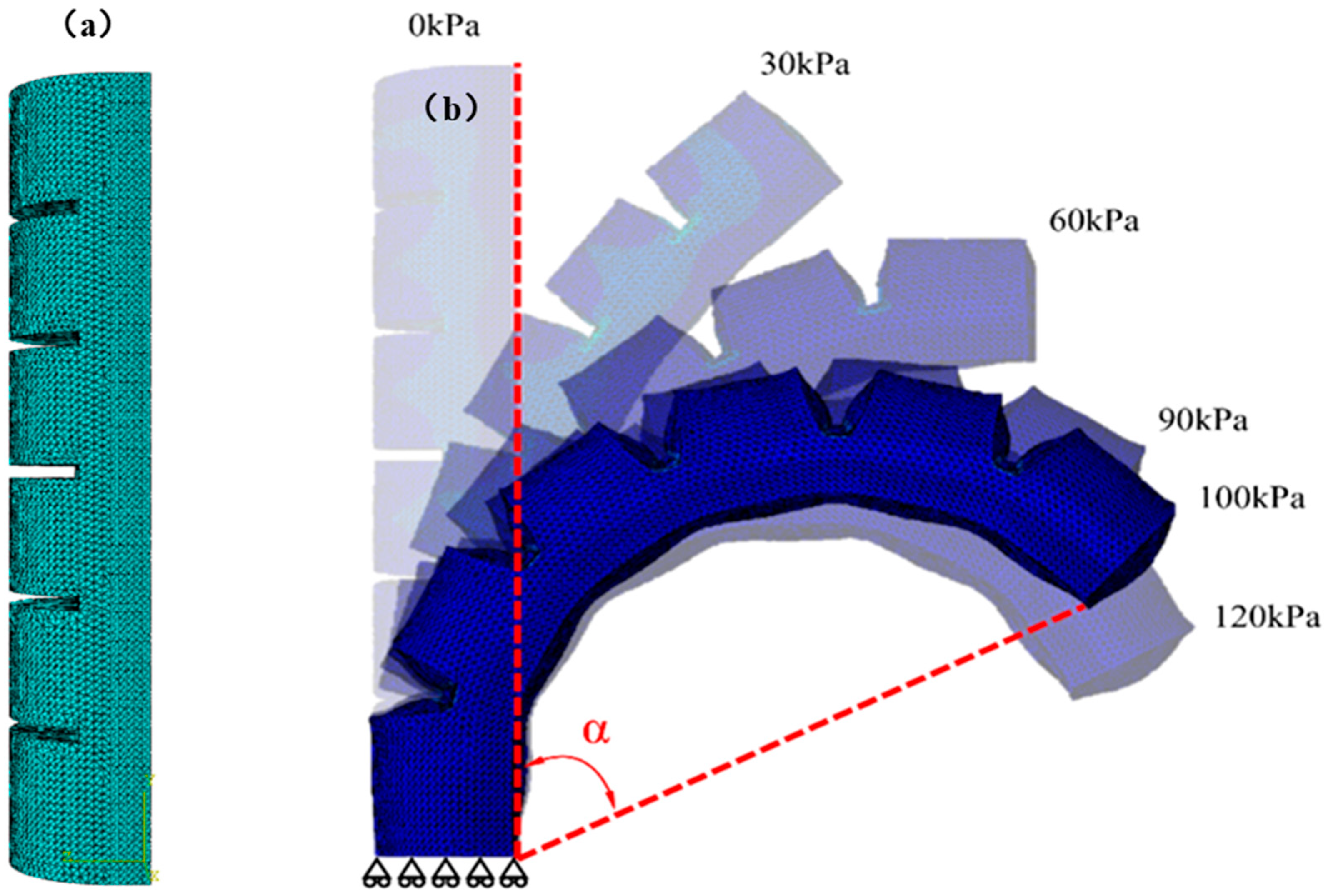
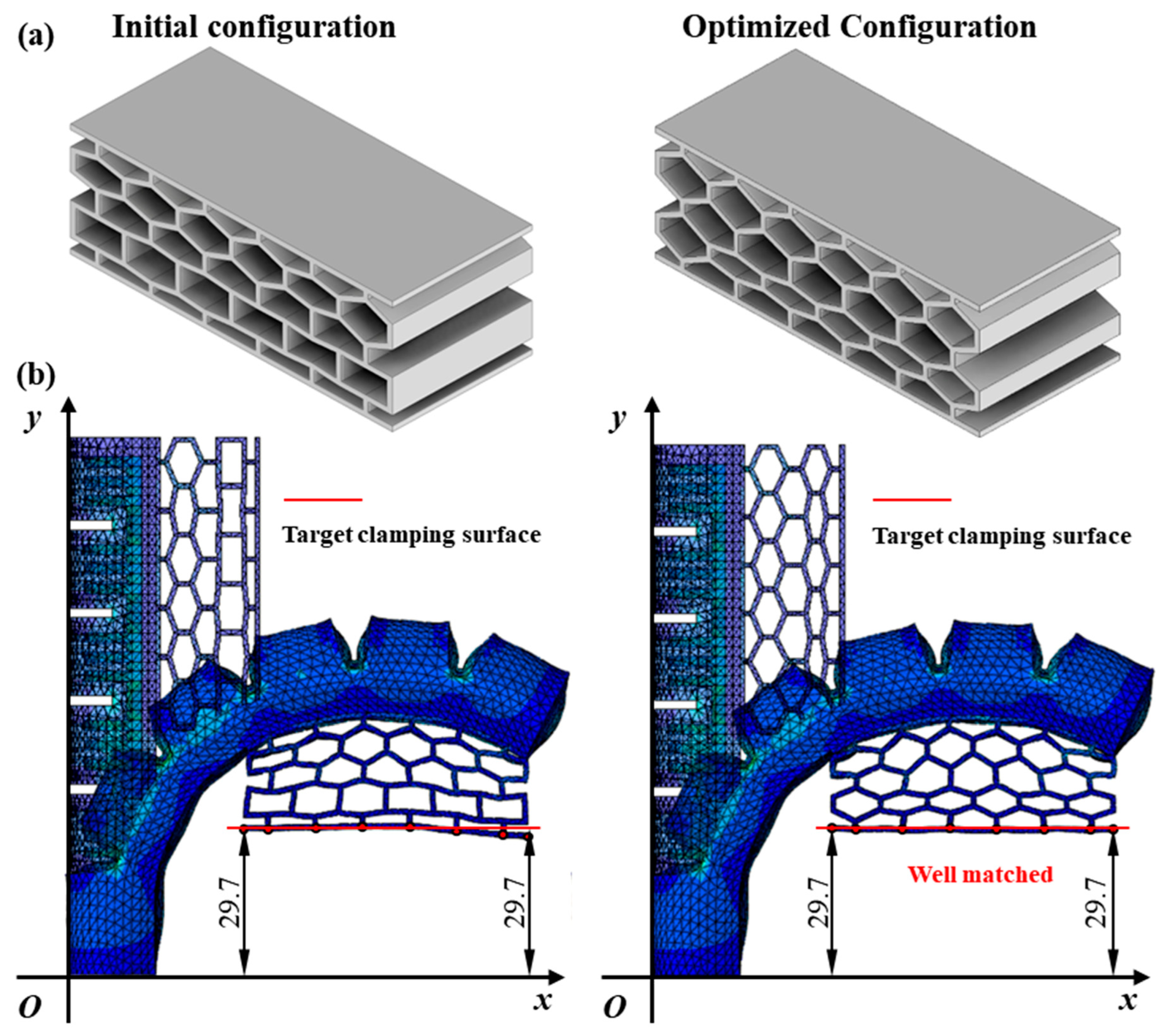
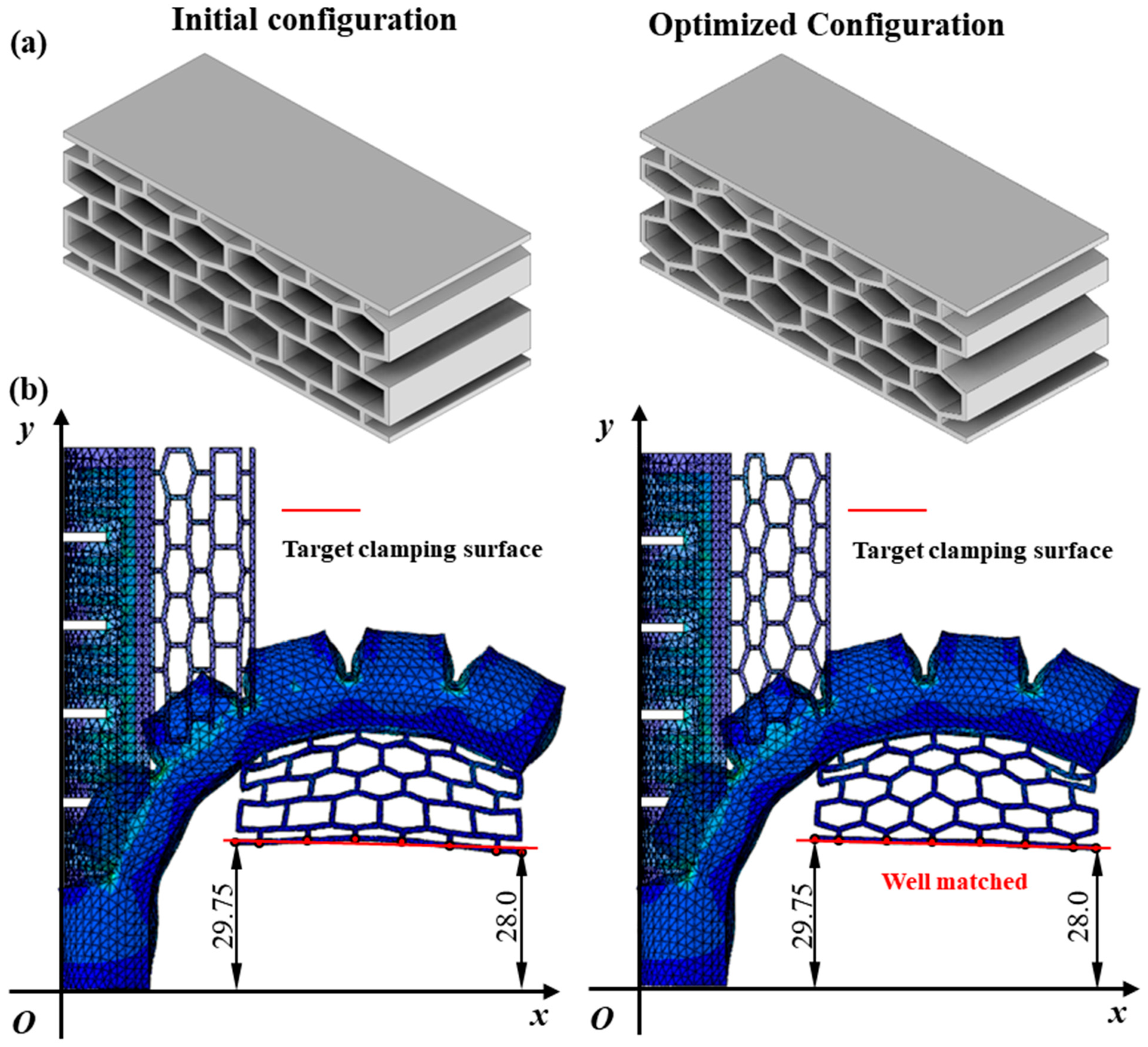
3.1. FEA on Traditional Gripper
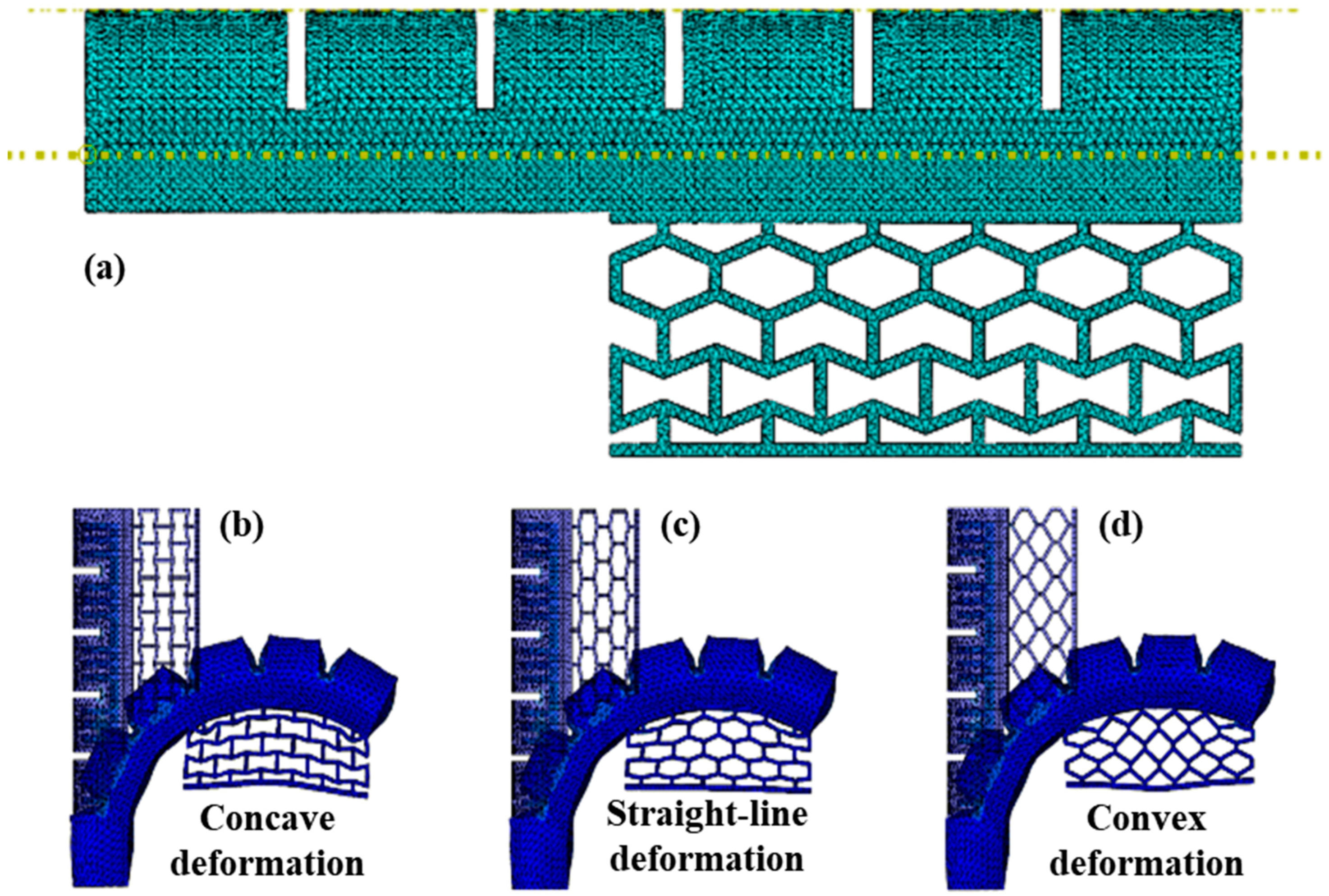
3.2. FEA on Novel Assembled Gripper
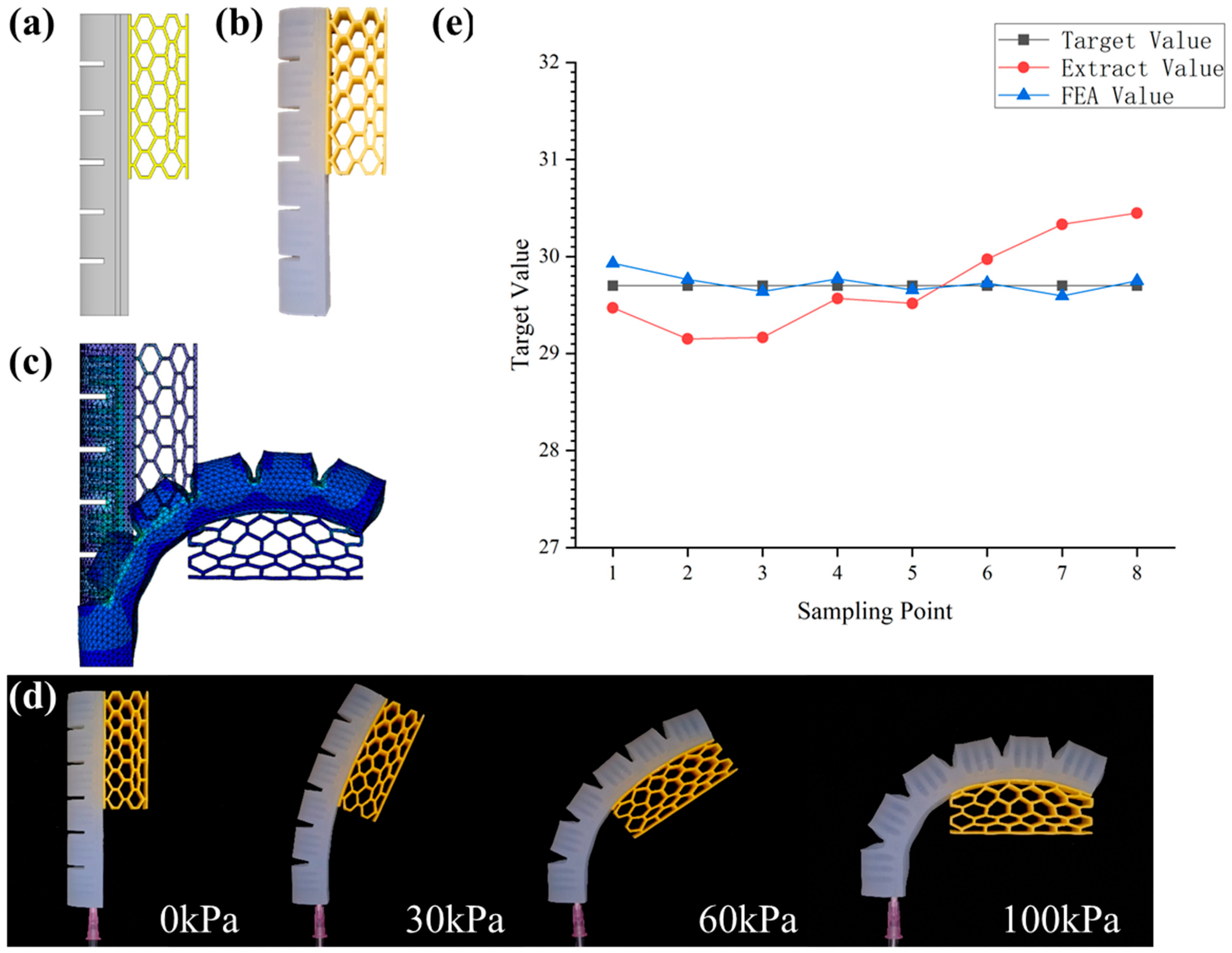
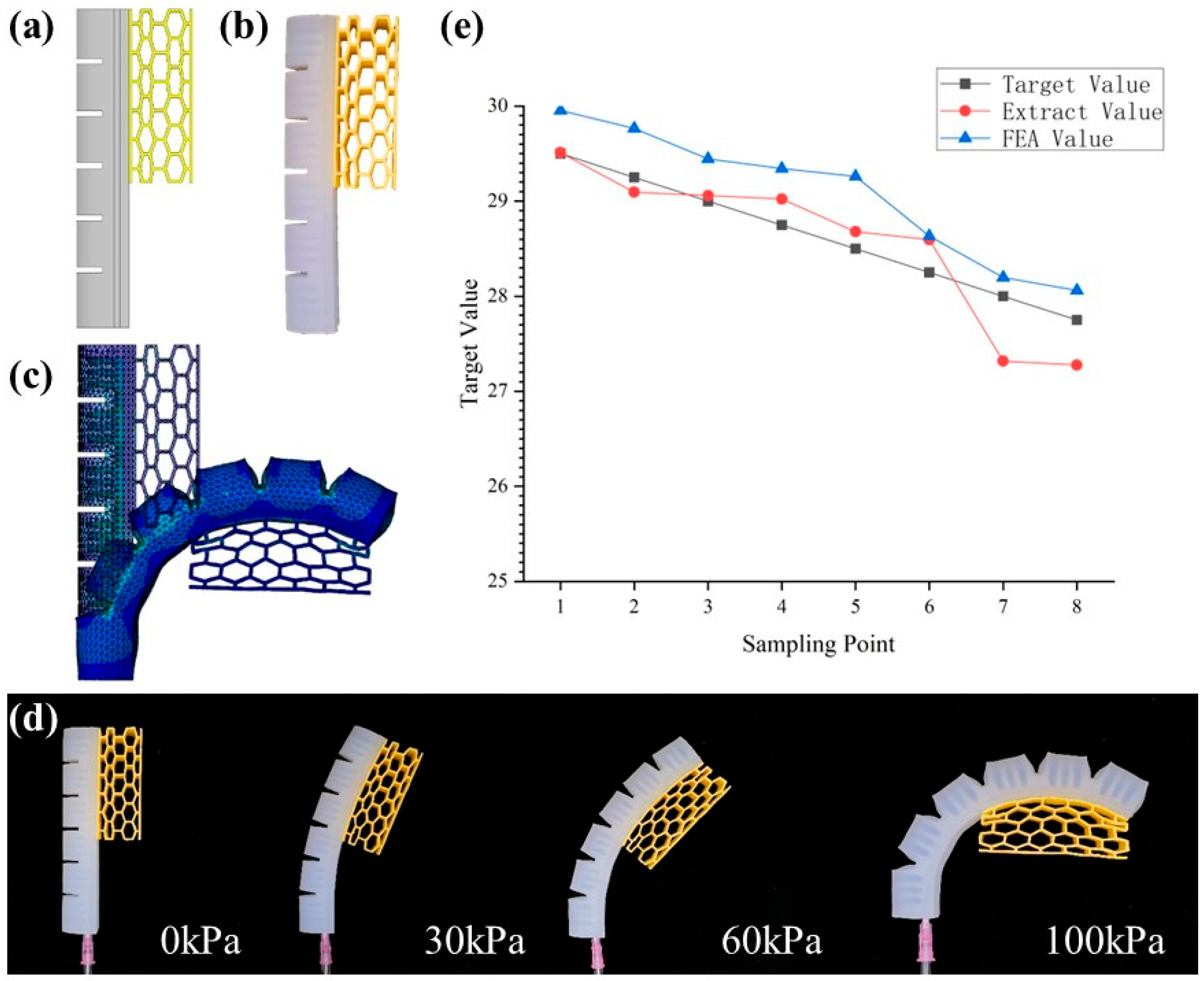
4. Data-Driven Inverse Design of Novel Assembled Gripper
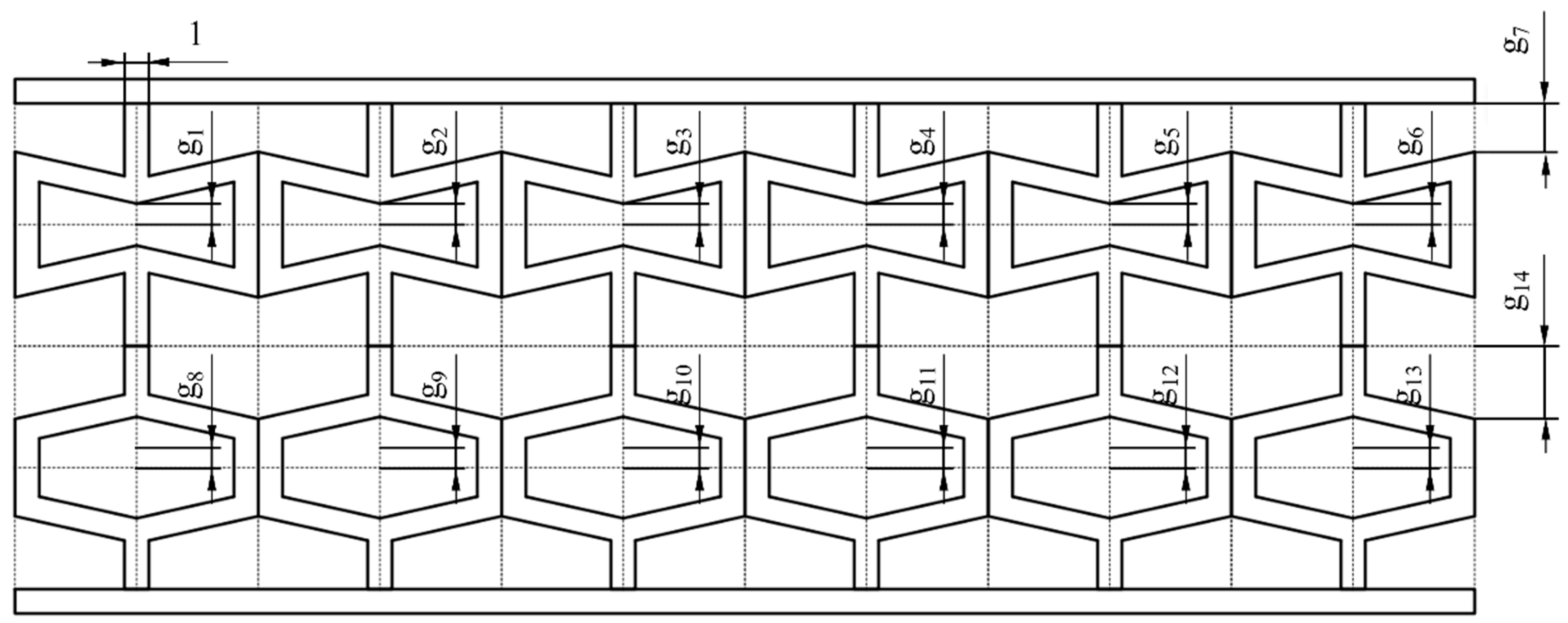
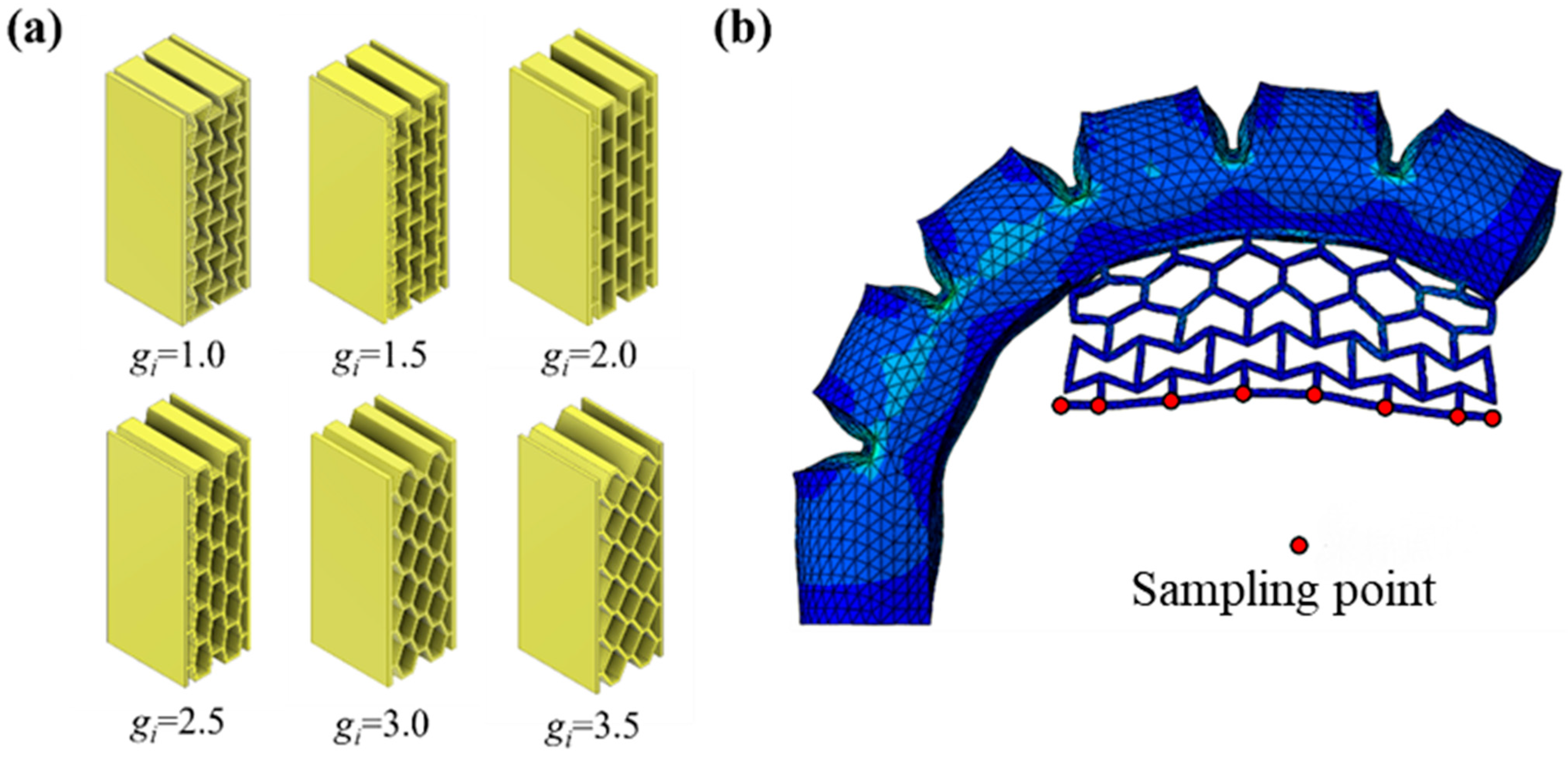
4.1. Parametric Finite Element Analysis Model
4.2. Generation of Dataset for Deep Learning
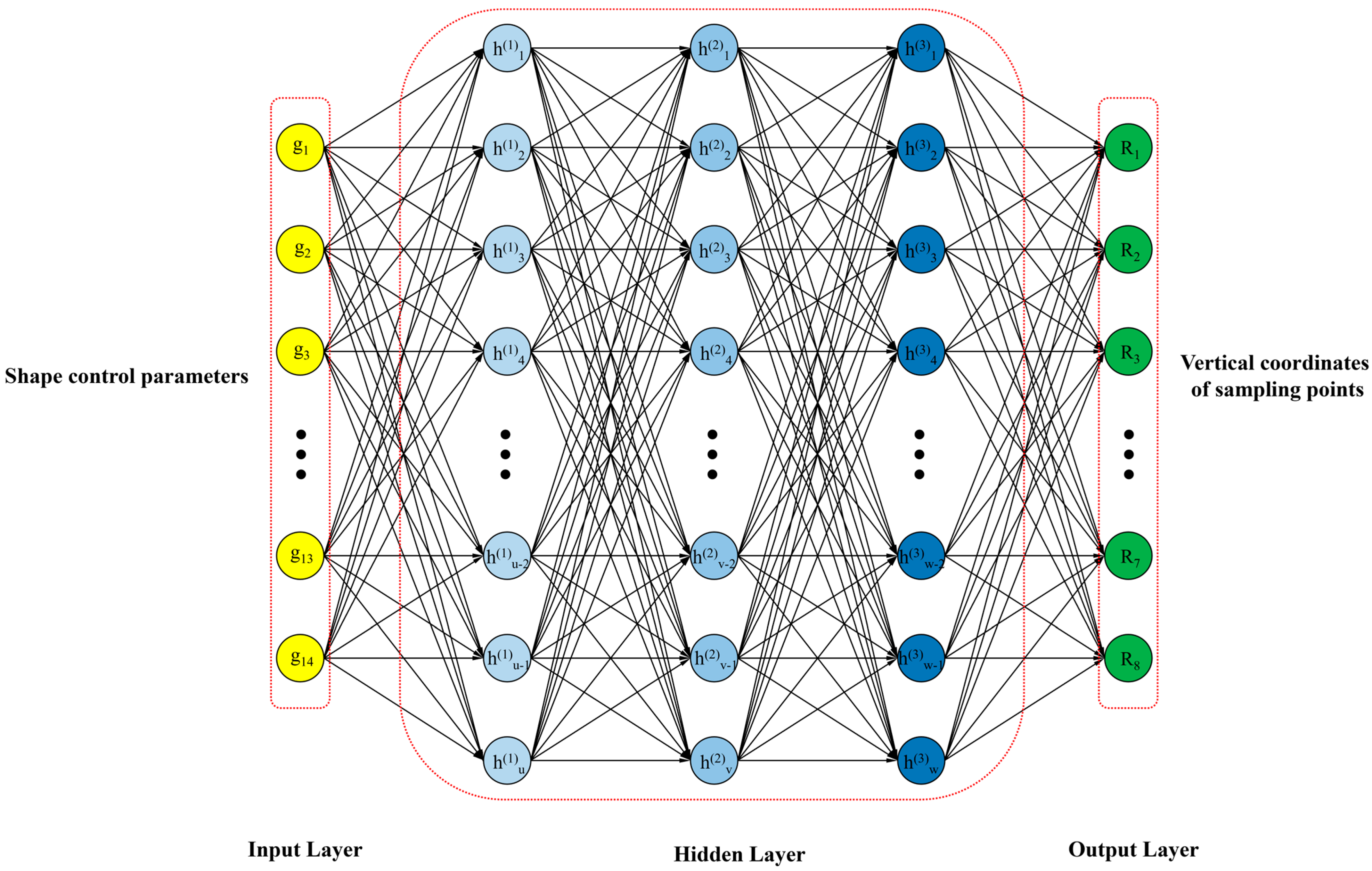
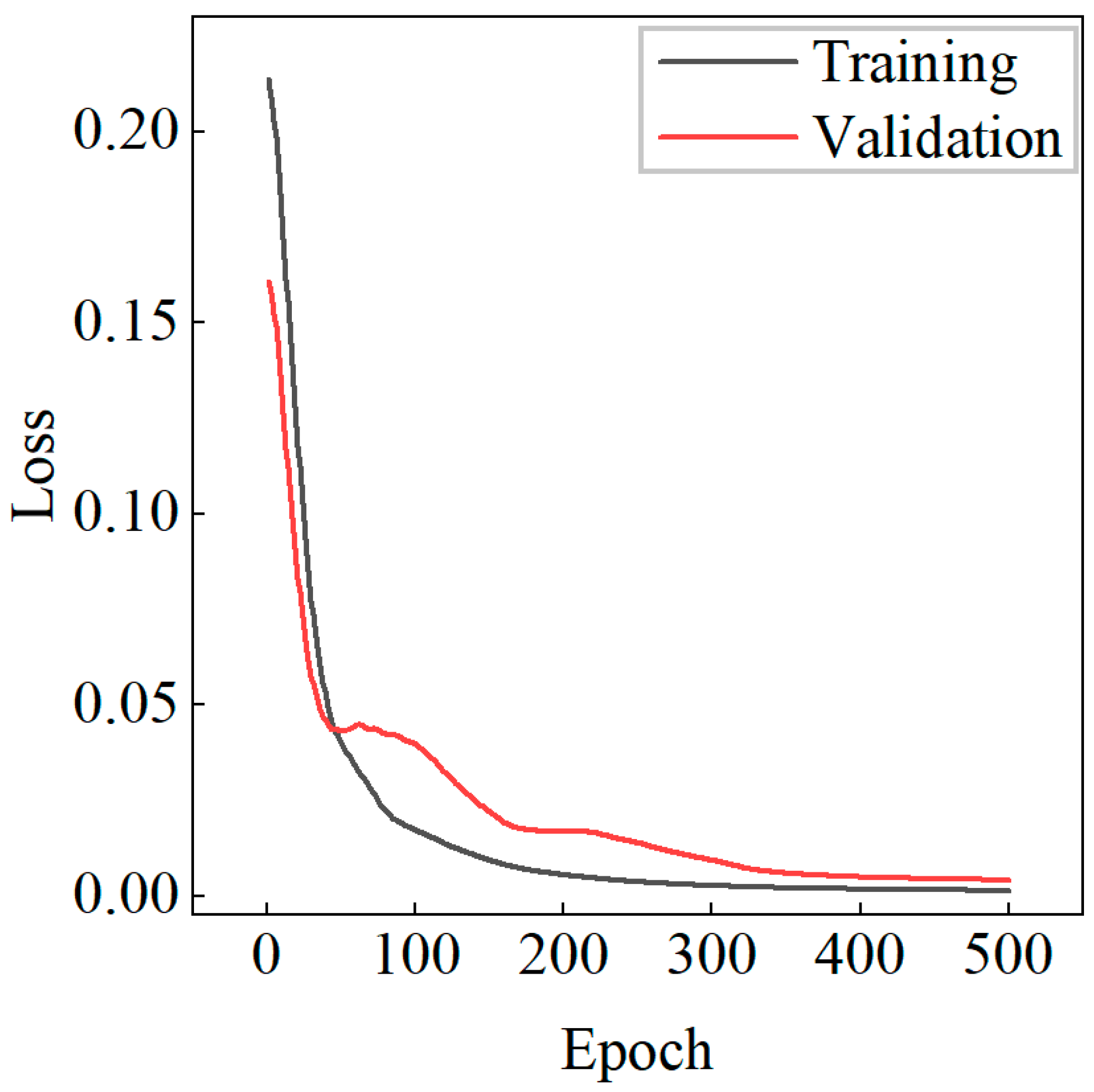
4.3. Forward Design Neutral Network
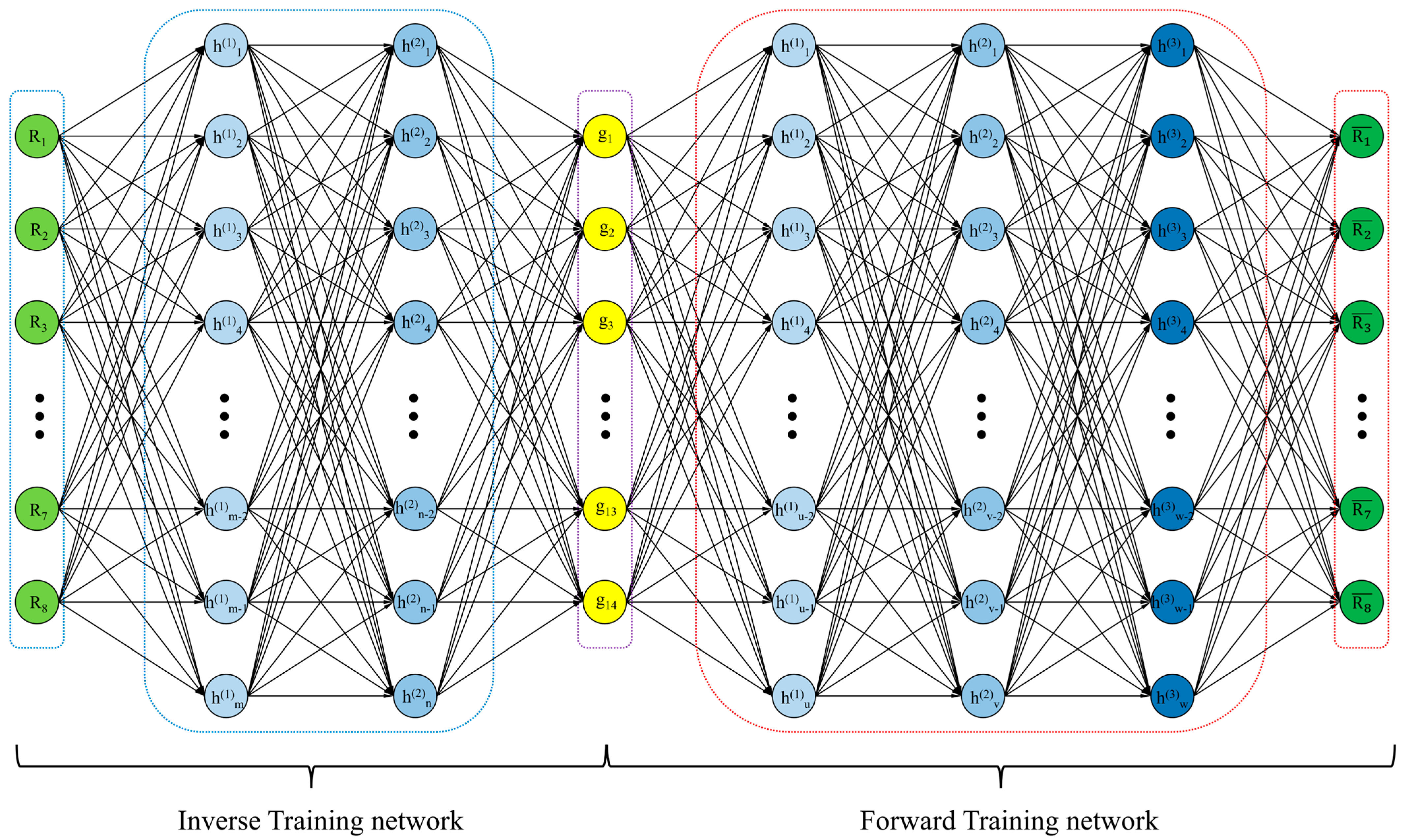
4.4. Inverse Design Neutral Network
4.5. Design Results
5. Experiments and Validation
5.1. Preparation of the Novel Assembled Gripper
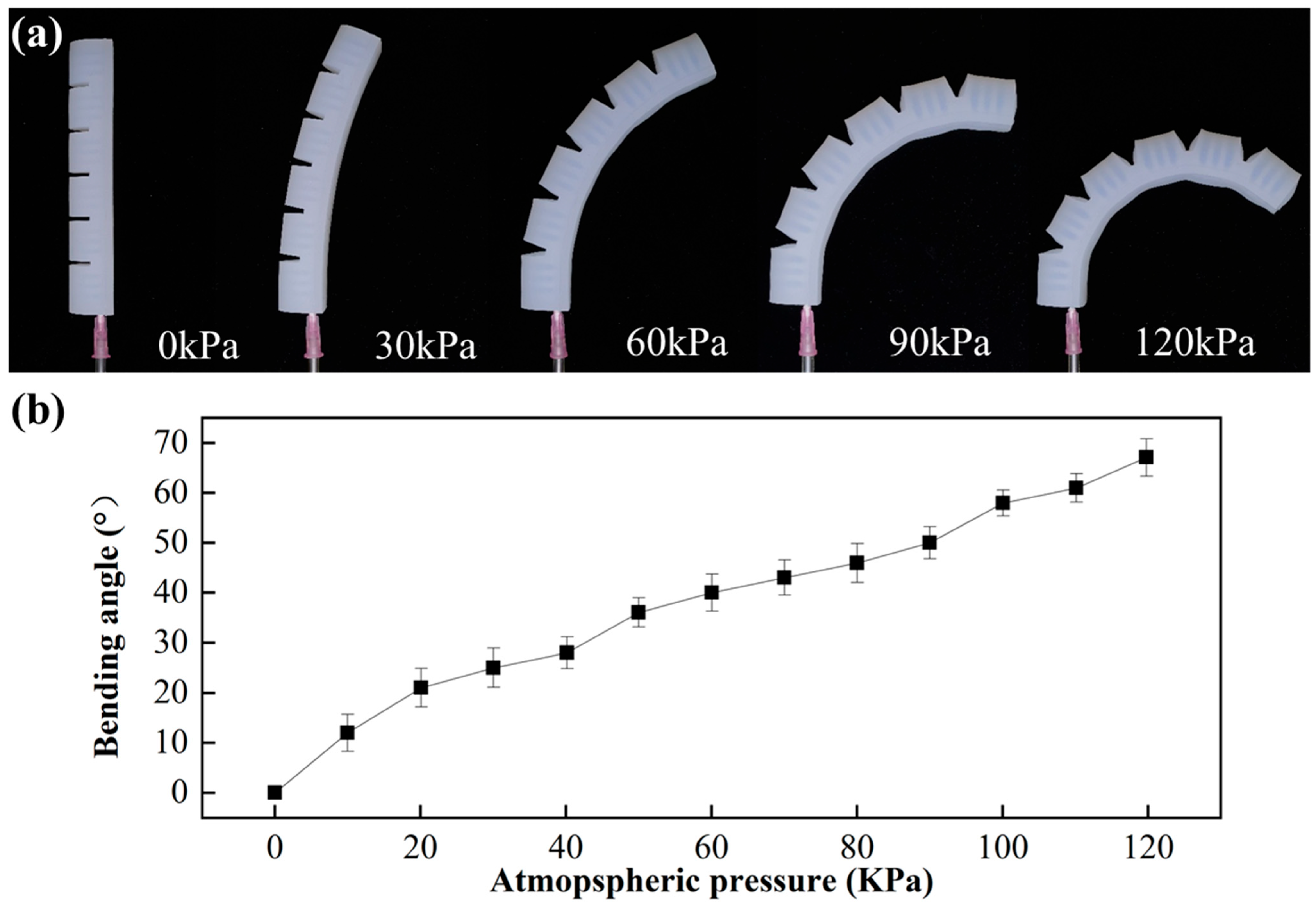
5.2. Performance Testing and Results Discussion
5.3. Deformation of Soft Grippers with Integrated Mechanical Metamaterials
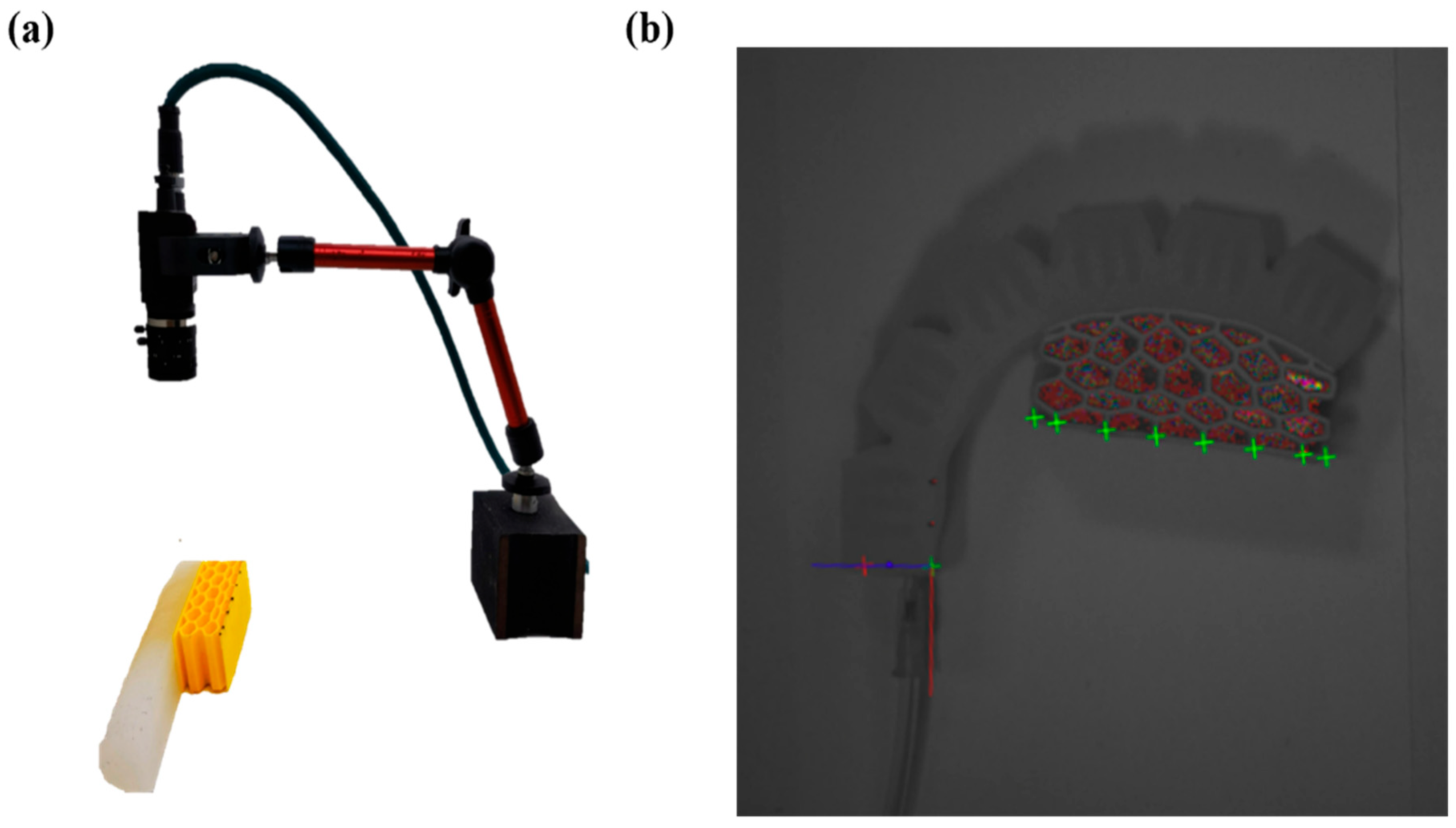
5.4. Experimental Validation of Shape-Matching Control in Soft Grippers
5.5. Discussion and the Limitations
- (1)
- Structural Design: Metamaterials are silicone-bonded “patches” on the fingertip (not integral). Long-term cyclic bending may cause adhesive failure (shear fatigue, peeling, creep); adhesive thickness/coating errors affect stiffness/Poisson’s ratio, with no quantified error sensitivity or tolerance control yet.
- (2)
- Overly Simple Optimization Objective: The deep learning loss function only uses sampling point z-coordinate deviation (focusing on geometric fit), ignoring gripping force, peak contact stress, fatigue life, and airtight safety margin. This risks crushing fragile objects (despite good profile matching) or early cracking.
- (3)
- Inadequate Experimental Coverage: Experiments only used two samples (planar, wedge-shaped; monotonic curvature, no depressions), failing to verify “high adaptability to complex/fragile targets.” Tests used only single-pressure loading (no cyclic tests) and lacked pressure retention/profile drift records, providing no basis for industrial service life.
6. Conclusions
- (1)
- This study presents the structural design of an integrated gripper, validated through FEA to ensure feasible deformation under pneumatic loads. The incorporation of Gibson hexagonal unit-based metamaterials enables tailored surface deformation, significantly improving contact conformity with complex object geometries.
- (2)
- This study develops a robust deep learning framework, comprising forward and inverse neural networks, which efficiently predicts gripping surface deformation and enables inverse design of metamaterial parameters for desired shapes, significantly reducing design complexity. This data-driven approach allows rapid generation of high-quality design solutions, overcoming the limitations of traditional trial-and-error methods.
- (3)
- This study demonstrates successful fabrication via 3D printing and silicone casting, with experimental results confirming that the optimized gripper achieves remarkable shape-matching performance and stable gripping of test objects. Machine vision-based validation demonstrated average shape deviation reductions of over 80% compared to initial designs, highlighting the practical effectiveness of the proposed method.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, D.; Baek, S.R.; Kim, M.S.; Park, C.Y.; Lee, I.H. Design and manufacturing process of pneumatic soft gripper for additive manufacturing. Sens. Actuators A Phys. 2024, 370, 115218. [Google Scholar] [CrossRef]
- Sinuo, Z.; Cong, N.C.; Thien, H.T.; Nho, D.T.; HoangPhuong, P. Transparent Pneumatic Tactile Sensors for Soft Biomedical Robotics. Sensors 2023, 23, 5671. [Google Scholar] [CrossRef]
- Li, X.; Fan, D.; Sun, Y.; Xu, L.; Li, D.; Sun, B.; Nong, S.; Li, W.; Zhang, S.; Hu, B. Porous magnetic soft grippers for fast and gentle grasping of delicate living objects. Adv. Mater. 2024, 36, 2409173. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, W.; Yang, H.; Yang, H. Application of Soft Grippers in the Field of Agricultural Harvesting: A Review. Machines 2025, 13, 55. [Google Scholar] [CrossRef]
- Schreiber, F.; Frohn-Sörensen, P.; Engel, B.; Manns, M. Applicability of models to predict the bending behavior of soft pneumatic grippers. Int. J. Adv. Manuf. Technol. 2025, 138, 273–286. [Google Scholar] [CrossRef]
- Qu, J.; Yu, Z.; Tang, W.; Xu, Y.; Mao, B.; Zhou, K. Advanced technologies and applications of robotic soft grippers. Adv. Mater. Technol. 2024, 9, 2301004. [Google Scholar] [CrossRef]
- Knospler, J. Design and Control of a Versatile Modular Soft Robotic System with Integrated Resource Sharing and Self-Reconfiguration Capabilities. Master’s Thesis, Rowan University, Glassboro, NJ, USA, 2025. [Google Scholar]
- Dzedzickis, A.; Petronienė, J.J.; Petkevičius, S.; Bučinskas, V. Soft grippers in robotics: Progress of last 10 years. Machines 2024, 12, 887. [Google Scholar] [CrossRef]
- Kozhemyatov, K.; Bulauka, Y. The improving of the safety level of the equipment working under excessive pressure. In Topical Issues of Rational Use of Natural Resource; CRC Press: Boca Raton, FL, USA, 2019; Volume 2, pp. 822–831. [Google Scholar]
- Al-Rubaiai, M.; Pinto, T.; Qian, C.; Tan, X. Soft Actuators with Stiffness and Shape Modulation Using 3D-Printed Conductive Polylactic Acid Material. Soft Robot. 2019, 6, 318–332. [Google Scholar] [CrossRef] [PubMed]
- Ilievski, F.; Mazzeo, A.D.; Shepherd, R.F.; Chen, X.; Whitesides, G.M. Soft robotics for chemists. Angew. Chem. (Int. Ed. Engl.) 2011, 50, 1890–1895. [Google Scholar] [CrossRef]
- Thien, H.T.; Sheng, Q.J.J.; Thanh, T.M.; Thien, P.P.; Hamilton, L.N.; Nho, D.T. Soft robotic fabric gripper with gecko adhesion and variable stiffness. Sens. Actuators A Phys. 2021, 323, 112673. [Google Scholar]
- Kumar, S.; Wang, X.; Strachan, J.P.; Yang, Y.; Lu, W.D. Dynamical memristors for higher-complexity neuromorphic computing. Nat. Rev. Mater. 2022, 7, 575–591. [Google Scholar] [CrossRef]
- Duan, F.; Wei, D.; Chen, A.; Zheng, X.; Wang, H.; Qin, G. Efficient modulation of thermal transport in two-dimensional materials for thermal management in device applications. Nanoscale 2023, 15, 1459–1483. [Google Scholar] [CrossRef]
- Yao, H.; Guo, B.; Zhang, T.; Tao, W. Photocurrent enhancement of topological insulator by femtosecond laser controlled surface structure. Eur. Phys. J. Plus 2023, 138, 562. [Google Scholar] [CrossRef]
- Valipour, A.; Kargozarfard, M.H.; Rakhshi, M.; Yaghootian, A.; Sedighi, H.M. Metamaterials and their applications: An overview. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 2171–2210. [Google Scholar] [CrossRef]
- Liu, G.-Q.; Liu, H.-T. Synergistic design of curved beam metastructure with tunable nonlinearity deformation and Poisson’s ratio. Eng. Fract. Mech. 2025, 316, 110897. [Google Scholar] [CrossRef]
- Shunshun, R.; Zhao, G. Mechanical characterization of a metamaterial with negative Poisson’s ratio under compressive loading: Experimental along with FEM. Mech. Adv. Mater. Struct. 2025, 1–10. [Google Scholar] [CrossRef]
- Jenett, B.; Cameron, C.; Tourlomousis, F.; Rubio, A.P.; Ochalek, M.; Gershenfeld, N. Discretely assembled mechanical metamaterials. Sci. Adv. 2020, 6, eabc9943. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Zhang, J.; Bai, Y. In-plane mechanics of a novel cellular structure for multiple morphing applications. Compos. Struct. 2019, 207, 598–611. [Google Scholar] [CrossRef]
- Dikici, Y.; Jiang, H.; Li, B.; Daltorio, K.A.; Akkus, O. Piece-by-piece shape-morphing: Engineering compatible auxetic and non-auxetic lattices to improve soft robot performance in confined spaces. Adv. Eng. Mater. 2022, 24, 2101620. [Google Scholar] [CrossRef]
- Dudek, K.K.; Kadic, M.; Coulais, C.; Bertoldi, K. Shape-morphing metamaterials. Nat. Rev. Mater. 2025, 10, 783–798. [Google Scholar] [CrossRef]
- Qi, P.; ShiTong, C.; FeiFei, C.; XiangYang, Z. Programmable soft bending actuators with auxetic metamaterials. Sci. China (Technol. Sci.) 2020, 63, 2518–2526. [Google Scholar]
- Charbel, T.; Rahim, M.; Gursel, A. A 3D Printed Modular Soft Gripper Integrated with Metamaterials for Conformal Grasping. Front. Robot. AI 2022, 8, 799230. [Google Scholar] [CrossRef] [PubMed]
- Xinjie, Z.; Elisha, O.A.; Ke, M.; Shouyi, Y. Entirely soft valve leveraging snap-through instability for passive flow control. Sens. Actuators B Chem. 2022, 367, 132035. [Google Scholar]
- Zhang, X.; Yu, S.; Dai, J.; Oseyemi, A.E.; Liu, L.; Du, N.; Lv, F. A Modular Soft Gripper with Combined Pneu-Net Actuators. Actuators 2023, 12, 172. [Google Scholar] [CrossRef]
- Vesco, S.; Salvi, D. Fuzzy skin in fused filament fabrication: Enhancing morphology, wettability, and friction through a full-factorial experimental plan. Prog. Addit. Manuf. 2025, 1–25. [Google Scholar] [CrossRef]








| L | W | H | R | ti | to | d | r | w |
|---|---|---|---|---|---|---|---|---|
| 110 mm | 26 mm | 19 mm | 16 mm | 2 mm | 3 mm | 3 mm | 13 mm | 2 mm |
| Exposure Time | Light-Off Time | Bottom Exposure Time | Number of Bottom Layers | Z-Axis Lift Height | Z-Axis Lift Speed | Z-Axis Retract Speed |
|---|---|---|---|---|---|---|
| 2.2 s | 2 s | 40 s | 5 | 5 mm | 4 mm/s | 4 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Zhang, B.; Sun, W.; Xu, Z.; Chen, X.; Weng, S.; Zhang, X. Novel Pneumatic Soft Gripper Integrated with Mechanical Metamaterials for Enhanced Shape Matching Performance. J. Manuf. Mater. Process. 2025, 9, 330. https://doi.org/10.3390/jmmp9100330
Han Z, Zhang B, Sun W, Xu Z, Chen X, Weng S, Zhang X. Novel Pneumatic Soft Gripper Integrated with Mechanical Metamaterials for Enhanced Shape Matching Performance. Journal of Manufacturing and Materials Processing. 2025; 9(10):330. https://doi.org/10.3390/jmmp9100330
Chicago/Turabian StyleHan, Zhengtong, Boqing Zhang, Wentao Sun, Ze Xu, Xiang Chen, Shayuan Weng, and Xinjie Zhang. 2025. "Novel Pneumatic Soft Gripper Integrated with Mechanical Metamaterials for Enhanced Shape Matching Performance" Journal of Manufacturing and Materials Processing 9, no. 10: 330. https://doi.org/10.3390/jmmp9100330
APA StyleHan, Z., Zhang, B., Sun, W., Xu, Z., Chen, X., Weng, S., & Zhang, X. (2025). Novel Pneumatic Soft Gripper Integrated with Mechanical Metamaterials for Enhanced Shape Matching Performance. Journal of Manufacturing and Materials Processing, 9(10), 330. https://doi.org/10.3390/jmmp9100330






