Extension of a Contact Subroutine for Composite Ring Rolling to Include Temperature Dependency

Abstract

By combining the ring rolling and roll bonding processes, the product spectrum can be additionally expanded. Since a successful composite ring rolling process requires a higher growth tendency for the inner ring, previous publications commonly included a softer inner ring to reduce the flow resistance of the inner ring or specific geometries for rings and tools. In this work, the material combination of a 100Cr6 (DIN 1.3505, AISI 52100) outer ring and a 42CrMo4 (DIN 1.7225, AISI 4140) inner ring is used to show that the composite ring rolling process is also possible for material combinations with a balanced flow stress ratio and equal wall thicknesses. In earlier publications, the influence of temperature was neglected. As the influence on the yield stress and thus on the success of the process has a significant influence, this should be considered in order to be able to make a reliable statement. For this purpose, the bond formation of the two materials was investigated by bonding experiments, and an existing bond formation model was extended with respect to the temperature dependency. On the basis of this model, the process control parameters were investigated using FE simulations, and a ring rolling experiment was carried out.

1. Introduction

Ring rolling is an incremental pressure-forming process for the production of seamless concentric rings. Due to their good mechanical properties and the wide range of geometries and materials, ring-rolled products are used in many technical areas, such as industrial plant engineering and mechanical engineering [1]. The process is divided into the initial, main and final (or: rounding) rolling phases. The initial rolling phase, where only radial rolling takes place, serves to correct defects of the preform such as uneven wall thicknesses due to asymmetric piercing of the preform. In the main rolling phase, a radial and axial reduction in the ring takes place, and a high Ring Growth Rate (RGR) is reached. In the end rolling phase, the ring roundness is improved, and the RGR is reduced in relation to the main rolling phase [2].

Due to the technological combination of ring rolling and roll bonding by composite ring rolling, this product spectrum can be extended even further. In this process, two concentrically arranged rings made of different materials are rolled together in one ring rolling process and joined by the existing normal stresses and surface enlargement (SE) in the joining surfaces. The composite ring rolling process can thus be used for rings whose local properties are adapted to the application by the choice of material so that expensive material or further processing of the component can be saved [3].

For example, a ring that needs to be wear resistant on the inside, such as the outer ring of a roller bearing, could be more economically produced if that ring is made of a composite material. Only the functional surface on the inside, which is in contact with the rolling elements, is made of bearing steel, while the outer ring that carries the load is replaced with cheaper quenched and tempered steel. Despite its similarity to roll bonding and the lack of alternative processes for the production of seamless composite rings with the mechanical properties of forged/rolled parts, the composite ring rolling process has hardly been investigated to date.

In comparison to roll bonding, the composite ring rolling process is more complex because of the thermal conditions, the small pass reductions, the long process time and the constantly changing forming parameters due to the repeated roll gap passes. The resulting fluctuating stress states can be problematic for achieving a permanently stable material bond. For a stable material bond, it is important that the rings do not separate during rolling. This is one of the biggest challenges of the process. As the flow stresses play a decisive role here, the temperature of the individual rings is just as important [4]. Previous investigations and models on roll bonding can only be transferred to the composite ring rolling process to a limited extent, as they neglect, for example, the temperature drop during the process. The longer process time of ring rolling compared to roll bonding leads to dramatic temperature fluctuations and has a major impact on the process and the bond.

Due to the high costs for experiments, today’s investigations usually start with simulative studies. However, due to the long calculation time, earlier bonding models for the rolling of composite rings did not consider the influence of temperature changes [5,6].

In this paper, the composite ring rolling process for the material combination 100Cr6 (DIN 1.3505, AISI 52100) outer ring and 42CrMo4 (DIN 1.7225, AISI 4140) inner ring is to be investigated. Due to the very good hardenability and wear resistance of 100Cr6 and the high toughness and strength of 42CrMo4, a composite ring made of these materials can serve as an inner ring for a roller bearing ring. The aim of this work is to enable a reliable production of composite rings made of these two materials by developing the contact subroutine VUINTER in Abaqus to simulate the temperature dependence of the bond strength.

2. State of the Art

2.1. Bonding of Material Established by Forming

The variety of processes to obtain a material bond between two materials is wide [7]. Typical processes to achieve a bond are surface coating, gluing, welding and casting processes. In addition, there are some metal forming processes like composite extrusion [8], explosion welding [9], composite forging [10] and the industrially well-established process of roll bonding [11] in use. In roll bonding, two strips or slabs are joined together by one or more flat rolling passes. The contact surfaces are enlarged by rolling and stretching the material. The existing compressive stresses together with the creation of new surfaces during the stretching of the material lead to a welding of the two materials without the need for a liquid phase [12]. However, none of these processes makes it possible to produce rings with the excellent mechanical properties of a forged or rolled part. The composite ring rolling process, a combination of ring rolling and roll bonding, would offer the possibility of combining materials with significantly different properties that meet local requirements on the inner and outer lateral surfaces. There are currently no other options to produce a seamless ring with different material properties on both surfaces in combination with a fine-grained microstructure resulting from forming processes.

2.2. Bonding Models

In order to describe the bond formation, different models can be used. The first model for bond formation was published by Bay et al. [13] in roll bonding of scratch-brushed aluminum sheets. The material, which was strain hardened due to brushing, was considered to have a brittle cover layer of surface oxides together with a ductile contaminant film on both contacting surfaces. According to the model, the height reduction and the elongation of the sheets start two mechanisms. At first, the brittle oxide layer breaks up and, if the pressure stresses are high enough, virgin material is extruded through the cracks.

The material is bonded under high pressure in the area where the new material of both partners is in contact on an atomic level. The ductile-contaminated film on the surface is considered in the second mechanism. The ductile film thins out until a threshold surface enlargement (SE) breaks it. After the film breaks, the second mechanism takes place when the two materials contact and bonding is achieved.

This model was expanded by Cooper and Allwood [14] to predict bond strength based on physical assumptions. They take the roughness of the contact area into account. For simplicity, one surface of this pair of surfaces is assumed to be flat. The other is expected to have a topology that approximates two rough surfaces in contact. This allows the calculation of the true amount of exposed aluminum metal. The necessary extrusion pressure for the aluminum metal is estimated with a calculation of the typical crack width between cracked oxide fragments. These extrusion pressures are depending on the longitudinal strain, shear, strain rate, normal and shear contact stresses and the contact temperature. Experiments showed that for bonding, a minimum strain or surface enlargement (SE) is required. This minimum strain is influenced by the temperature, normal contact stress or shear stress and is predicted by the model correctly, but for higher temperatures, it underestimates the bond strength and the influence of the strain rate.

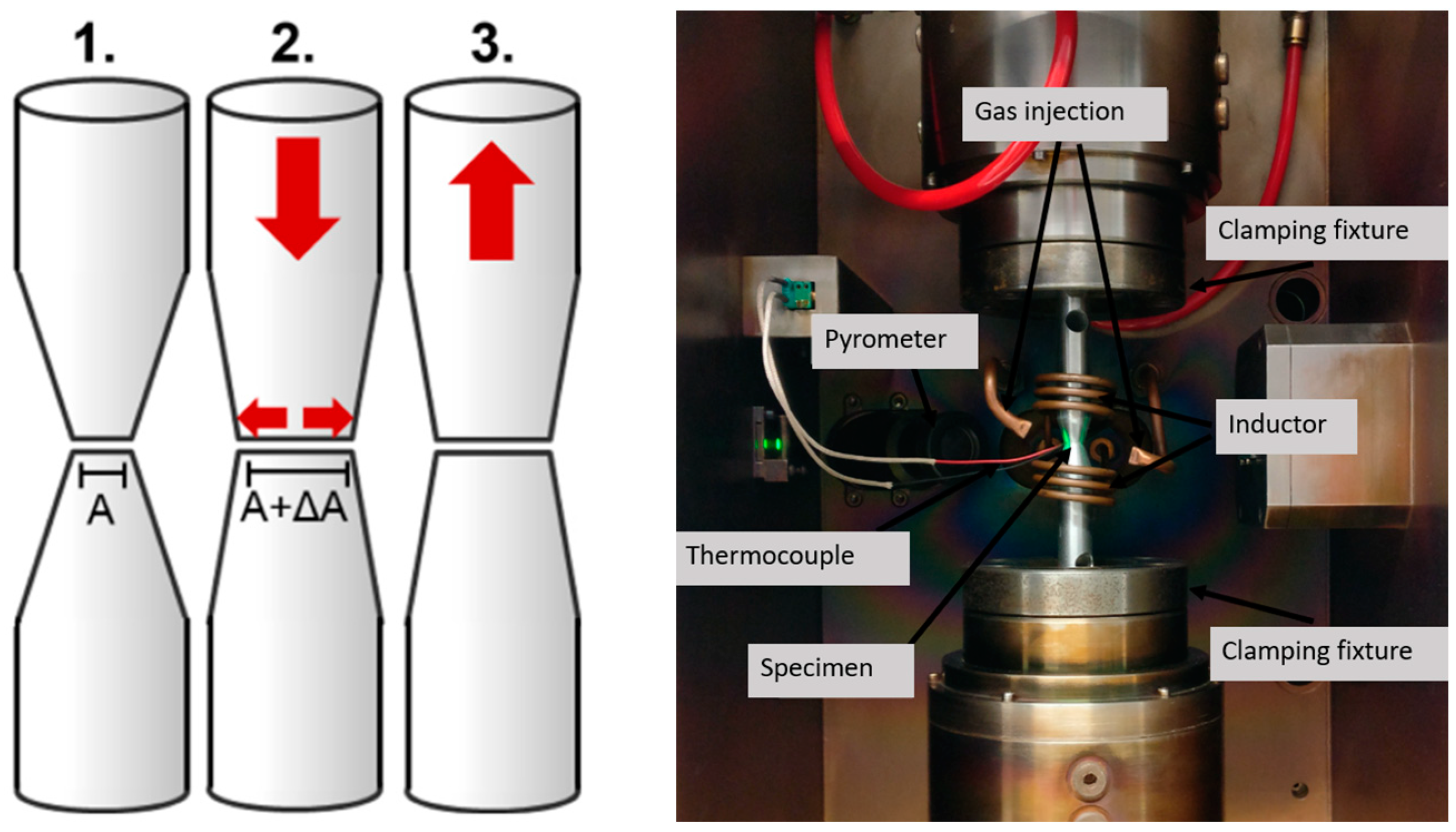
Bambach et al. [15] developed a framework which can describe the bond strength with good accuracy. To calibrate this empirical bonding model, Mikloweit et al. [16] presented a bond strength experiment for pressure welding processes at room temperature such as cold roll bonding. In these experiments, two truncated-cone shaped samples of the investigated material combination (cf. Figure 1) are first heated to process temperature and then upset according to different compression distances to investigate the bond strength in dependence of the upsetting path. After that, the movement is reversed, and the samples are immediately tensile tested by measuring the forces and movement of the specimen holder of the upper sample. The results show a tensile force to debond the two samples. Simple FE simulations of these tests deliver the SE in % for the investigated upsetting path. With this information, the calculation of the bond strength is possible by correlating the tensile forces and contact area at the time of bond failure. For different temperatures and upsetting paths, the bond strength can be calculated. By conducting these tests at different temperatures and compression distances, the temperature and strain-dependent bond strength model can be calibrated.

One possible way to implement the framework presented by Bambach et al. [15] into an FE software is an interaction subroutine, which can also consider the results of empirically determined bonding values as depicted above.

The models explained above were developed for low temperatures and are therefore not directly applicable for hot ring rolling. In hot forming processes, the complex interrelations on the microscale need to be considered. Furthermore, the framework [15] needs adjustments for the hot composite ring rolling of steel, because it was designed to describe single step or continuous forming processes. Neither diffusion nor the large number of rolling passes are considered originally.

2.3. Simulation of the Bonding Behavior in Ring Rolling

For a successful ring rolling process, it is imperative that the final ring geometry matches the target geometry, that the rings are bonded together accurately and that the joint line runs parallel to the surface lines. A number of simulation studies have been carried out on this topic in the past.

Seitz et al. [17] investigated the composite ring rolling process by using a closed-loop controlled ring rolling model previously developed by Jenkouk et al. [18]. Using a friction coefficient of 0.3 and “hard contact” in the normal direction between all contact partners, an asymmetrical joint line in the ring’s cross-section was observed, resulting from the rolling tables’ influence on the material flow in the radial roll gap. With uneven material flow across the ring height as the underlying cause, a larger height-to-wall thickness ratio could reduce or prevent this issue. Furthermore, a softer inner ring does not necessarily lead to a successful composite ring, because the inner ring may grow out of the outer ring if a considerably faster tendency for ring growth cannot be inhibited by the composite ring [17]. The start of the process turned out to be the most critical time period for the process, because maintaining the contact between the rings becomes easier with increasing ring diameters [19]. Based on the results of Mikloweit [16] and Pietryga [20], Guenther et al. [5,6] extended the FE model by Jenkouk [18] with the bond strength model linked to the SE by using the interaction subroutine VUINTER to consider the contact behavior of the materials and both bonding and debonding processes. By adding the third dimension to the subroutine, one normal and two tangential directions need to be considered. However, the influence of temperature was neglected in these investigations, as only a single parameter set was used for just one temperature. The cooling of the ring during transportation to the ring rolling mill or the heating due to dissipation during the process was therefore neglected, which can lead to considerable differences between the simulation and experiment.

2.4. Conclusion from the State of the Art

The composite ring rolling process enables the production of seamless rolled rings made of different materials on the inside and outside. Due to its complexity, a precise FE-simulation model including a bonding model is needed to enable a favorable and reliable process design. Nevertheless, previous simulation models have not been able to consider the temperature dependence. Since temperature has a significant influence on the forming and bonding behavior of the rings and the rings may cool down considerably during transport from the furnace to the machine as well as during the rolling process, this temperature dependence must be considered in order to reliably produce well-bonded composite rings.

In earlier publications of the recent authors, the bonding subroutine, based on the framework of Bambach [15], was used to simulate the composite ring rolling process, whereby the temperature was neglected. Cleaver et al. [4] showed that the flow stress ratio has a significant impact on the success of the composite ring rolling process; thus, the temperature should not be neglected while investigating the process. This publication describes the extension of the temperature dependence within the bonding model used in the FE simulations of ring rolling of composite materials. The subroutine VUINTER is extended to consider the bonding behavior of the investigated material combination.

3. Calibration of Subroutine VUINTER

To calibrate the Abaqus subroutine VUINTER for the investigated materials, it is necessary to investigate the parameters of the bonding. The material-specific values result from bonding tests, which provide a dependence between the bond strength and the SE due to forming.

3.1. Bonding Experiments with the Plastometer

In this study, a material combination of 100Cr6 for the outer ring and 42CrMo4 for the inner ring is examined. To characterize the bonding behavior of the chosen materials, a torsion plastometer STD812 was used; the procedure and the experimental setup are shown in Figure 1. The process procedure was described more in detail in Section 2.2. For more detailed information, see earlier publications [5,6]. Reproducible test results can be achieved with the torsion plastometer, whereby the deformation paths, temperature, heating rates, speed and ambient atmosphere can be controlled. The plastometer tests were carried out at different temperatures and different compression paths in order to investigate the bonding of the material combination. The temperature range was between 1150 and 1250 °C, with 1200 °C as the chosen rolling temperature for this material combination and possible cooling during transport as well as heating of the interface area due to dissipation in the rolling process. The compression paths varied between 0.05 and 2 mm, leading to surface enlargements of up to 12% for the highest temperature, for which a strong bond is established.

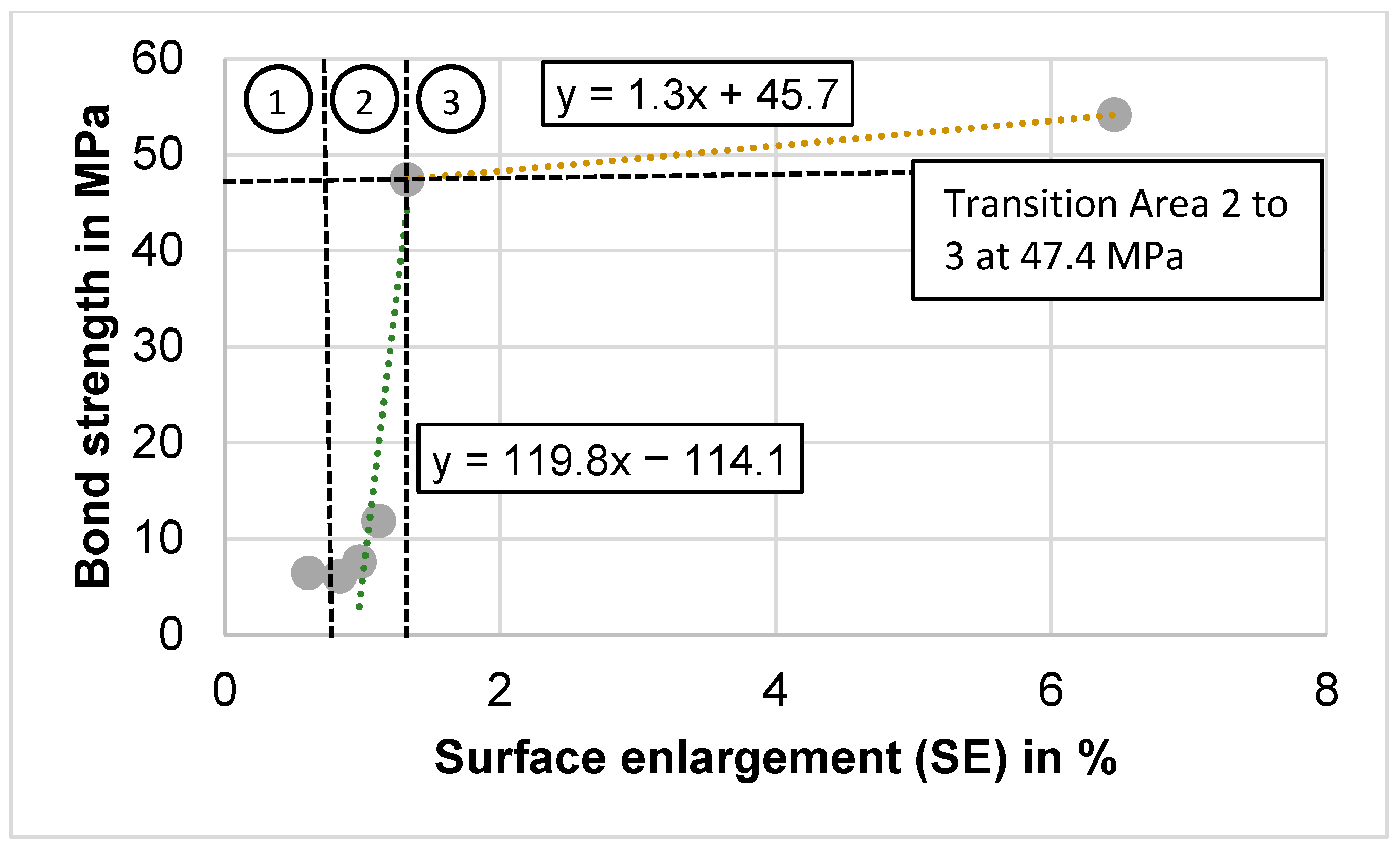
Figure 2 shows the bond strength at 1150 °C for different SE values, respectively, compression paths. The bond strength was determined by tensile tests on the plastometer. Due to the high bond strength achieved by the compression paths, the subsequent tensile test results in relevant necking of the bonding area, which prevents direct measurement of the surface enlargement. Therefore, the surface enlargement for the individual compression paths was determined by hard contact simulations of the experiment.

The figure shows that the course of the bond strength, similar to the observations of Guenther et al. [5], can be divided in three different areas. In area 1, there is no nominal increase in bond strength due to SE, as the brittle oxide layers are starting to break up. The bond strength remains below 7 MPa until an SE of approx. 0.9% is reached. In area 2, the bond strength increases significantly due to the larger surface area, as the virgin material is extruded through the cracks. A linear regression through two data points shows a gradient of 119 MPa/(% SE). Starting from a value of approx. 47 MPa of the bond strength, area 3 begins. Here, the bond strength increases very slowly over the SE, which is mainly due to the hardening of the base material. The gradient in this area shows 1.3 MPa/(% SE).

Table 1. Values of the bond strength for different temperatures.

Temperature in °C	Gradient Area 2 [MPa/%]	Bond Strength at Transition Point [MPa]	Gradient Area 3 [MPa/%]
1150 1200 1250	119.8	47.4	1.3
	150.5	36.2	2.0
	300.8	35.4	3.5

shows the values of the bond strength for the investigated temperatures.

In the first area, the oxide layers on the contact surfaces do not crack enough to allow the extruding of clean material at the present contact normal pressure, resulting in no bond strength. Instead, the measured values are expected to be surface roughness peaks becoming entangled with each other (cf. Cooper et al. [14]). For a conservative design of the bonding model, these affects will be neglected. For the further investigations, it is therefore assumed that no bond occurs in area 1 and that the bond strength can only be assumed in combination with a minimum SE. For the calculation of the minimum SE, it is assumed that the neglected effects predominate up to an SE of 0.8% and a bond strength of 7 MPa, since this was similar for all courses. These values represent the approximate average values of the transition point from area 1 to area 2 for all three investigated temperatures (cf. Figure 2).

As the temperature increases, the material combination shows an increasingly stronger affinity for bonding, which is due to the increased kinetics of the thermodynamic processes involved. At the same time, the yield stress of the material is lower so that the maximum achievable bond strength is reached earlier.

3.2. Development of the Contact Model

The used user subroutine containing the bonding model is based on the framework of Bambach et al. [15]. The model was developed for cold roll bonding, so the influence of temperature was neglected. In hot ring rolling, however, the high starting temperatures as well as long process times lead to a significant cooling of the ring during the process. To take this into account, an extension of the model described by Guenther et al. [5] is required to allow the use of temperature-dependent connection parameters.

For this purpose, the gradients of the bond strength as a function of the SE, given in Table 1, are plotted against temperature. Figure 3 shows a corresponding example for area 2.

A quadratic fitting of the data points for every characteristic value is calculated by Equation (1), which describes the bonding parameters for one investigated temperature in the range from 1150 to 1250 °C.

$$p_{B{S}_i}=p_{B{S}_{i1}}·{\left({\displaystyle \frac{T}{100}}\right)}^2+p_{B{S}_{i2}}·\left({\displaystyle \frac{T}{100}}\right)+p_{B{S}_{i3}}$$

(1)

$$p_{B{S}_{ij}}=\mathrm{Bonding} \mathrm{Parameters},T=\mathrm{Temperature}$$

The three original bonding parameters are therefore each made up of three individual composite parameters and are recalculated for each time the VUINTER is called in the simulation. The boundary values for temperatures lower than 1150 °C and higher than 1250 °C are assumed to be constant, because the joint line temperatures during the critical part of the rolling process will stay in this range. The beginning of the process is the most critical time window for separation, and therefore, the first few seconds should be simulated as accurately as possible.

Table 2. Bonding parameters.

	${\mathit{p}}_{\mathit{B}{\mathit{S}}_{\mathit{i}1}}$	${\mathit{p}}_{\mathit{B}{\mathit{S}}_{\mathit{i}2}}$	${\mathit{p}}_{\mathit{B}{\mathit{S}}_{\mathit{i}3}}$
i = 1; Gradient Area 2	239.1	−5556.9	32,405.6
i = 2; Transition area 2 to 3	20.9	−514.4	3194.6
i = 3; Gradient Area 3	1.6	−36.6	208.6

shows the bonding parameters for the areas.

The calculation of the bond strength ${\sigma }_B$, which is based on the SE, was changed to an incremental calculation. This allows calculation of the bond strength for every increment with a dependence of the temperature; subsequently, the temperature change over the process can be considered. Equation (2) shows the calculation scheme for ${\sigma }_{B,t}$ in area i.

$${\sigma }_{B,t}={\sigma }_{B,t-1}+dSE·p_{B{S}_{\mathrm{i}}}$$

(2)

t = time, i = area of bonding

The bond strength ${\sigma }_B$ will be calculated based on the bond strength of the previous time step, the surface enlargement change (dSE) and the bonding parameter $p_{B{S}_i}$.

The minimum surface enlargement SE_min which is necessary for bond formation (see Section 3.1) is calculated for the material combination tested here as

$${SE}_{min}=0.8\%-{\displaystyle \frac{7\mathrm{MPa}}{p_{{BS}_1}}}$$

(3)

A limit value for the bond strength is also implemented. As the ring passes through several passes during ring rolling, it is possible to achieve a calculated bond strength that is many times higher than the yield stresses of the two materials, which is not physically possible. As a conservative estimate for the FE simulation, the limit value is therefore set to the lower yield stress of the two materials as a function of temperature.

3.3. Implementation and Macroscopic Validation of the Contact Model

For the validation of the determined composite parameters and the extended subroutine VUINTER in Abaqus, the above discussed parameters are implemented in the simulation. The plastometer experiment, described in Section 2.2, will be simulated using this setup.

Figure 4 shows the bond strength of the plastometer tests as a function of the SE for a temperature of 1200 °C. In addition, the figure shows the bond strength of an exemplary node on the face of a plastometer sample calculated by VUINTER for a plastometer simulation at the same temperature.

The course of the bond strength calculated by the VUINTER corresponds to that of the plastometer tests in the characteristic points. However, the bond strength is underestimated by 3 to 10 MPa in the entire tested range (areas 2 and 3) due to the conservative estimate of the simulation. One reason for this could be the minimum surface enlargement that must be achieved in order to establish a bond in the simulation. The minimum surface enlargement could be too low so that the bonding starts too late in the simulation or earlier in the experiment.

Since the aim was precisely this conservative estimate, this deviation is acceptable. Since in reality a higher bond strength occurs, a positive prediction of the simulation should lead to an even better result in the ring rolling process.

4. FE Simulation of the Ring Rolling Process

For the investigations presented in this paper, a fully closed-loop controlled FE model (Abaqus) [18] was used, which includes motion control for all tools via the subroutine VUAMP (cf. Figure 5).

Even though the motion control of the radial–axial ring rolling mill treats the composite ring as a monolithic ring, no adjustment to the control algorithm was necessary, as the composite ring rolling process requires joining both rings in the early phases of the process. The subroutine VUAMP is used to simulate the system behavior and used to control the tool movements within the simulation. The ring geometries and the materials are summarized in

Table 3. Material and geometry of the investigated rings.

Materials
Outer ring (OR) Inner ring (IR)	100Cr6 42CrMo4
Initial geometry
Outer diameter Inner diameter Height Wall thickness OR ($s_{OR}$) Wall thickness IR ($s_{IR}$)	290 mm 186 mm 130 mm 26 mm 26 mm
Final geometry
Outer diameter Inner diameter Height Total wall thickness	502 mm 450 mm 130 mm 26 mm

.

The initial wall thickness ratio $s_{OR}/s_{IR}$ of the investigated ring is 1:1. The height of the ring is held constant throughout the rolling process. As a first investigation point, a convergence analysis was carried out in which the influence of the mass scaling, the friction coefficient and the mesh density were examined. The results show that a friction coefficient between the tools and the rings of 0.3 is suitable, and a mass scaling of 50 and an element count of 24,600 are recommended for the investigated geometry for achieving realistic results with appropriate computational times. Both rings had 120 elements in the circumferential direction. The inner ring had five elements and the outer ring had four elements in the direction of the wall thickness. Across the ring height, the inner ring featured 25 elements and the outer ring featured 20 elements. As the growth of the inner ring is decisive for the bond, it was meshed more finely. The temperature of the ring at the start of the process was 1200 °C. The influence of different tool geometries and process parameters for maintaining a geometric fit between the rings, i.e., the rings remain in contact throughout the whole process, was analyzed.

To investigate the influence of the contact subroutine VUINTER on the simulation results, in a first step, simulations are carried out without the subroutine using “hard contact” due to there being shorter computational times. This prevents the slave surface from penetrating the master surface, and no tensile stresses are transferred across the interface. In order to qualitatively consider a possible bonding, the friction coefficient between the two rings was set to 0.45. To ensure that the ring is within the investigated temperature range, the process was simulated at 1200 °C.

4.1. Ring Rolling Simulation without the Contact Subroutine VUINTER

During the simulation, the separation of the rings—respectively, the gap between the rings—is monitored. In order to minimize the influence of the individual rolling phases, a relatively low RGR in relation to earlier investigations was selected in each case (see

Table 4. Combined process parameters.

Parameter	RGR Initial Rolling Phase [mm/s]	RGR Main Rolling Phase [mm/s]	Diameter of the Mandrel [mm]
Value	0.75	3	75

).

Figure 6 shows the evolution of the rings during the first 20 s of the rolling process. This figure shows the cross-sections of the ring in the axial rolling gap so that a separation of the rings becomes visible. At the start of the process, it can be seen that the rings have come into contact. Right after the start of the ring rolling process, the outer ring has a larger ring growth than the inner ring, and the two rings separate. The figure shows that a clearly recognizable gap forms after just 3 s. Due to the displacement of the inner ring in the direction of the radial roll gap exit, the gap can be observed in the axial roll gap. A gap in an experiment would immediately lead to scaling. The gap between the rings then closes again and is no longer visible after a process time of 15 s. The reason for this behavior is the ring curvature. At the beginning of the process, the ring curvature is larger, and therefore, the pressed length at the mandrel is larger than the pressed length at the main roll, so that the outer ring initially grows faster. In the course of the process, the ring curvature changes so that from a certain point in time, the pressed length on the main roll is larger than the pressed length on the mandrel, so that from this point in time, the inner ring grows more than the outer ring (cf. Figure 6), and the rings then come into contact.

4.2. Ring Rolling Simulation Including the Contact Subroutine VUINTER

As a second step, more accurate but more computationally intensive simulations including the contact subroutine VUINTER were used to validate these process parameters including the bonding behavior. Other than the different contact behavior, the same process parameters as for the simulations using hard contacts were used (cf. Table 4). It should be noted that the subroutine VUINTER forces the use of a penalty contact. Figure 7 shows the ring geometry at different times. When suitable parameters (cf. Table 4) for the forming processes are chosen, the simulation including the contact subroutine VUINTER shows no separation of the rings in comparison to the results without the subroutine (cf. Figure 6). The simulation shows no debonding of the two rings in any timestep. The outgrowth of the outer ring, as seen in the hard contact simulation, was completely prevented by the bonding strength between the rings. The developing bond strength, calculated by VUINTER, leads to a permanent contact of the rings in the simulation.

The results suggest that a composite ring can be successfully rolled using the process parameters from the simulation. Separating is completely prevented, and a permanent contact between the rings is achieved.

5. Experimental Validation

A composite ring rolling test was carried out on the IBF radial–axial ring rolling mill, Wagner Banning H100/V80 (see Figure 8). The mill was built by the J. Banning AG, based in Hamm, Germany, which is now part of the SMS group GmbH, Mönchengladbach, Germany.

Seamless rolled rings were used as the preform for the production of the composite rings. To produce the pre-ring for the composite ring rolling, two concentrically arranged rings were pressed into each other. In order to achieve the best possible bond, the surface between the rings should be as clean as possible (cf. Cooper et al. [14]). For this reason, the rings were machined at the joint line and then cleaned with citric acid and ethanol. In order to achieve an interference fit between the rings, an excess of 0.9 mm was used to ensure the best possible contact during heating. The excess requires heating of the outer ring to 120 °C to press the rings into each other with the use of a hydraulic press. The inner ring remains at room temperature. To prevent oxidation while heating the rings, the upper and lower contact lines were welded and sealed. The dimensions of the ring pairing of outer and inner ring (OR and IR) after machining are summarized in

Table 5. Dimensions of the ring pairing after machining.

Single Rings	Outer Diameter [mm]	Inner Diameter [mm]	Wall Thickness [mm]	Height [mm]
Outer ring	308.4	238.4	35.1	130
Inner ring	239.3	174.5	32.4	135

.

For the rolling procedure, the rings are heated up to 1200 °C. The RGR was chosen as in the simulations to be 0.75, 3 and 1 mm/s in the initial, main and final rolling phase (see Table 4). Figure 9 shows the rolled composite ring of the experiment.

The experiments have shown that the predictions of the simulation, including the contact subroutine, were correct. The rolled composite ring had the target geometry, a joint line running parallel to the surface lines, and the bonding between the rings was strong enough to remain after sawing. No further tests were carried out at this stage, as the focus was on the feasibility of the process. The rolling of the composite ring was successful.

6. Conclusions

In this work, the composite ring rolling process for the material combination of a 100Cr6 outer ring and a 42CrMo4 inner ring was investigated by means of simulations using a contact model that considers bonding and debonding between the rings. In earlier investigations, the influence of the temperature on the bonding was neglected. Since the cooling of the rings during transport or during the process has an important influence on the success of the process, the subroutine VUINTER was expanded to simulate the contact behavior between the two surfaces, including the temperature dependency. By switching to an incremental calculation and temperature-dependent composite parameters, temperature changes are considered, as they should not be neglected in composite ring rolling. A minimum surface enlargement and a bond strength limit were successfully implemented to represent the material-dependent behavior and prevent the calculation of bond strengths exceeding the base materials’ flow stresses.

In order to investigate the bonding in the relevant area, a bonding experiment was carried out to determine the parameters as a function of temperature. The calibrated and extended contact model underestimates the bond strength by 3 to 10 MPa over the entire tested range. One reason for this could be the conservative assumption of the bonding model or the minimum surface area required to create a bond between the materials.

This contact model was then used for composite ring rolling simulations. The results of the simulation could thus be brought closer to reality by taking both the bonding and the temperature change into account. To validate the subroutine, ring rolling simulations were first carried out without the contact subroutine. Subsequently, the same parameters were used for simulation with the contact subroutine. The results show no separation of the rings. Based on this, a composite ring with a wall thickness ratio of 1:1 and a flow stress ratio of 1:1 was successfully manufactured.

Further investigations should focus on different material combinations for specific applications for the composite rings. The subroutine enables the simulation to consider different material properties and the different cooling behavior of the two materials. A reliable and cost-effective analysis is possible. One more possible application of such composite rings is pressure vessel shells. The inner ring of such a composite ring must be corrosion-resistant, and the outer ring provided the mechanical properties. In this case, a different combination of materials could offer the possibility of saving material costs, as the expensive corrosion-resistant material could be saved by using a cheaper material on the outside to achieve the mechanical properties.