Abstract
This paper introduces a complete real-time algorithm, where the chatter is detected and eliminated by spindle speed manipulation via the chatter energy feedback calculated from the axis encoder measurement. The proposed method does not require profound knowledge of the machining dynamics; instead, the entire algorithm exploits the fact that milling vibrations consist of forced vibrations at spindle speed harmonics and chatter vibrations that are close to one of the natural modes, with sidebands which are spread at the multiples of spindle speed frequency above and below the chatter frequency. The developed algorithm is able to identify the amplitude, phase and frequency of all the harmonics constituting the periodic forced and chatter vibrations. The key challenge is to select dominant chatter frequencies for the calculation of a robust and accurate chatter energy ratio feedback; this is achieved by utilizing the frequency estimation variance of EKF as a novel chatter indicator. Based on the chatter energy ratio feedback, the controller overrides the spindle speed in order to suppress the chatter energy below a particular threshold value. The varying spindle speed challenge is handled by updating the state transition matrices of the Kalman filters and real-time calculation of the band-pass filter coefficients, based on the derived discrete time transfer functions. The developed algorithm is tested on a Deckel FP5cc CNC which is in-house retrofitted and has a PC-based controller for the real-time application of the proposed algorithm. It is shown that the real-time chatter frequency and amplitude estimates are compatible with off-line FFT analysis, and chatter can be successfully eliminated by energy feedback.
1. Introduction
Chatter is the undesired self-excited vibrations that causes bad surface finish, increased tool wear/breakage and excessive noise, and it limits productivity. Chatter can be avoided by the selection of the proper machining parameters. For that purpose, stability lobe diagrams are used to select the best suitable spindle speed and depth of cut combinations [1]. Those diagrams are formed based on the mathematical model of the machine tool–workpiece system. The mathematical model relies on the frequency response function (FRF) measurements and the cutting force models. However, during the milling process, the physical system might deviate from the physical model. For example, the FRF of the rotating spindle might be different from the stationary measurements during high-speed machining operations [2]; likewise, the position changes of the axes will change the stiffness characteristics [3], and the workpiece dynamics will deviate with the varying mass reduction during the process [4]. Besides the physical model, the input force model also reserves uncertainties. The tool wear causes varying force coefficients; furthermore, practical engagement problems like the unknown tool runout cause deviations in the prediction of force models.
All those problems force an online chatter detection and control solution. Online speed regulation to suppress the chatter is a known and old technique. In 1994, Liao and Young utilized the cutting force signal of a dynamometer; by the use of FFT, they detected the chatter frequency. The new spindle speed was determined in order to keep a /2 phase difference in between the present and previous cuts [5]. In 1998, Soliman utilized dynamometer measurement; rather than computing the new spindle speed set point, they utilized a closed-loop-like solution and regulated the ramp rate of the spindle according to a statistical indicator, the R-value [6]. Although those techniques are called online, they are not appropriate for real-time operations since the signal processing requires a large amount of data. In 2010, van Dijk developed control strategies for the automatic adaptation of the spindle speed. They used a Kalman filter and a second-order TF to detect the dominant chatter frequency [7].
Continuous spindle speed variation (SSV) is another known technique for chatter suppression. Stability properties can be improved by spindle speed variation [8]. The spindle speed is varied around its nominal value in a sinusoidal form. Selection of the frequency and amplitude parameters of the speed variations is a challenging task; Urbikain [9] achieved real-time implementation in turning operation and discussed the power consumption limitations for parameter selection. Al-regib [10] proposed a simple amplitude ratio determination criterion based on the fractional phase portion of the chatter vibrations associated with the mean spindle speed. The method requires only chatter frequency and spindle speed knowledge for online application; the effectiveness is shown for the turning process. Ding developed active control methods for determining the amplitude and frequency of SSV in turning operations [11,12]. Besides sinusoidal, the effect of different profiles has been investigated. Seguy [13] showed the amplitude has a greater effect on stability than the frequency, and the triangular shape is more effective than a sinusoidal variation, while Li [14] utilized a piecewise profile.
Suppression of chatter provides a further increase in the stability and real-time applications require the accurate detection of the onset of chatter. The online detection algorithms consist of data acquisition, signal processing, feature extraction and classification model steps [15]. The percentage of the signal types processed in the chatter detection literature up to 2023 is classified by Navarro [16]. According to his review paper, 39% of the chatter detection studies utilize vibration signals, 25% utilize force signals, 10% acoustic signals and 13% utilize other signals such as laser displacements, thin film piezo, non-conventional embedded sensors [17], etc. Seven percent of chatter detection studies are classified as sensorless methods. Those studies utilize the internal signals of the CNC like set spindle motor current [18] and intrinsic signals like electric phase monitoring [19]. The remaining 6% of the chatter detection studies consists of the multi-sensor approaches, which gained attention in the last few years. Kuljanic [20] utilized a rotating dynamometer, accelerometers, and acoustic and electrical power sensors, and used different chatter indicators. They compared the robustness and accuracy of multi-sensor to single-sensor systems. Depending on the signal type, signal number and also the signal processing and feature extraction techniques, multi-sensor systems may achieve accuracy in chatter detection [21], or give no significant difference in the single-sensor case [22]. Zheng investigated the effectiveness of CNC internal signals for the external acceleration signal [23]. Although they listed the encoder measurement as an available signal, the comparison is made only with the integral component of the current command and the actual torque value signals.
To the best of the author’s knowledge and based on the review papers [15,16,24], there is a lack of literature on direct chatter detection methods that rely solely on axis encoder measurements. Encoder signals in conjunction with motor current signals are only exploited by Sugiyama [25] and Yamada [26]. They employ a dynamic model of the machining system to estimate the cutting force and have introduced the MEF (mechanical energy factor) index for chatter detection purposes, which reflects the phase difference between displacement and estimated force.
In the feature extraction step, there are different signal processing methods that can be classified into three main groups: time domain, frequency domain and time–frequency domain. In time domain analysis, either the raw signal or the filtered one is analyzed, and statistical indicators are calculated as chatter indicators. However, the lack of frequency information is the main limitation of the statistical analysis. Also, for the cases where machining conditions change, statistical methods may not detect the onset of chatter effectively [27]. However, with the use of model-based observers, the chatter frequency can be accurately tracked in time [28,29,30]. In frequency domain analysis, FFT is the most commonly used indicator. Although frequency domain analysis provides accurate and reliable chatter detection, the lack of time information is the main limitation of that approach. Therefore, the methods based on frequency domain analysis are not suitable for real-time chatter detection. Conversely, time–frequency domain analysis provides both the time and frequency information at the same time which makes it favorable for real-time applications. In time–frequency domain analysis, short-time Fourier Transform (STFT) [31], wavelet pocket transform (WPT) [32] and Hilbert–Huang Transform [33] are the most commonly used techniques. Once the chatter frequency is extracted, chatter can be eliminated, by adjusting a new spindle speed in such a way that the new tooth passing frequency equals a multiple value of the chatter frequency [34].
The commonly utilized signals for chatter identification in the milling process in the literature include force signals, vibration signals, acoustic signals, motor current signals and acoustic emission signals. This paper proposes a solution that relies solely on linear encoder measurements and does not require any dynamic system model. The proposed algorithm is the extension of the previous research, where a generalized detection algorithm for acoustic, acceleration, dynamometer and motor spindle current signals was presented based on the chatter energy ratio [29]. The earlier algorithm employed a Kalman filter to distinguish between the periodic and chatter components of the signal and used a non-linear Teager–Kaiser energy operator (NEO) to identify chatter frequencies. In this work, the algorithm is extended to incorporate encoder measurements and updated to address the challenge of varying spindle speeds. Moreover, the frequency estimation process is now conducted using an extended Kalman filter (EKF), providing greater robustness and accuracy compared to the NEO. In addition to the chatter energy ratio, this approach introduces frequency estimation variance as a novel indicator for chatter detection and the selection of dominant frequencies. Additionally, a control strategy has been developed that uses the chatter energy ratio as a feedback signal. The entire algorithm operates in real time, with the controller adjusting the spindle speed to maintain the chatter energy below a predefined threshold. The developed algorithm is tested on the Deckel FP5cc CNC, which has been retrofitted with Beckhoff servo motors, drivers, IO modules and a PC-based controller.
2. Materials and Methods
2.1. The Proposed Algorithm
The proposed method does not require profound knowledge of the machining dynamics; instead, the entire algorithm is based on the vibration characteristics of the milling processes. Besides the encoder measurement, the algorithm only requires spindle speed and commanded axis feedrate as the inputs.
The vibration signals related with the milling processes primarily includes three types of elements: forced periodic components, abnormal chatter vibration components [35] and random components due to noise and tool–workpiece inconsistencies. These random components are treated as measurement noise in the Kalman filter and are not included in the ideal plant mode. The forced vibrations occur at known tooth passing frequency and its harmonics; on the other hand, chatter vibrations occur close to one of the natural modes; in addition, there are sidebands which are spread at the multiples of tooth passing frequency above and below the chatter frequency. In this paper, considering the tool runout effect, the chatter frequency and its sidebands are assumed to be located between two spindle speed harmonics [36], rather than the tooth passing frequency. The resulting vibration signal due to milling process is expressed as follows.
The proposed method makes use of Equation (1) and consists of six steps and is illustrated in Figure 1. In the 1st step, the axis position measurement is processed through a kinematic Kalman filter and the velocity variations around the feed command are estimated. In the 2nd step, a periodic Kalman filter block identifies all the spindle speed harmonics of the velocity variations. Here, the filter make use of the known spindle frequency input and identifies the unknown magnitudes and phases of all spindle harmonics. The periodic component of the signal is reconstructed by summing all the spindle harmonics. The chatter component is extracted by subtracting the stable component from the estimated feed speed variation .
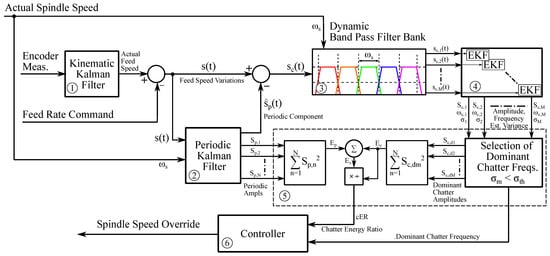
Figure 1.
The schematic of the proposed algorithm.
Different from the periodic forcing components, besides the amplitude and phase, the frequency of the chatter signal is also unknown. Therefore, it is not possible to detect all chatter frequencies with a single observer. As a solution, in the 3rd step, a single chatter prone frequency is isolated in between two consecutive spindle harmonics by a band-pass filter, which will then be fed through an allocated extended Kalman filter (EKF) observer. The challenge with the BPFs is the varying spindle speed. Since the manipulated output of the chatter controller is the spindle speed, the corner frequencies and the band length of the filter have to be adapted with the varying speed. Therefore, a dynamics band-pass algorithm is derived which updates the filter coefficients in real time as a function of spindle speed. In the 4th step, EKF searches for a possible unknown chatter frequency and identifies its amplitude and phase. For stable cases there is no chatter frequency in between the two consecutive spindle harmonics resulting in junk estimation. Therefore, a novel decision algorithm is made, where the dominant chatter frequencies are selected based on the frequency estimation variance of the EKF.
In the 5th step, the energy of the chatter and the periodic components are calculated. Energy ratio of chatter over the total signal, ER, is fed back to the chatter controller. The 6th step is the automatic chatter controller (ACC). It consists of a finite state machine and a regulator. Once the chatter is detected, regulator manipulates the spindle speed in order to minimize the chatter energy ratio.
2.2. Derivation of Feed Variation from Axis Encoder
Linear encoder is built in all CNC systems; therefore, in considering chatter detection, it is superior to external signals like acceleration, microphone or force measurements. However, raw position measurements are not appropriate for signal processing, since it does not have a zero mean, but has an increasing or decreasing trend due to its inherent integral behavior. On the other hand, the feed is constant throughout the cutting process and, subtracting the actual velocity from the feed command, a zero mean Gaussian signal can be obtained. The actual axis velocity signals are already available inside the PLC unit. However, they are not suitable for identification purposes since they are low-pass filtered in order to remove the high-frequency content for motion control purposes. Conversely, relatively high-frequency signals that are well above the position and velocity control loop bandwidths are of interest in the chatter detection algorithm. Therefore, in this study, the raw encoder signals are utilized in the chatter detection algorithm instead of intrinsic PLC signals. The axis velocity is derived from the raw encoder measurements via a kinematic Kalman filter. The filter is called kinematic since the model does not include any dynamic terms like inertia and friction, but is only based on the kinematic relation in between the position and velocity. The state equations are given as follows.
Here, the state vector consists of position and velocity states. In the first row, position is incremented by the velocity state at T time step. On the other hand, in the second row, the velocity is kept constant since no acceleration state is defined. Considering the machining process, constant feed assumption is a fairly good model. Note that, although acceleration is not a separate state, it is introduced as a noise input w to the model. The magnitude of process noise w represents how much the speed and position estimations may vary during one sampling time T. The magnitude of w can be considered as a low-pass filter. Decreasing the acceleration noise, Kalman filter trusts more on the constant speed model resulting in a small bandwidth LPF. On the other hand, increasing the w, the filter trusts more on the measurement and this corresponds to a higher bandwidth. The Kalman filter equations are standard and can be found in literature [37]; they are also repeated here as follows.
These equations are solved at each kth time step recursively. Here, the is the state matrix as defined in Equation (2), is the measurement noise covariance and is the process noise covariance matrix determined by the acceleration noise as , where is the expectation operator
In the above equations, the position unit is not meter but ‘increment’ and the velocity unit is selected to be ‘increment/sample’. Encoder counter is the input of the algorithm and one count corresponds to the resolution of the linear encoder. Here, the sampling time is indicating one sample. In this way, the condition number of the matrix is enhanced, which is important for numerical stability in real-time operation. Moreover, the system is made independent of sampling time. In that way, the algorithm can be applied with any sampling frequencies without requiring an update for the covariance matrices. Lambda is the weight factor for adjusting the process noise. It is selected to be meaning that the feed speed may vary 20 increments/sample in 1 sample. Once the axis velocity is derived from the raw encoder data, it is subtracted from the commanded feed velocity. In this way, zero mean velocity variation data are obtained for the chatter detection algorithm.
2.3. Estimating Spindle Speed Harmonics
The forced vibrations generate the periodic oscillations at the harmonics of spindle frequency. The periodic part of the signal given in Equation (1) can be reconstructed with a finite number N of harmonics in discrete time domain as follows:
where and are the unknown amplitude and phase of the -th spindle harmonic () with frequency at discrete time step . For notational convenience, the sampling time, T, is omitted and the discrete time varying quantities are represented by subscript k only.
The state variable representation of a single cosine signal is given as follows [29]:
where is the process noise and accounts for the time variation in the amplitude and phase. Selecting the first state as the measured signal, i.e., , the measurement equation with the signal and measurement noise, , becomes the following:
The above state space representation can be generalized to N-number of spindle harmonics given in Equation (5), expressed as follows:
where with is the state transition matrix used to model the n-th harmonic.
Likewise, the kinematic KF from Equation (3) is utilized for periodic Kalman filter. Only the dimensions of the elements will change, where is the estimated state vector, is the error covariance matrix and the superscript denotes prior estimate. is the recursively updated Kalman gain matrix. is the diagonal process noise covariance matrix and R is the covariance of the measurement noise . R is found by taking the covariance of measured air cutting signal, and the process noise covariance is assumed to be where is tuned as . The periodic part of the measured signal is estimated as follows:
and subtracting it from the measured signal the chatter part is found and is expressed in discrete time with M—number of harmonics as follows:
2.4. Isolating the Chatter Frequencies: Bank of Dynamic Band-Pass Filters
The chatter component given in Equation (11) is assumed to consist of M-many components. Therefore, M-number of band-pass filters are utilized, where chatter prone frequency is isolated in between two consecutive spindle frequency harmonics, .
In the proposed method, the spindle speed is not constant but can be manipulated by the ACC. Therefore, in order to adapt the corner frequencies of the filter with the varying spindle speeds, analytical derivation of the filter coefficients in discrete time domain is made. The band-pass filter is designed based on the normalized 4th-order prototype Butterworth LPF whose transfer function is represented as follows [38]:
with the constants and .
The above prototype filter has unity cut-off frequency. An arbitrary analog filter with cut of frequency can be obtained by inserting . Likewise, an analog band-pass filter can be designed by inserting
where q is the quality factor defined as
Here, is the bandwidth, corresponding to spindle frequency, while is the resonant frequency defined with the corner frequencies, i.e., the two consecutive spindle speed harmonics, as follows:
Inserting Equation (13) into prototype filter Equation (12) with unity resonant frequency , the normalized BPF is found as follows:
with coefficients
This normalized BPF can be transformed to an arbitrary BPF with a resonant at by simply inserting . However, first, the continuous time correspondence of the desired corner frequencies which are defined in discrete time is calculated by utilizing frequency pre-warping ( in rad/s).
Then, the continuous time transfer function (Equation (16)) can be transformed to discrete time by using bi-linear transformation.
The procedure for converting normalized BPF, , to an equivalent discrete form by the change of Laplace variable s is summarized in Equation (19). First, the filter resonant frequency is switched to . Then, the continuous time is written in terms of the desired resonant frequency and in the last step Tustin transformation is applied.
After defining the variable , the resulting discrete BPF in z-domain with resonant frequency at is presented as follows:
where the denominator coefficients are
The real-time implementation of a single BPF is illustrated as a block diagram in Figure 2. The advantage of this implementation scheme is the decreased number of delay terms by defining a new variable . Note that direct implementation of Equation (20) requires 1 summer and 8 + 4 = 12 delay terms. However, if the BPF is implemented as in the block diagram representation, it requires two summer and eight delay terms only. Considering there are M-many band-pass filters, decreasing delay terms saves considerable memory.
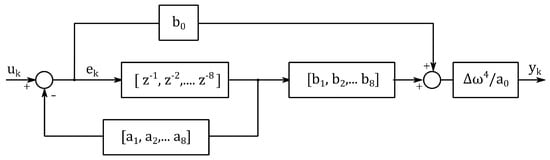
Figure 2.
Block diagram representation of the real–time implementation of a single BPF.
2.5. Identification of Chatter Components with EKF
BPF bank outputs totally M-many time series. EKF identified the unknown frequency , amplitude and phase of the chatter signal given in Equation (11). Here, the subscript index m represents the mth band-pass filter output, while c is for chatter. Different from the periodic Kalman estimation, the unknown frequency state creates a non-linearity. Thus, the linear Kalman algorithm given in Equation (3) can not be applied here. The EKF is the extension of Kalman filter and utilizes the linearized state equations calculated at each sample time. The state equations of a chatter signal are obtained by augmenting the periodic signal states with unknown frequency state as follows:
Like the periodic Kalman, the first state is the signal itself, , the second state is the sine counterpart and the third state is the unknown frequency . Although the unknown frequency is modeled to be constant, it is allowed to change with the noise variable w. Due to the non-linear relation between the states, the a priori covariance calculation step of the Kalman filter algorithm, that corresponds to the first two of Equation (3), is modified as follows.
In the a priori covariance calculation , a Jacobian matrix is utilized instead of a state matrix . Jacobian matrix is derived by linearizing the non-linear state vector calculated with the previous state estimation as follows.
Here, the hat is for the estimation and the superscript bar is for a priori estimation. Similar to the periodic force component estimation case, measurement matrix selects the first state . The magnitude and phase can be calculated by utilizing and , and the 3rd state is the unknown frequency.
2.6. Calculating the Vibration Energy
In the 5th step, all the unknown parameters of the velocity variation signal given in Equation (1) are identified. The energy of periodic and chatter components can be calculated by sum of the squares of the identified amplitudes as follows.
Calculation of the vibration energy with amplitude only is physically realizable. Considering a mass spring system, the free vibrations occur at the resonant frequency in the form of . The total energy of the system will be . Considering the force equilibrium , where m is the mass and k is the spring constant, total energy can be represented as . Inserting the first and second derivatives of and using trigonometric relations, the total energy becomes . Note that, since mass is constant and corresponds to velocity amplitude, the energy of the chatter and periodic components can be calculated directly by the identified signal amplitudes.
2.7. Selection of Chatter Components via Variance Energy Calculation
The detection of the chatter is determined by the ratio of chatter energy to the total vibration energy of the signal.
Direct calculation of the chatter energy by including all the M-many components results in a biased and noisy signal, which results in false alarms. In order to remove the noise, the energy of the chatter component is calculated by considering only the dominant frequencies.
The determination of the dominant chatter frequency among the M-many EKF outputs is not a trivial task. For this purpose, two approaches were tested: in the first approach, selection was based on an amplitude threshold value and, in the second approach, it was selected based on a frequency estimation variance threshold. As a result it is observed that frequency estimation variance is a very robust and accurate indicator of chatter onset.
Using frequency variance instead of amplitude is physically realizable; once the chatter occurs, the filtered signal in between the two consecutive spindle harmonics is dominated by a certain frequency. Therefore, the frequency variance is low. On the other hand, if there is no dominant frequency in the interval, since the EKF tries to fit a sinusoidal signal, it outputs a high variance frequency estimation. On the other hand, chatter amplitude may vary during stable or unstable cutting process. Note that the variance of the estimation frequency does not requires an extra calculation; it is inherently available inside the EKF algorithm. The frequency variance corresponds to the component of the covariance matrix.
2.8. Automatic Chatter Control with Spindle Speed Regulation
The automatic chatter controller (ACC) has two main tasks, (i) detection of the chatter onset and (ii) once it is started eliminating the chatter by manipulating the spindle speed. Both tasks are performed by the chatter energy ratio (ER) feedback, which is a measure of chatter energy over the whole signal. Note that ER feedback is created at the end of the whole above-mentioned algorithm. It is robust and accurate measure of chatter, since only the dominant chatter modes are selected by utilizing the frequency estimation variance parameter of the EKF. Based on the ER feedback and a predefined threshold, the onset of the chatter is detected. Then, a regulator with zero ER reference manipulates the spindle speed to decrease the ER below a predefined lower threshold value.
In order to apply the chatter control in real-time process, a finite state machine is constructed as shown in Figure 3 and is implemented in the TwinCAT software (version 4022) as a TcObject. The state machine has two parallel states, Energy state shown on the top and automatic chatter controller (ACC) state shown on the bottom of Figure 3. The Energy state is either stable or chatter; the switching in between the two sub-states is performed by checking the chatter energy ratio, ER. A In order to prevent continuous switching in between the two states, an additional hysteresis is also defined. Throughout the experiments, the energy ratio and the hysteresis are selected to be 50% and 25%. As a result, if the ER is higher than the upper threshold 75%, the ACC switches to the chatter state and manipulates the speed; if the ER is lower than lower threshold 25%, it switches back to the stable state keeping the manipulated spindle speed unchanged.
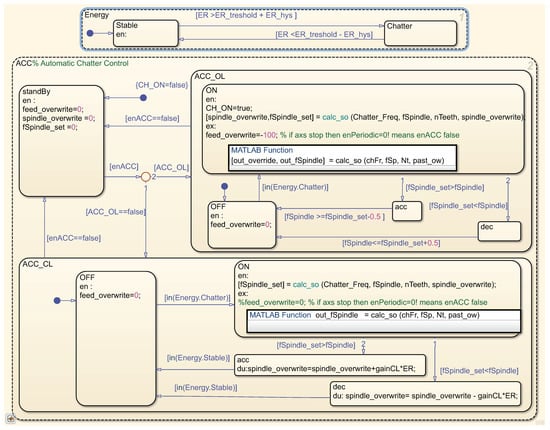
Figure 3.
The finite state machine for the application of automatic chatter control algorithm.
The ACC has three sub-states. The initial state is the standby. If the ACC is not enabled by an external command, there is no spindle and feed overwrite. The second and third states are the open-loop and closed-loop control modes. In the open-loop control case, the spindle speed is calculated based on the identified chatter frequency. Once the chatter frequency is known, it is trivial to match the spindle speed with the subharmonics of chatter. The selection of the new speed is performed as follows.
Here, is the number of inserts, is the current spindle speed and is the estimated chatter frequency.
The third state is the closed-loop control mode. The controller is acting as a regulator aiming to keep the reference chatter energy ratio at zero. Here, an integral-like control strategy is applied; the spindle override command is calculated as follows.
Here, the response time of the controller is adjusted with the parameter. It is known from the stability lobe diagrams that the processes can be stabilized either by increasing or decreasing the spindle speed. Furthermore, the maximum spindle speed override is limited to 20%. Therefore, a sign function is utilized in order to determine whether to speed up or slow down the spindle speed. Based on the OL speed calculation, the controller decides the direction by checking with the override limit. The CL controller is off when the energy states switch from chatter to stable, i.e., the ER is below the lower ER threshold.
OL or CL control configuration is selected by the user and is fixed during the operation. If there exist multiple dominant frequencies, applying OL control is not trivial, since the different chatter frequencies result in different spindle speed set points. However, in the CL case, the correct speed is selected automatically. During several tests, it is seen that CL performance is well above the OL case. Therefore, in this paper, only the CL control performance is illustrated; the OL speed calculation is used only for direction selection.
3. Results, Experimental Validation
The application and verification of the proposed method are explained in three steps. The first step is the introduction of the hardware and the software capabilities of the in-house retrofitted Deckel FP5cc CNC. In the second part, the chatter frequency detection performance of the EKF is verified. The decision for the selection of dominant chatter frequencies based on estimation variance is illustrated. In this step, a varying radial depth of cut test is performed, and ACC is not enabled. In the third step, ACC is enabled and its performance is illustrated. Two different cutting tests, full slot and varying radial depth of cut, are performed showing that the chatter is eliminated by manipulating the spindle speed.
3.1. The Test Set Up and Algorithm Implementation
Figure 4 shows the before and after photo of the in-house retrofitted CNC machine tool. The CNC has five independent axes; all axes are driven by Beckhoff servo motors; the servo motors are coupled to the ball-screw via a timing belt transmission. All axis positions are measured by Heidenhain encoders. The motor drivers, IO units and controllers are all replaced with Bechfhoff automation products. The controller is PC based and it enables the chatter detection and control algorithm running synchronously with the motion control. The control PC has four CPU cores: CPU 1 is used for the regular Windows applications like the HMI interface. CPU 2 is reserved for real-time motion control applications and CPU’s 3,4 are reserved for the ACC algorithm. The algorithm is developed in the MATLAB Simulink environment and implemented in TwinCAT by utilizing TcCOM objects.

Figure 4.
The in-house retrofitted Deckel FP5cc/T CNC; a PC-based controller with TwinCAT software allows the implementation of ACC algorithm together with the CNC-related motion control tasks.
Two different chatter tasks are defined for the whole algorithm. Task-1 includes the algorithms given in Section 2.2, Section 2.3 and Section 2.4. Task-2 includes the algorithms given in Section 2.5, Section 2.6, Section 2.7 and Section 2.8. It is observed that Task-1 is completed in 55.2 s and Task-2 is completed in 21.8 s. The computation time of Task-1 is relatively higher than Task-2; this is mainly due to the periodic Kalman filter. The algorithm identifies 24 spindle speed harmonics which correspond to a state transition matrix. On the other hand, Task-2 runs the EKF algorithm including M = 36 separate 3 × 3 state matrices. Since the number of harmonics is constant, the frequency range of detection depends on the spindle speed. For 3800 rpm spindle speed and N = 24, spindle harmonics up to 1520 Hz are identified, while M = 36 corresponds to chatter identification up to 2280 Hz. Since the periodic oscillation amplitudes decrease with increasing frequency and thus do not significantly contribute to the signal energy, it is reasonable to choose N < M to improve computational efficiency.
The base-cycle time for the chatter tasks is selected to be 125 s which corresponds to a 4 kHz Nyquist frequency limit. The base-cycle time of the PLC is 1 ms; however, the ACC algorithm can reach all the signals of the CNC, i.e., encoder measurement, spindle speed, etc., at 8 kHz sampling frequency. The encoders used in the X-Y-Z axes are the Heidenhain LS403 type with 1 m resolution. The output signal is the TTL type and read by an EL5101 terminal. The hardware and software properties of the CNC are summarized in Table 1.

Table 1.
Hardware and software properties of the retrofitted CNC.
3.2. EKF Performance and Selection of Dominant Chatter Frequencies
The EKF fits a sinusoidal signal for each band-pass filter output, i.e., a candidate chatter frequency is estimated in between each consecutive spindle speed harmonic. If there is no chatter signal in that interval, the estimation variance of the amplitude and frequency grows, which results in noisy chatter energy feedback for the controller. A noisy chatter energy calculation also results in false detection decisions. In order to prevent this, the dominant chatter frequency is selected based on a threshold for the estimation variance.
A varying radial depth of cut test is conducted to demonstrate the performance of the EKF. The spindle speed is 3500 rpm, the axial depth of cut is 2.5 mm and the radial depth of cut varies from 2 mm to 10 mm with 1000 mm/min feed speed. The tool diameter is 20 mm and it has three inserts. The workpiece is AL7075.
The variation in feed velocity is obtained with the kinematic Kalman filter and is illustrated in Figure 5. The chatter frequencies are found offline via an FFT analysis, and are provided as a sub-plot. The X-axis ticks are formed as multiples of the spindle frequency which corresponds to 59 Hz, and the dashed-green lines are the tooth passing frequency of 175 Hz. The left figure is the FFT of the time interval of 6.3–6.4 s, while the right one covers the FFT from 6.4 to 6.5 s. A relatively small time 0.1 s window is selected in order to illustrate the varying chattering behavior and comparison with the EKF performance. It is seen that in the first interval dominant chatter frequencies are 860 Hz and 1030 with amplitudes 936 and 386 units, respectively. In the second interval, the chatter frequencies are 862 Hz and 1033 Hz, while the amplitudes are 649 and 573 units, respectively. Although the chatter frequencies are varying with time, it has to be noted that they are inside the frequency resolution of 1/0.1 = 10 Hz. However, the significant variation in the amplitude has to be noted. This varying amplitude is clearly observed in real time with the EKF.

Figure 5.
The chatter frequency analysis by offline FFT analysis. (a) FFT of 6.3 to 6.4 s; (b) FFT of 6.4 to 6.5 s.
The frequency estimation performance of the EKF is illustrated in Figure 6a. Each horizontal-like line is the EKF estimate of a BPF output. The estimates instantly deviated from their initial value after the engagement at time 2 s. If there is no chatter in the signals, the frequency variation is high; this can be clearly seen in the detail figure provided on the right. It is seen that, after the start of chatter at time 6 s, two of the frequency estimates, shown with thicker linewidth, are stabilized around particular values which actually correspond to dominant chatter frequencies found by FFT analysis, 855 Hz and 1030 Hz. Besides the frequency, EKF also estimates the amplitudes, provided in Figure 6c. The two dominant chatter amplitudes differ from the rest when chatter starts at time 6. The amplitudes are not constant but varying with time. In the detailed figure, around time 6.5 s, the amplitude is varying in between 600 and 1000 units and the second one is varying from 300 to 600 units. Those variations are compatible with the FFT provided in Figure 5. It can be concluded that EKF is successful in estimating the frequency and amplitude of chatter vibrations in real time and the results are compatible with the off-line FFT analysis.
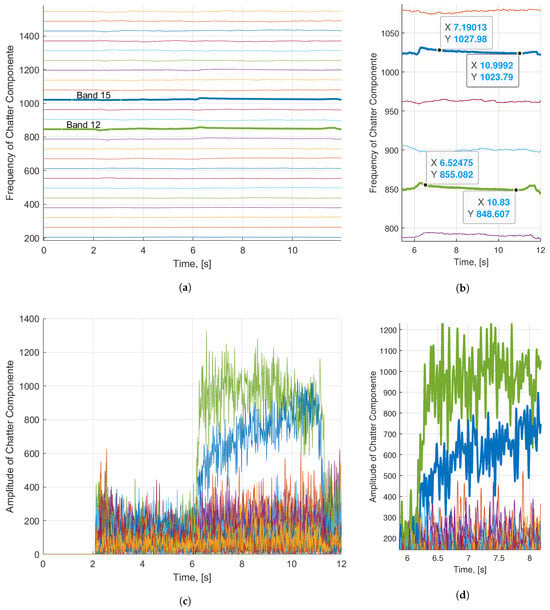
Figure 6.
The frequency and amplitude estimation performance of EKF. (a) Chatter frequency estimate; (b) detailed view; (c) amplitude estimates; (d) detailed view.
The calculation of chatter energy is crucial for accurately detecting the onset of chatter. Due to varying chatter amplitudes, selecting the dominant chatter frequencies is not straightforward. Some methods for calculating chatter energy are illustrated in Figure 7a. The purple line represents the energy of the periodic components. During the stable zone between 2 and 6 s, this energy increases gradually with the increasing radial depth of cut and drops abruptly at the onset of chatter. The blue line represents the chatter energy calculated by including all the amplitude estimates of the EKF. As shown, this method is problematic due to the biased chatter energy observed during the stable zone. To avoid this error, the energy ratio calculation is performed according to a threshold value. The energy of each EKF output is compared with the energy of the periodic component, and amplitudes with an energy ratio of less than 10% are disregarded. This results in the graph shown by the yellow line. The bias in the stable zone is significantly reduced compared to the blue graph; however, it still shows abrupt changes without a specific pattern. These changes make chatter identification challenging and may lead to false indications of chatter onset.
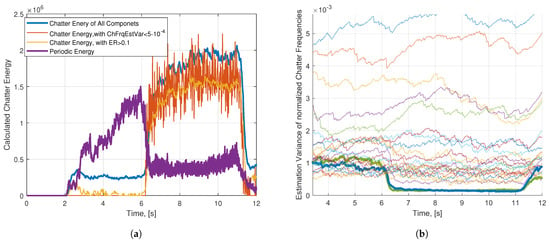
Figure 7.
Chatter energy calculation with different methods. (a) Chatter energy; (b) the frequency estimation variance of EKF.
The orange line in Figure 7a represents the chatter energy where the EKF estimates are selected based on a variance threshold. If the frequency estimation variance is below the threshold, its amplitude is included in the energy calculation. As seen, this method provides accurate results, with the chatter energy remaining nearly zero in the stable zone. To better visualize the comparison of the frequency variance with the threshold value, the frequency variances of all components estimated by the EKF are shown in Figure 7b. The estimation variance value is inherently available in the Kalman filter covariance matrix. It is evident that, during stable operations, the variance in all estimated frequencies is high and consistent. This is an expected outcome, as the EKF attempts to fit a sinusoidal signal for each BPF output, but no dominant chatter signal exists. This situation changes at the sixth second, where two dominant modes become significantly different from the others. As chatter begins to form and energy shifts to certain frequencies, the EKF can estimate these frequencies with high accuracy, causing the variance in these frequencies to decrease. The frequencies shown in blue and green with thicker line widths are the dominant chatter frequencies, and their amplitudes increase rapidly after the sixth second, as shown in Figure 6c.
3.3. Performance of the ACC
To illustrate the performance of the ACC, a full slot test is performed. The tool used is a 20 mm diameter cutter with three inserts, and the workpiece material is AL7075. The spindle speed is set at 3800 rpm, with an axial depth of cut of 0.3 mm and a feedrate of 1500 mm/min. Two consecutive tests are conducted: In the first test, the ACC is disabled, resulting in a constant spindle speed and unmitigated chatter. In the second test, the ACC is enabled, allowing for automatic spindle speed regulation. The tool position in the Y direction and tool–workpiece engagement points are labeled in Figure 8b. The time period from 2.9 s to 9.6 s is the ACC-disabled case, while the time period from 18.4 s to 25.1 s is the ACC-enabled case. The corresponding chatter energy ratio is shown in Figure 8c. It is seen that in the ACC-disabled region the chatter energy ratio constituted nearly 80–90% of the total vibration energy. However, with the ACC enabled, the energy ratio (ER) dropped to an average of 30%.
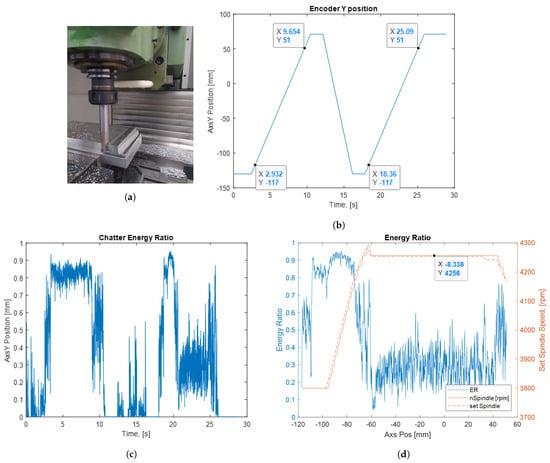
Figure 8.
Full slot tests; first the ACC is off, then ACC is on, 3500 rpm, 1000 mm/min, AL7075 workpiece, 20 mm 3 insert toll, 0.3 mm depth of cut. (a) Tool–workpiece; (b) Y–axis positions; (c) chatter energy: ACC enabled vs. disabled; (d) the spindle speed manipulation and ER response.
The ER, together with the spindle speed manipulation on the right y-coordinate is provided in Figure 8d. The x-coordinate is selected to be the tool position instead of time. Note that the engagement occurs at Y-117 mm. The ACC is enabled manually from the HMI after the engagement; this is to eliminate the false alarms that will occur at the engagement instant. The transient vibrations of the engagement are not in the scope of this study but remain for a future study. It is seen that after the ACC is enabled the spindle speed increases gradually. However, the response of the chatter energy does not decrease at that instant; when the speed exceeds 4256 rpm, the ER decreased abruptly. The ACC switches to the OFF state when the ER is below the lower threshold and the spindle speed remains unchanged. Note that although the ER oscillates the ACC does not switch back to the ON state due to the upper threshold determined by the hysteresis.
The ACC algorithm is also verified with a varying radial depth of cut test. The radial depth is changed from 10 mm (half slot) to 20 mm (full slot); the tool path is shown in Figure 9a. In this test, the axial depth of cut is 0.25 mm, the spindle speed is 3800 rpm, the feed is along the Y axis, the speed is 1500 mm/min and the closed-loop gain is . The test includes two consecutive cutting phases. During the first cutting, ACC is disabled and in the next cutting ACC is enabled. The Y-axis measurements and the tool–workpiece engagement instants are shown in Figure 9c.
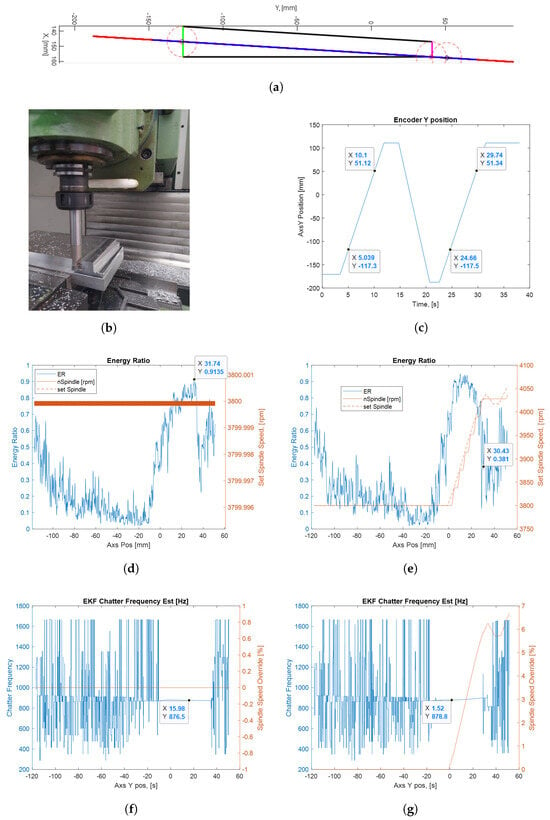
Figure 9.
Performance of ACC with varying depth of cut. (a) Tool path of varying radial depth of cut; (b) tool–workpiece; (c) Y–axis position; (d) ACC off chatter energy ratio; (e) ACC on chatter energy ratio; (f) EKF chatter frequency estimate; (g) EKF chatter frequency estimate.
The ACC-disabled cutting phase covers the time interval from 5.4 to 10.1 s. The related chatter energy ratio is illustrated in Figure 9d, with the Y axis position on the X–coordinate instead of time. It is observed that there is a sudden increase in energy around Y–117 due to engagement, which dissipates shortly thereafter as it is not a sustained vibration. Chatter energy begins to rise around Y-10 mm. The tool reaches the workpiece end surface at Y31 mm and totally disengages at Y51 mm. This progression is clearly visible in the energy graph. The chatter energy peaks around Y31 mm and then decreases immediately afterward. The dominant frequency estimation graph for this test is shown in Figure 9f. Initially, due to the absence of chatter, the algorithm cannot accurately estimate the dominant chatter frequency and thus oscillates between various band-pass filter outputs. However, beyond Y–20 mm (before significant growth), the algorithm accurately estimates the chatter frequency as 878 Hz. Beyond this point, as chatter occurs, the accuracy of the EKF prediction is high.
The second cutting phase covers the time interval from 24.7 to 29.7 s. Automatic chatter control is active during this cutting phase. Figure 9e presents the energy ratio specific to this test. It is seen that, close to the Y0mm position, the ER exceeds the upper threshold value. After switching to the ACC ON state, the spindle speed manipulation is started. As the spindle speed reaches 4030 rpm, the energy ratio decreases. The ACC switches to the OFF state once the lower threshold is crossed. It is clearly visible that, at Y31 mm, where the tool reaches the end of the workpiece, the energy ratio has already dropped, indicating the elimination of chatter. Figure 9g illustrates the EKF frequency estimation of this cutting phase. Similar to unstable cutting, there is initially no definite chatter frequency. However, once the chatter begins, it is estimated with high accuracy. However, unlike the ACC-disabled cutting case, here, when chatter is eliminated, around Y30 mm, the chatter frequency fluctuates between band-pass filter signals and does not remain within a single band. This is an expected result; since the chatter is eliminated, there is no dominant chatter frequency, the estimation variance increases and the candidate chatter frequency is selected from different band-pass filters outputs.
4. Discussion and Conclusions
Detection of chatter and its frequency without false alarms is essential to achieve self-optimizing, intelligent CNC machine tools. This paper presents a complete study, including chatter detection and control with speed manipulation. The algorithms are applicable in real time with a varying spindle speed. A linear encoder is built in all CNC systems; therefore, considering the cost, it is superior to external signals like acceleration, microphone or force measurements for chatter detection applications.
The proposed method relies solely on linear encoder measurements and does not require profound knowledge of the machining dynamics. The entire algorithm is based on the vibration characteristics of the milling processes. Besides the encoder measurement, the algorithm only requires spindle speed and commanded axis feedrate which are also intrinsic PLC signals. The linear encoder signal has an inherent integrator behavior. A zero mean vibration signal is obtained by utilizing a kinematic Kalman filter and subtracting the velocity estimate from the feed command. Selecting a relatively high process noise, the bandwidth of the filter and thus the frequency range of the identification can be increased.
Varying spindle speed requires a real-time update of the state transition matrices of the periodic Kalman filter and EKF. Furthermore, analytical derivation of the BPF transfer functions are presented, where the coefficients can be calculated and updated in real time with the varying speed. The periodic forced vibration components of the feed variation are identified by the periodic Kalman filter. After the chatter component is extracted, with the use of a BPF and EKF, the unknown frequency, amplitude and phase are identified.
The chatter energy ratio is calculated based on the amplitude estimates and utilized for chatter detection and control purposes. The key challenge is to separate the dominant chatter frequencies. The chatter energy ratio calculation given in Figure 7a reveals that, in order to detect chatter, not all the identified chatter components but only the dominant ones have to be included. The proposed frequency estimation variance in the EKF is shown to be a robust and accurate indicator for the selection of dominant chatter frequencies.
A finite state machine is constructed for the real-time application of the algorithm. ACC ON and OFF states are switched based on an upper and lower ER threshold. The introduced hysteresis prevents continuous switching between the control modes. ACC has open-loop and closed-loop options. In the OL option, the spindle speed determination is trivial based on the detected chatter frequency. However, for multiple dominant frequencies, it results in different speeds. The CL control on the other hand is a regulator manipulating the spindle speed in order to minimize the chatter energy ratio calculated based on all dominant frequencies. CL control is preferred to eliminate chatter; however, the direction of the speed rate is determined based on the OL output.
The proposed algorithm is implemented in real time using TwinCAT software. The cutting tests were conducted on an in-house retrofitted Deckel FP5cc CNC machine. All motors, drivers and IO modules have been updated with Beckhoff products. The PC-based controller allows the ACC algorithm to run in real time alongside the CNC motion control tasks. Two cores of the PC are utilized, with a base-cycle time of 125 s, and the algorithm is completed in less than half of the base-cycle time. Twenty-four periodic components are identified by the periodic Kalman filter, and thirty-six chatter-prone components are identified by the EKF. The cutting tests reveal that the chatter onset can be accurately detected and eliminated using the chatter energy ratio based on frequency estimation variance.
The spindle speed controller and response time to override commands significantly affects the chatter control performance; however, tuning the controller is left for future study since the spindle motor is not a Beckhoff product and needs to be identified to determine the correct properties. Additionally, although the current study uses single-axis measurements, future research could extend the algorithm to other axes, leveraging the benefits of multi-sensor systems. Moreover, since the algorithm does not depend on machine dynamics, it could be adapted to utilize other internal signals, such as spindle current, or external signals, such as acceleration acoustics, using the same approach.
It is believed the proposed algorithm has a potential for practical industrial applications. Although most of the CNC machine tools do not use a PC-based controller, an external edge PC may be utilized for the ACC algorithm and can be integrated with conventional CNC controllers for external spindle override command.
Funding
This research was funded by The Scientific and Technological Research Council of Türkiye (TÜBİTAK), 1001—the scientific and technological research project funding program with grant number 218M430 https://tubitak.gov.tr/en (accessed on 7 August 2024).
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
I appreciate Orkun Özşahin’s review and thoughtful comments on the paper and Umut Orguner’s guidance for the EKF design.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACC | Automatic Chatter Control Algorithm |
| EKF | Extended Kalman Filter |
| ER | Chatter Energy Ratio |
| KF | Kalman Filter |
| LPF | Low-Pass Filter |
| BPF | Band-Pass Filter |
| OL | Open Loop |
| CL | Close Loop |
| FFT | Fast Fourier Transform |
| FRF | Frequency Response Function |
References
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Postel, M.; Özsahin, O.; Altintas, Y. High speed tooltip FRF predictions of arbitrary tool-holder combinations based on operational spindle identification. Int. J. Mach. Tools Manuf. 2018, 129, 48–60. [Google Scholar] [CrossRef]
- Law, M.; Phani, A.S.; Altintas, Y. Position-dependent multibody dynamic modeling of machine tools based on improved reduced order models. J. Manuf. Sci. Eng. Trans. ASME 2013, 135, 021008. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Time-domain modeling of varying dynamic characteristics in thin-wall machining using perturbation and reduced-order substructuring methods. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 011015. [Google Scholar] [CrossRef]
- Liao, Y.S.; Young, Y.C. A new on-line spindle speed regulation strategy for chatter control. Int. J. Mach. Tools Manuf. 1996, 36, 651–660. [Google Scholar] [CrossRef]
- Soliman, E.; Ismail, F. A Control System for Chatter Avoidance by Ramping the Spindle Speed. J. Manuf. Sci. Eng. 1998, 120, 674–683. [Google Scholar] [CrossRef]
- van Dijk, N.J.; Doppenberg, E.J.; Faassen, R.P.; van de Wouw, N.; Oosterling, J.A.; Nijmeijer, H. Automatic in-process chatter avoidance in the high-speed milling process. J. Dyn. Syst. Meas. Control. Trans. ASME 2010, 132, 031006. [Google Scholar] [CrossRef]
- Zhang, H.; Jackson, M.J.; Ni, J. Stability analysis on spindle speed variation method for machining chatter suppression. Int. J. Mach. Mach. Mater. 2009, 5, 107–128. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; de Lacalle, L.N.; Elías-Zúñiga, A. Spindle speed variation technique in turning operations: Modeling and real implementation. J. Sound Vib. 2016, 383, 384–396. [Google Scholar] [CrossRef]
- Al-Regib, E.; Ni, J.; Lee, S.H. Programming spindle speed variation for machine tool chatter suppression. Int. J. Mach. Tools Manuf. 2003, 43, 1229–1240. [Google Scholar] [CrossRef]
- Ding, L.; Sun, Y.; Xiong, Z. Active Chatter Suppression in Turning by Simultaneous Adjustment of Amplitude and Frequency of Spindle Speed Variation. J. Manuf. Sci. Eng. Trans. ASME 2020, 142, 021004. [Google Scholar] [CrossRef]
- Ding, L.; Sun, Y.; Xiong, Z. Model-Free Adaptive Sliding Mode Control-Based Active Chatter Suppression by Spindle Speed Variation. J. Dyn. Syst. Meas. Control. Trans. ASME 2022, 144. [Google Scholar] [CrossRef]
- Seguy, S.; Gilles, D.; Lionel, A.; Tamas, I. Control of chatter by spindle speed variation in high-speed milling Sébastien. Adv. Mater. Res. 2010, 112, 179–186. [Google Scholar] [CrossRef]
- Li, Z.; Song, Q.; Liu, Z.; Wang, B.; Cai, Y. Chatter suppression mechanism and parameters configuration of the spindle speed variation with piecewise characteristics. Int. J. Adv. Manuf. Technol. 2022, 122, 3041–3055. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, C. Recent progress of chatter prediction, detection and suppression in milling. Mech. Syst. Signal Process. 2020, 143, 106840. [Google Scholar] [CrossRef]
- Navarro-Devia, J.H.; Chen, Y.; Dao, D.V.; Li, H. Chatter detection in milling processes—A review on signal processing and condition classification. Int. J. Adv. Manuf. Technol. 2023, 125, 3943–3980. [Google Scholar] [CrossRef]
- Kim, D.H.; Song, J.Y.; Cha, S.K.; Son, H. The development of embedded device to detect chatter vibration in machine tools and CNC-based autonomous compensation. J. Mech. Sci. Technol. 2011, 25, 2623–2630. [Google Scholar] [CrossRef]
- Aslan, D.; Altintas, Y. On-line chatter detection in milling using drive motor current commands extracted from CNC. Int. J. Mach. Tools Manuf. 2018, 132, 64–80. [Google Scholar] [CrossRef]
- Yamato, S.; Hirano, T.; Yamada, Y.; Koike, R.; Kakinuma, Y. Sensor-less on-line chatter detection in turning process based on phase monitoring using power factor theory. Precis. Eng. 2018, 51, 103–116. [Google Scholar] [CrossRef]
- Kuljanic, E.; Sortino, M.; Totis, G. Multisensor approaches for chatter detection in milling. J. Sound Vib. 2008, 312, 672–693. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, X.; Wang, J. Online machining chatter forecast based on improved local mean decomposition. Int. J. Adv. Manuf. Technol. 2016, 84, 1045–1056. [Google Scholar] [CrossRef]
- Arriaza, O.V.; Tumurkhuyagc, Z.; Kim, D.W. Chatter Identification using Multiple Sensors and Multi-Layer Neural Networks. Procedia Manuf. 2018, 17, 150–157. [Google Scholar] [CrossRef]
- Zheng, X.; Arrazola, P.; Perez, R.; Echebarria, D.; Kiritsis, D.; Aristimuño, P.; de Buruaga, M.S. Exploring the effectiveness of using internal CNC system signals for chatter detection in milling process. Mech. Syst. Signal Process. 2023, 185, 109812. [Google Scholar] [CrossRef]
- Liu, B.; Liu, C.; Yu, X.; Zhou, Y.; Wang, D. Prediction, detection, and suppression of regenerative chatter in milling. Adv. Mech. Eng. 2022, 14, 16878132221129746. [Google Scholar] [CrossRef]
- Sugiyama, A.; Yamada, Y.; Yamato, S.; Kakinuma, Y. Development of Sensorless Chatter Detection Method in Ball Screw Drive System Applying Mode Decoupling. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar]
- Yamada, Y.; Yamato, S.; Kakinuma, Y. Mode decoupled and sensorless cutting force monitoring based on multi-encoder. Int. J. Adv. Manuf. Technol. 2017, 92, 4081–4093. [Google Scholar] [CrossRef]
- Wang, W.K.; Wan, M.; Zhang, W.H.; Yang, Y. Chatter detection methods in the machining processes: A review. J. Manuf. Process. 2022, 77, 240–259. [Google Scholar] [CrossRef]
- van Dijk, N.J.; Doppenberg, E.J.; Faassen, R.P.; van de Wouw, N.; Oosterling, J.A.; Nijmeijer, H. Robust active chatter control in the high-speed milling process. Transactions on Control Systems Technology IEEE 2012, 20, 901–907. [Google Scholar] [CrossRef]
- Caliskan, H.; Kilic, Z.; Altintas, Y. On-line energy-based milling chatter detection. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 111012. [Google Scholar] [CrossRef]
- Li, K.; He, S.; Li, B.; Liu, H.; Mao, X.; Shi, C. A novel online chatter detection method in milling process based on multiscale entropy and gradient tree boosting. Mech. Syst. Signal Process. 2020, 135, 106385. [Google Scholar] [CrossRef]
- Albertelli, P.; Braghieri, L.; Torta, M.; Monno, M. Development of a generalized chatter detection methodology for variable speed machining. Mech. Syst. Signal Process. 2019, 123, 26–42. [Google Scholar] [CrossRef]
- Yao, Z.; Mei, D.; Chen, Z. On-line chatter detection and identification based on wavelet and support vector machine. J. Mater. Process. Technol. 2010, 210, 713–719. [Google Scholar] [CrossRef]
- Wan, S.; Li, X.; Chen, W.; Hong, J. Investigation on milling chatter identification at early stage with variance ratio and Hilbert–Huang transform. Int. J. Adv. Manuf. Technol. 2018, 95, 3563–3573. [Google Scholar] [CrossRef]
- Bediaga, I.; Muñoa, J.; Hernández, J.; de Lacalle, L.N.L. An automatic spindle speed selection strategy to obtain stability in high-speed milling. Int. J. Mach. Tools Manuf. 2009, 49, 384–394. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G.; Bayly, P.V.; Mann, B.P. Multiple chatter frequencies in milling processes. J. Sound Vib. 2003, 262, 333–345. [Google Scholar] [CrossRef]
- Insperger, T.; Mann, B.P.; Surmann, T.; Stépán, G. On the chatter frequencies of milling processes with runout. Int. J. Mach. Tools Manuf. 2008, 48, 1081–1089. [Google Scholar] [CrossRef]
- Brown, R.G.; Hwang, P.Y. Introduction to Random signals and Applied Kalman Filtering: With MATLAB Exercises, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Zölzer, U. Digital Audio Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).