Abstract
Industrial robots are increasingly prevalent due to their large workspace and cost-effectiveness. However, their limited static and dynamic stiffness can lead to issues like mode coupling chatter and regenerative chatter in robotic milling processes, even at shallow cutting depths. These problems significantly impact performance, product quality, tool longevity, and can damage robot components. An active inertial actuator was deployed at the milling spindle to enhance dynamic stiffness and suppress low-frequency vibrations effectively. It was identified that the characteristics of the actuator change with its mounting orientation, a common scenario in robotic machining processes. This variation has not been reported in the literature. Our study includes the identification of model parameters for the actuator in both horizontal and vertical mountings. Additionally, the novelty of the present work lies in the specific design and implementation of compensation filters tailored for the active inertial actuator in both horizontal and vertical configurations. These filters address the unique challenges posed by low-frequency vibrations in robotic milling, offering significant improvements in dynamic stiffness and vibration suppression. Traditional model-based compensators were effective for vertical mounting, while pole-zero placement techniques with minimum phase systems were optimal for horizontal mounting. These compensators significantly enhanced dynamic stiffness, reducing maximum low-frequency robot structural modes by approximately 100% in horizontal mounting and approximately 214% in the vertical configuration of the actuator. This advancement promises to enhance industrial robot capabilities across diverse machining applications.
1. Introduction
Due to substantial workspace flexibility, cost-effectiveness, and reduced setup time, industrial robotics has become increasingly popular, particularly in milling large, lightweight aerospace components and metal additively manufactured parts, and finishing and polishing operations. However, robots exhibit lower static and dynamic stiffness compared to conventional machine tools, hindering their application in various machining processes [1,2,3,4]. This lack of dynamic stiffness in robotic milling systems leads to regenerative chatter even at minimal depths of cut, which can negatively impact productivity, product quality, and potentially cause tool wear or machine damage [5]. Furthermore, robots possess identical eigenfrequencies in their two principal directions, which can induce self-excited mode coupling chatter and lead to unstable robotic milling processes [5,6,7]. To address these limitations, this study explores the use of active damping systems to counteract vibrations and improve the overall performance of robotic milling.
Robotic milling machines exhibit two distinct vibration types: high-frequency and low-frequency vibrations. As documented in prior research [8,9,10], the low-frequency modes are inherent to the robot’s structure and depend on its pose (configuration). These pose-dependent modes are particularly susceptible to instability during the low-speed cutting of challenging materials (high-strength or thermally resistant) due to phenomena like regenerative chatter and self-excited mode coupling chatter [6,8,9,11]. Conversely, high-frequency vibrations, associated with the milling spindle and tool combination, are nearly independent of the robot’s pose. These high-frequency modes become problematic at high spindle speeds when cutting lightweight materials [8,9,10]. This distinction between vibration sources is further supported by analyzing the system dynamics of the tool and robot structure in the present study and the system’s mode shapes [9]. In the high-frequency mode, the tool experiences significant vibration while the robotic structure remains stable. In contrast, the low-frequency mode exhibits pronounced vibration at the robotic joints, with the tool undergoing a rigid body swing accompanied by end effector vibration. Since the dynamics of the low-frequency robot structure mode are more prominent than those of the high-frequency tool mode, the present study is focused on increasing the dynamic stiffness of low-frequency robot modes and avoiding chatter at the minimal depth of cut.
At the initial stage, self-excited mode coupling chatter or regenerative chatter due to low-frequency milling robot modes can be avoided and/or mitigated by selecting stable cutting conditions from the predicted stability chart. Several authors have developed chatter stability models for the robotic milling process, incorporating three-dimensional frequency response functions (FRFs) using time and frequency domain methods [8], chip wave phase difference analysis and chatter participation degree analysis [12], mode coupling effects [6,7,11], and surface renewal functions while considering tool jumping-out-of-cut nonlinearities [9]. Although these models are useful for selecting stable cutting conditions, which may change as the robot’s pose changes, they do not improve the inherent low dynamic stiffness of the robot. Therefore, various researchers have attempted to increase the low-frequency dynamic stiffness using passive, active, and semi-active damping control strategies.
Cen and Melkote developed a Conservative Congruence Transformation (CCT) stiffness model to mitigate low-frequency mode coupling chatter by accounting for the effect of milling forces on robot stiffness. The CCT technique does not require changing the tool feed direction or the workpiece orientation, but rather adjusting the angle between the average cutting force direction and the maximum principal stiffness of the robot [11]. H. Vieler et al. presented the theoretical simulation results of a robot feed drive-based active control model that uses encoder data as the input, converting it into velocity feedback for the active control loop. This proportionately adds damping to the robot joints. The model performed well in simulations; however, the authors did not consider nonlinearity and backlash in robot joints, which are prevalent in real scenarios [13]. Chen and Zhao designed and developed an eddy current damper to suppress robotic milling tool tip vibrations. The damper, mounted on the spindle, reportedly increased the critical stable depth of cut by 23.5% [14]. Wang and Keogh utilized a voice coil-type inertial actuator with a maximum force capacity of 15.6 N and MEMS-based accelerometers with velocity feedback to actively control tool tip vibrations. Using a single actuator mounted at the spindle and in the feed direction, they achieved up to a 26% reduction in machining vibrations [15].
Nguyen et al. developed an optimal control strategy based on a Linear Quadratic Regulator (LQR) to estimate pose-dependent controller gains for mitigating tool tip vibrations. Instead of using external actuators, they controlled the robot’s drive directly, resulting in significant reductions in machining vibrations—up to 51% in the X-direction and 43% in the Z-direction [16]. Guo et al. introduced a method called active contact robotic milling, featuring a novel milling cutter that has three components such as regular cutting edges, a plain rod, and a needle bearing. The needle bearing maintains contact with the workpiece, and the resultant contact force, measured by a force sensor, is used as a feedback signal to actively control the contact forces between the robot and the workpiece, in addition to the milling forces. The authors claimed that this approach significantly expanded the stable zone of robotic milling [17]. Furthermore, Ozsoy et al. theoretically investigated various active control strategies, including direct velocity feedback (DVF), PID control, LQR control, H∞, and µ-synthesis controls [18]. Subsequently, they conducted experimental validation and developed an actuator saturation model. Their findings indicated that while the active control laws theoretically stabilize the machining process, the actuators tested in experiments exhibited saturation due to limited force capacity, thereby hindering further control over the cutting process. Therefore, they recommended integrating the actuator saturation model for real-world industrial cutting scenarios [19]. Kim et al. designed and implemented a piezo-actuator-based active spindle holder for a robotic milling machine aimed at enhancing the low-frequency dynamic stiffness of the robot structure. Experimental results demonstrated an improvement of up to 18% in surface quality [20].
Wu et al. developed a passive damper, known as a tuned mass damper, to mitigate low-frequency and lateral frequency robot modes, which correspond to modes aligned with and perpendicular to the tool axis. Significant damping effects were observed in both directional modes; however, the effectiveness diminished with changes in robot pose altering the robot mode [21]. Several efforts have been undertaken to tackle the challenge of low-frequency vibrations and pose dependence in robotic structures through semi-active damping techniques. Yuan et al. pioneered a Magnetorheological Elastomer (MRE) with adjustable stiffness, introducing a novel mode-coupling chatter suppression scheme. Their approach employed an MRE integrated on the spindle alongside a semi-active controller to modulate the applied current, enabling resonance tracking and the effective absorption of low-frequency vibration energy [22]. In a similar vein, Zhao et al. explored the application of an MRE vibration absorber in robotic milling, positioning it at the end effector of the robot, asymmetrically. Their study showcased a notable reduction of over 69% in power spectral density at peak frequencies, resulting in significant enhancements in surface finish with workpiece roughness decreasing by more than 16.5% [23]. Building upon this foundation, recent advancements include modifications to the MRE design, transforming it into a symmetrical configuration installed at the robot’s end effector. This development achieved substantial reductions of 73%, 88%, and 79% in vibration peak values along the X-, Y-, and Z-axes, respectively [24]. In order to improve the structural rigidity of the robot, Xin et al. devised a Joint Wearable Structural Reinforcing Device (JWSRD) with the help of an MR damper. This technique strengthened the robot dynamic stiffness by approximately 23%, preserving robot flexibility while mitigating vibrations [25]. Furthermore, Xin et al. introduced a Magnetorheological Joint Damper (MRJD) strategically placed across different robot joints. By optimizing the MRJD through robot joint angle adjustments, they achieved significant advancements: a 60% reduction in low-frequency chatter vibrations and a 35% suppression under stable conditions [26].
Despite advancements in chatter control and stability models, limited research has been conducted on the use of active inertial actuators for vibration suppression in the robotic milling processes. In previous studies, robot dynamics were emulated using a cantilever beam structure with an inertial actuator (8.4 Hz) mounted on it [18,19]. In this work, a flexure-mounted workpiece was analyzed, with system dynamics dominated at 142.1 Hz because chatter occurs around 142 Hz. Typically, robot structure modes are more dominant than workpiece or tool dynamics, leading to chatter near the robot structural modes (~10–30 Hz) when cutting at low speeds. Under these conditions, the inertial actuator used in [18,19] would be ineffective, as the actuator’s mode and the robot’s mode would be in close proximity. It is important to note that commercially available inertial actuators integrated into industrial robots often possess eigenfrequencies ranging from 5 to 30 Hz [18,19,27,28,29]. Utilizing such actuators for active damping in robotic milling presents a challenge. Resonances between the robot’s structural modes and the actuator’s modes can potentially amplify vibrations instead of mitigating them. This issue of low-frequency vibration mitigation is also encountered in gantry-type portal milling machines [30]. A common approach to address this challenge involves designing an actuator compensator that reduces the influence of the actuator’s mode. Bilbao-Guillerna et al. proposed various compensatory filter designs to expand the linear range of inertial actuators and enhance milling stability in ram-type portal milling machines [31]. However, these filters often exhibit significant effects at very low frequencies, including up to 5 Hz. This can potentially amplify low-frequency signals and compromise the robustness of active damping. To overcome this limitation, this study proposes a novel compensator filter design that effectively suppresses the actuator mode without inducing instability, ensuring that very low-frequency modes are not amplified.
The rest of the paper is organized as follows: Section 2 presents the results of the experimental modal analysis of the robotic milling machine with and without the mounting of an actuator, alongside the dynamic characterization of the actuator in horizontal and vertical mounting configurations. Section 3 characterizes the dynamic behavior of the inertial actuator. Section 4 details the three different design methodologies for the compensation filter, including the selection of additional filter parameters. Section 5 describes the development of a Simulink model to facilitate active damping experiments and assess the closed-loop system’s stability. Section 6 discusses the results of the experimental modal analysis performed on the robotic milling system with active damping, followed by conclusions in Section 7 summarizing the key findings of the paper.
2. Modal Analysis of the Robotic Milling Machine
To understand the dynamics of a robotic machine tool, which is essential for predicting and improving the stability of the milling process, a comprehensive modal analysis was conducted under various conditions. The experimental setup for the modal analysis of the robotic milling machine is depicted in Figure 1a. The existing literature indicates that the dynamics of low-frequency structural modes are position-dependent, whereas high-frequency tool spindle modes are relatively unaffected by changes in the robot’s tool position [8,9,10]. Therefore, this section focuses on conducting modal analysis for both the cutting tools and the milling spindle head. The spindle unit of the robotic milling system has a maximum speed of 30,000 rpm. For this analysis, a high-speed steel end-mill cutter with a diameter of 10 mm, two flutes, a helix angle of 30 degrees, and a tool overhang of 105 mm was selected. The cutting tool is secured using a collet chuck type tool holder. The modal analysis includes the identification of direct and cross FRFs for both the cutting tool and the spindle head at a specific robot position. To facilitate the analysis, a medium-sized impact hammer (Make: Dytran, Model: 5800B4), a miniature uniaxial accelerometer (Make: Dytran, Model: 322F1), and a tri-axial accelerometer (Make: PCB, Model: JTLB356B08) were employed. The miniature uniaxial accelerometer measures the dynamics of the tool at the tool center point (TCP), while the tri-axial accelerometer captures the dynamics of the milling spindle head and the robot structure combination, as illustrated in Figure 1a and Figure 2a.
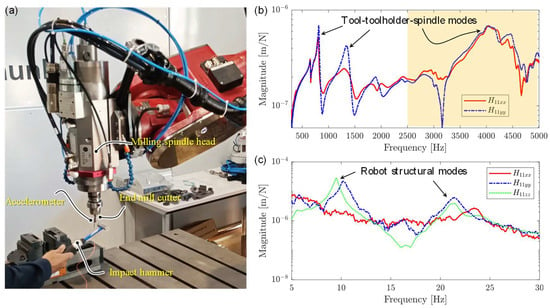
Figure 1.
(a) Experimental setup for modal testing of robotic milling machine. (b) Direct FRFs at the TCP in the X- and Y-directions [yellow shade represents approximate FRFs beyond half power spectrum]. (c) Direct FRFs at the TCP in X-, Y-, and Z-directions showing robot structural modes.
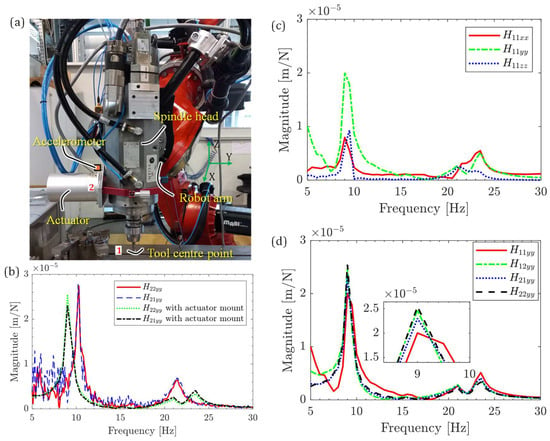
Figure 2.
(a) Robotic milling system with actuator mount at the spindle head. (b) FRFs of the robot structure with and without mounting of actuator. (c) Direct FRFs at the tool tip in X-, Y-, and Z-directions. (d) Direct and cross FRFs at the tool tip and at the actuator mounting location.
Since the uniaxial accelerometer mounted at the TCP cannot accurately measure frequencies below 20 Hz, which pertain to the robot structure and are observable at the TCP, a tri-axial accelerometer is magnetically mounted near the shank of the tool on the tool holder. The mass of the accelerometer has a negligible influence on the measured dynamics below 30 Hz, as eigenfrequencies below 30 Hz primarily correspond to the robot’s structural modes. The measured direct FRFs of the tool tip in the X- and Y-directions, obtained using the uniaxial accelerometer, are presented in Figure 1b. Additionally, the measured FRFs near the TCP, acquired using the tri-axial accelerometer, are combined and illustrated in Figure 1c. We observed that the direct FRF in the Z-direction, corresponding to the tool–toolholder combination, has a magnitude one or more orders higher than that in the X- and Y-directions due to the tool’s significant stiffness in its axial direction. Consequently, we have omitted the Z-direction FRF in Figure 1b. Conversely, the low-frequency robot structural modes shown in Figure 1c in all three directions (X, Y, and Z) have magnitudes approximately 35 times higher than the FRFs in Figure 1b. These modes critically impact machining stability, justifying the inclusion of all three directional FRFs in Figure 1c.
Figure 1b reveals that the observed tool dynamics between 500 Hz and 2500 Hz have four modes and are nearly symmetric in both the X- and Y-directions. However, beyond 2500 Hz, the measurements exhibit variations. This deviation can be attributed to the excitation bandwidth of the impact hammer, which reaches around 2500 Hz, whereas the accelerometer can measure acceleration signals up to 5000 Hz. Consequently, measurements beyond 2500 Hz are less accurate and only indicate the presence of high-frequency modes of the cutting tool at approximately 4050 Hz and 4400 Hz. These modes may be excited and lead to instability during high-speed cutting processes. Figure 1c suggests that the structural modes of the robot exhibit greater dominance compared to those of the cutting tool. These modes directly influence the minimum stability of the milling process. Practically, low-frequency modes of the robot may become unstable when performing low-speed cutting on high-strength materials, whereas high-frequency modes of the cutting tool may experience instability during high-speed cutting processes.
It is evident from Figure 1b,c that robotic milling machine has both low- and high-frequency modes. The low-frequency robot structural modes, as illustrated in Figure 1c, are more dominant and significant compared to the high-frequency modes of the cutting tool-tool holder combination shown in Figure 1b. Quantitatively, the magnitude of the low-frequency modes depicted in Figure 1c is approximately 35 times greater than that of the high-frequency modes shown in Figure 1b. Even though high-frequency modes may destabilize during high-speed cutting process, this paper is focused on stabilizing low-frequency modes using active control technique by mounting inertial actuator (Make: Micromega Dynamics; Model: ADD45) at the spindle head and integrating the most reliable direct velocity feedback control law [19,27,28,32], see Figure 2a. Conditions other than the actuator mounting are the same as the conditions mentioned for Figure 1. The tool tip is designated as location 1, while location 2 corresponds to the actuator mounting location (AML). The actuator was securely screw-mounted in place. To measure vibrations and serve as a feedback sensor, an external accelerometer (Make: PCB, Model: JTLB356B08) was strategically positioned near location 2. The accelerometer’s signal was then transmitted to the controller for further analysis and monitoring.
To evaluate the impact of the actuator mass on robot dynamics, modal testing was performed in two scenarios: with and without the actuator mounted. For the analysis, the Y-direction was specifically selected. The results of these tests are presented in Figure 2b. The notation represents the cross FRF at the location where the actuator is mounted. The excitation occurs at location 1, while the measurement is performed at location 2. Both the excitation and measurement directions are aligned with the Y-direction. Considering the accelerometer’s reliable measurement range starting from 5 Hz, the plotted FRFs in Figure 2b are presented only after the 5 Hz threshold. This decision ensures that the displayed FRFs are based on reliable and accurate accelerometer data. The direct FRFs at the TCP in the X-, Y-, and Z-directions are presented in Figure 2c. Since the cross FRFs at the TCP are not utilized in this investigation, their plots are omitted. Furthermore, as the actuator is mounted on the spindle head (location 2) oriented in the Y-direction of the robot, the direct and cross FRFs in the Y-direction are presented in Figure 2d to observe the effect of active damping at the TCP (location 1) and at the actuator mounting location (location 2).
It is clear from Figure 2b that the natural frequency of the robot’s structural mode decreases at lower frequencies due to the inclusion of the actuator mass. This reduction in frequency also causes a shift in the peak mode around 20 Hz, splitting it into two distinct peaks. Consequently, further experiments were conducted using the same configuration, specifically with the actuator mounted. This configuration accurately reflects real cutting experimentation scenarios where active control is employed. To measure these low-frequency modes at the tool tip, a tri-axial accelerometer was magnetically mounted near the shank of the tool at the tool holder. This accelerometer was utilized to directly measure the FRFs at the tool tip, denoted as (, , , and ). Given that the actuator is mounted in the Y-direction, the direct and cross FRFs at the Actuator Mounting Location (AML) were exclusively measured in the Y-direction, as demonstrated in Figure 2a. This approach allowed for a focused analysis of the actuator’s effects on the system’s response in the Y-direction (see Figure 2d). From Figure 2c, it is clear that the FRF in the Y-direction is more dominant than that in the X- and Z-directions. This dominance in the Y-direction can be attributed to the alignment of the robot arms. In the X-direction, the robot exhibits high strength as the robot arms are aligned along the X-axis, providing substantial rigidity. In the Z-direction, the presence of spindle and tool supports contributes additional strength to this axis.
Furthermore, analyzing the cross and direct FRFs in the Y-direction shown in Figure 2d, we observe that their peak magnitudes and FRF characteristics are approximately similar. This similarity occurs because these low-frequency modes are inherent to the robot structure, and their magnitudes remain consistent when measured at the TCP (tool center point). These low-frequency structural modes are observable at the TCP, indicating that the vibrations measured at different points on the robot structure (near to the spindle and tool) have similar characteristics due to the intrinsic properties of the robot.
The modal parameters corresponding to the FRFs depicted in Figure 2c,d have been estimated through the utilization of the residue method, as outlined in reference [33]. These modal parameters, crucial for the theoretical calculation of stability within the closed-loop active damping system, are compiled and presented in Table 1.
wherein , (note: if the system has only one mode), natural frequency of the robot, damping ratio of the robot, number of modes, measurement direction, excitation direction, measurement location, excitation location, real part of the residue, and imaginary part of the residue.

Table 1.
Modal parameters of the direct and cross FRFs of the robot.
To understand the dynamic behavior of the actuator, systemic characterization of the actuator has been presented subsequently.
3. Characterization and Model Identification of Actuator
The experimental setup for characterizing the actuator is depicted in Figure 3. The actuator was securely mounted onto the Kistler Dynamometer (Model: 9255B, SN: 485906) to ensure stability and accurate force measurements. The primary objective of this study was not to measure spindle-speed-dependent cutting forces or actuator forces. Instead, we focused on measuring the actuator force within the frequency range of 1 Hz to 200 Hz to determine its natural frequency and bandwidth. To generate the necessary input signals for testing, LabVIEW 2021 was employed; see Figure 3a. Sine chirp signals at various voltages were generated, covering a wide frequency range. This comprehensive range allowed for a thorough characterization of the actuator’s performance across different frequencies. To facilitate data acquisition and signal transmission, a Compact RIO controller (Model: NI cRIO 9047) was utilized as depicted in Figure 3b. It integrated an analog-to-digital converter (Model: NI 9232) to receive the force signal from the Kistler dynamometer, which came through a charge amplifier. Simultaneously, a digital-to-analog converter (Model: NI 9263) was employed to transmit voltage signals to the actuator via a power amplifier (Figure 3c). The actuator force is obtained through the charge amplifier of the dynamometer, which converts the voltage signal into a force signal by multiplying it with the sensitivity, as illustrated in Figure 3d,e. Given that the working configuration of the robot varies depending on the specific use case, the actuator was tested exclusively in both vertical and horizontal orientations, as illustrated in Figure 4.
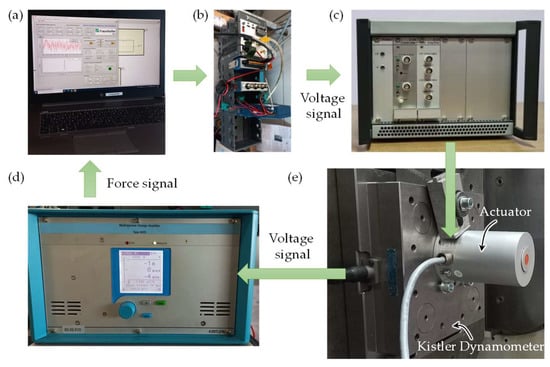
Figure 3.
Experimental setup for characterizing the actuator. (a) Signal generation and data recording using LabVIEW. (b) Compact RIO controller with analog I/O modules. (c) Power amplifier of the actuator. (d) Charge amplifier of the dynamometer. (e) Actuator mounted on the dynamometer.

Figure 4.
Actuator mounted on the dynamometer in (a) vertical position and (b) horizontal position.
A sine chirp signal ranging from 1 Hz to 200 Hz was generated and applied for a duration of 30 s, with a magnitude of 1 V. The response of the system, in terms of the measured input voltage to the actuator and the corresponding force in the Z-direction as measured by the dynamometer, was recorded for both the vertical and horizontal mounting configurations of the actuator. These measurements are visually represented in Figure 5. Furthermore, the frequency response of the system, indicating the relationship between input frequency and output force, is illustrated in Figure 6.
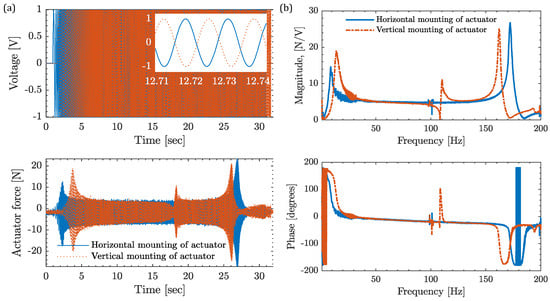
Figure 5.
Time and frequency characteristics of actuator in horizontal and vertical mounting of actuator. (a) Measured time domain signal of input voltage and output force from the actuator. (b) Estimated force-to-voltage frequency characteristics of the actuator from the measured time domain signal.
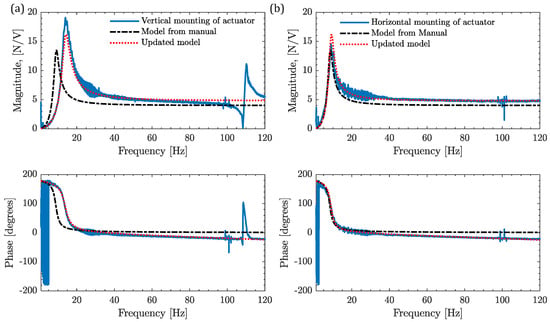
Figure 6.
Measured and modeled force-to-voltage frequency characteristics of the actuator at different voltages. (a) Vertical mounting of the actuator. (b) Horizontal mounting of actuator.
It is clear from Figure 5b that the frequency response of the actuator varies in the horizontal and vertical positions. According to the actuator’s user manual, the specified natural frequency is 8.4 Hz [18,29]. However, when the actuator is mounted in horizontal and vertical configurations, the measured natural frequency changes, ranging from 9 Hz to 14 Hz. Interestingly, additional natural frequencies are observed near 110 Hz and within the range of 160–180 Hz, which are also influenced by the mounting orientation of the actuator. It should be noted that the modes observed beyond 150 Hz correspond to the eigenfrequencies of the Kistler dynamometer in the Y- and Z-directions (172 Hz in horizontal mounting and 162.2 Hz in vertical mounting of actuator). To assess the linearity of the actuator, experiments were conducted at three different voltage levels for each mounting configuration and found that linearity holds for 1–3Vpp and up to 120 Hz. The primary objective of this study was to enhance the low-frequency dynamic stiffness of the robot (below 30 Hz) using active damping, and thus, frequency responses up to 120 Hz were analyzed, as shown in Figure 6.
The actuator exhibits a flat working bandwidth ranging from approximately 30 Hz to 120 Hz. Although there is a slight variation in magnitude near the actuator’s natural frequency, this difference is considered negligible. As a result, data obtained from the input voltage of 1V have been selected for modeling the actuator dynamics, which will be discussed subsequently. The general transfer function of the actuator, as derived from Preumont [34] and the actuator’s user manual [29], is provided below:
wherein 4 N/V, 0.15, and 8.4 rad/s.
Since Equation (2) does not fit well with the measured data shown Figure 6, a delay term has been introduced to exactly fit the phase frequency characteristics of the actuator. The updated transfer function of the actuator with a delay term is given below:
In this way, model parameters of the actuator in horizontal and vertical configuration of the actuator have been tuned manually and identified as listed in Table 2. It is noted that only the natural frequency of the actuator changes when we change its mounting configuration. The model fitted frequency responses along with the measured FRFs for both mounting configurations are shown in Figure 6.

Table 2.
Dynamic parameters of the actuator in horizontal and vertical configuration.
It is evident from Figure 6 that the model fitted frequency responses for both mounting configurations matches well with the measured response. Interestingly, for the case of vertical mounting of the actuator, its dynamics are significantly different than those reported in the user manual of the actuator. While the frequency response functions (FRFs) corresponding to the vertical mounting of the actuator deviate from those presented in the user manual, the FRFs for the horizontal mounting of the actuator, shown in Figure 6b, match well with the user manual of the actuator. This discrepancy arises because the user manual reports experimental results only for the horizontal mounting of the actuator and does not address changes in actuator dynamics with different mounting configurations. The actuator has predominantly been used in horizontal mounting configurations in robots and machine tools. However, in robotic machining, the actuator may be vertically mounted depending on the robot’s pose.
The change in the dynamics of the actuator with different mounting configurations is primarily due to the inherent mass of the actuator and the effect of gravitational forces on its overall stiffness in both horizontal and vertical mounting configurations.
Having characterized the actuator and identified its model parameters, the subsequent step involves utilizing this information to design an active control strategy that effectively enhances the dynamic stiffness of the robot structure. By doing so, the overall productivity of the robotic milling processes can be increased. However, since the actuator mode (9 Hz) is in close proximity to the robot mode (9.2 Hz), the actuator will not dampen the robot mode, but rather amplify it. Consequently, a compensation filter needs to be devised to initially compensate for the actuator mode. The procedure for designing such a compensation filter is outlined below.
4. Design and Testing of Actuator Mode Compensator
The compensation filter was designed to suppress the actuator modes at 9 Hz and 14 Hz. The objective was to ensure that the actuator’s FRF magnitude remains at 0 dB, meaning that when the robot vibrates at its natural frequencies, the actuator does not amplify these vibrations but rather suppresses them. Additionally, it should maintain stability, meaning that the pole of the compensator must be located in the left half of the complex plane. In this study, two types of compensation filters are presented, each offering a distinct approach to address the requirements. The first approach is based on the actuator model itself, leveraging its characteristics to design the compensation filter. This method utilizes the known properties and behavior of the actuator to devise a filter that effectively attenuates the actuator mode and assists in vibration suppression. The second approach uses pole-zero placement. In this case, the compensation filter is designed by strategically selecting the location of poles and zeros to achieve the desired attenuation of the actuator mode and overall stability.
4.1. Model-Based Design of Compensation Filter
The model-based approach for designing compensation filter has been adapted from [35]. The transfer function of the compensation filter:
wherein rad/s is the cut frequency of the compensation filter, is the damping ratio of the actuator, is the natural frequency of the actuator. These actuator parameters are listed in Table 2. The selection of the cut frequency for the compensation filter is determined based on various factors. The cutoff frequency for the compensation filter was optimally chosen to be 0.5 Hz after experimenting with various values between 0.1 Hz and 5 Hz, with 0.5 Hz providing the best performance. At this cutoff frequency, the actuator mode achieved a flat response with a magnitude of 0 dB. The value of has been kept same for both the cases of horizontal and vertical mounting of actuator. By selecting a cut frequency of 0.5 Hz, the compensation filter effectively addresses the frequency range affected by the actuator. The bode plot of the compensation filter, is presented in Figure 7a.
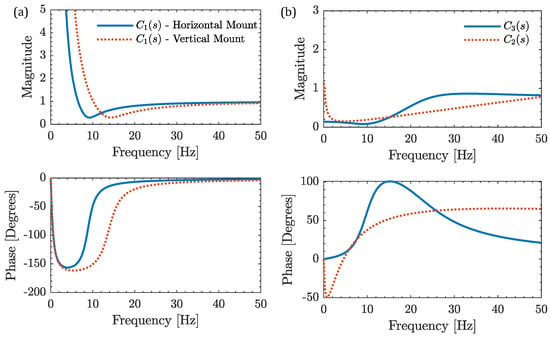
Figure 7.
Frequency response of compensation filters. (a) Model-based technique; (b) non-model-based techniques. Note: and are designed for both horizontal and vertical mounting configurations.
Figure 7a demonstrates a notch effect at the natural frequency of the actuator in both the horizontal and vertical mounting cases. However, there is a notable high magnitude observed at lower frequencies, specifically around 5 Hz. This high magnitude at lower frequencies could potentially amplify the inherent 3 Hz (found after separate investigation) low-frequency vibration of the robot. The implications of this behavior on the stability of the closed-loop active control system will be discussed in Section 5, where the stability analysis will be presented.
In addition to the presented compensation approach, this work also introduces another method known as pole-zero placement for designing a compensation filter for the actuator. This alternative approach aims to minimize the magnitude at lower frequencies, thereby addressing the issue of amplifying the low-frequency vibration of the robot. The details and discussion of this approach will be presented in subsequent sections.
4.2. Pole-Zero-Placement-Based Design of Compensation Filter
In this technique, the MATLAB Control System Designer toolbox has been employed to design the compensation filter. Within this toolbox, the Bode editor feature has been utilized, allowing for the strategic placement of poles and zeros to achieve the desired Bode plot. Placing a pole results in a 20 dB per decade decay in magnitude and a −90° phase shift, while adding zero leads to a −20 dB per decade increase in magnitude and a +90° phase shift. The criteria for the compensation filter entail its ability to exhibit a significantly low magnitude at the natural frequency of the actuator, as well as at frequencies below 5 Hz, to prevent amplification of inherent robot’s 3 Hz vibrations. However, it is important to note that the addition of poles and zeros also impacts the phase of the system. Therefore, there exists a trade-off between obtaining the desired magnitude and phase plot, as the overall stability of the active control system relies on the phase characteristics of the system as well. Consequently, the placement of poles and zeros within the compensation filter is carefully determined to ensure system stability.
To achieve a stable system, two versions of the compensation filter have been designed using a pole-zero-placement-based method. One version, denoted as , is directly designed using the Bode editor and is employed in the experiments. The second version, denoted as , is obtained by inverting the transfer function that was initially constructed as an actuator transfer function using the Bode editor tool. In contrast to the actuator transfer function developed in the previous section, this newly constructed transfer function possesses a characteristic of exhibiting high magnitude at lower frequencies. This inversion is deemed more suitable for compensating low-frequency vibrations. The resulting transfer function of the actuator, after inversion, is provided below:
However, due to the nonminimum phase behavior of the above transfer function, direct inversion is not always possible. To address this issue, we utilize the invfreqz function available in MATLAB, which allows us to transform the transfer function into a minimum phase form [36]. This transformation involves minimizing the weighted sum of the squares of the errors between the absolute magnitudes of the actual transfer function and the ratio of the polynomial, evaluated at various frequencies.
It is important to note that the invfreqz function operates in the discrete domain. In the present case, a time step of dt = 5 ms is chosen as it aligns well with the frequency response of the continuous system. By utilizing this function and selecting an appropriate time step, we can achieve a minimum phase representation of the transfer function, thus addressing the nonminimum phase behavior.
An inverted version of with minimum phase compensation filter transfer function is given below:
Another compensation filter, that is directly designed using the pole-zero placement method in Bode editor as given below:
The frequency responses of the compensation filters are presented below in Figure 7b.
Figure 7b clearly illustrates that the Bode plot magnitude remains significantly low for frequencies below 20 Hz. Additionally, it is apparent that the magnitude plot of reaches unity after 25 Hz, but it introduces a substantial phase shift, unlike . These filters have been integrated into the LabVIEW 2021 as part of the active control system, as detailed in the subsequent section. A separate experiment for characterizing compensation filters in an open loop has also been done and shows its effectiveness in making actuator mode flat. The subsequent section deals with the closed loop stability of the active damping system.
5. Closed-Loop Active Damping Model
The schematic diagram and a Simulink model illustrating the closed-loop active damping model of the robotic milling machine can be observed in Figure 8a and Figure 8b, respectively. To conduct the entire active damping experiments, one position of the robot was specifically chosen, as detailed in Section 2. In this study, a well-established non-model-based direct velocity feedback (DVF) control law, previously documented in references [18,19,27,28,32], was utilized.
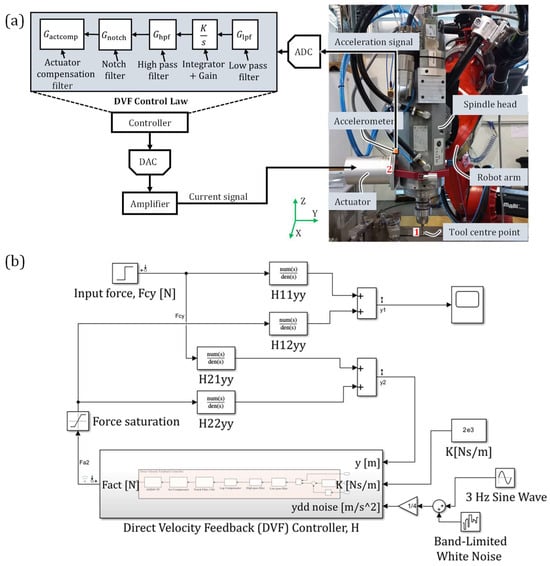
Figure 8.
(a) Robotic milling system with integrated active inertial actuator, (b) Simulink model of the robotic milling system with integrated inertial actuator.
The acceleration signal captured by the accelerometer, positioned near the actuator mounting location (location 2), undergoes a series of signal processing stages including a low-pass filter, an integrator with control gain, a high-pass filter, a notch filter, and a compensation filter. The control parameters for these filters are implemented within LabVIEW 2021. For the control system, a Compact RIO controller based on FPGA (Make: National Instrument, Model: cRIO9047) was employed. This controller is equipped with analog-to-digital (ADC, Model: NI9225) and digital-to-analog converter (DAC, Model: NI9263) modules, which support IEPE (Integrated Electronic Piezoelectric) functionality. The controller is connected to a PC, where LabVIEW 2021 is utilized to manage and regulate the actuator.
The present study acknowledges the presence of nonlinearity and backlash in robot joints as factors that can affect the overall stiffness and damping of the robot. However, the active damping technique employed in this study utilizes a direct velocity feedback control law, which does not necessitate the consideration of the robot structure’s dynamics or a detailed nonlinear robot joint model. In this method, an accelerometer directly measures the vibration, which is then converted into velocity using an integrator. By multiplying this velocity with a control gain, an active damping force is produced, proportionately suppressing the vibrations. Thus, the present study does not primarily analyze the impact of nonlinearity and backlash in the robot joints on damping. In Figure 8b, the direct and cross FRFs of the robotic milling system have been selected specifically for the Y-direction, as the actuator is mounted in that direction, yielding the most significant impact. To account for the inherent above-mentioned vibrations of the robot structure occurring at 3 Hz, a 3 Hz white noise signal has been incorporated into the acceleration signal. Notably, the receptance FRFs (x/F) have been utilized in the Simulink model to obtain the displacement signal as an output. Consequently, a differentiator (s) has been employed to derive the velocity signal from the displacement signal, enabling further analysis and evaluation of the control strategy’s effectiveness. The direct velocity feedback controller (DVF), in Figure 8 is given below:
where (Ns/m) is the closed loop control gain of the DVF controller. The stability of the closed-loop active control system has been theoretically checked using a root locus technique, which is not presented here. The transfer function of the closed-loop active control system when feedback is taken from location 2 is given by:
wherein, is the transducer constant whose values are given Table 2. The denominator of Equation (9), i.e., the characteristics equation governs the stability of the closed-loop system. The system’s stability is ensured if all poles of the characteristic equation lie in the left half of the s-plane. For the given transfer function, the characteristic equation becomes:
Using Equation (12), , stability of the closed-loop system has been checked using root locus method in MATLAB for all three compensation filters and are used in the experiments. To apply the root locus method, we need to plot the loci of the roots of this equation as varies from 0 to ∞. The system is stable if the poles of the closed-loop transfer function are in the left half-plane (i.e., have negative real parts). Using the root locus, we ensure that: (i) for , the real parts of all poles must be negative, (ii) no poles should cross into the right half-plane for any value of K.
Furthermore, it is well understood that the implementation of filters introduces phase lead or phase lag to the system and influences the magnitude of the response [28,37,38]. In the present study, considering the utilization of various combinations of filters for different purposes, the behavior of the DVF controller may deviate from an ideal case. The impact of filters on the magnitude can be adjusted by modifying the control gain to smaller or larger values. However, it is crucial to carefully examine the phase characteristics of the filters, which will be discussed sequentially in the following paragraphs.
Compensation filter (CF) denoted as : In this study, three versions ( = 3) of CF were designed to compensate for the actuator mode and counteract the robot structure mode. The transfer functions and FRFs for all three CFs have been previously reported and elucidated in detail in Section 4.1 and Section 4.2. At the natural frequency of the actuator (9.2 Hz), the phase shifts provided by the CFs are as follows: , and .
High-pass filter (HPF) denoted as : The purpose of the HPF is to eliminate low-frequency signals. Since an integrator is employed to obtain the velocity signal from the acceleration signal, it introduces a DC offset during real-time integration, resulting in a continuous accumulation of DC offsets in the integrated signal. These DC offsets represent low-frequency signals that can be effectively removed using an HPF. Additionally, since the robot structure inherently exhibits vibrations at 3 Hz, a cutoff frequency of 4 Hz and a damping ratio of = 0.707 were selected for the HPF. The transfer function of the implemented second-order HPF is provided below. Notably, the HPF introduces a positive phase shift of approximately +37° at the natural frequency of the actuator (9.2 Hz).
Notch filter (NF) denoted as : The notch filter was employed to reduce the magnitude of the inevitable 3 Hz mode. The transfer function for the utilized notch filter is presented below. Notch filter provides a positive phase shift of +26° at the natural frequency of robot structure (9.2 Hz).
Low pass filter (LPF) denoted as : It is an essential component in measurement and control systems as it effectively eliminates high-frequency noise. Unlike most previous filters that introduce a large positive phase shift, LPF stands out by providing a negative phase shift. To evaluate the response of a second-order LPF with various cutoff frequencies, a thorough analysis has been conducted. The transfer function of a second-order LPF can be expressed as follows:
Here, represents the natural frequency of the LPF in rad/sec, while = 0.707 denotes the damping ratio. The frequency responses of the LPF have been studied for different cutoff frequencies ( ranging from 2000 Hz to 50 Hz. Additionally, 50 Hz and 100 Hz LPFs have been included due to the limited negative phase provided by LPFs in the range of 2000 Hz to 500 Hz. It is worth noting that doubling the implementation of the 50 Hz mode leads to a maximum phase shift of −30.1° at the natural frequency (9.2 Hz) of the robot. Further reduction of the LPF’s cutoff frequency below 50 Hz is not advisable since it would introduce a substantial negative phase shift at another natural frequency (23.6 Hz) of the robot. Consequently, for this study, two second-order LPFs with a cutoff frequency of 50 Hz have been cascaded to achieve the desired filtering characteristics.
6. Results of the Robotic Milling Machine with Active Damping
The modal analysis of a robotic milling machine with active damping is conducted using a custom-made application developed in LabVIEW 2021. Active damping experiments are conducted for both horizontal and vertical mounting of the actuator at the same position of the robot as we had done the modal experiments without active damping. Initially, the effect of the actuator compensation filter on active damping is evaluated by performing modal experiments with and without the compensator, with the robot drives both on and off. In these experiments, a compensation filter (), a low-pass filter (LPF) with a cutoff frequency of 2000 Hz, a high-pass filter (HPF) with a cutoff frequency of 4 Hz, and only the direct FRFs of the robot at the actuator mounting location (location 2) in the Y-direction are chosen, as depicted in Figure 9a.
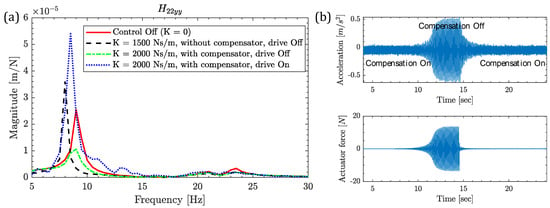
Figure 9.
(a) Direct FRFs of the robot at the actuator mounting location () with compensation On/Off and drive On/Off, (b) Time domain accelerations and actuator force with compensation On and Off. In this case, the drive was Off and K = 1500 Ns/m.
The black-dashed curve in Figure 9a shows that the magnitude of the FRF increases when the compensator is not used and the drive is off. In this case the combination of the actuator mode and the robot mode around 9 Hz amplifies the vibration. When the compensator is turned on with the drive turned off, significant damping is achieved (green dash-dotted curve). The time domain response of the acceleration signal and actuator force for this case is also illustrated in Figure 9b. However, when the compensator is active and, in addition, the robot’s drive is turned on, which is necessary for any cutting experiments, the magnitude of the FRF increases significantly, leading to system destabilization. This behavior can be attributed to the high magnitude of the compensator at low frequencies, which amplifies the robot’s inherent 3 Hz mode and impacts the robot mode as well. Note that these initial experiments were performed with a LPF cutoff frequency = 22000 rad/s, which was later also optimized.
Since the robot drives are always On during cutting experiments, active damping experiments presented from this point onwards are conducted with robot drive active. Consequently, the tuning of the active control strategy should aim to suppress the magnitude of the FRFs, thereby increasing the dynamic stiffness of the system. Following the preliminary active damping experiments, compensation filters , and with two second-order low-pass filters (LPFs) having a cutoff frequency of 50 Hz have been tested. These LPFs are employed to compensate for the large phase lead introduced by the notch filter, high-pass filter (HPF), and compensation filter. All filter parameters remain the same, comprising a second-order high-pass filter with a cutoff frequency of 4 Hz, a notch filter with a center frequency of 3 Hz and a bandwidth of 4 Hz. Modal experiments are conducted for both horizontal and vertical mounting of the actuator. The experiments are carried out sequentially as before, starting with testing the strategy solely with . If this proves successful, the experiments proceed to include , and , as illustrated in Figure 10 and Figure 11.
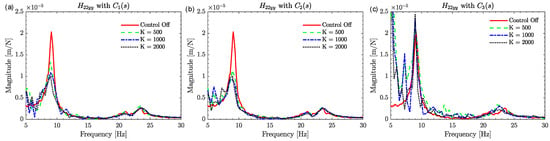
Figure 10.
Direct FRFs at location 2 with active control off and on, and with different compensation filters. (a) with , (b) with , (c) with . Horizontal mounting of actuator.
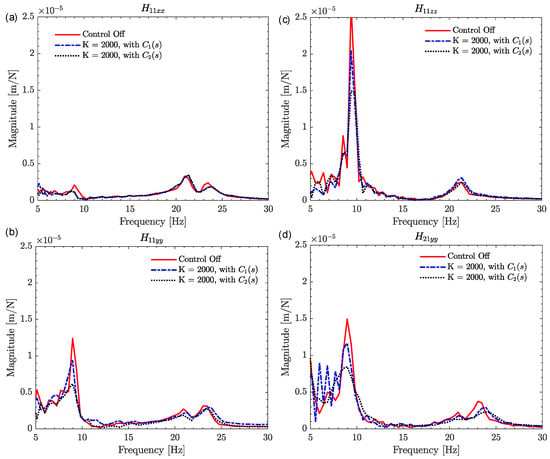
Figure 11.
Direct FRFs at the tool tip and cross FRF between tool tip and AML with active control off and on, and with different compensation filters. (a) , (b) , (c) , (d) . Horizontal mounting of actuator at position 3.
Figure 10 clearly demonstrates that compensators 1 and 2 effectively suppress the robot’s structural mode at different control gains, resulting in approximately 100% improvement in dynamic stiffness in both cases. However, compensator 3 is not as effective due to its introduction of a large positive phase at the robot’s eigenfrequency, rendering it ineffective. By utilizing and , the damping improvement in the system reaches saturation due to the predetermined 36 N active damping force acting as a saturation level for the actuator [18,28]. Since and provide damping improvement, modal experiments with active damping are performed for the direct FRF at the tool center point (TCP) in the X-, Y-, and Z-directions at K = 2000 Ns/m. These FRFs are directly linked to the minimum stability limit of the cutting process [8]. Furthermore, experiments are also conducted for the cross FRF between the TCP and AML, as presented in Figure 11d.
Figure 11 indicates that compensator 2 performs better than compensator 1 in suppressing robot mode vibrations at the TCP when using the same control gain. This is because compensator 2 has a smaller phase lead and is further compensated by a low-pass filter. Therefore, when aiming to effectively dampen low-frequency robot structural modes in the horizontal position of the actuator, compensator 2 is preferred. Since the actuator is mounted in the Y-direction, active damping is most effective in the same direction, resulting in a maximum improvement of approximately 100% in dynamic stiffness, as listed in Table 3.

Table 3.
Percentage improvement in dynamic stiffness with horizontal mounting of actuator.
Figure 12 depicts the experimental setup for active damping of robot structural vibration in the vertical mounting configuration of the actuator. To achieve the vertical position of the actuator, the tool center point (TCP) at position 3 is rotated 90° counterclockwise about the X-axis. The procedure for modal experiments with active damping in this configuration follows the same methodology as those reported for the horizontal mounting of the actuator.

Figure 12.
Experimental condition for vertical mounting of actuator.
In the case of the vertical mounting configuration, the actuator is oriented in the Z-direction. Hence, Figure 13 shows the direct frequency response functions (FRFs) in the Z-direction () at the actuator mounting location (AML) for various compensation filters and control gains.
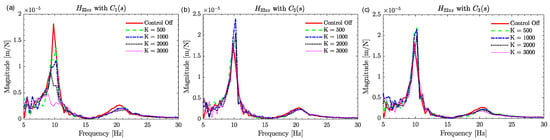
Figure 13.
Direct FRFs at location 2 with active control off and on, and with different compensation filters. (a) with , (b) with , (c) with . Vertical mounting of actuator.
It is evident from Figure 13 that compensator 1 outperforms compensators 2 and 3, achieving the highest damping with an improvement of approximately 277%. The damping of the robot structure increases with higher control gains. One reason for the effectiveness of compensator 1 is that the eigenfrequency of the actuator in the vertical mounting configuration is 14 Hz, while the dominant robot mode is at 9.8 Hz. The combined phase lead provided by the actuator and compensator 1 is negligible, and the phase lead provided by the notch filter and high-pass filter is approximately compensated by the low-pass filter. The direct and cross FRFs at the TCP and the AML with compensator 1 at a control gain of 2000 Ns/m are also tested, as shown in Figure 14, and the percentage improvement in dynamic stiffness is tabulated in Table 4.
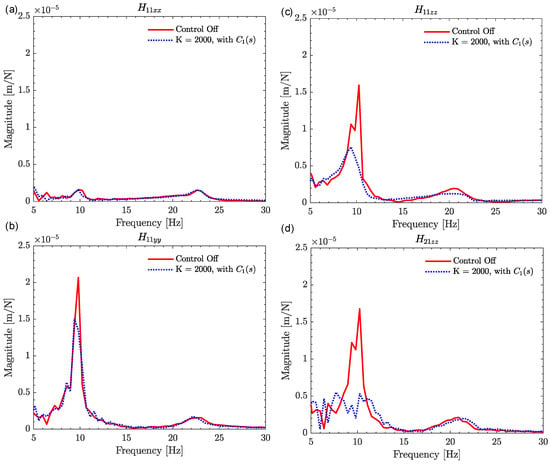
Figure 14.
Direct FRFs at the tool tip and cross FRF between tool tip and AML with active control off and on. (a) , (b) , (c) , (d) . Vertical mounting of actuator.

Table 4.
%age improvement in dynamic stiffness with vertical mounting of actuator.
It is clear from Figure 14 and Table 4 that the active damping effect is more prominent in the Z-direction, which is expected as the actuator is mounted in the Z-direction, applying vertical forces. There is also a slight damping effect achieved in the Y-direction (37.31%). Interestingly, excitation at the AML has a significant impact on suppressing vibrations at the TCP in the Z-direction ( and ), resulting in a 214% and 107% improvement in the dynamic stiffness of the robot structure, respectively.
7. Conclusions
This work presents a methodology to suppress the low-frequency structural modes of a robotic milling machine using a structurally integrated inertial actuator. Preliminary modal experiments revealed that among the various modes, the low-frequency modes were the most dominant. The dynamic characterization of the inertial actuator demonstrated that its dynamics change with different mounting configurations, an observation not previously reported in the literature. The model parameters of the actuator in both horizontal and vertical configurations were obtained, and they matched well with the measured actuator dynamics. These models will be valuable to the research community for future investigations.
The novel approach of using an inertial actuator with a compensation filter to suppress low-frequency robot modes has not been discussed before in the literature. Three designs of compensation filters for the inertial actuator are presented. When combined with other standard filters, these designs effectively suppress the low-frequency modes of the robotic milling machine, resulting in a maximum improvement in dynamic stiffness of approximately 100% in the horizontal configuration and approximately 214% in the vertical configuration of the actuator. This increase in dynamic stiffness will proportionately enhance the productivity of the robotic milling machine.
The planned future investigation includes robotic milling experiments with the designed active control parameters. The current work opens several opportunities for future research, such as experimentally testing the designed compensator at different robot postures. Furthermore, developing a more robust data-driven compensation filter to effectively suppress robot modes across various poses is a promising direction for enhancing the performance and stability of robotic milling systems.
Author Contributions
Conceptualization, G.N.S.; methodology, G.N.S. and A.O.; software, G.N.S.; validation, G.N.S.; formal analysis, G.N.S.; investigation, G.N.S. and A.O.; resources, A.O. and S.I.; data curation, G.N.S.; writing—original draft preparation, G.N.S.; writing—review and editing, G.N.S. and A.O.; visualization, G.N.S.; supervision, A.O. and S.I.; funding acquisition, G.N.S., A.O. and S.I. All authors have read and agreed to the published version of the manuscript.
Funding
The first author of this paper would like to express sincere gratitude for the support received from the IGSTC Post-Doctoral Industrial Fellowship (PDIF)—2021.
Data Availability Statement
Data will be shared on request basis.
Acknowledgments
The research presented in this paper was conducted exclusively at the Fraunhofer Institute for Machine Tools and Forming Technology, IWU, Germany. The first author greatly acknowledges the institute.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Verl, A.; Valente, A.; Melkote, S.; Brecher, C.; Ozturk, E.; Tunc, L.T. Robots in machining. CIRP Ann. 2019, 68, 799–822. [Google Scholar] [CrossRef]
- Wang, W.; Guo, Q.; Yang, Z.; Jiang, Y.; Xu, J. A state-of-the-art review on robotic milling of complex parts with high efficiency and precision. Robot. Comput. Manuf. 2022, 79, 102436. [Google Scholar] [CrossRef]
- González, M.; Rodríguez, A.; López-Saratxaga, U.; Pereira, O.; de Lacalle, L.N.L.; González, M.; Rodríguez, A.; López-Saratxaga, U.; Pereira, O.; de Lacalle, L.N.L. Adaptive edge finishing process on distorted features through robot-assisted computer vision. J. Manuf. Syst. 2024, 74, 41–54. [Google Scholar] [CrossRef]
- Rodríguez, A.; González, M.; Pereira, O.; de Lacalle, L.N.L.; Esparta, M. Edge finishing of large turbine casings using defined multi-edge and abrasive tools in automated cells. Int. J. Adv. Manuf. Technol. 2023, 124, 3149–3159. [Google Scholar] [CrossRef]
- Yuan, L.; Pan, Z.; Ding, D.; Sun, S.; Li, W. A Review on Chatter in Robotic Machining Process Regarding Both Regenerative and Mode Coupling Mechanism. IEEE/ASME Trans. Mechatron. 2018, 23, 2240–2251. [Google Scholar] [CrossRef]
- Wu, J.; Tang, X.; Peng, F.; Yan, R.; Xin, S. A novel mode coupling mechanism for predicting low-frequency chatter in robotic milling by providing a vibration feedback perspective. Mech. Syst. Signal Process. 2024, 216, 111424. [Google Scholar] [CrossRef]
- Gienke, O.; Pan, Z.; Yuan, L.; Lepper, T.; Van Duin, S. Mode coupling chatter prediction and avoidance in robotic machining process. Int. J. Adv. Manuf. Technol. 2019, 104, 2103–2116. [Google Scholar] [CrossRef]
- Cordes, M.; Hintze, W.; Altintas, Y. Chatter stability in robotic milling. Robot. Comput. Manuf. 2019, 55, 11–18. [Google Scholar] [CrossRef]
- Xin, S.; Tang, X.; Wu, J.; Peng, F.; Yan, R.; Yang, W. Investigation of the low-frequency chatter in robotic milling. Int. J. Mach. Tools Manuf. 2023, 190, 104048. [Google Scholar] [CrossRef]
- Swan, R.; Penney, J.; Corson, G.; Nazario, J.; Schmitz, T. Surface location error in robotic milling: Effect of combined low frequency and high frequency vibration modes. CIRP J. Manuf. Sci. Technol. 2024, 49, 203–215. [Google Scholar] [CrossRef]
- Cen, L.; Melkote, S.N. CCT-based mode coupling chatter avoidance in robotic milling. J. Manuf. Process. 2017, 29, 50–61. [Google Scholar] [CrossRef]
- Xin, S.; Peng, F.; Chen, C.; Tang, X.; Yan, R.; Li, Z.; Wu, J. Chip wave phase difference analysis of robotic milling and chatter dominant mode research. Int. J. Adv. Manuf. Technol. 2022, 122, 1431–1455. [Google Scholar] [CrossRef]
- Vieler, H.; Karim, A.; Lechler, A. Drive based damping for robots with secondary encoders. Robot. Comput. Manuf. 2017, 47, 117–122. [Google Scholar] [CrossRef]
- Chen, F.; Zhao, H. Design of eddy current dampers for vibration suppression in robotic milling. Adv. Mech. Eng. 2018, 10, 1687814018814075. [Google Scholar] [CrossRef]
- Wang, Z.; Keogh, P. Active vibration control for robotic machining. ASME Int. Mech. Eng. Congr. Expo. 2017, 58356, V002T02A079. [Google Scholar]
- Nguyen, V.; Johnson, J.; Melkote, S. Active vibration suppression in robotic milling using optimal control. Int. J. Mach. Tools Manuf. 2020, 152, 103541. [Google Scholar] [CrossRef]
- Guo, K.; Zhang, Y.; Sun, J. Towards stable milling: Principle and application of active contact robotic milling. Int. J. Mach. Tools Manuf. 2022, 182, 103952. [Google Scholar] [CrossRef]
- Ozsoy, M.; Sims, N.D.; Ozturk, E. Robotically assisted active vibration control in milling: A feasibility study. Mech. Syst. Signal Process. 2022, 177, 109152. [Google Scholar] [CrossRef]
- Ozsoy, M.; Sims, N.D.; Ozturk, E. Actuator Saturation during Active Vibration Control of Milling. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4853204 (accessed on 24 July 2024).
- Kim, T.-H.; Noe, S.-H.; Choi, Y.-M.; Lee, H.-J. Vibration-Damped Tool Holders in Industrial Robotic Machining Systems. Int. J. Precis. Eng. Manuf. 2023, 24, 1535–1548. [Google Scholar] [CrossRef]
- Wu, J.; Tang, X.; Xin, S.; Wang, C.; Peng, F.; Yan, R.; Mao, X. Low-frequency chatter suppression using tuned mass damper in robotic milling. MM Sci. J. 2023, 2023, 6824–6829. [Google Scholar] [CrossRef]
- Yuan, L.; Sun, S.; Pan, Z.; Ding, D.; Gienke, O.; Li, W. Mode coupling chatter suppression for robotic machining using semi-active magnetorheological elastomers absorber. Mech. Syst. Signal Process. 2019, 117, 221–237. [Google Scholar] [CrossRef]
- Zhao, W.; Tian, W.; Liu, P.; Li, B. Experimental study on vibration suppression for robotic milling using an MRE absorber. Smart Mater. Struct. 2023, 32, 105009. [Google Scholar] [CrossRef]
- Zhao, W.; Li, B.; Tian, W.; Liu, P.; Liao, W. Magnetorheological elastomer absorber-based chatter suppression in robotic milling. Robot. Comput. Manuf. 2024, 88, 102740. [Google Scholar] [CrossRef]
- Xin, S.; Peng, F.; Tang, X.; Wu, J.; Sun, Z.; Yan, R. A joint wearable structural reinforcing device for vibration suppression in robotic milling. MM Sci. J. 2023, 2023, 6989–6995. [Google Scholar] [CrossRef]
- Xin, S.; Tang, X.; Wu, J.; Peng, F.; Yan, R.; Sun, K. Low-frequency chatter suppression in robotic milling using Magnetorheological Joint Damper (MRJD). Chin. J. Aeronaut. 2024. [Google Scholar] [CrossRef]
- Sahu, G.N.; Deora, P.; Law, M.; Wahi, P. Adaptive Model-Free Gain Tuning for Active Damping of Machine Tool Vibrations. J. Vib. Eng. Technol. 2022, 10, 2799–2808. [Google Scholar] [CrossRef]
- Sahu, G.; Vashisht, S.; Wahi, P.; Law, M. Validation of a hardware-in-the-loop simulator for investigating and actively damping regenerative chatter in orthogonal cutting. CIRP J. Manuf. Sci. Technol. 2020, 29, 115–129. [Google Scholar] [CrossRef]
- Operation and Maintenance Manual, 45N Active Damping Devices; Micromega Dynamics: Fernelmont, Belgium, 2017.
- Abele, E.; Pfeiffer, G.; Jalizi, B.; Bretz, A. Simulation and development of an active damper with robust μ-control for a machine tool with a gantry portal. Prod. Eng. 2016, 10, 519–528. [Google Scholar] [CrossRef]
- Bilbao-Guillerna, A.; Azpeitia, I.; Luyckx, S.; Loix, N.; Munoa, J. Low Frequency Chatter Suppression using an Inertial Actuator. In Proceedings of the International Conference on High Speed Machining, Niigata, Japan, 15–16 August 2012. [Google Scholar]
- Sahu, N.; Law, M. Hardware-in-the-loop simulator for emulation and active control of chatter. HardwareX 2022, 11, e00273. [Google Scholar] [CrossRef] [PubMed]
- Altintas, Y. Manufacturing Automation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Preumont, A. Vibration Control of Active Structures, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mancisidor, I.; Munoa, J.; Barcena, R.; Beudaert, X.; Zatarain, M. Coupled model for simulating active inertial actuators in milling processes. Int. J. Adv. Manuf. Technol. 2015, 77, 581–595. [Google Scholar] [CrossRef]
- Magnevall, M.; Lundblad, M.; Ahlin, K.; Broman, G. High frequency measurements of cutting forces in milling by inverse filtering. Mach. Sci. Technol. 2012, 16, 487–500. [Google Scholar] [CrossRef]
- Sahu, G.; Jain, P.; Wahi, P.; Law, M. Emulating bistabilities in turning to devise gain tuning strategies to actively damp them using a hardware-in-the-loop simulator. CIRP J. Manuf. Sci. Technol. 2020, 32, 120–131. [Google Scholar] [CrossRef]
- Mancisidor, I.; Beudaert, X.; Etxebarria, A.; Barcena, R.; Munoa, J.; Jugo, J. Hardware-in-the-loop simulator for stability study in orthogonal cutting. Control Eng. Pract. 2015, 44, 31–44. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).