Stability of Micro-Milling Tool Considering Tool Breakage
Abstract
1. Introduction
2. Methodology
2.1. Methods for Obtaining FRFs of Micro-Milling Cutters
2.2. Method for Predicting Tool Breakage
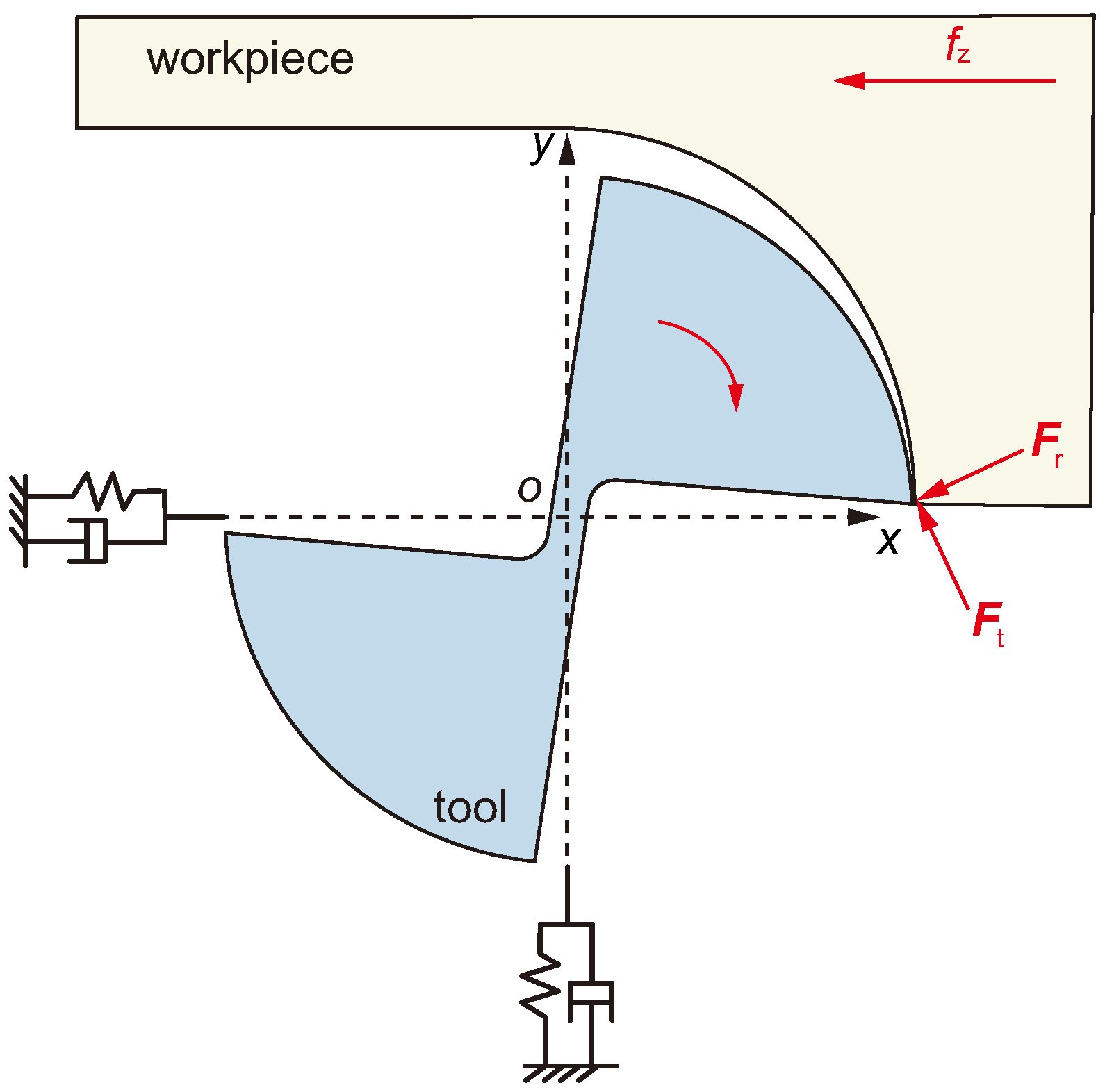
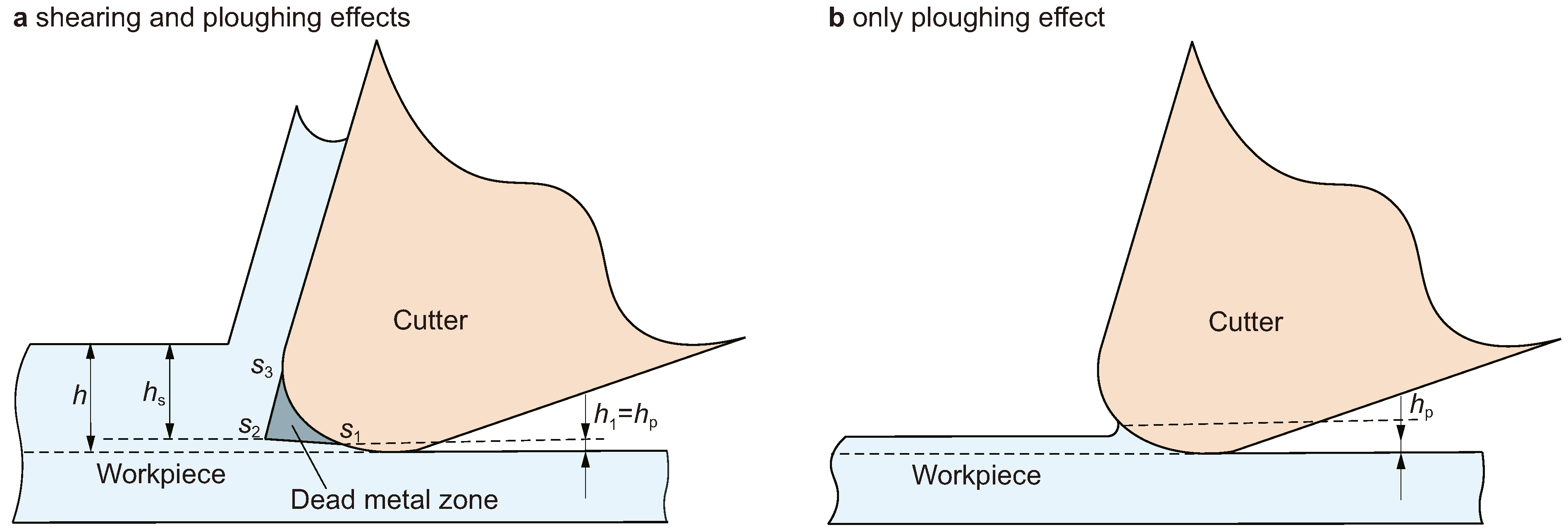
2.2.1. Micro-Milling Force Model
- If h >
- If h ≤
2.2.2. Calculation of the Maximum Bending Stress
2.2.3. Prediction of Stability Considering Tool Breakage
- case1If (, ) < 0.8 ∧ <(, ) ∈ (, )
- case2If (, ) ≥ 0.8 ∧ <(, ) ∈ (, )
- case3If (, ) < 0.8 ∧ ≥(, ) ∈ (, )
- case4If (, ) ≥ 0.8 ∧ ≥(, ) ∈ (, )
3. Experimental Validation
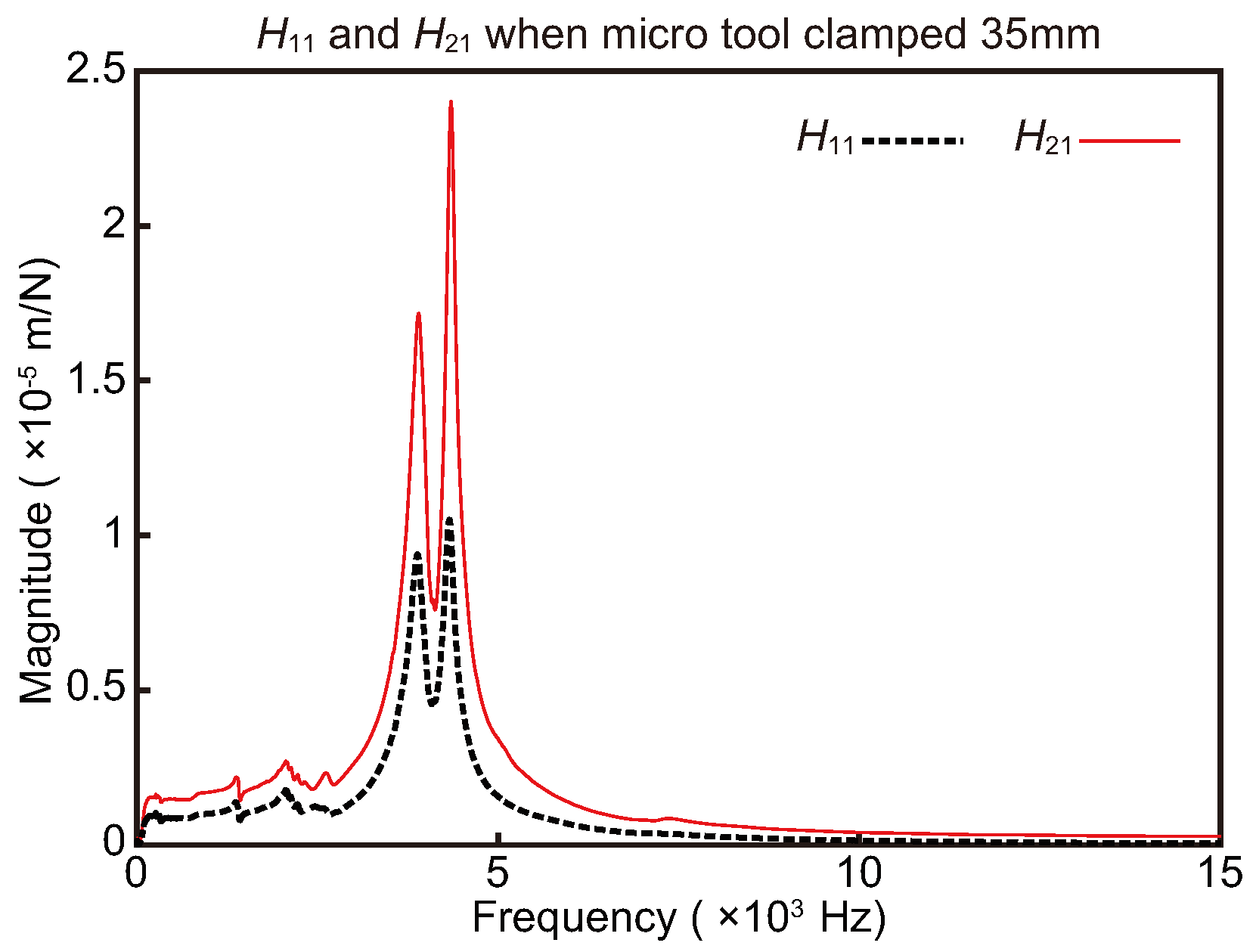
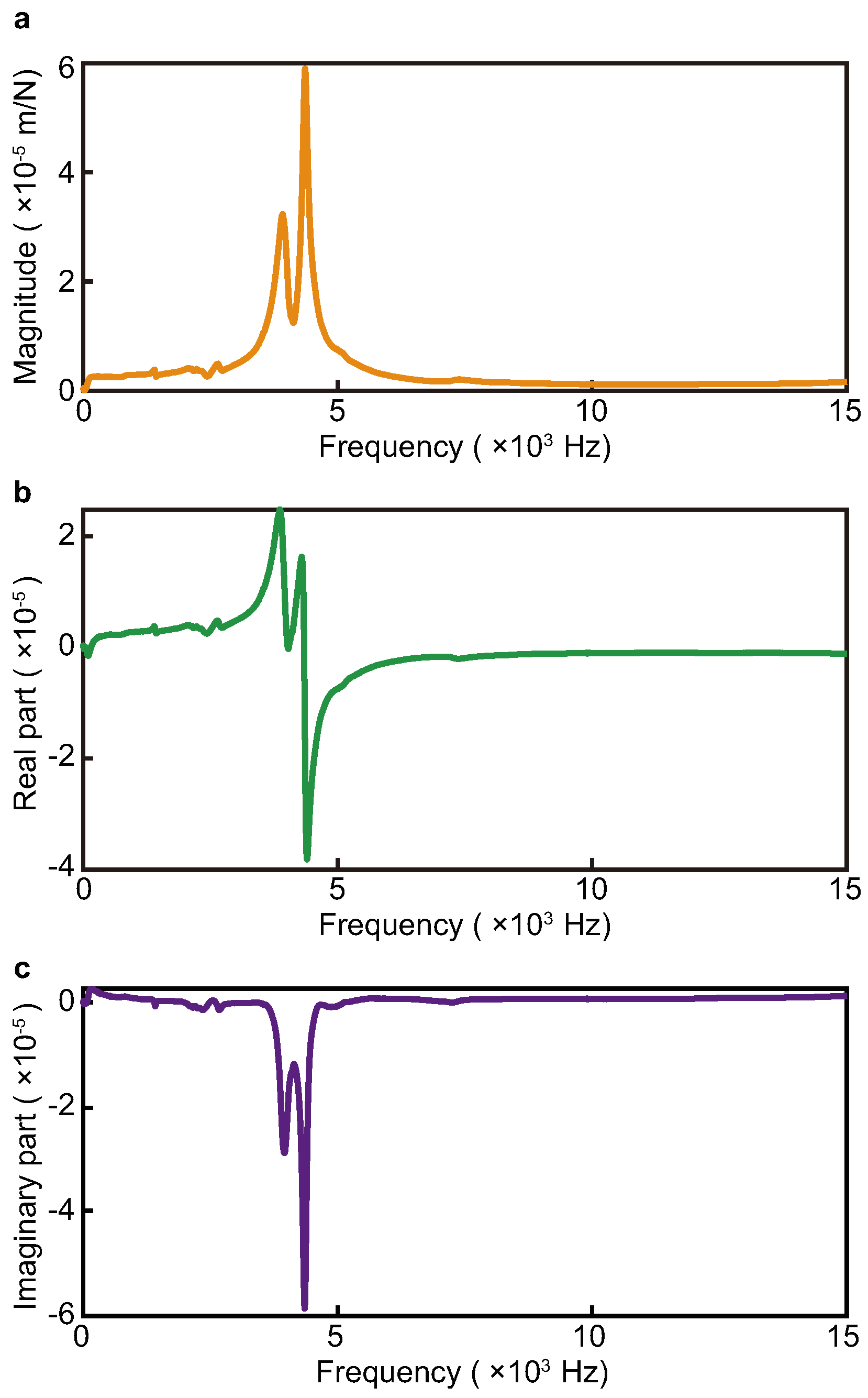
3.1. Verification of FRFs of Micro-Milling Tool
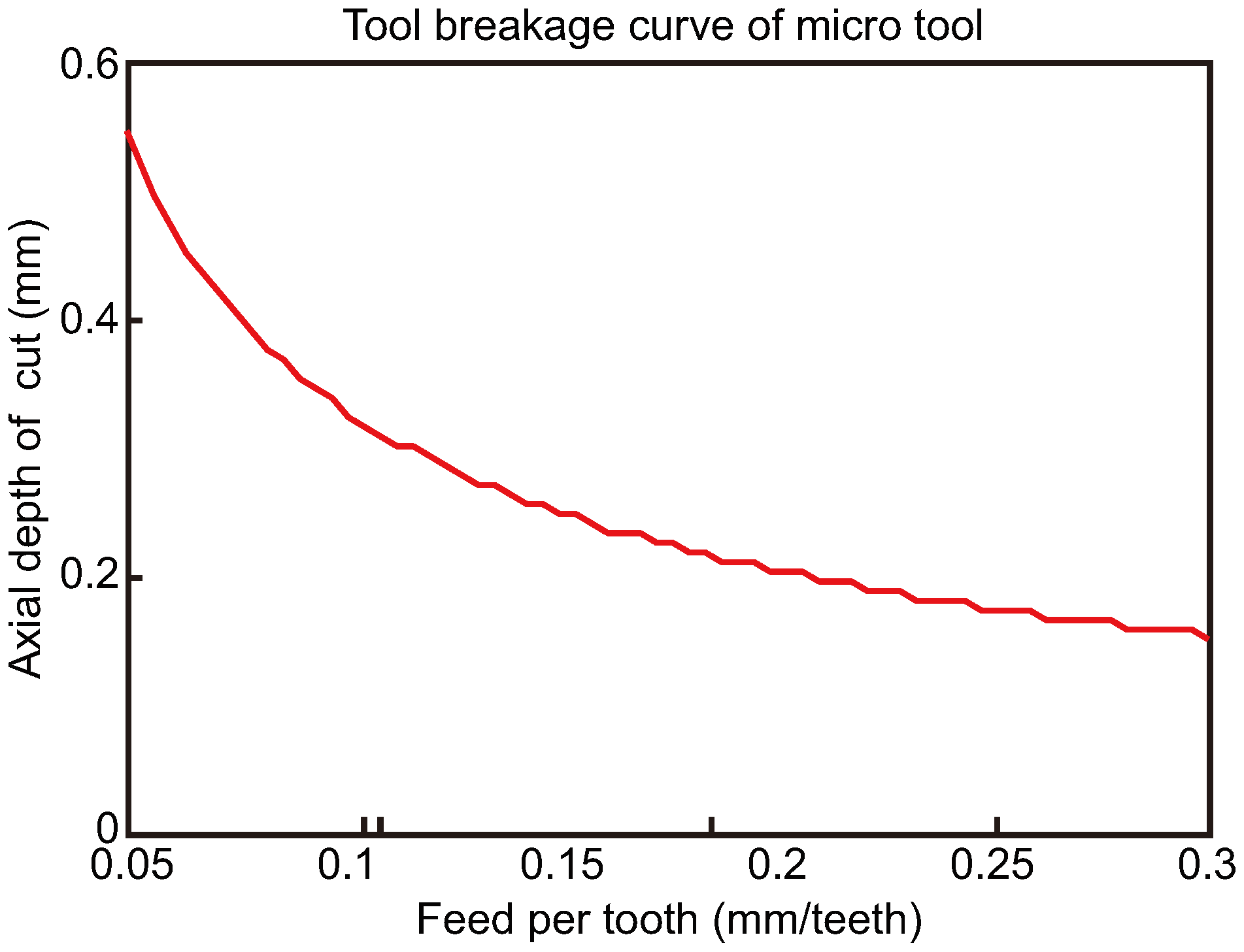
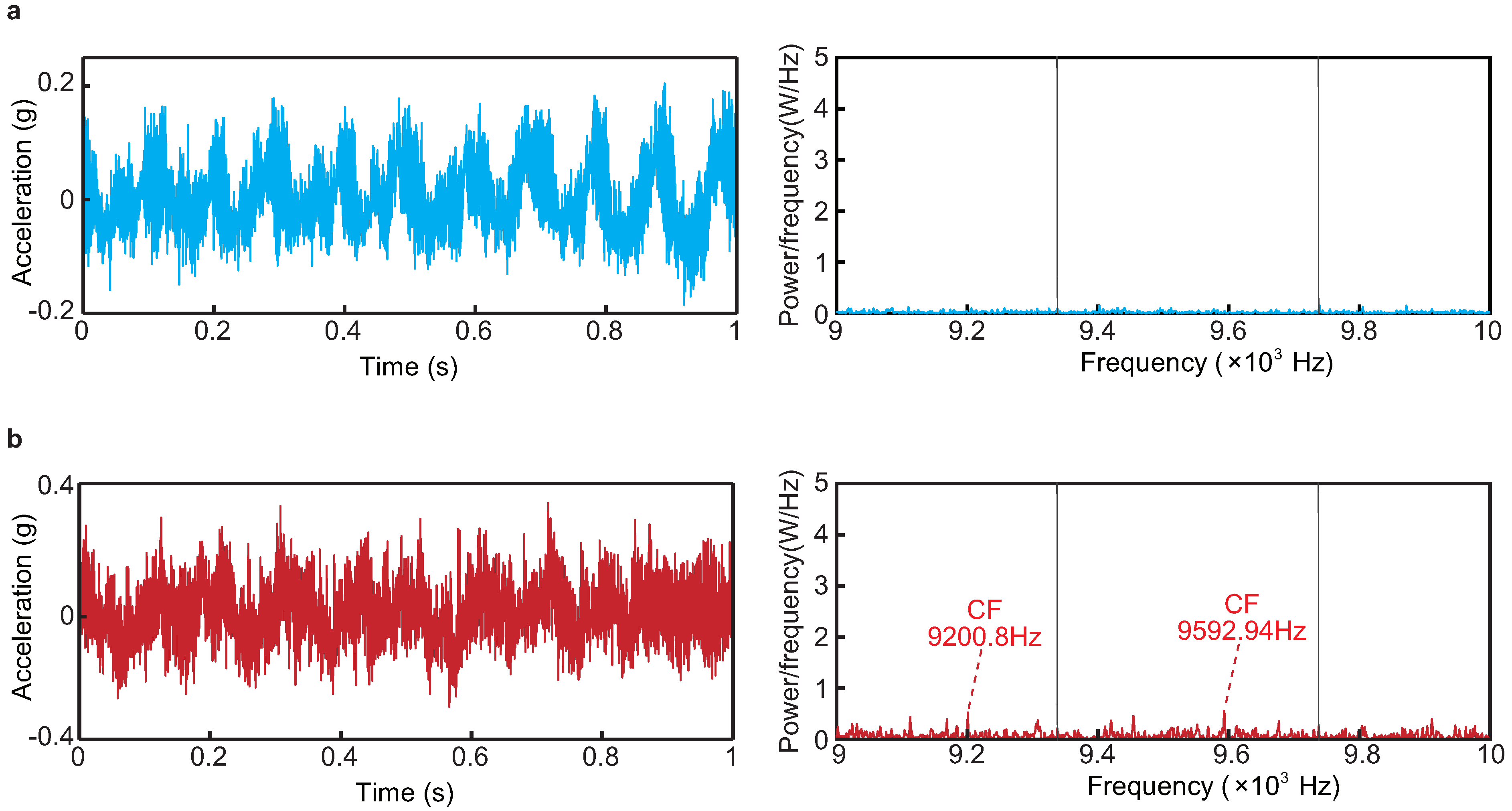
3.2. Verification of Tool Breakage
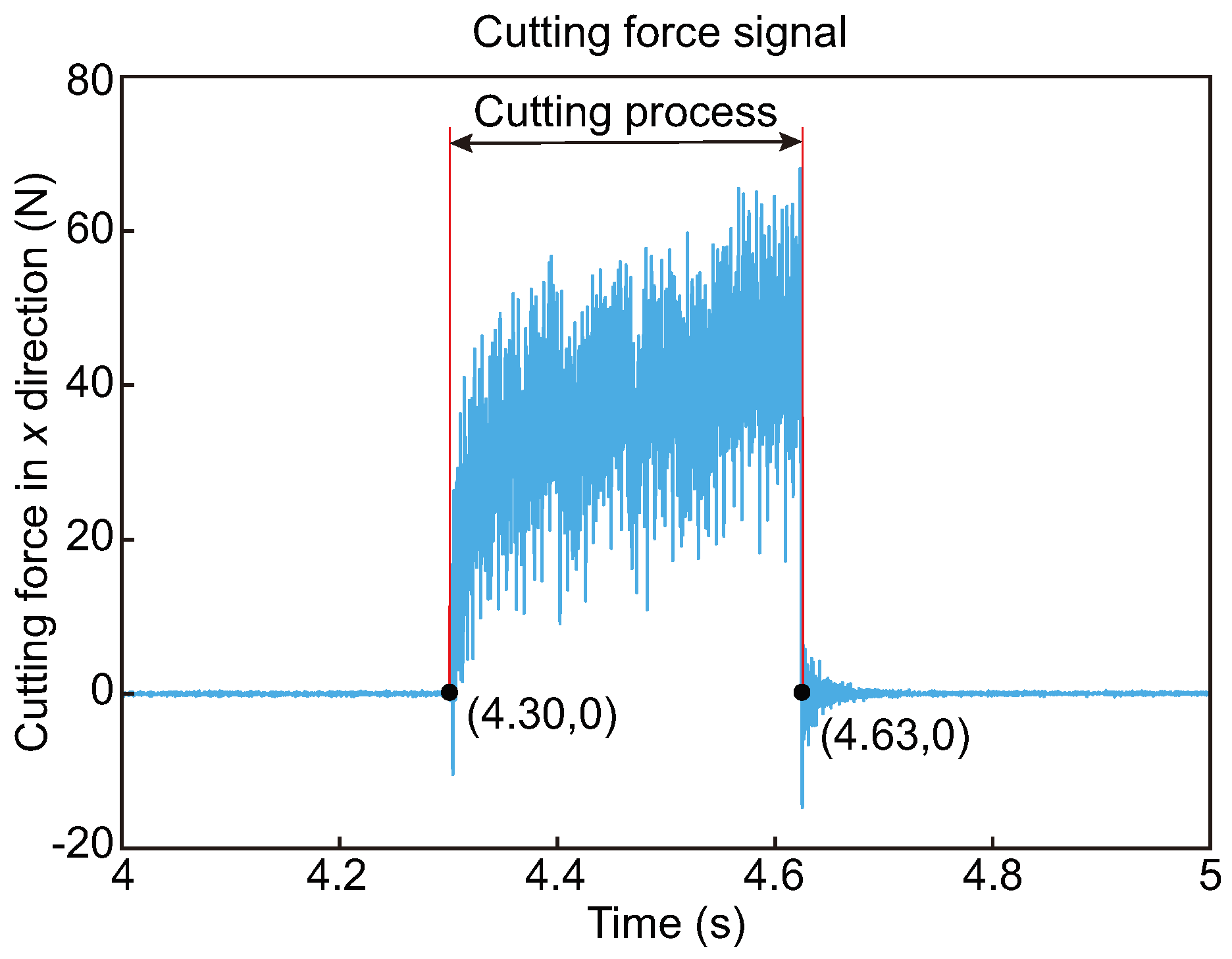
3.2.1. Determination of Ultimate Bending Stress
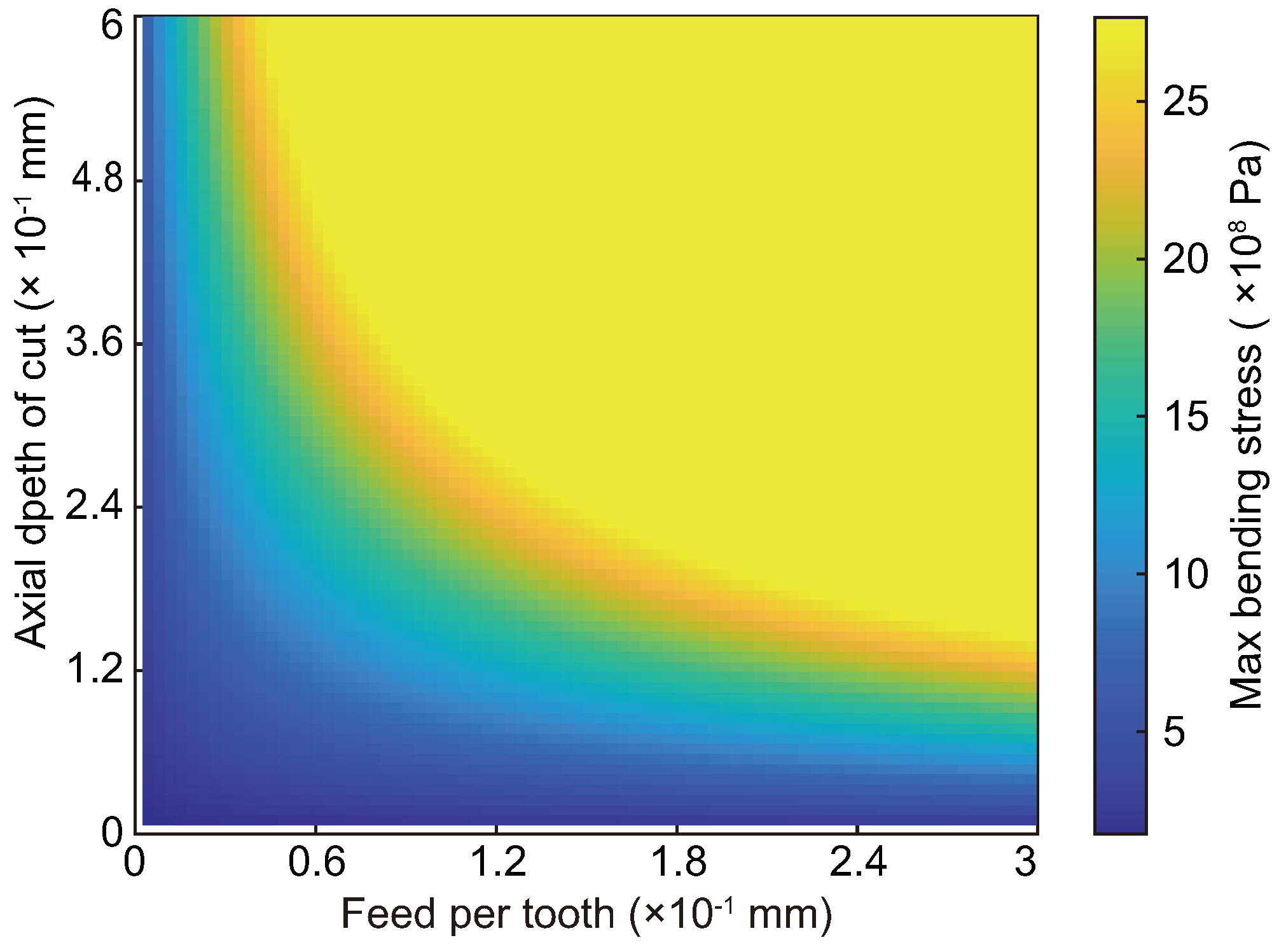
3.2.2. SLDs Considering Tool Breakage
4. Conclusions
- First, although the natural frequency of a micro-milling cutter increases rapidly with a decrease in tool overhang length, there is a large decrease in its modal mass. When the clamped length is shortened from 35 mm to 25 mm for the used tool, the first-order natural frequency increases by about 2.47 times, while the corresponding damping deceases to 0.16 times of the original value.
- Second, the breakage curve of a micro-milling cutter depends on the materials of both the workpiece and the tool. When the ratio of the axial depth of cut to tool length is large, the maximum bending stress of the tool can be approximately calculated based on a concentrated force.
- Third, after considering tool breakage, the original stable and chatter domains of SLDs are changed to four regions, i.e., stable and safe region, chatter and safe region, stable and unsafe region, and chatter and unsafe region. This implies that when planning machining processes, the stable and unsafe region needs to be removed from the stable area of SLDs in order to ensure both safe and stable micro-milling.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FRFs | Frequency response functions |
| SLDs | Stability lobe diagrams |
| RCSA | Receptance coupling substructure analysis |
| VFF-RLS | Variable forgetting factor recursive least-squares |
References
- Balazs, B.Z.; Geier, N.; Takacs, M.; Davim, J.P. A review on micro-milling: Recent advances and future trends. Int. J. Adv. Manuf. Technol. 2021, 112, 665–684. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Altintas, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–392. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Analytical Prediction of Chatter Stability in Milling—PartI: General Formulation. J. Dyn. Syst. Meas. Control. 1998, 120, 22–30. [Google Scholar] [CrossRef]
- Insperger, T.; Stepan, G. Analytical Prediction of Chatter Stability in Milling—PartI: General Formulation. J. Dyn. Syst. Meas. Control. 2004, 61, 117–141. [Google Scholar]
- Sanz-Calle, M.; Munoa, J.; Morelli, L.; Iglesias, A.; Lacalle, L.N.L.; Dombovari, Z. On the effect of radial engagement on the milling stability of modes perpendicular to the feed direction. CIRP J. Manuf. Sci. Technol. 2024, 49, 111–127. [Google Scholar] [CrossRef]
- Sanz-Calle, M.; Munoa, J.; Iglesias, A.; Lacalle, L.N.L.; Dombovari, Z. The influence of radial engagement and milling direction for thin wall machining: A semi-analytical study. Procedia CIRP 2021, 102, 180–185. [Google Scholar] [CrossRef]
- Iglesias, A.; Munoa, J.; Ciurana, J.; Dombovari, Z.; Stepan, G. Analytical expressions for chatter analysis in milling operations with one dominant mode. J. Sound Vib. 2016, 375, 403–421. [Google Scholar] [CrossRef]
- Qin, G.; Tan, Z.; Wu, Z.; Lou, W. High precision judgment method for milling stability based on Bernoulli distribution and hybrid-drive model. Mech. Syst. Signal Process. 2024, 212, 111266. [Google Scholar] [CrossRef]
- Wan, M.; Ren, Y.-Y.; Zhang, W.-H.; Yang, Y. Investigation of a cutting state-independent method for identifying in-process frequency response functions of the micro milling systeme. Mech. Syst. Signal Process. 2024, 213, 111353. [Google Scholar] [CrossRef]
- Jin, X.; Altintas, Y. Chatter Stability Model of Micro-Milling With Process Damping. J. Dyn. Syst. Meas. Control. 2013, 135, 031011. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Donalson, R.R. Predicting High-Speed Machining Dynamics by Substructure Analysis. CIRP Ann. 2000, 49, 303–308. [Google Scholar] [CrossRef]
- Park, S.S.; Altintas, Y.; Movahhedy, M. Predicting High-Speed Machining Dynamics by Substructure Analysis. Int. J. Mach. Tools Manuf. 2003, 43, 889–896. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Duncan, G.S. Three-Component Receptance Coupling Substructure Analysis for Tool Point Dynamics Prediction. Trans. ASME J. Manuf. Sci. Eng. 2005, 127, 781–790. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Powell, K.; Won, D.; Duncan, G.S.; Sawyer, W.G.; Ziegert, J.C. Shrink fit tool holder connection stiffness/damping modeling for frequency response prediction in milling. Trans. ASME J. Manuf. Sci. Eng. 2007, 47, 1368–1380. [Google Scholar] [CrossRef]
- Erturk, A.; Ozguven, H.N.; Budak, E. Analytical modeling of spindle-tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF. Trans. ASME J. Manuf. Sci. Eng. 2006, 46, 1901–1912. [Google Scholar] [CrossRef]
- Lu, X.; Jia, Z.; Liu, S.; Yang, K.; Feng, Y.; Liang, S.Y. Chatter Stability of Micro-Milling by Considering the Centrifugal Force and Gyroscopic Effect of the Spindle. Trans. ASME J. Manuf. Sci. Eng. 2019, 141, 111003. [Google Scholar] [CrossRef]
- Zhou, J.M.; Andersson, M.; Stahl, J.E. Cutting tool fracture prediction and strength evaluation by stress identification, part i: Stress model. Int. J. Mach. Tools Manuf. 1997, 37, 1691–1714. [Google Scholar] [CrossRef]
- Fang, F.Z.; Wu, H.; Liu, X.D.; Liu, Y.C.; Ng, S.T. Tool geometry study in micromachining. J. Micromech. Microeng. 2003, 13, 726. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, H.; Jia, Z.; Feng, Y.; Liang, S.Y. A New Method for the Prediction of Micro-Milling Tool Breakage. In Proceedings of the ASME 2017 12th International Manufacturing Science and Engineering Conference, Los Angeles, CA, USA, 4–8 June 2017. [Google Scholar]
- Huang, X.; Jiang, F.; Wang, Z.; Wu, X.; Huang, S.; Liu, Y.; Zhang, J.; Shi, X. A review on the balancing design of micro drills. Int. J. Adv. Manuf. Technol. 2023, 126, 4849–4871. [Google Scholar] [CrossRef]
- Uriarte, L.; Herrero, A.; Zatarain, M.; Santiso, G.; Lacalle, L.N.L.; Lamikiz, A.; Albizuri, J. Error budget and stiffness chain assessment in a micromilling machine equipped with tools less than 0.3 mm in diameter. Precis. Eng. 2007, 31, 1–12. [Google Scholar] [CrossRef]
- Uriarte, L.; Herrero, A.; Zatarain, M.; Santiso, G.; Lacalle, L.N.L.; Lamikiz, A.; Albizuri, J. Mechanistic modelling of the micro-end milling operation. In 4M 2006—Second International Conference on Multi-Material Micro Manufacture; Menz, W., Dimov, S., Fillon, B., Eds.; Elsevier: Oxford, UK, 2006; pp. 237–240. [Google Scholar]
- Wen, D.Y.; Wan, M.; Ren, Y.Y.; Zhang, W.H.; Yang, Y. Material piling up and spreading effects in the cutting processes with small feed rates. Mech. Syst. Signal Process. 2022, 171, 108839. [Google Scholar] [CrossRef]
- Li, K.; He, S.; Liu, H.; Mao, X.; Li, B.; Luo, B. Bayesian uncertainty quantification and propagation for prediction of milling stability lobe. Mech. Syst. Signal Process. 2020, 138, 106532. [Google Scholar] [CrossRef]
- Albertelli, P.; Goletti, M.; Monno, M. A new receptance coupling substructure analysis methodology to improve chatter free cutting conditions prediction. Int. J. Mach. Tools Manuf. 2013, 72, 16–24. [Google Scholar] [CrossRef]
- Ji, Y.; Bi, Q.; Zhang, S.; Wang, Y. A new receptance coupling substructure analysis methodology to predict tool tip dynamics. Int. J. Mach. Tools Manuf. 2018, 126, 18–26. [Google Scholar] [CrossRef]
- Ma, W.; Yang, Y.; Jin, X. Chatter suppression in micro-milling using shank-mounted Two-DOF tuned mass damper. Precis. Eng. 2021, 72, 144–157. [Google Scholar] [CrossRef]
- Wan, M.; Wen, D.Y.; Ma, Y.C.; Zhang, W.H. On material separation and cutting force prediction in micro milling through involving the effect of dead metal zone. Mech. Syst. Signal Process. 2019, 146, 103452. [Google Scholar] [CrossRef]
- Wan, M.; Wang, W.K.; Zhang, W.H.; Yang, Y. Chatter detection for micro milling considering environment noises without the requirement of dominant frequency. Mech. Syst. Signal Process. 2023, 199, 110451. [Google Scholar] [CrossRef]
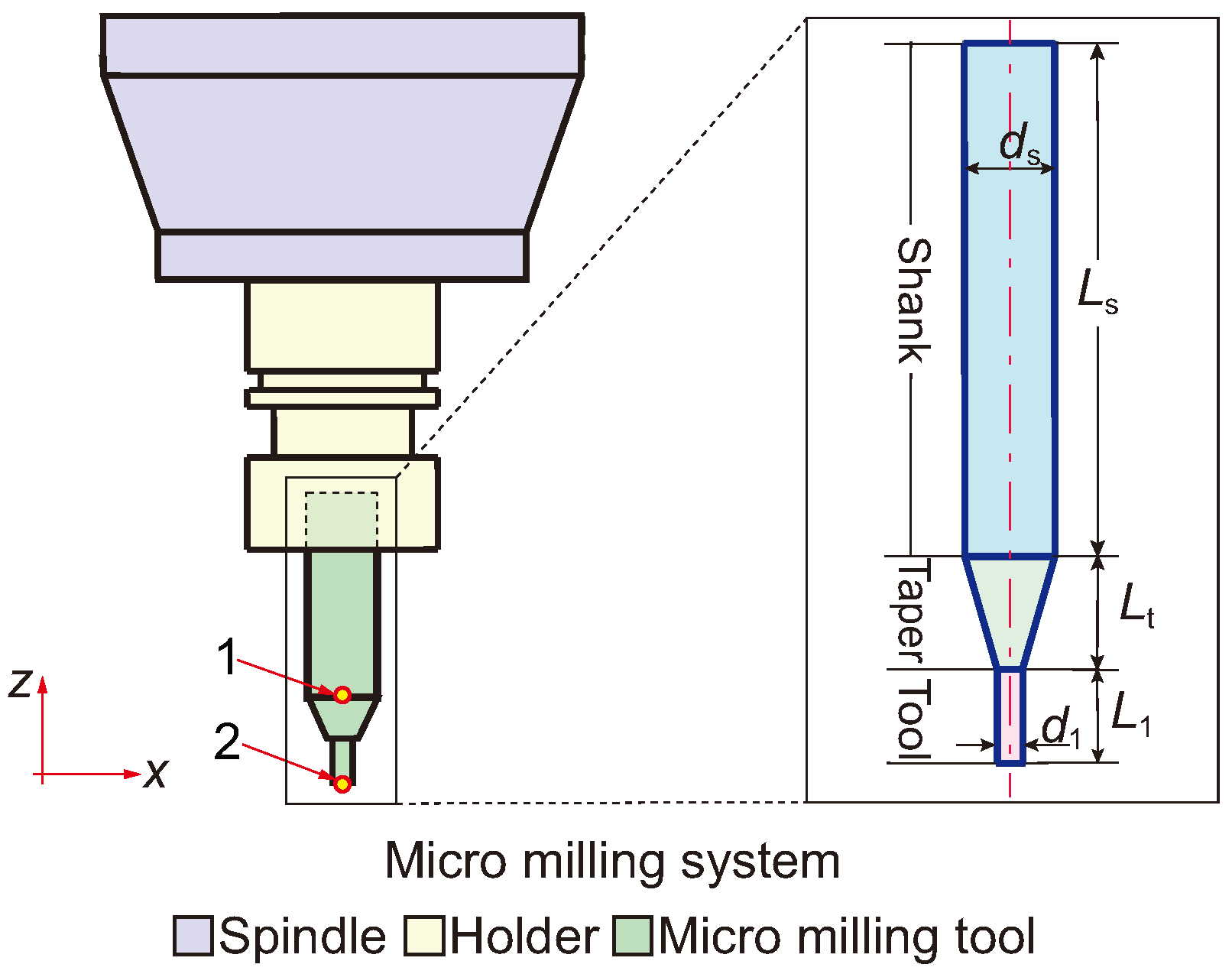






| (mm) | (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|---|
| 39 | 5 | 6 | 4 | 1 |
| Clamped Length (mm) | Order | Natural Frequency (Hz) | Modal Mass (kg) | Damping Ratio (%) |
|---|---|---|---|---|
| 35 | 1 | 3938.24 | 0.00131 | 2.36 |
| 35 | 2 | 4353.71 | 0.00098 | 1.24 |
| 25 | 1 | 9728.60 | 0.00021 | 1.48 |
| Workpiece Material | ||||||
|---|---|---|---|---|---|---|
| Al 7050-T7451 | 1182 | 0.8532 | 0.01174 | 1584 | 0.6071 | 0.2832 |
| Workpiece Material | ||||||
|---|---|---|---|---|---|---|
| Al 7050-T7451 | 851.3 | 0.6382 | 0.1023 | 402 | 0.9781 | −0.08319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.-Y.; Jia, B.-G.; Wan, M.; Tian, H. Stability of Micro-Milling Tool Considering Tool Breakage. J. Manuf. Mater. Process. 2024, 8, 122. https://doi.org/10.3390/jmmp8030122
Ren Y-Y, Jia B-G, Wan M, Tian H. Stability of Micro-Milling Tool Considering Tool Breakage. Journal of Manufacturing and Materials Processing. 2024; 8(3):122. https://doi.org/10.3390/jmmp8030122
Chicago/Turabian StyleRen, Yuan-Yuan, Bao-Guo Jia, Min Wan, and Hui Tian. 2024. "Stability of Micro-Milling Tool Considering Tool Breakage" Journal of Manufacturing and Materials Processing 8, no. 3: 122. https://doi.org/10.3390/jmmp8030122
APA StyleRen, Y.-Y., Jia, B.-G., Wan, M., & Tian, H. (2024). Stability of Micro-Milling Tool Considering Tool Breakage. Journal of Manufacturing and Materials Processing, 8(3), 122. https://doi.org/10.3390/jmmp8030122






