Particle Size Effect on Powder Packing Properties and Molten Pool Dimensions in Laser Powder Bed Fusion Simulation
Abstract
1. Introduction
2. Materials and Methods
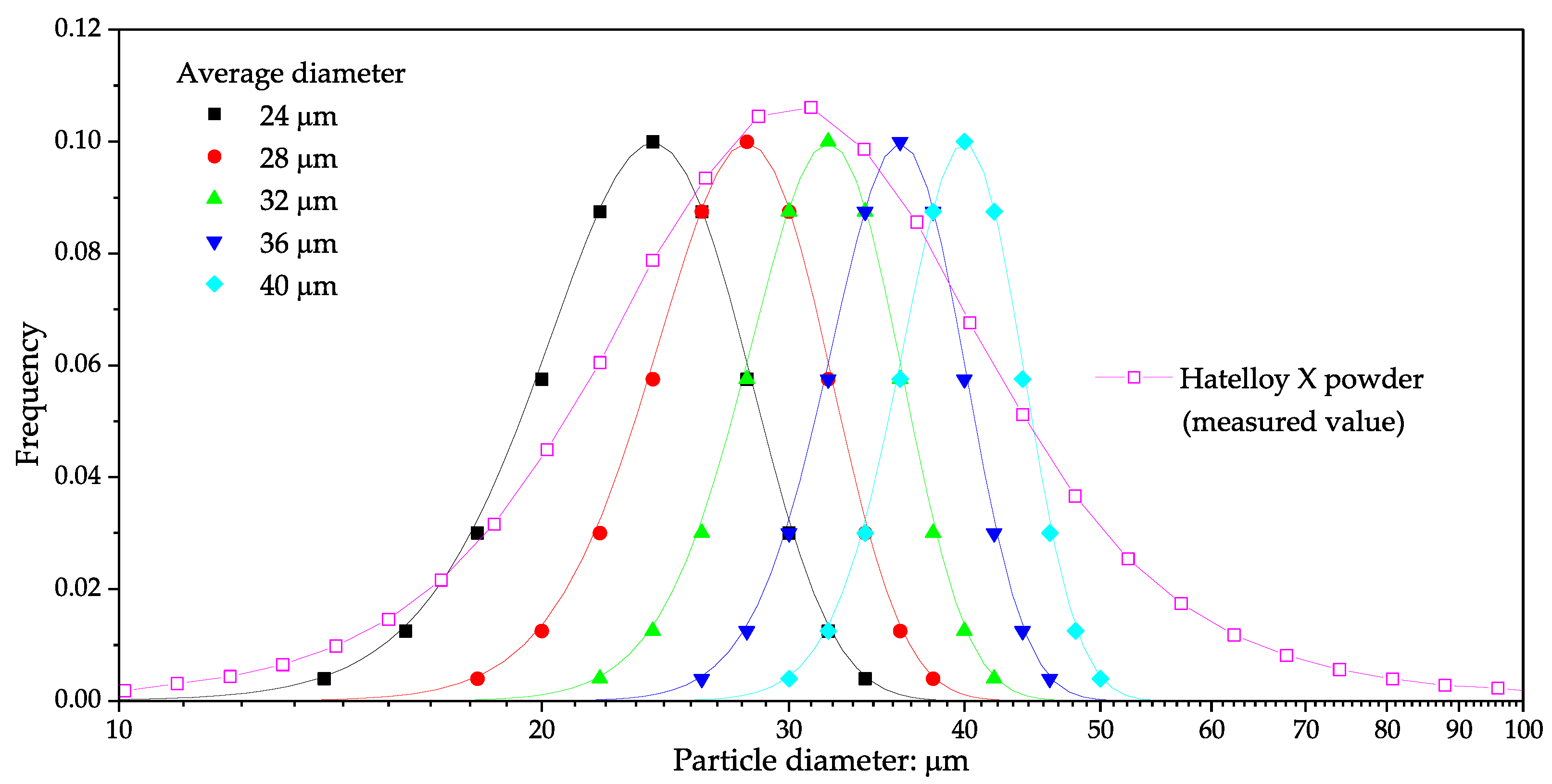
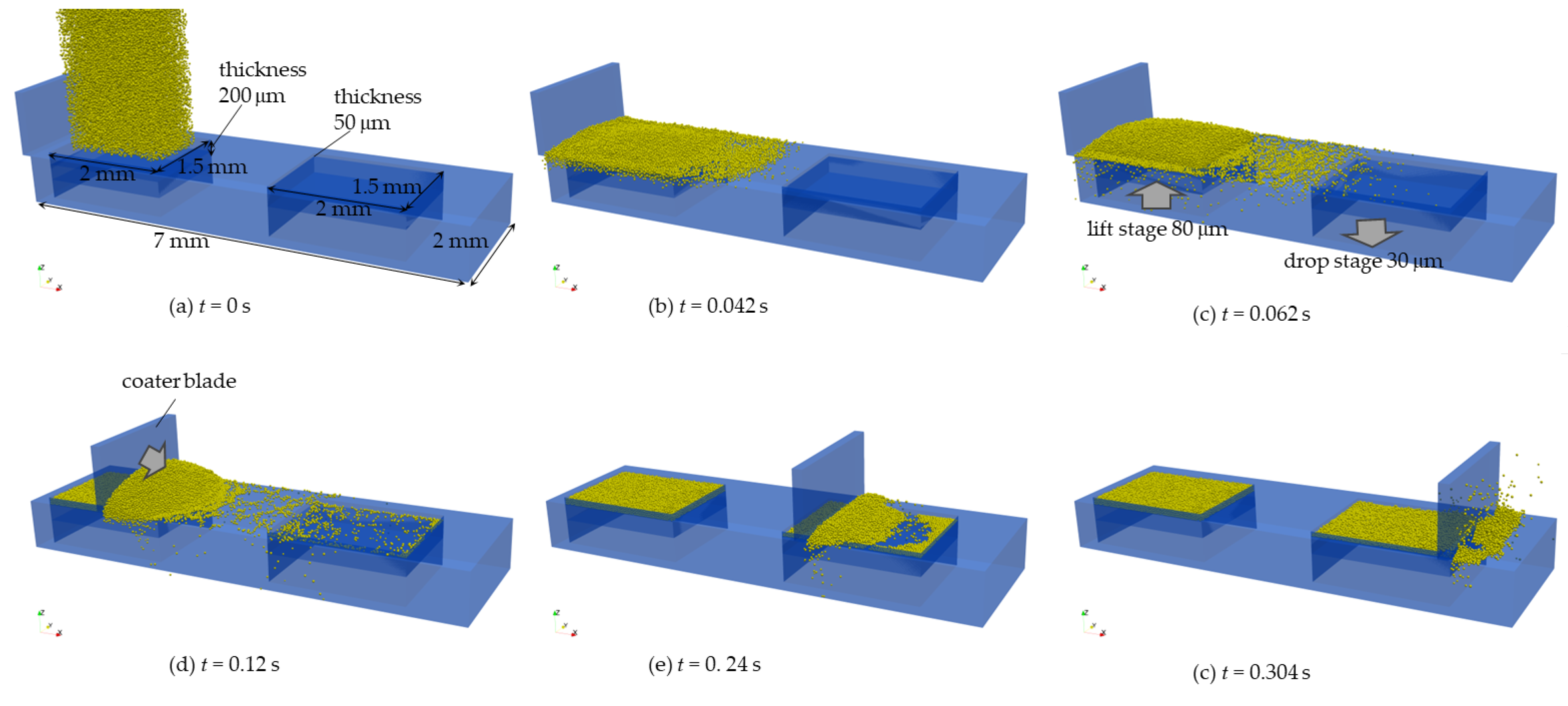
2.1. Powder Spreading Analysis
2.2. Overview of Multiphysics CFD Simulation
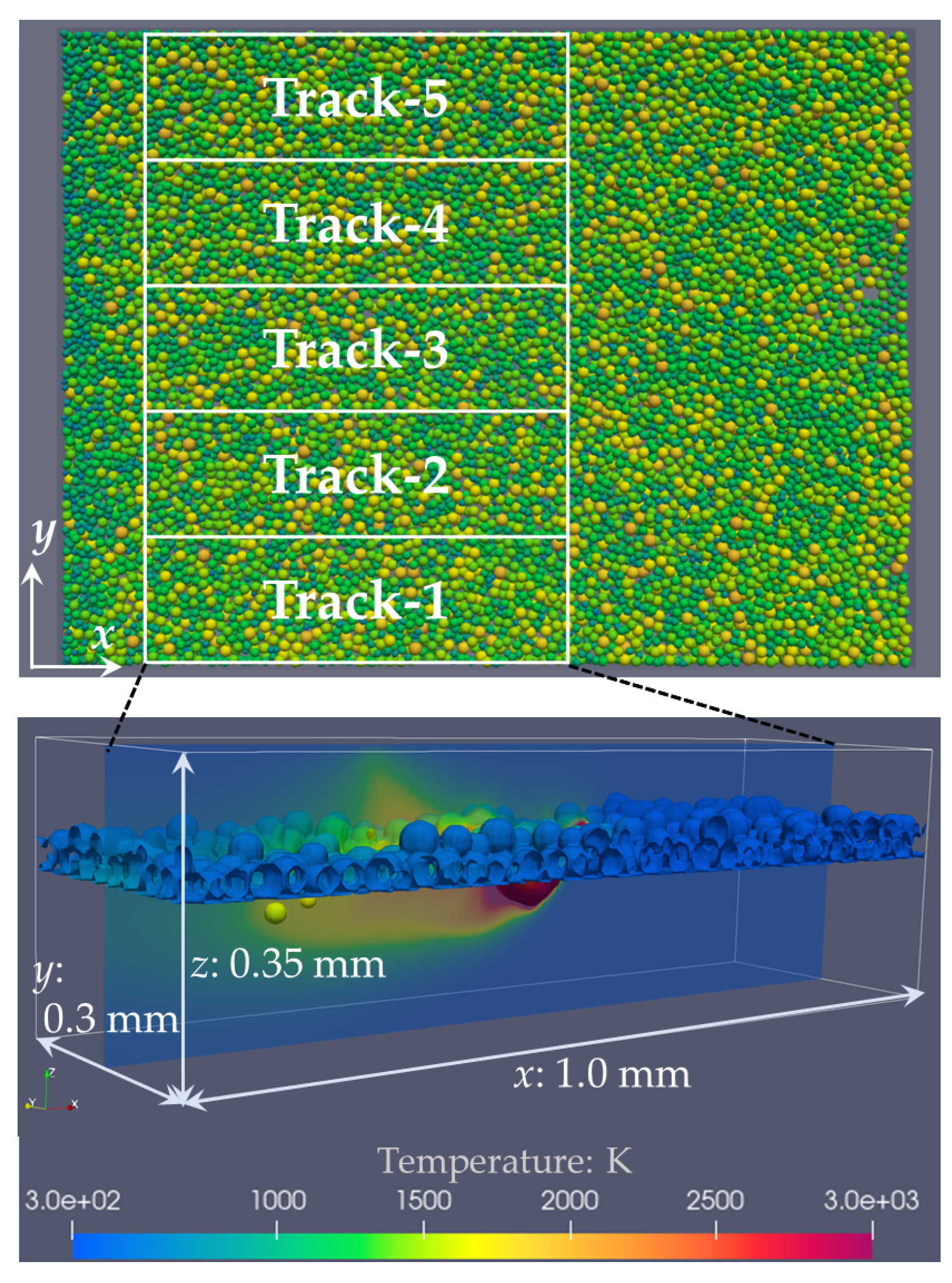
2.3. Single-Track Laser Scanning Simulations
2.4. Single-Track Laser Scanning Experiments
3. Results and Discussion
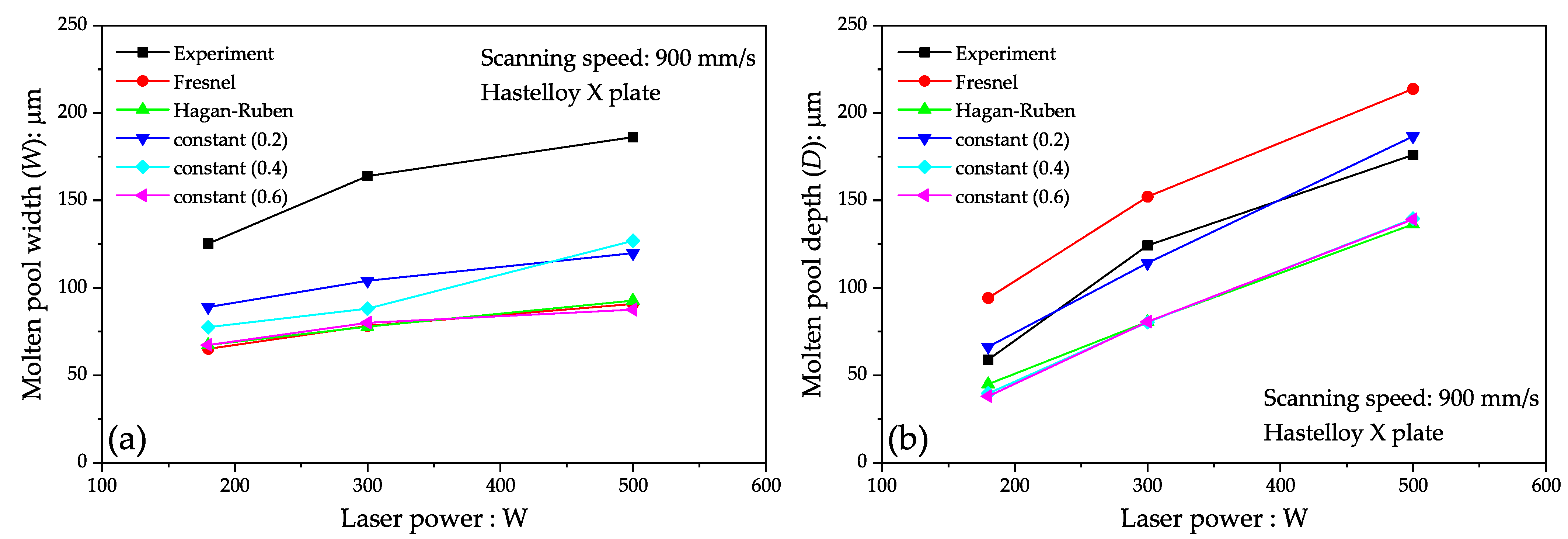
3.1. Preliminary Analysis: Experimental Validation
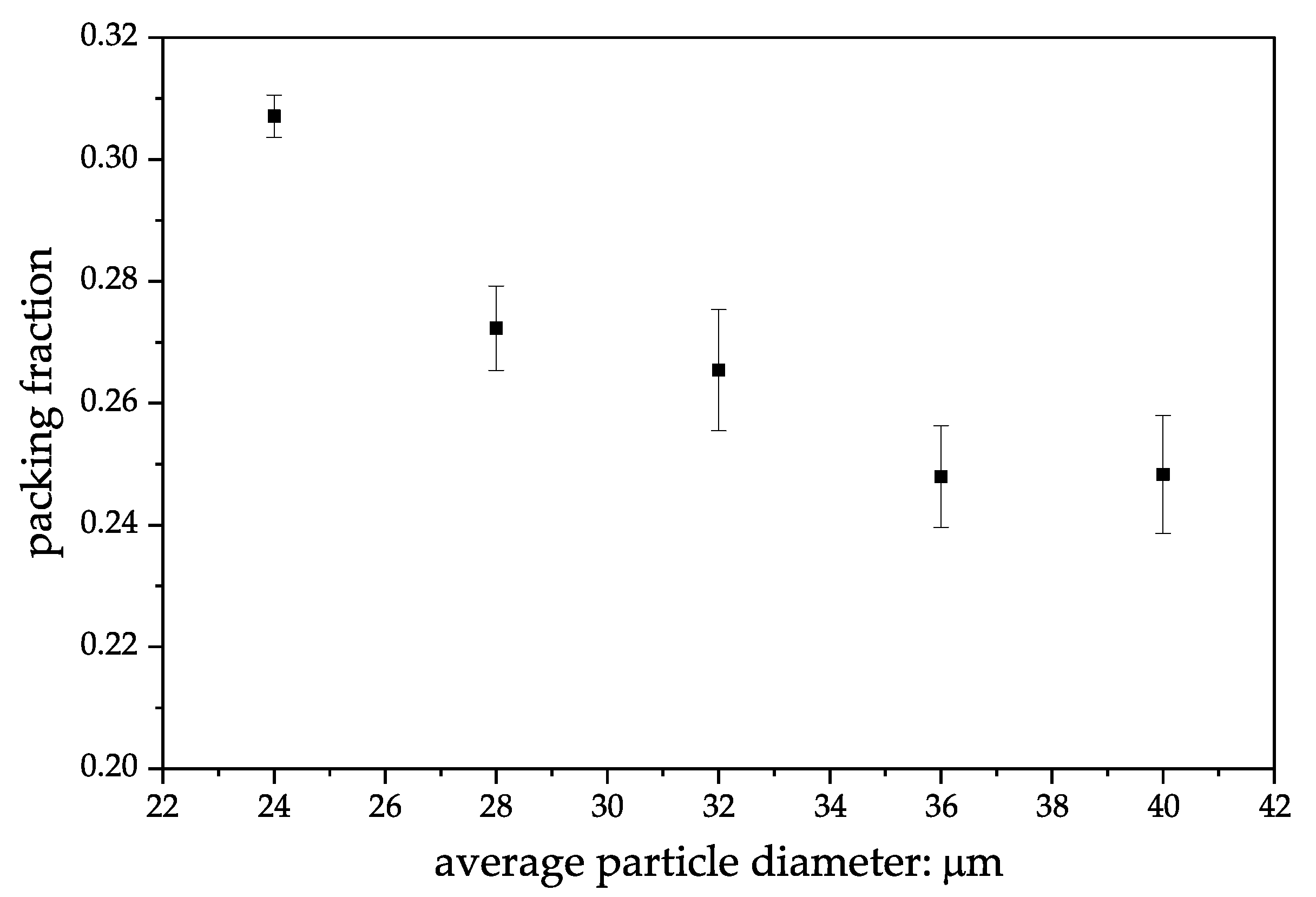
3.2. Packing Fraction of Powder Bed
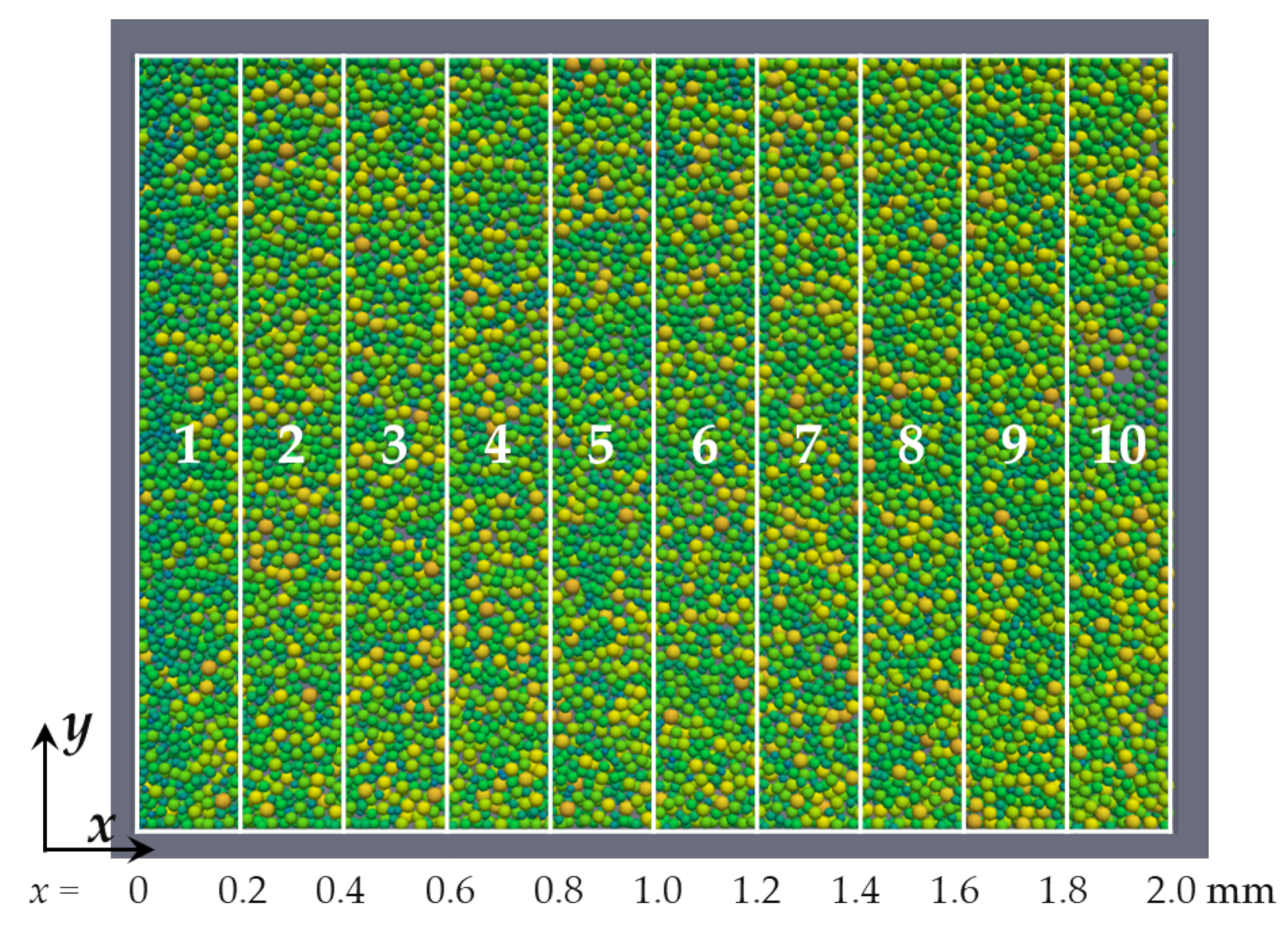
3.3. Packing Homogeneity
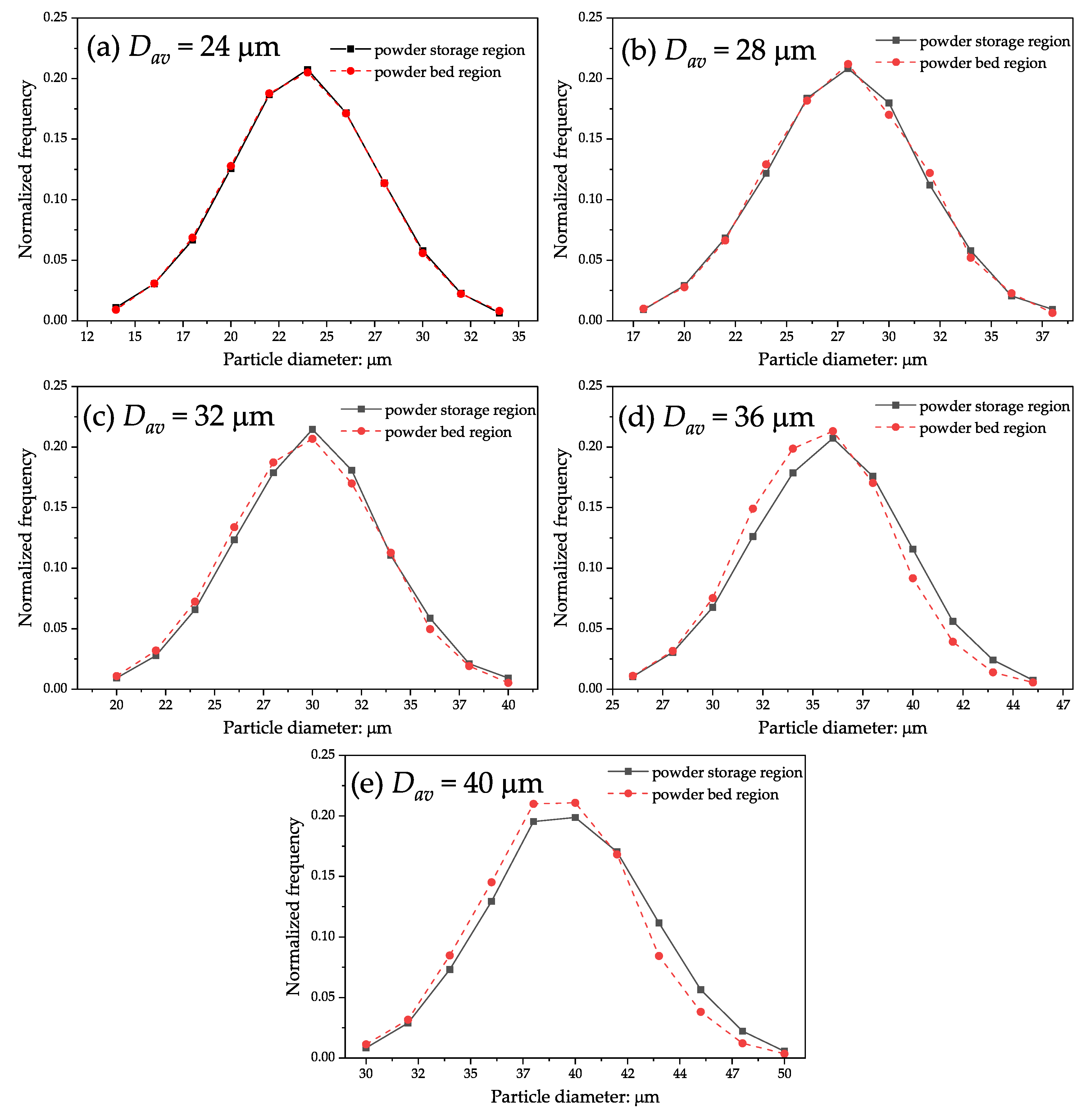
3.4. Equivalency of Particle Size Distribution
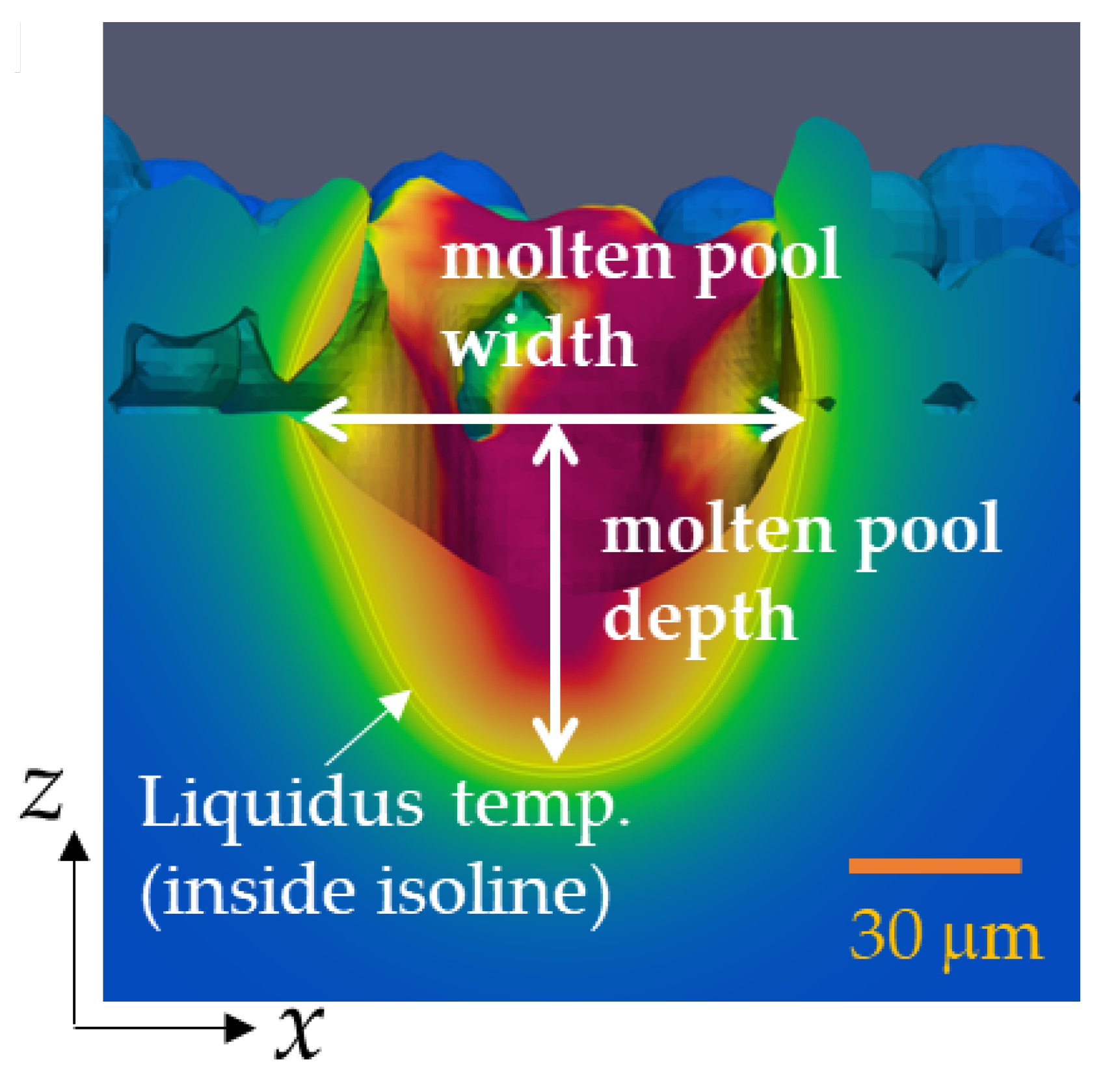
3.5. Molten Pool Dimensions
4. Conclusions
- The packing fraction increased as the average particle diameter decreased.
- Smaller particles tended to accumulate at the inlet edge of the powder bed formation region.
- As excess particles penetrated prior to powder spreading by the movement of the coater, the number of filled particles between the centre and the outlet edge of the powder bed formation region increased.
- The powder bed thickness increased as the average particle diameter decreased.
- Multiple particles piled up in the z direction when the average particle diameter was small, whereas the particles spread inhomogeneously with a thickness of one particle for large average diameters.
- The molten pool width was hardly dependent on the average particle diameter and was approximately equal to the laser spot diameter used in the simulation.
- The molten pool depth increased with decreasing average particle diameter. It was suggested that the region of the powder bed with a smaller average particle diameter absorbed greater thermal energy due to the greater specific surface area resulting from the large powder bed thickness and the accumulation of multiple particles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schneider, J.; Farris, L.; Nolze, G.; Reinsch, S.; Cios, G.; Tokarski, T.; Thompson, S. Microstructure Evolution in Inconel 718 Produced by Powder Bed Fusion Additive Manufacturing. J. Manuf. Mater. Process. 2022, 6, 20. [Google Scholar] [CrossRef]
- Peters, M.; Brodie, E.G.; Thomas, S.; Djumas, L.; Brameld, M.; Salasi, M.; Quadir, Z.; Iannuzzi, M.; Wang, J.; Sercombe, T.; et al. On the importance of nano-oxide control in laser powder bed fusion manufactured Ni-based alloys to enhance fracture properties. Materialia 2023, 32, 101958. [Google Scholar] [CrossRef]
- Kuo, Y.L.; Kamigaichi, A.; Kakehi, K. Characterization of Ni-Based Superalloy Built by Selective Laser Melting and Electron Beam Melting. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2018, 49, 3831–3837. [Google Scholar] [CrossRef]
- Sato, N.; Nakano, S.; Nagahari, T.; Nagoya, T.; Kakehi, K. Microstructure of Nickel-Based Superalloy Fabricated by Selective Laser Melting in Vacuum. J. Jpn. Soc. Powder Powder Metall. 2020, 67, 121–124. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, R.; Liu, Y.; Zhang, L. Understanding melt pool characteristics in laser powder bed fusion: An overview of single- and multi-track melt pools for process optimization. Adv. Powder Mater. 2023, 2, 100137. [Google Scholar] [CrossRef]
- Seede, R.; Shoukr, D.; Zhang, B.; Whitt, A.; Gibbons, S.; Flater, P.; Elwany, A.; Arroyave, R.; Karaman, I. An ultra-high strength martensitic steel fabricated using selective laser melting additive manufacturing: Densification, microstructure, and mechanical properties. Acta Mater. 2020, 186, 199–214. [Google Scholar] [CrossRef]
- Letenneur, M.; Kreitcberg, A.; Brailovski, V. Optimization of Laser Powder Bed Fusion Processing Using a Combination of Melt Pool Modeling and Design of Experiment Approaches: Density Control. J. Manuf. Mater. Process. 2019, 3, 21. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Kitano, H.; Kusano, M.; Tsujii, M.; Yumoto, A.; Watanabe, M. Process Parameter Optimization Framework for the Selective Laser Melting of Hastelloy X Alloy Considering Defects and Solidification Crack Occurrence. Crystals 2021, 11, 578. [Google Scholar] [CrossRef]
- Katagiri, J.; Kusano, M.; Minamoto, S.; Kitano, H.; Daimaru, K.; Tsujii, M.; Watanabe, M. Melt Pool Shape Evaluation by Single-Track Experiments and Finite-Element Thermal Analysis: Balling and Lack of Fusion Criteria for Generating Process Window of Inconel738LC. Materials 2023, 16, 1729. [Google Scholar] [CrossRef]
- Zhao, C.; Parab, N.D.; Li, X.; Fezzaa, K.; Tan, W.; Rollett, A.D.; Sun, T. Critical instability at moving keyhole tip generates porosity in laser melting. Science 2020, 370, 1080–1086. [Google Scholar] [CrossRef]
- Cunningham, R.; Zhao, C.; Parab, N.; Kantzos, C.; Pauza, J.; Fezzaa, K.; Sun, T.; Rollett, A.D. Keyhole threshold and morphology in laser melting revealed by ultrahigh-speed x-ray imaging. Science 2019, 363, 849–852. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Fleming, T.G.; Clark, S.J.; Marussi, S.; Fezzaa, K.; Thiyagalingam, J.; Leung, C.L.A.; Lee, P.D. Keyhole fluctuation and pore formation mechanisms during laser powder bed fusion additive manufacturing. Nat. Commun. 2022, 13, 1170. [Google Scholar] [CrossRef] [PubMed]
- Morgan, R.; Sutcliffe, C.J.; O’Neill, W. Experimental investigation of nanosecond pulsed Nd:YAG laser re-melted pre-placed powder beds. Rapid Prototyp. J. 2001, 7, 159. [Google Scholar] [CrossRef]
- Tolochko, N.K.; Mozzharov, S.E.; Yadroitsev, I.A.; Laoui, T.; Froyen, L.; Titov, V.I.; Ignatiev, M.B. Balling processes during selective laser treatment of powders. Rapid Prototyp. J. 2004, 10, 78–87. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Bertrand, P.; Smurov, I. Parametric analysis of the selective laser melting process. Appl. Surf. Sci. 2007, 253, 8064–8069. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Yadroitsava, I.; Bertrand, P.; Smurov, I. Factor analysis of selective laser melting process parameters and geometrical characteristics of synthesized single tracks. Rapid Prototyp. J. 2012, 18, 201–208. [Google Scholar] [CrossRef]
- Kruth, J.P.; Froyen, L.; Vaerenbergh, J.V.; Mercelis, P.; Rombouts, M.; Lauwers, B. Selective laser melting of iron-based powder. J. Mater. Process. Technol. 2004, 149, 616–622. [Google Scholar] [CrossRef]
- Gusarov, A.V.; Yadroitsev, I.; Bertrand, P.; Smurov, I. Heat transfer modelling and stability analysis of selective laser melting. Appl. Surf. Sci. 2007, 254, 975–979. [Google Scholar] [CrossRef]
- Guirguis, D.; Tucker, C.; Beuth, J. Accelerating process development for 3D printing of new metal alloys. Nat. Commun. 2024, 15, 582. [Google Scholar] [CrossRef] [PubMed]
- Kusano, M.; Watanabe, M. Heat Source Model Development for Thermal Analysis of Laser Powder Bed Fusion Using Bayesian Optimization and Machine Learning. Integr. Mater. Manuf. Innov. 2024, 13, 288–304. [Google Scholar] [CrossRef]
- Cheng, B.; Shrestha, S.; Chou, K. Stress and deformation evaluations of scanning strategy effect in selective laser melting. Addit. Manuf. 2016, 12, 240–251. [Google Scholar] [CrossRef]
- Carraturo, M.; Lane, B.; Yeung, H.; Kollmannsberger, S.; Reali, A.; Auricchio, F. Numerical Evaluation of Advanced Laser Control Strategies Influence on Residual Stresses for Laser Powder Bed Fusion Systems. Integr. Mater. Manuf. Innov. 2020, 9, 435–445. [Google Scholar] [CrossRef]
- Ninpetch, P.; Kowitwarangkul, P.; Mahathanabodee, S.; Chalermkarnnon, P.; Rattanadecho, P. Computational investigation of thermal behavior and molten metal flow with moving laser heat source for selective laser melting process. Case Stud. Therm. Eng. 2021, 24, 100860. [Google Scholar] [CrossRef]
- Alphonso, W.; Baier, M.; Carmignato, S.; Hattel, J.; Bayat, M. On the possibility of doing reduced order, thermo-fluid modelling of laser powder bed fusion (L-PBF)–Assessment of the importance of recoil pressure and surface tension. J. Manuf. Process. 2023, 94, 564–577. [Google Scholar] [CrossRef]
- Flint, T.F.; Robson, J.D.; Parivendhan, G.; Cardiff, P. laserbeamFoam: Laser ray-tracing and thermally induced state transition simulation toolkit. SoftwareX 2023, 21, 101299. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Chia, H.Y.; Yan, W. Mechanism of keyhole pore formation in metal additive manufacturing. NPJ Comput. Mater. 2022, 8, 22. [Google Scholar] [CrossRef]
- Wang, W.; Lin, W.; Yang, R.; Wu, Y.; Li, J.; Zhang, Z.; Zhai, Z. Mesoscopic evolution of molten pool during selective laser melting of superalloy Inconel 738 at elevating preheating temperature. Mater. Des. 2022, 213, 110355. [Google Scholar] [CrossRef]
- Li, E.L.; Wang, L.; Yu, A.B.; Zhou, Z.Y. A three-phase model for simulation of heat transfer and melt pool behaviour in laser powder bed fusion process. Powder Technol. 2021, 381, 298–312. [Google Scholar] [CrossRef]
- Bayat, M.; Mohanty, S.; Hattel, J.H. Multiphysics modelling of lack-of-fusion voids formation and evolution in IN718 made by multi-track/multi-layer L-PBF. Int. J. Heat Mass Transf. 2019, 139, 95–114. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, D.Z.; Fu, G.; Jiang, J.; Zhao, M. High-fidelity modelling of selective laser melting copper alloy: Laser reflection behavior and thermal-fluid dynamics. Mater. Des. 2021, 207, 109857. [Google Scholar] [CrossRef]
- Le, T.N.; Chou, K. Surface Formation of Sloping Features in Laser Powder–Bed Fusion by Multi-Track Multi-Layer Simulations. Metals 2023, 13, 976. [Google Scholar] [CrossRef]
- Fotovvati, B.; Chou, K. Multi-layer thermo-fluid modeling of powder bed fusion (PBF) process. J. Manuf. Process. 2022, 83, 203–211. [Google Scholar] [CrossRef]
- Ninpetch, P.; Chalermkarnnon, P.; Kowitwarangkul, P. Multiphysics Simulation of Thermal-Fluid Behavior in Laser Powder Bed Fusion of H13 Steel: Influence of Layer Thickness and Energy Input. Met. Mater. Int. 2023, 29, 536–551. [Google Scholar] [CrossRef]
- Cook, P.S.; Phua, A.; Davies, C.H.; Delaney, G.W. Modelling the influences of powder layer depth and particle morphology on powder bed fusion using a coupled DEM-CFD approach. Powder Technol. 2023, 429, 118927. [Google Scholar] [CrossRef]
- Bogdanova, M.; Chernyshikhin, S.; Zakirov, A.; Zotov, B.; Fedorenko, L.; Belousov, S.; Perepelkina, A.; Korneev, B.; Lyange, M.; Pelevin, I.; et al. Mesoscale Simulation of Laser Powder Bed Fusion with an Increased Layer Thickness for AlSi10Mg Alloy. J. Manuf. Mater. Process. 2024, 8, 7. [Google Scholar] [CrossRef]
- Fouda, Y.M.; Bayly, A.E. A DEM study of powder spreading in additive layer manufacturing. Granul. Matter 2020, 22, 10. [Google Scholar] [CrossRef]
- Yuan, W.; Chen, H.; Li, S.; Heng, Y.; Yin, S.; Wei, Q. Understanding of adopting flat-top laser in laser powder bed fusion processed Inconel 718 alloy: Simulation of single-track scanning and experiment. J. Mater. Res. Technol. 2022, 16, 1388–1401. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete element model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Katagiri, J.; Kusano, M.; Nomoto, S.; Watanabe, M. Influence of recoil pressure, mushy zone flow resistance and reflectivity on melt pool shape in laser powder bed fusion simulation. Case Stud. Therm. Eng. 2023, 50, 103477. [Google Scholar] [CrossRef]
- Cho, J.H.; Na, S.J. Implementation of real-time multiple reflection and Fresnel absorption of laser beam in keyhole. J. Phys. D Appl. Phys. 2006, 39, 5372–5378. [Google Scholar] [CrossRef]
- Fuchs, S.L.; Praegla, P.M.; Cyron, C.J.; Wall, W.A.; Meier, C. A versatile SPH modeling framework for coupled microfluid-powder dynamics in additive manufacturing: Binder jetting, material jetting, directed energy deposition and powder bed fusion. Eng. Comput. 2022, 38, 4853–4877. [Google Scholar] [CrossRef]
- Queva, A.; Guillemot, G.; Moriconi, C.; Metton, C.; Bellet, M. Numerical study of the impact of vaporisation on melt pool dynamics in Laser Powder Bed Fusion—Application to IN718 and Ti–6Al–4V. Addit. Manuf. 2020, 35, 101249. [Google Scholar] [CrossRef]
- Afrin, N.; Ji, P.; Chen, J.K.; Zhang, Y. Effects of Beam Size and Pulse Duration on the Laser Drilling Process; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Y.; Xie, Y.; Yang, S.; Hou, R.; Ge, Y.; Lang, L.; Gong, S.; Li, H. Observation of vapor plume behavior and process stability at single-track and multi-track levels in laser powder bed fusion regime. Metals 2021, 11, 937. [Google Scholar] [CrossRef]
- Wang, R.; Garcia, D.; Kamath, R.R.; Dou, C.; Ma, X.; Shen, B.; Choo, H.; Fezzaa, K.; Yu, H.Z.; Kong, Z. In situ melt pool measurements for laser powder bed fusion using multi sensing and correlation analysis. Sci. Rep. 2022, 12, 13716. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Li, H.; Lang, L.; Gong, S.; Ge, Y. Effects of scan speed on vapor plume behavior and spatter generation in laser powder bed fusion additive manufacturing. J. Manuf. Process. 2018, 36, 60–67. [Google Scholar] [CrossRef]
- Bitharas, I.; Parab, N.; Zhao, C.; Sun, T.; Rollett, A.D.; Moore, A.J. The interplay between vapour, liquid, and solid phases in laser powder bed fusion. Nat. Commun. 2022, 13, 2959. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Heng, H.; Li, F.; Wang, M. The influences of welding parameters on the metal vapor plume in fiber laser welding based on 3D reconstruction. Opt. Laser Technol. 2018, 107, 1–7. [Google Scholar] [CrossRef]
- Trapp, J.; Rubenchik, A.M.; Guss, G.; Matthews, M.J. In situ absorptivity measurements of metallic powders during laser powder-bed fusion additive manufacturing. Appl. Mater. Today 2017, 9, 341–349. [Google Scholar] [CrossRef]
- Xie, J.; Kar, A.; Rothenflue, J.A.; Latham, W.P. Temperature-dependent absorptivity and cutting capability of CO2, Nd:YAG and chemical oxygen–iodine lasers. J. Laser Appl. 1997, 9, 77–85. [Google Scholar] [CrossRef]
- Okugawa, M.; Isono, Y.; Koizumi, Y.; Nakano, T. Raking Process for Powder Bed Fusion of Ti6Al4V Alloy Powder Analyzed by Discrete Element Method+1. Mater. Trans. 2023, 64, 37–43. [Google Scholar] [CrossRef]
- Savage, S.B.; Lun, C.K.K. Particle size segregation in inclined chute flow of dry cohesionless granular solids. J. Fluid Mech. 1988, 189, 311–335. [Google Scholar] [CrossRef]
- Khakhar, D.V.; McCarthy, J.J.; Ottino, J.M. Mixing and segregation of granular materials in chute flows. Chaos Interdiscip. J. Nonlinear Sci. 1999, 9, 594–610. [Google Scholar] [CrossRef] [PubMed]
- Gray, J.M.N.T.; Chugunov, V.A. Particle-size segregation and diffusive remixing in shallow granular avalanches. J. Fluid Mech. 2006, 569, 365–398. [Google Scholar] [CrossRef]
- Wiederseiner, S.; Andreini, N.; Épely Chauvin, G.; Moser, G.; Monnereau, M.; Gray, J.M.N.T.; Ancey, C. Experimental investigation into segregating granular flows down chutes. Phys. Fluids 2011, 23, 013301. [Google Scholar] [CrossRef]
- Neveu, A.; Larcher, M.; Delannay, R.; Jenkins, J.T.; Valance, A. Particle segregation in inclined high-speed granular flows. J. Fluid Mech. 2022, 935, A41. [Google Scholar] [CrossRef]
- Phua, A.; Cook, P.S.; Davies, C.H.; Delaney, G.W. Powder spreading over realistic laser melted surfaces in metal additive manufacturing. Addit. Manuf. Lett. 2022, 3, 100039. [Google Scholar] [CrossRef]
- Kikuchi, K.; Tanifuji, Y.; Zhou, W.; Nomura, N.; Kawasaki, A. Experimental Characterization and Computational Simulation of Powder Bed for Powder Bed Fusion Additive Manufacturing. Mater. Trans. 2022, 63, 931–938. [Google Scholar] [CrossRef]
- Haeri, S. Optimisation of blade type spreaders for powder bed preparation in Additive Manufacturing using DEM simulations. Powder Technol. 2017, 321, 94–104. [Google Scholar] [CrossRef]





| Ni | Cr | Fe | Mo | Co | W | C | Al | B | Mn | N | O | P | S | Si | Ti | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Powder | Ni-bal. | 22.1 | 18.1 | 9.0 | 1.6 | 0.7 | 0.06 | 0.05 | <0.002 | 0.0 | 0.008 | 0.0013 | <0.005 | 0.003 | <0.1 | 0.09 |
| Bare plate | R48.22 | 21.56 | 18.38 | 8.86 | 1.01 | 0.59 | 0.08 | 0.19 | 0.005 | 0.48 | - | - | 0.008 | <0.002 | 0.46 | 0.02 |
| Model | Parameter [Unit] |
|---|---|
| Density | 8220 [kg/m3] |
| Spring constant | [N/m] |
| Poisson’s ratio | 0.3 |
| Restitution coefficient | 0.4 |
| Particle–particle friction coefficient | 0.3 |
| Particle–wall friction coefficient | 0.3 |
| Time increment | [s] |
| Parameter | Value [Unit] |
|---|---|
| Solid density | 8220 [kg/m3] |
| Liquid density | 8220 [kg/m3] |
| Density of gas | 1.780 [kg/m3] |
| Solidus temperature | 1533.15 [K] |
| Liquidus temperature | 1628.15 [K] |
| Evaporation temperature | 3100 [K] [44] |
| Thermal conductivity | 29.0 [W/(m·K)] |
| Latent heat of fusion | 27,600 [J/kg] |
| Latent heat of evaporation | 645,700 [J/kg] [44] |
| Specific heat capacity of metal | 677 [J/kg·K] |
| Specific heat capacity of gas | 523 [J/kg·K] |
| Surface tension coefficient () | T + 2.067 [N/m] [43] |
| Liquid viscosity () | 0.005 [Pa·s] |
| Gas viscosity | [Pa·s] |
| Mushy zone constant | 105 [kg/(m3s)] |
| Model | Model Parameter Value |
|---|---|
| Fresnel | = 0.25 |
| Hagan–Ruben | - |
| Constant | 0.2 |
| Constant | 0.4 |
| Constant | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katagiri, J.; Nomoto, S.; Kusano, M.; Watanabe, M. Particle Size Effect on Powder Packing Properties and Molten Pool Dimensions in Laser Powder Bed Fusion Simulation. J. Manuf. Mater. Process. 2024, 8, 71. https://doi.org/10.3390/jmmp8020071
Katagiri J, Nomoto S, Kusano M, Watanabe M. Particle Size Effect on Powder Packing Properties and Molten Pool Dimensions in Laser Powder Bed Fusion Simulation. Journal of Manufacturing and Materials Processing. 2024; 8(2):71. https://doi.org/10.3390/jmmp8020071
Chicago/Turabian StyleKatagiri, Jun, Sukeharu Nomoto, Masahiro Kusano, and Makoto Watanabe. 2024. "Particle Size Effect on Powder Packing Properties and Molten Pool Dimensions in Laser Powder Bed Fusion Simulation" Journal of Manufacturing and Materials Processing 8, no. 2: 71. https://doi.org/10.3390/jmmp8020071
APA StyleKatagiri, J., Nomoto, S., Kusano, M., & Watanabe, M. (2024). Particle Size Effect on Powder Packing Properties and Molten Pool Dimensions in Laser Powder Bed Fusion Simulation. Journal of Manufacturing and Materials Processing, 8(2), 71. https://doi.org/10.3390/jmmp8020071






