On the Influence of Wave-Shaped Tool Path Strategies on Geometric Accuracy in Incremental Sheet Forming
Abstract
1. Introduction
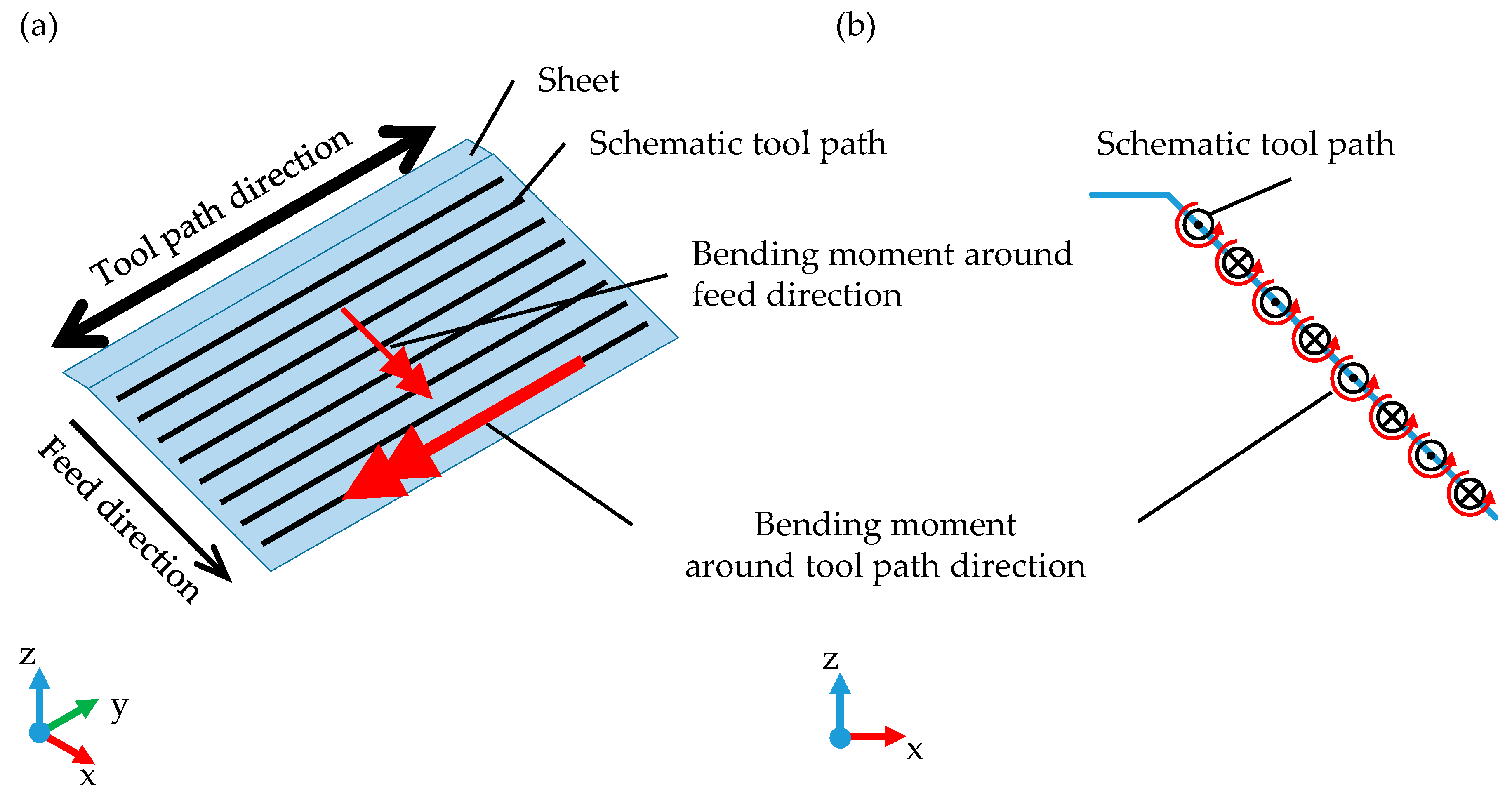
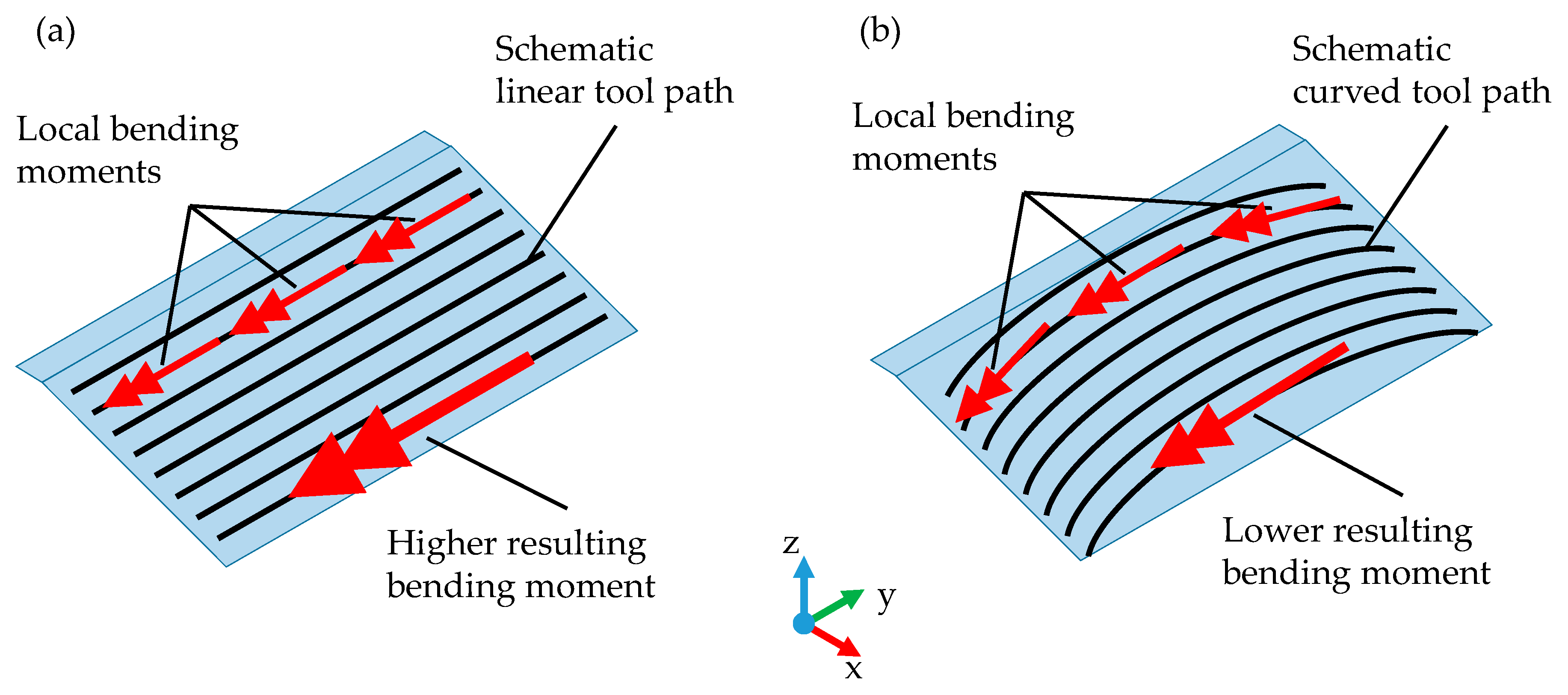
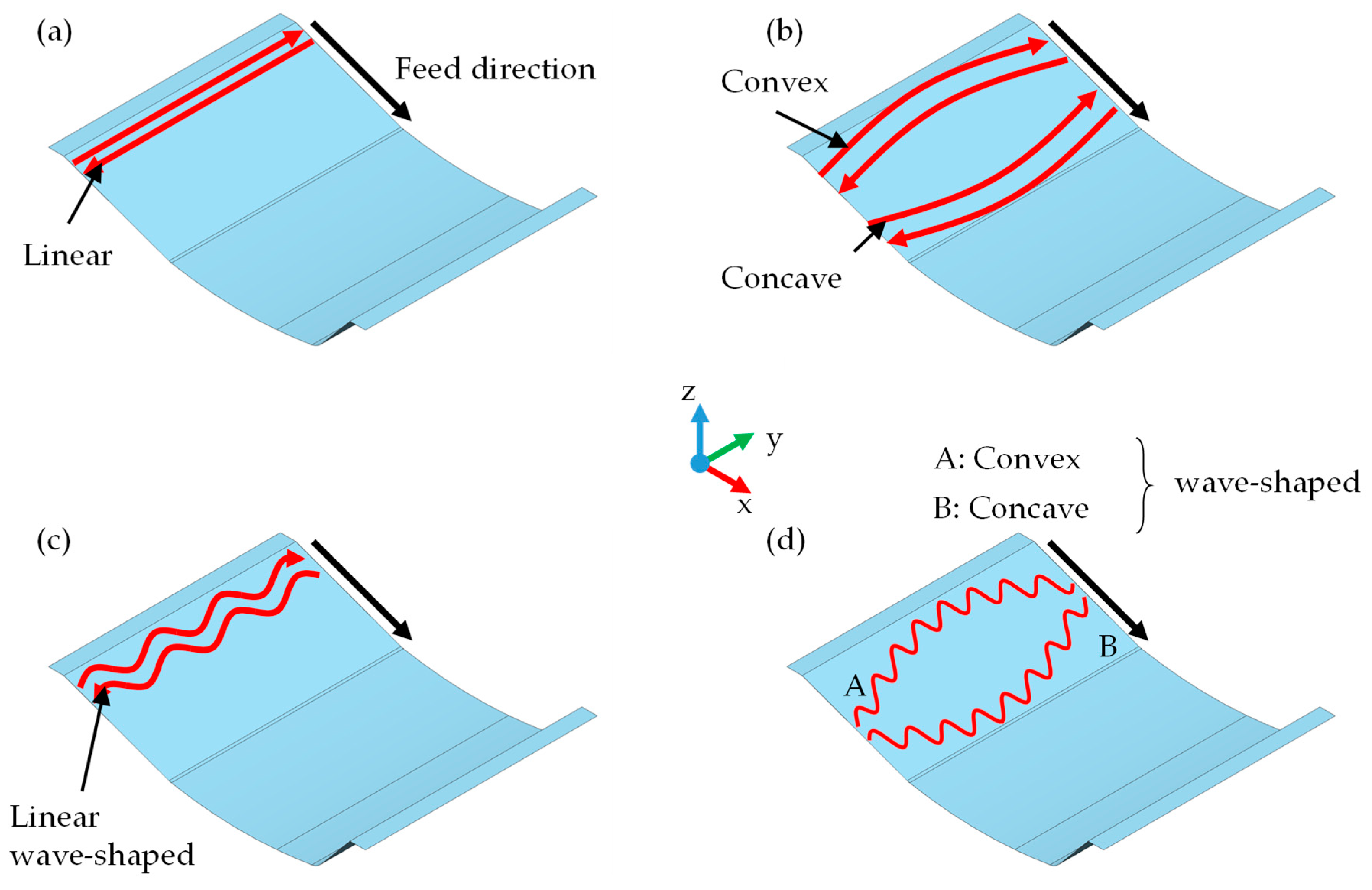
- On a linear and parallel tool path, all axes of local residual bending moments are also parallel, and an accumulated, amplified bending moment results around a united overall axis (see Figure 2a).
- On a curved tool path, the axes of local bending moments are tangential to the path and thus not parallel to each other. This prevents an accumulation of bending moments around a united overall axis and, in contrast, leads to a mutual interlocking of the bending moments, rather than an amplification (see Figure 2b).
State of the Art
2. Materials and Methods
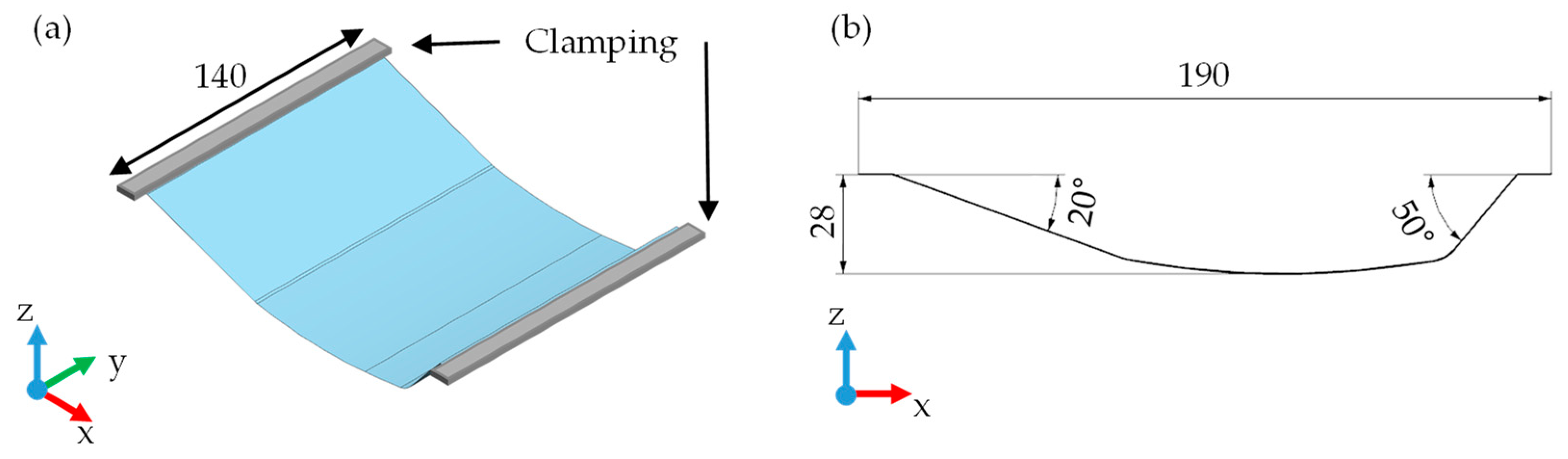
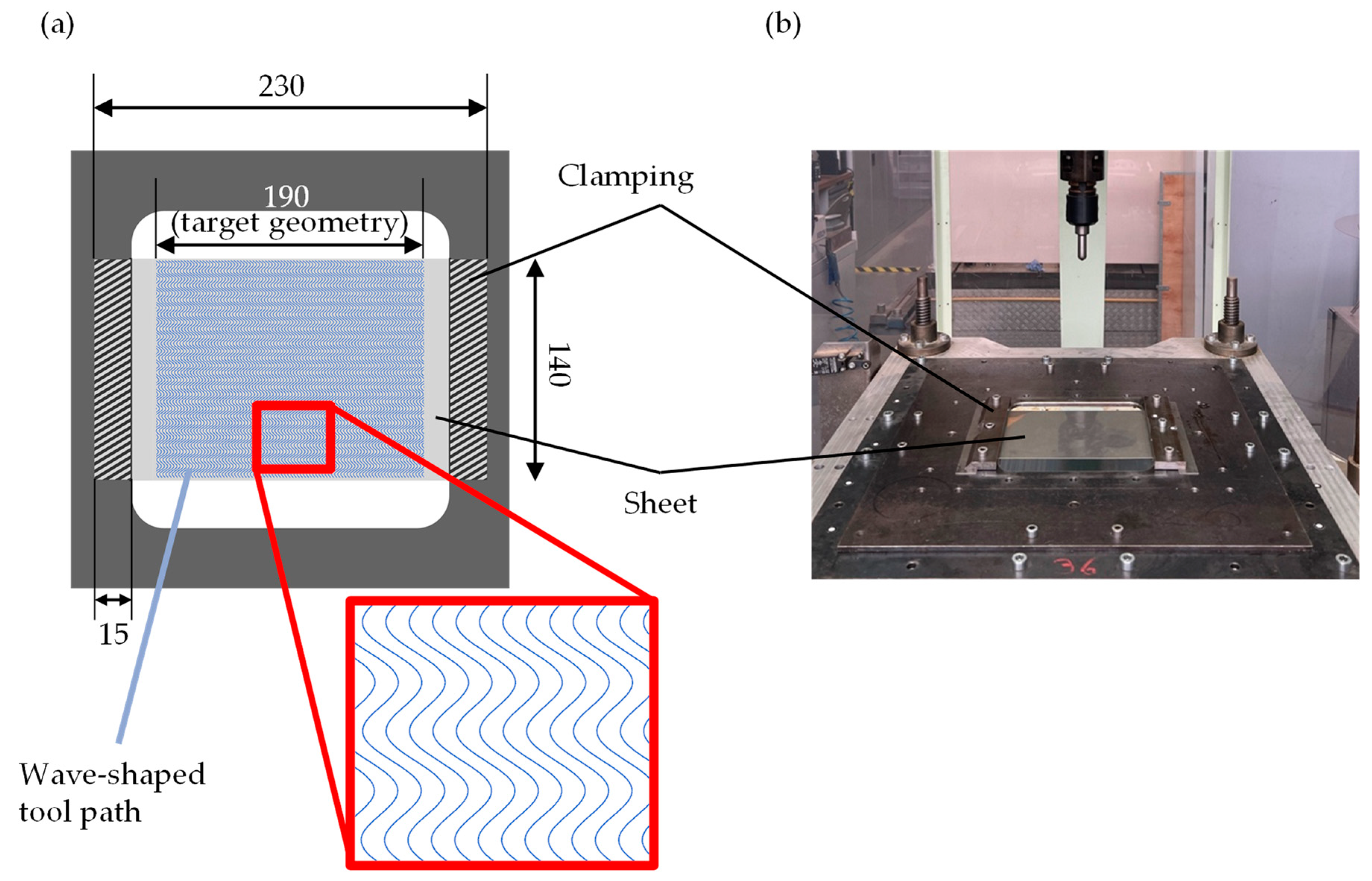
2.1. Experimental Setup
2.2. Finite Element (FE) Setup
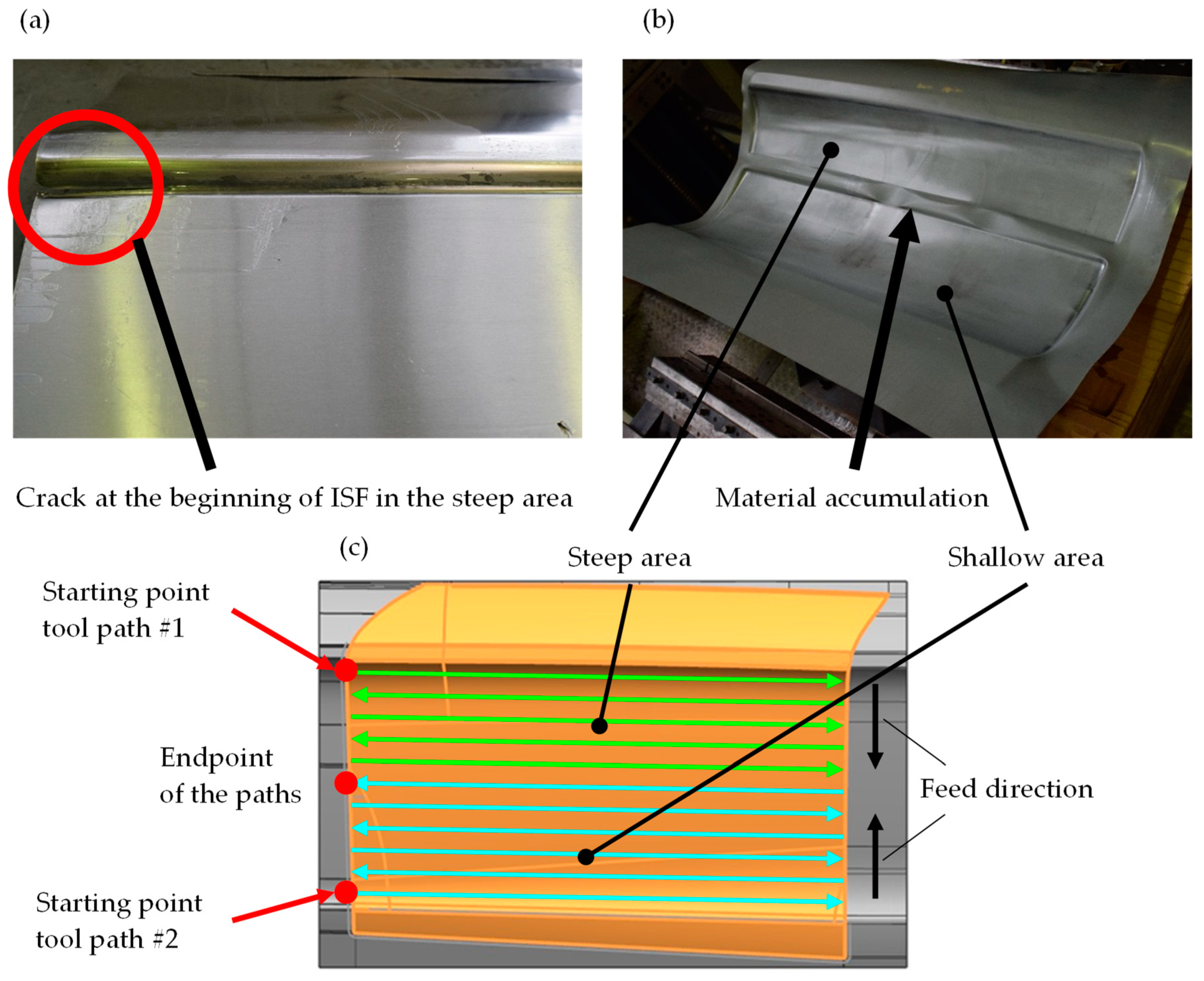
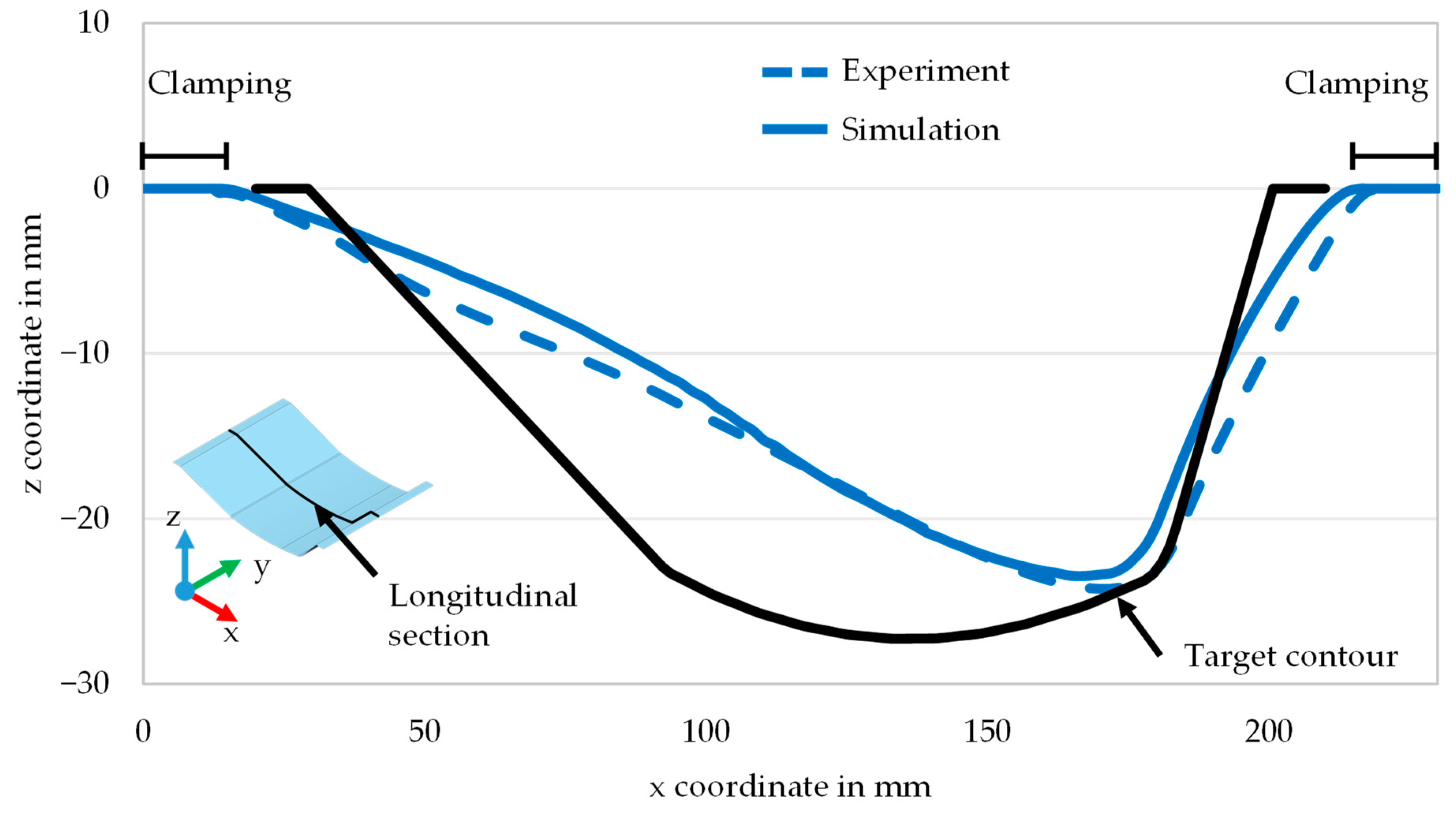
3. Results and Discussion
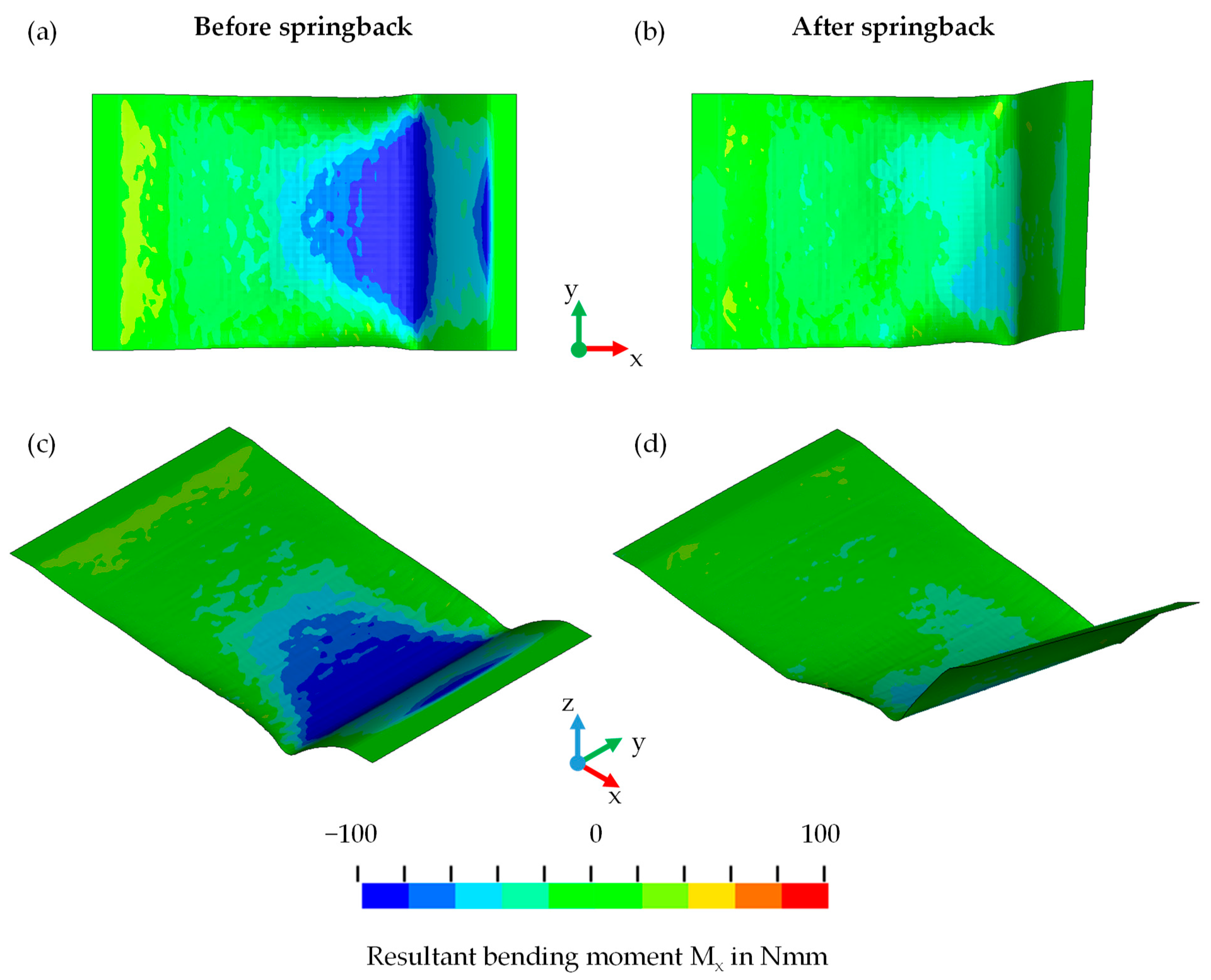
Bending Moments
4. Conclusions
- A linear tool path strategy leads to very high geometric deviation for the selected unstiffened part geometry that is sensitive to geometric distortions.
- The geometric deviation has been significantly reduced by some versions of wave-shaped path strategies. In particular, the combination of a convex wave (wave peak points opposite to feed direction) with a superimposed sine function resulted in the lowest geometric deviation.
- In general, it has been shown that convex strategies lead to a stronger reduction of the springback than concave (wave peak points in feed direction) path strategies. It is not yet fully understood why concave path strategies do not have the same positive effect but lead to a similarly high geometric deviation as linear paths.
- With the help of an FE model, the effect of the chosen path strategy on the residual bending moment has been analysed. The best wave-shaped path strategies resulted in a significant reduction of the residual bending moment around the main axis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allwood, J.M.; King, G.P.F.; Duflou, J. A structured search for applications of the incremental sheet-forming process by product segmentation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2005, 219, 239–244. [Google Scholar] [CrossRef]
- Hirt, G.; Kordtomeikel, R.; Bremen, T.; Laugwitz, M.; Bailly, D. On the Geometrical Accuracy in Incremental Sheet Forming. In Forming the Future; Daehn, G., Cao, J., Kinsey, B., Tekkaya, E., Vivek, A., Yoshida, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 507–521. ISBN 978-3-030-75380-1. [Google Scholar]
- Gatea, S.; Ou, H.; McCartney, G. Review on the influence of process parameters in incremental sheet forming. Int. J. Adv. Manuf. Technol. 2016, 87, 479–499. [Google Scholar] [CrossRef]
- Maqbool, F.; Bambach, M. Experimental and Numerical Investigation of the Influence of Process Parameters in Incremental Sheet Metal Forming on Residual Stresses. J. Manuf. Mater. Process. 2019, 3, 31. [Google Scholar] [CrossRef]
- Jeswiet, J.; Micari, F.; Hirt, G.; Bramley, A.; Duflou, J.; Allwood, J. Asymmetric Single Point Incremental Forming of Sheet Metal. CIRP Ann. 2005, 54, 88–114. [Google Scholar] [CrossRef]
- Bambach, M.; Taleb Araghi, B.; Hirt, G. Strategies to improve the geometric accuracy in asymmetric single point incremental forming. Prod. Eng. Res. Devel. 2009, 3, 145–156. [Google Scholar] [CrossRef]
- Lu, H.; Liu, H.; Wang, C. Review on strategies for geometric accuracy improvement in incremental sheet forming. Int. J. Adv. Manuf. Technol. 2019, 102, 3381–3417. [Google Scholar] [CrossRef]
- Araghi, B.T.; Manco, G.L.; Bambach, M.; Hirt, G. Investigation into a new hybrid forming process: Incremental sheet forming combined with stretch forming. CIRP Ann. 2009, 58, 225–228. [Google Scholar] [CrossRef]
- Wu, S.; Gao, L.; Matsuoka, Y.; Rashed, S.; Zhao, Y.; Ma, N. Multi-step toolpath approach of improving the dimensional accuracy of a non-axisymmetric part in incremental sheet forming and its mechanism analysis. J. Mech. Sci. Technol. 2022, 36, 1975–1985. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, L.; Liu, Y.; Kang, J. Research on the selective multi-stage two point incremental forming based on the forming angle. J. Mech. Sci. Technol. 2021, 35, 3643–3658. [Google Scholar] [CrossRef]
- Wei, B.; Zhang, F.; He, K.; Li, Z.; Du, R. Deformation and Springback Behavior of Sheet Metal with Convex-Shaped Surfaces in Heat-Assisted Incremental Bending Process Based on Minimum Energy Method. J. Manuf. Sci. Eng. 2022, 145, 31003. [Google Scholar] [CrossRef]
- Möllensiep, D.; Kulessa, P.; Thyssen, L.; Kuhlenkötter, B. Regression-based compensation of part inaccuracies in incremental sheet forming at elevated temperatures. Int. J. Adv. Manuf. Technol. 2020, 109, 1917–1928. [Google Scholar] [CrossRef]
- Chang, Z.; Huang, W.; Chen, J. A new tool path with point contact and its effect on incremental sheet forming process. Int. J. Adv. Manuf. Technol. 2020, 110, 1515–1525. [Google Scholar] [CrossRef]
- Grimm, T.J.; Ragai, I.; Roth, J.T. Utilization of Wavy Toolpath in Single-Point Incremental Forming. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition-2018, Pittsburgh, PA, USA, 9–15 November 2018; The American Society of Mechanical Engineers: New York, NY, USA, 2019. ISBN 978-0-7918-5201-9. [Google Scholar]
- Chang, Z.; Chen, J. Mechanism of the twisting in incremental sheet forming process. J. Mater. Process. Technol. 2020, 276, 116396. [Google Scholar] [CrossRef]
- Maqbool, F.; Bambach, M. Dominant deformation mechanisms in single point incremental forming (SPIF) and their effect on geometrical accuracy. Int. J. Mech. Sci. 2018, 136, 279–292. [Google Scholar] [CrossRef]
- Micari, F.; Ambrogio, G.; Filice, L. Shape and dimensional accuracy in Single Point Incremental Forming: State of the art and future trends. J. Mater. Process. Technol. 2007, 191, 390–395. [Google Scholar] [CrossRef]
- Schmitz, R.U.C.; Bremen, T.; Bailly, D.B.; Hirt, G.K.P. On the Influence of the Tool Path and Intrusion Depth on the Geometrical Accuracy in Incremental Sheet Forming. Metals 2020, 10, 661. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T. A model of large-strain cyclic plasticity and its application to springback simulation. Int. J. Mech. Sci. 2003, 45, 1687–1702. [Google Scholar] [CrossRef]
- Ul Hassan, H.; Maqbool, F.; Güner, A.; Hartmaier, A.; Ben Khalifa, N.; Tekkaya, A.E. Springback prediction and reduction in deep drawing under influence of unloading modulus degradation. Int. J. Mater. Form. 2016, 9, 619–633. [Google Scholar] [CrossRef]




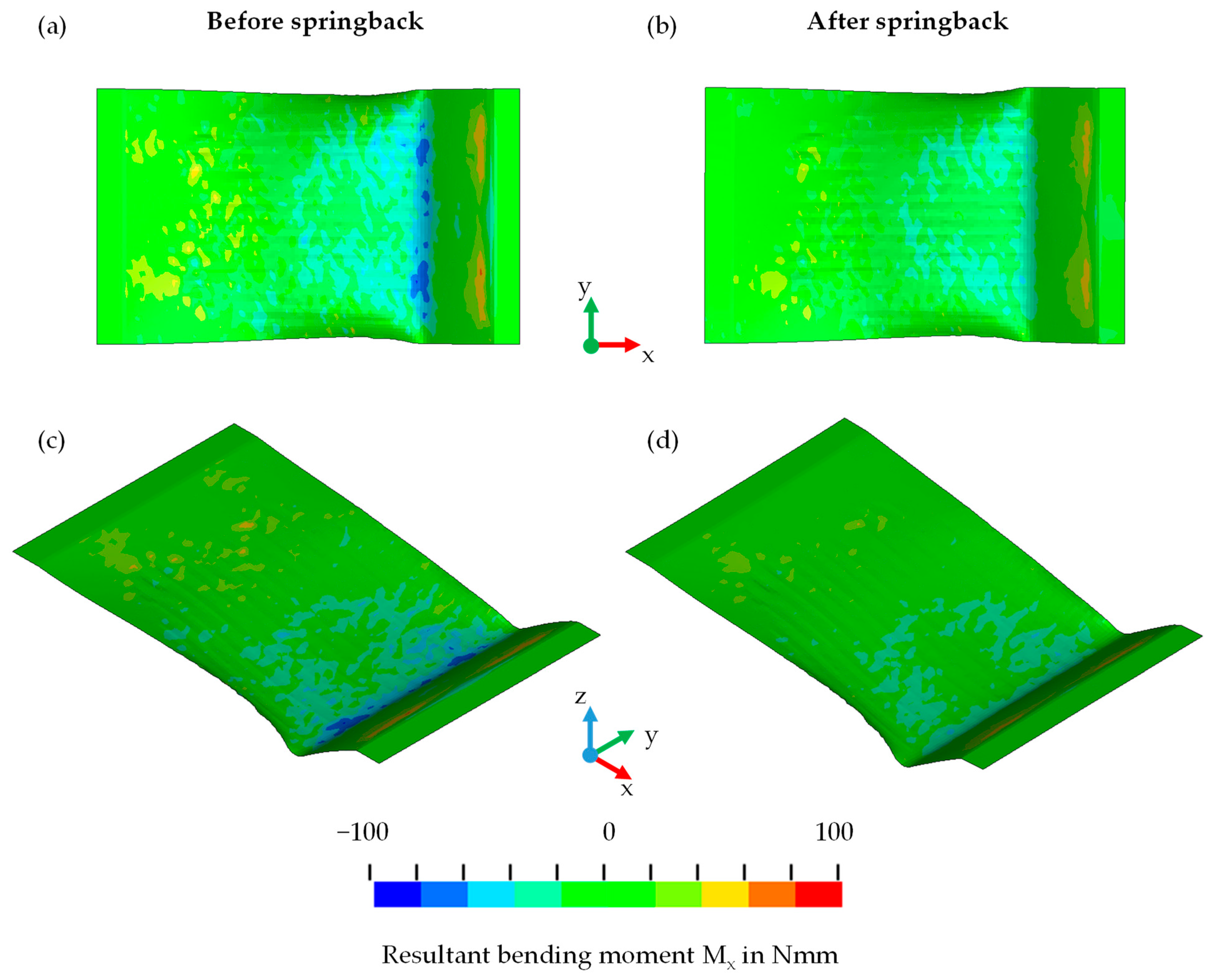
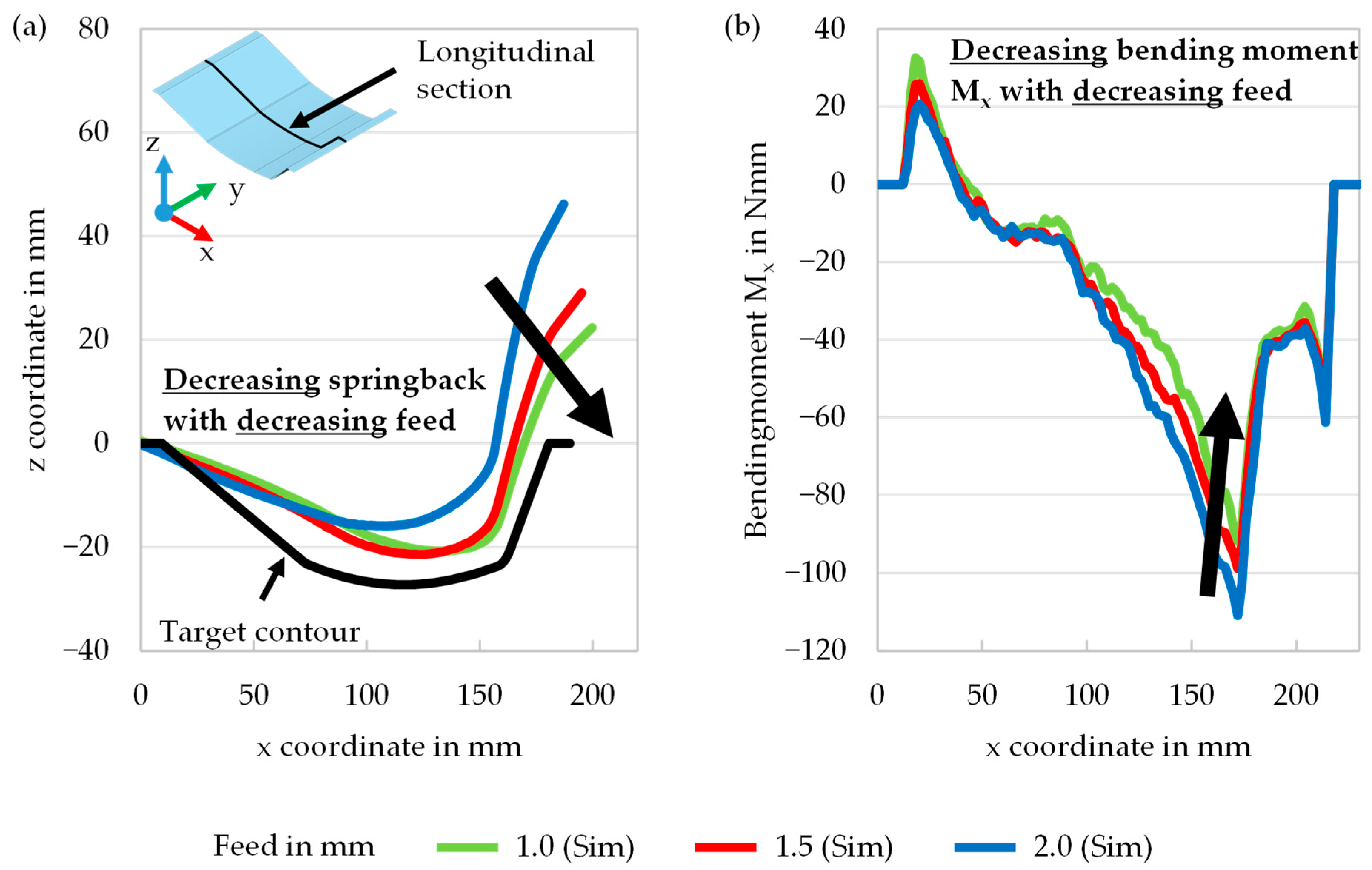

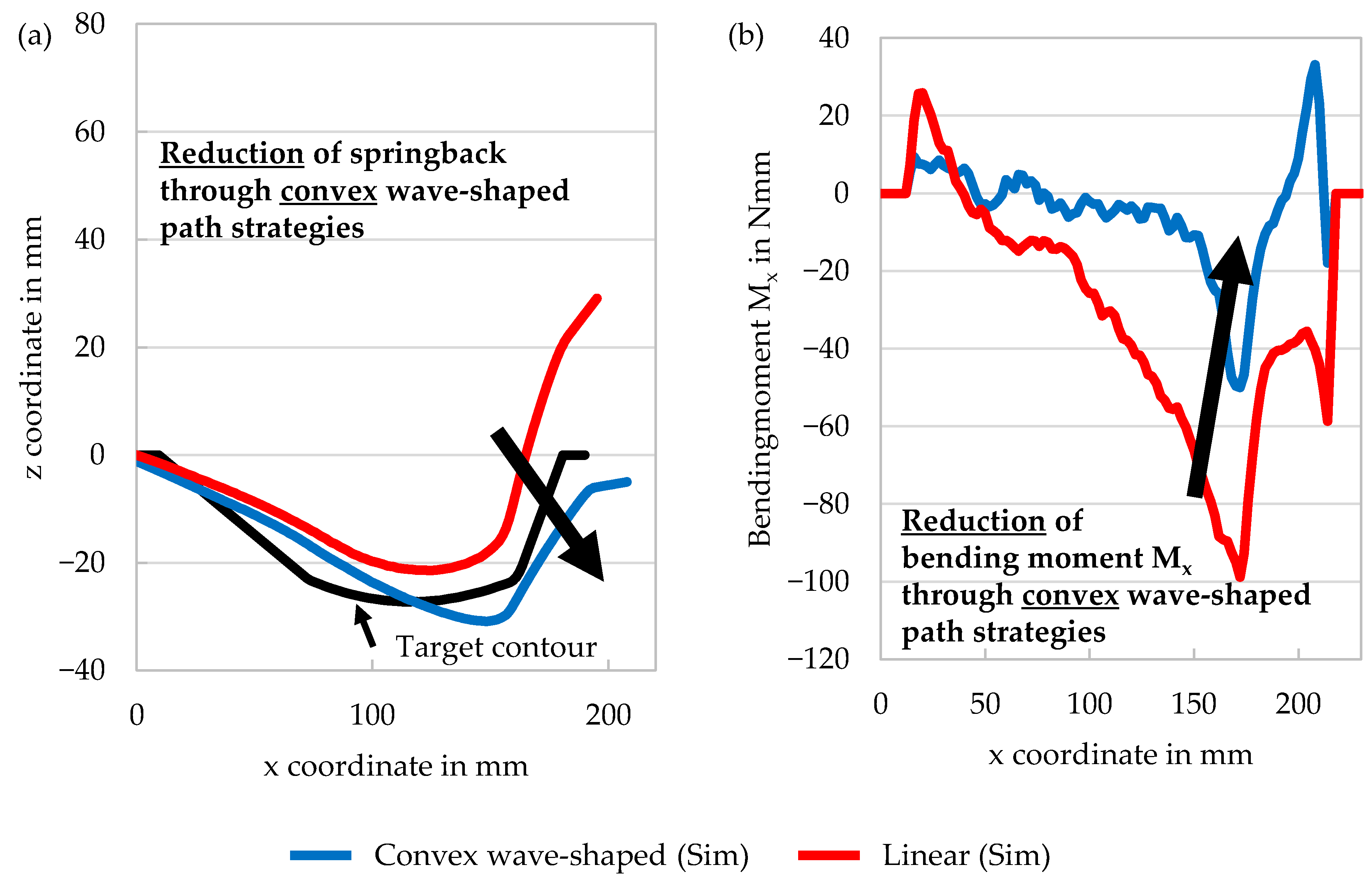
| Y in MPa | C | B in MPa | Rsat in MPA | m | h | b in MPa |
|---|---|---|---|---|---|---|
| 180 | 425 | 700 | 700 | 56 | 0.69 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bremen, T.; Bailly, D.B. On the Influence of Wave-Shaped Tool Path Strategies on Geometric Accuracy in Incremental Sheet Forming. J. Manuf. Mater. Process. 2024, 8, 27. https://doi.org/10.3390/jmmp8010027
Bremen T, Bailly DB. On the Influence of Wave-Shaped Tool Path Strategies on Geometric Accuracy in Incremental Sheet Forming. Journal of Manufacturing and Materials Processing. 2024; 8(1):27. https://doi.org/10.3390/jmmp8010027
Chicago/Turabian StyleBremen, Thomas, and David Benjamin Bailly. 2024. "On the Influence of Wave-Shaped Tool Path Strategies on Geometric Accuracy in Incremental Sheet Forming" Journal of Manufacturing and Materials Processing 8, no. 1: 27. https://doi.org/10.3390/jmmp8010027
APA StyleBremen, T., & Bailly, D. B. (2024). On the Influence of Wave-Shaped Tool Path Strategies on Geometric Accuracy in Incremental Sheet Forming. Journal of Manufacturing and Materials Processing, 8(1), 27. https://doi.org/10.3390/jmmp8010027






