Abstract
X-ray-computed tomography (CT) is today’s gold standard for the non-destructive evaluation of internal component defects such as cracks and porosity. Using automated standardized evaluation algorithms, an analysis can be performed without knowledge of the shape, location, or size of the defects. Both the measurement and the evaluation are based on the fact that the component has no internal structures or cavities. However, additive manufacturing (AM) and hybrid subtractive procedures offer the possibility of integrating internal structures directly during the building process. The examination of powder bed fusion (PBF) samples made of Ti64 and PA12 showed that the standardized evaluation methods were not able to identify internal structures correctly. Different evaluation methods for the CT-measured values were analyzed and recommendations on a procedure for measuring internal structures are given.
1. Introduction
Processes, such as additive manufacturing (AM) or hybrid subtractive manufacturing methods, facilitate the production of components with completely closed internal structures. Although these have rarely been utilized, they offer significant advantages over traditional manufacturing processes. Klahn et al. [1] reported an improved generation of shockwaves in medical devices through targeted cavities. Blakey-Milner et al. [2] described the possibility of mass reduction and internal cooling features for metals in the AM. In addition, internal structures could be used to evaluate the performance of the process by building small flaws [3]. Not exposing the core area, but only the contour of the part, could lead to the implementation of complex geometries or internal structures with laser powder bed fusion (L-PBF) [4]. However, the challenge in such cases is to transfer the geometric shape of the template to the real part, since the planned cavities are filled with powder during the build process, which can lead to as-built surface roughness, a reduction of the volume or a change in the shape of the desired structure [4]. This can affect the position, size, shape and detectability of internal structures and complicate a 2D evaluation, e.g., with a micrograph. Tammas-Williams et al. [5] investigated the influences of internal structures in Ti-6Al-4V components and analyzed the role of internal structural defects, such as channel openings and pores, as crack initiators, in addition to their influence on fatigue behavior. In addition, these factors can influence the static strength and ductility of materials, making porosity analysis a priority [6,7,8]. Cersullo et al. [9] evaluated the effects of lack-of-fusion pores through artificial internal defects to estimate a critical defect size for the component failure. Various methods have been presented to develop correlations between the observed monotonic tensile data and the fatigue properties of conventional materials, e.g., in [10,11]. However, it has been difficult to develop a sufficiently robust relationship between tensile and fatigue properties since fatigue behavior is much more sensitive to microstructural defect characteristics than tensile behavior.
As a non-invasive method, X-ray-computed tomography could help to evaluate and measure inner defects with a 3D relationship to the sample geometry [3,12]. Using a surface determination procedure on the generated volume data, all geometric dimensioning and tolerancing callouts (GD&T) can be measured and a deviation related to a reference geometry can be calculated. Lifton et al. [13] verified the use of CT for roughness measurements of surface-opened internal structures, in which there is often no access to the tactile method. Although CT is a possible method of evaluating internal defects, deviations of the detected surface from internal structures cannot be traced without knowledge of the reference geometry. Iassonov et al. [14] investigated influences of thresholding with and without local adaption segmentation techniques to industrial and synchrotron X-ray CT images of porous materials. Comparing directly observed and imaged porosities showed that using different segmentation methods, as well as manually thresholding, led to different results. According to Jaques et al. [15], determining a global threshold gray value for the surface did not perfectly describe the material transition of closed inner defects as well. They recommended the allegation of a workflow and measurement uncertainty. Villarraga-Gómez et al. [16] compared the dimensional accuracy of CT measurements with coordinate measure machine probing points on internal features and determined a deviation of about 5 µm. Razaei et al. [17] investigated the effectiveness of different thresholding techniques in estimating porosity in carbonates and recommended the use of the Otsu method (ISO 50%) for surface determination in order to reduce deviations. In addition, the material, CT settings, imaging artifacts [18] and nonmelted powder had an impact on the contrast between cavities and material—and thus, also, on the surface determination. Without the use of a local adaptive thresholding method, deviations greater than 5 µm can be expected if the cavities are powder-filled. As such, an evaluation of internal features with surface determination can be assumed to be inappropriate. An alternative—one that could evaluate structures of unknown size, shape and position, with or without surface determination—is artificial intelligence, specifically AI-based porosity algorithms. As a commercial solution, the software VGStudioMax from VolumeGraphix offers several different algorithms, such as VGEasypore, which can (largely automatically) determine a gray value threshold to separate pores from the material, or VGDefX, which requires a manual estimation. Both of these algorithms use AI-based image recognition algorithms and thresholding [19] to determine structures independently from surface determination and calculate a probability criterion for the detected defects. Another possibility is the Only Threshold method, which does not use AI. Although the algorithm is predestined for this task, i.e., the assessment of defects with surface openings, agglomeration of defects, and powder filled cavities, the algorithm does not always consider all structures due to the porosity probability criterion. Thus, it could be correct for planned features but could also make analyses more difficult. Another problem is powder trapped in the cavities. Powder can have a lower density than the bulk material and influence the X-ray absorption, making a comparison using micrographs more complicated when using global thresholding, as described in [20]. This work investigated the possibility of analyzing powder-filled internal geometrical features using the CT porosity algorithm. The focus was on documenting a workflow, detailing methods by which to parametrize analyses for the detection of internal features for different AM materials. The the results were then compared with alternative porosity determination methods.
2. Materials and Methods
2.1. Samples
The examination of internal features was carried out using two different AM materials: polyamide 12 (PA12) and the titanium alloy Ti-6Al-4V (Ti64). In order to determine clear differences in the internal structures, two different PBF processes were used for the metal Ti64. This served to investigate influences and effects on detectability and evaluability, as well as to illustrate possible adjustments in the workflow. In addition, the material dependence of the CT porosity analysis was investigated using comparison with another material, PA12. The sample geometry had a cylindrical shape based on the recommendations of ASTM 1570.11 [21]. Due to the rotational symmetry, the transmission length for the X-rays were kept roughly constant during CT measurement, which had a beneficial effect on the occurrence of CT artifacts. The specimen had a height of 8.7 mm (without reference and support structures) and a diameter of 5 mm. On top of the cylinder, there was a 1-mm-high triangular recess with a 90° angle (Figure 1a black line and 1c), which served as a reference structure and orientation mark for micrographs and CT analyses. The internal features were designed as cylindrical cavities and are shown in Figure 1a, in the top view. The diameter of each cylinder was 1.5 mm. The height of the cylindrical cavities varied from 0.05 mm to 0.4 mm. These were located at different heights in the sample, with spacing measured from the top edge of one to the bottom edge of the next of 0.7 mm, as shown in Figure 1b. The lower height limit was related to the layer thickness in the application process. Assuming that the smallest feature would not be buildable due to the remelting rate, the height of the largest structure was determined to be high enough to produce an internal defect. All cavities were built four times in the same layer for statistical assessment of the manufacturing capability.
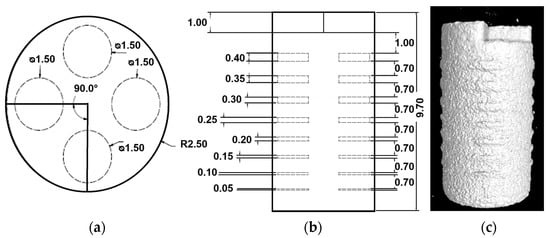
Figure 1.
(a) Cross-section (top view) of the sample with four planned inner structures; (b) cross-section (side view) of the sample, showing the position of the inner structures and the variation of the volume. (c) CT images of the build PA12 sample.
2.2. Manufacturing Processes
The samples were produced using three different additive processes. For the PA12 sample, a powder bed fusion of polymer (PBF-LB/P later referred as LBP) process was used. For Ti64 samples, an electron beam powder bed fusion (PBF-EB/M later referred as EBM) and laser-based powder bed fusion of metals process (PBF-LB/M, later denoted as LBM) was used. The process parameters are given in Table 1. Although the energy transfer values were different in the EBM and LBM methods, an attempt was made to approximate the parameters of both methods. As a stand-alone and non-comparable process, the parameters of the LBP process were optimized to the production of the component. For the EBM process, an electron-optic in situ imaging system (ELO) was available, and was described in more detail in [22]. For the production of the polymer sample, the experiments were conducted using PA12 powder PA 2200 from EOS GmbH (Krailling, Germany). The powder was used with a refreshing rate of 50% of used powder. The used powder was taken from overflow containers of previous experiments. Therefore, only a slight influence of high ambient temperatures on the powders and experiments was expected. For the EBM process, a plasma-atomized Ti-6AL-4V powder from Tekna Plasma Europe (Macon, France) was used, while for the LBM process, a plasma-atomized Ti-6AL-4V powder from AP&C (Saint-Eustache, Canada) was used. These were used with a powder fraction from 45 to 105 µm and from 20 to 40 µm, respectively.

Table 1.
Process parameters of EBM, LBM for the Ti64-samples, and LBP for the PA12 sample.
As all three processes were powder bed-based, the powder remained within the planned structure and was not removed. Since the powder had a lower density than the bulk material, it was assumed that a contrast difference would be detected on CT or, in certain circumstances, voids (or rather, pores) would be created by partial melting due to the remelting rate.
2.3. CT Measurement
The CT measurements of all samples were performed on an industrial X-ray computer tomograph Metrotom 1500 (Zeiss, Germany). The detector had a pitch of 2048 × 2048 pixels with a pixel pitch of 0.2 mm. The detector parameters were set to a gain of 16, integration time of 2000 ms. A prefilter made of copper, with a thickness of 0.5 mm, was used. The samples were rotated 360° with a step size of 0.2°, which corresponded to 1800 projection images in total. Because of material-specific X-ray absorption, the cathode parameters differed for PA12 and Ti64; this helped to achieve a maximum in contrast. As [23] recommends, the voltage should be set as low as possible and the current should be increased until a sufficient material contrast is achieved. For PA12, a voltage of 140 kV and a current of 150 µA were used, whereas 150 kV and 70 µA were used for Ti64. These settings resulted in focal spot sizes (Br) of 22 µm, and 7 µm, respectively, and led to native voxel sizes (vx) of 8 µm and 7.32 µm (manufacturer information), respectively. The CT parameters used were specific for the system utilized and could differ upon use with other CT devices; they also depended upon the sample size. The chosen parameter sets were related to the Zeiss CT CookBook [23], with a voltage of 180 kV and a current of 100 µm for Ti64 and [24] a voltage of 110 kV and a current of 130 µm for PA12, used on a different CT device. The images were saved in Unit16 format and reconstructed using a Feldkamp–Davis–Kress (FDK) reconstruction algorithm [25] with a Shepp–Logan filter.
2.4. Metrological Evaluation
The metrological processing for the gray value-based volume data was done using VGStudio Max Version 2022.2 (VolumeGraphix, Heidelberg, Germany). For the study, an automated workflow, with minimal or no user input and an advanced workflow with user input, was examined. A surface determination was carried out, after the CT scan and the reconstruction of the radiographic image on the 3D volume. Optionally, volume data filtering could be performed beforehand. After selecting a segmentation method and calculation, dimensional measurements could be carried out on the 3D volume, or the data set could be used for evaluation with a porosity algorithm. Without limiting the parameters or methods used, a workflow of this procedure is shown in Figure 2.
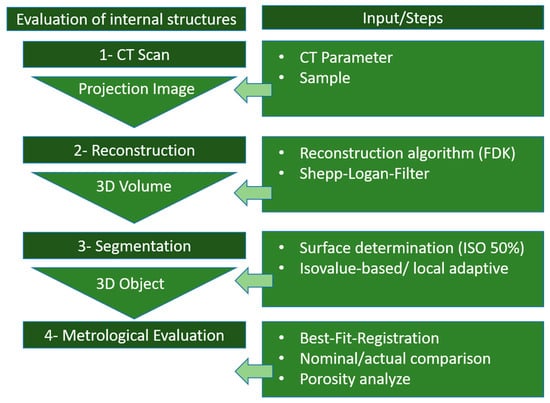
Figure 2.
Workflow of the CT analysis with metrological evaluation.
2.4.1. Voxel Data Filter
Optional filtering of the voxel data set could be provided to reduce noise, while internal structures and edges are preserved or highlighted. For this research, a non-local means filter [26] was used with a 1.0 smoothing factor and disabled opacity mapping. Since this was an unnecessary step, it was not included in the workflow in Figure 2.
2.4.2. Surface Determination
Isovalue-based method: The surface determination calculated the boundaries between the material and background by allocating a single gray value to the material and background. Using the isovalue-based method—based on the Otsu threshold method [27]—the material and background gray value levels could be automatically calculated. The surface line, with an interpolated subvoxel accuracy, was drawn at half of the gray values of both peaks in the histogram (ISO 50%) by default. The single gray value represented the mean of the material and background peak of the gray value histogram, respectively. The surface line/area could be used for probing or as a start contour for porosity analysis.
Advanced (classic) method: A calculated surface with the advanced approach determined the material boundary concerning local gray value, comparable to the Kittler–Illingworth method [28]—in contrast to the global assessment of the isovalue-based method. In comparison, the advanced surface determination reduced the influences of local deviations like artifacts and reconstructed the geometry of the sample more closely [29]. Furthermore, the mean gray value could be calculated manually using regions of interest (ROIs).
2.4.3. Coordinate Measurement Functions
This measurement tool applied a fit of a geometry element to the determined surface mesh and allows a calculation of the deviation from the standard geometry. Concerning the planned internal structures, shown in Figure 1a, a cylinder fit or a freeform surface fit was suitable. The chosen fit for both, with the least squares method, with manually set initial fit points with auto-expand options, for a disk with a diameter of 0.06 mm and a step width of 0.015 mm for each point. The sampling method used a step width of 0.0075 mm and a maximum number of probing points of 10,000. The fit was performed with two iterations and the fit points were filtered with a search distance of 0.3 mm, a maximum gradient of 20° and a safety distance of 0.015 mm.
2.5. Porosity Analysis
The porosity analysis was developed to aid in finding internal defects like pores and inclusions within the voxel data set. The algorithm was built in two filter stages. On the one hand, a threshold value criterion for the gray value was checked. Potential defects were grouped if there was a connection to the next one (nearest neighbor). Optionally, the results were filtered by user-defined restrictions. Image processing algorithms calculated a probability value evaluating all potential defects. For the evaluation, three different algorithms were available. The differences have been mentioned herein.
VGEasypore: This porosity algorithm can be automatically performed by estimating a global threshold (absolute method) or a locally-defined threshold (relative method) and used for automatic workflow. However, this analysis could also be used in cases involving defects with connections to the surrounding background where a surface sealing function is not available. In addition, the algorithm has no noise reduction function, which could increase the detected results. The surface determination was implemented as start contour for the search, which could not be disabled. Since noise increases detectable porosity and the estimation of the threshold was not documented, it was likely that the analyzer would calculate too high a porosity, in terms of volume and number in the bulk area of the component. Additionally, it could calculate, on the other hand, too low a porosity in the edge area, due to the lack of surface sealing. Furthermore, the AI-based filtering of defects can only be partially influenced, which could lead to loss of defects.
VGDefX: This algorithm uses a global threshold value, determined by the material gray value from the histogram and adjustable as a deviation from the mean value in units of the standard deviation σ. However, the maximum pores gray value has to be set manually. The algorithm can take advantage of the surface determination in the form of a start contour for the search, or as a filter for clustering for potential defect candidates. This option can be disabled to improve pore detectability. Furthermore, the algorithm can use a surface sealing and noise reduction function to improve the detection of defects near the surface or with low gray value contrast, e.g., small pores. Compared to VGEasypore, this permitted a much better handling of noise and rough surfaces.
Only Threshold: As an additional option, the algorithm can be performed without the algorithm filtering methods using an Only Threshold method, which does not apply any filters to the initial result. This allowed for a direct comparison with the results of VGDefX- and AI-based filtering.
All porosity analysis methods were performed with default settings. These provided the surface finding as a starting point for the search for defects, in addition to filtering with regard to the shape of the results, such as their sphericity or compactness. The minimum volume of a defect was limited to 8 vx and the maximum to a volume of about 5,100,000 vx. The probability criterion was set to 1, which excluded defects with probability values lower than 1. The edge distance filter considered all defects with distances of 0 to 8000 mm. Defects created by CT artifacts were not ignored and the option “Check neighbourhood” was enabled, which included defects influenced by artifacts. Modifications of the settings and their impacts on results were discussed in Section 3.
3. Results
The investigation aimed to find a suitable workflow, as shown in Figure 2, to evaluate internal structures and features. Therefore, a surface determination was done on all samples using the isovalue-based method. An optional non-local means of volume filtering was applied to the data as needed. In the next step, a geometry fit was executed on the surface data, and the geometry was evaluated. In addition, the main focal points were the testing of the porosity algorithms and adaptations of the settings to detect internal structures. Although dimensional accuracy was certainly considered important, the analyses focused on improving the possibility of detection. An assessment was made comparing the results with micrographs and pycnometer measurements for PA12 and Ti64 (LBM, EBM) and ELO only for Ti64 (EBM).
3.1. Metrological Evaluation
The internal cavities were evaluated based on geometric fits, as described in Section 2.4.3, after a surface determination. Figure 3 shows deviations in the determined surface area of one internal cavity at the height of 7.5 mm in Ti64 (EBM). Figure 3d–f used different calculation workflows. Even if the background value was shifted to the mean gray value of large internal voids, i.e., using the mean gray value of the ROIs or using a local iterative method, it was assumed that the transition likely did not fully describe the geometric shape of the structures using an ISO 50% value. It was assumed that this was caused by unmelted powder, which had different CT contrast than the bulk material due to differences in density. Although the surface, shown in Figure 3c,f,I, showed promise for possible evaluation of internal structures, the gray value, determined by the ROI, depended on influences like CT artifacts. It was calculated with only a few voxels due to the limited size, which had an impact on the reproducibility of the results. The results of Ti64 (LBM) were very similar to Ti64 (EBM). With PA12, as shown in Figure 3a–c, on the other hand, the influence of the choice of surface determination on the metals was significantly lower, which was attributed to the low selectivity. Nevertheless, an advanced (classic) surface determination with an iterative local weighting, see Figure 3b,e,h, was the best, most reliable choice for the examination of internal structures, since there was no need for user input. It was used for all subsequent evaluations.


Figure 3.
CT cross-section of internal structures in PA12 (a–c), Ti64 (LBM) (d–f) and Ti64 (EBM) (g–i). The white lines show the determined surface calculated: (a,d,g) with the Isovalue-based method (ISO 50%); (b,e,h) with the iterative advanced (classic) method (ISO 50%) and the use of ROIs of the background and material; and (c,f,i) with the advanced (classic) method (ISO 50%) and ROIs of the material and the gray value of an internal defect.
In consequence, using the surface determination line to fit the geometry provided too few supporting points of the actual structure for the automatic orientation of the ideal geometry. Figure 4a demonstrates the use of a circular fit using the least square (LS) method to determine the diameter of the internal structure for the chosen CT slice, while the cylindrical fit (LS) seen in Figure 4b did not follow the direction of the geometry correctly. Adding more supporting points manually did not improve the evaluation. This surface-dependent evaluation complicated the estimation of the volume and surface area since the structure could be divided into several smaller parts.
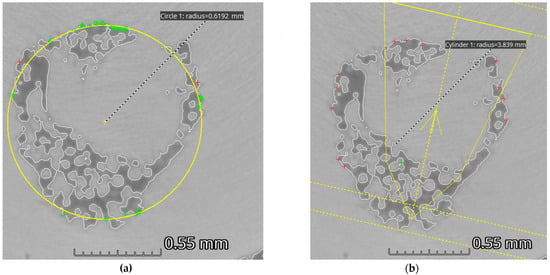
Figure 4.
Zoomed CT slice of an internal feature of Ti64 (EBM) at the height of 7.5 mm. (a) Circular Gaussian least square fit on the surface points. (b) Cross-section of the cylindrical fit on the surface of the internal structure perpendicular to the cylindrical axis.
Using the best fit method facilitated an assessment of the deviation related to the CAD template. This method was sensitive to the deviation of the external shape, especially the reference structure on top of the sample. Figure 5a shows a mismatch in the CAD model caused by manufacturing deviations of the reference structures. Performing a nominal/actual comparison with an aligned template did not lead to beneficial results, since the manufacturing process initiated channel opening and caused deviations in the position of the internal structures, as shown in Figure 5b.
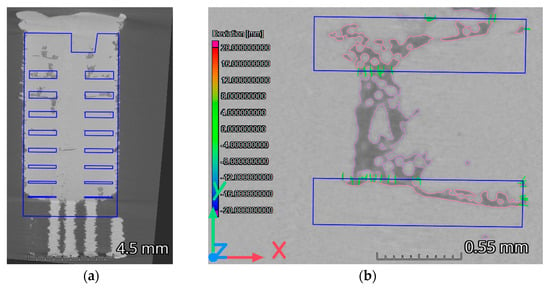
Figure 5.
Dependence of best fit registration of the CAD template on manufacturing deviation on the reference structures, on the top for the intersection plane (a). (b) Nominal/actual comparison of the CAD model and Ti64 (EBM).
3.2. Volume Filtering
Analyzing material with low X-ray contrast values or rough surfaces can lead to an incoherent component surface determination. Subsequent porosity analyses cannot be correctly undertaken. Starting with a surface determination as described in Section 2.4.2 and performing the VGEasyPore analysis, as described in Section 2.5, showed a great influence on the result since the algorithm used the surface data to determine closed voids in the material. Due to noisy gray data sets, a porosity analysis can fail for materials with low X-ray contrast, e.g., for PA12. Figure 6a (inset) shows that the surface determination for PA12 (white line) was separated into several smaller volumes instead. Performing a porosity analysis enabled the search for voids inside the separated volume (green area) and ignored nearly the entire component. Volume filtering is one way to avoid inhomogeneous surface determinations. Filters can have an impact on the selectivity between material and background, especially in reducing noise [30].

Figure 6.
Cross-section of PA12 sample at a height of 7.5 mm. (a) Performing VGEasyPore algorithm on the noisy surface data set (green) with the aligned CAD model (blue) to locate the internal structures. (b) Cross-section of the voxel data of PA12 after non-local-means filtering.
The non-local-means volume filter reduces noise and sharpens edge transitions, as shown in Figure 5b. As such, it affects surface determination. Furthermore, it has a smoothing effect on surface roughness, which can close defects with connections to the surface. For this study, volume filtering was used as a precaution for all volume data sets.
Porosity Analysis
The main focus of this examination was to adapt the parameters of the porosity algorithms as best as possible in order to evaluate internal structures. Using the default settings, as described in Section 2.5, the best possible results, in terms of maximum detection of internal structures, minimum noise and fewer process-related pores were considered. The changes to the default settings for each algorithm are displayed in Table 2. The outcome was colored with respect to the volume, ascending from small volume in blue (min. 8 vx) to red (max. 11,220 vx). Using the direction variability with a normal vector aligned to the building direction (z-axis) and a resolution of 1 vx/slice, the porosity within the cross-section in the perpendicular xy plane was summed up and plotted as a function of the z-axis, as seen in Figure 7a for PA12 and Figure 7b for Ti64 (LBM). The direction depending porosity was measured and plotted for VGEasypore (orange), VGDefX (yellow) and Only Threshold (purple).

Table 2.
Modification on the default setting of the porosity algorithm VGEasyPore, VGDefX, and the Only Threshold method for the Ti64-samples and the PA12 sample.
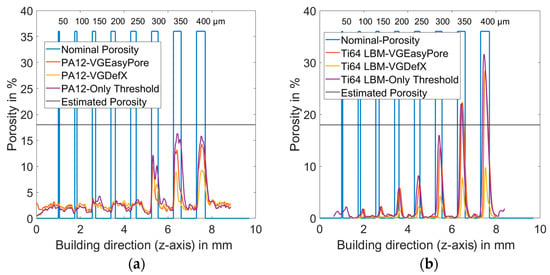
Figure 7.
Direction variability of the porosity along the building direction for (a) PA12-sample and (b) Ti64-sample (LBM), calculated using VGEasyPore (orange), VGDefX (yellow), and the Only Threshold Method (purple). The nominal porosity (blue) of the CAD is aligned to the data and an estimated porosity value is drawn in black.
The theoretical planned nominal porosity of the CAD file was plotted in blue. According to the data sheets of the powder used, the bulk density of the unmelted powder was about half. Estimating the realistic volume of a powder-filled internal structure with respect to the powder volume, only half of the nominal porosity (black solid line) could be achieved within the planned structures (blue line). The results of the porosity algorithms are shown in Figure 8a–i.
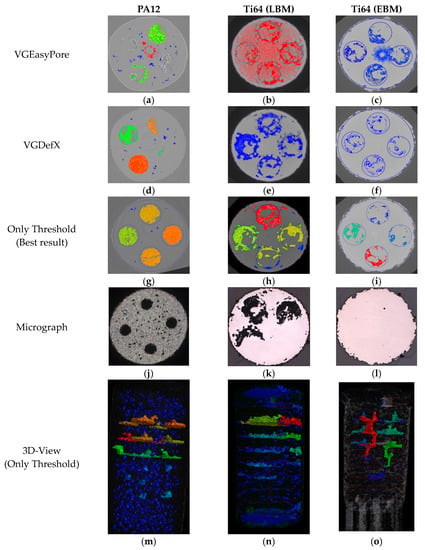
Figure 8.
(a–i) Cross-sections of the results of the porosity algorithms (colored area) at a height of 7.5 mm. VGEasyPore (a–c), VGDefX (d–f) and Only Threshold methods (g–i). (j–l) Micrograph images of the analyzed area. (m–o) The best possible result for the 3D evaluation of internal structures.
4. Discussion
4.1. VGEasyPore
Considering the automatic calculation of the gray value threshold, this analysis already took internal structures into account when the probability threshold was set to zero. Noise (Ti64 LBM) and ring artifacts (PA12 red area, Ti64 EBM) strongly influenced the results of the detected porosity, as seen in Figure 8a–c. According to the P203 guideline [31], the deviation of the threshold value from the mean material gray value was not high enough, since material voxels were already taken into account in the analysis area. These could be classified as false detections due to their size and shape. Although changing the global threshold to relative or using the noise particle function can impact detection efforts, there is no parametrization that completely removes noise and keeps all internal structures within the analyzing area at the same time. This problem could be solved by using adjusted volume filtering with a greater smoothing effect on the material peak. Since the Ti64 EBM measurement was more strongly influenced by ring artifacts, a greater smoothing factor of the non-local means filter could not provide significant improvement;. Ring artifacts were due to systematic influence and the filter primarily filtered out statistical effects. Changing the internal cleaning within the calculation of the surface determination, or at the porosity algorithm, could reduce this influence; however, the position of the ring artifact center contacted some internal structures. This would have an impact on the results. As illustrated in PA12 in Figure 8a, some bigger structures were missing. Considering the absence of the structures in the analyzed area, most of the defects were rejected, caused by an opening to the sample surface. Further variations of the parameters, such as relative threshold values or surface sealing, did not have a significant impact on closing these connections. Although the filter effectivity of noise, issues with connections to the surface and the gray value threshold were not estimated perfectly, the VGEasyPore algorithm was able to manage the detection of internal defects with a minimum of user adjustments.
4.2. VGDefX
Using the VGDefX algorithm with default settings, it was necessary to define a manual threshold value. In consideration of the size of the internal defects, a grey value with a difference of -1 times σ from the material peak of the gray value histogram and a probability criterion of 0 offered the best prerequisites to detect all internal structures. Even though the threshold was not high enough to suppress noise particles, better separation between noise particles and defects could be achieved with the VGDefX algorithm (see Figure 8e), since the noise reduction function was available. CT artifacts like ring artifacts could be eliminated for Ti64 (EBM) without the use of a ring artifact correction, as seen in Figure 8f. Nevertheless, surface-opened defects were not included in the analyzing area. Similarly to the VGEasyPore analyses, for PA12, the same internal structures were missing. Enabling the surface sealing function, the main part of the material-defect transition could be added to the analyzing area, which allowed for surface determinations and dimensional measurements, as shown in Figure 9a. Although the contours of the internal structures were accessible, the volume of obtained defects remained almost empty, which led to the results shown in Figure 9b and Figure 8d. Concerning the dimensional accuracy, the shape was affected by the surface determination line, which led to an underestimation of the actual volume and size in relation to the analysis, seen in Figure 3b. Switching the material definition from “use determined surface” to “defined manually” (same threshold) led to an absolute loss of the internal structures, demonstrated in the results shown in Figure 9c, while the analyzing area remained similar to that shown in Figure 8a. In comparison, the VGDefX analysis calculated a smaller volume for internal defects, which can be seen in Figure 7.

Figure 9.
CT cross-section of PA12. (a) Analyzing area (yellow) of the considered defects with the VGDefX algorithm. (b) Results of the VGDefX analysis, obtained using the settings mentioned in Table 2 for PA12, and (c) results of the VGDefX analysis obtained by switching the material definition to manual.
4.3. Only Threshold-Method
The remaining analysis method, Only Threshold, was performed with similar settings as VGDefX, except for the fact that the threshold was adjusted manually without reference to the gray value histogram. To determine a capable threshold value, the threshold value was manually increased, stepwise, until the analyzing area reached the boundaries of the aligned CAD template in the top view cross-section—instead of using the surface line of a clearly recognizable defect, as recommended in P203 [31]. This procedure maximized the probability of evaluation of inner structures, whereby a significantly-increased global porosity could be expected. However, since the defects differed in size, volume and position compared to process-related porosity, a filtering of the results may be possible. Setting a threshold value equal to approximately −2 x σ, a probability criterion of 0 and disabling the “use of the surface determination“ setting, the detection of internal structures in PA12 and Ti64 (LBM) was maximized and the volume was fully taken into account. The same settings used for Ti64 (EBM) removed most of the noise from the analysis region and larger internal structures.
These structures were the same as those sorted out by the VGDefX algorithm when selecting a probability criterion greater than 0. These defects showed extensive surface openings, which could not be taken into account by changing the parameterization. A cylindrical ROI that followed the surface line of the sample, with a spacing of 10 voxels as a workaround, could be used as a surface-sealing method without a significant impact on the total porosity calculation. These results are displayed in Figure 8g–i. The calculated porosity, in relation to the building direction along the z-axis, is displayed in Figure 7 (purple line). A similar result was determined for the Ti64 samples using the VGEasyPore and Only Threshold methods. In comparison to the PA12 sample, there were differences in the calculated porosity of the larger internal structures, which could be explained by the missing defects in the results of the VGEasypore analysis.
4.4. Evaluating the Porosity Measurement
In order to investigate the accuracy of the parameterization of the porosity algorithm, a micrograph was created at the height of the largest internal defect, and the porosity was determined by thresholding. Please note that the black areas in the ELO image could have been generated due to pores or powder. The results for the micrographs are shown in Figure 9j,k,l. For the porosity algorithms, the maximum value achieved within the planned structure from Figure 7 at the same height was used for comparison.
The results of VGEasyPore and the Only Threshold method showed good agreement with the micrographs for the Ti64 LBM. For the Ti64 EBM, the micrograph showed almost no porosity. Assuming that the micrograph missed the internal structure, a comparison was made with the in-process ELO measurement, taken during the build process and shown in Figure 10a. The porosity shown here was usually overestimated due to the subsequent temperature effect of the overlaying layers. It was therefore likely that the porosity could have changed in shape and position and was at least plausible in relation to the micrograph shown in Figure 8l. Figure 10b shows a powder-filled cavity before it was fused with the next layer, seen in Figure 10c, after closing the internal feature with one layer. A comparison of the porosity from the ELO image, in Figure 10c, achieved a porosity of 22%, which was significantly higher than the measured values from the CT. However, as the ELO provided a snapshot of the porosity during the building process, it commonly overestimated porosity.

Figure 10.
In situ ELO images of the Ti64 (EBM) sample during the building process at a height of 7.5 mm. (a) Image of a layer between two planned internal structures. (b) Image of the internal structure filled with powder. (c) Image of a layer above the internal structure.
The micrograph of the PA12 sample showed circular defects, but these were significantly smaller in diameter. At the same time, the proportion of process-dependent pores appeared to be larger. Thus, the cross-section of the micrograph cut the bulging of the defects (visible in Figure 8m) and not the actual defect in particular. Nevertheless, the analysis still needs to be optimized, since the results strongly depended on the goodness of the registration, as shown in Figure 5, and shape deviations of the reference structure. An evaluation of the component porosity in the micrograph, as well as the total component porosity, was carried out by pycnometry measurement, according to [32]; the results are shown in Table 3 with corresponding CT analyses.

Table 3.
Comparison between the porosity, calculated with porosity algorithms, and micrographs at the middle of the largest internal structure (400 µm).
As seen in Figure 7, the results of the CT analysis methods differed greatly. The best agreement of porosity in the micrograph was achieved by the Only Threshold algorithm for PA12 and Ti64 (LBM. A much better agreement was achieved in the evaluation of the total component porosity for both Ti64 samples when comparing the CT data with the pycnometer measurement. Here, all porosity algorithms showed good agreement—and the Only Threshold method showed the lowest deviation. As the CT analysis aimed to detect as many internal structures as possible, and these were the major contributors to porosity, it was not surprising that this also led to better agreement. However, there was a great deviation in the case of PA12, which could be explained by the low X-ray contrast, which could have influenced the filter operation and the surface determination, thereby impacting the material volume calculation.
5. Conclusions
5.1. Recommendation for Metrolocigal Assessment with CT
- Without going further into the CT scan, a volume filtering method like the non-local means method was considered a useful tool with which to prepare the volume data for surface determination, since the transition between material and background/defects could be improved.
- Regarding surface determination, the transition between the material and internal defects was influenced by the chosen method of calculation. Although optimization of the transition could be achieved using an ROI-based iterative surface determination with the mean gray value of an internal defect, better replicability could be accomplished with an automatic calculation of the mean value of the background peak.
- Based on the differences in surface determinations, the evaluation should be performed without the use of the surface determination as a starting point for the porosity algorithm.
5.2. Recommendations on the Procedure for Measuring Internal Structures
In summary, a recommendation for a procedure for analyzing internal defects was derived from the results of different materials, processes and analyses. The workflow illustrated in Figure 2 should be added to the workflow shown in Figure 11 for the analysis of CT porosity. For the adaption of the algorithm there were three main steps:
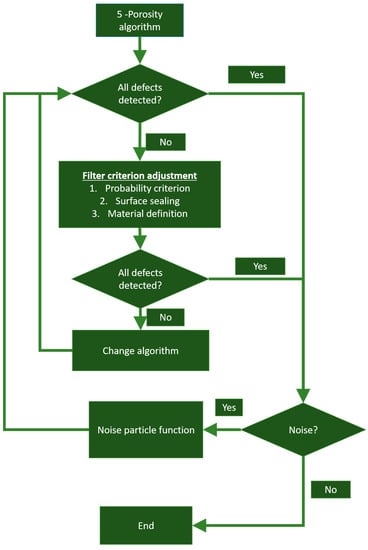
Figure 11.
Workflow of the parameterization of the CT porosity algorithm to improve the detection of internal powder filled features in Ti64 and PA12.
- Reduce the filter criterions e.g., the material threshold to add internal defects to the analyzing area.
- Disable filtering of the results due to AI. Automatically estimating or manually setting the threshold value can influence the detectable volume and shape of the internal structures and noise. The probability criterion must be set to 0.
- Close surface-connected defects.
Among the three algorithms examined, the Only Threshold method was able to fulfill the three steps, filtering noise efficiently and considering contrast transitions by disabling the use of surface determination. One major problem encountered while employing this analyzing method, however, was the selection of the threshold value, which had to be set manually. In contrast, VGEasyPore performed with an estimated threshold value, achieving very similar results with less user input. However, this method had to deal with more noise.
Author Contributions
T.H. oversaw project administration, contributed to the conceptualization, writing, editing, review and supervision process. M.M. contributed to the conceptualization, writing and supervision process. B.B. contributed to the conceptualization, writing (original draft), data curation, formal analysis, investigation methodology, software, validation and visualization. S.G., R.R., C.B. and J.R. contributed samples, investigations, resources, software and visualization. T.H., D.D., M.S. and C.K. contributed supervision, subproject administration, editing, funding acquisition and the review process. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 61375930–SFB814, Subproject B2, B3, B5, and C4. This financial support is gratefully acknowledged.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Support from the Erlangen Graduate School in Advanced Optical Technologies (SAOT) in the framework of DFG’s excellence initiative is also gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klahn, C.; Leutenecker, B.; Meboldt, M. Design for Additive Manufacturing—Supporting the Substitution of Components in Series Products. Procedia CIRP 2014, 21, 138–143. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; Du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Villarraga-Gómez, H.; Peitsch, C.; Ramsey, A.; Smith, S. The Role of Computed Tomography in Additive Manufacturing. Am. Soc. Precis. Eng. 2018, 69, 201–209. [Google Scholar]
- Du Plessis, A.; Yadroitsava, I.; Yadroitsev, I. Effects of defects on mechanical properties in metal additive manufacturing: A review focusing on X-ray tomography insights. Mater. Des. 2020, 187, 108385. [Google Scholar] [CrossRef]
- Tammas-Williams, S.; Withers, P.J.; Todd, I.; Prangnell, P.B. The Influence of Porosity on Fatigue Crack Initiation in Additively Manufactured Titanium Components. Sci. Rep. 2017, 7, 7308. [Google Scholar] [CrossRef]
- Zhang, L.; Lifton, J.; Hu, Z.; Hong, R.; Feih, S. Influence of geometric defects on the compression behaviour of thin shell lattices fabricated by micro laser powder bed fusion. Addit. Manuf. 2022, 58, 103038. [Google Scholar] [CrossRef]
- Gapinski, B.; Wieczorowski, M.; Grzelka, M.; Arroyo Alonso, P.; Bermudez Tome, A. The application of micro computed tomography to assess quality of parts manufactured by means of rapid prototyping. Polimery 2017, 62, 53–59. [Google Scholar] [CrossRef]
- Du Plessis, A.; Yadroitsava, I.; Yadroitsev, I.; Le Roux, S. X-Ray microcomputed tomography in additive manufacturing: A review of current technology and applications. 3D Print. Addit. Manuf. 2018, 5, 3. [Google Scholar] [CrossRef]
- Cersullo, N.; Mardaras, J.; Emile, P.; Nickel, K.; Holzinger, V.; Hühne, C. Effect of Internal Defects on the Fatigue Behavior of Additive Manufactured Metal Components: A Comparison between Ti6Al4V and Inconel 718. Materials 2022, 15, 6882. [Google Scholar] [CrossRef]
- Masuo, H.; Tanaka, Y.; Morokoshi, S.; Yagura, H.; Uchida, T.; Yamamoto, Y.; Murakami, Y. Effects of Defects, Surface Roughness and HIP on Fatigue Strength of Ti-6Al-4V manufactured by Additive Manufacturing. Procedia Struct. Integr. 2017, 7, 19–26. [Google Scholar] [CrossRef]
- Gates, N.; Fatemi, A. Friction and roughness induced closure effects on shear-mode crack growth and branching mechanisms. Int. J. Fatigue 2016, 92, 442–458. [Google Scholar] [CrossRef]
- Caillé, J.-M.; Salamon, G. (Eds.) Computerized Tomography; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Lifton, J.; Bakar, A.A.; Tan, J.T.; Malcolm, A. Internal Surface Roughness Measurement of Metal AM Channels via X-ray Computed Tomography: A Case Study. In Proceedings of the Singapore International NDT Conference & Exhibition, (SINCE 2022), Singapore, 7–8 November 2022. [Google Scholar]
- Iassonov, P.; Gebrenegus, T.; Tuller, M. Segmentation of X-ray computed tomography images of porous materials: A crucial step for characterization and quantitative analysis of pore structures. Water Resour. Res. 2009, 45, W09415. [Google Scholar] [CrossRef]
- Jaques, V.A.J.; Du Plessis, A.; Zemek, M.; Šalplachta, J.; Stubianová, Z.; Zikmund, T.; Kaiser, J. Review of porosity uncertainty estimation methods in computed tomography dataset. Meas. Sci. Technol. 2021, 32, 122001. [Google Scholar] [CrossRef]
- Villarraga-Gómez, H.; Lee, C.; Smith, S.T. Dimensional metrology with X-ray CT: A comparison with CMM measurements on internal features and compliant structures. Precis. Eng. 2018, 51, 291–307. [Google Scholar] [CrossRef]
- Rezaei, F.; Izadi, H.; Memarian, H.; Baniassadi, M. The effectiveness of different thresholding techniques in segmenting micro CT images of porous carbonates to estimate porosity. J. Pet. Sci. Eng. 2019, 177, 518–527. [Google Scholar] [CrossRef]
- Du Plessis, A.; Le Roux, S.G.; Waller, J.; Sperling, P.; Achilles, N.; Beerlink, A.; Métayer, J.-F.; Sinico, M.; Probst, G.; Dewulf, W.; et al. Laboratory X-ray tomography for metal additive manufacturing: Round robin test. Addit. Manuf. 2019, 30, 100837. [Google Scholar] [CrossRef]
- Abera, K.A.; Manahiloh, K.N.; Nejad, M. The effectiveness of global thresholding techniques in segmenting two-phase porous media. Constr. Build. Mater. 2017, 142, 256–267. [Google Scholar] [CrossRef]
- Payel, R.; Saurab, D.; Nilanjan, D.; Gaotami, D.; Sayan, C.; Ruben, R. Adaptive thresholding: A comparative Study. In Proceedings of the 2014 International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kanyakumari District, India, 10–11 July 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- ASTM E1570-11; Standard Practice for Computed Tomographic (CT) Examination. ASTM International: West Conshohocken, PA, USA, 2011.
- Bäreis, J.; Semjatov, N.; Renner, J.; Ye, J.; Zongwen, F.; Körner, C. Electron-optical in-situ crack monitoring during electron beam powder bed fusion of the Ni-Base superalloy CMSX-4. Prog. Addit. Manuf. 2022, 7, 1–6. [Google Scholar] [CrossRef]
- ZEISS. ZEISS CT Cookbook-English Edition: Best Practice Guide for ZEISS METROTOM Settings; ZEISS: Jena, Germany; Available online: https://shop.metrology.zeiss.de/INTERSHOP/web/WFS/IMT-DE-Site/de_DE/-/EUR/ViewProduct-Start?SKU=600033-2022-016&CategoryName=240100&CatalogID=200000&ExtendedNavigation=true (accessed on 15 March 2023).
- Bellens, S.; Vandewalle, P.; Dewulf, W. Deep learning based porosity segmentation in X-ray CT measurements of polymer additive manufacturing parts. Procedia CIRP 2021, 96, 336–341. [Google Scholar] [CrossRef]
- Feldkamp, J.A.; Davis, J.C.; Kress, J.W. Practical cone-beam algortihm. J. Opt. Soc. Am. 1984, 1, 612–619. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Sapiro, G. Fast image and video denoising via nonlocal means of similar neighborhoods. IEEE Signal Process. Lett. 2005, 12, 839–842. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Kittler, J.; Illingworth, J. Minimum Error Thresholding. Pattern Recognit. 1986, 19, 41–47. [Google Scholar] [CrossRef]
- Cho, S.; Haralick, R.; Yi, S. Improvement of kittler and illingworth’s minimum error thresholding. Pattern Recognit. 1989, 22, 609–617. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. A Non-Local Algorithm for Image Denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 60–65, ISBN 0-7695-2372-2. [Google Scholar]
- Bundesverband der Deutschen Gießerei-Industrie e.V. BDG. BDG-Richtlinie P203: Porositätsanalyse und -Beurteilung Mittels Industrieller Röntgen-Computertomographie (CT); Bundesverband der Deutschen Gießerei-Industrie e.V. BDG: Düsseldorf, Germany, 2019. [Google Scholar]
- DIN EN ISO 1183-3:2000-05; Kunststoffe—Bestimmung der Dichte von Nicht Verschäumten Kunststoffen—Teil 3: Gas-Pyknometer-Verfahren. Beuth Verlag: Berlin, Germany, 2000; 83.080.01. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).