Design Optimization of Hot Isostatic Pressing Capsules
Abstract
1. Introduction
2. Methodology
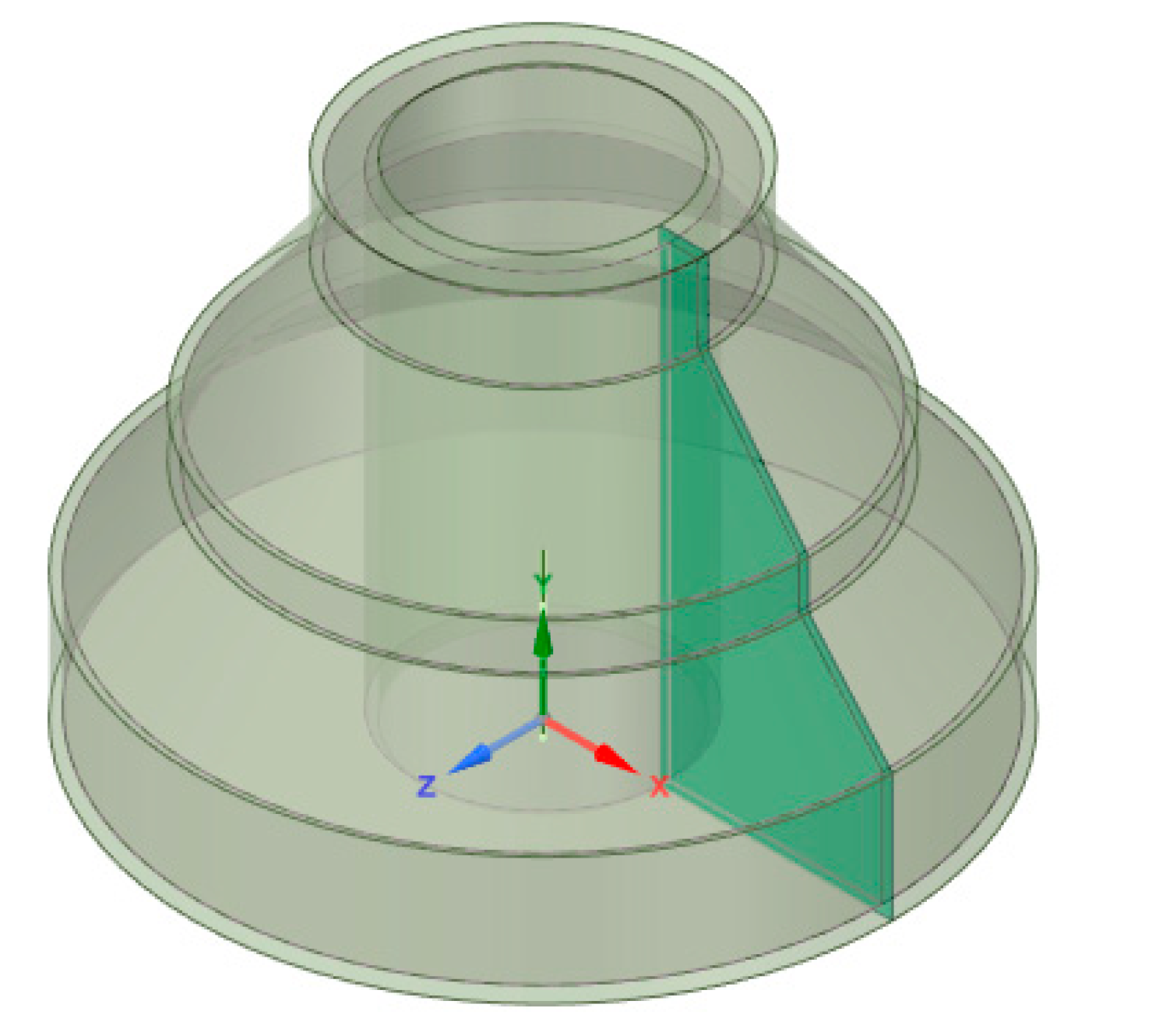
2.1. The Desired Component
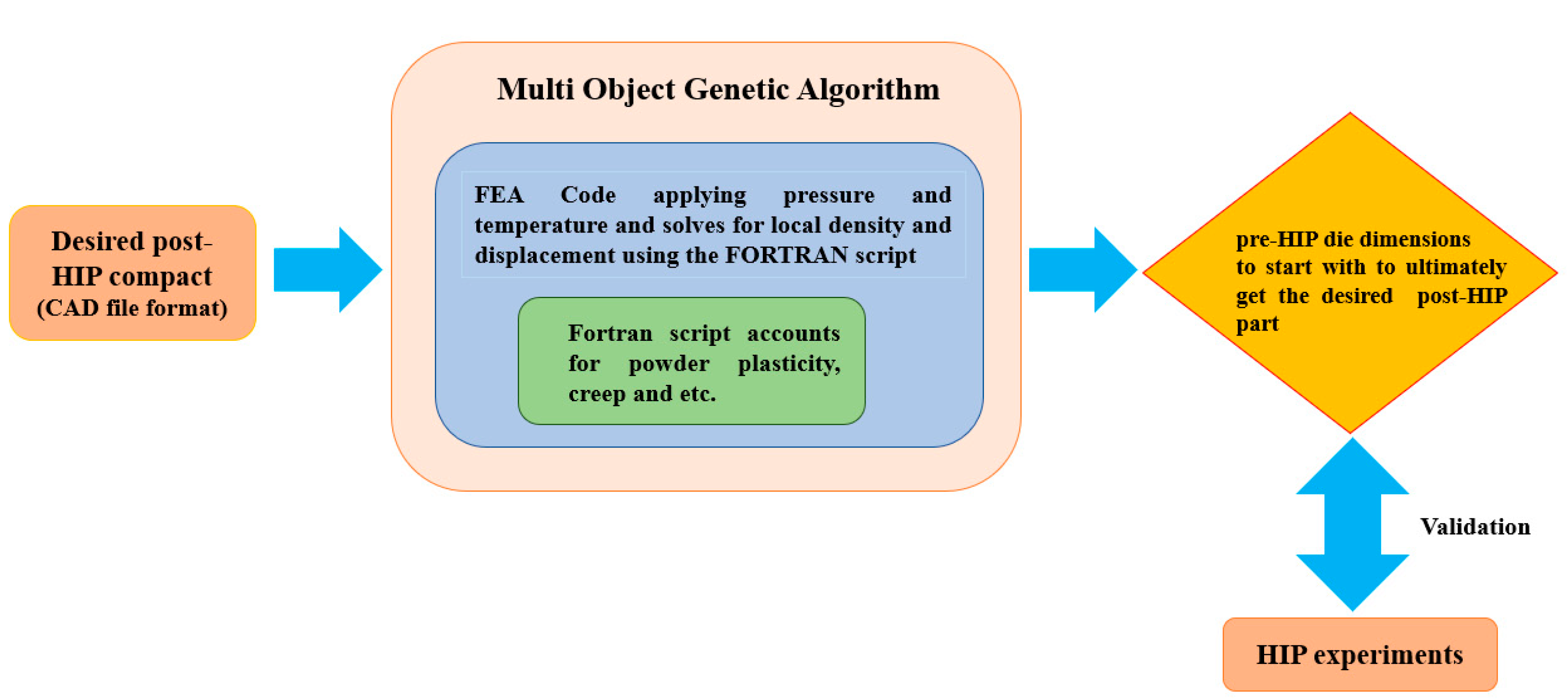
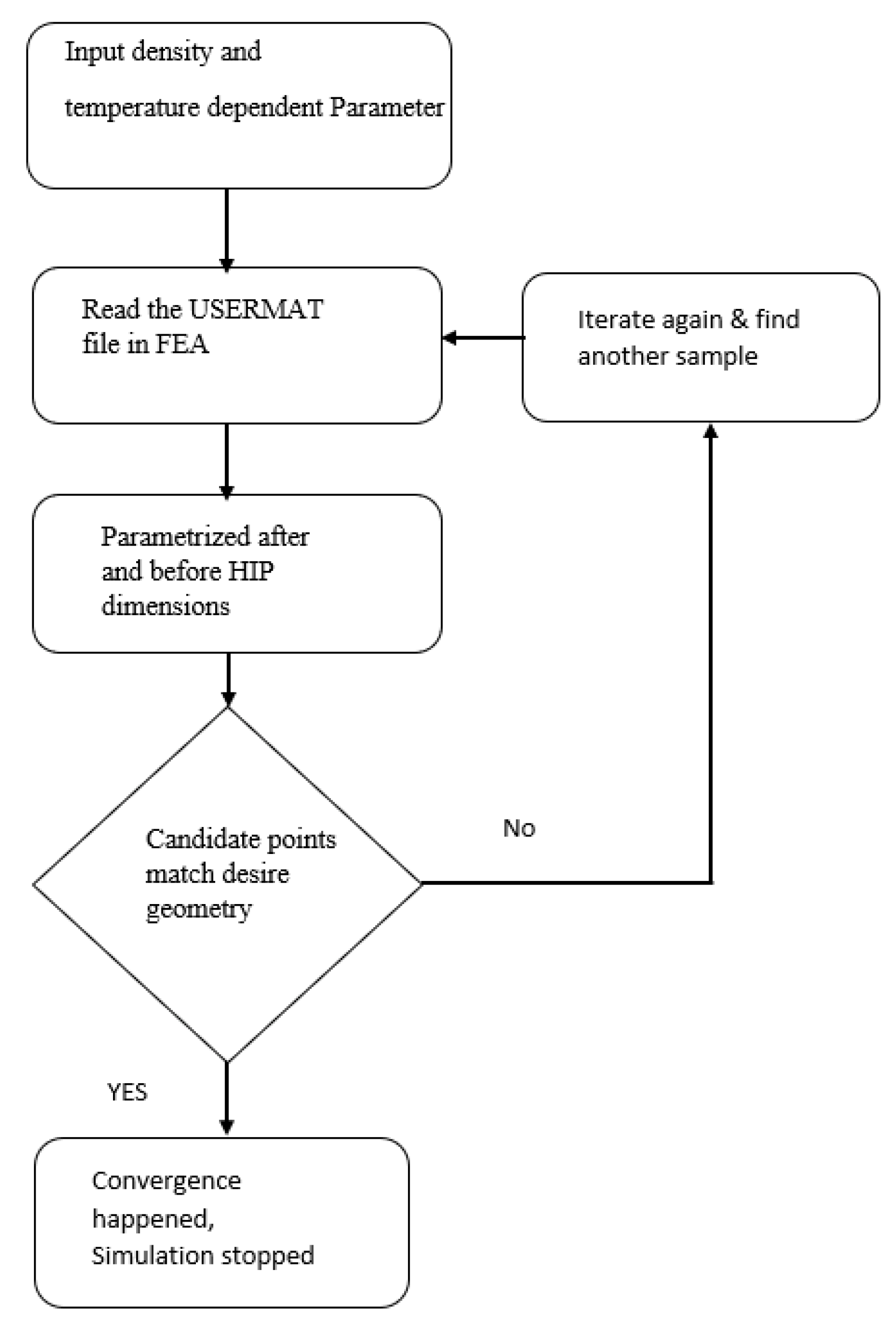
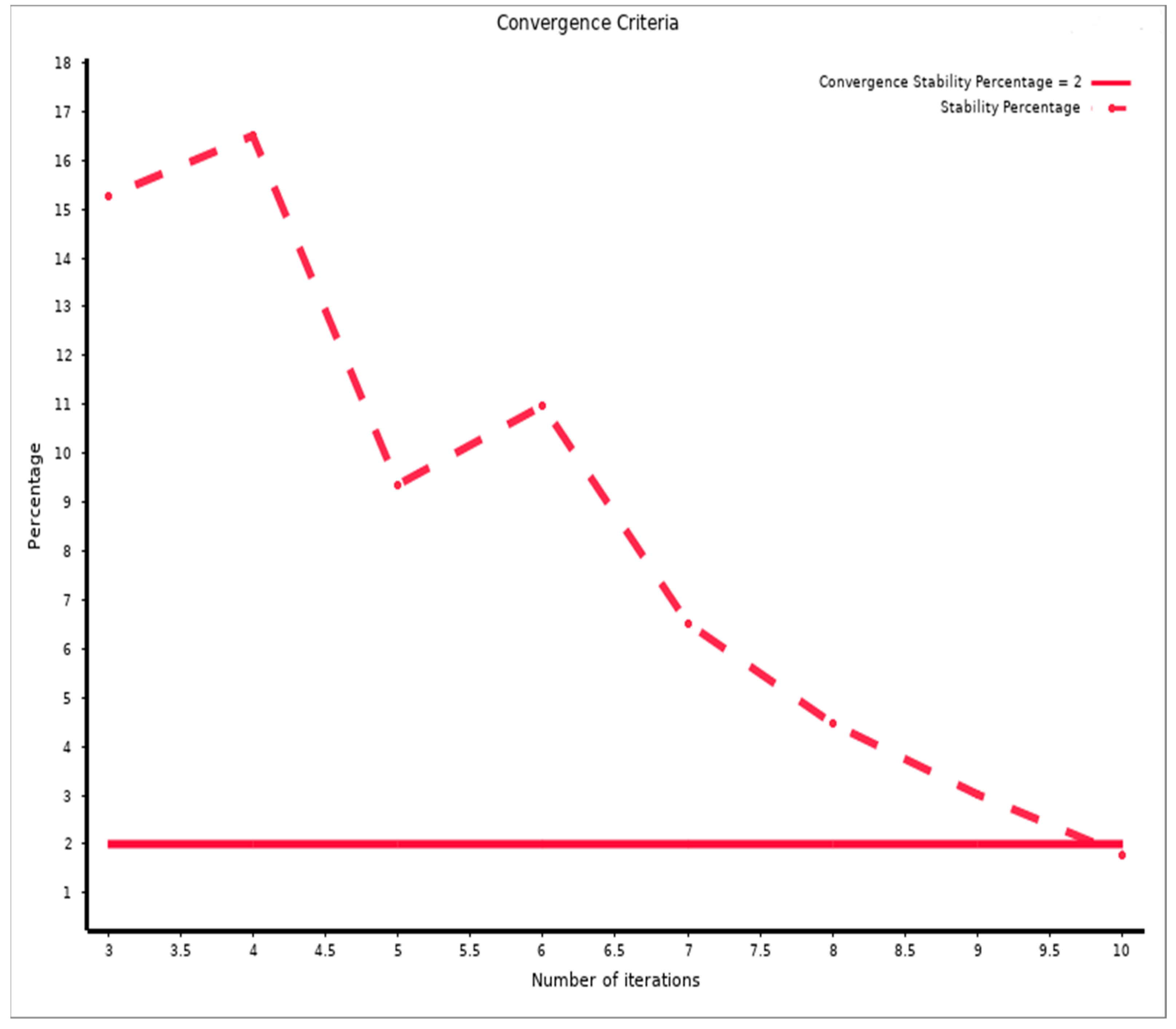
2.2. The Optimization Procedure
2.3. Constitutive Model
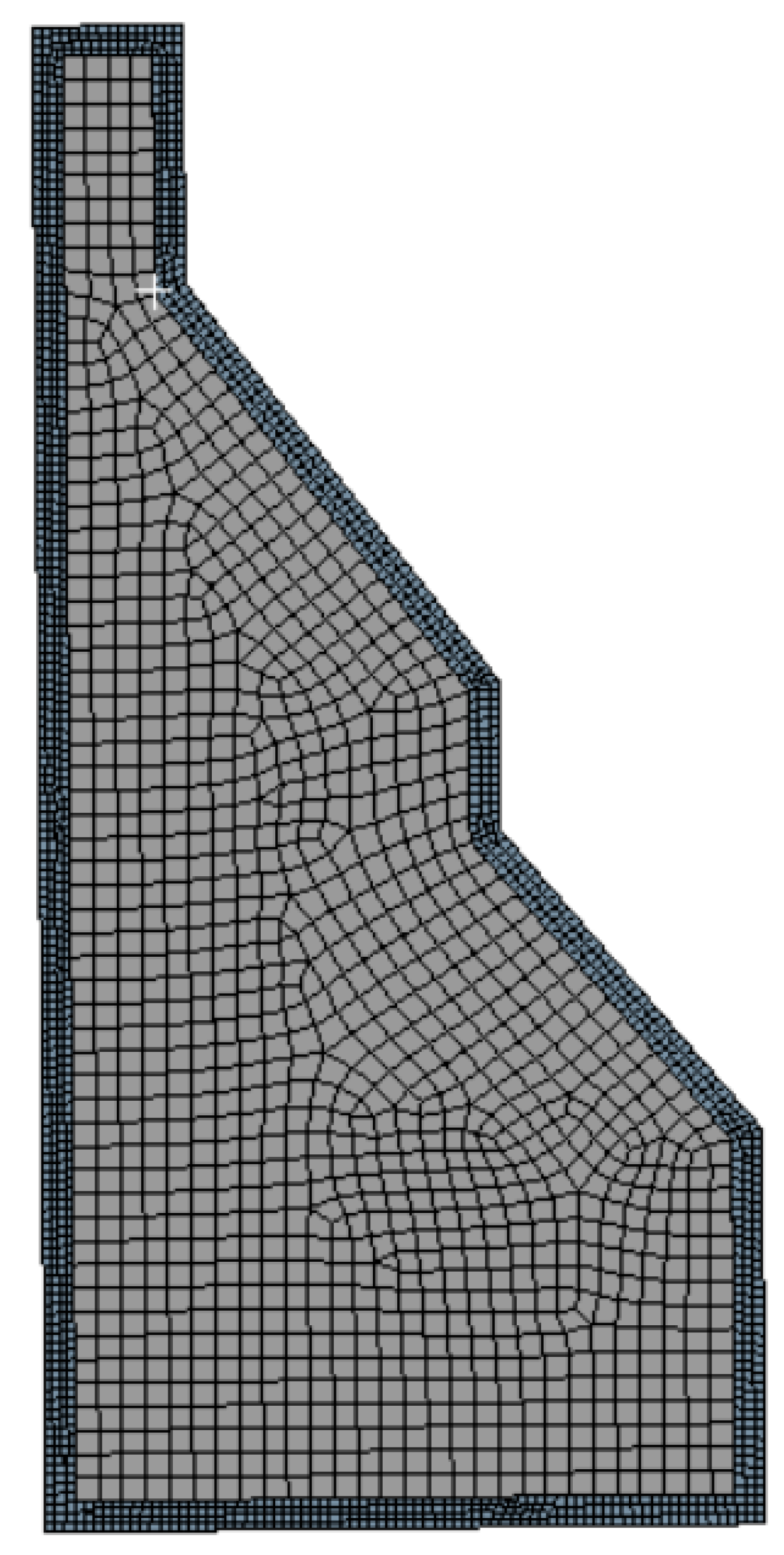
2.4. Simulation Setup
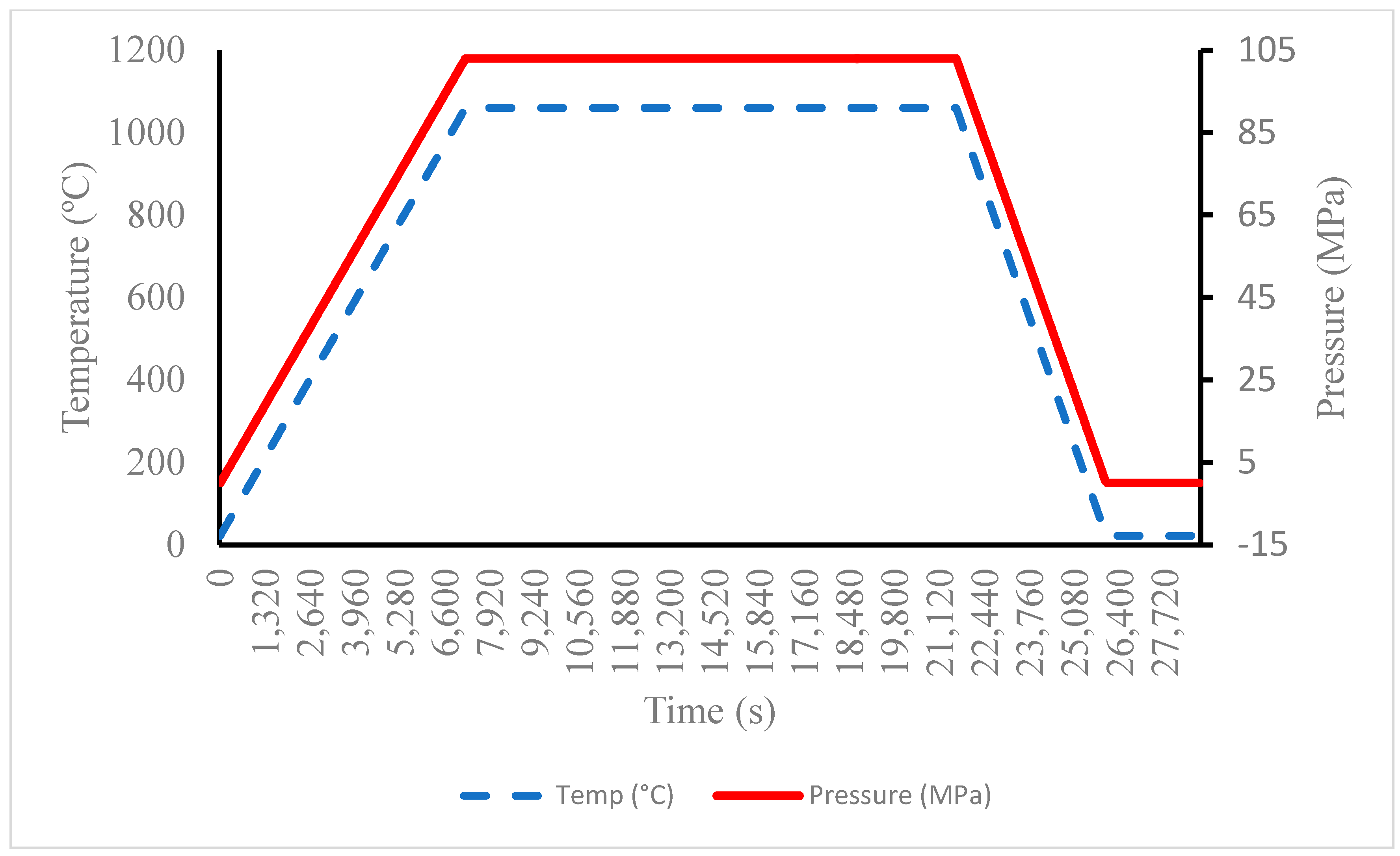
2.5. Experiment
- (1)
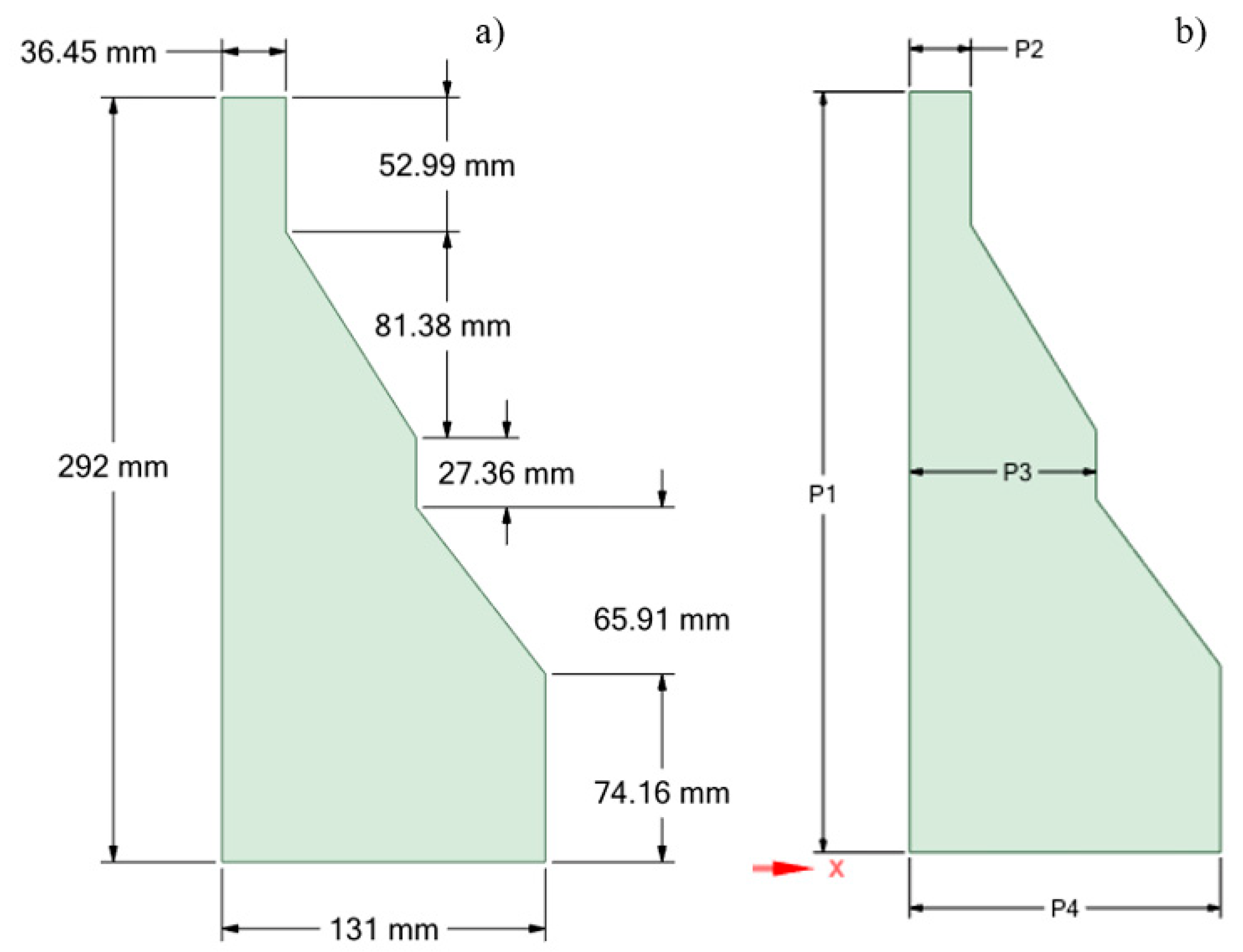
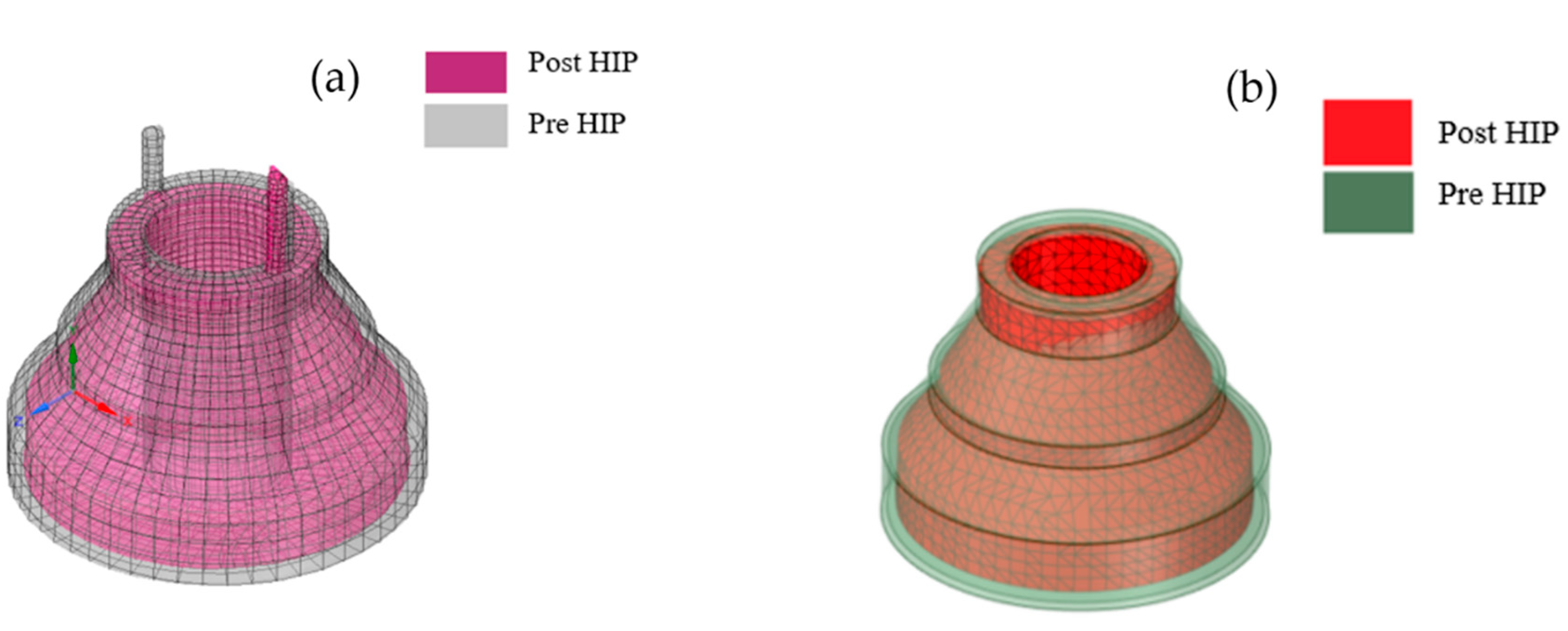
- The pre-HIP capsule design dimensions arbitrarily chosen for a prototypic component shown in Figure 3a;
- (2)
- A physical capsule was fabricated from 6.35-mm-thick mild carbon steel according to the pre-HIP capsule design dimensions chosen in Step 1) above;
- (3)
- The fabricated pre-HIP capsule physical dimensions were 3D-scanned;
- (4)
- The 3D-scanned data (point cloud data) were converted to a 3D CAD model and imported into ANSYS;
- (5)
- The compaction simulation was run on the imported pre-HIP 3D physical scan dimensions to determine the FEM post-HIP dimensions;
- (6)
- The physical capsule was filled with 316L powder and consolidated via the HIP cycle shown in Figure 7;
- (7)
- The physical post-HIP consolidated component (with the capsule shell still on) was 3D-scanned and converted to 3D CAD.
3. Results and Discussion
3.1. Densification Behavior
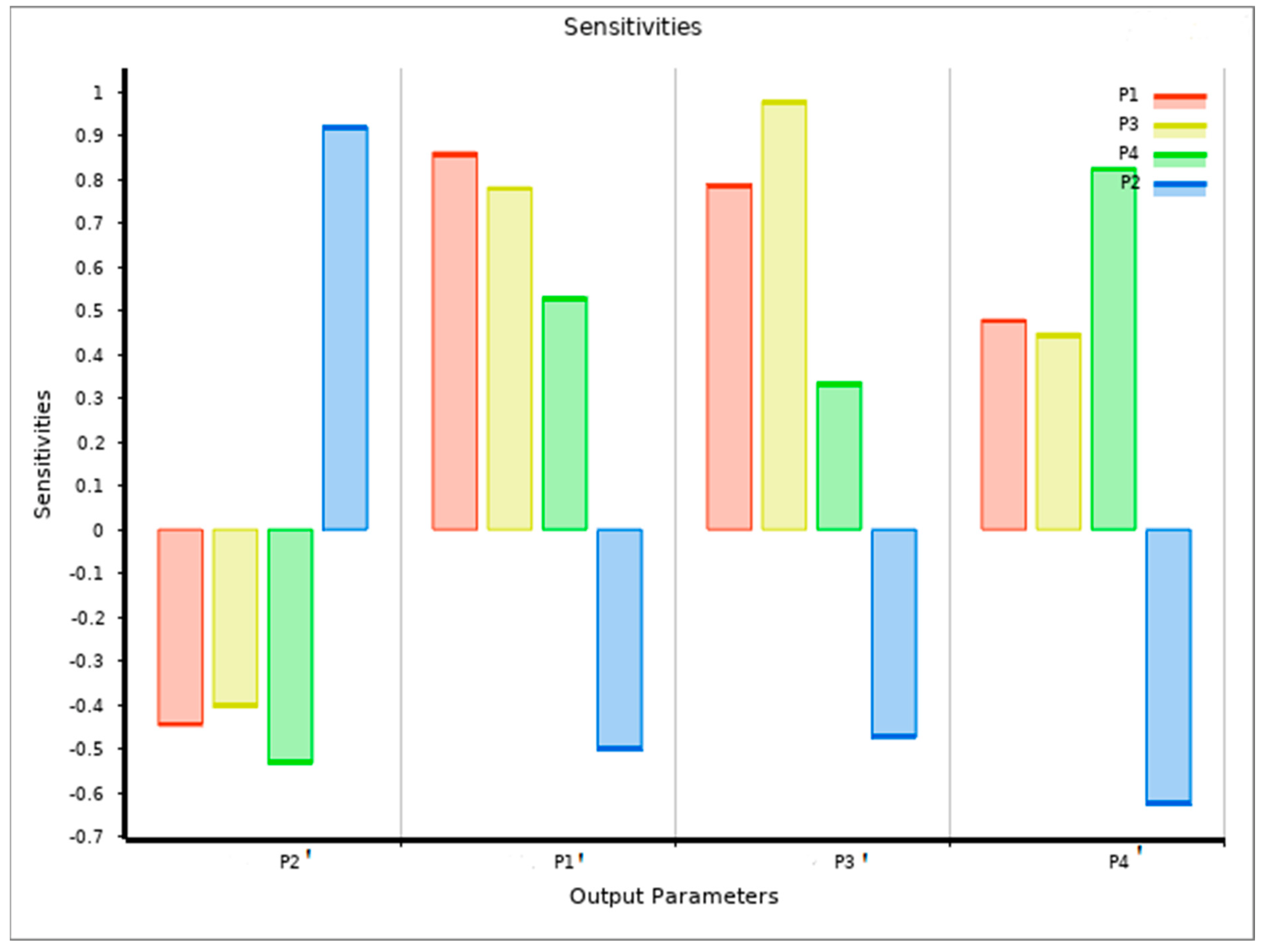
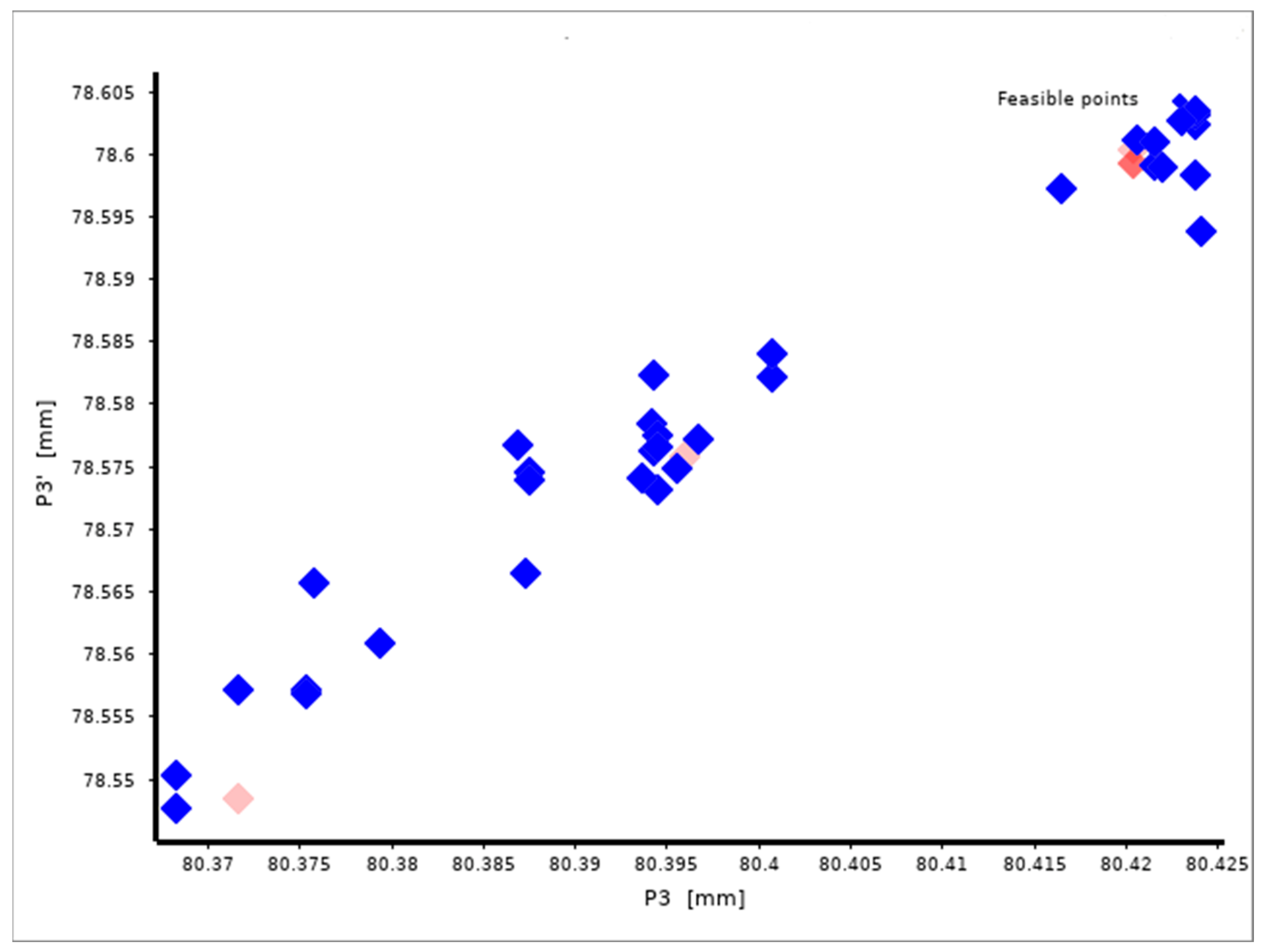
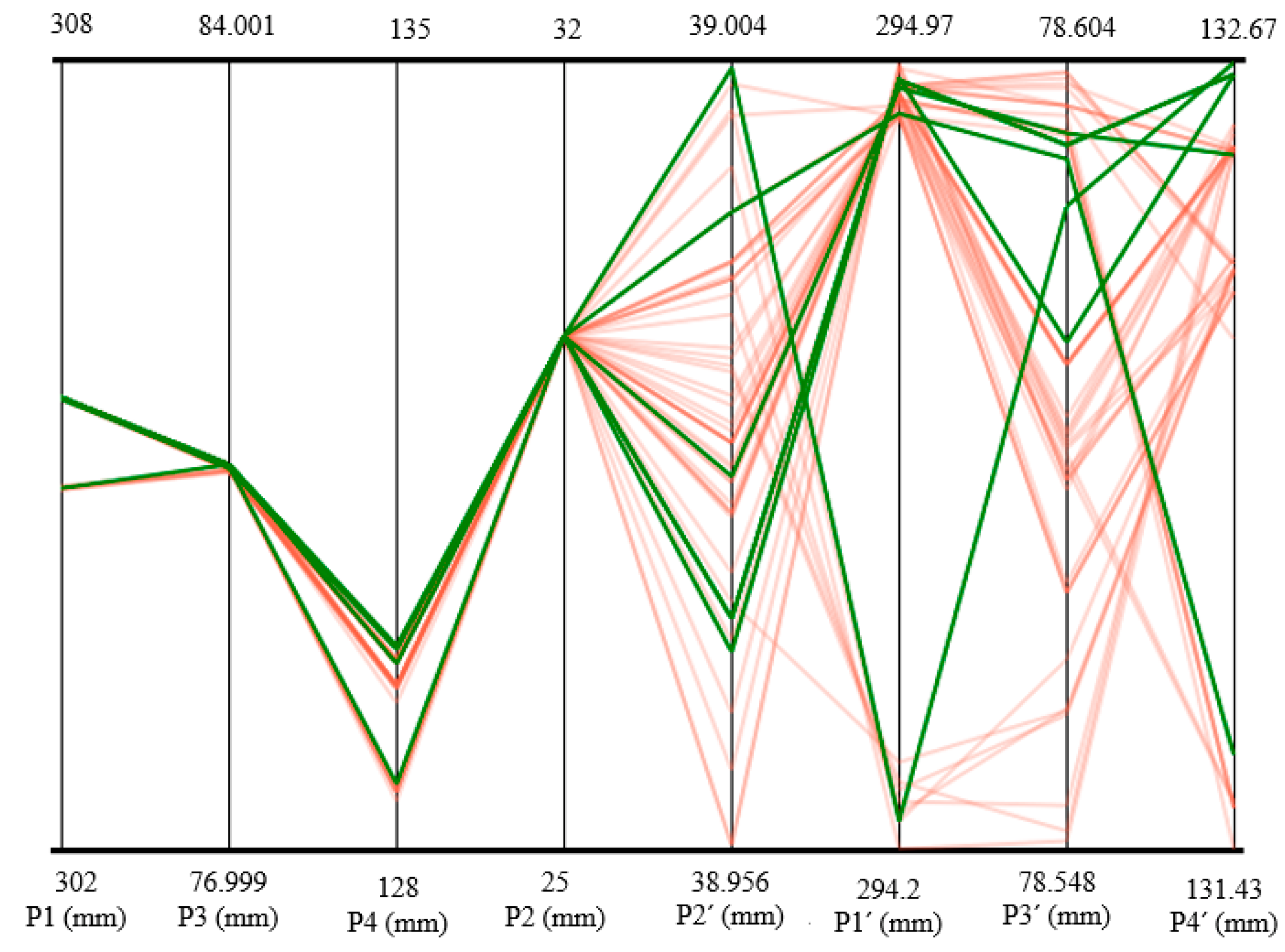
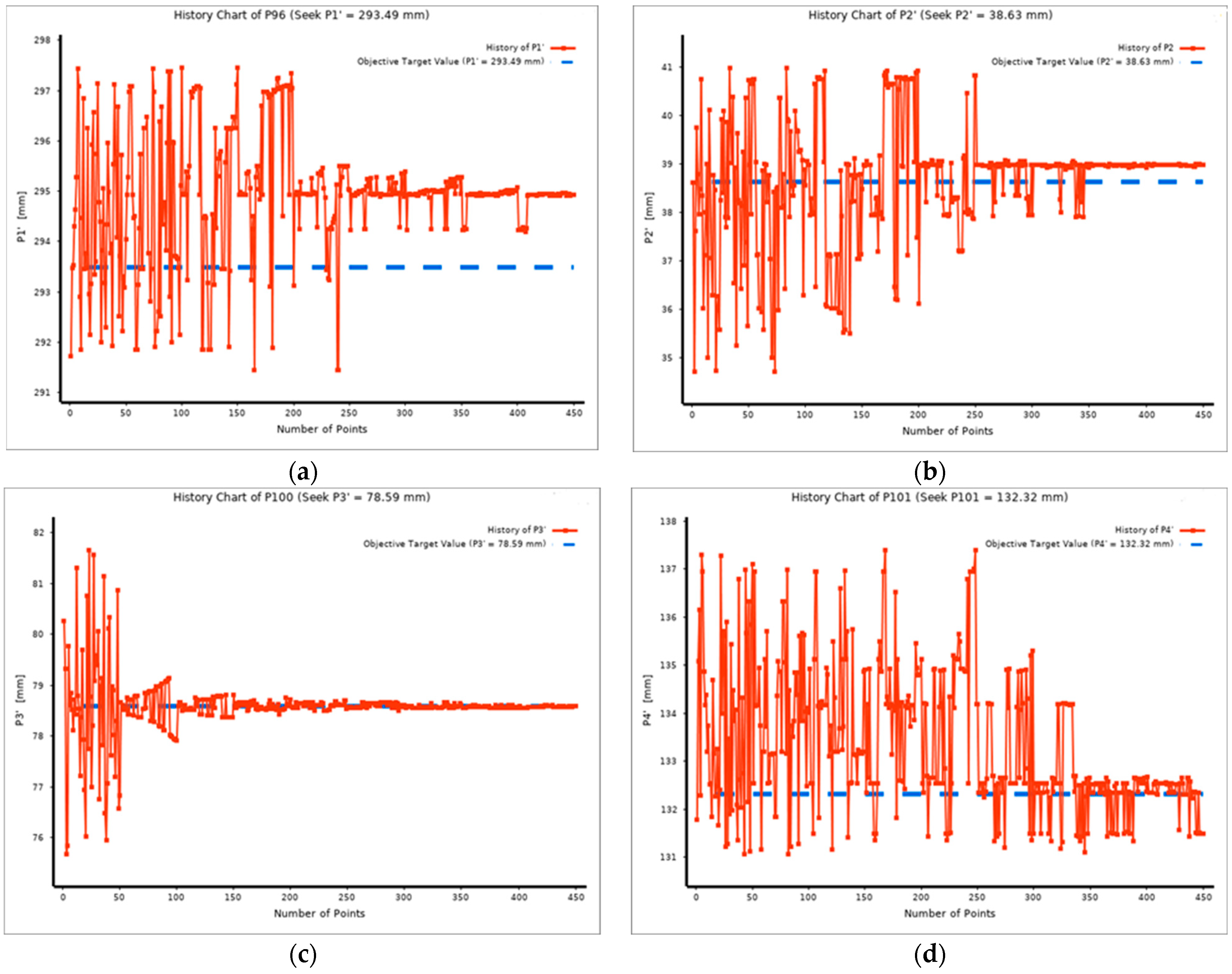
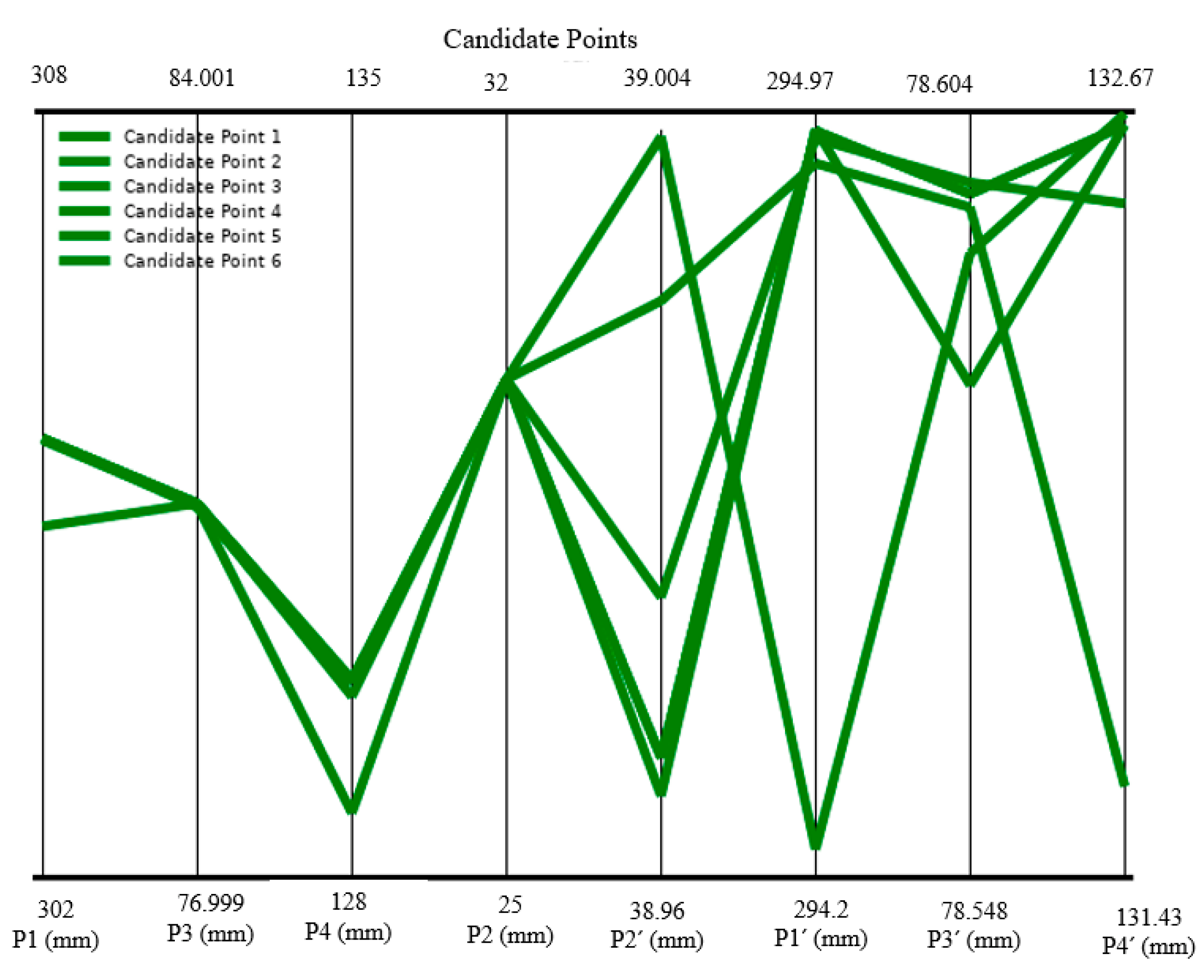
3.2. Optimization Results
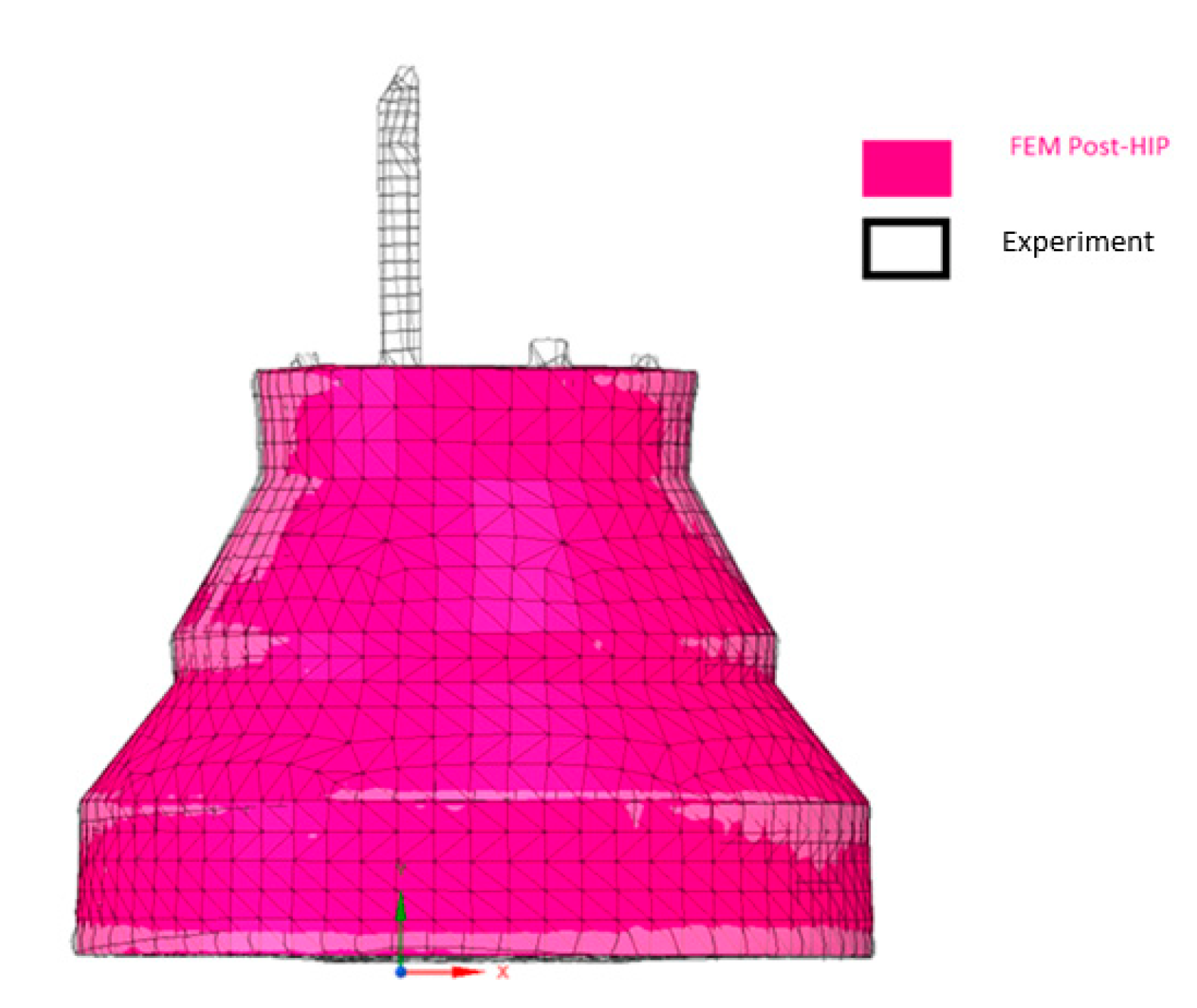
3.3. Experimental Results
4. Conclusions
- 1.
- The combined constitutive model, which includes time-independent plasticity, creep and thermal strain, was used here to predict the densification process of the powder. The model was incorporated into FEA software using the USERMAT Fortran code. The compact and capsule shrank uniformly, while the relative density harmoniously reached 1 in the majority of the volume.
- 2.
- The optimization procedure based on a multi-objective genetic algorithm (MOGA) was aimed at obtaining the desired pre-PM-HIP capsule dimensions, such that the post-HIP compact required minimal or no post-machining and dimensioning adjustments. The desired post-HIP compact dimensions were set as targets and the pre-HIP dimensions were calculated over almost 500 points. Five candidate points that met all the constraints were selected.
- 3.
- An HIP experiment was conducted to confirm the modeling outcome. The results showed that the simulation and experiment had the same target and their results closely matched, ending in a post-HIP part that was less than 3% deviation or approximately 1.0 to 1.5 mm deviation from target.
Author Contributions
Funding
Conflicts of Interest
References
- Deng, Y.; Kaletsch, A.; Bezold, A.; Broeckmann, C. Precise Prediction of Near-Net-Shape HIP Components through DEM and FEM Modelling. In Proceedings of the Conference on Hot Isostatic Pressing: HIP’17, Sydney, Australia, 5–8 December 2017; Volume 10, pp. 182–189. [Google Scholar] [CrossRef]
- Khoei, A.R.; Molaeinia, Z.; Keshavarz, S. Modeling of hot isostatic pressing of metal powder with temperature-dependent cap plasticity model. Int. J. Mater. Form. 2012, 6, 363–376. [Google Scholar] [CrossRef]
- Kohar, C.P.; Martin, É.; Connolly, D.S.; Patil, S.; Krutz, N.; Wei, D.; Inal, K. A new and efficient thermo-elasto-viscoplastic numerical implementation for implicit finite element simulations of powder metals: An application to hot isostatic pressing. Int. J. Mech. Sci. 2019, 155, 222–234. [Google Scholar] [CrossRef]
- Nguyen, C.V.; Bezold, A.; Christoph, B. Anisotropic shrinkage of hot isostatically pressed components. In Proceedings of the 11th International Conference on Hot Isostatic Pressing, Stockholm, Sweden, 9–13 June 2014; pp. 369–382. [Google Scholar]
- Van Nguyen, C.; Deng, Y.; Bezold, A.; Broeckmann, C. A combined model to simulate the powder densification and shape changes during hot isostatic pressing. Comput. Methods Appl. Mech. Eng. 2017, 315, 302–315. [Google Scholar] [CrossRef]
- Deng, Y.; Birke, C.; Rajaei, A.; Kaletsch, A.; Broeckmann, C. Numerical Study of Hot Isostatic Pressing with Integrated Heat Treatment of PM-HIP Cold Work Steel D7. In Proceedings of the WorldPM 2018, Peking, China, 16–20 September 2018; pp. 442–453. [Google Scholar]
- Van Nguyen, C.; Bezold, A.; Broeckmann, C. Modelling of HIP: Influence of Initial Powder Distribution after Pre-Densification on the Consolidation of Stainless Steel 316L during HIP. In European PM Conference Proceedings, Proceedings of the European Congress and Exhibition on Powder Metallurgy, Gothenburg, Sweden, 5–18 September 2013; The European Powder Metallurgy Association: Brussels, Belgium, 2013; p. 1. [Google Scholar]
- Chung, S.H.; Park, H.; Jeon, K.D.; Kim, K.T.; Hwang, S.M. An Optimal Container Design for Metal Powder Under Hot Isostatic Pressing. J. Eng. Mater. Technol. Trans. ASME 2001, 123, 234–239. [Google Scholar] [CrossRef]
- Abouaf, M.; Chenot, J.L.; Raisson, G.; Bauduin, P. Finite element simulation of hot isostatic pressing of metal powders. Int. J. Numer. Methods Eng. 1988, 25, 191–212. [Google Scholar] [CrossRef]
- Oyane, M.; Shima, S.; Kono, Y. Thoery of Plasticity for Porous Metals. Bull. JSME 1973, 16, 1254–1262. [Google Scholar] [CrossRef]
- Kühn, H.A.; Downey, C.L. Material Behavior in Powder Preform Forging. J. Eng. Mater. Technol. 1972, 95, 41–46. [Google Scholar] [CrossRef]
- Jeon, Y.; Kim, K. Near-net-shape forming of 316L stainless steel powder under hot isostatic pressing. Int. J. Mech. Sci. 1999, 41, 815–830. [Google Scholar] [CrossRef]
- Sofronis, P.; Mcmeeking, R.M. Creep of Power-Law Material Containing Spherical Voids. J. Appl. Mech. Trans. ASME 1992, 59, S88–S95. [Google Scholar] [CrossRef]
- Jinka, A.G.; Lewis, R.W. Finite element simulation of hot isostatic pressing of metal powders. Comput. Methods Appl. Mech. Eng. 1994, 114, 249–272. [Google Scholar] [CrossRef]
- Yuan, W.; Mei, J.; Samarov, V.; Seliverstov, D.; Wu, X. Computer modelling and tooling design for near net shaped components using hot isostatic pressing. J. Mater. Process. Technol. 2007, 182, 39–49. [Google Scholar] [CrossRef]
- Wikman, B. Modelling and Simulation of Powder Pressing with Consideration of Friction Modelling and Simulation of Powder Pressing with Consideration of Friction. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 1999. [Google Scholar]
- Aryanpour, G. Constitutive Modeling for Hot Isostatic Pressing of Metal Powders. J. Porous Media 2006, 9, 15–34. [Google Scholar] [CrossRef]
- Aryanpour, G.; Mashl, S.; Warke, V. Elastoplastic–viscoplastic modelling of metal powder compaction: Application to hot isostatic pressing. Powder Metall. 2013, 56, 14–23. [Google Scholar] [CrossRef]
- Liu, G.-C.; Shi, Y.-S.; Wei, Q.-S.; Xue, P.-J. Simulation of pressure effects on hot isostatic pressing of stainless steel powder. J. Cent. South Univ. 2012, 19, 55–62. [Google Scholar] [CrossRef]
- Abdelhafeez, A.; Essa, K. Influences of Powder Compaction Constitutive Models on the Finite Element Simulation of Hot Isostatic Pressing. Procedia CIRP 2016, 55, 188–193. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, J.-L.; Kaletsch, A.; Broeckmann, C. Modelling and simulation of densification and σ-phase precipitation in PM duplex steel AISI 318LN during hot isostatic pressing. Mater. Today Commun. 2021, 29, 102901. [Google Scholar] [CrossRef]
- You, D.; Wang, Y.; Yang, C.; Li, F. Comparative analysis of the hot-isostatic-pressing densification behavior of atomized and milled Ti6Al4V powders. J. Mater. Res. Technol. 2020, 9, 3091–3108. [Google Scholar] [CrossRef]
- Shima, S.; Oyane, M. Plasticity theory for porous metals. Int. J. Mech. Sci. 1976, 18, 285–291. [Google Scholar] [CrossRef]
- Hu, B.; Cai, G.; Fu, J.; Xin, Y.; Zhang, D.; Yuan, Y.; Guo, S. Densification behavior of tungsten alloy powders during hot isostatic pressing. Mater. Today Commun. 2022, 31, 103576. [Google Scholar] [CrossRef]
- Reddy, J. Introduction to the Finite Element Method; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Wikman, B.; Svoboda, A.; Häggblad, H. A combined material model for numerical simulation of hot isostatic pressing. Comput. Methods Appl. Mech. Eng. 2000, 189, 901–913. [Google Scholar] [CrossRef]
- Ishibuchi, H. MOGA: Multi-objective genetic algorithms n.d. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, Australia, 29 November–1 December 1995. [Google Scholar]
- Huang, B.; Wang, Z.; Xu, Y. Multi-Objective Genetic Algorithm for Hybrid Electric Vehicle Parameter Optimization. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5177–5182. [Google Scholar]
- Keshavarz, S.; Khoei, A.R.; Molaeinia, Z. Genetic algorithm-based numerical optimization of powder compaction process with temperature-dependent cap plasticity model. Int. J. Adv. Manuf. Technol. 2013, 64, 1057–1072. [Google Scholar] [CrossRef]
- Gao, Y.; Shi, L.; Yao, P. Study on multi-objective genetic algorithm. In Proceedings of the World Congress on Intelligent Control and Automation (WCICA), Hefei, China, 28 June–2 July 2000; Volume 1, pp. 646–650. [Google Scholar] [CrossRef]
- Chou, S.-H.; Song, Y.-L.; Hsiau, S.-S. A Study of the Mixing Index in Solid Particles. KONA Powder Part. J. 2017, 34, 275–281. [Google Scholar] [CrossRef]
- Mechanics Group. ANSYS USER Material Subroutine USERMAT Technology; ANSYS, Inc.: Canonsburg, PA, USA, 1999; pp. 1–22. [Google Scholar]
- Essa, K.; Khan, R.; Hassanin, H.; Attallah, M.M.; Reed, R. An iterative approach of hot isostatic pressing tooling design for net-shape IN718 superalloy parts. Int. J. Adv. Manuf. Technol. 2016, 83, 1835–1845. [Google Scholar] [CrossRef]


| Material Properties | Stainless Steel 316L | Mild Carbon Steel |
|---|---|---|
| Young modulus (MPa) | ) | |
| Poisson ratio | ) | |
| Yield stress (MPa) | ||
| Thermal conductivity (w/mmk) | ||
| Specific heat (J/kgk) | ||
| Input and Output | Candidate Point 1 | Deviation | Candidate Point 2 | Deviation | Candidate Point 3 | Deviation | Candidate Point 4 | Deviation | Candidate Point 5 | Deviation | Target |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 304.76 | 305.44 | 305.43 | 305.44 | 305.45 | ||||||
| P2 | 29.57 | 29.57 | 29.56 | 29.57 | 29.56 | ||||||
| P3 | 80.42 | 80.40 | 80.41 | 80.42 | 80.42 | ||||||
| P4 | 129.82 | 129.78 | 128.60 | 129.80 | 129.66 | ||||||
| P1′ | 294.2 | 0.2 | 294.95 | 0.49 | 294.91 | 0.48 | 294.94 | 0.5 | 294.94 | 0.5 | 293.49 |
| P2′ | 39.00 | 0.95 | 38.96 | 0.85 | 38.99 | 0.93 | 38.96 | 0.85 | 38.97 | 0.88 | 38.63 |
| P3′ | 78.59 | 0 | 78.58 | 0 | 78.59 | 0 | 78.59 | 0 | 78.59 | 0 | 78.59 |
| P4′ | 132.66 | 0.3 | 132.65 | 0.25 | 131.58 | −0.55 | 132.65 | 0.25 | 132.52 | 0.2 | 132.32 |
| Feature No | Pre-HIP (mm) | FEM (mm) | Experiment (mm) | Deviation% |
|---|---|---|---|---|
| P1 | 304.97 | 291.9 | 293.49 | 0.54 |
| P2 | 28.405 | 37.52 | 38.63 | 2.87 |
| P3 | 79.93 | 76.86 | 78.89 | 2.57 |
| P4 | 131.07 | 129.66 | 132.52 | 2.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobhani, S.; Albert, M.; Gandy, D.; Tabei, A.; Fan, Z. Design Optimization of Hot Isostatic Pressing Capsules. J. Manuf. Mater. Process. 2023, 7, 30. https://doi.org/10.3390/jmmp7010030
Sobhani S, Albert M, Gandy D, Tabei A, Fan Z. Design Optimization of Hot Isostatic Pressing Capsules. Journal of Manufacturing and Materials Processing. 2023; 7(1):30. https://doi.org/10.3390/jmmp7010030
Chicago/Turabian StyleSobhani, Samaneh, Marc Albert, David Gandy, Ali Tabei, and Zhaoyan Fan. 2023. "Design Optimization of Hot Isostatic Pressing Capsules" Journal of Manufacturing and Materials Processing 7, no. 1: 30. https://doi.org/10.3390/jmmp7010030
APA StyleSobhani, S., Albert, M., Gandy, D., Tabei, A., & Fan, Z. (2023). Design Optimization of Hot Isostatic Pressing Capsules. Journal of Manufacturing and Materials Processing, 7(1), 30. https://doi.org/10.3390/jmmp7010030







