Multi-Response Optimization of Ti6Al4V Support Structures for Laser Powder Bed Fusion Systems
Abstract
1. Introduction
2. Methodology
2.1. Design of Experiments (DOE)
2.2. Printings
2.3. Performance Measures
3. Results and Discussion
3.1. Support Volume Analysis
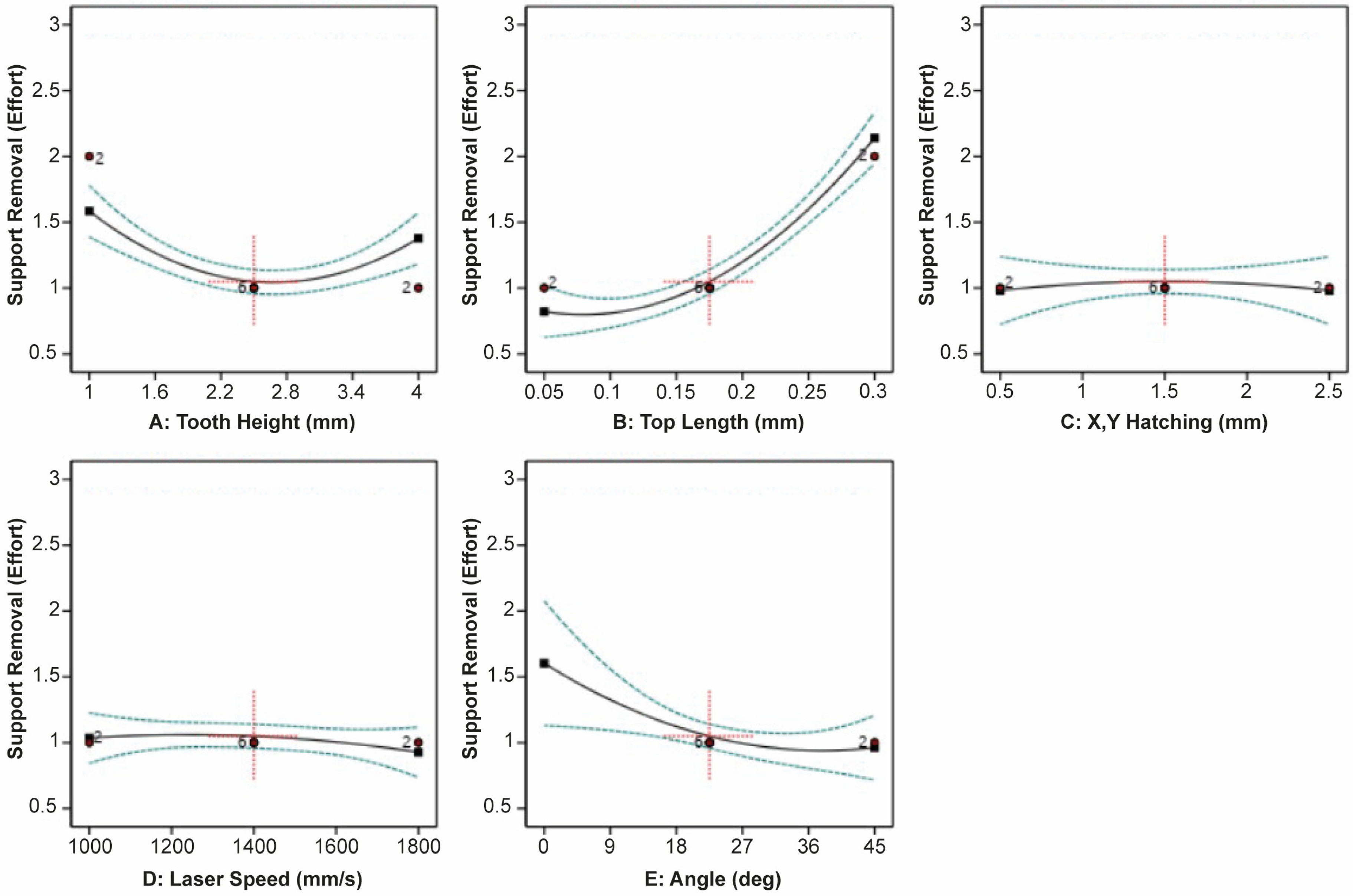
3.2. Support Removal Effort Analysis
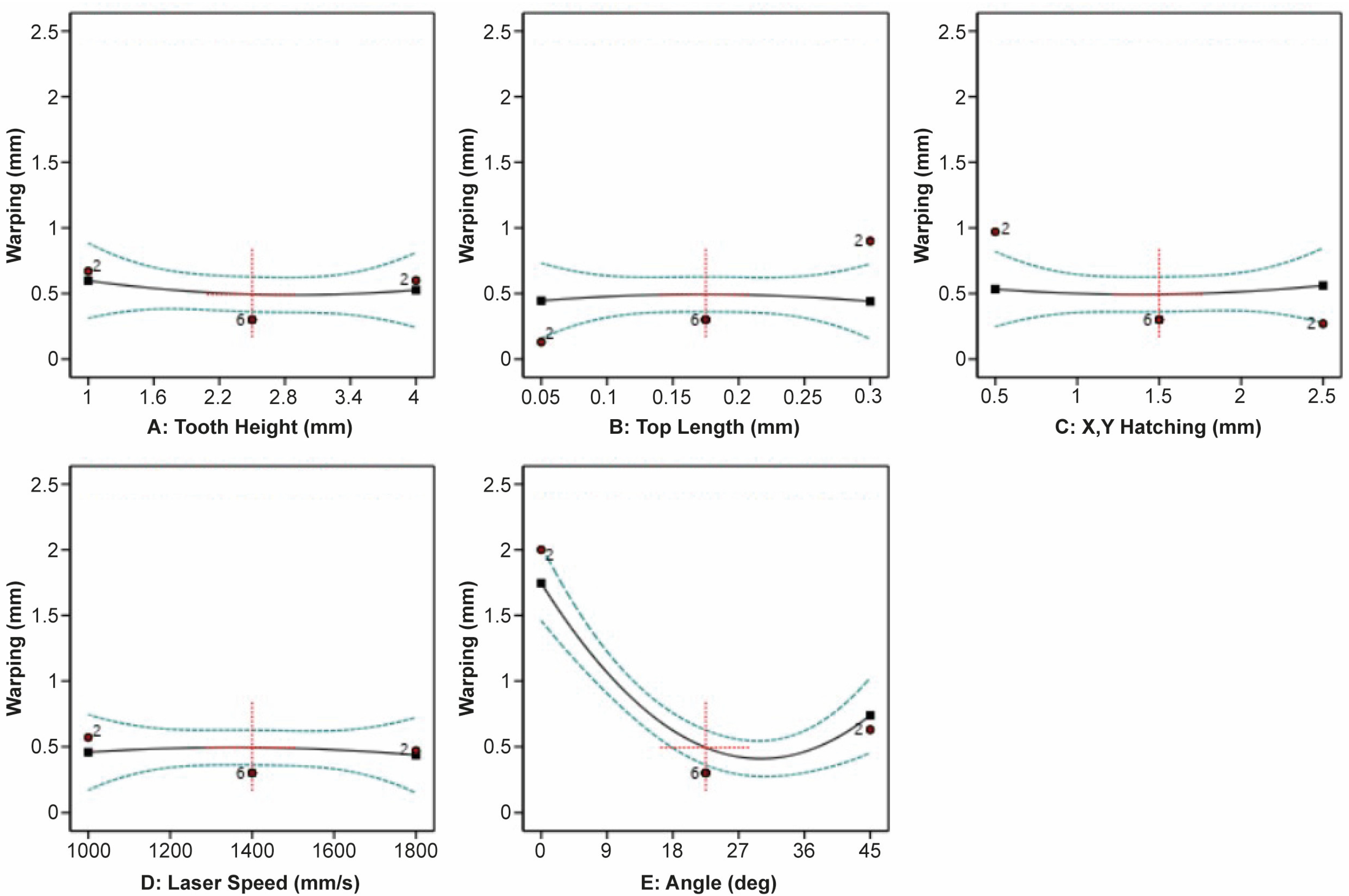
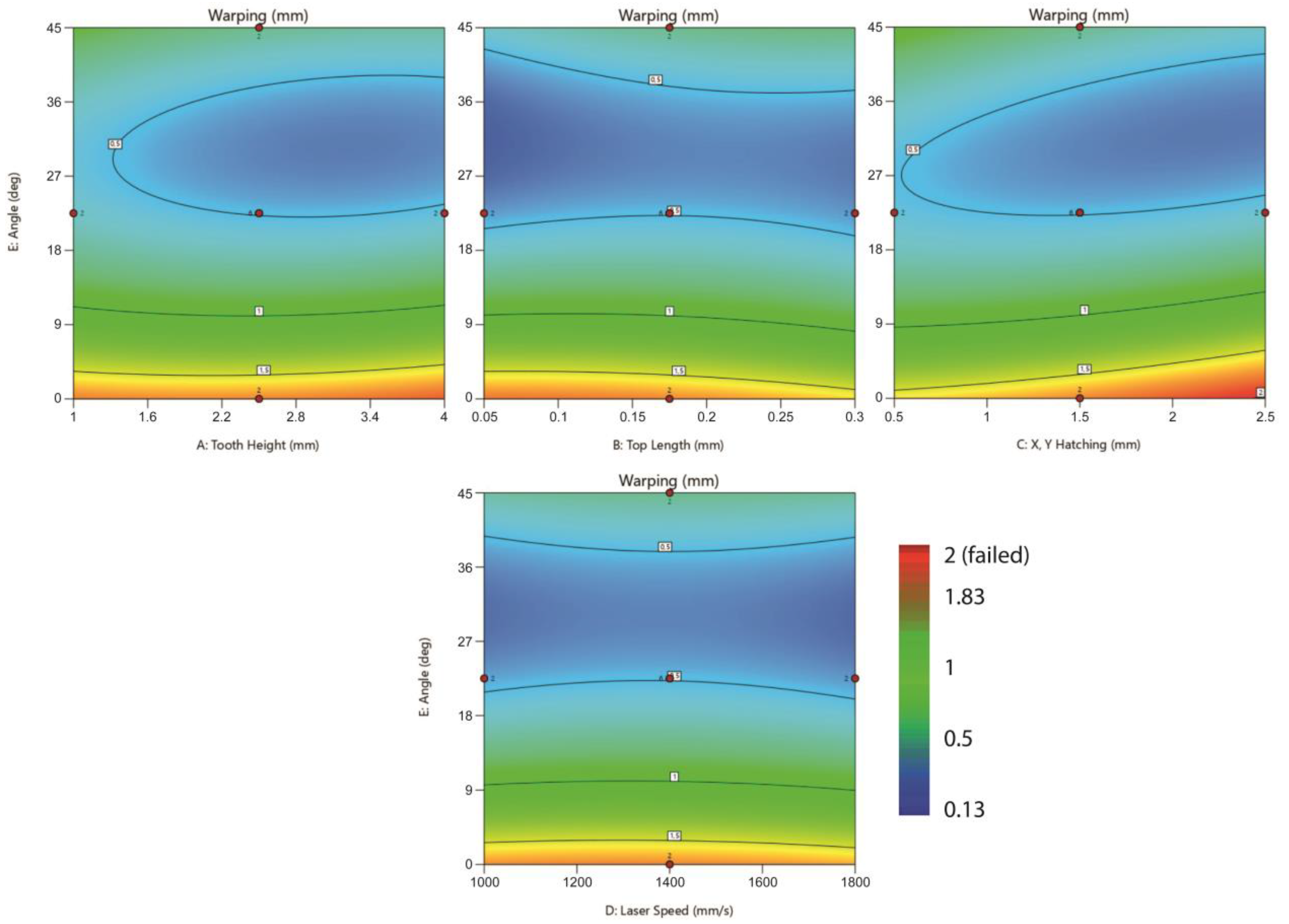
3.3. Warping Deformation Analysis
3.4. Numerical Optimization
3.5. Comparison of the Findings with Previously Published Work on LPBF and Other AM Methods
4. Conclusions
- The lack of 0° specimens due to printing failures significantly affected the optimization process. As a result, a limited number of optimal configurations was suggested for these specimens without efficiently minimizing Support Volume and Warping Deformation.
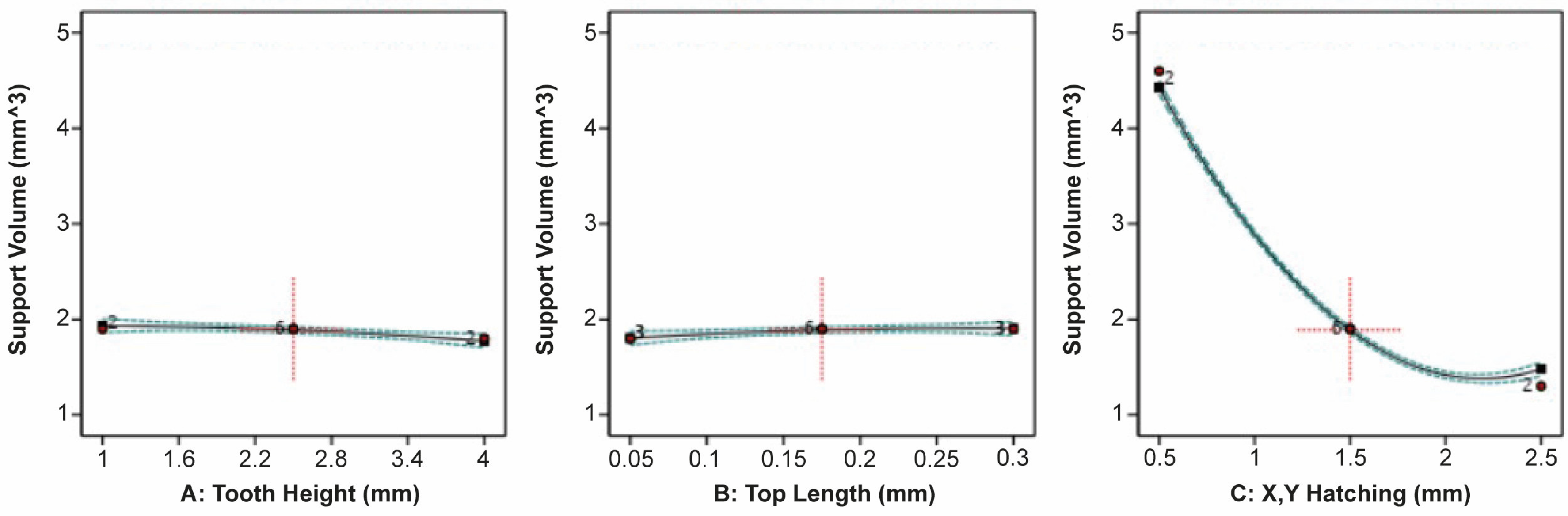
- X, Y Hatching has the most significant effect on Support Volume. The minimum Support Volume was observed at higher levels of X, Y Hatching (4 mm), while Tooth Height and Tooth Top Length barely affect Support Volume.
- Tooth Top Length has the most significant effect on Support Removal Effort. The minimum Support Removal Effort was found at lower levels of Tooth Top Length (0.05 mm), while the other parameters do not significantly affect the support removal.
- Overhang Angle has the most significant effect on Warping Deformation. The minimum Warping Deformation was observed at higher levels of Overhang Angle (45°), while the other parameters barely affect Warping Deformation.
- For 0° overhangs, the optimal solution was characterized by an average Tooth Height (2.74 mm), large Tooth Top Length (0.23 mm), low X, Y Hatching (0.72 mm), and high Laser Speed (1800 mm/s).
- For 22.5° overhangs, the optimal solution was characterized by a large Tooth Height (3.56 mm), low Tooth Top Length (0.05 mm), high X, Y Hatching (2.23 mm), and high Laser Speed (1799.9 mm/s).
- For 45° overhangs, the optimal solution was characterized by a large Tooth Height (4 mm), low Tooth Top Length (0.05 mm), high X, Y Hatching (2.5 mm), and high Laser Speed (1800 mm/s).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dilberoglu, U.M.; Gharehpapagh, B.; Yaman, U.; Dolen, M. The Role of Additive Manufacturing in the Era of Industry 4.0. Procedia Manuf. 2017, 11, 545–554. [Google Scholar] [CrossRef]
- Haleem, A.; Javaid, M. Additive Manufacturing Applications in Industry 4.0: A Review. J. Ind. Integr. Manag. 2019, 4, 1930001. [Google Scholar] [CrossRef]
- Facts & Factors. With 20.50% CAGR, Global Additive Manufacturing Market Size Worth USD 34,846.25 Million by 2028: Additive Manufacturing Industry Trends, Share, Growth, Segmentation, Analysis & Forecast Report. Globe Newswire News Room, 5 September 2022. [Google Scholar]
- Chowdhury, S.; Yadaiah, N.; Prakash, C.; Ramakrishna, S.; Dixit, S.; Gupta, L.R.; Buddhi, D. Laser powder bed fusion: A state-of-the-art review of the technology, materials, properties & defects, and numerical modelling. J. Mater. Res. Technol. 2022, 20, 2109–2172. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies, 3rd ed.; Chapter 5; Springer International Publishing: Manhattan, NY, USA, 2021. [Google Scholar]
- Poyraz, Ö.; Yasa, E.; Akbulut, G.; Orhangül, A.; Pilatin, S. Investigation of Support Structures for Direct Metal Laser Sintering (DMLS) of IN625 Parts; University of Texas at Austin: Austin, TX, USA, 2015. [Google Scholar]
- Cheng, B.; Kevin, C. Thermal Stresses Associated with Part Overhang Geometry in Electron Beam Additive Manufacturing: Process Parameter Effects; University of Texas at Austin: Austin, TX, USA, 2014. [Google Scholar]
- ISO/ASTM 52911-1:2019. Additive Manufacturing—Design—Part 1: Laser-Based Powder Bed Fusion of Metals. ISO: Geneva, Switzerland, 2019.
- Ameen, W.; Al-Ahmari, A.; Mohammed, M.K.; Kaid, H. Multi-objective optimization of support structures for metal additive manufacturing. Int. J. Adv. Manuf. Technol. 2021, 116, 2613–2632. [Google Scholar] [CrossRef]
- Ameen, W.; Al-Ahmari, A.; Alkhalefah, H. Design the Support Structures for Easy Removal of Un-Melted Powder in Metal Additive Manufacturing. Int. J. Adv. Sci. Technol. 2020, 29, 1847–1854. [Google Scholar]
- Järvinen, J.-P.; Matilainen, V.; Li, X.; Piili, H.; Salminen, A.; Mäkelä, I.; Nyrhilä, O. Characterization of Effect of Support Structures in Laser Additive Manufacturing of Stainless Steel. Phys. Procedia 2014, 56, 72–81. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R.; Young, P. Advanced lattice support structures for metal additive manufacturing. J. Mater. Process. Technol. 2013, 213, 1019–1026. [Google Scholar] [CrossRef]
- Lindecke, P.N.J.; Blunk, H.; Wenzl, J.-P.; Möller, M.; Emmelmann, C. Optimization of support structures for the laser additive manufacturing of TiAl6V4 parts. Procedia CIRP 2018, 74, 53–58. [Google Scholar] [CrossRef]
- Cloots, M.; Spierings, A.B.; Wegener, K. Assessing new support minimizing strategies for the additive manufacturing technology SLM ETH Zurich. In 24th International SFF Symposium; University of Texas at Austin: Austin, TX, USA, 2013. [Google Scholar]
- Jhabvala, J.; Boillat, E.; André, C.; Glardon, R. An innovative method to build support structures with a pulsed laser in the selective laser melting process. Int. J. Adv. Manuf. Technol. 2012, 59, 137–142. [Google Scholar] [CrossRef]
- Cao, Q.; Bai, Y.; Zhang, J.; Shi, Z.; Fuh, J.Y.H.; Wang, H. Removability of 316L stainless steel cone and block support structures fabricated by Selective Laser Melting (SLM). Mater. Des. 2020, 191, 108691. [Google Scholar] [CrossRef]
- Lefky, C.S.; Zucker, B.; Wright, D.; Nassar, A.R.; Simpson, T.W.; Hildreth, O.J. Dissolvable Supports in Powder Bed Fusion-Printed Stainless Steel. 3D Print. Addit. Manuf. 2017, 4, 3–11. [Google Scholar] [CrossRef]
- Zeng, K. Optimization of Support Structures for Selective Laser Melting. Ph.D. Thesis, University of Louisville, Louisville, KY, USA, 2015. Available online: https://ir.library.louisville.edu/etd/2221/ (accessed on 1 November 2022).
- Jiang, J.; Xu, X.; Stringer, J. Support Structures for Additive Manufacturing: A Review. J. Manuf. Mater. Process. 2018, 2, 64. [Google Scholar] [CrossRef]
- Singh, R.; Gupta, A.; Tripathi, O.; Srivastava, S.; Singh, B.; Awasthi, A.; Rajput, S.; Sonia, P.; Singhal, P.; Saxena, K.K. Powder bed fusion process in additive manufacturing: An overview. Mater. Today Proc. 2020, 26, 3058–3070. [Google Scholar] [CrossRef]
- Cobbinah, P.V.; Nzeukou, R.A.; Onawale, O.T.; Matizamhuka, W.R. Laser Powder Bed Fusion of Potential Superalloys: A Review. Metals 2020, 11, 58. [Google Scholar] [CrossRef]
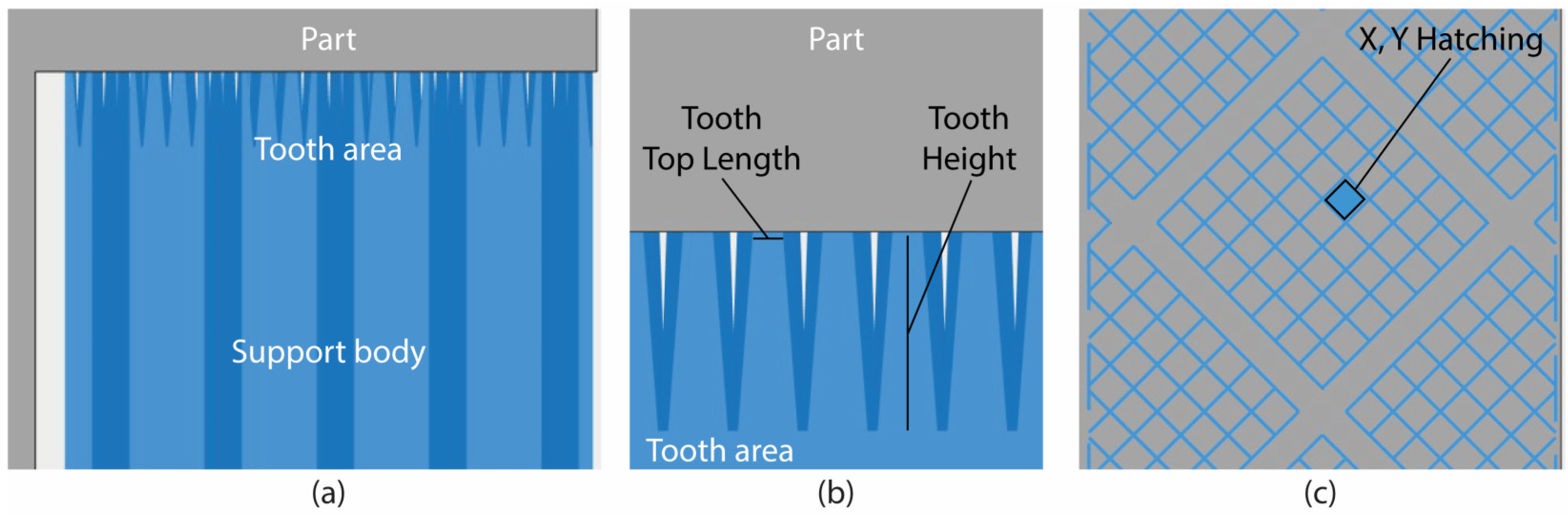
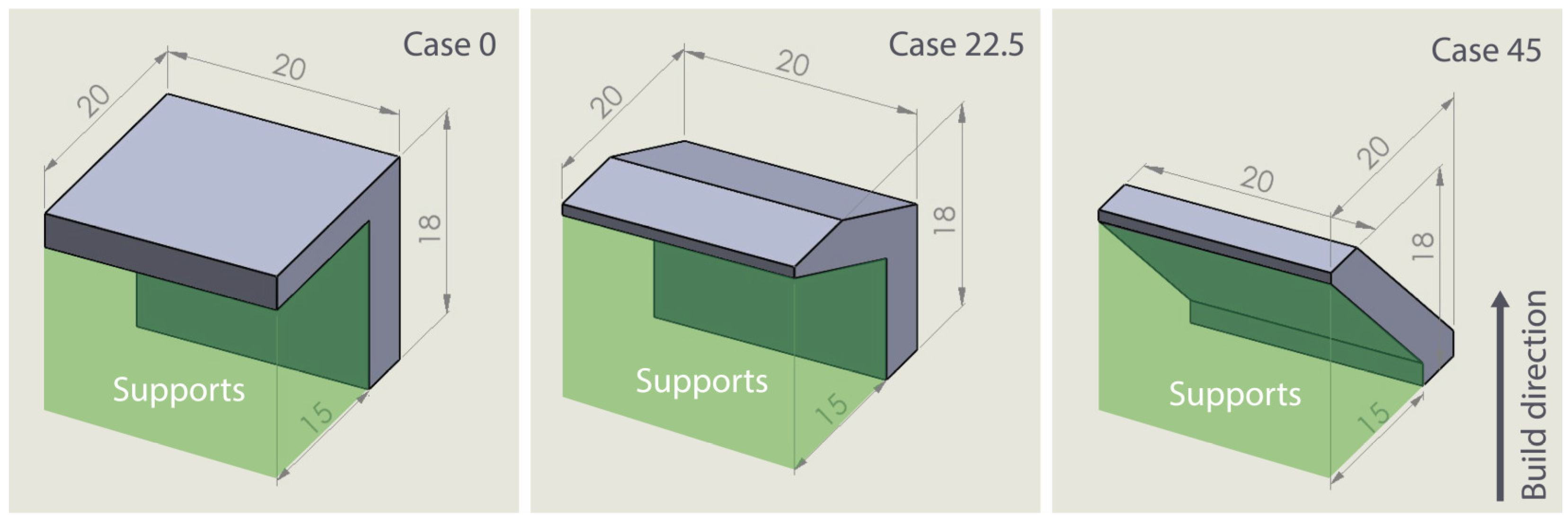


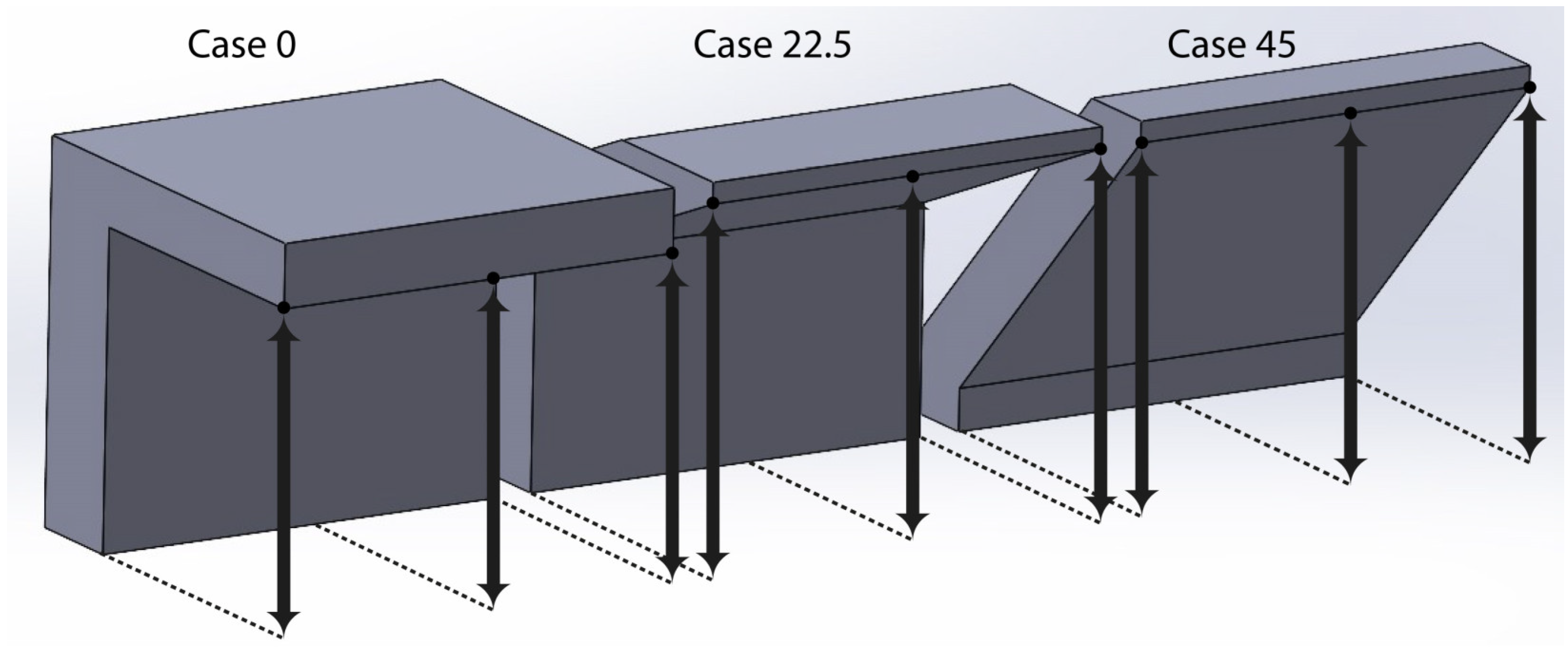



| Parameter | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Tooth Height Tooth Top Length X, Y Hatching Laser Speed Overhang Angle | 1 mm 0.05 mm 0.5 mm 1000 mm/s 0° | 2.5 mm 0.175 mm 1.5 mm 1400 mm/s 22.5° | 4 mm 0.3 mm 2.5 mm 1800 mm/s 45° |
| Tooth Base Interval | Tooth Base Length | Z Offset | Thickness | Fragmentation Interval | Separation Width | Rotation Angle |
|---|---|---|---|---|---|---|
| 0.1 mm | 1 mm | 0.06 mm | 0.2 mm | 8 mm | 1 mm | 45 deg |
| Std. Dev. Mean C.V. % | 0.0741 2.48 2.99 | R2 Adjusted R2 Predicted R2 Adeq Precision | 0.9979 0.9972 0.9962 112.346 |
| Source | Sum of Squares | Mean Square | F-Value | p-Value |
|---|---|---|---|---|
| Model A-Tooth Height B-Top Length C-X, Y Hatching D-Laser Speed E-Angle AB AC AD AE BC BD BE CD CE DE A2 B2 C2 D2 E2 Residual Lack of Fit Pure Error Cor Total | 176.50 0.4288 0.1700 147.65 0.0006 11.20 0.0400 0.0900 0.0025 0.0025 0.1225 0.0000 0.0000 0.0000 4.41 0.0025 0.0057 0.0057 5.60 0.0057 0.1667 0.3793 0.3793 0.0000 176.88 | 8.82 0.4288 0.1700 147.65 0.0006 11.20 0.0400 0.0900 0.0025 0.0025 0.1225 0.0000 0.0000 0.0000 4.41 0.0025 0.0057 0.0057 5.60 0.0057 0.1667 0.0055 0.0172 0.0000 | 1605.40 78.01 30.93 26,859.87 0.1070 2037.92 7.28 16.37 0.4548 0.4548 22.29 0.0000 0.0000 0.0000 802.26 0.4548 1.03 1.03 1018.50 1.03 30.33 | <0.0001 <0.0001 <0.0001 <0.0001 0.7446 <0.0001 0.0088 0.0001 0.5023 0.5023 <0.0001 1.0000 1.0000 1.0000 <0.0001 0.5023 0.3127 0.3127 <0.0001 0.3127 <0.0001 |
| Std. Dev. Mean C.V. % | 0.1838 1.62 11.36 | R2 Adjusted R2 Predicted R2 Adeq Precision | 0.9669 0.9529 0.9323 22.3995 |
| Source | Sum of Squares | Mean Square | F-Value | p-Value |
|---|---|---|---|---|
| Model A-Tooth Height B-Top Length C-X, Y Hatching D-Laser Speed E-Angle AB AC AD AE BC BD BE CD CE DE A2 B2 C2 D2 E2 Residual Lack of Fit Pure Error Cor Total | 46.47 0.2439 9.94 0.0000 0.0894 0.3404 0.0762 0.2503 0.0698 0.0052 3.41 0.0766 0.0074 0.1149 0.3472 0.0006 0.8610 0.8610 0.0215 0.0215 0.0858 1.59 1.59 0.0000 48.06 | 2.32 0.2439 9.94 0.0000 0.0894 0.3404 0.0762 0.2503 0.0698 0.0052 3.41 0.0766 0.0074 0.1149 0.3472 0.0006 0.8610 0.8610 0.0215 0.0215 0.0858 0.0338 0.1444 0.0000 | 68.75 7.22 294.14 0.0000 2.64 10.07 2.25 7.41 2.06 0.1543 101.04 2.27 0.2177 3.40 10.27 0.0192 25.48 25.48 0.6364 0.6364 2.54 | <0.0001 0.0100 <0.0001 1.0000 0.1106 0.0027 0.1399 0.0091 0.1574 0.6962 <0.0001 0.1390 0.6430 0.0715 0.0024 0.8904 <0.0001 <0.0001 0.4290 0.4290 0.1178 |
| Std. Dev. Mean C.V. % | 0.2876 1.08 26.68 | R2 Adjusted R2 Predicted R2 Adeq Precision | 0.8503 0.8069 0.7403 14.2794 |
| Source | Sum of Squares | Mean Square | F-Value | p-Value |
|---|---|---|---|---|
| Model A-Tooth Height B-Top Length C-X, Y Hatching D-Laser Speed E-Angle AB AC AD AE BC BD BE CD CE DE A2 B2 C2 D2 E2 Residual Lack of Fit Pure Error Cor Total | 32.40 0.0861 0.0005 0.0124 0.0076 17.22 0.0049 0.0182 0.1444 0.4225 1.20 0.0025 0.6084 0.0132 2.81 0.0169 0.0232 0.0130 0.0142 0.0106 2.76 5.71 5.71 0.0000 38.11 | 1.62 0.0861 0.0005 0.0124 0.0076 17.22 0.0049 0.0182 0.1444 0.4225 1.20 0.0025 0.6084 0.0132 2.81 0.0169 0.0232 0.0130 0.0142 0.0106 2.76 0.0827 0.2594 0.0000 | 19.59 1.04 0.0058 0.1505 0.0922 208.23 0.0592 0.2204 1.75 5.11 14.50 0.0302 7.36 0.1599 33.92 0.2044 0.2809 0.1570 0.1716 0.1279 33.39 | <0.0001 0.3111 0.9397 0.6992 0.7623 <0.0001 0.8084 0.6402 0.1907 0.0270 0.0003 0.8625 0.0084 0.6905 <0.0001 0.6526 0.5978 0.6932 0.6800 0.7217 <0.0001 |
| Name | Goal | Lower Limit | Upper Limit |
|---|---|---|---|
| A: Tooth Height B: Tooth Top Length C: X, Y Hatching D: Laser Speed Support Volume Support Removal Warping Deformation | in range in range in range in range minimize minimize minimize | 1 mm 0.05 mm 0.5 mm 1000 mm/s 1 (normalised) Condition 1 0.13 mm | 4 mm 0.3 mm 2.5 mm 1800 mm/s 5 (normalised) Condition 2 1.5 mm |
| Angle. | Tooth Height | Tooth Top Length | X, Y Hatching | Laser Speed | Support Volume | Support Removal | Warping Deform. | Desirability |
|---|---|---|---|---|---|---|---|---|
| 0° 22.5° 45° | 2.738 3.557 4.000 | 0.230 0.050 0.050 | 0.722 2.227 2.500 | 1800 1799.9 1800 | 4.074 1.216 1.000 | 1.700 1.000 1.000 | 1.437 0.313 0.195 | 0.147 0.936 0.984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimopoulos, A.; Zournatzis, I.; Gan, T.-H.; Chatzakos, P. Multi-Response Optimization of Ti6Al4V Support Structures for Laser Powder Bed Fusion Systems. J. Manuf. Mater. Process. 2023, 7, 22. https://doi.org/10.3390/jmmp7010022
Dimopoulos A, Zournatzis I, Gan T-H, Chatzakos P. Multi-Response Optimization of Ti6Al4V Support Structures for Laser Powder Bed Fusion Systems. Journal of Manufacturing and Materials Processing. 2023; 7(1):22. https://doi.org/10.3390/jmmp7010022
Chicago/Turabian StyleDimopoulos, Antonios, Ilias Zournatzis, Tat-Hean Gan, and Panagiotis Chatzakos. 2023. "Multi-Response Optimization of Ti6Al4V Support Structures for Laser Powder Bed Fusion Systems" Journal of Manufacturing and Materials Processing 7, no. 1: 22. https://doi.org/10.3390/jmmp7010022
APA StyleDimopoulos, A., Zournatzis, I., Gan, T.-H., & Chatzakos, P. (2023). Multi-Response Optimization of Ti6Al4V Support Structures for Laser Powder Bed Fusion Systems. Journal of Manufacturing and Materials Processing, 7(1), 22. https://doi.org/10.3390/jmmp7010022








