Friction Resistance of Uncured Carbon/Epoxy Prepregs under Thermoforming Process Conditions: Experiments and Modelling
Abstract
1. Introduction
2. Characterisation of the Frictional Behaviour
2.1. Prepreg Material
2.2. Experimental Set-Up
2.3. Test Results
3. Characterisation of the Contact Surfaces
Surface Examination
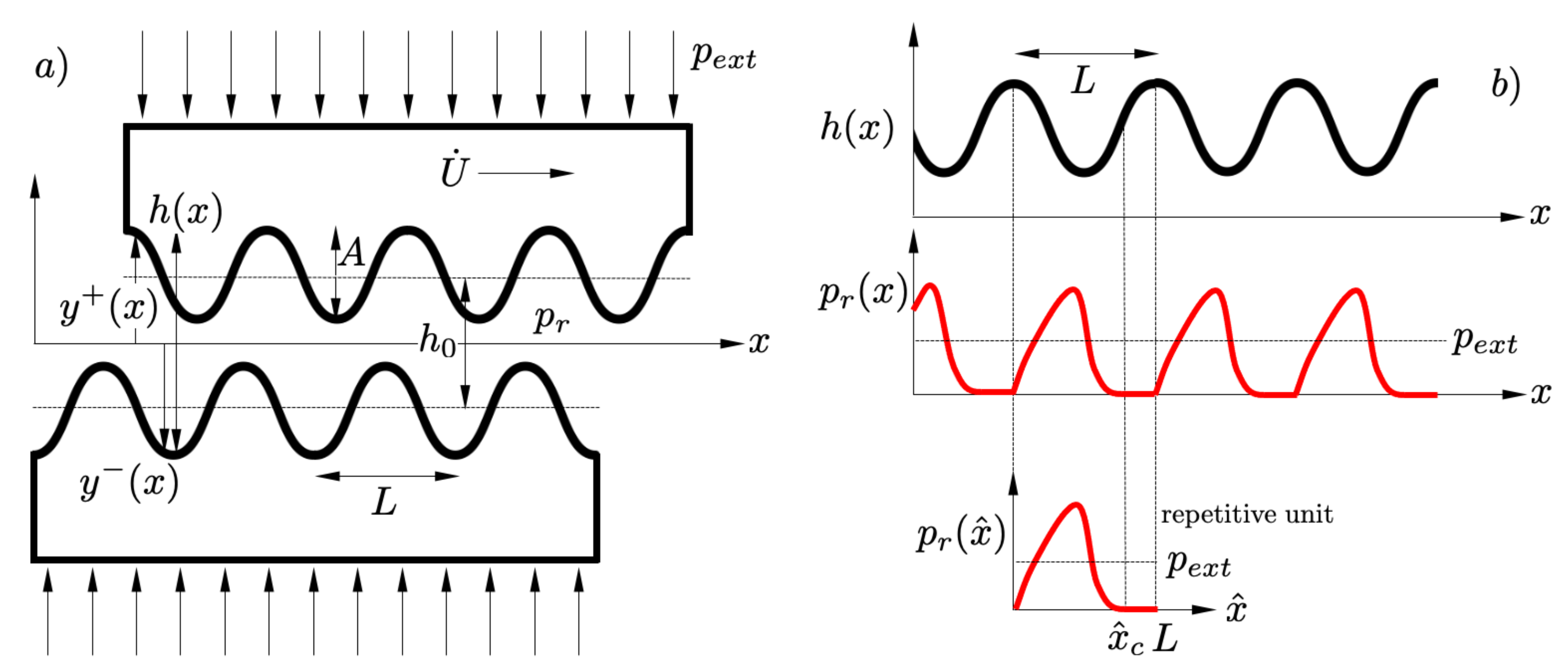
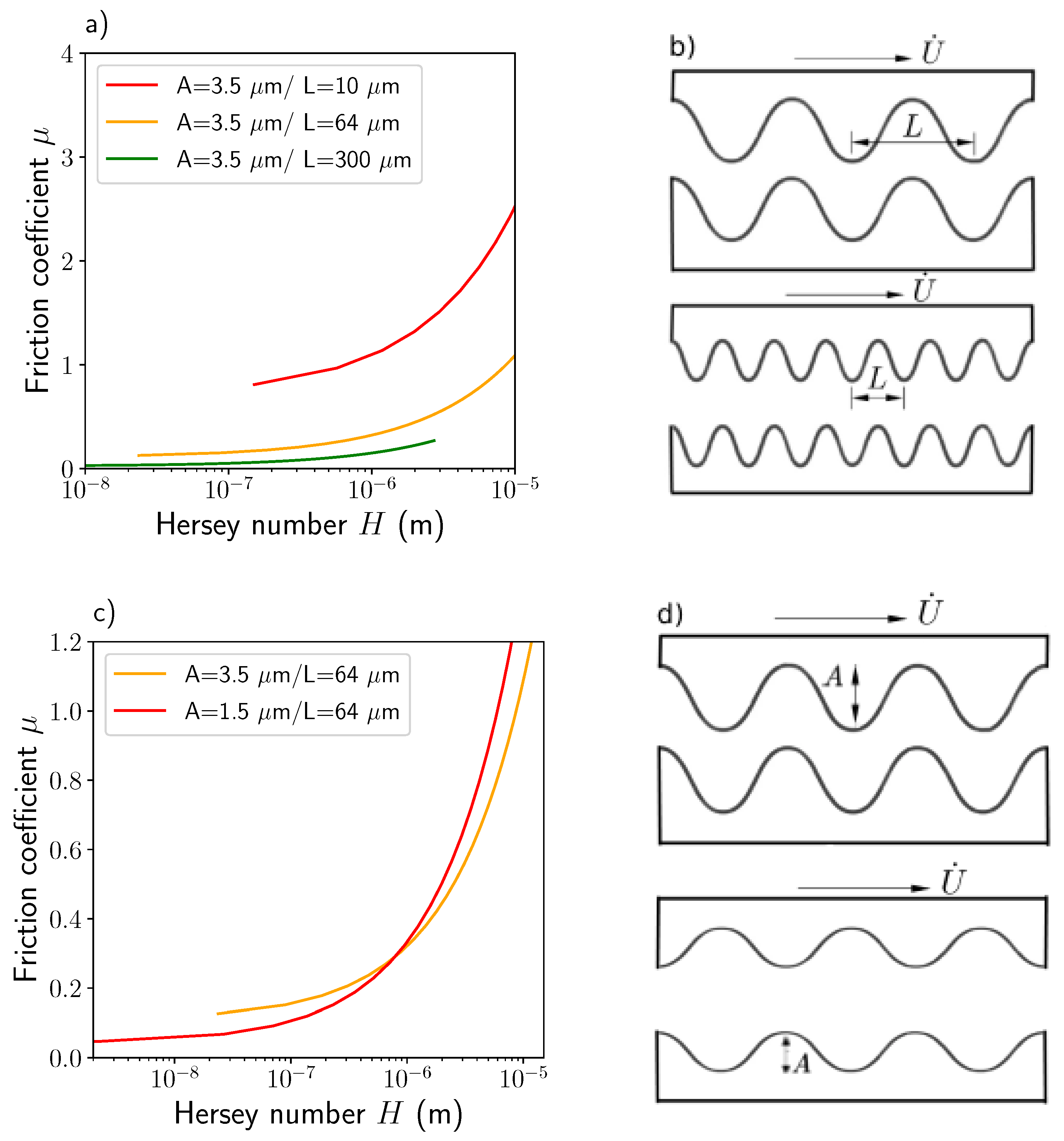
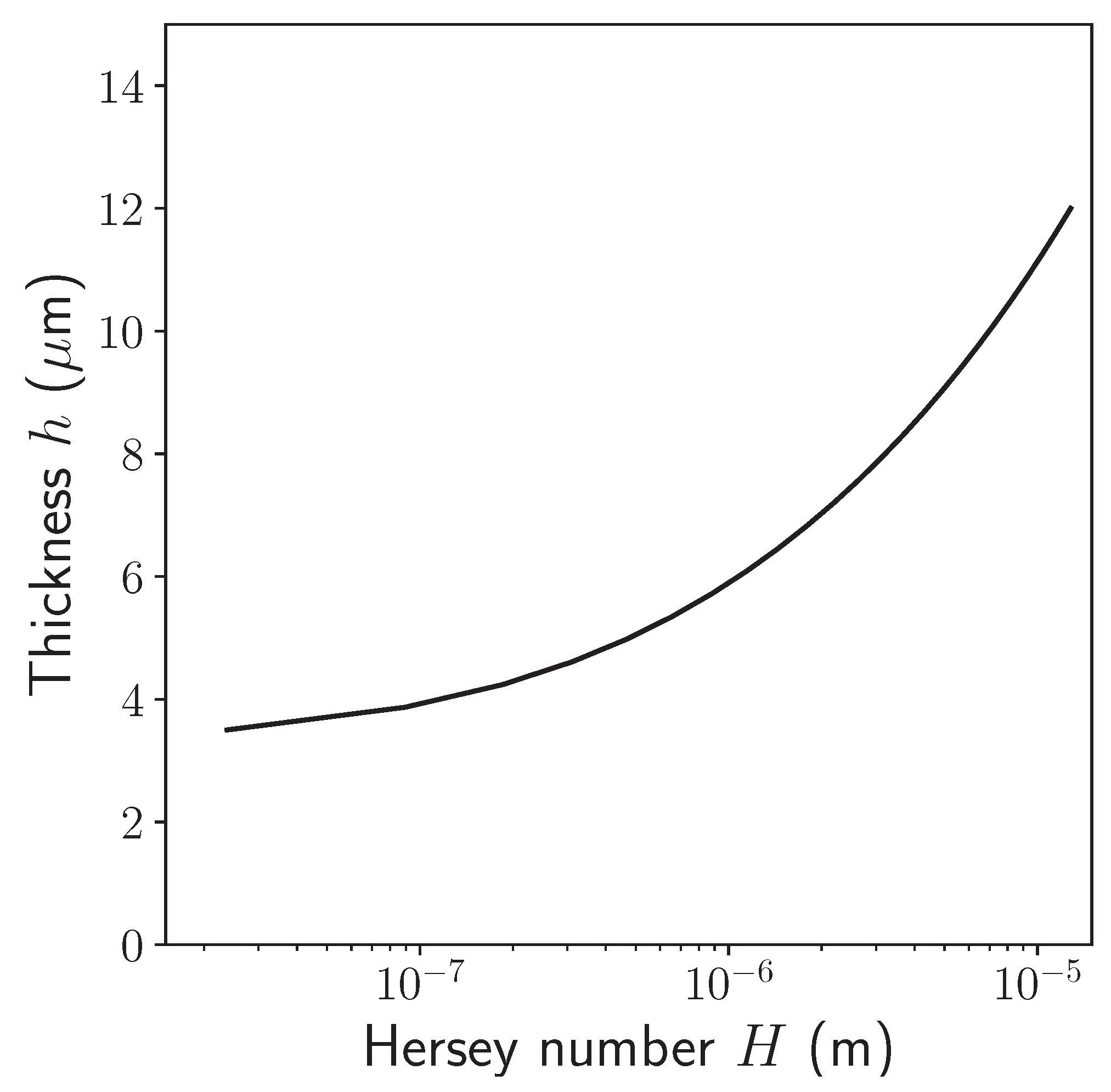
4. Modelling
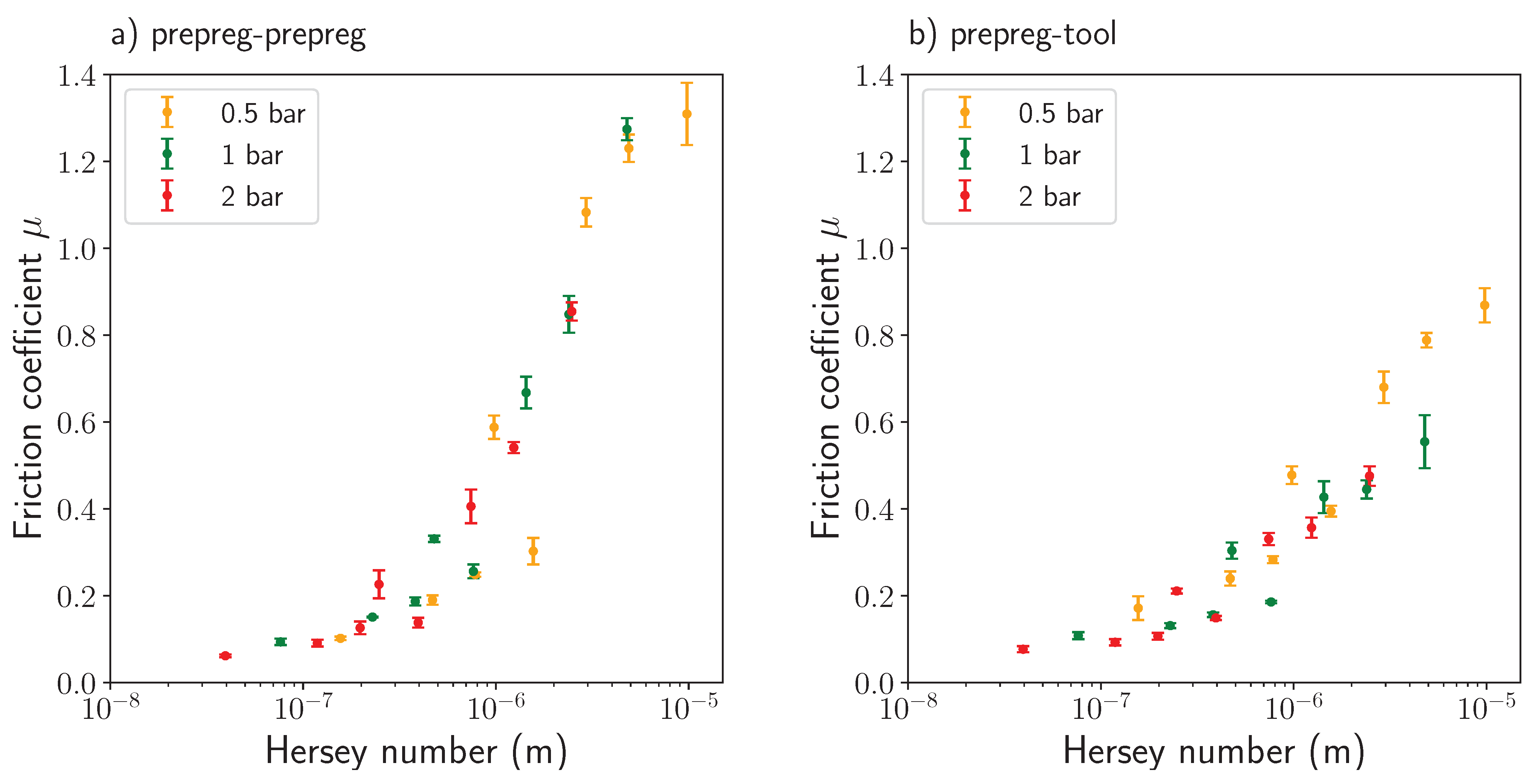
Lubrication Theory
5. Discussion
6. Conclusions
- For a sort of temperatures, pressures, and velocities, a set of friction coefficients were obtained for uncured AS4/8552 UD prepreg composite. The friction mechanism observed was in accordance with the theoretical behaviour expected, e.g., by reducing viscosity with a temperature increment, low friction coefficients were measured. A better representation of these effects was built through a Stribeck curve which also helped to identify our friction case study within the hydrodynamic lubrication regime.
- The prepreg surface examination after friction revealed geometrical characteristics like resin accumulations, exposed fibres and surface roughness which were quantified to contemplate the use of the lubrication theory. After applying microscopical techniques, we conclude that the resin layer between two prepreg plies acts as a lubrication layer. Therefore, the lubrication theory is reasonable for the phenomena explanation. The influence of this lubrication layer was taken into account in the model by quantifying its distribution and accumulation in terms of an equivalent sinusoidal shape with a given wavelength and roughness.
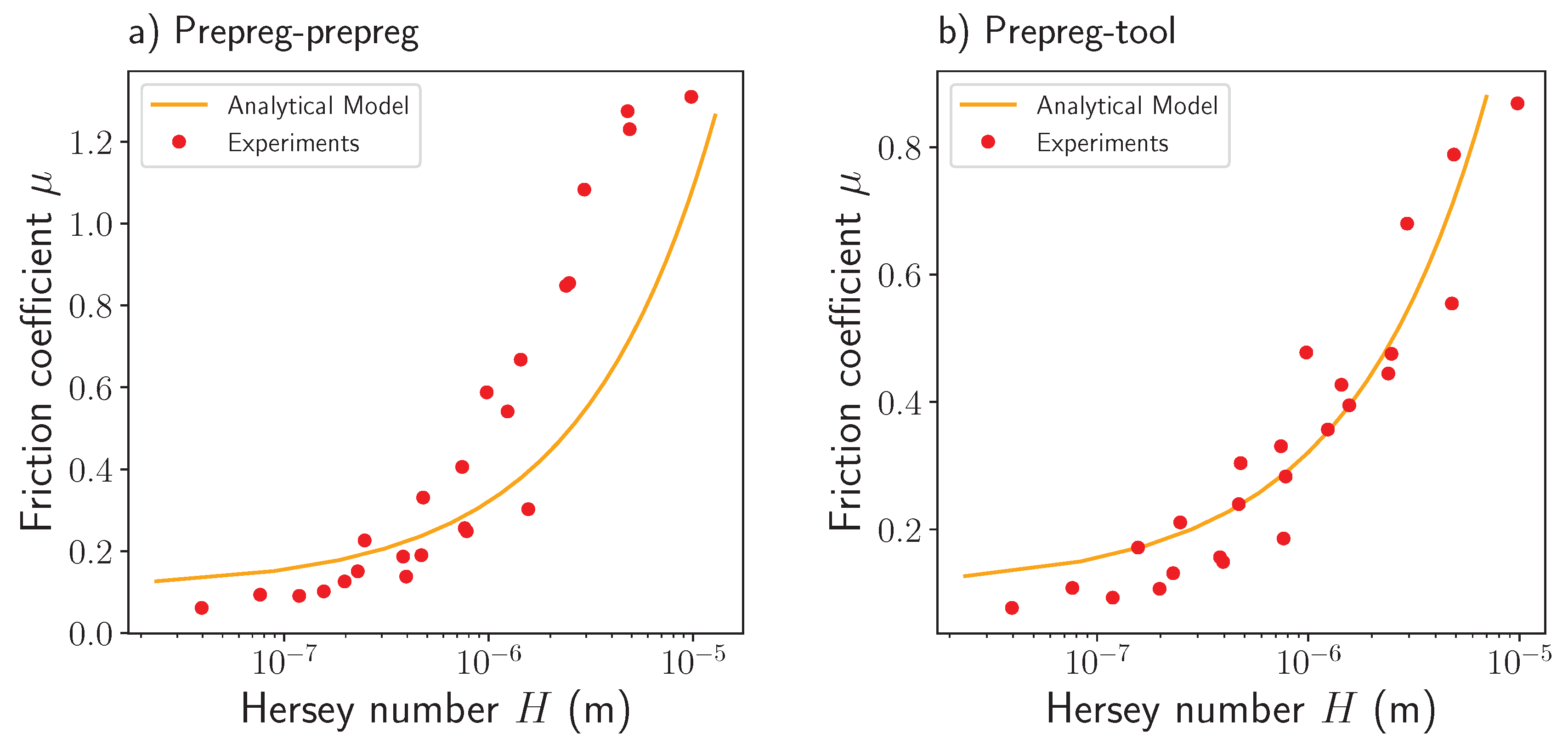
- An analytical model was conceived with a basis on the lubrication theory and the Reynolds equation. The inputs of this model are the wavelength and amplitude of the resin accumulations detected on the prepreg surface. The model results showed that a good characterisation of the rough surface geometry of the prepregs allows the calculation of reliable friction coefficients through the formulation mentioned above. When comparing the model and experimental results, a slight divergence is observed in the prepreg-prepreg contact at 40 °C. The divergence at this temperature was understood as the effect of dry lubrication due to a dominant solid-to-fluid response of the resin. This divergence was not observed in the ply-tool case since the metal surface presents fewer asperities allowing a more smooth slide between the surfaces.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
References
- González, C.; Vilatela, J.; Molina-Aldareguía, J.; Lopes, C.; LLorca, J. Structural composites for multifunctional applications: Current challenges and future trends. Prog. Mater. Sci. 2017, 89, 194–251. [Google Scholar] [CrossRef]
- Dhinakaran, V.; Surendar, K.; Riyaz, M.H.; Ravichandran, M. Review on study of thermosetting and thermoplastic materials in the automated fiber placement process. Mater. Today Proc. 2020, 27, 812–815. [Google Scholar] [CrossRef]
- Brasington, A.; Sacco, C.; Halbritter, J.; Wehbe, R.; Harik, R. Automated fiber placement: A review of history, current technologies, and future paths forward. Compos. Part C Open Access 2021, 6, 100182. [Google Scholar] [CrossRef]
- Boisse, P.; Colmars, J.; Hamila, N.; Naouar, N.; Steer, Q. Bending and wrinkling of composite fiber preforms and prepregs. A review and new developments in the draping simulations. Compos. Part B Eng. 2018, 141, 234–249. [Google Scholar] [CrossRef]
- Guzman-Maldonado, E.; Wang, P.; Hamila, N.; Boisse, P. Experimental and numerical analysis of wrinkling during forming of multi-layered textile composites. Compos. Struct. 2019, 208, 213–223. [Google Scholar] [CrossRef]
- Hsiao, H.M.; Daniel, I.M. Effect of fiber waviness on stiffness and strength reduction of unidirectional composites under compressive loading. Compos. Sci. Technol. 1996, 56, 581–593. [Google Scholar] [CrossRef]
- Garnich, M.R.; Karami, G. Finite element micromechanics for stiffness and strength of wavy fiber composites. J. Compos. Mater. 2004, 38, 273–292. [Google Scholar] [CrossRef]
- Potter, K.; Khan, B.; Wisnom, M.; Bell, T.; Stevens, J. Variability, fibre waviness and misalignment in the determination of the properties of composite materials and structures. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1343–1354. [Google Scholar] [CrossRef]
- Bloom, L.D.; Wang, J.; Potter, K.D. Damage progression and defect sensitivity: An experimental study of representative wrinkles in tension. Compos. Part B Eng. 2013, 45, 449–458. [Google Scholar] [CrossRef]
- Karami, G.; Garnich, M. Effective moduli and failure considerations for composites with periodic fiber waviness. Compos. Struct. 2005, 67, 461–475. [Google Scholar] [CrossRef]
- Lightfoot, J.S.; Wisnom, M.R.; Potter, K. A new mechanism for the formation of ply wrinkles due to shear between plies. Compos. Part A Appl. Sci. Manuf. 2013, 49, 139–147. [Google Scholar] [CrossRef]
- Guzman-Maldonado, E.; Hamila, N.; Naouar, N.; Moulin, G.; Boisse, P. Simulation of thermoplastic prepreg thermoforming based on a visco-hyperelastic model and a thermal homogenization. Mater. Des. 2016, 93, 431–442. [Google Scholar] [CrossRef]
- Çinar, K.; Ersoy, N. Effect of fibre wrinkling to the spring-in behaviour of L-shaped composite materials. Compos. Part A Appl. Sci. Manuf. 2015, 69, 105–114. [Google Scholar] [CrossRef]
- Belnoue, J.P.; Nixon-Pearson, O.J.; Thompson, A.J.; Ivanov, D.S.; Potter, K.D.; Hallett, S.R. Consolidation-driven defect generation in thick composite parts. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 071006. [Google Scholar] [CrossRef]
- Rashidi, A.; Keegan, C.; Milani, A.S. Analysis of inter-ply friction in consolidation process of thermoset woven prepregs. AIP Conf. Proc. 2019, 2113, 1–7. [Google Scholar] [CrossRef]
- Sun, J.; Gu, Y.; Li, M.; Ma, X.; Zhang, Z. Effect of forming temperature on the quality of hot diaphragm formed C-shaped thermosetting composite laminates. J. Reinf. Plast. Compos. 2012, 31, 1074–1087. [Google Scholar] [CrossRef]
- Larberg, Y.; Åkermo, M. In-plane deformation of multi-layered unidirectional thermoset prepreg—Modelling and experimental verification. Compos. Part A Appl. Sci. Manuf. 2014, 56, 203–212. [Google Scholar] [CrossRef]
- Wang, L.; Xu, P.; Peng, X.; Zhao, K.; Wei, R. Characterization of inter-ply slipping behaviors in hot diaphragm preforming: Experiments and modelling. Compos. Part A Appl. Sci. Manuf. 2019, 121, 28–35. [Google Scholar] [CrossRef]
- Pasco, C.; Khan, M.; Gupta, J.; Kendall, K. Experimental investigation on interply friction properties of thermoset prepreg systems. J. Compos. Mater. 2019, 53, 227–243. [Google Scholar] [CrossRef]
- Sun, J.; Li, M.; Gu, Y.; Zhang, D.; Li, Y.; Zhang, Z. Interply friction of carbon fiber/epoxy prepreg stacks under different processing conditions. J. Compos. Mater. 2014, 48, 515–526. [Google Scholar] [CrossRef]
- Liang, B.; Hamila, N.; Peillon, M.; Boisse, P. Analysis of thermoplastic prepreg bending stiffness during manufacturing and of its influence on wrinkling simulations. Compos. Part A Appl. Sci. Manuf. 2014, 67, 111–122. [Google Scholar] [CrossRef]
- Larberg, Y.R.; Åkermo, M. On the interply friction of different generations of carbon/epoxy prepreg systems. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1067–1074. [Google Scholar] [CrossRef]
- Ersoy, N.; Potter, K.; Wisnom, M.R.; Clegg, M.J. An experimental method to study the frictional processes during composites manufacturing. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1536–1544. [Google Scholar] [CrossRef]
- Ten Thije, R.H.; Akkerman, R.; Ubbink, M.; Van Der Meer, L. A lubrication approach to friction in thermoplastic composites forming processes. Compos. Part A Appl. Sci. Manuf. 2011, 42, 950–960. [Google Scholar] [CrossRef]
- Murtagh, A.M.; Lennon, J.J.; Mallon, P.J. Surface friction effects related to pressforming of continuous fibre thermoplastic composites. Compos. Manuf. 1995, 6, 169–175. [Google Scholar] [CrossRef]
- Lee, J.M.; Kim, B.M.; Lee, C.J.; Ko, D.C. A characterisation of tool-ply friction behaviors in thermoplastic composite. Procedia Eng. 2017, 207, 90–94. [Google Scholar] [CrossRef]
- Sachs, U.U. Friction and Bending in Thermoplasctic Composites Forming Processes; University of Twente: Enschede, The Netherlands, 2014; p. 101. [Google Scholar]
- Fetfatsidis, K.A.; Gamache, L.M.; Gorczyca, J.L.; Sherwood, J.A.; Jauffrès, D.; Chen, J. Design of an apparatus for measuring tool/fabric and fabric/fabric friction of woven-fabric composites during the thermostamping process. Int. J. Mater. Form. 2013, 6, 1–11. [Google Scholar] [CrossRef]
- Alshahrani, H.; Hojjati, M. Bending behavior of multilayered textile composite prepregs: Experiment and finite element modeling. Mater. Des. 2017, 124, 211–224. [Google Scholar] [CrossRef]
- Sachs, U.; Akkerman, R.; Fetfatsidis, K.; Vidal-Sallé, E.; Schumacher, J.; Ziegmann, G.; Allaoui, S.; Hivet, G.; Maron, B.; Vanclooster, K.; et al. Characterization of the dynamic friction of woven fabrics: Experimental methods and benchmark results. Compos. Part A Appl. Sci. Manuf. 2014, 67, 289–298. [Google Scholar] [CrossRef]
- Cornelissen, B.; Sachs, U.; Rietman, B.; Akkerman, R. Dry friction characterisation of carbon fibre tow and satin weave fabric for composite applications. Compos. Part A Appl. Sci. Manuf. 2014, 56, 127–135. [Google Scholar] [CrossRef]
- Rashidi, A.; Montazerian, H.; Yesilcimen, K.; Milani, A. Experimental characterization of the inter-ply shear behavior of dry and prepreg woven fabrics: Significance of mixed lubrication mode during thermoset composites processing. Compos. Part A Appl. Sci. Manuf. 2020, 129, 105725. [Google Scholar] [CrossRef]
- ten Thije, R.H.; Akkerman, R.; van der Meer, L.; Ubbink, M.P. Tool-ply friction in thermoplastic composite forming. Int. J. Mater. Form. 2008, 1, 953–956. [Google Scholar] [CrossRef]
- Singh Grewal, H. Characterization of Interply Shear Behaviour of Out-of-Autoclave Thermosetting Prepreg Composites; Technical Report; Concordia University: Montreal, QC, Canada, 2015. [Google Scholar]
- Kappel, E.; Stefaniak, D.; Spröwitz, T.; Hühne, C. A semi-analytical simulation strategy and its application to warpage of autoclave-processed CFRP parts. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1985–1994. [Google Scholar] [CrossRef]
- Joven, R.; Tavakol, B.; Rodriguez, A.; Guzman, M.; Minaie, B. Characterization of shear stress at the tool-part interface during autoclave processing of prepreg composites. J. Appl. Polym. Sci. 2013, 129, 2017–2028. [Google Scholar] [CrossRef]
- Groves, D.J. A characterization of shear flow in continuous fibre thermoplastic laminates. Composites 1989, 20, 28–32. [Google Scholar] [CrossRef]
- Scherer, R.; Friedrich, K. Inter- and intraply-slip flow processes during thermoforming of cf/pp-laminates. Compos. Manuf. 1991, 2, 92–96. [Google Scholar] [CrossRef]
- Morris, S.R.; Sun, C.T. An investigation of interply slip behaviour in AS4/PEEK at forming temperatures. Compos. Manuf. 1994, 5, 217–224. [Google Scholar] [CrossRef]
- Gorczyca-Cole, J.L.; Sherwood, J.A.; Chen, J. A friction model for thermostamping commingled glass-polypropylene woven fabrics. Compos. Part A Appl. Sci. Manuf. 2007, 38, 393–406. [Google Scholar] [CrossRef]
- Kim, J.Y.; Hwang, Y.T.; Baek, J.H.; Song, W.Y.; Kim, H.S. Study on inter-ply friction between woven and unidirectional prepregs and its effect on the composite forming process. Compos. Struct. 2021, 267, 113888. [Google Scholar] [CrossRef]
- Shoaib, T.; Espinosa-Marzal, R.M. Advances in Understanding Hydrogel Lubrication. Colloids Interfaces 2020, 4, 54. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, T.; Li, H.; Zhang, B. Characterization of prepreg-prepreg and prepreg-tool friction for unidirectional carbon fiber/epoxy prepreg during hot diaphragm forming process. Polym. Test. 2020, 84, 106440. [Google Scholar] [CrossRef]
- Nikas, G.K. Recent Developements in Wear Prevention, Friction, and Lubrication; Research Signpost: Thiruvananthapuram, India, 2010; p. 314. [Google Scholar]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, A.; Crawford, B.; Olfatbakhsh, T.; Milani, A.S. A mixed lubrication model for inter-ply friction behaviour of uncured fabric prepregs. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106571. [Google Scholar] [CrossRef]
- Burstein, L. Effect of sinusoidal roughened surfaces on pressure in lubricating film. Int. J. Surf. Sci. Eng. 2008, 2, 52–70. [Google Scholar] [CrossRef]
- Heshmat, H.; Walton, J.F. Starved Hydrodynamic Gas Foil Bearings-Experiment, Micromechanical Phenomenon, and Hypotheses. J. Tribol. 2016, 138, 1–14. [Google Scholar] [CrossRef]

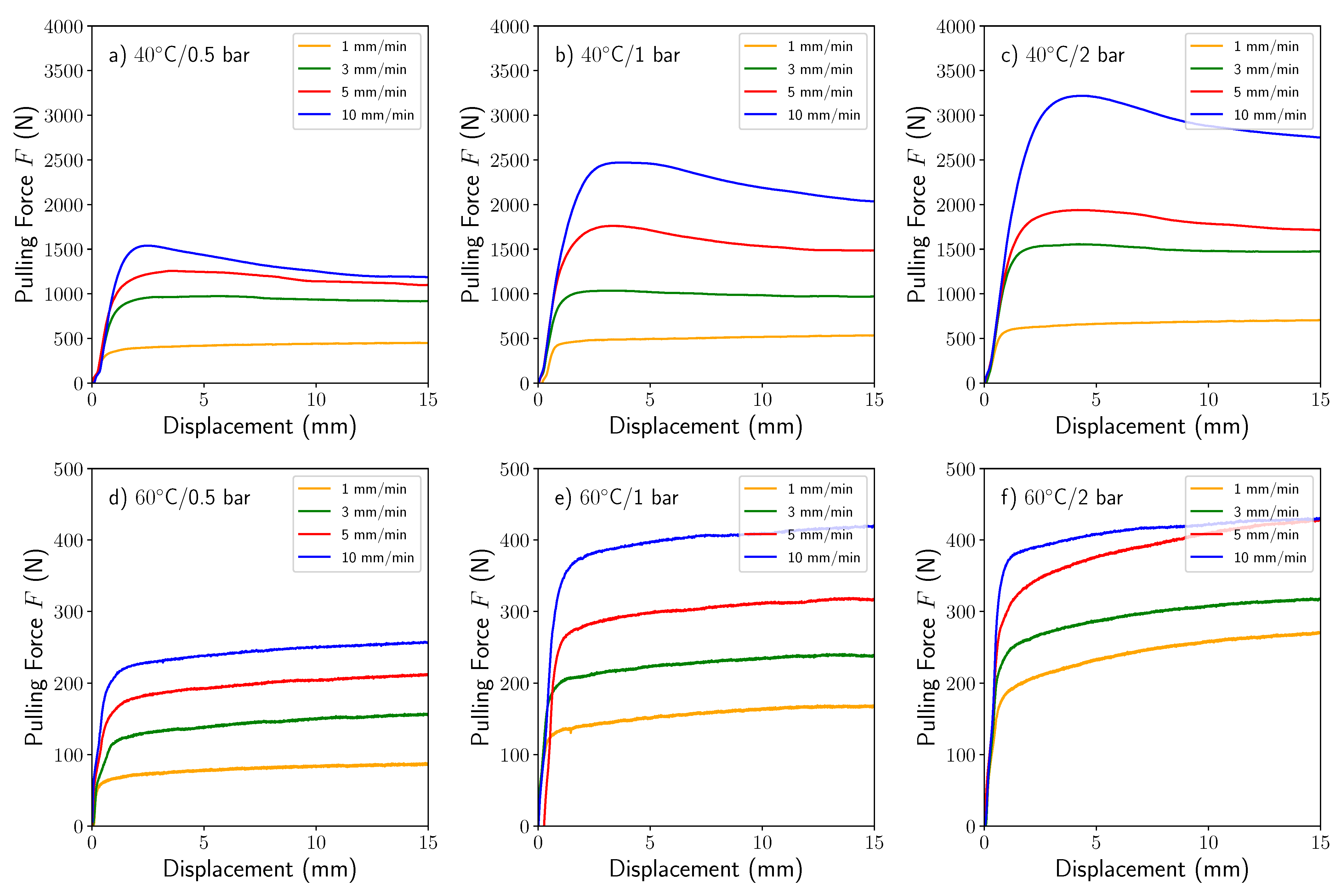
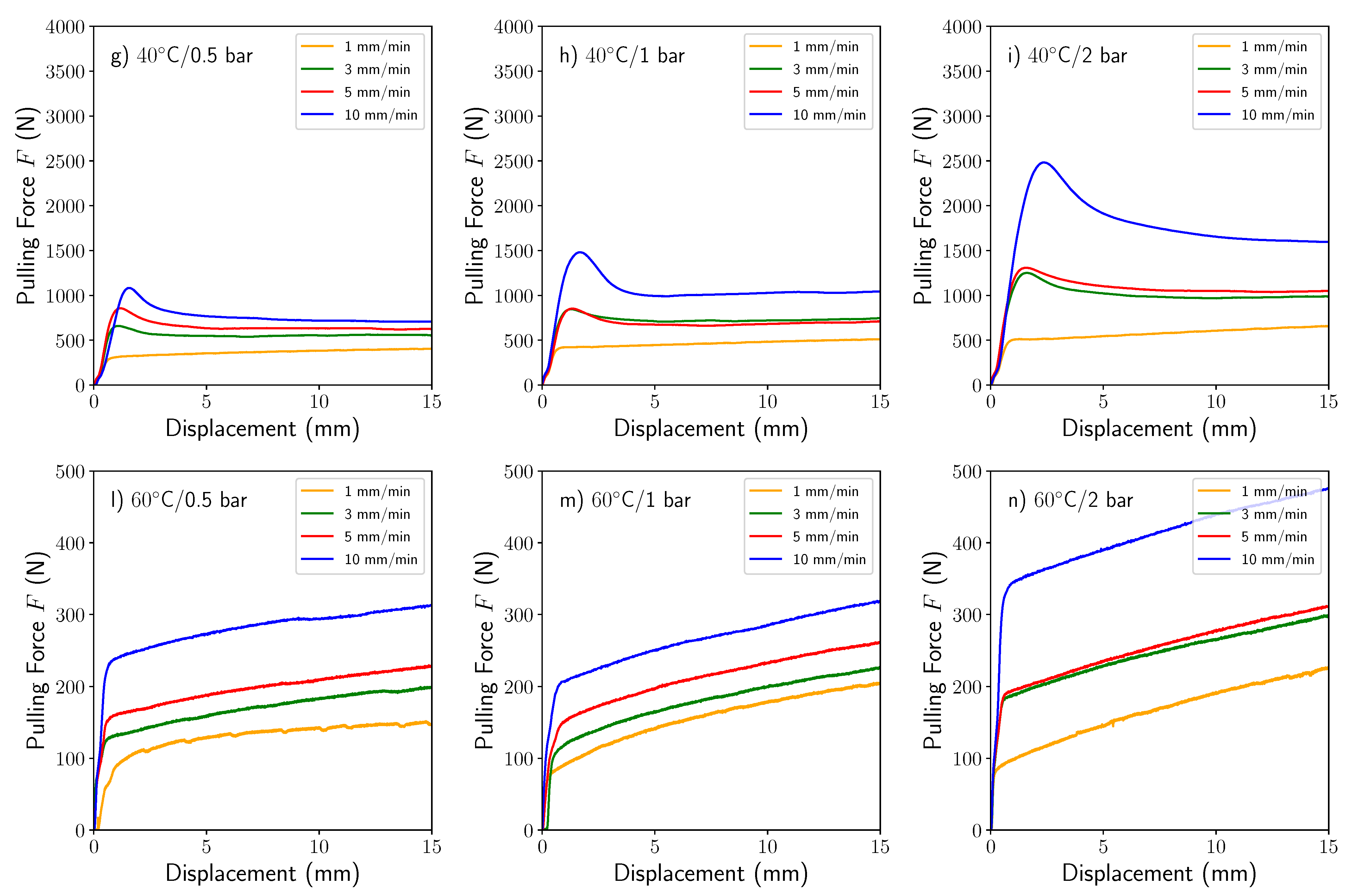
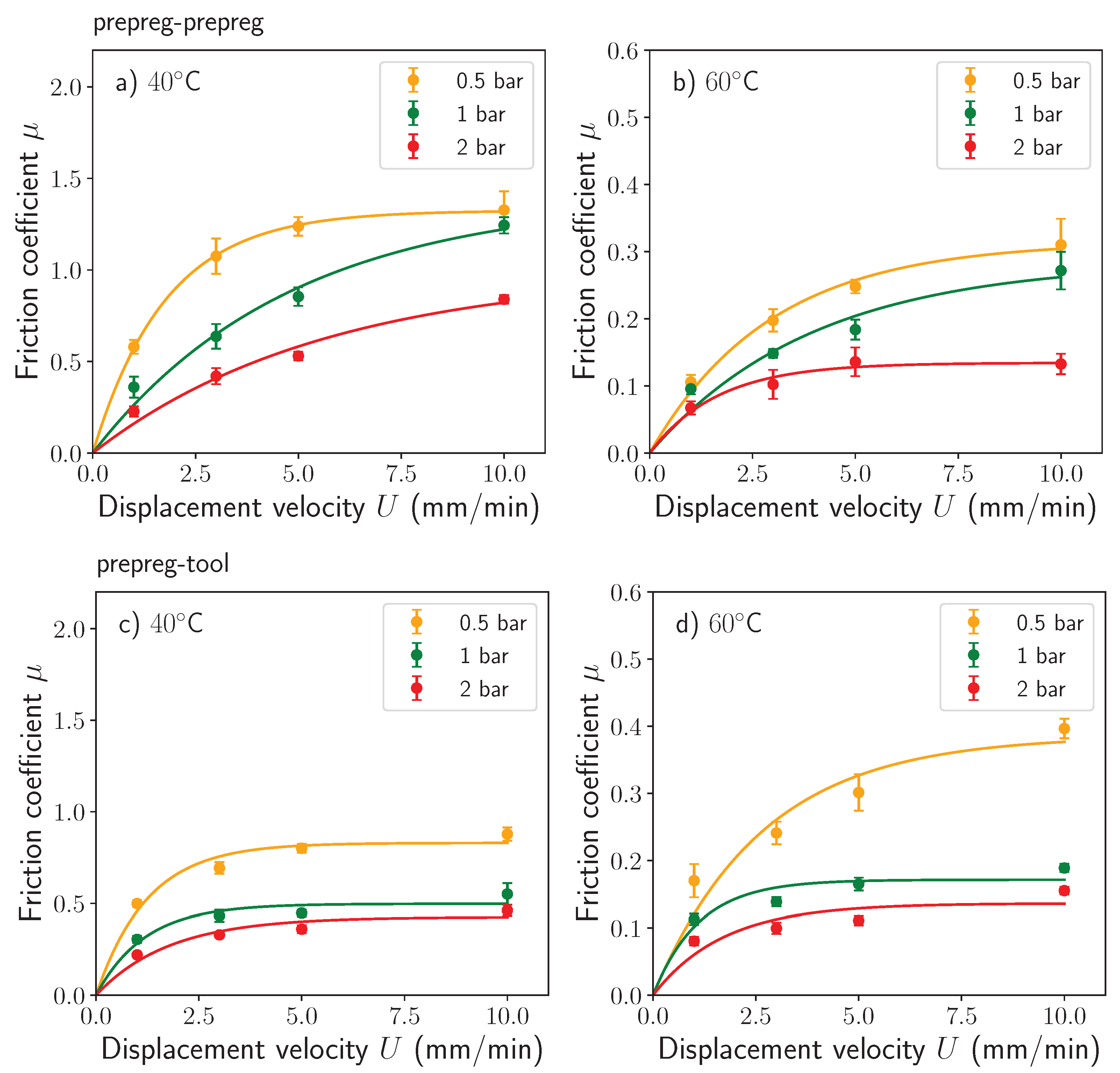


| Clamping Pressure (bar) | Pulling Velocity (mm/min) | Friction Coefficients at 40 °C Ply-Ply | Friction Coefficients at 40 °C Ply-Tool | Friction Coefficients at 60 °C Ply-Ply | Friction Coefficients at 60 °C Ply-Tool |
|---|---|---|---|---|---|
| 0.5 | 1 | 0.59 ± 0.03 | 0.47 ± 0.02 | 0.1 ± 0.004 | 0.17 ± 0.03 |
| 3 | 1.08 ± 0.03 | 0.68 ± 0.02 | 0.19 ± 0.01 | 0.23 ± 0.02 | |
| 5 | 1.23 ± 0.03 | 0.78 ± 0.02 | 0.25 ± 0.005 | 0.28 ± 0.008 | |
| 10 | 1.31 ± 0.07 | 0.86 ± 0.04 | 0.3 ± 0.03 | 0.39 ± 0.01 | |
| 1 | 1 | 0.33 ± 0.007 | 0.30 ± 0.02 | 0.09 ± 0.007 | 0.10 ± 0.008 |
| 3 | 0.67 ± 0.04 | 0.42 ± 0.04 | 0.15 ± 0.001 | 0.13 ± 0.007 | |
| 5 | 0.85 ± 0.04 | 0.44 ± 0.02 | 0.19 ± 0.009 | 0.15 ± 0.008 | |
| 10 | 1.27 ± 0.03 | 0.55 ± 0.06 | 0.26 ± 0.02 | 0.18 ± 0.005 | |
| 2 | 1 | 0.23 ± 0.03 | 0.21 ± 0.006 | 0.06 ± 0.003 | 0.07 ± 0.007 |
| 3 | 0.41 ± 0.04 | 0.33 ± 0.01 | 0.09 ± 0.008 | 0.09 ± 0.007 | |
| 5 | 0.54 ± 0.01 | 0.35 ± 0.02 | 0.13 ± 0.01 | 0.19 ± 0.008 | |
| 10 | 0.85 ± 0.02 | 0.47 ± 0.02 | 0.14 ± 0.01 | 0.14 ± 0.005 |
| Contact Type | 40 °C | 60 °C |
|---|---|---|
| Prepreg-prepreg | 3.22 ± 0.23 | 3.17 ± 0.66 |
| Prepreg-tool | 3.93 ± 0.46 | 3.10 ± 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aveiga, D.; Gómez, D.G.; Mocerino, D.; López-Romano, B.; González, C. Friction Resistance of Uncured Carbon/Epoxy Prepregs under Thermoforming Process Conditions: Experiments and Modelling. J. Manuf. Mater. Process. 2023, 7, 14. https://doi.org/10.3390/jmmp7010014
Aveiga D, Gómez DG, Mocerino D, López-Romano B, González C. Friction Resistance of Uncured Carbon/Epoxy Prepregs under Thermoforming Process Conditions: Experiments and Modelling. Journal of Manufacturing and Materials Processing. 2023; 7(1):14. https://doi.org/10.3390/jmmp7010014
Chicago/Turabian StyleAveiga, David, David Garoz Gómez, Davide Mocerino, Bernardo López-Romano, and Carlos González. 2023. "Friction Resistance of Uncured Carbon/Epoxy Prepregs under Thermoforming Process Conditions: Experiments and Modelling" Journal of Manufacturing and Materials Processing 7, no. 1: 14. https://doi.org/10.3390/jmmp7010014
APA StyleAveiga, D., Gómez, D. G., Mocerino, D., López-Romano, B., & González, C. (2023). Friction Resistance of Uncured Carbon/Epoxy Prepregs under Thermoforming Process Conditions: Experiments and Modelling. Journal of Manufacturing and Materials Processing, 7(1), 14. https://doi.org/10.3390/jmmp7010014






