Thermal Contact Resistance between Mold Steel and Additively Manufactured Insert for Designing Conformal Channels: An Experimental Study
Abstract
:1. Introduction
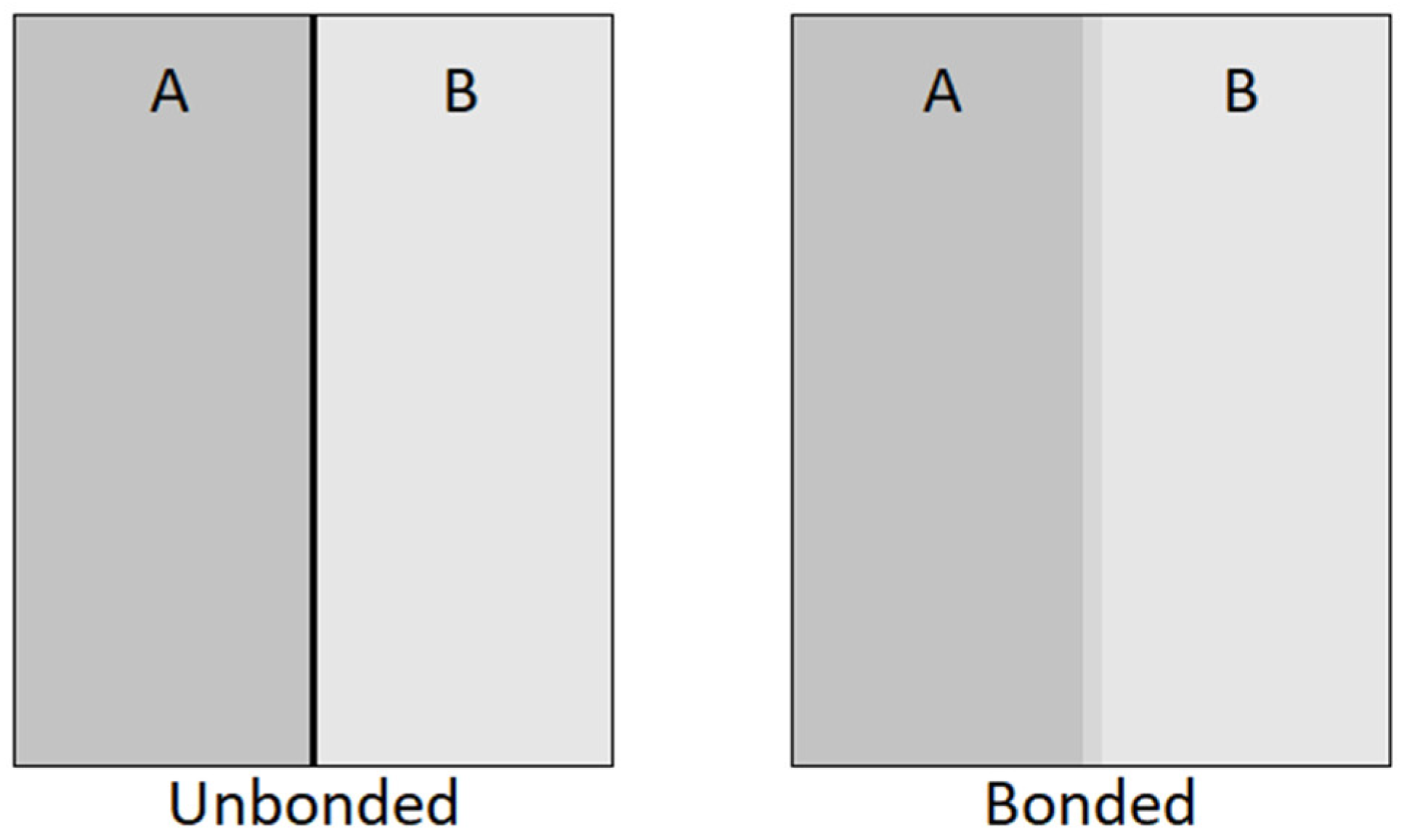
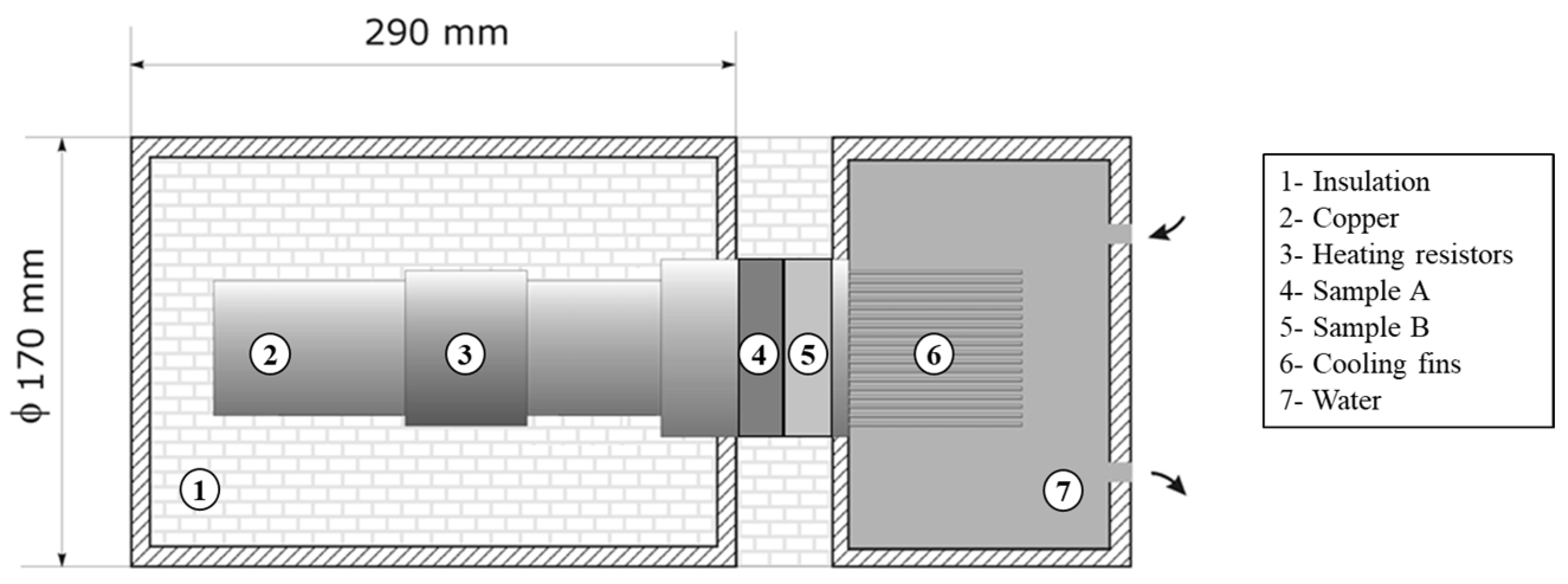
2. Materials and Methods
2.1. Sample Preparations
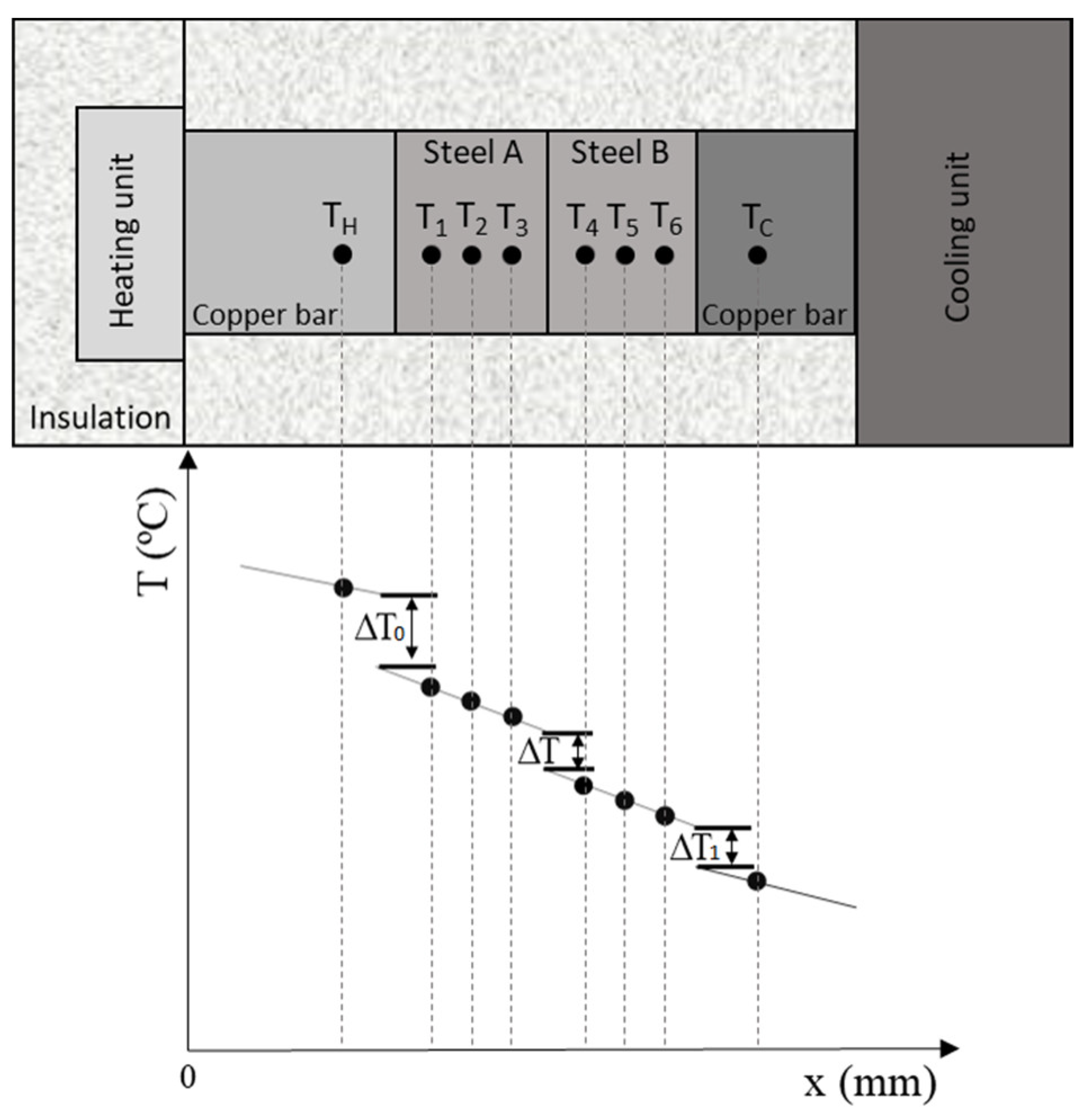
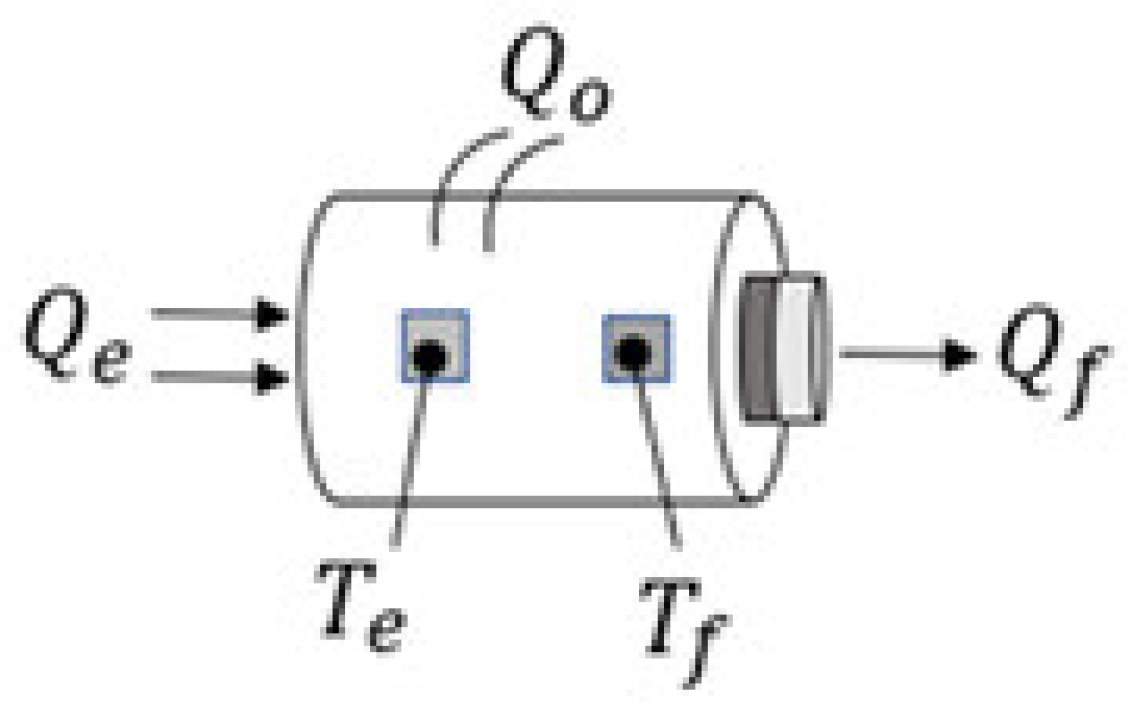
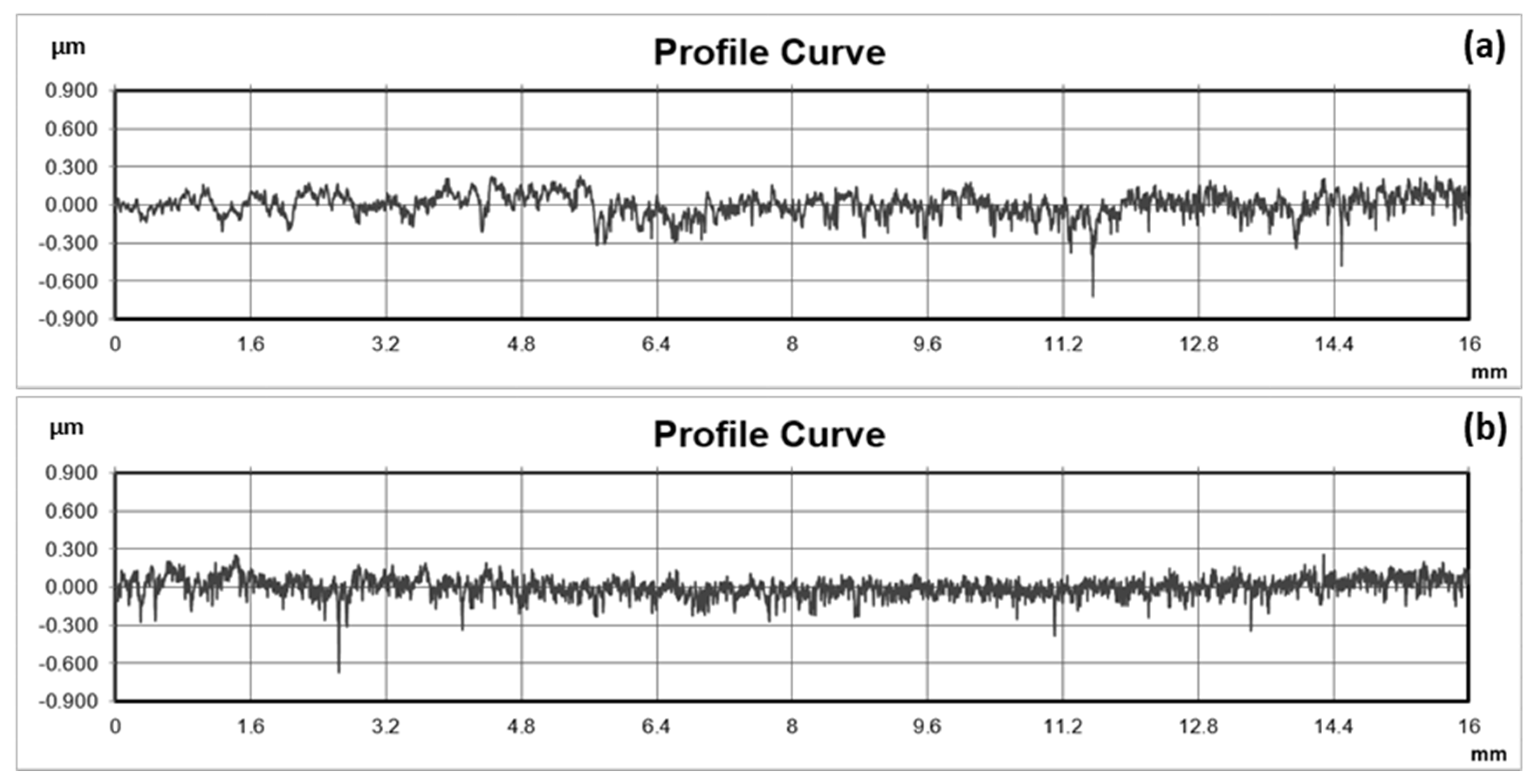
2.2. Sample Characterization
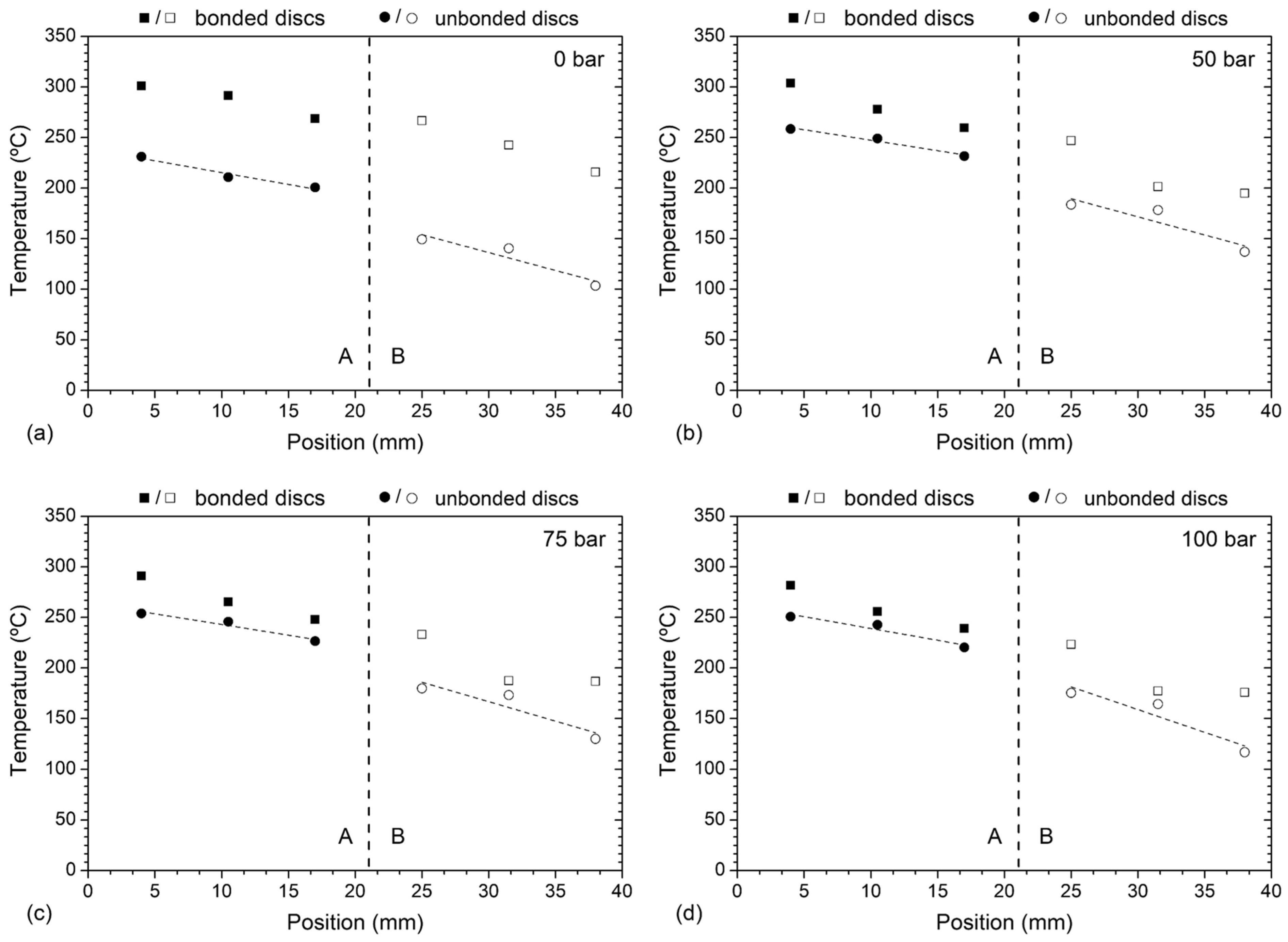
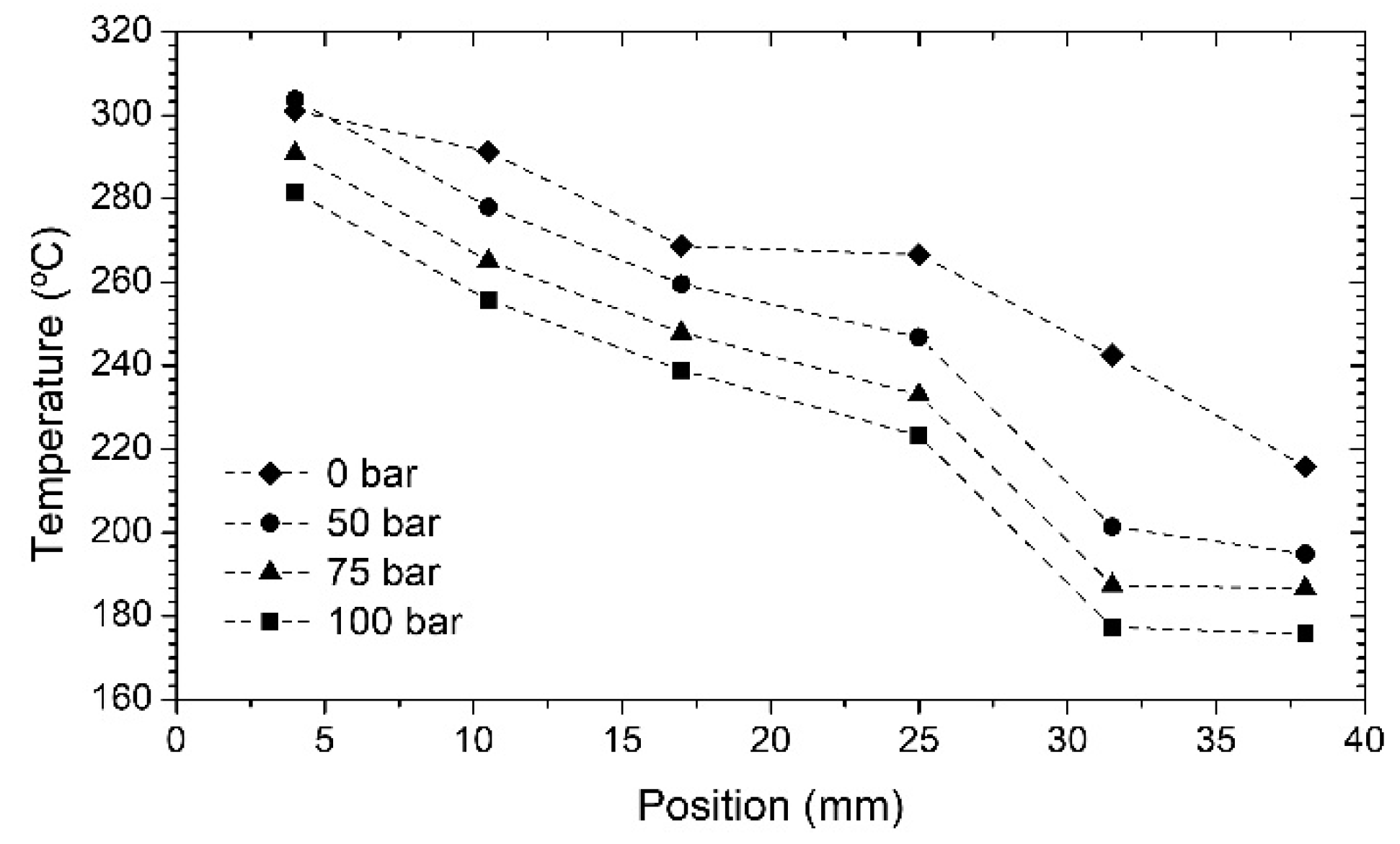
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hsu, F.H.; Wang, K.; Huang, C.T.; Chang, R.Y. Investigation on conformal cooling system design in injection molding. Adv. Prod. Eng. Manag. 2013, 8, 107–115. [Google Scholar] [CrossRef]
- Kurtulus, K.; Bolatturk, A.; Coskun, A.; Gürel, B. An experimental investigation of the cooling and heating performance of a gravity die casting mold with conformal cooling channels. Appl. Therm. Eng. 2021, 194, 117105. [Google Scholar] [CrossRef]
- Shinde, M.S.; Ashtankar, K.M. Additive manufacturing—Assisted conformal cooling channels in mold manufacturing processes. Adv. Mech. Eng. 2017, 9, 1687814017699764. [Google Scholar] [CrossRef]
- Heogh, W.; Yeon, S.M.; Kang, D.S.; Park, S.; Park, S.; Ryu, K.; Ha, C.W. The design and additive manufacturing of an eco-friendly mold utilized for high productivity based on conformal cooling optimization. Mater. Des. 2022, 222, 111088. [Google Scholar] [CrossRef]
- Tan, C.; Wang, D.; Ma, W.; Chen, Y.; Chen, S.; Yang, Y.; Zhou, K. Design and additive manufacturing of novel conformal cooling molds. Mater. Des. 2020, 196, 109147. [Google Scholar] [CrossRef]
- Davis, W.; Lunetto, V.; Priarone, P.C.; Centea, D.; Settineri, L. An appraisal on the sustainability payback of additively manufactured molds with conformal cooling. Procedia CIRP 2020, 90, 516–521. [Google Scholar] [CrossRef]
- Whal, J.P.; Niedermeyer, J.; Bernhard, R.; Hermsdorf, J.; Kaierle, S. Design of additively manufacturable injection molds with conformal cooling. Procedia CIRP 2022, 111, 97–100. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Murugan, P.D.; Vijayananth, S.; Natarajan, M.P.; Jayabalakrishnan, D.; Arul, K.; Jayaseelan, V.; Elanchezhian, J. A current state of metal additive manufacturing methods: A review. Mater. Today Proc. 2022, 59, 1277–1283. [Google Scholar] [CrossRef]
- Tomasoni, D.; Colosio, S.; Giorleo, L.; Ceretti, E. Design for additive manufacturing: Thermoforming mold optimization via conformal cooling channel technology. Procedia Manuf. 2020, 47, 1117–1122. [Google Scholar] [CrossRef]
- Clemente, M.R.; Oliveira Panão, M.R. Introducing flow architecture in the design and optimization of mold inserts cooling systems. Int. J. Therm. Sci. 2018, 127, 288–293. [Google Scholar] [CrossRef]
- Fiorentini, F.; Curcio, P.; Armentani, E.; Rosso, C.; Baldissera, P. Study of two alternative cooling systems of a mold insert used in die casting process of light alloy components. Procedia Struct. Integr. 2019, 24, 569–582. [Google Scholar] [CrossRef]
- Wang, A.L.; Zhao, J.F. Review of prediction for thermal contact resistance. Sci. China Technol. Sci. 2010, 53, 1798–1808. [Google Scholar] [CrossRef]
- Li, X.; Luo, R.; Zhang, W.; Liao, H. Method for measuring thermal contact resistance of graphite thin film materials. Measurement 2016, 93, 202–207. [Google Scholar] [CrossRef]
- Ren, X.J.; Ding, H.; Dai, Y.J.; Tu, J.Y.; Chen, X.; He, J.Y.; Tao, W.Q. Experimental study on thermal contact resistance of carbon fiber reinforced silicon carbide composite with 3D needled preform (3DN C/SiC). Int. Commun. Heat Mass Transf. 2021, 124, 105271. [Google Scholar] [CrossRef]
- Bi, D.; Chen, H.; Ye, T. Influences of temperature and contact pressure on thermal contact resistance at interfaces at cryogenic temperatures. Cryogenics 2012, 52, 403–409. [Google Scholar] [CrossRef]
- Hsiao, F.-B.; Wang, D.-B.; Jen, C.-P. Numerical investigation of thermal contact resistance between the mold and substrate on laser-assisted imprinting fabrication. Numer. Heat Transf. A-Appl. 2006, 49, 669–682. [Google Scholar] [CrossRef]
- Goodarzi, K.; Ramezani, S.R.; Hajati, S. Reducing thermal contact resistance using nanocoating. Appl. Therm. Eng. 2014, 70, 641–646. [Google Scholar] [CrossRef]
- Fletcher, L.S.; Smuda, P.A. Thermal contact resistance of selected low-conductance interstitial materials. AIAA J. 1969, 7, 1302–1309. [Google Scholar] [CrossRef]
- Mikic, B.B. Thermal contact conductance; theoretical considerations. Int. J. Heat Mass Transf. 1974, 17, 205–214. [Google Scholar] [CrossRef]
- McCool, J.I.; April, R. Comparison of models for the contact of rough surfaces. Wear 1986, 107, 37–60. [Google Scholar] [CrossRef]
- Dai, Y.-J.; Gou, J.-J.; Ren, X.-J.; Bai, F.; Fang, W.-Z.; Tao, W.-Q. A test-validated prediction model of thermal contact resistance for Ti-6Al-4V alloy. Appl. Energy 2018, 228, 1601–1617. [Google Scholar] [CrossRef]
- Gou, J.-J.; Ren, X.-J.; Dai, Y.-J.; Li, S.; Tao, W.-Q. Study of thermal contact resistance of rough surfaces based on the practical topography. Comp. Fluids 2018, 164, 2–11. [Google Scholar] [CrossRef]
- Ren, X.-J.; Dai, Y.-J.; Gou, J.-J.; Tao, W.-Q. Numerical prediction of thermal contact resistance of 3D C/C-SiC needled composites based on measured practical topography. Int. J. Heat Mass Transf. 2019, 131, 176–188. [Google Scholar] [CrossRef]
- Liu, D.; Luo, Y.; Shang, X. Experimental investigation of high temperature thermal contact resistance between high thermal conductivity C/C material and Inconel 600. Int. J. Heat Mass Transf. 2015, 80, 407–410. [Google Scholar] [CrossRef]
- Madhusudana, C.V. Accuracy in thermal contact conductance experiments-the effect of heat losses to the surroundings. Int. Commun. Heat Mass Transf. 2000, 27, 877–891. [Google Scholar] [CrossRef]
- Dongmei, B.; Huanxin, C.; Shanjian, L.; Limei, S. Measurement of thermal diffusivity/thermal contact resistance using laser photothermal method at cryogenic temperatures. Appl. Therm. Eng. 2017, 111, 768–775. [Google Scholar] [CrossRef]
- Cousineau, J.E.; Bennion, K.; Devoto, D.; Narumanchi, S. Experimental characterization and modeling of thermal resistance of electric machine lamination stacks. Int. J. Heat Mass Transf. 2019, 129, 152–159. [Google Scholar] [CrossRef]
- Le, V.T.; Goo, N.S.; Kim, J.Y. Experimental investigation on thermal contact resistance of alumina fibrous insulation material with Ti-6Al-4V alloy at high temperature and its effective thermal conductivity. Heat Mass Transf. 2019, 55, 1705–1721. [Google Scholar] [CrossRef]
- Choi, Y.S.; Kim, M.S. Experiments on Thermal Contact Conductance between Metals below 100 K. Adv. Cryog. Eng. AIP Conf. Proc. 2014, 1573, 1070–1077. [Google Scholar]

| Contact Pressure (bar) | Qf (W) | hc (W/m2·°C) | TCR × 104 (m2·K/W) |
|---|---|---|---|
| Unbonded (A/B) configuration | |||
| 0 | 385 | 4395 | 2.28 |
| 50 | 386 | 4574 | 2.19 |
| 75 | 388 | 5142 | 1.94 |
| 100 | 389 | 6791 | 1.47 |
| Bonded (A.B.) configuration | |||
| 0 | 374 | 26,160 | - |
| 50 | 375 | 21,417 | - |
| 75 | 379 | 22,415 | - |
| 100 | 383 | 23,401 | - |
| Contact Pressure (bar) | T1–T6 Temperature Reduction (°C) | |
|---|---|---|
| Unbonded (A/B) Configuration | Bonded (A.B.) Configuration | |
| 0 | 91 | 85 |
| 50 | 112 | 109 |
| 75 | 112 | 104 |
| 100 | 115 | 106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, A.; Capela, P.; Lopes, V.; Prior, F.; Puga, H.; Soares, D.; Teixeira, J. Thermal Contact Resistance between Mold Steel and Additively Manufactured Insert for Designing Conformal Channels: An Experimental Study. J. Manuf. Mater. Process. 2022, 6, 99. https://doi.org/10.3390/jmmp6050099
Souza A, Capela P, Lopes V, Prior F, Puga H, Soares D, Teixeira J. Thermal Contact Resistance between Mold Steel and Additively Manufactured Insert for Designing Conformal Channels: An Experimental Study. Journal of Manufacturing and Materials Processing. 2022; 6(5):99. https://doi.org/10.3390/jmmp6050099
Chicago/Turabian StyleSouza, Andrews, Paulina Capela, Vítor Lopes, Filipe Prior, Hélder Puga, Delfim Soares, and José Teixeira. 2022. "Thermal Contact Resistance between Mold Steel and Additively Manufactured Insert for Designing Conformal Channels: An Experimental Study" Journal of Manufacturing and Materials Processing 6, no. 5: 99. https://doi.org/10.3390/jmmp6050099
APA StyleSouza, A., Capela, P., Lopes, V., Prior, F., Puga, H., Soares, D., & Teixeira, J. (2022). Thermal Contact Resistance between Mold Steel and Additively Manufactured Insert for Designing Conformal Channels: An Experimental Study. Journal of Manufacturing and Materials Processing, 6(5), 99. https://doi.org/10.3390/jmmp6050099









