Abstract
Acoustic emission-based monitoring of the milling process holds the potential to detect undesired damages of fibre-reinforced plastic workpieces, such as delamination or matrix cracking. In addition, abrasive tool wear, tool breakage, or coating failures can be detected. As measurements of the acoustic emission are impacted by attenuation, dispersion, and reflection as it propagates from source to sensor, the waveforms, amplitudes, and frequency content of a wave packet differ depending on the propagation length in the workpiece. Since the distance between acoustic emission sources and a stationary sensor attached to the workpiece changes continually in circumferential milling, the extraction of meaningful information from the raw measurement data is challenging and requires appropriate signal processing and frequency-dependent amplification. In this paper, practical and robust approaches, namely experimentally identified transfer functions and frequency gain parameter tables for attenuation modelling, which in reverse enable the reconstruction of frequency spectra emitted at the acoustic emission source, are presented and discussed. From the results, it is concluded that linear signal processing can largely compensate for the influence of attenuation, dispersion, and reflection on the frequency spectra and can therefore enable acoustic emission based process monitoring.
1. Introduction
The milling of carbon fibre-reinforced plastics (CFRP) remains a challenging process in manufacturing. Since the carbon fibres are highly abrasive, high tool wear rates occur. To enhance tool life, state-of-the-art milling tools with diamond coatings and segmented cutting edges are employed in industry. Nevertheless, even with these improvements, machining with a worn tool leads to higher cutting temperatures and increasing cutting forces [1]. These result in poor surface quality and undesired workpiece damages, such as matrix cracking, delamination or fibre protrusion [2]. Damage to the workpiece reduces fatigue strength considerably, and therefore workpieces must be inspected by quality control and reworked or disposed of, if necessary.
One approach to avoid workpiece damages and thus eliminate laborious workpiece inspections is acoustic emission (AE) based process monitoring. AE is emitted by the release of strain energy, e.g., by deformation, friction, breakage or impact in the cutting zone. Therefore, it holds the potential to monitor the tool wear state as well as undesired workpiece damages. However, because these different phenomena are meant to be quantified with one measurand, special care needs to be taken when analysing AE generation, propagation, sensor coupling and transduction. The same applies to the parameterisation of the downstream signal processing algorithms e.g., for process monitoring. Often neglected in academic works on AE process monitoring for machining are effects like attenuation, dispersion and reflection in the AE propagation path. The impact of these effects on measurement signals depends on material properties, geometric setup and workpiece clamping equipment. They pose a serious challenge for AE-based process monitoring approaches. To fill this research gap, practical and robust experimental algorithms which account for such phenomena are presented and discussed in this paper.
As AE propagates through a solid, it is subjected to attenuation, dispersion and reflection. Therefore, measured waveforms, amplitudes and frequency content of a wave packet depend on the distance and the positioning of AE source and sensor. The effects of attenuation, dispersion, reflection, and positioning are significant and, in most cases, must not be neglected when evaluating different AE measurement results. A short introduction on the theoretical background of these phenomena is given in the following section.
Attenuation can be observed as a decline in signal amplitude due to geometric spread as well as material absorption and internal friction resulting from the viscoelastic nature of the workpiece. Attenuation coefficients α(f) are frequency-dependent and can be identified experimentally using Equation (1) [3,4,5,6].
where Vm1 and Vm2 are the amplitudes of a discrete signal frequency at the radial distances x1 and x2. If the attenuation coefficients α(f) are constant for different distances to the source x, which might not always be given, amplitude Vm can be calculated using Equation (2) [7].
where V is the amplitude at the AE source. Ono and Gallego [3] identified attenuation coefficients for aluminium as well as unidirectional, cross-ply and quasi-isotropic CFRP. Abdulaziz et al. [8] identified the attenuation coefficients for different distances and angles between glass fibres and the AE propagation path experimentally. High directivity, meaning dependence of the attenuation coefficient on the angle between fibres and the propagation path, was reported. It was also shown that external bending load on the CFRP specimen can impact attenuation coefficients significantly [6]. Theoretical modelling of attenuation, e.g., with numerical approaches, are based on Voigt-Kelvin or Boltzmann models for the relationship of tension σ and elongation ε but might not be applicable for complex part geometries and material properties [9,10,11].
Dispersion denotes the effect of frequency-dependent phase velocity vp. Higher frequencies may propagate, depending on the wave mode, with a different velocity than lower frequencies. Therefore, the shape of a wave packet changes along the propagation path. Different wave velocities have been reported for AE propagation in unidirectional CFRP, depending on the angle between the signal path and the fibre orientation [12]. Phase velocities can be obtained experimentally or estimated based on workpiece material properties [13]. For the frequency spectrum of around 0–250 kHz, which is induced during the milling and drilling process, significant differences in phase velocities are reported, thus a strong influence of dispersion is to be expected [14].
Reflection of AE occurs at workpiece edges. Once the wavepacket hits an interface with the angle ϴ1, it is reflected under angle ϴ1 and refracted and propagates further under a certain angle ϴ2 which can be estimated with the indices of refraction c1 and c2 using Equation (3).
In most cases, reflections and refractions are considered a disturbance. Therefore, experimental setups are often realised to minimise the effects of reflection on measurements. Generic dispersion curves for the wave modes A0 and S0 as well as a simplified illustration of the propagation of an AE wave as it is reflected at the workpiece edges are presented in Figure 1.
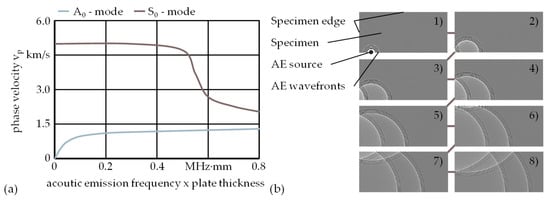
Figure 1.
Dispersion and reflection; (a) dispersion curves; (b) reflection of AE at workpiece edges of the specimen.
The impact of the discussed attenuation, dispersion and reflection phenomena on an AE wave packet emitted by a Hsu-Nielsen source close to a workpiece edge to provoke reflection is shown in Figure 2. It can be observed that AE propagation distances of several centimetres in CFRP already have a significant impact on the transduced measurement signal as the maximum amplitude decreases due to attenuation and the waveform distorts due to dispersion.
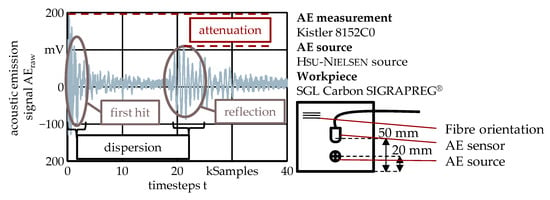
Figure 2.
AE measurement demonstrating the effects of attenuation, dispersion and reflection.
AE-based approaches are applied for different monitoring tasks for a variety of machining processes [15,16,17]. In grinding, the contact recognition of the grinding wheel and workpiece, as well as the detection of grinding burn, can be realised [18,19]. Therefore, AE monitoring is common in industrial grinding applications. Boaron et al. [20] developed a quick-test method for the characterization of grinding wheel topography based on AE. Bi et al. [21] developed a tool condition monitoring system for grinding based on AE and a long short-term memory network. For milling, Giriray et al. [22] used the root mean squares (RMS) of an AE signal to predict the flank wear on a tool using an artificial neural network (ANN). Marinescu and Axinte [23] detected surface anomalies in the workpieces and entrances of individual cutting edges. For micro-milling, Uhlmann et al. [24] used AE measurements for tool contact detection. Prakash et al. [25] showed a relation between the AE signal and tool wear for high-speed edge trimming. Möhring et al. [26] reported on the correlation of the AE signal with tool wear and surface quality in comparison to other process measurands like cutting forces and workpiece vibrations in milling CFRP. For the drilling process, Arul et al. [27] showed the correlation of AE RMS values with tool wear and thrust force.
In all examined and presented publications, sensors were attached to the workpiece or the workpiece clamping. Signal processing algorithms to compensate for the effects of attenuation, dispersion and reflection are not applied. However, when attaching the AE sensor to the workpiece and machining at different distances to the sensor, several authors report significant disturbances on measurements [28,29]. Above all, a drastic reduction in signal amplitude with increasing distance between source and sensor is observed. Since the stationary sensor needs to be attached to each new workpiece, the coupling conditions may only be poorly reproducible in a way that may not allow consistent comparability of the measurements across workpieces during machining [3]. Everson and Cheraghi therefore recommend digressing from workpiece sided AE sensors and rather to attach the sensor on the tool holder [30]. A comprehensive literature review on state-of-the art machining of CFRP and polymers is given by Che et al. [31]. Further applications and challenges of AE measurement in machining processes are analysed and reviewed by Kishawy et al. [32].
Nevertheless, stationary AE measurement can be a practical approach for application-specific monitoring tasks in machining. However, to improve the quality of processed AE signals, a more sophisticated evaluation of the measurements, the discussed drawbacks and challenges, such as the influence of attenuation, dispersion, and reflection on the measured signal need to be considered. This is especially true for the machining of CFRPs, which have much higher attenuation coefficients than for example, metals and in the milling process, where the distances between AE source and sensor are allowed to vary considerably as the tool travels at the edge of large CFRP parts. Both the influence of different distances between AE source and sensor as well as signal path and fibre orientation must be compensated for, the latter due to the anisotropic nature of most CFRPs.
2. Materials and Methods
AE were induced by the milling process or alternatively, with compressed air at a pressure of p = 8 bar.
Experiments with compressed air can be easily conducted outside of the machine tool and can be used to pre-parameterise models which are then applied to the milling process measurements. The milling experiments have been conducted using an Ultrasonic C260 Composites of the company Sauer Gmbh, Stipshausen, Germany. As a workpiece, plates of unidirectional Cfrp Sigrapreg® supplied by the company SGL Carbon Se, Wiesbaden, Germany, with a thickness of 2 mm were used. AE was measured with a stationary sensor Type 8152C0 manufactured by the company Kistler Instrumente Gmbh, Sindelfingen, Germany, attached to the workpiece. The sensor has a high sensitivity of S = 57 dB V/(m/s) in the range of 50 kHz to 400 kHz. The signal is filtered by a bandpass with the cut-off frequencies fcLL = 50 kHz and fcUL = 1000 kHz in a piezotron coupler 5125. Another AE sensor AE9039, rotating, was attached with a frictional connection to the tool holder powRgrip HSK F63/PG25x100H of the company Rego-Fix AG, Tenniken, Switzerland. The signal of the rotating sensor is amplified by a control card AEMS5522Q. The rotating sensor, the stator as well as the control card are supplied by the company Accretech Sbs Inc., Portland, OR, USA. Both sensor signals are digitalised using a PicoScope 5444D from the company Pico Technology Ltd., Cambridgeshire, UK with a sampling rate of 2.906 MS/s with a vertical resolution of r = 15 Bits. Since the machine tool axis amplifiers induce high frequencies into the power grid, which can disturb the AE measurement, low pass filters were applied to the power supplies of all AE equipment. For the milling processes, an uncoated R&D milling tool FE100S manufactured by the company Hufschmied Zerspanungssysteme, Bobingen, Germany, was employed. For all machining experiments dry, down milling processes were applied. All measurement programs, signal processing and model parameterisation scripts are written with Python 3.9.5 from Python Software Foundation, Wilmington, USA. Sensors, clamping setup, and AE sources were configured in such a way that reflection was negligible. AE signals are emitted at different distances d and under different angles β between the signal path and fibre orientation. A representation of the experimental setup is given in Figure 3.
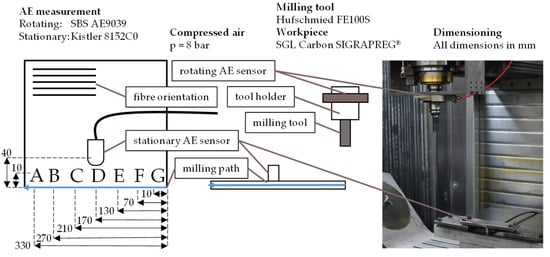
Figure 3.
Sensor placement and AE source positioning for the AE experiments.
For this setup, the angle between fibre direction and AE propagation path β is in the range of 10.6° < β < 90° with the AE propagating distance d in the range of 30 mm < d < 162 mm. Since the angle between AE propagation path and fibre direction as well as the distance between the sensor and AE source is always known, models for their influence on the AE measurement signal can be parameterised in further signal processing steps.
Linear time-invariant (LTI) transfer functions and frequency gain parameter tables have been implemented to obtain models, which can be used to reconstruct attenuated, and dispersed frequency spectra of measurement data to its shape and amplitude emitted at the AE source. Approaches to reconstruct the time-domain data of the AE emitted at the source have been tested with two identical AE sensors but did not achieve satisfying model performance. ANN and autoregressive exogenous models (ARX) have been applied on the acquired datasets as well, but robust and acceptable modelling could not be accomplished. Further investigation of these approaches was aborted due to the excessive computing effort during model teaching. To identify a transfer function TF(s), a generic structure of the filter function was assumed for the optimization algorithm according to Equation (4).
When a certain threshold of n is surpassed, only marginal model performance improvement is accomplished whereas computational effort for optimisation increases sharply for higher orders of TF(s). Therefore, model order n is first set to n = 1 and then gradually increased. Parameters an to a0 and bn to b0 of the TF filter were subject to variation by the optimisation algorithm. AE induced with a minimal distance to the sensor with negligible effect of attenuation, dispersion, and reflection were defined as target signals. To evaluate the filter parameters proposed by the optimisation algorithm, frequency spectra of both the attenuated and filtered and the target acoustic emission measurement data were determined by Fourier transform. Since the amplitudes of these frequency spectra are calculated for discrete frequencies, the deviations can be calculated for each. Deviations can be taken as absolute value and then summed. The sum of all absolute deviations defines the quality criterion of the filter function to be minimised by the optimisation algorithm. To avoid numerical issues when executing the algorithm, sample time can be used as timebase.
Frequency spectra can also be reconstructed using large-scale frequency gain parameter tables. For each frequency in the spectra, a specific gain can be identified. Attenuation coefficients are widely used in literature and easy to calculate. However, the approach may be difficult to implement as it delivers gains only for discrete frequencies in the spectra and does not represent a physically realisable filter. To increase the robustness of this approach, frequency gains are smoothed using a Savitzky-Golay filter with a window length of 1001 and a polynomial order of 3. The procedure for both algorithms is presented in Figure 4.
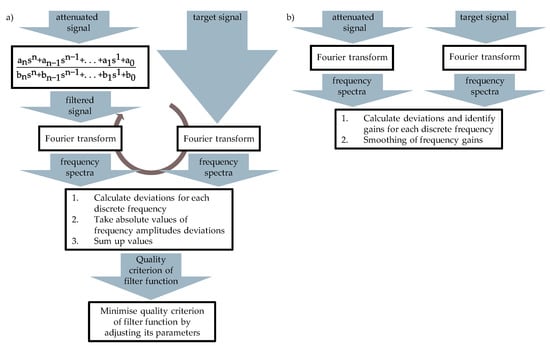
Figure 4.
Algorithms for model identification; (a) LTI transfer function; (b) frequency gain parameter table.
For both approaches presented, it should be noted that they cannot account for the effects of signal dispersion and reflection in the time domain. Therefore, only the reconstruction of frequency spectra according to their shape and amplitudes emitted at the AE source is investigated. Additionally, applying LTI transfer functions induces a frequency-dependent phase shift into the time domain signal, which is not to be confused with the effects of different phase velocities vp caused by dispersion. However, phase shift is irrelevant, when only frequency spectra are evaluated for process monitoring. As both presented and applied algorithms are linear, nonlinear effects in attenuation, dispersion, and reflection cannot be accounted for.
3. Results
For both the AE induced by compressed air as well as by the milling process, strong dependencies of the distance between AE source and sensor and angle between signal path and fibre orientation on the transduced frequency spectra are observed. For both sources, AE in a wide frequency range is emitted. However, peak and centroid frequency in the frequency spectra differ significantly, as AE emitted by milling is more broadband with strong frequency components of up to 240 kHz and high peaks below 90 kHz, whereas inducing AE with compressed air produces predominantly a single peak in the frequency spectrum of around 150 kHz with an overall lower amplitude magnitude, as shown in Figure 5.
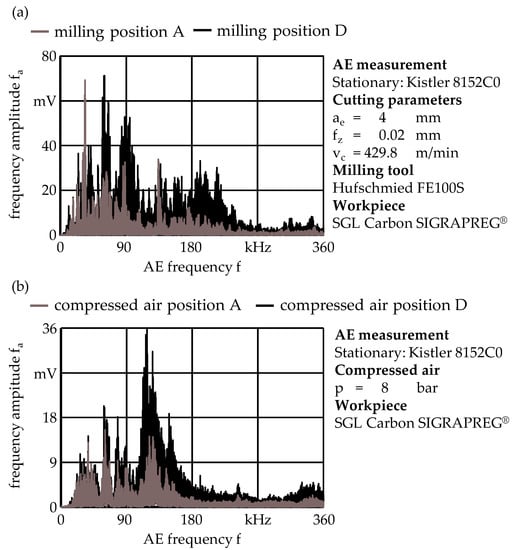
Figure 5.
Different AE frequency spectra at different source positions; (a) induced by the milling process; (b) induced by compressed air.
The impact of attenuation can also be observed in the time domain. It can be shown that the transduced AE signal amplitude is heavily dependent on the AE source position. When the distance between sensor and AE source is changed by a few centimetres, the maximum transduced amplitude can decrease by a factor of 0.3–0.5. The maximum amplitudes for the different source positions A-G for AE induced by the milling process and by compressed air, their distance from source to sensor d, as well as the propagation angle β are presented in Table 1.

Table 1.
Maximum amplitudes of different AE sources for the different source positions.
Equivalent results are obtained when AE signals transduced by the rotating and the stationary sensor are compared. For position D, waveforms in the time domain are much alike with relative high signal-to-noise ratio SNRD. The effect of the deviation of the effective tool radius for the four different cutting edges on the AE measurement can easily be determined. For position A, the maximum amplitude of the time domain signal is significantly attenuated. The shape of the waveform differs considerably from the measurement signals obtained by the rotating sensor and the difference between the maximum amplitudes across the different cutting edges diminishes. Consequently, the SNR drops considerably. Time domain measurement data obtained during the milling process of a CFRP plate with the measurement setup presented in Figure 3 at the two extremal positions A and D, obtained by the stationary AE sensor and the rotating AE sensor, are presented in Figure 6.
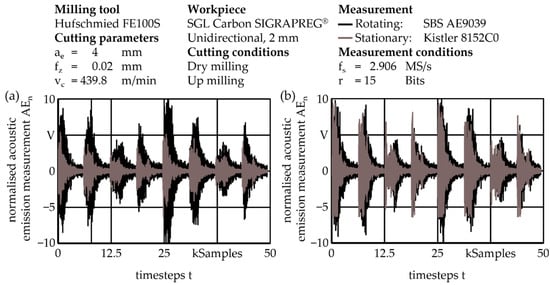
Figure 6.
Time domain signals transduced by the rotating and the stationary AE sensor; (a) position A; (b) position D.
Analysing the measurement results highlights the challenges that attenuation and dispersion pose regarding stationary AE sensor placement. The maximum amplitude of the transduced signal, as well as frequency spectra, vary significantly when sensor to source distance is changed by only several centimetres. Monitoring of larger CFRP parts with high distance variations between sensor and AE source, therefore, appears to be difficult to implement, as the effect of attenuation is so predominant. However, for not too large distances between sensor and AE source, reconstruction of the emitted signal appears feasible. The performance of the two applied approaches to compensate for attenuation and dispersion and estimate the target frequency spectra emitted at the AE source with transduced measurement data is presented in the following section.
4. Signal Processing and Algorithm Evaluation
Applying the transfer function identification algorithm on the measurement data by the compressed air experiments, convergence is obtained for less than nine parameters. For more than nine parameters, optimisation computing time increases drastically and the probability of convergence of the optimisation algorithm is drastically reduced due to high dimensionality of the transfer function TF. In this case, no meaningful model function parameters may be identified by different optimisation algorithms. For six parameters, a strong increase in model performance can be observed. For seven and eight parameters, performance increase is only marginal. It is expected that adding further parameters will increase the performance of the LTI transfer function model as the dynamic behaviour of the physical system is replicated more and more precisely. The performance of the transfer function model according to the normalised quality criterion for quality function as well as the identified numerator and denominator parameter values for different numbers of parameters k, are presented and tabulated in Figure 7. The quality criterion is normalised by defining the deviation value of the quality criterion of the transfer function TF1(s) = 1 as 1.
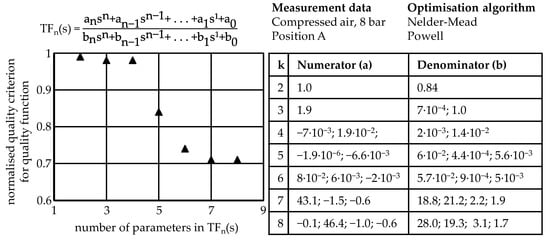
Figure 7.
Performance of the identified LTI transfer functions for different numbers of parameters k for the compressed air experiments.
The identified, optimised transfer functions magnitude response for eight parameters shows a high positive gain around 150 kHz with steep decrease into attenuation for lower frequencies. Higher frequencies are amplified with smaller positive gains. However, when comparing against the frequency gain parameter table, very equivalent results can be observed. The Bode plots illustrating the magnitude response of the optimised LTI transfer function and the identified frequency gain parameter table are presented in Figure 8.
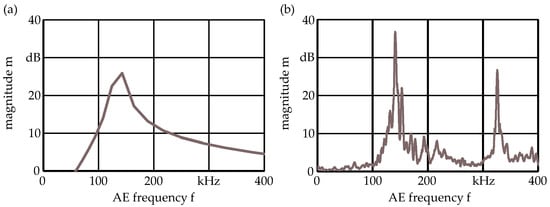
Figure 8.
Identified models; (a) magnitude response of the identified, optimised LTI transfer function with eight parameters; (b) frequency gain parameter table.
When applying the identified LTI transfer function on the attenuated signal for validation, it can be shown that the frequency spectra can, to a certain extent, be reconstructed to the frequency spectra emitted at the AE source. The high gain around 150 kHz in the transfer function reconstructs the peak in the frequency spectra from several mV to more than 80 mV. The peak in the target spectra, however, exceeds 120 mV. The investigated frequency spectra of the attenuated signal and the target signal as well as the spectra reconstructed by the LTI transfer function and by frequency gain parameter table are presented in Figure 9.
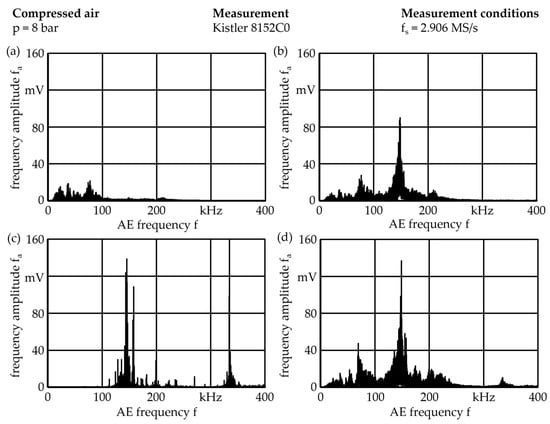
Figure 9.
Frequency spectra of AE signals emitted by compressed air (a) attenuated signal; (b) spectrum reconstructed by LTI transfer function; (c) spectrum reconstructed by frequency gain parameter table; (d) spectrum of the target signal.
The same procedure can be applied to the measurement data obtained during the milling process. Model performance as well as numerator and denominator values for different numbers of parameters are presented in Figure 10. The quality criterion is normalised by defining the deviation value of the transfer function TF(s) = 1 as 1.

Figure 10.
Performance of the identified LTI transfer functions for different numbers of parameters k for the milling experiments.
The identified, optimized transfer functions magnitude response for eight parameters shows a high positive gain around 220 kHz with steep decrease into attenuation for lower frequencies and higher frequencies. However, when comparing against the table of frequency gains, equivalent results can be observed, even though the frequency gain parameter table shows a much less smooth progression. The Bode plot illustrating the magnitude response and the frequency gain parameter table are presented in Figure 11.
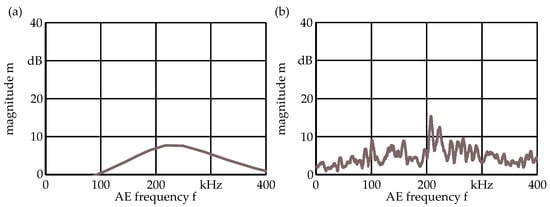
Figure 11.
Identified models; (a) Magnitude response of the identified, optimised LTI transfer function with eight parameters; (b) frequency gain parameter table.
Since the spectra emitted by the milling process yield multiple peaks, the used low order transfer functions result in poor model performance. For the spectra obtained by filtering, higher amplitudes around 200 kHz are amplified, whereas the peaks at 50 kHz and 25 kHz are only poorly reconstructed. Better results are obtained by applying the frequency gain parameter table, which reproduces the different characteristic peaks of the target signal much better. The investigated frequency spectra are presented in Figure 12.
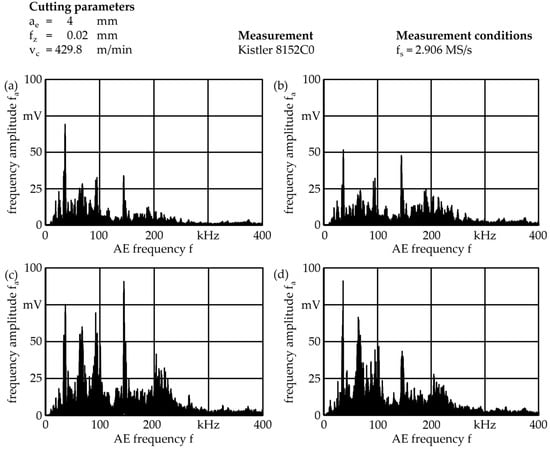
Figure 12.
Frequency spectra of AE signals emitted by the milling process (a) attenuated signal; (b) spectrum reconstructed by LTI transfer function; (c) spectrum reconstructed by frequency gain parameter table; (d) spectrum of the target signal.
5. Discussion
With the experiments and model identifications conducted, it was shown that reconstructing attenuated, dispersed and reflected frequency spectra using LTI transfer functions and frequency gain parameter tables is a feasible approach. Models with acceptable performance are identified with a reasonable amount of computing effort. Models for the milling process can be pre-parameterised using compressed air experimental measurement data. Additionally, inverted models can be employed to model the effect of attenuation of AE along the propagation path in the workpiece. Therefore, the major drawback of acoustic emission sensors attached to the workpiece can be accounted for. When evaluating the performance of the algorithms, however, it can be observed that both models may incorrectly identify frequency gains when the frequency spectrum is very unsteady or specific frequency components are highly influenced by noise. When comparing experimental data transduced by the rotating and the stationary sensor, it can be shown that certain AE frequency bands are not transduced by the rotating sensor. Therefore, the stationary sensor placement for process monitoring might be worthwhile, even though the processing of the measurement data in order to account for the effects of attenuation, dispersion and reflection is laborious. The frequency spectra of the AE signals transduced by the rotating sensor and the stationary sensor, however, differ significantly, even for the source position D with minimal propagation path in the CFRP. This can be attributed to the different signal paths, component interfaces of the tool clamping as well as the different frequency response spectra of the two sensors. Also, some phenomena in the cutting zone might induce AE events that only propagate to the stationary or the rotating sensor and not to the other one. For example, because the milling tool is not always in contact with the workpiece. The reconstruction of time domain AE signals using LTI transfer functions appears, according to the experimental data obtained in this work, to be an approach that may be feasible in a controlled environment. In industrial applications however, due to complex workpiece geometries, the clamping setup and the rough environment in the machine tool, the measurement signal appears to be too disturbed for time domain processing. Nonetheless, LTI transfer functions and frequency gain parameter tables can successfully be used to reconstruct AE frequency spectra. The following steps should be considered in further research:
- Applying nonlinear dynamic transfer functions on the measurement data
- Transduce AE signals with several identical sensors
- Realising identification algorithms for LTI transfer functions with higher number of parameters
- Investigation of performance of the proposed algorithms for the specific process monitoring tasks in milling
- Investigation of the influence of different cutting tool geometries and their respective emitted frequency spectra on the applicability of the proposed algorithms
Author Contributions
Conceptualization, E.U., T.H. and R.C.; methodology, T.H.; software, T.H.; validation, T.H; formal analysis, T.H. and R.C.; investigation, T.H. and R.C.; resources, T.H.; data curation, T.H.; writing—original draft preparation, T.H.; writing—review and editing, E.U. and R.C.; visualization, T.H. and R.C.; supervision, E.U. and R.C.; project administration, E.U. and R.C.; funding acquisition, E.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deutsche Forschungsgemeinschaft (DFG), Bonn, Germany grant number 420609123.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- El-Hofy, M.H.; Soo, S.L.; Aspinwall, D.K.; Sim, W.M.; Pearson, D.; Saoubi, R.M.; Harden, P. Tool temperature in slotting of CFRP composites. Procedia Manuf. 2017, 10, 371–381. [Google Scholar] [CrossRef]
- Uhlmann, E.; Sammler, F.; Richarz, S.; Reucher, G.; Hufschmied, R.; Frank, A.; Stawiszynski, B.; Protz, F. Machining of carbon and glass fiber reinforced composites. Procedia CIRP 2016, 46, 63–66. [Google Scholar] [CrossRef]
- Gallego, A.; Ono, K. An Improved Acousto-Ultrasonic Scheme with Lamb Wave Mode Separation and Damping Factor in CFRP Plates. In Proceedings of the 30th European Conference on Acoustic Emission Testing & 7th International Conference on Acoustic Emission University of Granada, Granada, Spain, 12–15 September 2012. [Google Scholar]
- Asamene, K.; Hudson, L.; Sundaresan, M. Influence of attenuation on acoustic emission signals in carbon fiber reinforced polymer panels. Ultrasonics 2015, 15, 86–93. [Google Scholar] [CrossRef]
- Sreekumar, P.; Ramadas, C.; Anand, A.; Joshi, M. Attenuation of Ao Lamb mode in hybrid structural composites with nanofillers. Compos. Struct. 2015, 132, 198–204. [Google Scholar] [CrossRef]
- Wirtz, S.F.; Bach, S.; Söffker, D. Experimental Results of Acoustic Emission Attenuation Due to Wave Propagation in Composites. In Proceedings of the Annual Conference of the PHM Society, Scottsdale, AZ, USA, 23 September 2019. [Google Scholar] [CrossRef]
- Sofer, M.; Cienciala, J.; Fusek, M.; Pavlíček, P.; Moravec, R. Damage Analysis of Composite CFRP Tubes Using Acoustic Emission Monitoring and Pattern Recognition Approach. J. Mater. 2021, 4, 786. [Google Scholar] [CrossRef] [PubMed]
- Abdulaziz, A.H.; Holford, K.M.; McCrory, J.P.; Hedaya, M. Effects of Honeycomb Core on Acoustic Emission Wave Propagation in Glass Fibre Composite Plates. In Proceedings of the 58th Annual Conference of British Institute of Non-Destructive Testing, Telford, UK, 3–5 September 2019; pp. 1–11. [Google Scholar]
- Möser, M.; Kropp, W. Körperschall, 1st ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Aggelis, D.G.; Matikas, T.E. Effect of plate wave dispersion on the acoustic emission parameters in metals. Comput. Struct. 2012, 98, 17–22. [Google Scholar] [CrossRef]
- Hamam, Z.; Godin, N.; Fusco, C.; Monnier, T. Modelling of Acoustic Emission Signals Due to Fiber Break in a Model Composite Carbon/Epoxy: Experimental Validation and Parametric Study. Appl. Sci. 2019, 23, 5124. [Google Scholar] [CrossRef]
- Lopresto, V.; Leone, C.; Caprino, G.; Iorio, I. Analysis of acoustic emission signals produced by different carbon fibre reinforced plastic laminates. In Proceedings of the 17th International Conference on Composite Materials ICCM-17, Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Wu, Y.; Perrin, M.; Pastor, M.-L.; Casari, P.; Gong, X. On the determination of acoustic emission wave propagation velocity in composite sandwich structures. Compos. Struct. 2021, 259, 113231. [Google Scholar] [CrossRef]
- Pohl, J.; Szewieczek, A.; Hillger, W.; Mook, G. Ermittlung der Dispersion von Lamb-Wellen zur Zustandsüberwachung in Anisotropen Bauteilen; DGZfP-Jahrestagung: Erfurt, Germany, 2010. [Google Scholar]
- Marinescu, I.D.; Hitchiner, M.; Uhlmann, E.; Rowe, W.B.; Inasaki, I. Handbook of Machining with Grinding Wheels, 1st ed.; Taylor & Francis: London, UK, 2007. [Google Scholar]
- Heisel, U.; Klocke, F.; Uhlmann, E.; Spur, G. Handbuch Spanen, 1st ed.; Hanser: München, Germany, 2014. [Google Scholar]
- Uhlmann, E.; Laghmouchi, A.; Ehrenpfordt, R.; Hohwieler, E.; Geisert, C. Intelligentes Elektroniksystem für Condition Monitoring in Industrie 4.0. ZwF 2016, 111, 855–857. [Google Scholar] [CrossRef]
- Boaron, A.; Weingaertner, W. Contact recognition between grinding wheel and workpiece. COBEM 2009, 1, 1–10. [Google Scholar]
- Gao, Z.; Lin, J.; Wang, X.; Liao, Y. Grinding Burn Detection Based on Cross Wavelet and Wavelet Coherence Analysis by Acoustic Emission Signal. Chin. J. Mech. Eng. 2019, 32, 859–869. [Google Scholar] [CrossRef]
- Boaron, A.; Weingaertner, W.L.; Uhlmann, E. A quick-test method based on acoustic emission for the in-process characterization of conventional grinding wheels. Ilmenau Sci. Colloq. 2014, 58, 1–15. [Google Scholar]
- Bi, G.; Liu, S.; Su, S.; Wang, Z. Diamond Grinding Wheel Condition Monitoring Based on Acoustic Emission Signals. Sensors 2021, 21, 1054. [Google Scholar] [CrossRef] [PubMed]
- Giriraj, B.; Raja, V.P.; Gandhinadhan, R.; Ganeshkumar, R. Prediction of tool wear in high speed machining using acoustic emission technique and neural network. Indian J. Eng. Mater. Sci. 2006, 13, 275–280. [Google Scholar]
- Marinescu, I.; Axinte, D. A time–frequency acoustic emission-based monitoring technique to identify workpiece surface malfunctions in milling with multiple teeth cutting simultaneously. Int. J. Mach. Tools Manuf. 2009, 49, 53–65. [Google Scholar] [CrossRef]
- Uhlmann, E.; Raue, N.; Gabriel, C. Acoustic Emission-based micro milling tool contact detection as an integrated machine tool function. In Proceedings of the 13th Euspen International Conference, AMRC, Berlin, Germany, 13 March 2013. [Google Scholar]
- Prakash, R.; Krishnaraj, V.; Zitoune, R.; Ahmad, J.S. High-Speed Edge Trimming of CFRP and Online Monitoring of Performance of Router Tools Using Acoustic Emission. Materials 2016, 9, 798. [Google Scholar] [CrossRef]
- Möhring, H.-C.; Eschelbacher, S.; Kimmelmann, M. Material failure detection for intelligent process control in CFRP machining. Procedia CIRP 2018, 77, 387–390. [Google Scholar] [CrossRef]
- Arul, S.; Vijayaraghavan, L.; Malhotra, S.K. Online monitoring of acoustic emission for quality control in drilling of polymeric composites. J. Mater. Process. Technol. 2007, 185, 184–190. [Google Scholar] [CrossRef]
- LeMoal, G.; Rabate, P.; Moraru, G.; Veron, P.; Douilly, M. A Robust Method for Drilling Monitoring using Acoustic Emission. In Proceedings of the 9th International Conference on High Speed Machining, San Sebastian, Spain, 15 March 2012. [Google Scholar]
- Leng, S.; Wang, Z.; Min, T.; Dai, Z.; Chen, G. Detection of Tool Wear in Drilling CFRP/TC4 Stacks by Acoustic Emission. J. Vib. Eng. Technol. 2020, 8, 463–470. [Google Scholar] [CrossRef]
- Everson, C.E.; Cheraghi, S.H. The application of acoustic emission for precision drilling process monitoring. Int. J. Mach. Tools Manuf. 1999, 39, 371–387. [Google Scholar] [CrossRef]
- Che, D.; Saxena, I.; Han, P.; Guo, P.; Ehmann, K.F. Machining of Carbon Fiber Reinforced Plastics/Polymers: A Literature Review. J. Manuf. Sci. Eng. 2014, 136, 034001. [Google Scholar] [CrossRef]
- Kishawy, H.A.; Hegab, H.; Umer, U.; Mohany, A. Application of acoustic emissions in machining processes: Analysis and critical review. Int. J. Adv. Manuf. Technol. 2018, 98, 1391–1407. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).