Tool Condition Monitoring Using Machine Tool Spindle Electric Current and Multiscale Analysis while Milling Steel Alloy
Abstract
:1. Introduction
2. Methodology
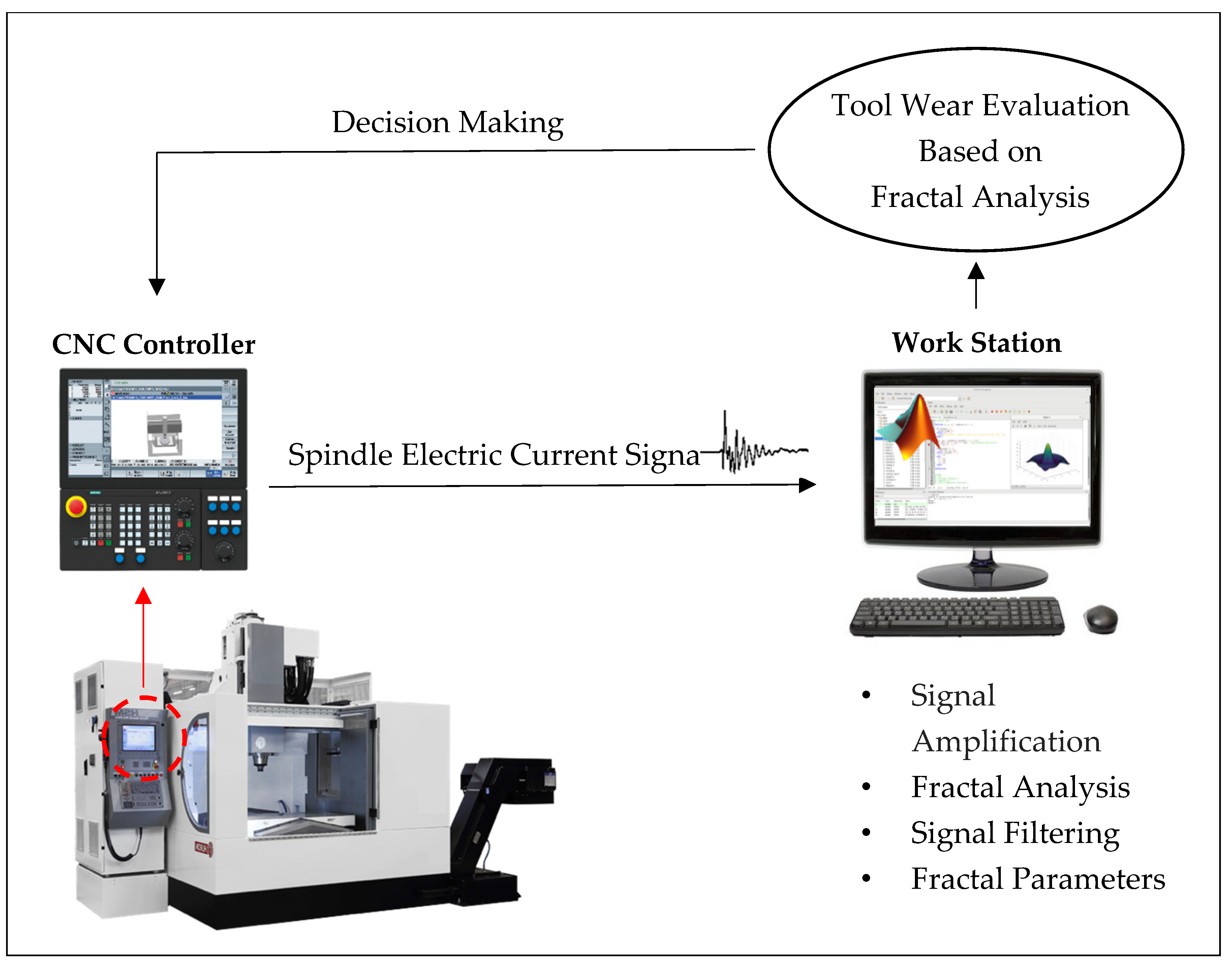
2.1. Materials and Experimental Setup
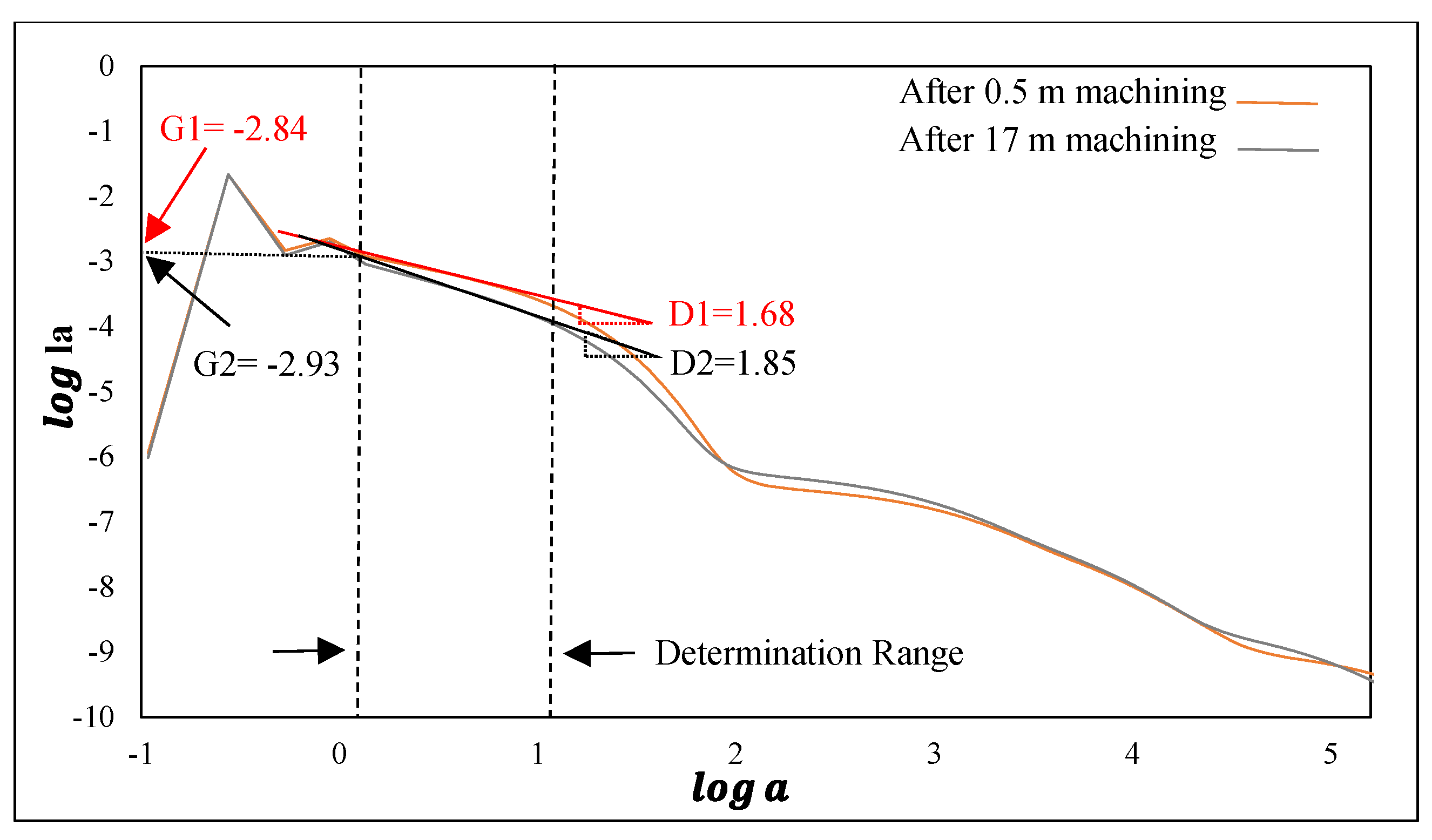
2.2. Fractal Analysis for Feature Extraction
3. Results and Discussion
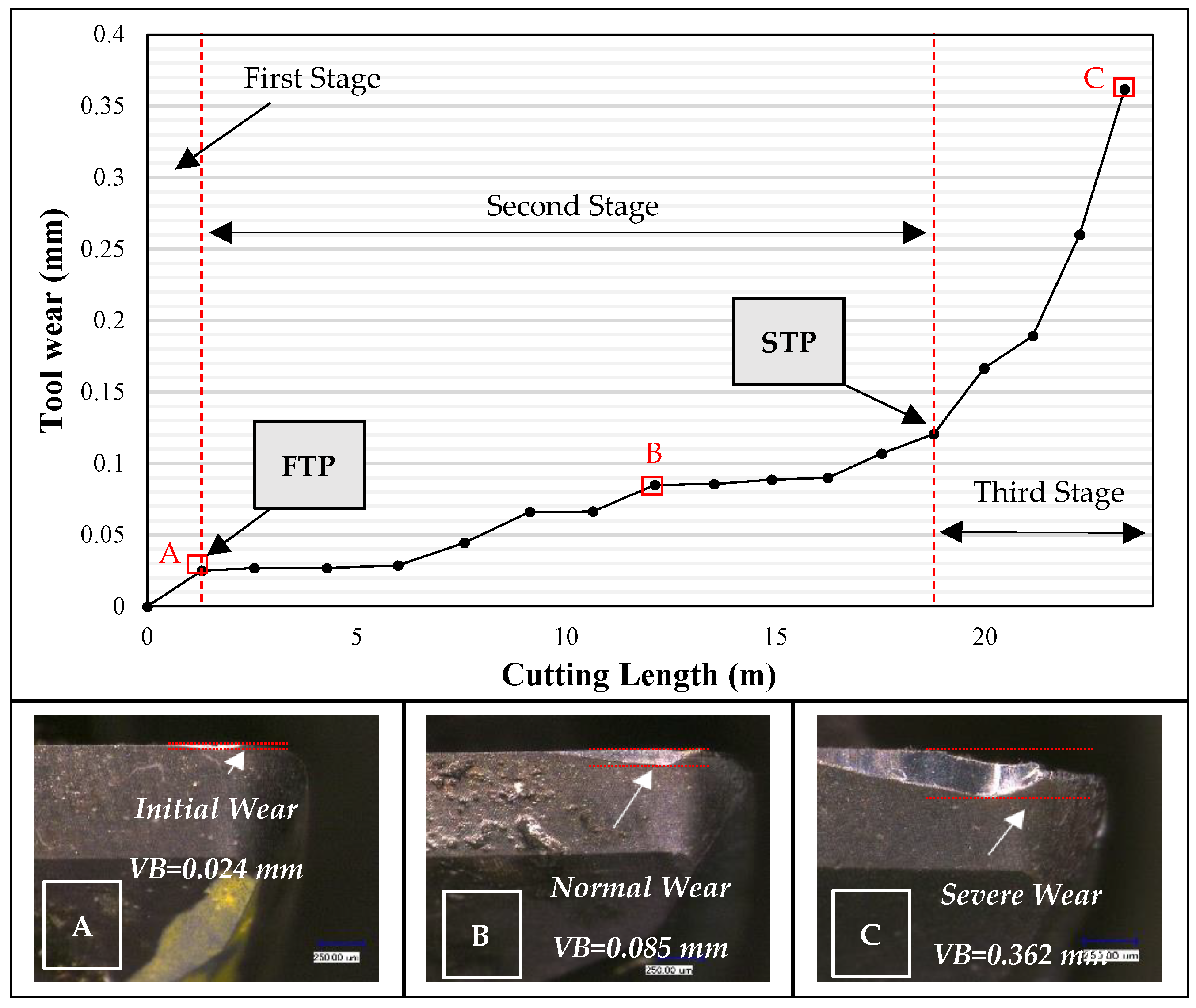
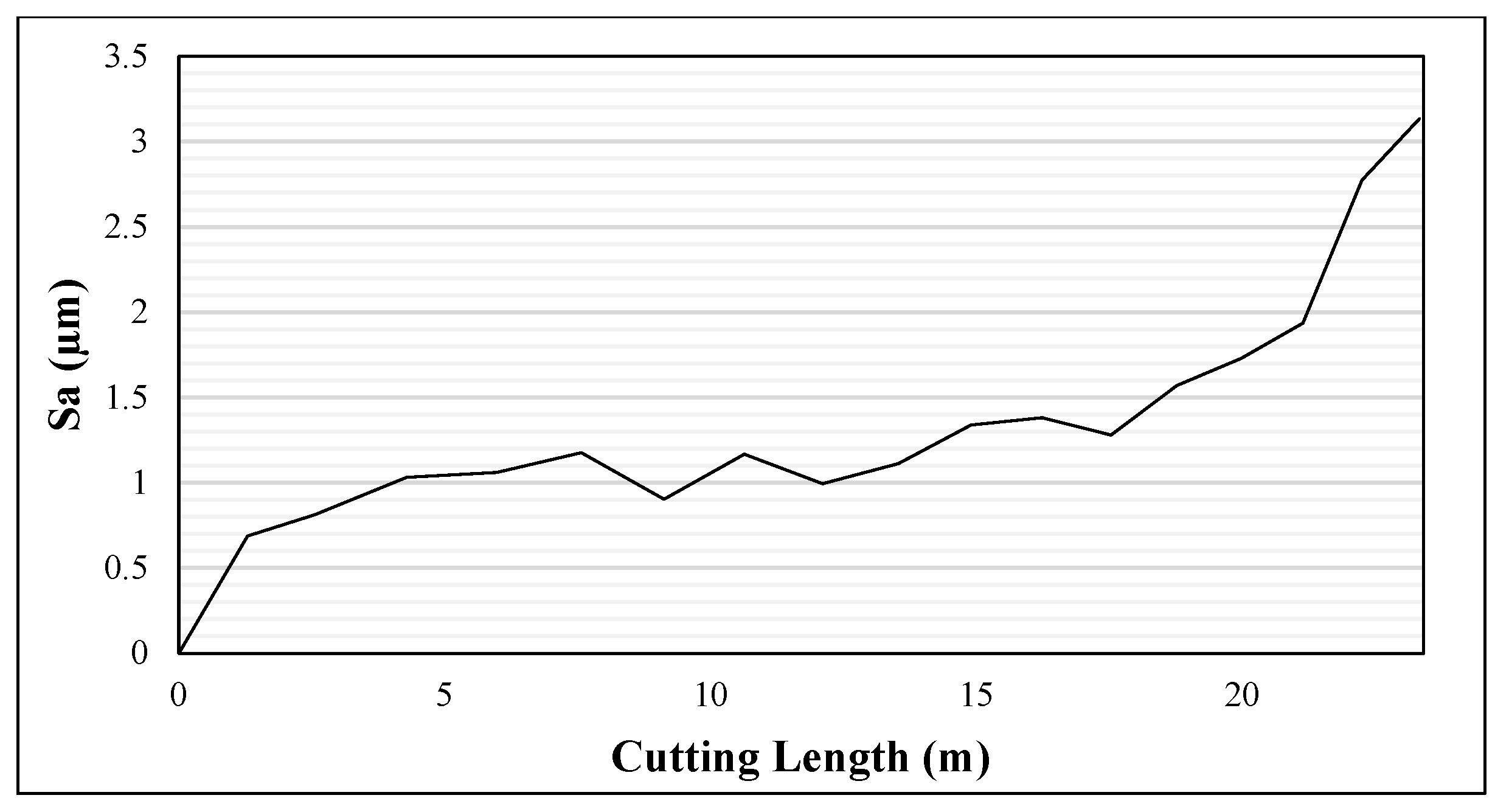
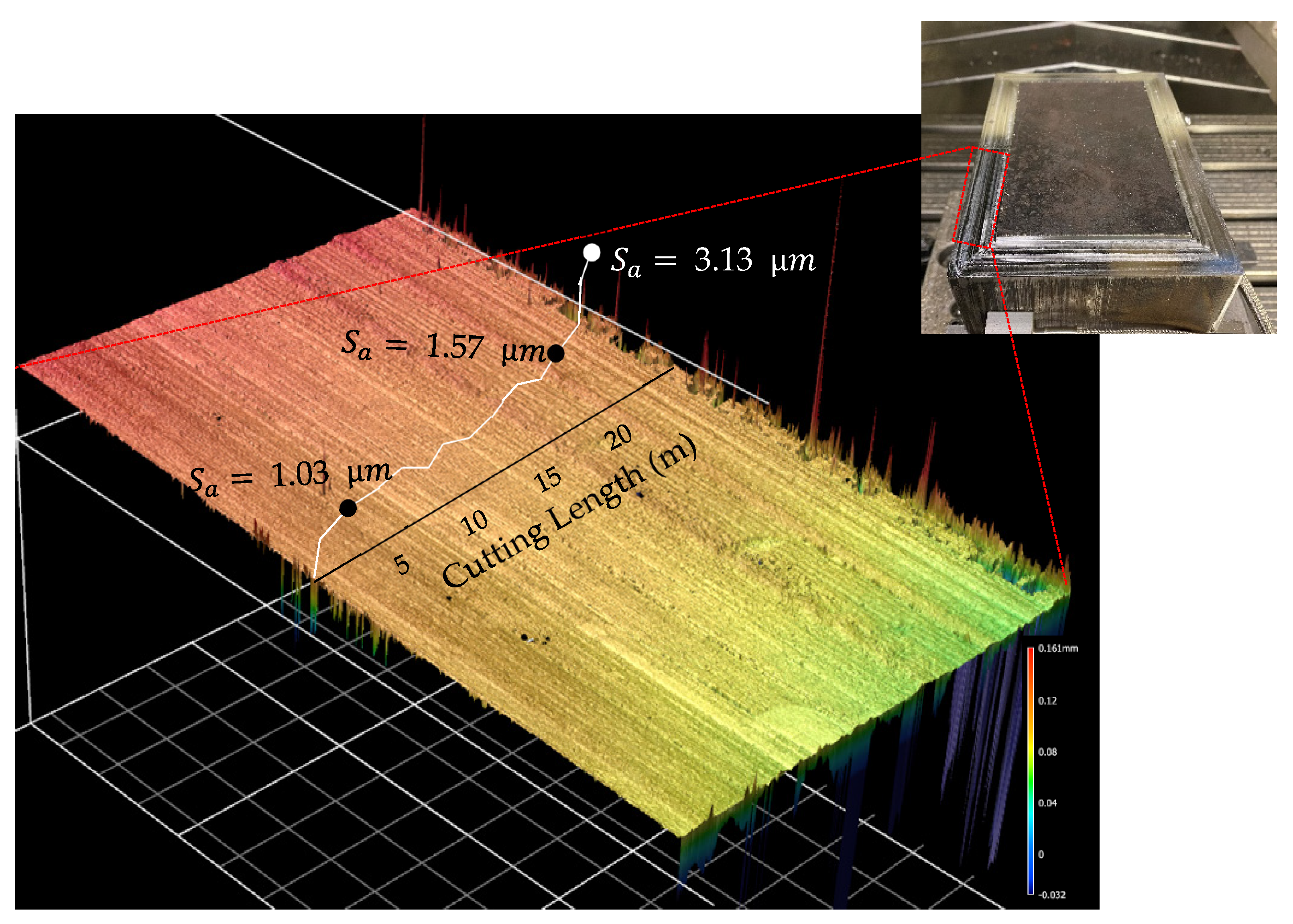
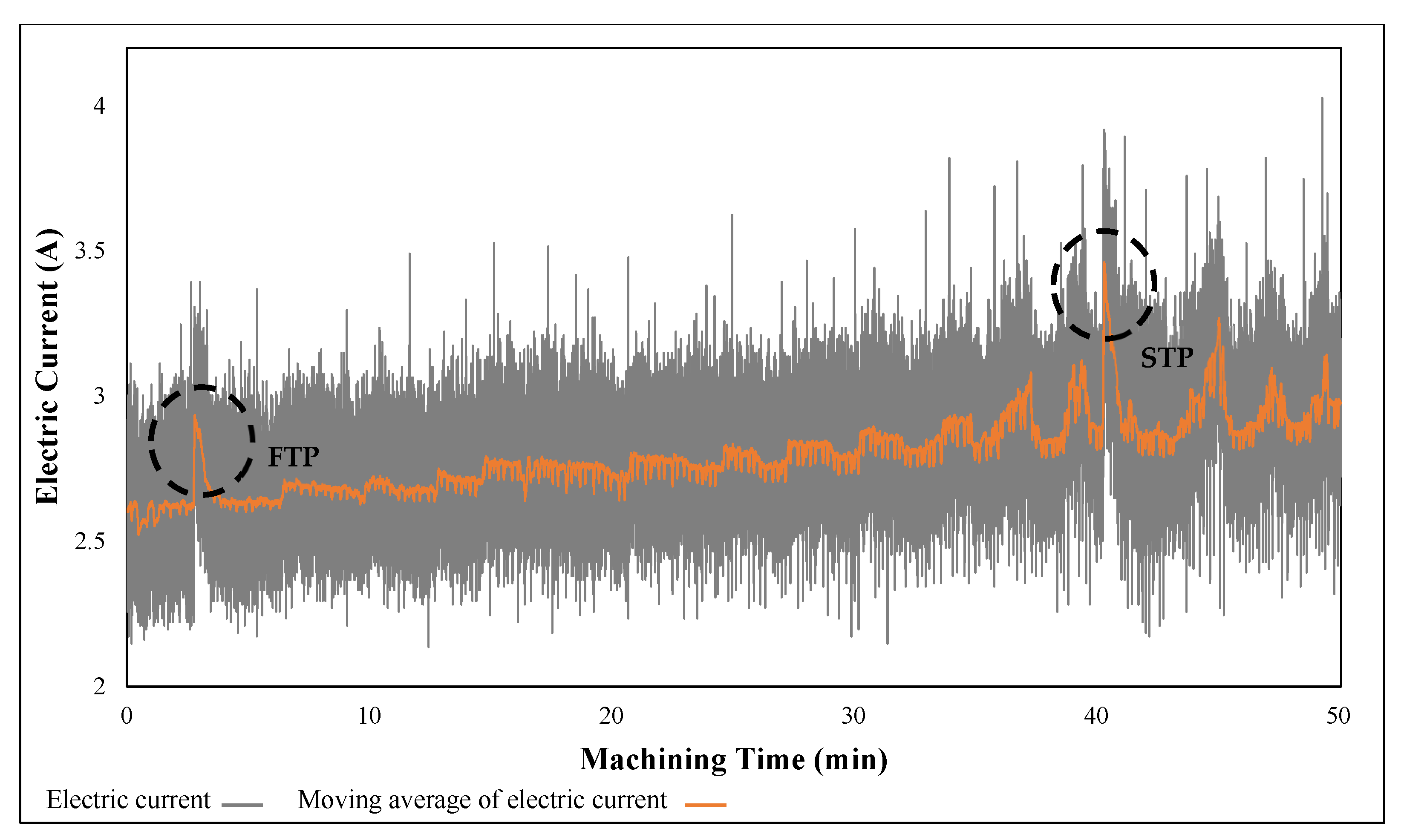
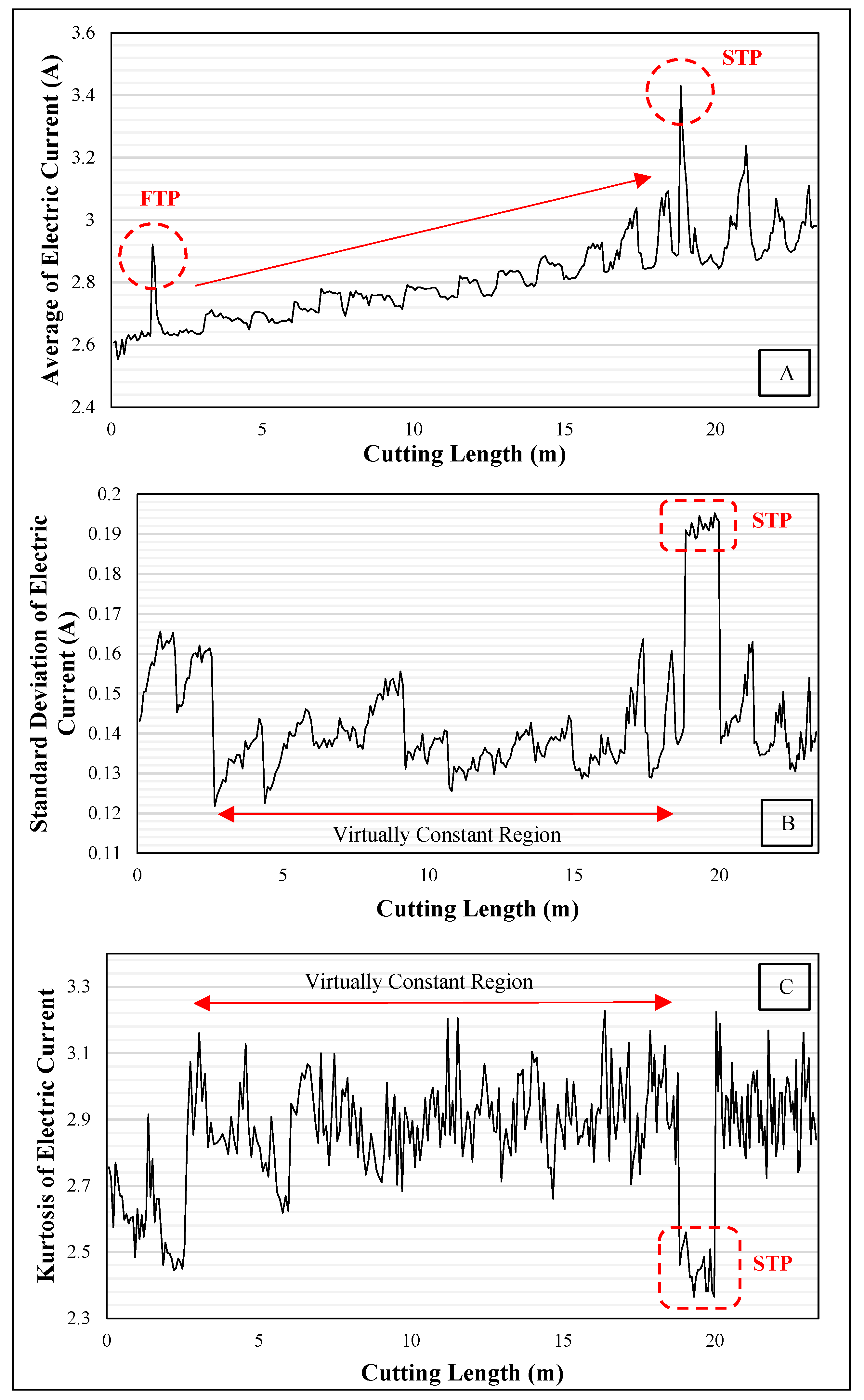
3.1. Conventional Analysis
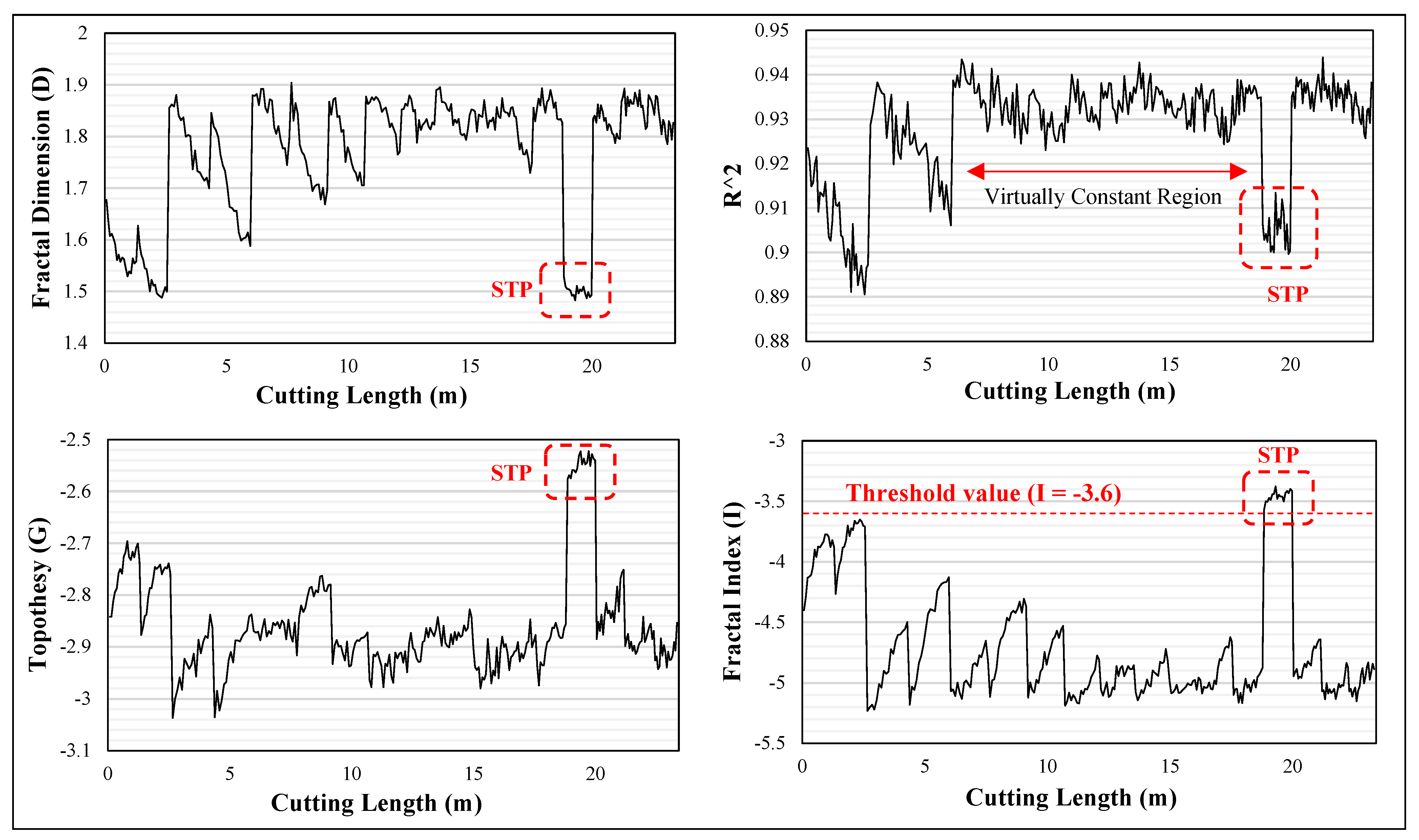
3.2. Fractal Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Drouillet, C.; Karandikar, J.; Nath, C.; Journeaux, A.-C.; El Mansori, M.; Kurfess, T. Tool life predictions in milling using spindle power with the neural network technique. J. Manuf. Process. 2016, 22, 161–168. [Google Scholar] [CrossRef]
- Grzesik, W. Wear development on wiper Al2O3–TiC mixed ceramic tools in hard machining of high strength steel. Wear 2009, 266, 1021–1028. [Google Scholar] [CrossRef]
- Li, N.; Chen, Y.; Kong, D.; Tan, S. Force-based tool condition monitoring for turning process using v-support vector regression. Int. J. Adv. Manuf. Technol. 2016, 91, 351–361. [Google Scholar] [CrossRef]
- Nouri, M.; Fussell, B.K.; Ziniti, B.L.; Linder, E. Real-time tool wear monitoring in milling using a cutting condition independent method. Int. J. Mach. Tools Manuf. 2015, 89, 1–13. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.-Y.; Zhao, Y.; Hou, C.-Y.; Zhu, X.; Cai, Y.-D.; Jin, Z.-J.; Kang, R.-K. On-machine measurement of tool nose radius and wear during precision/ultra-precision machining. Adv. Manuf. 2022, 10, 368–381. [Google Scholar] [CrossRef]
- Jamshidi, M.; Chatelain, J.-F.; Rimpault, X.; Balazinski, M. Tool condition monitoring based on the fractal analysis of current and cutting force signals during CFRP trimming. Int. J. Adv. Manuf. Technol. 2022, 1–16. [Google Scholar] [CrossRef]
- Liao, X.; Zhou, G.; Zhang, Z.; Lu, J.; Ma, J. Tool wear state recognition based on GWO–SVM with feature selection of genetic algorithm. Int. J. Adv. Manuf. Technol. 2019, 104, 1051–1063. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Yue, C.; Liang, S.Y.; Wang, L. Systematic review on tool breakage monitoring techniques in machining operations. Int. J. Mach. Tools Manuf. 2022, 176, 103882. [Google Scholar] [CrossRef]
- Rmili, W.; Ouahabi, A.; Serra, R.; Leroy, R. An automatic system based on vibratory analysis for cutting tool wear monitoring. Measurement 2016, 77, 117–123. [Google Scholar] [CrossRef]
- Li, D.-D.; Zhang, W.-M.; Li, Y.-S.; Xue, F.; Fleischer, J. Chatter identification of thin-walled parts for intelligent manufacturing based on multi-signal processing. Adv. Manuf. 2020, 9, 22–33. [Google Scholar] [CrossRef]
- Choi, Y.J.; Park, M.S.; Chu, C.N. Prediction of drill failure using features extraction in time and frequency domains of feed motor current. Int. J. Mach. Tools Manuf. 2008, 48, 29–39. [Google Scholar] [CrossRef]
- Wang, K.-S. Towards zero-defect manufacturing (ZDM)—A data mining approach. Adv. Manuf. 2013, 1, 62–74. [Google Scholar] [CrossRef]
- Arslan, H.; Er, A.O.; Orhan, S.; Aslan, E. Tool Condition Monitoring in Turning Using Statistical Parameters of Vibration Signal. Int. J. Acoust. Vib. 2016, 21, 371–378. [Google Scholar] [CrossRef]
- Pyatykh, A.S.; Savilov, A.V.; Timofeev, S.A. Method of Tool Wear Control during Stainless Steel End Milling. J. Frict. Wear 2021, 42, 263–267. [Google Scholar] [CrossRef]
- Jamshidi, M.; Rimpault, X.; Balazinski, M.; Chatelain, J.-F. Fractal analysis implementation for tool wear monitoring based on cutting force signals during CFRP/titanium stack machining. Int. J. Adv. Manuf. Technol. 2020, 106, 3859–3868. [Google Scholar] [CrossRef]
- ISO 8688-2:1989; Tool Life Testing in Milling—Part 2: End Milling. American National Standards Institute (ANSI): Co-lumbia, WA, USA, 1989.
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1982. [Google Scholar]
- Chuangwen, X.; Hualing, C. Fractal analysis of vibration signals for monitoring the condition of milling tool wear. Proc. Inst. Mech. Eng. Part J: J. Eng. Tribol. 2009, 223, 909–918. [Google Scholar] [CrossRef]
- Zuo, X.; Zhu, H.; Zhou, Y.; Yang, J. Estimation of fractal dimension and surface roughness based on material characteristics and cutting conditions in the end milling of carbon steels. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 231, 1423–1437. [Google Scholar] [CrossRef]
- Sahoo, P.; Barman, T.; Davim, J.P. Fractal Analysis in Machining; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Feng, Z.; Zuo, M.J.; Chu, F. Application of regularization dimension to gear damage assessment. Mech. Syst. Signal Process. 2010, 24, 1081–1098. [Google Scholar] [CrossRef]
- Rimpault, X.; Chatelain, J.-F.; Klemberg-Sapieha, J.; Balazinski, M. Tool wear and surface quality assessment of CFRP trimming using fractal analyses of the cutting force signals. CIRP J. Manuf. Sci. Technol. 2017, 16, 72–80. [Google Scholar] [CrossRef]
- Rimpault, X.; Bitar-Nehme, E.; Balazinski, M.; Mayer, J. Online monitoring and failure detection of capacitive displacement sensor in a Capball device using fractal analysis. Measurement 2018, 118, 23–28. [Google Scholar] [CrossRef]
- Guo, M.-X.; Liu, J.; Pan, L.-M.; Wu, C.-J.; Jiang, X.-H.; Guo, W.-C. An integrated machine-process-controller model to predict milling surface topography considering vibration suppression. Adv. Manuf. 2022, 10, 443–458. [Google Scholar] [CrossRef]
- ISO 25178-2; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2012; p. 47.

| Element | Fe | Mn | Cr | C | Si | S | P |
|---|---|---|---|---|---|---|---|
| Content (%) | 97.395–98.07 | 0.7–0.9 | 0.7–0.9 | 0.38–0.43 | 0.15–0.3 | ≤0.04 | ≤0.035 |
| Properties | Tensile Strength | Yield Strength | Elastic Modulus | Poisson’s Ratio | Hardness |
|---|---|---|---|---|---|
| 570 MPa | 295 MPa | 189,998–210,000 MPa | 0.27–0.30 | 167 (Brinell) |
| Cutting Speed | Feed Rate | Radial Depth of Cut (RDOC) | Axial Depth of Cut (ADOC) |
|---|---|---|---|
| 18336 RPM | 465.73 mm/min | 0.64 mm | 3 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamshidi, M.; Chatelain, J.-F.; Rimpault, X.; Balazinski, M. Tool Condition Monitoring Using Machine Tool Spindle Electric Current and Multiscale Analysis while Milling Steel Alloy. J. Manuf. Mater. Process. 2022, 6, 115. https://doi.org/10.3390/jmmp6050115
Jamshidi M, Chatelain J-F, Rimpault X, Balazinski M. Tool Condition Monitoring Using Machine Tool Spindle Electric Current and Multiscale Analysis while Milling Steel Alloy. Journal of Manufacturing and Materials Processing. 2022; 6(5):115. https://doi.org/10.3390/jmmp6050115
Chicago/Turabian StyleJamshidi, Maryam, Jean-François Chatelain, Xavier Rimpault, and Marek Balazinski. 2022. "Tool Condition Monitoring Using Machine Tool Spindle Electric Current and Multiscale Analysis while Milling Steel Alloy" Journal of Manufacturing and Materials Processing 6, no. 5: 115. https://doi.org/10.3390/jmmp6050115
APA StyleJamshidi, M., Chatelain, J.-F., Rimpault, X., & Balazinski, M. (2022). Tool Condition Monitoring Using Machine Tool Spindle Electric Current and Multiscale Analysis while Milling Steel Alloy. Journal of Manufacturing and Materials Processing, 6(5), 115. https://doi.org/10.3390/jmmp6050115






