Characterization of the Interaction of Metalworking Fluids with Grinding Wheels
Abstract
:1. Introduction
2. Approach and Procedure
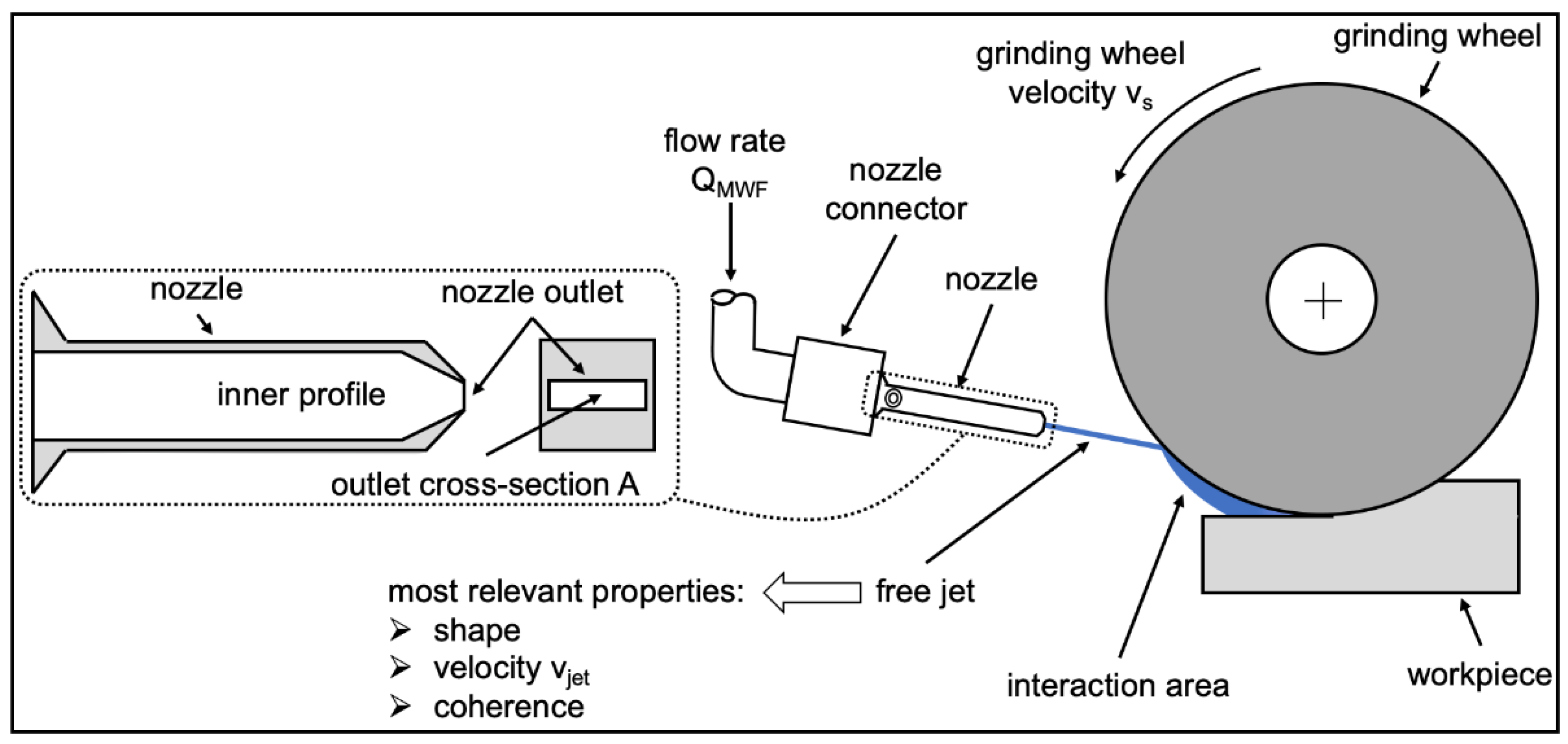
2.1. Experimental Setup
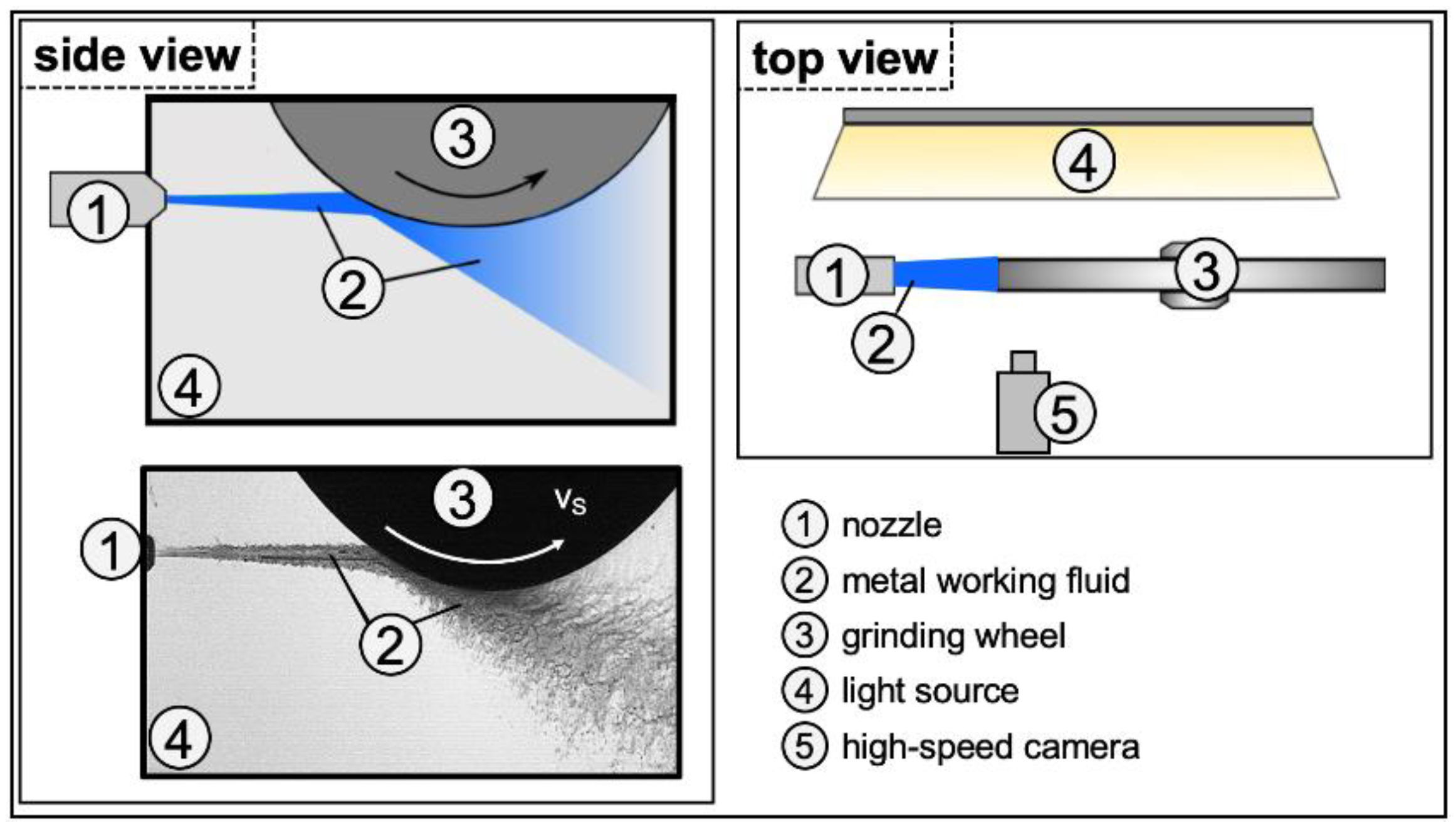
2.1.1. Setup for the High-Speed Recordings
2.1.2. Nozzle Design
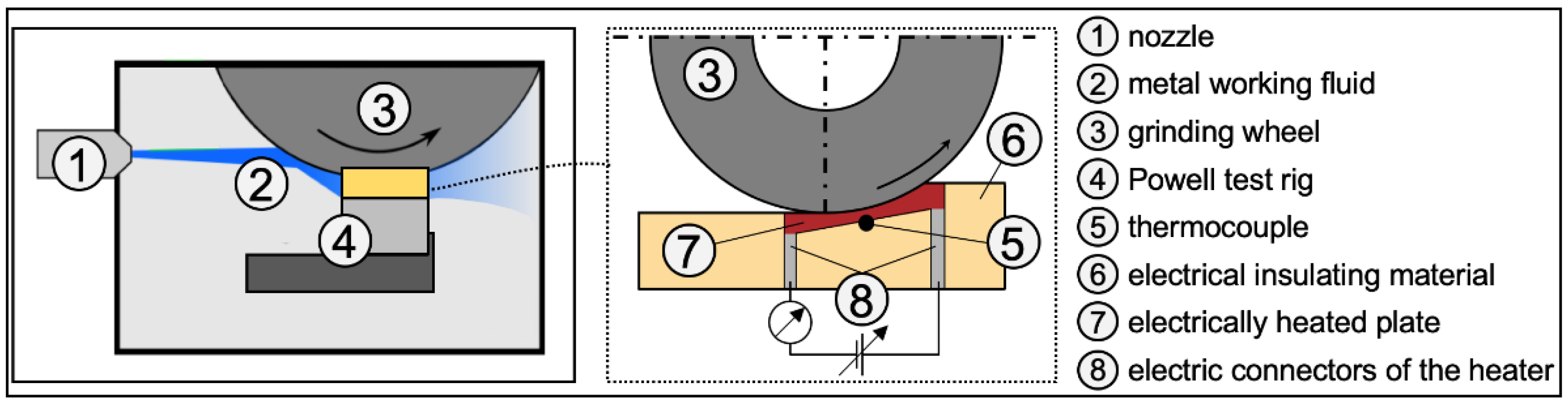
2.1.3. Setup for the Evaluation of the Cooling Capacity of the MWF Supply
2.2. Methods of Analysis
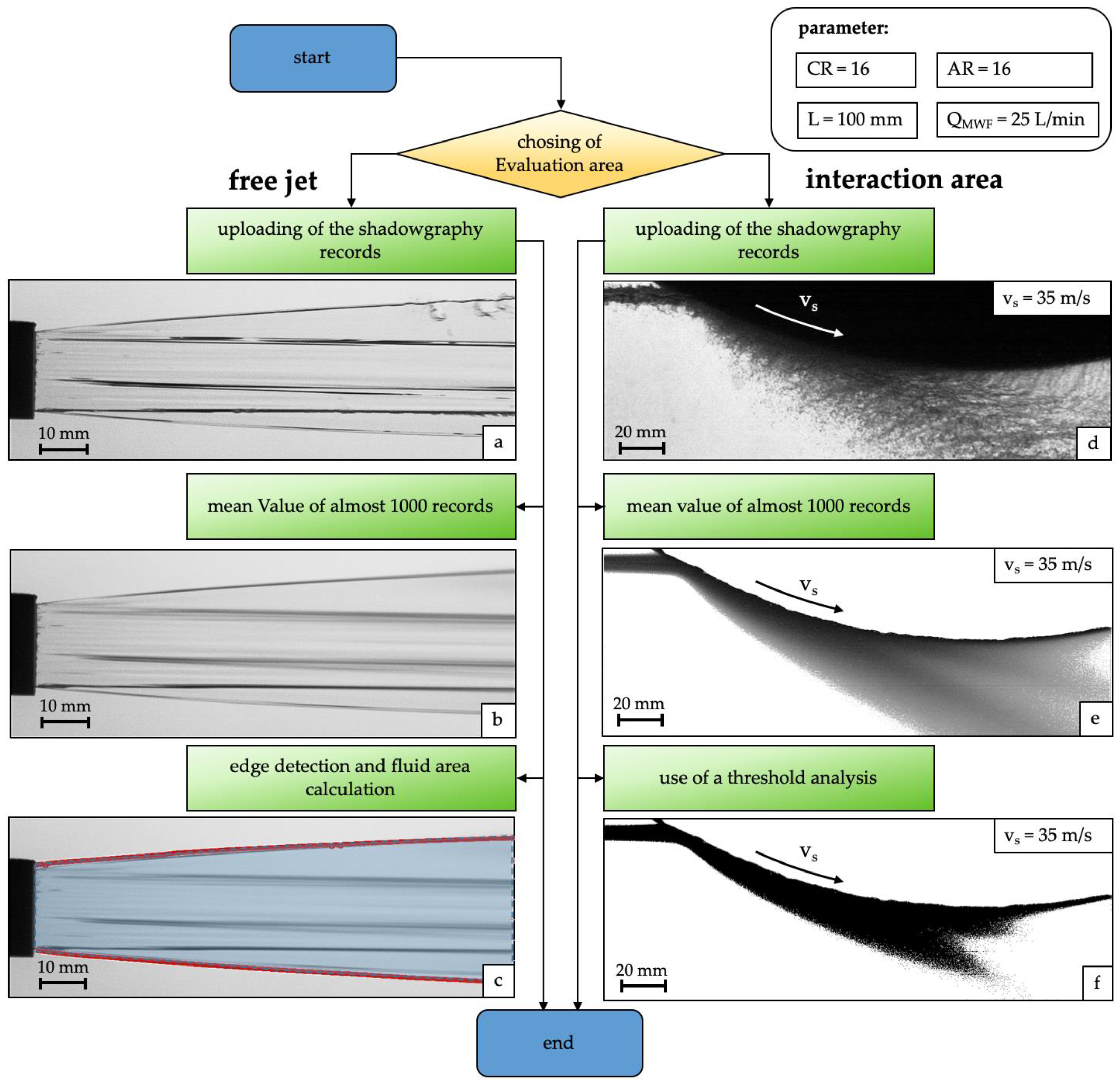
2.2.1. Shadow Image Velocimetry
2.2.2. Processing of the Shadowgraphy Recordings
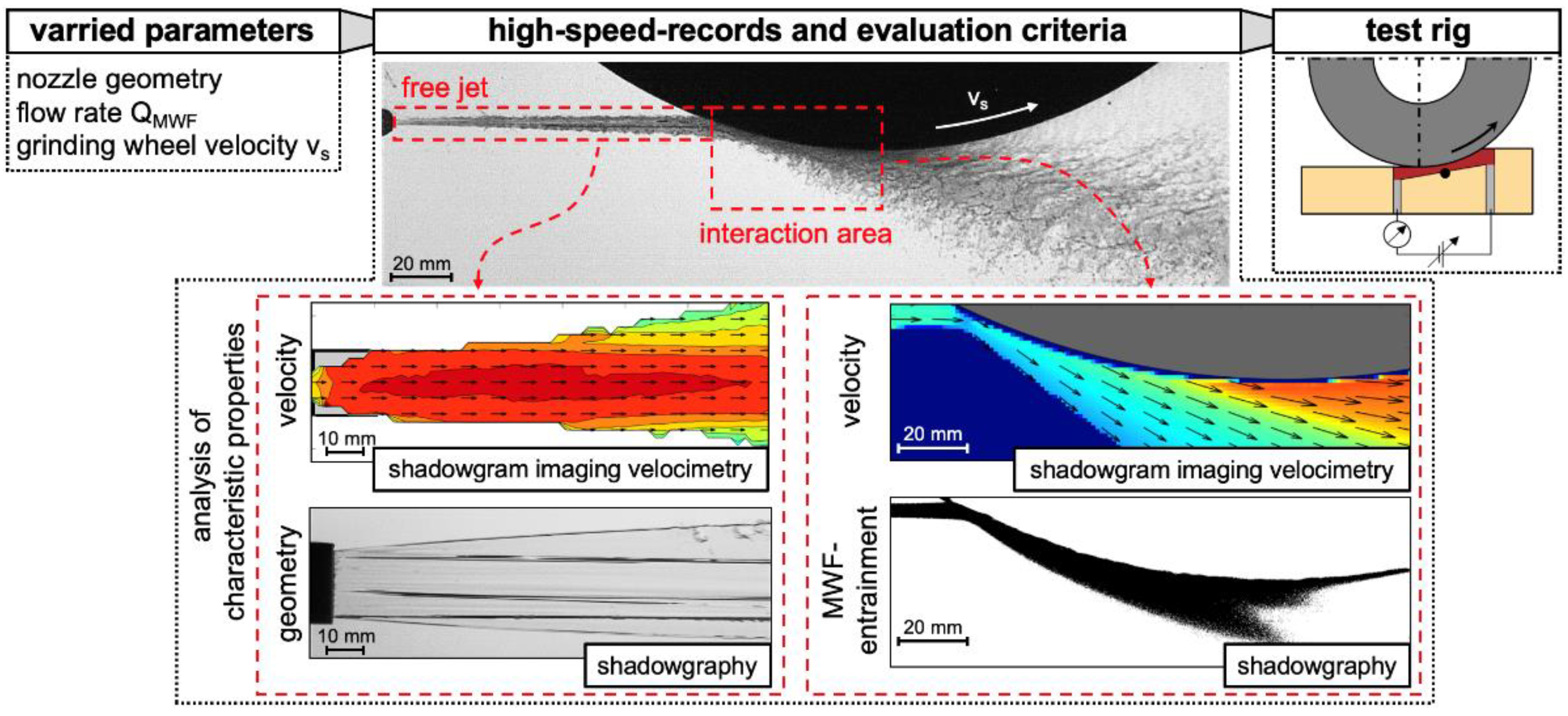
3. Results
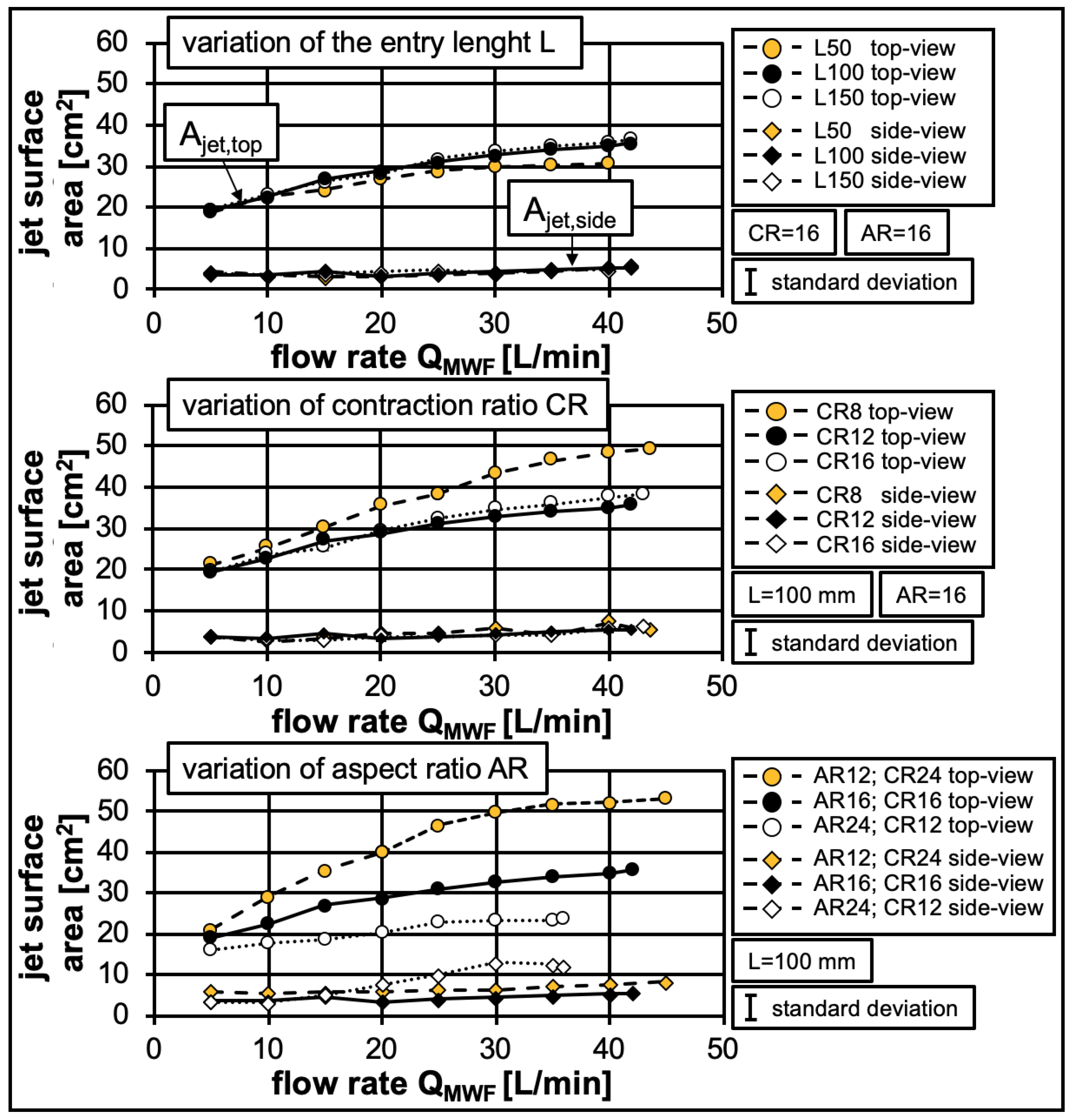
3.1. Free Jet—Geometry
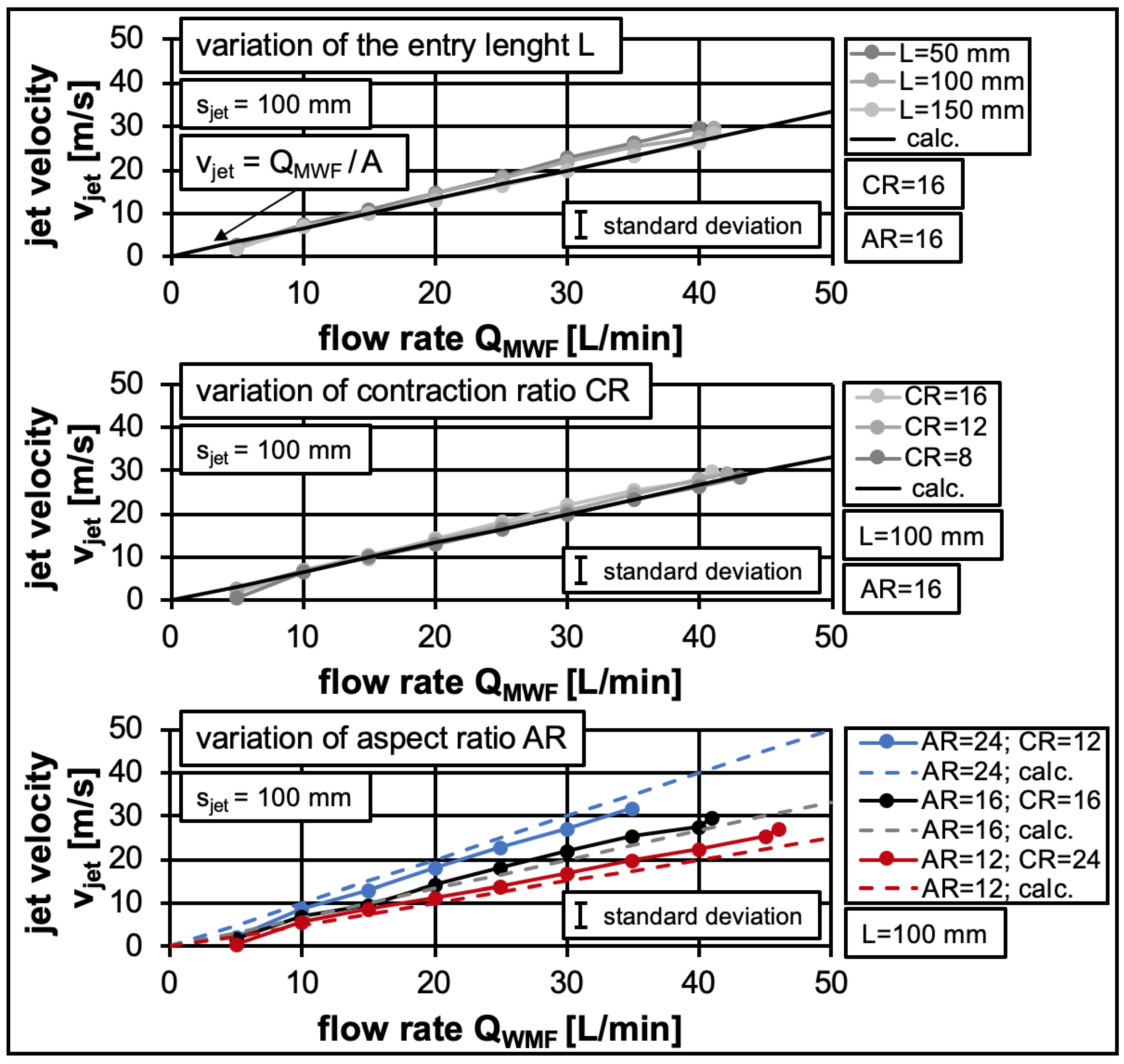
3.2. Free Jet—Velocity Distribution
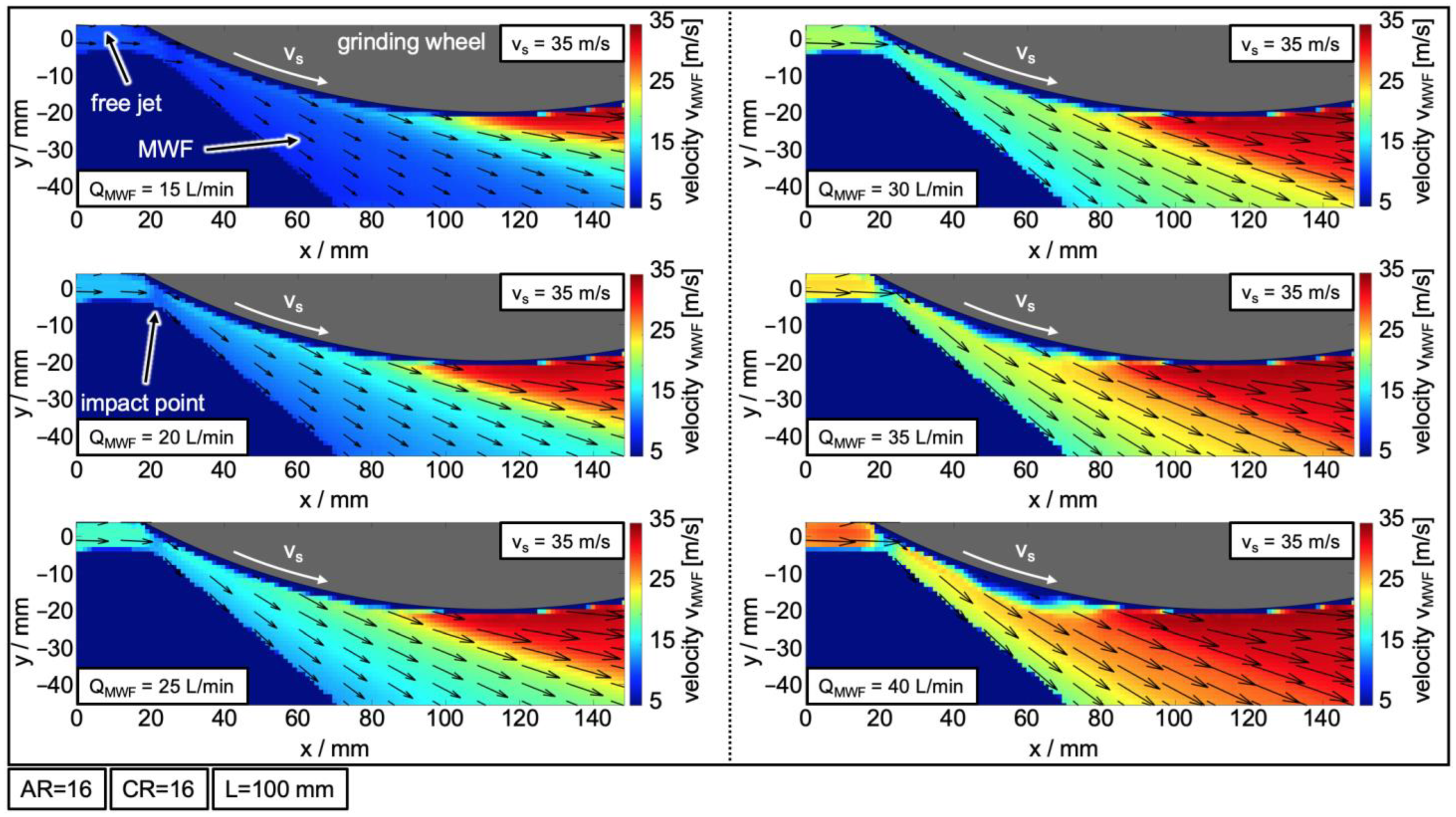
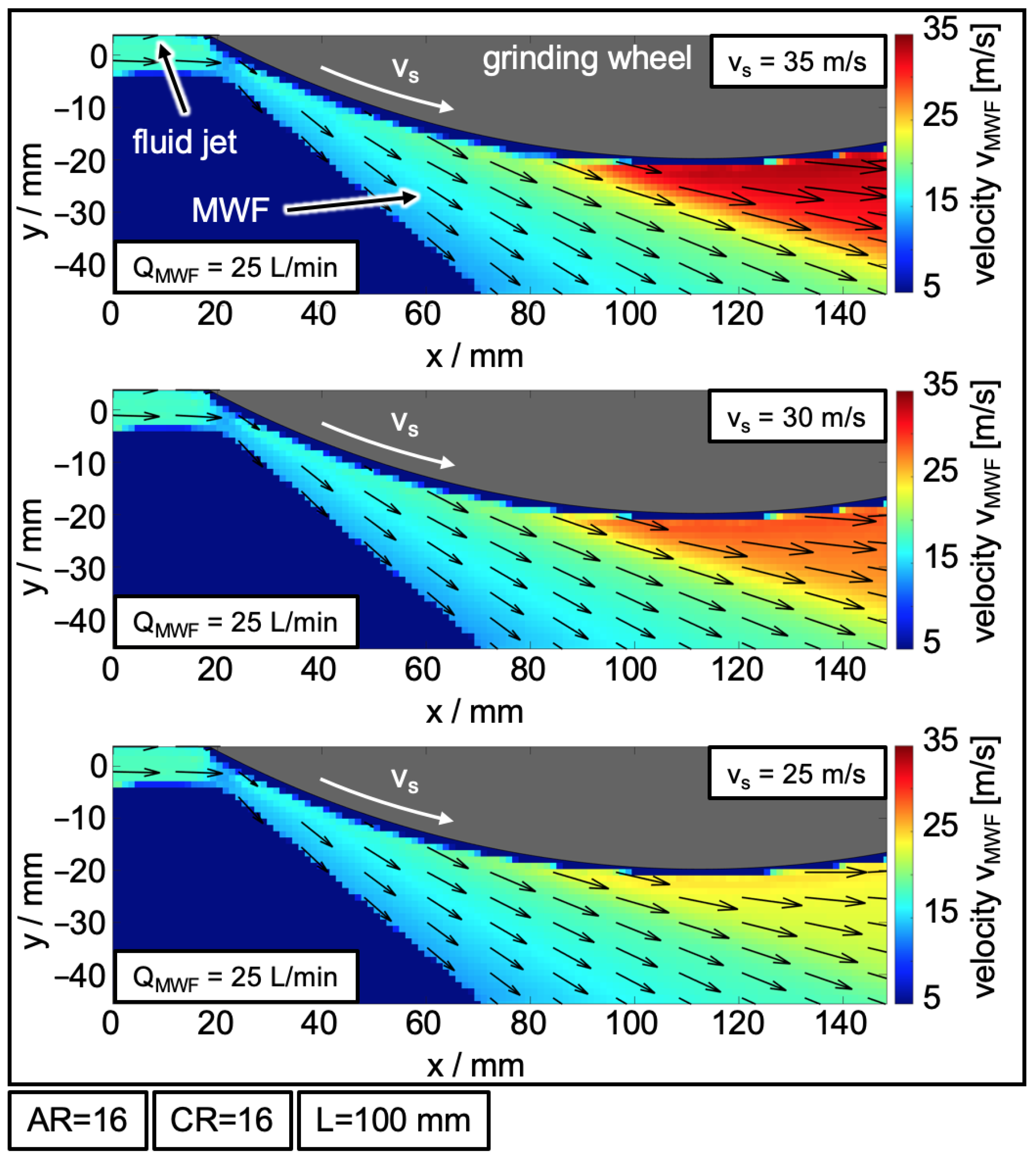
3.3. Interaction Area—Velocity Distribution
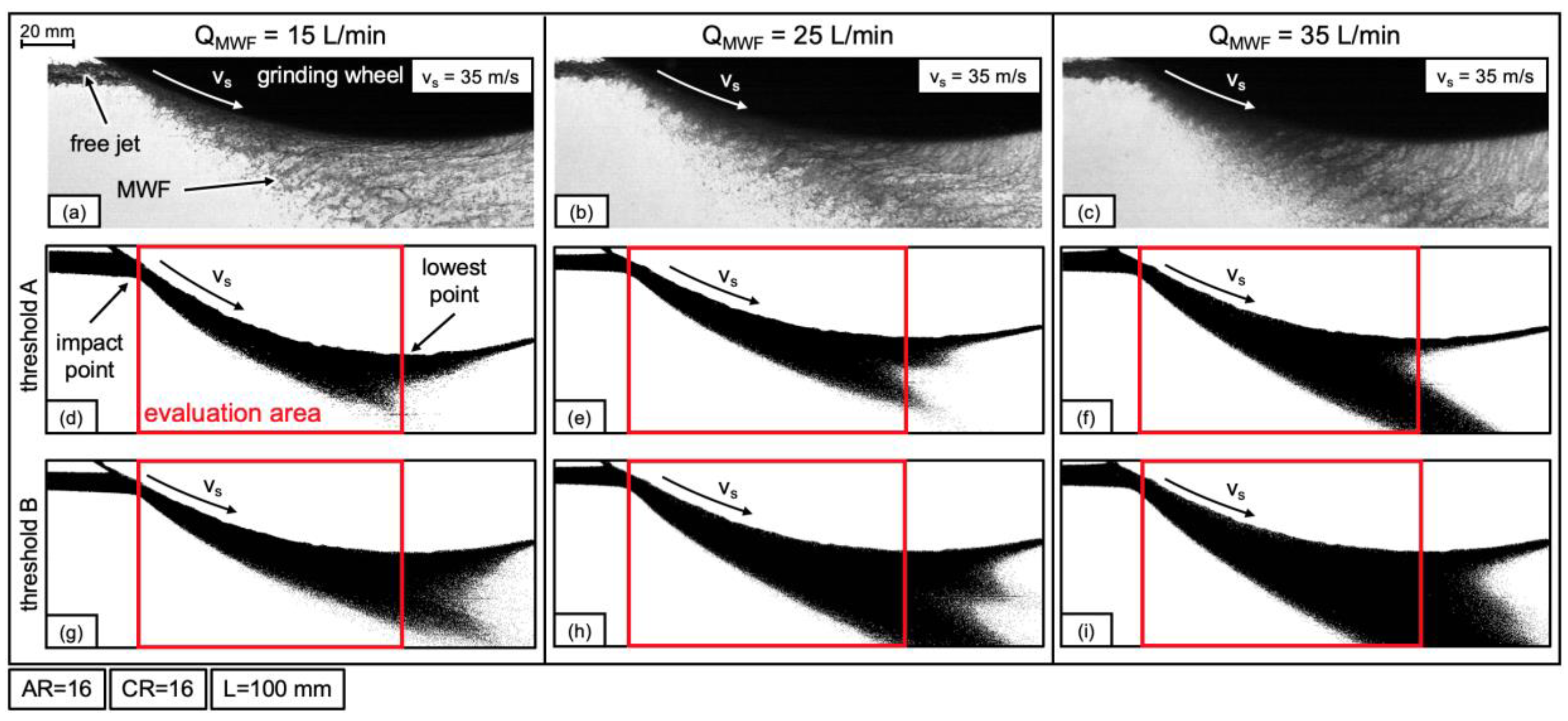
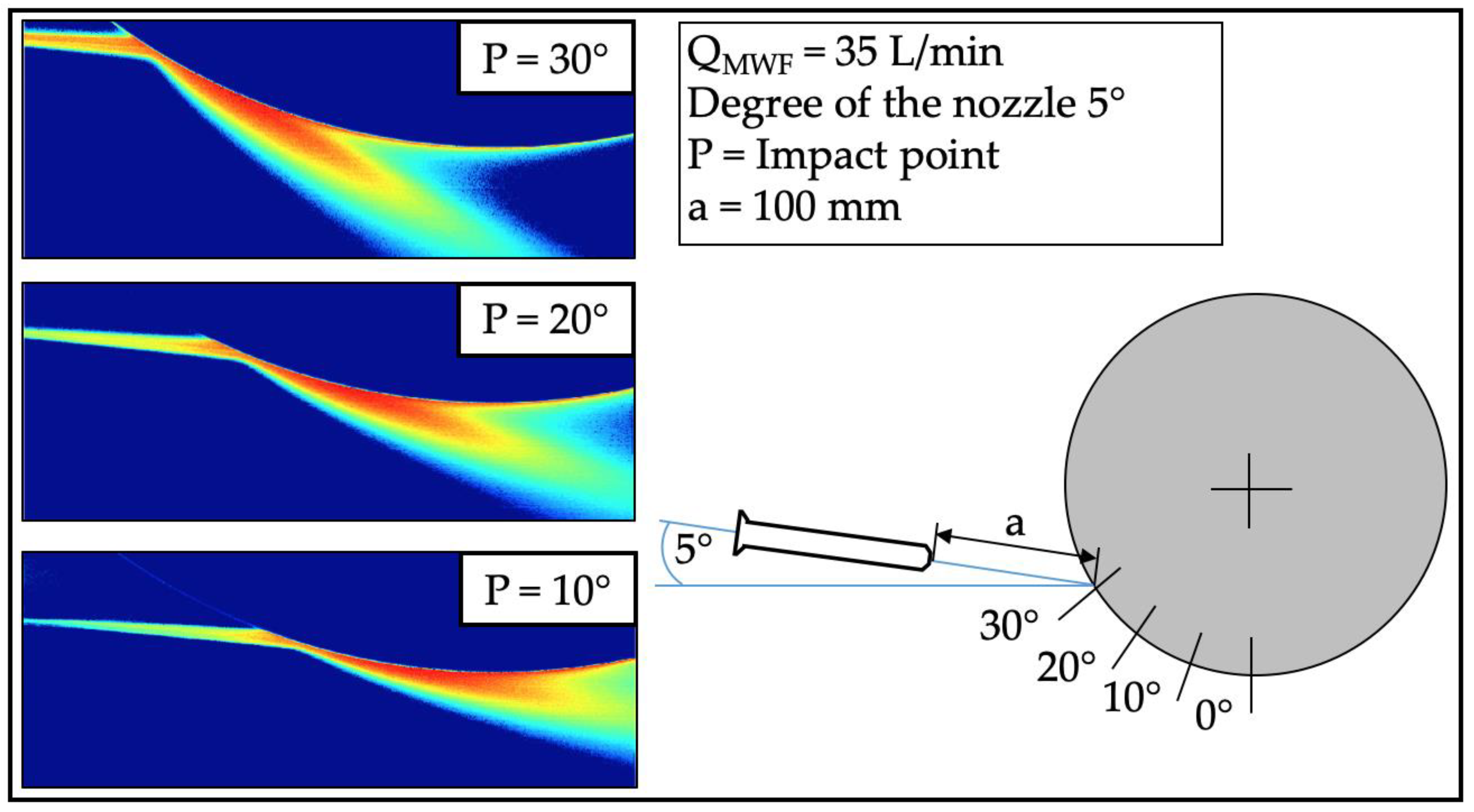
3.4. Analysis of the MWF Supply with Shadowgraphy
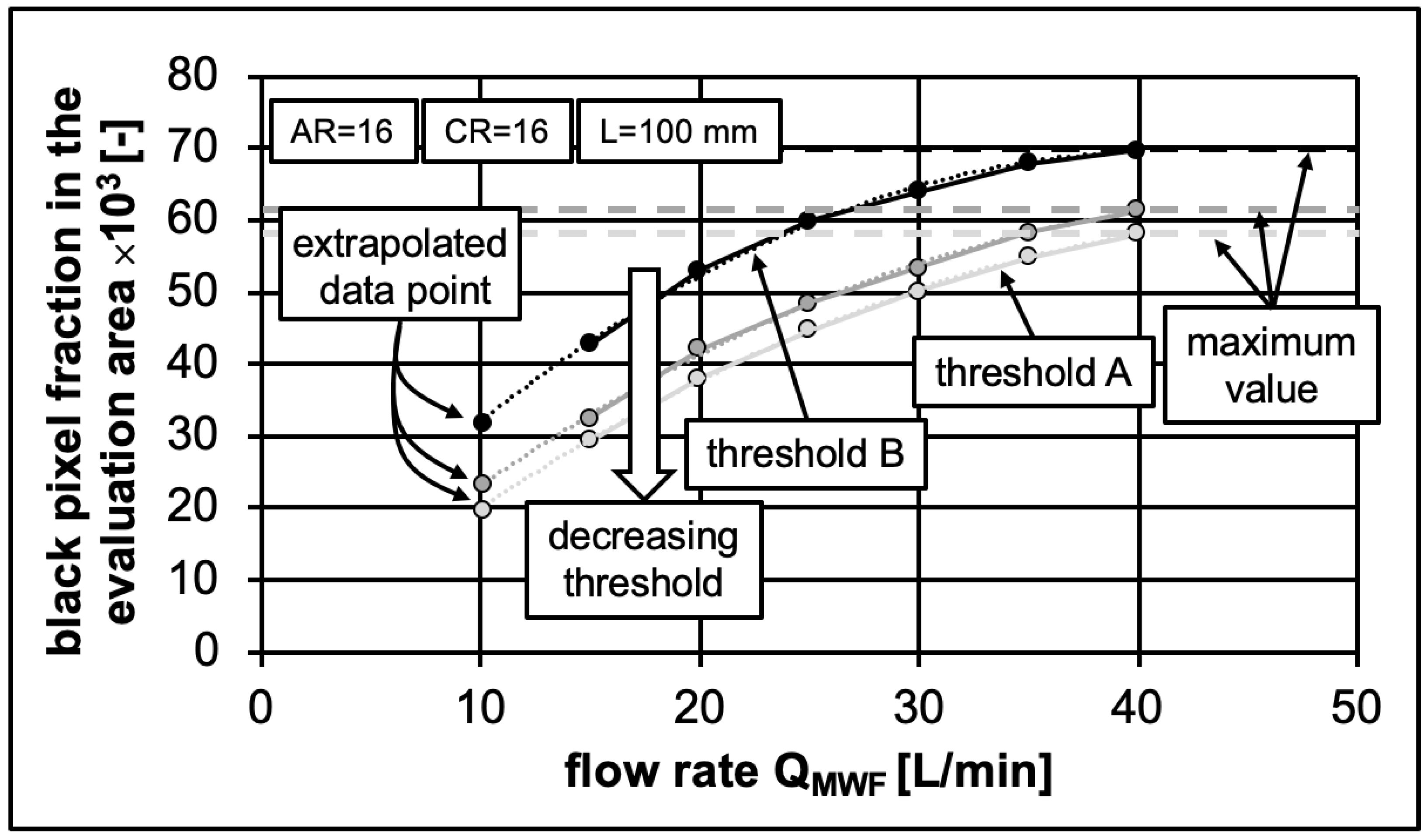
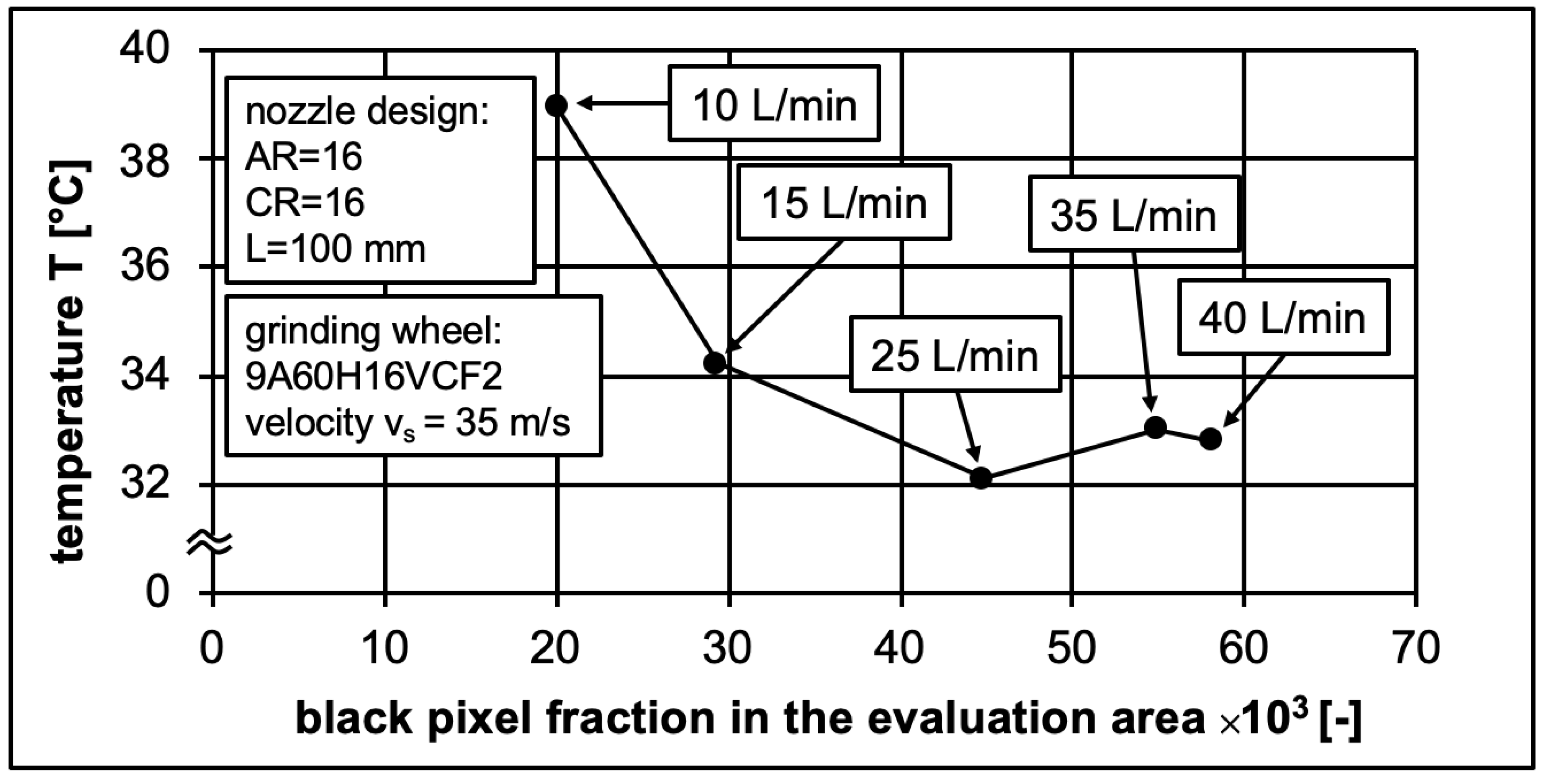
3.5. Evaluation of the Cooling Capacity Depending on MWF Supply Conditions
4. Conclusions and Outlook
- (1)
- For the applied MWF nozzle, the jet velocity remains approximately constant in a defined free jet cross-section, even at high distances from the nozzle outlet. This confirmed that a valid estimate of the jet velocity in the relevant free jet area is obtained with the aid of Equation (1).
- (2)
- Despite constant velocities, the free jet geometry can differ significantly when the entrance length L and contraction ratio CR are varied.
- (3)
- The velocity distribution in the interaction area is mainly influenced by the flow rate. The grinding wheel velocity has an influence limited to an area below the grinding wheel.
- (4)
- The new parameter black pixel fraction was derived for the evaluation of the MWF supply to the contact zone.
- (5)
- The informative value of this new image parameter was verified with the aid of a suitable test rig.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kohl, E.; Heinzel, C.; Eich, M. Evaluation of Hardness and Resiual Stress Changes of AISI 4140 Steel Due to Thermal Load during Surface Grinding. J. Manuf. Mater. Process. 2021, 5, 73. [Google Scholar]
- Srivastava, A.; Awale, A.; Vashista, M.; Yusufzai, M.Z.K. Monitoring of thermal damages upon grinding of hardened steel using Barkhausen noise analysis. J. Mech. Sci. Technol. 2020, 34, 2145–2151. [Google Scholar] [CrossRef]
- Neslusan, M.; Cizek, J.; Kolarik, K.; Minarik, P.; Cillikova, M.; Melokhova, O. Monitoring of grinding burn via Barkhausen noise emission in case-hardened steel in large-bearing production. J. Mater. Process. Technol. 2017, 240, 104–117. [Google Scholar] [CrossRef]
- Meyer, D.; Wagner, A. Influence of metalworking fluid additives on the thermal conditions in grinding. CIRP Ann. Manuf. Technol. 2016, 65, 313–316. [Google Scholar] [CrossRef] [Green Version]
- Rowe, W.B.; Black, S.C.E.; Mills, B.; Qi, H.S.; Morgan, M.N. Experimental Investigation of Heat Transfer in Grinding. Ann. CIRP 2018, 44, 329–332. [Google Scholar] [CrossRef]
- Schwienbacher, S. Einfluss von Schleifbrand auf die Flankentragfähigkeit einsatzgehärteter Zahnräder. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2008. [Google Scholar]
- Aurich, J.C.; Kirsch, B. Improved coolant supply through slotted grinding wheel. CIRP Ann. Manuf. Technol. 2013, 62, 363–366. [Google Scholar] [CrossRef]
- Heinzel, C.; Kirsch, B.; Meyer, D.; Webster, J. Interactions of grinding tool and supplied fluid. CIRP Ann. Manuf. Technol. 2020, 69, 624–645. [Google Scholar] [CrossRef]
- Kirsch, B. The impact of contact zone flow rate and bulk cooling on the cooling efficiency in grinding applying different nozzle designs and grinding wheel textures. CIRP-JMST 2017, 18, 179–187. [Google Scholar] [CrossRef]
- Sieniawski, J.; Nadolny, K. Experimental study into the grinding force in surface grinding of steel CrV12 utilizing a zonal centrifugal coolant provision system. Proc. Inst. Mech. Eng. Part. B J. Eng. Manuf. 2018, 232, 394–403. [Google Scholar] [CrossRef]
- Baumgart, C.; Radziwill, J.J.; Kuster, F.; Weger, K. A Study of the interaction between coolant jet nozzle flow and the airflow around a grinding wheel in cylindrical grinding. Procedia CIRP 2017, 58, 517–522. [Google Scholar] [CrossRef]
- Zhao, Z.; Qian, N.; Fu, Y. Coolant condition and spindle power high-efficiency-deep-grinding of nickel-based superalloy profile part. Mater. Manuf. Process. 2021, 36, 1–13. [Google Scholar] [CrossRef]
- Smith, E.D.; Curtis, D. An investigation of additively manufactures coolant nozzles for cylindrical grinding applications and progression to high stock removal. Procedia CIRP 2021, 101, 162–165. [Google Scholar] [CrossRef]
- Rouse, H. Experimental investigation of fire monitors and nozzles. Trans. Am. Soc. Civil Eng. 1952, 117, 1147. [Google Scholar] [CrossRef]
- Stachurski, W.; Sawicki, J.; Krupanek, K.; Nadolny, K. Numerical analysis of coolant flow in the grinding zine. Int. J. Adv. Manuf. Technol. 2019, 104, 1999–2012. [Google Scholar] [CrossRef] [Green Version]
- Hosokawa, A.; Shimizu, R.; Kiwata, T.; Koyano, T.; Furumoto, T.; Hashimoto, Y. Studies on Eco-Friendly Grinding with an Extremely Small Amount of Coolant–Applicability of Contact-Type Flexible Brush-Nozzle. Int. J. Autom. Technol. 2019, 13, 648–656. [Google Scholar] [CrossRef]
- Parthasarathy, A.; Malkin, S. Effect of fluid application conditions on grinding behaviour. Mech. Eng. B J. Eng. 2010, 24, 225–235. [Google Scholar] [CrossRef]
- Brevern, P. Untersuchungen zur Kühlschmierstoffversorgung beim Tiefschleifen von Hartmetall. Ind. Diam. Rundsch. 2008, 42, 34–38. [Google Scholar]
- Heinzel, C.; Meyer, D.; Kolkwitz, B.; Eckebrecht, J. Advanced approach for a demand-oriented fluid supply in grinding. CIRP Ann. Manuf. Technol. 2015, 64, 333–336. [Google Scholar] [CrossRef] [Green Version]
- Morgan, M.N.; Jackson, A.R.; Wu, H.; Baines-Jones, V. Optimisation of fluid application in grinding. CIRP Ann. Manuf. Technol. 2008, 57, 363–366. [Google Scholar] [CrossRef]
- Denkena, B.; Becker, J.; Jung, M.; Catoni, F. Optimization of the cooling conditions in continuous generating grinding of gears. In Proceedings of the 3rd International Conference and Exhibition on Design and Production of Dies Molds, Bursa, Turkey, 17–19 June 2004; pp. 339–344. [Google Scholar]
- Ott, H.W. Richtig gekühlt ist halb geschliffen-Eine eher physikalische Betrachtung. Semin. Mod. Schleiftechnol. Feinstbearbeitung 2002, 32, 1–7. [Google Scholar]
- Webster, J.A.; Cui, C.; Mindek, R.B. Grinding fluid application system design. CIRP Ann. Manuf. Technol. 1995, 44, 333–338. [Google Scholar] [CrossRef]
- Geilert, P.; Heinzel, C.; Wagner, A. Grinding fluid jet characteristics and their effect on a gear profile grinding process. Inventions 2017, 2, 27. [Google Scholar] [CrossRef] [Green Version]
- Wittmann, M. Methode zur Bewertung der Kühlwirkung des Kühl-schmierstoff-Zufuhrsystems beim Schleifen. In Proceedings of the 14th International Colloq Tribology-Tribology and Lubrication, Esslingen, Germany, 13–15 January 2004. [Google Scholar]
- Kirsch, B. Wirkmechanismen der Kühlschmierstoff-Zufuhr beim Schleifen: Analyse externer und interner Kühlschmierstoff-Zufuhrmethoden. Ph.D. Thesis, Technical University of Kaiserslautern, Kaiserslautern, Germany, 2013. [Google Scholar]
- Kirsch, B.; Aurich, J.C. Kontaktzonenvolumenstrom und Überflutungskühlung -Kühlmechanismen von Freistrahl- und Schuhdüsen bei hoher Wärmebelastung. Jahrb. Schleif. Honen Läppen Polier. 2013, 66, 81–99. [Google Scholar]
- Qiu, B.; Yin, J.; Ding, W.; Xu, J.; Guo, Q. Flow field and cooling capacity in workpiece-tool contact zone during ultra-high-speed grinding. Int. J. Adv. Manuf. Technol. 2020, 111, 2349–2359. [Google Scholar] [CrossRef]
- Stabauer, R.; Saxler, W. Investigation of the Influence of the Airflow Around a Grinding Wheel on the Coolant Supply. WMMES 2021, 1190, 1–10. [Google Scholar] [CrossRef]
- Gviniashvili, V.; Webster, J.; Rowe, B. Fluid flow and pressure in the grinding wheel-workpiece interface. J. Manuf. Sci. 2005, 127, 198–205. [Google Scholar] [CrossRef]
- Mandal, B.; Singh, R.; Das, S.; Banerjee, S. Improving grinding perfomance by controlling air flow around a grinding wheel. Int. J. Mach. Tool Manu. 2011, 51, 670–676. [Google Scholar] [CrossRef]
- Webster, J.A. Optimizing coolant application systems for high productivity grinding. Abras. Mag. 1999, 34–41. [Google Scholar]
- Gori, F.; Petracci, I.; Angelino, M. Flow evolution of a turbulent submerged two-dimensional rectangular free jet of air. Average Particle Image Velocimetry (PIV) visualizations and measurements. Int. J. Heat Fluid Flow 2013, 44, 764–775. [Google Scholar] [CrossRef]
- Espenhahn, B.; Schumski, L.; Vanslow, C.; Stöbener, D.; Meyer, D.; Fischer, A. Optical flow field measurements of the coolant in a grinding machine. Appl. Sci. 2021, 11, 24. [Google Scholar] [CrossRef]
- Powell, J. The Application of Grinding Fluid in Creep Feed Grinding. Ph.D. Thesis, University of Bristol, Bristol, UK, 1979. [Google Scholar]
- Howes, T.D.; Neailey, K.; Harrison, J. Fluid Film Boiling in Shallow Cut Grinding. Ann. CIRP 1990, 39, 313–316. [Google Scholar] [CrossRef]
- Wittmann, M.; Heinzel, C.; Brinksmeier, E. Evaluating the Efficiency of Coolant Supply Systems in Grinding, Production Engineering Research and Development. Ann. WGP 2004, 6, 39–42. [Google Scholar]
- Wittmann, M. Bedarfsgerechte Kühlschmierung Beim Schleifen; VDI Verlag: Düsseldorf, Germany, 2007. [Google Scholar]
- Mindek, R.B.; Webster, J. Minimizing thermal damage of aero-space components using coolant nozzle and coolant system optimization. IGTI ASME Cogen-Turbo 1994, 9, 97–104. [Google Scholar]
- Canny, J. A Comutational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Czenkusch, C. Technologische Untersuchungen und Prozessmodelle zum Rundschleifen; VDI Verlag: Düsseldorf, Germany, 2000. [Google Scholar]
- Vits, R. Technologische Aspekte der Kühlschmierung Beim Schleifen; VDI Verlag: Düsseldorf, Germany, 1985. [Google Scholar]
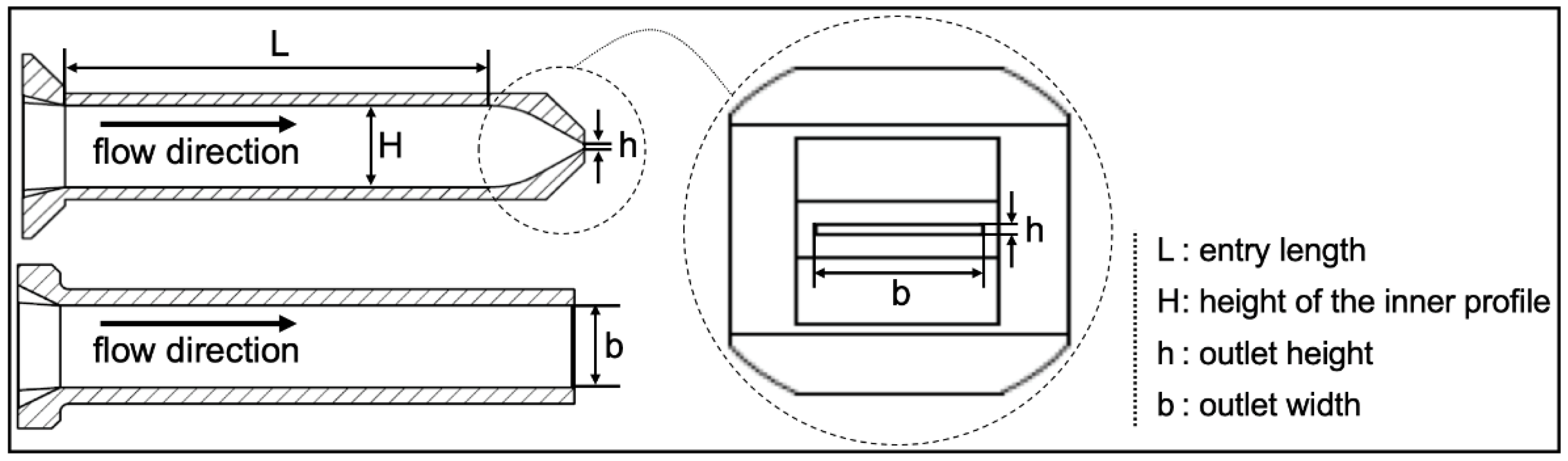




| Height H of the Inner Profile | Outlet Height h of the Nozzle | Outlet Width b of the Nozzle | Entry Length L | Contraction Ratio CR | Aspect Ratio AR |
|---|---|---|---|---|---|
| 10 mm | 0.83 mm | 20 mm | 50 mm | 8 | 8 |
| 15 mm | 1.25 mm | 20 mm | 100 mm | 12 | 16 |
| 20 mm | 1.67 mm | 20 mm | 150 mm | 16 | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schumski, L.; Guba, N.; Espenhahn, B.; Stöbener, D.; Fischer, A.; Meyer, D. Characterization of the Interaction of Metalworking Fluids with Grinding Wheels. J. Manuf. Mater. Process. 2022, 6, 51. https://doi.org/10.3390/jmmp6030051
Schumski L, Guba N, Espenhahn B, Stöbener D, Fischer A, Meyer D. Characterization of the Interaction of Metalworking Fluids with Grinding Wheels. Journal of Manufacturing and Materials Processing. 2022; 6(3):51. https://doi.org/10.3390/jmmp6030051
Chicago/Turabian StyleSchumski, Lukas, Nikolai Guba, Björn Espenhahn, Dirk Stöbener, Andreas Fischer, and Daniel Meyer. 2022. "Characterization of the Interaction of Metalworking Fluids with Grinding Wheels" Journal of Manufacturing and Materials Processing 6, no. 3: 51. https://doi.org/10.3390/jmmp6030051
APA StyleSchumski, L., Guba, N., Espenhahn, B., Stöbener, D., Fischer, A., & Meyer, D. (2022). Characterization of the Interaction of Metalworking Fluids with Grinding Wheels. Journal of Manufacturing and Materials Processing, 6(3), 51. https://doi.org/10.3390/jmmp6030051








