Abstract
The processes involved in the metallurgical industry consume significant amounts of energy and materials, so improving their control would result in considerable improvements in the efficient use of these resources. This study is part of the MORSE H2020 Project, and it aims to implement an operator support system that improves the efficiency of the oxygen blowing process of a real cast steel foundry. For this purpose, a machine learning agent is developed according to a reinforcement learning method suitable for the dynamics of the oxygen blowing process in the cast steel factory. This reinforcement learning agent is trained with both historical data provided by the company and data generated by an external model. The trained agent will be the basis of the operator support system that will be integrated into the factory, allowing the agent to continue improving with new and real experience. The results show that the suggestions of the agent improve as it gains experience, and consequently the efficiency of the process also improves. As a result, the success rate of the process increases by 12%.
1. Introduction
The fourth industrial revolution, also called Industry 4.0, has increased the digitisation and automation of many industrial sectors through the development of smart factories [1]. The objective is to enhance production through processes optimisation, environmental protection and data management, among other factors [2]. To this end, the integration of AI-based techniques is playing an important role, highlighting a machine learning (ML) paradigm called reinforcement learning (RL). Thanks to its capability for learning from interaction, this ML paradigm has become a clear alternative to classic control methods to control industrial processes [3]. In fact, in many cases, RL control methods enhance process efficiencies [4,5], such as welding with robot manipulators [6] and controlling cooling water systems [7] and chemical processes [8].
The steel industry has a broad scope for efficiency improvements due to its high rates of energy and material consumption. Moreover, most techniques used in the steelmaking processes are based on the know-how and professional experience of experts in the sector [9]. Focusing on cast steel foundries with an electric arc furnace (EAF) in their production chain [10], some EAF processes have scope for improvement regarding the time and material efficiency. On the one hand, agent-based systems have been used to reduce electricity consumption in these factories [11] and to increase production [12]. On the other hand, some machine learning algorithms have been applied to EAF steelmaking processes in order to improve the efficiency of the electrical energy consumption [13], the quality of the steel [14] and the dephosphorisation of the melt [15].
This paper presents the implementation of a reinforcement learning agent that will be the core of an operator support system (OSS) that will be used to control the oxygen blowing process of a real cast steel foundry. The agent will have to suggest the most suitable amount of oxygen to blow in order to achieve the target state. To this end, the agent will be designed according to the process dynamics and its objectives, and then it will be trained with the historical data from EAF facilities, which correspond to operational data taken from MFL (Maschinenfabrik Liezen und Gießerei Ges.m.b.H.) facilities. Moreover, a second training phase of the agent will be performed thanks to the integration of a digital twin able to model and reproduce similar conditions to the ones obtained in the current facilities. This training with simulated experience generated by this model is necessary to improve the performance of the agent, as in [16] where an artificial neural network (ANN) is trained with a model to predict the stability behaviour in turn. The final aim of applying this kind of control to this process is to increase the material and time efficiency and productivity.
The paper is organised as follows. Section 2 contextualises the application of the RL agent, describing the process and available resources used to design and develop the agent and explaining the necessary theoretical background regarding reinforcement learning. Section 3 describes the development and training of the agent. Section 4 presents the results of the second training phase of the agent, which illustrates its future performance. Finally, Section 5 includes the conclusions.
2. Materials and Methods
Figure 1 illustrates the role of the RL agent in the decision-making process related to the oxygen blowing process. The operator could request how much oxygen has to be blown and carry out the suggested action or not, but in any case the agent will gain experience that enhances its performance.
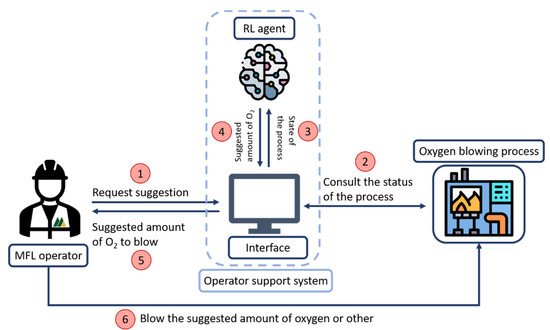
Figure 1.
Diagram of the decision process with the assistance of the operator support system (the order of the steps is indicated by the numbers in red circles; oxygen blowing process icon made by Vitaly Gorbachev from www.flaticon.com; accessed 14 April 2021).
2.1. Oxygen Blowing Process
This case is an EU-funded Horizon 2020 SPIRE Project called MORSE (Model-Based Optimisation for Efficient Use of Resources and Energy) [17], which addresses the implementation of an ML-based OSS to enhance the material and time efficiency of the oxygen blowing process. The castings catalog of the MFL factory is extensive, from rails to components of cars. Furthermore, these products are made of different steel grades, such as unalloyed, low-alloyed quenched and tempered, high-alloyed heat-resistant and Mn-hard alloyed. As stated in [17], the process chain in this factory consists of 5 steps, as is also briefly described in Figure 2. The RL agent will be applied in the second step.
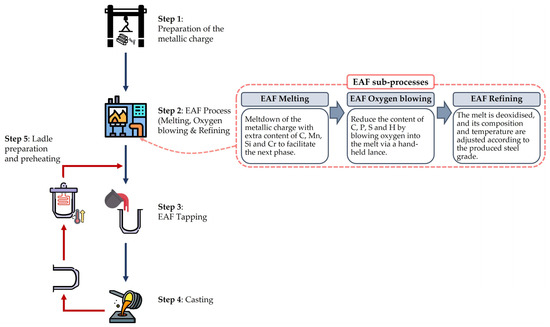
Figure 2.
Scheme of the overall process chain in MFL with the subprocesses that compose the EAF process (to predict the stability behaviour in turning; icons made by Smashicons, Freepik and Gorbachev from www.flaticon.com; accessed 14 April 2021).
The agent is involved in the decision-making process of the second subprocess in the EAF process, i.e., the EAF oxygen blowing process (as seen in Figure 1). These subprocesses (right diagram of Figure 2) are sequential, and before moving on to the next one the melt composition and temperature are measured, then the melt is deslagged.
In order to produce the best decision-making process, the agent is focused on the whole oxygen blowing process, as shown in Figure 3. In this process, the oxygen reacts with C, P, S and H to reduce their contents in the melt, and the slag, which contains the liquid and solid oxide impurities, is formed. Nevertheless, blowing oxygen promotes undesired but unavoidable exothermic chemical reactions that further increase the temperature of the melt and cause the loss of valuable metallic alloy elements such as chromium. These unwanted events are presented on the right side of the figure. Moreover, it should be noted that oxygen can be blown more than once until the target content of chemical elements related to the oxygen blowing process is achieved. This occurs after the EAF refining subprocess, because in many cases a complete composition measurement cannot be obtained beforehand and it is not possible to know whether the C, P, S and H contents have been sufficiently reduced, especially the hydrogen content. This repetition of the EAF oxygen blowing process entails reductions in time and material efficiency for the entire EAF process.
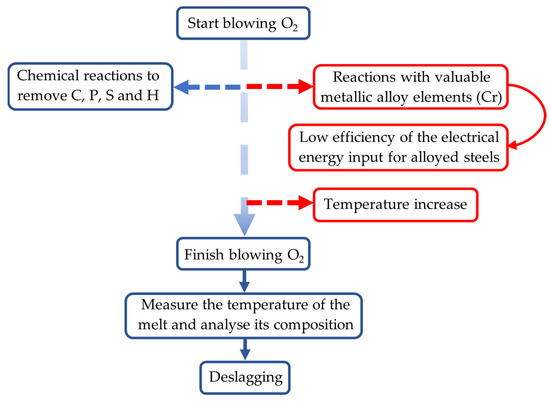
Figure 3.
Scheme of the EAF oxygen blowing process.
From the descriptions of the subprocesses, it is possible to see the relation between the three subprocesses and how improvements in the EAF oxygen blowing process have an effect on the efficiency of the entire production chain. Regarding the material efficiency, it is increased by blowing the minimum amount of oxygen to achieve the target contents of C, P, S and H, which are determined by the initial metallic charge. In this way, the melt does not overheat, which avoids having to wait for it to cool. This, together with the reduction in the duration of the EAF refining process due to the lower residual oxygen in the melt to be deoxidised, results in time savings. As a result, the productivity of the plant is enhanced.
2.1.1. Provided Data
The data used to train the RL agent correspond to the real operation parameters from the EAF processes from 2019. The historical data include all of the information from a real oxygen blowing process, with 204 lots gathered in total, also called heats. All of these lots correspond to a single unalloyed steel grade, called G22Mn7. As an example, the data corresponding to a representative heat are included in Table A1 of Appendix A. Since these historical data are the real outputs of the operations carried out in a foundry to measure each parameter, some cells contain a dash (‘-’) or ‘NULL’. The dash symbol represents the parameters that were not measured during the measurement process. For instance, in the second row of Table A1, the single parameter measured is the temperature of the melt. A similar case occurs when a parameter is measured and its measurement is not available for any reason, represented by ‘NULL’. An example of this can be observed in row 8 of Table A1, where the contents of all chemical elements are measured, except the hydrogen content.
As can be seen in Table A1, the duration of each operation performed in the EAF process is registered with a start time and end time. The temperature of the melt is measured in °C, and it is monitored throughout the EAF process (EAF melting, EAF oxygen blowing and EAF refining). There are four weights given for each heat in kg: (i) the requested weight, which is the weight necessary for the moulding process; (ii) the scrap weight, which is the weight of the scrap needed to ensure that there is sufficient melt available for casting; (iii) the total weight, which is the sum of all materials added to the furnace (the metallic charge and the additions in the three EAF subprocesses) and the slag materials; (iv) the tapping weight, which is the weight of the molten steel that is poured into the ladle. The contents of 32 chemical elements are measured and expressed in percentages, except the hydrogen content, which is given in parts per million (ppm). Portions of these chemical elements are determined by the selected metallic charge in the first step and then adjusted to the target composition of the steel grade to be worked through EAF oxygen blowing and EAF refining process operations.
As mentioned before, the composition of the melt is measured at the end of each EAF subprocess. In those cases, the samples taken to carry out those measurements are assigned the sample numbers 1, 2 and 3, respectively. Moreover, in the event that it is necessary to repeat the EAF oxygen blowing process, the sample numbers will be higher than three. In any case, the same 32 chemical elements are always measured in the samples. The target contents of the chemical elements to be reduced in the EAF oxygen blowing process for the steel grade G22Mn7 are 0.2–023% for C, <0.02% for P, <0.01% for S and <6 ppm for H. In addition, regarding the temperature objective, the target tapping temperature for this steel grade is 1719 ± 15 °C.
2.1.2. Oxygen Blowing Process Model
Due to the short extension of the real dataset, the RL agent is trained with the simulated experience generated by a digital twin model developed by VDEh-Betriebsforschungsinstitut GmbH (BFI) [18,19,20]. Indeed, training an ML model with simulated experience and then applying it to a real process is increasingly common practice [21]. In this case, this training improves the learning process and the future performance of the RL agent.
The dynamic EAF process model is based on energy and mass balances using thermodynamic equilibrium states and reaction or transport kinetic equations without taking into account spatial variations of the heat state. Thus, the model calculates the mean temperatures and compositions of steel and slag, as well as their actual weights, as is explained in [20]. The related ordinary differential equations are solved cyclically along the time axis, considering the respective input data from the cyclic process (such as the electrical energy input needed to keep the EAF on), as well as acyclic events (e.g., material additions). The thermodynamic model calculations may be complemented by balances based on off-gas analyses if available, e.g., regarding decarburisation.
In order to observe the thermal process state, the current energy content is cyclically calculated within an energy balance from the difference in energy gains and energy losses. The energy gains result from the electrical and chemical energy inputs. The energy losses take into account the losses from cooling water, off-gas, radiation and convection. The molten steel temperature is obtained from the difference in current energy content and the energy requirement for the meltdown, which has to be calculated from the reference enthalpies (i.e., specific energies at reference temperature) of the charged materials (scraps, alloys and slag formers), whereby the hot heel (molten steel from a previous heat) is also taken into account. Further details of the model can be found in [19].
This dynamic model is adapted as a digital twin to support the EAF furnace process with good results regarding the achieved calculation, optimisation and control accuracies. The model has been tested and validated in [18]. Thanks to this model, a batch of heats is simulated based on the data of the real historical database, allowing the RL agent to interact with “the oxygen blowing process” and train and improve its performance.
2.2. Finite Markov Decision Process
Markov decision processes (MDPs) are mathematical and idealised interpretations of the reinforcement learning problem. Most of these problems may adopt the MDP structure thanks to the abstraction and flexibility of its framework [22]. The interaction between an agent and its environment is reduced to three signals: one signal to symbolise the decisions of the agent (the actions), another one to indicate the situation of the environment (the state) and a final signal to indicate the target to be achieved by the agent (the rewards). This framework is illustrated in Figure 4.
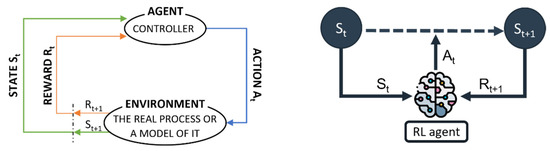
Figure 4.
Adapted scheme of the Markov decision process structure to the control of the EAF process. The image on the left is a generic diagram of the structure of a Markov Decision Process, while the image on the right is a more simplified diagram that corresponds more closely to the development of the agent (icon made by Freepik from www.flaticon.com, accessed 14 April 2021).
Figure 4 expresses the interaction between an agent and its environment following the MDP structure; that is to say, the agent selects and takes actions () according to how it perceives the environment () and it responds to them by presenting new situations (), which gives rise to rewards () [23]. This reward signal plays the most crucial role in an RL problem because it is the channel whereby the agent perceives how good or bad taking action in state is [24]. These numerical rewards are essential to indicate to the agent what objective it must achieve and not how it must accomplish it. In fact, the agent understands the goal of the problem as maximising the accumulative reward in the long run; that is, it seeks to maximise the expected return ().
As explained in [23], depending on the set T, understood as the instants in which the agent can observe the state of the environment and make a decision, the problem can be classified in two ways as a continuous or discrete time and as a finite or infinite horizon. In the interpretation of the oxygen blowing process as an MDP problem, the agent and the environment interact at each discrete time step t (t = 0, 1, 2, 3,…), which gives rise to a state–action–reward sequence: , , , , , , , , . Depending on the RL problem, this sequence can naturally be broken down into subsequences or not. Regardless, the (sub)sequences are determined by the environment dynamics. The dynamics are defined mathematically as the probability that the agent receives a reward , and the environment passes to state from state after taking action :
for all , and . Moreover, since it has been considered that the sets of states, actions and rewards (, and ) for this problem all have a finite number of elements, this will be addressed as a finite MDP according to [23]. Thus, from this point forward, finite MDPs will always be referred to, even if not explicitly indicated.
Finally, as can be seen from the expression above, the probability of each possible value for and only depends on the immediately preceding state and action, without considering the followed trajectory until then. However, this is not actually true because, that state is a result of the past agent–environment interaction [22]. This is known as the Markov property, and it is assumed throughout this research.
2.3. Reinforcement Learning Method Selection
Reinforcement learning is a machine learning paradigm, together with supervised and unsupervised learning. This paradigm stands out from the rest for two reasons. Firstly, it is suited to interacting with sequential decision-making processes, which perfectly fit the MDP structure. Secondly, it does not depend on a large volume of historical data on which to base its learning, as the agent learns as it gains experience in interacting with the actual process or a model of it. All of this makes an agent based on reinforcement learning very appropriate for the control of the EAF oxygen blowing process, because in addition to being a sequential decision-making process, scarce historical data are available and an algorithm capable of learning as it interacts with the process is required.
There are many RL methods, but all of them have the same core and way of learning. This core is composed of the policy and the value function. The former defines the agent’s behaviour because it decides which action must be taken in each state [24]. The policy may be greedy (the agent exploits its current knowledge to maximise the accumulative reward in the long run) or not (the agent tends to explore new paths to achieve the target). Moreover, the policy is deduced from the value function of the agent, which estimates the values of the states according to the received rewards [22]. There are two types of value function:
- State–value function for policy (): This function calculates the expected return when starting in and following thereafter;
- Action–value function for policy (): This defines the expected return starting from , taking action and following policy .
The achievement of the optimal policy and value function is through the generalised policy iteration (GPI) [25]. In this process, both elements interact, changing until they converge to the optimal state. In the case of the value function update, it follows an update rule that depends on the RL method because each one estimates the new values differently. The generic update rule is formulated as:
where is the estimated return in each state and the expression is an error in the estimation [26]. Moreover, the variable , known as alpha, controls how much the agent learns about its experience. This parameter is between 0 and 1, and it may be constant or variable [22].
Regarding the choice of the most suitable RL method to implement the agent, given the oxygen blowing process characteristics, only the RL tabular methods were considered. These methods, which are composed of dynamic programming (DP), Monte Carlo (MC) and temporal difference (TD) methods, are explained in Appendix B.
In the decision process, dynamic programming was not considered to implement the agent because of its requirement of a perfect model of the environment. For that reason, the selection was between Monte Carlo and temporal difference methods. Although both learn directly from raw experience without a model of the environment, MC methods update estimates at the end of each episode, whereas TD methods do it after each step based in part on other learned estimations. This online learning, together with faster convergence, meant that the TD method was chosen.
Within temporal difference learning methods, it was necessary to choose between on-policy and off-policy algorithms. The first type base their decisions on the same policy that is improved. In contrast, off-policy methods perform these operations with two different policies: the behaviour policy (which generates data) and the target policy (which is enhanced with said data). This last kind of TD method was selected to implement the RL agent because it offers the advantage of improving the policy deduced from the historical database and exploring new paths to achieve the target state at the same time. In other words, this method allows one to initialise the RL agent with data from the provided database and improve its policy as it gains experience. Therefore, this initial policy is the target policy, whereas the behaviour policy may be an explorative one or may be substituted by the actions taken by an operator. This explorative policy is usually an ε-greedy policy with which the agent chooses the greediest action most of the time, although with probability ε it selects an action at random.
The temporal difference off-policy control method is called Q-learning, for which the update rule is:
Comparing this expression with Equation (2), it can be deduced that the algorithm estimates the action–value function for each state–action pair at time t. In addition, the step–size parameter is represented by α and the Target by the expression . The latter consists of three elements:
- : This is the reward that the agent receives after applying action in state ;
- γ: This parameter is called the discount factor, and it determines the present value of future rewards, that is, how much the agent trusts its estimates;
- : This expression indicates the maximum q-value of the action–value function by applying the action that corresponds to this state–action pair.
Equation (3) shows that the agent updates its estimation of greedily because the estimated q-value of the next state is the maximum. The pseudocode of the learning process of a Q-learning agent is shown in Algorithm 1. Detailed information about the process to update the q-value function with this algorithm can be found in [25].
| Algorithm 1: Q-Learning Algorithm |
| * Initialisation* Algorithm parameters: Step size α and discount factor γ ϵ (0, 1], small ε > 0 Initialise Q(s, a) for all states and actions arbitrarily, except Q(terminal, a) = 0 Loop for each episode: Loop for each step of the episode: according to the behaviour policy Update the action–value function with the following expression: Until S is terminal |
2.4. Data Processing
Once the available data to implement the RL agent and the theoretical knowledge necessary for the implementation have been explained, it is necessary to carry out two tasks before developing the agent. The first step is to analyse the historical dataset and the results obtained to assess the performance of the agent. Secondly, one must proceed to define the three signals of the MDP structure in order to understand the oxygen blowing process as an RL problem.
2.4.1. Assessment of the Historical Data
The aim of this step was to analyse the original historical dataset to make it simpler and to remove the defectively recorded heats. To this end, some columns were deleted, and the result was a database whose columns contained the following data: timestamps, temperature measurements, requested weights (to give a representative weight of the heat), sample numbers, blown oxygen and the contents of the chemical elements directly modified in this process (C, P, S, H and O). For example, Table A2 illustrates the measurements of an example heat from Table A1 after removing the columns mentioned before. In addition, all heats of the original dataset were analysed, and 31 invalid heats were detected. The leading anomalies were disordered sample numbers, lack of blown oxygen records and manual input failures. Therefore, the resultant database consisted of 173 heats.
According to the requested weights of the heats, MFL categorises them as medium heats if the requested weight is around 4 tonnes and large heats if the requested weight is about 7 tonnes. Nonetheless, all heats of the provided database are medium heats, so the design and application of the RL agent are developed according to this type of heat.
After analysing the historical database, it was observed that 78 of the 173 heats end the EAF oxygen blowing process successfully, representing less than 45% of the total. For this calculation, the final state of the EAF oxygen blowing process has been taken from the first sample after the last oxygen blowing. Moreover, the heats that were considered successful were those that show that the contents of all chemical elements that were modified in the oxygen blowing process (C, P, S, H and O) were within their target intervals, or the same but with the C content slightly below its target content (this criterion is detailed explained in State Signal). However, this does not mean that the remaining heats were rejected because 40% of the heats were unsuccessful due to an excessive reduction in the C content, and this can be corrected by adding carbon in the EAF refining process. Furthermore, focusing on the temperature at the end of the oxygen blowing process, 5% of the heats overheated due to the excessive amount of oxygen blown. These data were obtained from the temperature measurements taken immediately after sample 2, since in this case it was known that the temperature increase was directly related to the oxygen blown. Moreover, it should be noted that any measurement above the upper limit of the target tapping temperature (1734 °C) was considered as overheating. Finally, regarding the number of actions taken, in 83% of the heats, oxygen was blown only once, and 63 of those heats ended the oxygen blowing process successfully, while the rest of the heats required 2, 3 or 4 actions (see Figure 5). In these cases, delays were incurred due to the repetition of composition measurements and extra oxygen blowing. Therefore, the productivity of the plant was reduced.
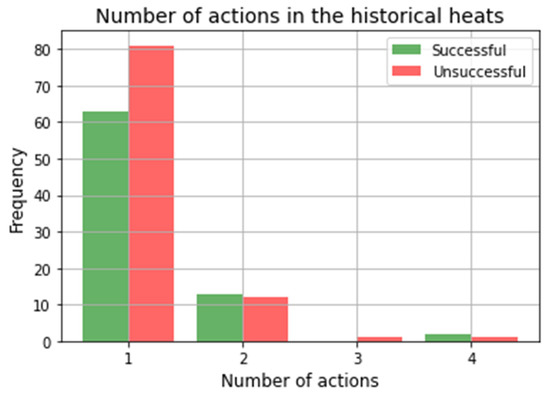
Figure 5.
Number of actions taken in the heats of the historical database and how many of them achieved the target state.
2.4.2. Adaptation to Finite Markov Decision Process Structure
In this section, the finite MDP structure signals are defined according to the normal development of the process and its objectives. Then, these definitions are used to construct a dataset that is understandable by the agent.
State Signal
As shown in Figure 4, the state and reward signals are the only two channels whereby the RL agent receives information about the environment. In the case of the state signal, it reflects the current situation of the environment, which is the information on which the agent bases its next action, and which must indicate when the target has been achieved. Therefore, the agent is only interested in information about the reductions in contents of undesired chemical elements; that is, the remaining chemical contents in the molten steel of C, P, S and H. However, since the melt overheats if oxygen is blown in excess, it is necessary to include an indicator to control it. For this reason, the oxygen content is incorporated into the state definition, which has a twofold benefit: (i) to save material, such as oxygen and other chemical elements that are used in the deoxidation of the EAF refining process; and (ii) to save time by avoiding waiting for cooling due to overheating of the molten steel.
Once the components of the state have been chosen, it is necessary to discretise those data to obtain a delimited state space. On the basis of the target intervals for each chemical element presented in Section 2.1.1 and the analysis of the evolution of the content of the chemical elements included in the state definition, other ranges are established for each chemical element in order to measure how far their contents are from their target intervals. In this way, numeric chemical elements contents are classified into three main categories: target, close to target and far from target. In the case of C, there are two more intervals below its target interval because its content must not be reduced to a minimum: far exceeded target and slightly exceeded target. The numerical contents of the chemical elements are substituted by a corresponding label, which is customised for each chemical element. The intervals for the steel grade G22Mn7 are gathered in Table 1.

Table 1.
Discretisation intervals for the chemical elements of the state.
Action Signal
In the same way that the state signal is defined, the action signal definition is a trade-off between simplicity and efficiency. In this case, the only action in the process is blowing oxygen, which determines the definition of the state signal because oxygen directly modifies the content of the chosen state chemical elements. Therefore, the action signal will represent the amount of oxygen to blow. Some of the enhancements that may be achieved if the optimal actions are taken are as follows:
- The melt will not overheat, and consequently the waiting time for cooling will be avoided;
- This will increase the number of heats that require single oxygen blowing to achieve the target state;
- Delays will be avoided because of the fulfilment of the previous points;
- At the end of the process, the oxygen content will be negligible and the amount of chemical elements used to deoxidise the melt will be reduced.
Although there is an optimal action according to the features of each heat, the action space must be finite. To this end, the definition of the new action space is based on the actions taken in the provided historical database. As a result, two action spaces are defined, one for each weight category (medium and large). However, as was mentioned before, this paper focuses on the medium heats for which historical data are available to compare with the future performance of the RL agent. In this case, the action space consists of 12 actions which are the possible amounts of oxygen in cubic metres that the agent can recommend blowing. These are 2, 4, 8, 10, 20, 30, 35, 40, 45, 50, 55 and 60 m3 of oxygen.
The agent will choose the most suitable action based on the current state and its experience. In this sense, higher amounts of oxygen should be blown when the composition of the molten steel is very far from the target state. In contrast, if the current state is close to the target, lower amounts of oxygen should be blown so as not to reduce the C content in excess or overheat the melt.
Reward Signal
As stated previously, the reward signal and the state signal are the two channels whereby the agent receives information about the environment. The role of this signal is crucial in attaining suitable RL control performance because the agent learns based on this signal. Thus, actions that make all chemical elements of the current state pass to be in their target intervals will be awarded more. Consequently, the dynamics of the process must be considered.
In the case of steel grade G22Mn7, the heats successfully complete the oxygen blowing process in two different states: achieving all the content targets for the chemical elements composing the state signal in their target ranges (‘target’ intervals of Table 1), or with the C content slightly below its target content. In the latter case, P, S, H and O are in their ‘target’ intervals, whereas the C content is in the ‘slightly exceeded target’ interval. This final state occurs when a C content reduction below its target intervals is needed in order to reduce the contents of P and S. In this case, it is then necessary to add carbon in the EAF refining process to achieve the target interval. Therefore, there are two final successful states for the EAF oxygen blowing process: the “super-successful” target state (with C, P, S, H and O in their ‘target’ intervals) and the “simple-successful” target state (P, S, H and O in their ‘target’ intervals and C in the ‘slightly exceeded target’ interval). In contrast, a rejected state will be achieved if, after 6 actions, any of the previous successful states have been reached or if the content of C has been reduced in excess, i.e., below 0.1%. Thus, reaching a rejected state does not imply the rejection of the heat but rather that the oxygen blowing process has not been completed according to the standards sought by MFL. Considering this, the chosen rewards are as follows:
- +10: This is the largest positive reward, which is given when the “super-successful” target state is achieved;
- 0: This reward is received by the agent when the “simple-successful” target state is achieved;
- −10: This is the negative reward that the agent receives if any of the previous target states are reached;
- −50: This is an extra negative reward that the agent receives when the content of C is reduced in excess; that is, below 0.1%. When this occurs, the heat is automatically considered unsuccessful. Thus, this state, together with the other target states explained above, are the only final states.
This distribution of rewards makes the agent see that the most important thing is reaching the state in which the contents of all chemical elements are in their target intervals, i.e., the “super-successful” target state. Nevertheless, if this is not possible, the agent must achieve the “simple-successful” target state. In addition, negative rewards indicate to the agent that it is better to take more than one action (4 or less) to reach one of the target states than to blow excess oxygen and reduce the carbon content below 0.1%.
3. Development of the Agent and Training
In this section, the whole process to develop the agent and train it is explained, as is shown in Figure 6. The first operation is the adaptation of the historical database from EAF operations to the MDP structure according to the definition of the signals described in Section 2.4.2. The next step is the training of the agent with this historical experience. Subsequently, a second training with the simulated experience generated by the process model developed by BFI is carried out in order to improve the performance of the agent. The training with the simulated experience will enhance the learning process because it will allow for the training to be extended with a model that reproduces the EAF process conditions. Finally, the assessment of the performance of the agent will be performed based on the results of this second training. All of these operations are programmed in Python 3.7 [27], mainly using Pandas library (release 1.0.1.) [28] to deal with datasets.
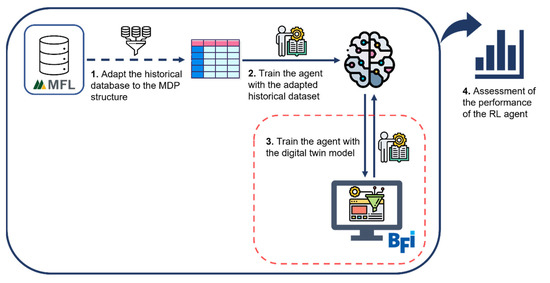
Figure 6.
Process to train the RL agent (historical data from MFL and simulated data from BFI; icons made by Becris, Flat Icons, Eucalyp, and Freepik from www.flaticon.com; accessed 14 April 2021).
3.1. Historical Dataset Creation with Finite Markov Decision Process Structure
This point illustrates the creation of a dataset with the sequences of states, actions, next states and rewards. The first step is to detect consecutive actions, which are those without a composition measurement between them, and combine them into a single action by adding their amounts of oxygen. This logical operation is essential because the number of actions determines how many sequences are there in each heat. Secondly, the initial null composition measurements are detected and substituted by their initial mean values, except the hydrogen, whose concentration is unknown at the beginning of the heat. This approximation is justified by the normal distribution of the initial contents of these chemical elements, as is shown in Figure 7.

Figure 7.
Initial contents of carbon (a), phosphorus (b) and sulphur (c) modelled as normal distributions.
The next step is the selection of the states for each heat according to the taken actions. On the one hand, the states, , are taken from the contents of C, P, S, H and O measured in the sample immediately previous to each action. On the other hand, the next states, , consist of the C, P, S, H and O measurements belonging to the sample that is immediately subsequent to the action taken as a reference to define the previous state. In the event that the measurement of a chemical element content is not available in the sample from which the next state is taken, the composition measurement of the next closest sample would be considered and before the next oxygen blowing phase if applicable. This anomaly is very common for hydrogen because its content cannot be measured until sample 3 in many cases.
This criterion allows for the isolation of each oxygen blowing phase, mitigating possible interference of the operations of the EAF refining process. Therefore, the RL agent will learn the consequences of applying each action in each visited state. Table 2 shows the results of applying the described process to the data of the representative heat included in Appendix A.

Table 2.
Sequence of states and actions for an example heat.
Finally, the discretisation of the states and actions is carried out by conforming to the criteria explained in the definitions of these signals. Moreover, the rewards are added, as stated in Reward Signal. Table 3 presents the measurements of the example heat adapted to the MDP structure and discretised. In this case, it is necessary to remark that the original amounts of blown oxygen are two of the possible factors included in the action space, so they do not change.

Table 3.
Data for the example heat adapted to the MDP structure and discretised. Legend of states: F: ‘far from target’; C: ‘close to target’; T: ‘target’; L: ‘slightly exceeded target’; E: ‘far exceeded target’).
The process represented in the tables below is applied to the 173 heats of the historical database, resulting in a database with 204 sequences. Given the extension of this database, at most 204 state–action pairs are visited, yet the agent distinguishes 405 states according to the possible combinations of the discretisation labels defined in State Signal. Therefore, it can be stated that the extent of the historical database is insufficient to train the agent completely, although training with it will allow the agent to learn the first target policy. For this reason, in addition to the training with the real historical dataset of the process, a second training phase will be necessary. For this second training phase, the simulated experience generated by the model will be used to improve the learning of the agent and its performance.
3.2. Training with the Historical Database
In this section, the implementation and results of the first training phase of the RL agent are described, which involves the historical database adapted to the MDP structure. This training phase is programmed based on the pseudocode shown in Algorithm 1, which is known as batch updating because it always processes the same batch of training data. In this case, the historical dataset serves as the data generated by the behaviour policy of the Q-learning algorithm. After each complete update of the action–value function, an error is calculated as the maximum variation between the current Q and the previous one. When this training error is below a certain threshold, it is considered that the RL agent is trained. The parameters of the training are as follows:
- : A low value is assigned to the step-size parameter so as not to imitate the performance of the operators because it is not optimal. If the agent expects to improve this performance, it must learn the environment dynamics;
- : A discount factor is not necessary to train the agent because it is based on historical data;
- : This maximum accepted training error shows that a variation below the fourth decimal is insignificant.
Once the code is executed, the training requires 895 sweeps of the batch to finish. As a result, Figure 8a is obtained, which illustrates the evolution of the training error throughout the process. This graph shows how the error is sharply reduced during the first sweeps, and then this decreasing trend slows down until the action–value function converges (Figure 8b).
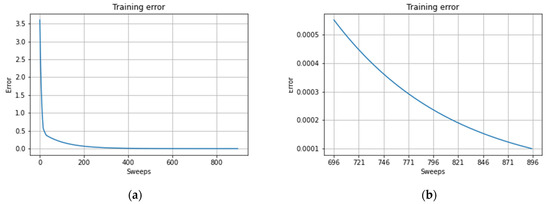
Figure 8.
(a) Evolution of the training error during the training with historical data. (b) Convergence of the training error.
The training result is an estimated action–value function based on the historical data. Because of the short extension of the provided database, the value function does not have values for all state–action pairs, meaning significant improvements may not be observed. Nonetheless, if the most visited states are considered, some well-founded deductions may be made. Figure 9 depicts the visits to each state in the historical dataset, differentiating between states and final states. According to this graph, the agent will gain more experience in the states CTTFT, FTTFT, FTCFT, FCTFT and FCCFT after the training, whereas most heats end in the states ETTTT, LTTTT and TTTT, which are the target states. In the latter cases, the agent does not gain any experience for those states because no actions are taken (these are the final states). These states are expressed in abbreviated form in which each letter corresponds to the discretised content of a chemical element of the state in the order C, P, S, H and O. Thus, there are 5 possible letters: F: ‘far from target’; C: ‘close to target’; T: ‘target’; L: ‘slightly exceeded target’; E: ‘far exceeded target’. Henceforth, this abbreviated nomenclature of the states will be used in text as well as in the figures and tables.
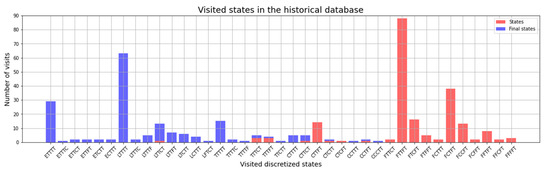
Figure 9.
Visited states in the historical database.
The visits also reflect the process dynamics because the final states (blue ones) are closer to the target state, whereas the states further from the target (red ones) are initial or intermediate. For this reason, the state FTTFT is the most visited one, as it is the most common initial state. The values of for the states are shown in Table 4, while the number of visits to their state–action pairs is shown in Table 5.

Table 4.
Values of the state–action pairs of the most visited states.

Table 5.
Number of visits of the state–action pairs of the most visited states.
To analyse Table 4, it must be considered how many times each action is taken in each of those states (Table 5). Considering this last information, it is noted that larger amounts of oxygen are blown in those states further from the target one (states FTTFT, FTCFT, FCTFT and FCCFT), whereas small actions are preferred for states closer to the goal (state CTTFT). Although the acquired experience is limited, this tendency is reflected in the q-values of Table 4 because the agent will take those actions with greater values; that is, the agent will recommend blowing more than 35 m3 of oxygen for states far from the target, which is in accordance with the target amount of oxygen calculated by MFL (40 m3 of oxygen for medium heats), and less than 8 m3 for states close to the target. A clear example of this is state FTTFT, which is the most visited state. Focusing on the actions that are taken most often in that state, the most recommendable action is blowing 40 m3 of oxygen, as MFL estimates. Therefore, the estimated q-values of the most visited states demonstrate that the agent learned the process dynamics. Nevertheless, the training must continue so that the agent gains a broad experience and the suggestions are improved.
3.3. Training with the Model
This section explains the training of the RL agent with the digital twin model of the oxygen blowing process. This process comprises the configuration of the RL agent and its integration with the model to train it with the simulated experience generated by the model. Since the agent is focused on the oxygen blowing process, the only model functions that will be used throughout the simulation will be measurements of the composition, weight and temperature of the molten steel and the blowing of oxygen into it. Thus, the model will act as a “black box” because its internal functioning is unknown to the agent. Furthermore, although the more experience the agent gains, the better its suggestions are, this training has to be limited due to its computational cost. For this reason, here we decide to simulate 30,000 heats, which we consider sufficient to observe significant improvements.
Regarding the RL agent, its parameters are modified according to the type of training. Firstly, an ε-greedy policy is used as a behaviour policy. In this case, the parameter ε starts from 0.5 and is reduced throughout the simulation until 0, which is achieved mid-simulation. Since the operator support system will work with the greedy behaviour of the RL agent, this will show the future performance of the system. Secondly, the step-size parameter increases to 0.1 in order to accelerate the learning process, and the discount factor is 0.9. Finally, the rest of the parameters are the same as the previous training.
The dynamics of the training with the model is as follows (see Figure 10).

Figure 10.
Interactions between the RL agent and the BFI model during the training (icons made by Eucalyp and Freepik from www.flaticon.com; accessed 14 April 2021).
First, each heat is initialised based on the historical ones (Figure 10, step 1). On the one hand, the weight is randomly chosen as being between 4 and 5.6 tonnes, which is the range of most frequently required weights in the historical dataset. On the other hand, the initial melt temperature and the content of the 32 analysed chemical elements are approximated to normal distributions so that their initial values for the simulated heats are generated from those distributions. For this reason, the mean and standard deviation of these measurements are calculated. Regarding the temperature, the mean and standard deviation are 1521.221 and 49.121 °C, respectively. Figure 11 shows how the temperature may be modelled as a normal distribution. For the chemical composition of the melt, the 32 chemical elements must be initialised in order to replicate the conditions of a real heat. Table 6 includes the mean initial content and standard deviation of the chemical elements most relevant to the process. In this line, the standard deviation is necessary to generate all possible initial contents, especially of the elements of interest (C, P, S, H and O), changing the assigned discretisation labels.
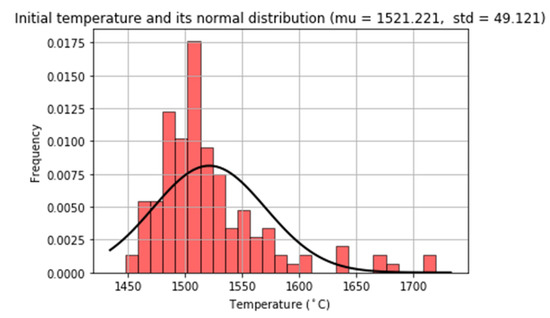
Figure 11.
Initial temperature modelled as a normal distribution.

Table 6.
Mean and standard deviation of the normal distributions corresponding to each analysed chemical element.
After the initialisation, step 2 of Figure 10 starts. The chemical composition of the melt is read and the state is obtained. According to this and the current experience of the agent, the model takes the most suitable action. The model simulates the chosen amount of oxygen being blowen (Figure 10, step 3). For this action, an approximate constant flow rate at the oxygen valve of 8 m3/min is considered. Then, the chemical composition is measured:
- If the state is a target state (“super-successful” or “simple-successful” target states), the heat ends and the agent receives a positive reward of 10 or 0, respectively;
- If the C content of the state is below 0.1%, the heat ends, regardless of the contents of the other chemical elements of the state, and the agent receives a very negative reward of −50;
- If the state does not fit above criteria, the reward is −10. If the number of actions taken by the agent surpasses six the heat ends, otherwise another suitable action is taken (return to step 2).
- After the end of the heat simulation, whether successful or unsuccessful, the training continues with the initilisation of a new heat (return to step 1 of Figure 10).
4. Results
After executing the training with the model described above, the generated experience and the performance of the RL agent in that training phase were evaluated. To this end, several aspects were analysed. The first and most general one was the number of successful heats, where failures were considered as those that surpassed the maximum number of actions per heat or where the carbon was excessively reduced (below 0.1%). The training assessment was that 16,034 of the total 30,000 simulated heats ended the oxygen blowing process successfully, representing 53.45% of the heats. However, it is more interesting to focus on the performance of the agent during the exploitation period (from heat 15,000 when ε = 0) because this will be how the operator support system will behave when it is operational. In the exploitation period, which corresponds to the second half of the training with the model, the agent exploits the knowledge gained during the first half of the training in order to achieve the target state. Considering this part of the simulation, the evaluation was slightly enhanced and 57.34% of the heats in this period were successful. Table 7 shows the number of heats successfully ended by their final states.

Table 7.
Successful heats during the simulation.
From the table above, it can be deduced that the exploitation training meant that the agent tended to end the oxygen blowing process successfully, as reflected by a 14% increase in successful heats when the agent behaved greedily. Comparing the performance of the agent in the exploitation phase with the results obtained historically with the decisions of the operators, the success rate improves from 45.09% to 57.34%, which represents an increase of just over 12%. This general improvement summarises the benefits of using the OSS:
- Time, materials and energy are saved, as the resources spent on the previous steps are less likely to be wasted;
- As a consequence of the above, there is an increase in productivity;
- Both of the above benefits would positively affect the profits of the company.
Regarding the blown oxygen, Figure 12 presents the total amount of blown oxygen from the successful heats during the exploitation phase. This figure shows that most heats needed to blow 40 or 45 m3 of oxygen. However, the super-successful target state was most often reached with the first of the two aforementioned rates. Moreover, it can be observed that less than 50 m3 of oxygen was blown in many successful heats. This is in line with the approximation mentioned in Section 3.2 that states that the target amount of oxygen to be blown for medium heats is around 40 m3.
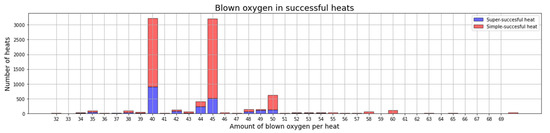
Figure 12.
Amount of blown oxygen in the successful heats in the exploitation period of the training.
Although the amount of blown oxygen influences the duration of the EAF oxygen blowing process, the number of actions taken is also relevant. This is because blowing oxygen after the first time involves other operations, such as preparing the handheld lance and taking a sample to analyse the melt composition, which further increases the duration of the process.
The results regarding this indicator have can be interpreted in two ways. On the one hand, if all simulated heats in the exploitation period are considered, it can be observed that there is an increase of 3% of the number of successful heats achieved when blowing once (63 heats out of 173 heats in the historical database against 5949 heats out of 15,000 heats). On the other side, if only successful heats are taken into account, the RL agent causes an increase in the number of actions per heat, reducing the number of successful heats with a single action by 10%. This slightly increases the average duration of the process due to the operations involved in blowing oxygen. However, this is preferable if a higher success rate is achieved, as in the overall computation the processing time for each heat is reduced. Furthermore, this follows the dynamics described in Reward Signal, with reaching the target in more than one action being preferable to blowing excess oxygen and having to reject the heat.
Figure 13 shows the number of actions taken in the successful heats of the exploitation period. This indicates that the majority of heats required one action to end the process successfully. Furthermore, thanks to the three intervals into which the number of successful heats has been divided, it is clear that there is a tendency for the number of heats requiring a single action to reach the target state to increase. Thus, there is room for improvement, and the number of actions could be reduced as the agent gains experience.
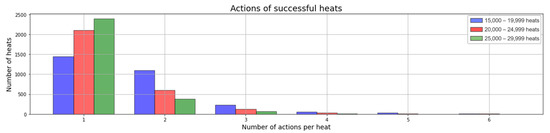
Figure 13.
Number of actions taken in the successful heats of the exploitation phase divided into three intervals.
Lastly, the melt temperature at the end of the EAF oxygen blowing process did not increase in excess. The mean value for this temperature was 1556.33 °C, while Figure 14 presents the distribution. Given that only one heat out of the 15,000 heats of the exploitation period exceeded the target tapping temperature, it can be stated that overheating of the melt was avoided. Thus, the achieved improvement was maximal regarding the historical data, where 5% of the heats overheated. The benefit of this is two-fold. On the one hand, time is saved because waiting times for cooling are not necessary, which is crucial to keeping the factory running to schedule. On the other hand, this also shows that the amount of blown oxygen is not excessive and that this material is saved.
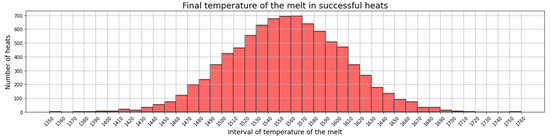
Figure 14.
Temperature of the melt at the end of the EAF oxygen blowing process for the successful heats in the exploitation phase.
5. Conclusions
This paper presents an analysis of the application of a reinforcement learning agent to control the oxygen blowing process carried out in the EAF of a cast steel foundry. The agent was developed based on the process dynamics and its objectives. Furthermore, it was trained with a real historical database and simulated experience generated by a dynamic process model.
The resultant RL agent showed quite positive behaviour compared to that deduced from the historical database. First, the RL agent increased the success rate of the process by 12%, which involved reducing heat rejections and lower rates of material and time wastage. Secondly, waiting times for cooling were avoided because only 1 out of 15,000 heats in the exploitation period ended the oxygen blowing process with the temperature of the molten steel above the target tapping temperature. Finally, the performance of the RL agent showed a tendency to achieve the target state with fewer actions, yet the number of successful heats with a single action in the group of successful heats was reduced by 10% with respect to the historical data. Nonetheless, an overall reading of the performance of the agent revealed that this indicator increased by 3% regarding all heats.
Therefore, the enhancements achieved with the application of the RL agent to control the oxygen blowing process entailed increasing the time and material efficiency of the process. This demonstrated that the Q-learning algorithm is suitable to learn from steelmaking processes and support operators in the decision-making process. Moreover, this paper encourages further investigation in this direction to open new ways of improving productivity and sustainability in the steelmaking sector. Hence, future studies should include an overview of the complete operator support system, training of the agent with more experience and applications of the model in other steelmaking processes.
Author Contributions
Conceptualization, Á.O.R., D.S.A. and A.d.R.T.; data curation, G.G.; funding acquisition, M.H. and C.L.G.; methodology, Á.O.R.; project administration, M.H., C.L.G. and A.d.R.T.; resources, M.S.; software, Á.O.R. and M.S.; supervision, L.E.A.G., M.H. and C.L.G.; validation, G.G.; writing—original draft, Á.O.R.; writing—review and editing, G.G., M.S., L.E.A.G., M.H., C.L.G., F.D.N. and A.d.R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This study was performed under the MORSE project, which has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 768652.

Data Availability Statement
Not applicable.
Acknowledgments
This study reflects only the authors’ views and the commission is not responsible for any use that may be made of the information contained herein.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Measurements of a representative heat included in the historical database provided by MFL. In each row, the results of a single operation are included because several operations cannot be carried out in parallel. There are four types of operations: (i) weight measurement, which is always the first operation in a heat; (ii) measurement of the melt temperature; (iii) composition analysis, for which a sample of the melt is taken (sample number) and the contents of the chemical elements presented in the melt are measured; (iv) blowing oxygen, which is the only possible action in EAF oxygen blowing process and is indicated by the amount of blown oxygen. Here, cells marked “-” correspond to parameters that are not measured in an operation, whereas NULL means that the parameter has been measured but it failed or was not possible.
Table A1.
Measurements of a representative heat included in the historical database provided by MFL. In each row, the results of a single operation are included because several operations cannot be carried out in parallel. There are four types of operations: (i) weight measurement, which is always the first operation in a heat; (ii) measurement of the melt temperature; (iii) composition analysis, for which a sample of the melt is taken (sample number) and the contents of the chemical elements presented in the melt are measured; (iv) blowing oxygen, which is the only possible action in EAF oxygen blowing process and is indicated by the amount of blown oxygen. Here, cells marked “-” correspond to parameters that are not measured in an operation, whereas NULL means that the parameter has been measured but it failed or was not possible.
| Type of Process | Start Time | End Time | Requested Weight | Scrap Weight | Total Weight | Tapping Weight | Blowing O2 | Temperature | Sample Number | C | Si | Mn | P | S | N | Al | Cr | Cu | Mo | Ni | H | O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EAF Melting | 2019-02-01 01:26:21.630 | 2019-02-01 05:02:25.293 | 5000 | 5050 | 5322.2 | 5480 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 2019-02-01 02:59:01.513 | 2019-02-01 02:59:01.873 | - | - | - | - | - | 1461 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2019-02-01 03:11:17.187 | 2019-02-01 03:11:17.500 | - | - | - | - | - | 1570 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2019-02-01 03:15:58.000 | - | - | - | - | - | - | 1 | 0.946 | 0.26 | 1.11 | 0.022 | 0.0042 | 0.018 | 0.215 | 0.12 | 0.053 | 0.02 | 0.06 | - | 0.034 | ||
| EAF Oxygen Blowing | 2019-02-01 03:22:29.157 | 2019-02-01 03:22:29.517 | - | - | - | - | - | 1577 | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 2019-02-01 03:24:02.593 | 2019-02-01 03:34:33.213 | - | - | - | - | 50 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2019-02-01 03:33:26.120 | 2019-02-01 03:33:26.433 | - | - | - | - | - | 1700 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2019-02-01 03:36:46.000 | - | - | - | - | - | - | 2 | 0.286 | 0 | 0.82 | 0.0147 | 0.004 | 0.007 | 0.371 | 0.12 | 0.051 | 0.02 | 0.06 | NULL | 0.032 | ||
| 2019-02-01 03:38:17.153 | 2019-02-01 03:41:30.263 | - | - | - | - | 6 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2019-02-01 03:44:45.000 | - | - | - | - | - | - | 3 | 0.184 | 0 | 0.74 | 0.0138 | 0.0045 | 0.006 | 0.231 | 0.11 | 0.052 | 0.02 | 0.06 | NULL | 0.002 | ||
| EAF Refining | 2019-02-01 03:52:21.247 | 2019-02-01 03:52:21.560 | - | - | - | - | - | 1707 | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 2019-02-01 04:08:15.490 | 2019-02-01 04:08:15.850 | - | - | - | - | - | 1728 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2019-02-01 04:13:02.000 | - | - | - | - | - | NULL | 4 | 0.208 | 0.29 | 1.48 | 0.0199 | 0.0036 | 0.006 | 0.052 | 0.14 | 0.056 | 0.02 | 0.06 | 3.397 | 0.021 | ||

Table A2.
Columns used for the development of the RL agent. Measurements of the same representative heat as shown in Table A1.
Table A2.
Columns used for the development of the RL agent. Measurements of the same representative heat as shown in Table A1.
| Type of Process | Start Time | End Time | Requested Weight | Blowing O2 | Temperature | Sample Number | C | P | S | H | O |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EAF Melting | 2019-02-01 01:26:21.630 | 2019-02-01 05:02:25.293 | 5000 | - | - | - | - | - | - | - | - |
| 2019-02-01 02:59:01.513 | 2019-02-01 02:59:01.873 | - | - | 1461 | - | - | - | - | - | - | |
| 2019-02-01 03:11:17.187 | 2019-02-01 03:11:17.500 | - | - | 1570 | - | - | - | - | - | - | |
| 2019-02-01 03:15:58.000 | - | - | - | 1 | 0.946 | 0.022 | 0.0042 | - | 0.034 | ||
| EAF Oxygen Blowing | 2019-02-01 03:22:29.157 | 2019-02-01 03:22:29.517 | - | - | 1577 | - | - | - | - | - | - |
| 2019-02-01 03:24:02.593 | 2019-02-01 03:34:33.213 | - | 50 | - | - | - | - | - | - | - | |
| 2019-02-01 03:33:26.120 | 2019-02-01 03:33:26.433 | - | - | 1700 | - | - | - | - | - | - | |
| 2019-02-01 03:36:46.000 | - | - | - | 2 | 0.286 | 0.0147 | 0.004 | NULL | 0.032 | ||
| 2019-02-01 03:38:17.153 | 2019-02-01 03:41:30.263 | - | 6 | - | - | - | - | - | - | - | |
| 2019-02-01 03:44:45.000 | - | - | - | 3 | 0.184 | 0.0138 | 0.0045 | NULL | 0.002 | ||
| EAF Refining | 2019-02-01 03:52:21.247 | 2019-02-01 03:52:21.560 | - | - | 1707 | - | - | - | - | - | - |
| 2019-02-01 04:08:15.490 | 2019-02-01 04:08:15.850 | - | - | 1728 | - | - | - | - | - | - | |
| 2019-02-01 04:13:02.000 | - | - | - | 4 | 0.208 | 0.0199 | 0.0036 | 3.397 | 0.021 | ||
Appendix B
For the implementation of the RL agent, only RL tabular methods were considered for the choice of the most suitable control method. This RL branch is appropriate for problems whose state and action spaces are enough small to be represented as arrays or tables. RL tabular methods are divided into three groups of techniques:
- Dynamic Programming (DP) [29]: these algorithms are the basis of RL, and they are capable of computing optimal policies if a perfect model of the environment is given. This requirement, together with the tremendous computational cost, limits the utility of this kind of algorithms.
- Monte Carlo (MC) methods [30]: in comparison with dynamic programming, these methods have lower computational expenses, and they do not need a perfect model of the environment to attain an optimal policy. Therefore, knowing the dynamics of the environment is not required because the agent learns from direct interaction. These methods only need a simulated or actual experience of this interaction in the form of state–action-reward sequences. Another distinctive feature is that they estimate value functions by averaging sample returns. Thus, MC methods are very suitable for episodic tasks, and they do not bootstrap because they base their estimations on the outcome of the interaction and not on other estimates.
- Temporal-Difference (TD) methods [26]: this group of methods combine the most striking features of the two previous ones. From MC methods, TD methods take the ability to learn directly from raw experience, whereas DP and TD methods share that they base their estimates on other learned ones (they bootstrap). Therefore, TD methods do not require a complete model of the environment, and the learning is online and fully incremental. This last feature makes them very appropriate to deal with continuing tasks and episodic tasks whose episodes are very long. Although it has not been proved mathematically, the efficiency and speed of convergence of these methods improve those of MC methods.
References
- Oztemel, E.; Gursev, S. Literature Review of Industry 4.0 and Related Technologies. J. Intell. Manuf. 2018, 31, 127–182. [Google Scholar] [CrossRef]
- Hozdić, E. Smart Factory for Industry 4.0: A Review. Int. J. Mod. Manuf. Technol. 2015, 7, 28–35. [Google Scholar]
- Tsai, Y.T.; Lee, C.H.; Liu, T.Y.; Chang, T.J.; Wang, C.S.; Pawar, S.J.; Huang, P.H.; Huang, J.H. Utilization of a Reinforcement Learning Algorithm for the Accurate Alignment of a Robotic Arm in a Complete Soft Fabric Shoe Tongues Automation Process. J. Manuf. Syst. 2020, 56, 501–513. [Google Scholar] [CrossRef]
- Spielberg, S.; Tulsyan, A.; Lawrence, N.P.; Loewen, P.D.; Gopaluni, R.B. Toward Self-Driving Processes: A Deep Reinforcement Learning Approach to Control. AIChE J. 2019, 65, e16689. [Google Scholar] [CrossRef] [Green Version]
- Alves Goulart, D.; Dutra Pereira, R. Autonomous PH Control by Reinforcement Learning for Electroplating Industry Wastewater. Comput. Chem. Eng. 2020, 140, 106909. [Google Scholar] [CrossRef]
- Pane, Y.P.; Nageshrao, S.P.; Kober, J.; Babuška, R. Reinforcement Learning Based Compensation Methods for Robot Manipulators. Eng. Appl. Artif. Intell. 2019, 78, 236–247. [Google Scholar] [CrossRef]
- Qiu, S.; Li, Z.; Li, Z.; Li, J.; Long, S.; Li, X. Model-Free Control Method Based on Reinforcement Learning for Building Cooling Water Systems: Validation by Measured Data-Based Simulation. Energy Build. 2020, 218, 110055. [Google Scholar] [CrossRef]
- Cassol, G.O.; Campos, G.V.K.; Thomaz, D.M.; Capron, B.D.O.; Secchi, A.R. Reinforcement Learning Applied to Process Control: A Van Der Vusse Reactor Case Study. Comput. Aided Chem. Eng. 2018, 44, 553–558. [Google Scholar] [CrossRef]
- Zarandi, M.H.F.; Ahmadpour, P. Fuzzy Agent-Based Expert System for Steel Making Process. Expert Syst. Appl. 2009, 36, 9539–9547. [Google Scholar] [CrossRef]
- Cavaliere, P. Electric Arc Furnace: Most Efficient Technologies for Greenhouse Emissions Abatement. In Clean Ironmaking and Steelmaking Processes; Cavaliere, P., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 303–375. [Google Scholar] [CrossRef]
- Marchiori, F.; Belloni, A.; Benini, M.; Cateni, S.; Colla, V.; Ebel, A.; Lupinelli, M.; Nastasi, G.; Neuer, M.; Pietrosanti, C.; et al. Integrated Dynamic Energy Management for Steel Production. Energy Procedia 2017, 105, 2772–2777. [Google Scholar] [CrossRef]
- Aksyonov, K.; Antonova, A.; Goncharova, N. Analysis of the Electric Arc Furnace Workshop Logistic Processes Using Multiagent Simulation. Adv. Intell. Syst. Comput. 2017, 678, 390–397. [Google Scholar] [CrossRef]
- Carlsson, L.S.; Samuelsson, P.B.; Jönsson, P.G. Predicting the Electrical Energy Consumption of Electric Arc Furnaces Using Statistical Modeling. Metals 2019, 9, 959. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, E.; Ferreño, D.; Cuartas, M.; Lloret, L.; Ruiz Del Árbol, P.M.; López, A.; Esteve, F.; Gutiérrez-solana, F. Machine Learning Methods for the Prediction of the Inclusion Content of Clean Steel Fabricated by Electric Arc Furnace and Rolling. Metals 2021, 11, 914. [Google Scholar] [CrossRef]
- Chen, C.; Wang, N.; Chen, M. Optimization of Dephosphorization Parameter in Consteel Electric Arc Furnace Using Rule Set Model. Steel Res. Int. 2021, 92, 200719. [Google Scholar] [CrossRef]
- Cherukuri, H.; Perez-Bernabeu, E.; Selles, M.; Schmitz, T. Machining Chatter Prediction Using a Data Learning Model. J. Manuf. Mater. Processing 2019, 3, 45. [Google Scholar] [CrossRef] [Green Version]
- Vimpari, J.; Lilja, J.; Paananen, T.; Leyva, C.; Stubbe, G.; Kleimt, B.; Fuchs, P.; Gassner, G.; Helaakoski, H.; Heiskanen, M.; et al. D1.1 Use Case Descriptions and Analysis. 2018. Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5a0fdfd41&appId=PPGMS (accessed on 29 March 2021).
- Pierre, R.; Kleimt, B.; Schlinge, L.; Unamuno, I.; Arteaga, A. Modelling of EAF Slag Properties for Improved Process Control. In Proceedings of the 11th European Electric Steelmaking Conference, Venice, Italy, 25–27 May 2016; p. 10. [Google Scholar]
- Kleimt, B.; Pierre, R.; Dettmer, B.; Jianxiong, D.; Schlinge, L.; Schliephake, H. Continuous Dynamic EAF Process Control for Increased Energy and Resource Efficiency. In Proceedings of the 10th European Electric Steelmaking Conference, Graz, Austria, 25–28 September 2012; p. 10. [Google Scholar]
- Rekersdrees, T.; Snatkin, H.; Schlinge, L.; Pierre, R.; Kordel, T.; Kleimt, B.; Gogolin, S.; Haverkamp, V. Adaptative EAF Online Control Based on Innovative Sensors and Comprehensive Models. In Proceedings of the 3rd European Steel Technology & Application Days, Vienna, Austria, 26–29 June 2017; p. 12. [Google Scholar]
- Dankar, F.K.; Ibrahim, M. Fake It till You Make It: Guidelines for Effective Synthetic Data Generation. Appl. Sci. 2021, 11, 2158. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An. Introduction, 2nd ed.; Bach, F., Ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Martin, L.P. Chapter 8 Markov Decision Processes. Stoch. Model. 1990, 2, 331–434. [Google Scholar]
- Stork, J.; Zaefferer, M.; Bartz-Beielstein, T.; Eiben, A.E. Understanding the Behavior of Reinforcement Learning Agents. I. In Proceedings of the 9th International Conference on Bioinspired Optimisation Methods and Their Applications, BIOMA 2020, Brussels, Belgium, 19–20 November 2020; pp. 148–160. [Google Scholar] [CrossRef]
- Buchli, J.; Farshidian, F.; Winkler, A.; Sandy, T.; Giftthaler, M. Optimal and Learning Control for Autonomous Robots. arXiv 2017, arXiv:1708.09342. [Google Scholar]
- Kaisaravalli Bhojraj, G.; Surya Achyut, M.Y. Policy-Based Reinforcement Learning Control for Window Opening and Closing in an Office Building. Master’s Thesis, Dalarna University, Falun, Sweden, 2020. [Google Scholar]
- The Python Standard Library—Python 3.7.10 Documentation. Available online: https://docs.python.org/3.7/library/index.html (accessed on 29 March 2021).
- User Guide—Pandas 1.0.1 Documentation. Available online: https://pandas.pydata.org/pandas-docs/version/1.0.1/user_guide/index.html (accessed on 29 March 2021).
- Barto, A.G. Reinforcement Learning and Dynamic Programming. IFAC Proc. Vol. 1995, 28, 407–412. [Google Scholar] [CrossRef]
- Mondal, A.K. A Survey of Reinforcement Learning Techniques: Strategies, Recent Development, and Future Directions. arXiv 2020, arXiv:2001.06921. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).