Anticipatory Online Compensation of Tool Deflection Using a Priori Information from Process Planning
Abstract
:1. Introduction
1.1. Recontouring by Automated Machining
1.2. Adaptive Machining Approaches for High Geometrical Accuracy
1.3. Objective and Approach
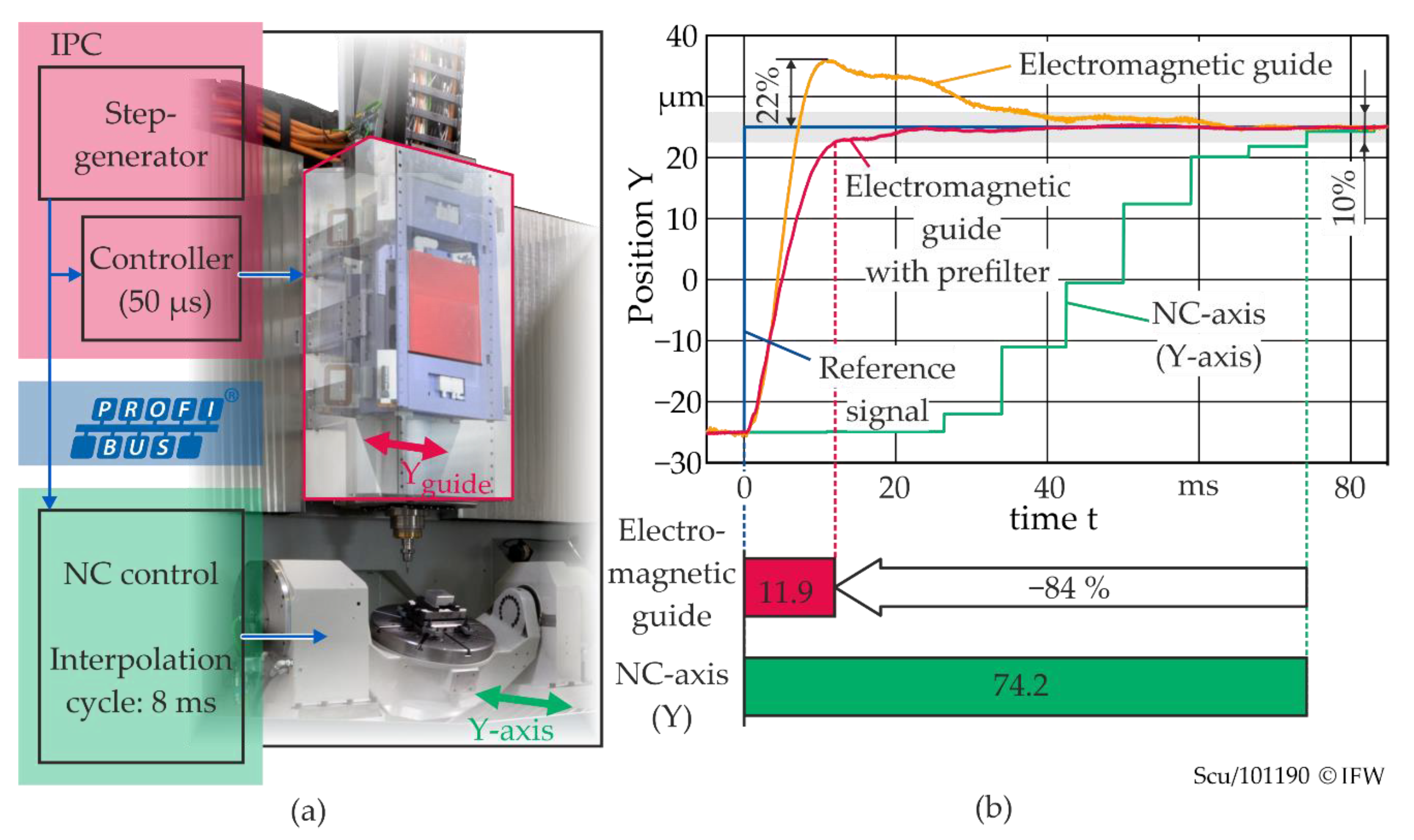
2. Machine Tool Prototype Neximo
2.1. Properties
2.2. Dynamic Positioning Response
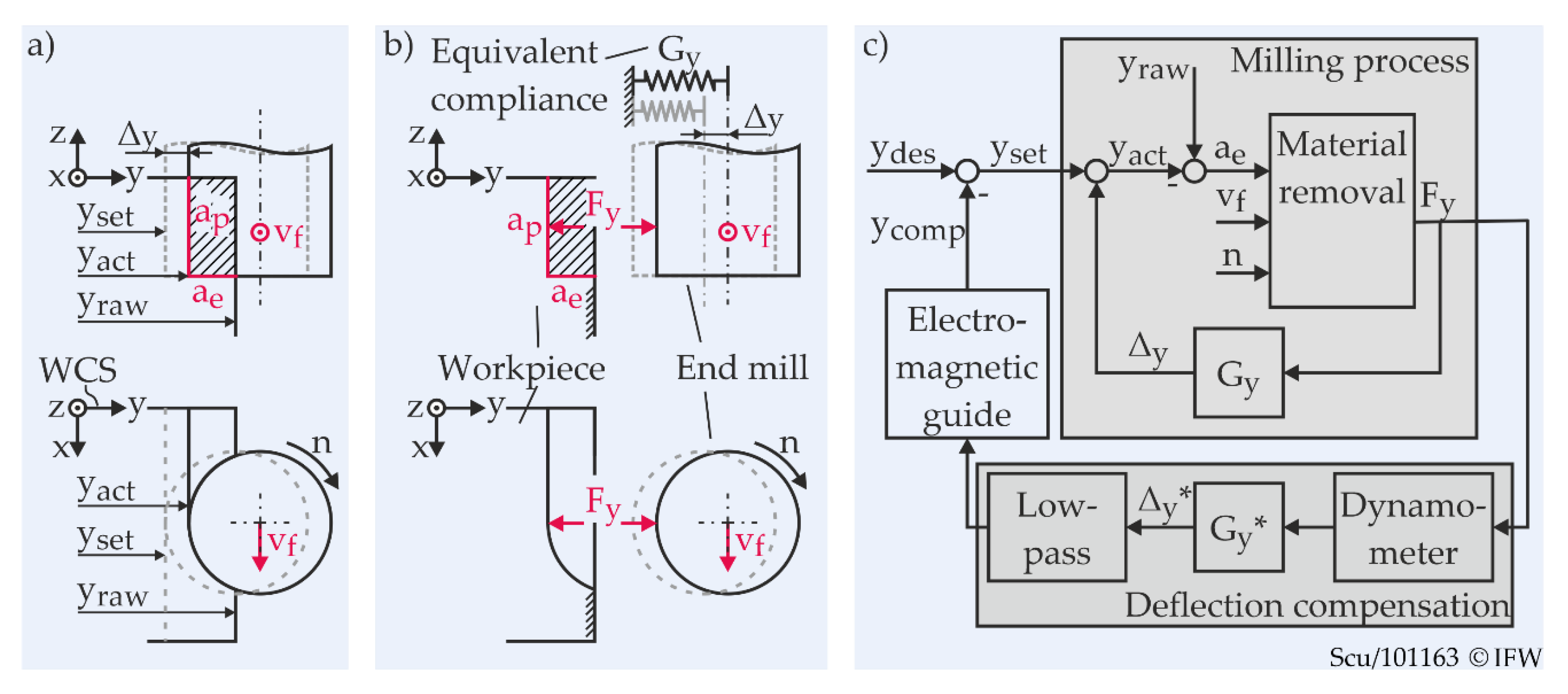
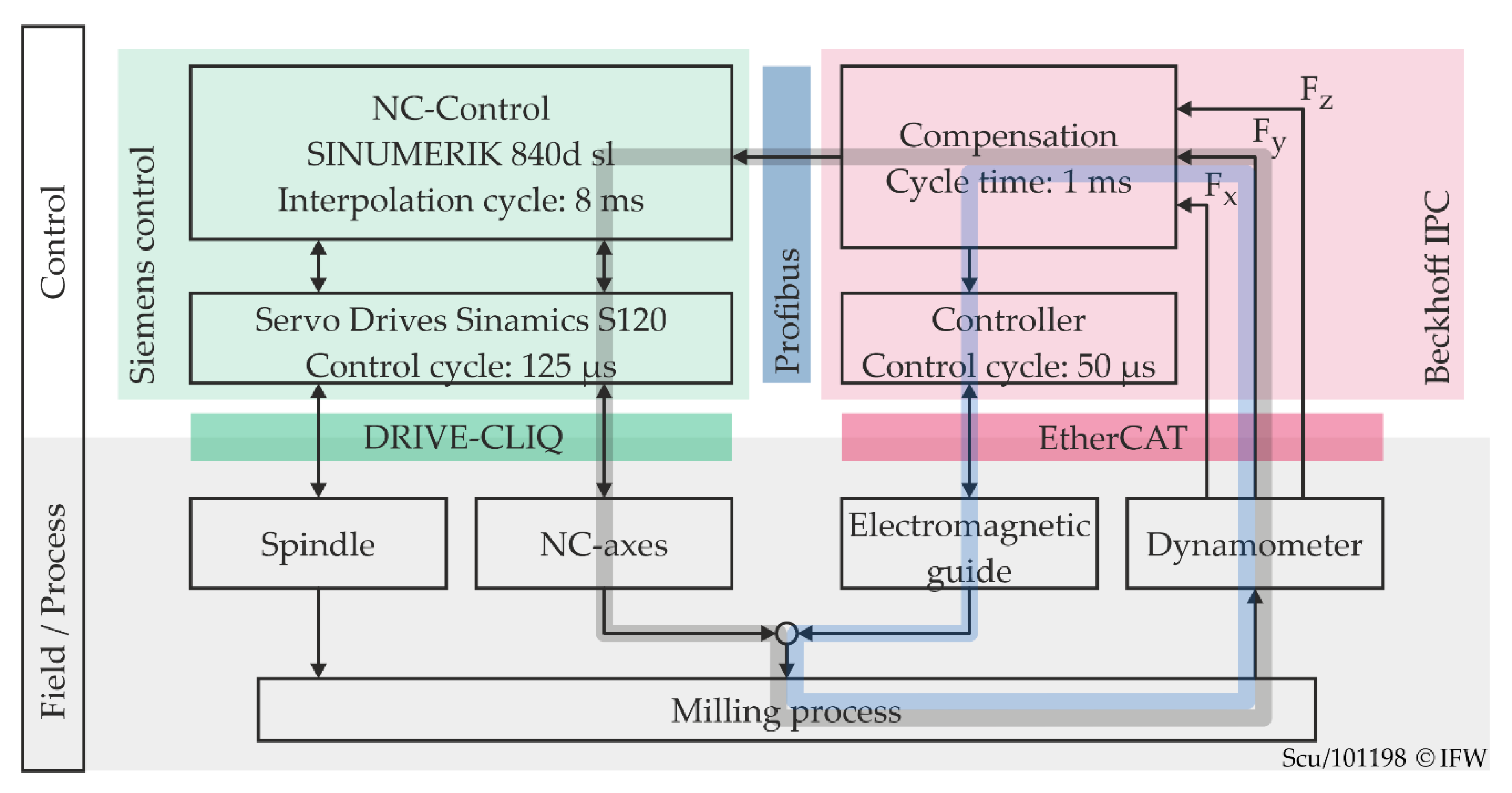
3. Deflection Compensation
3.1. Reactive Deflection Compensation
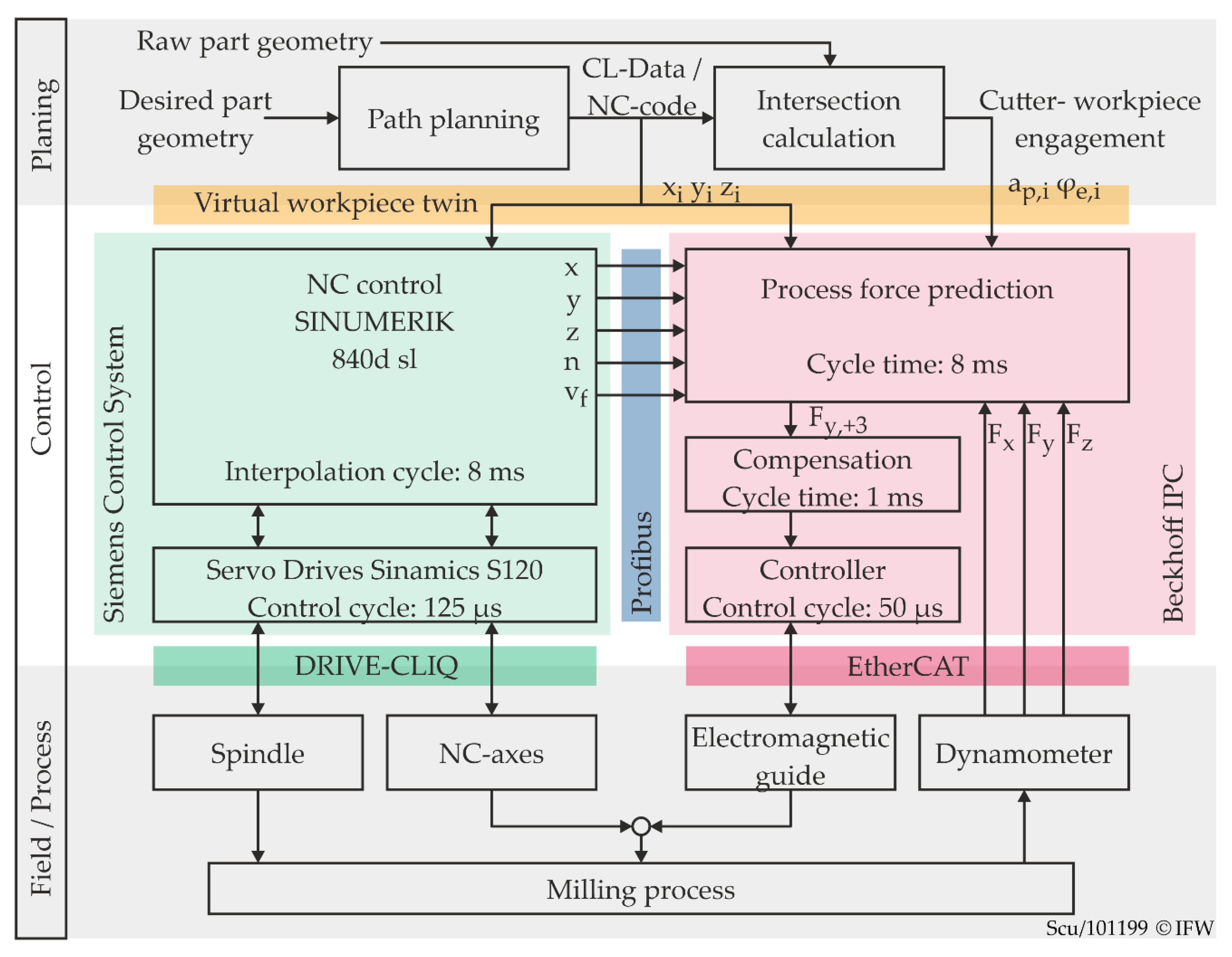
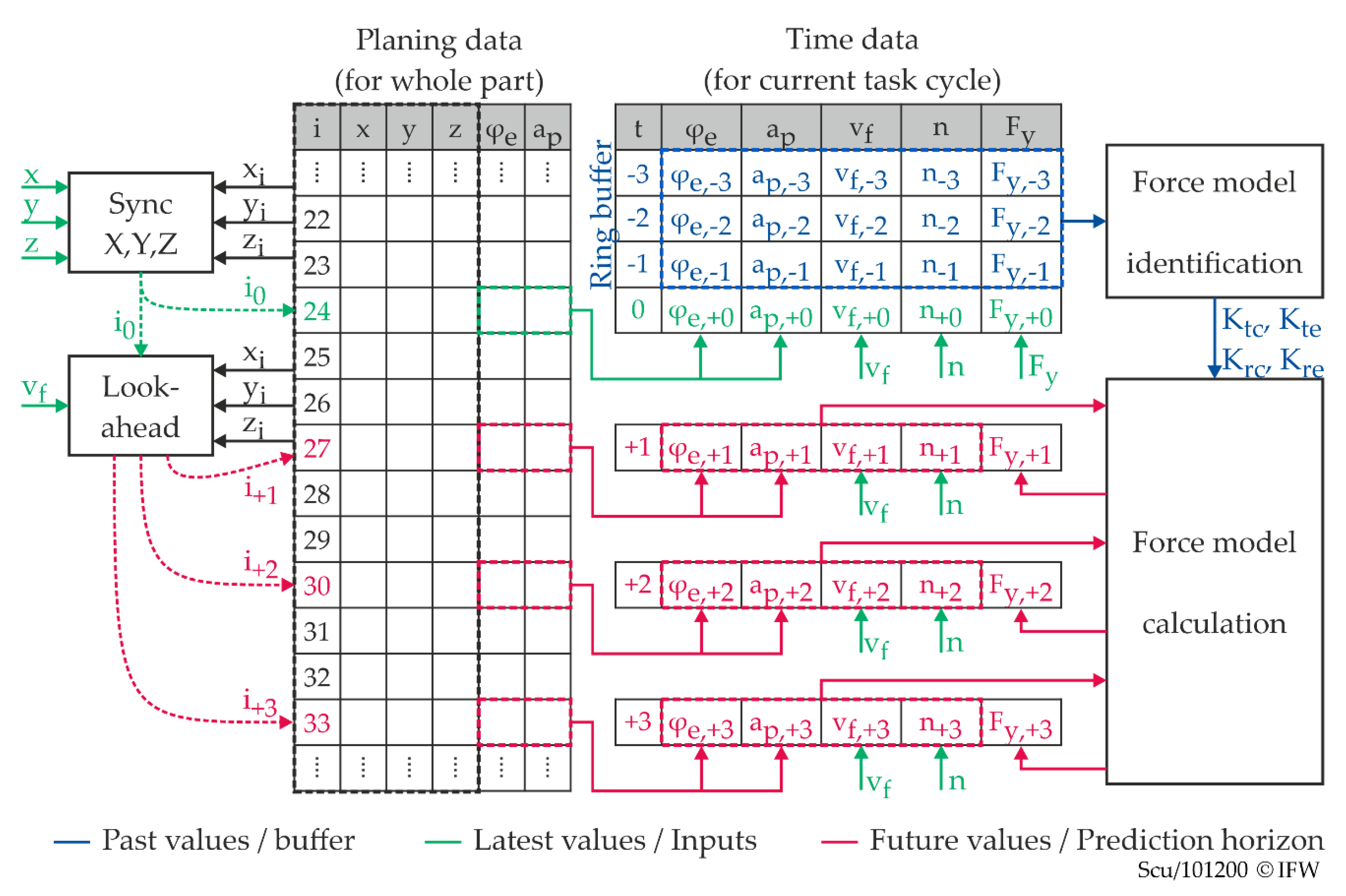
3.2. Anticipatory Deflection Compensation
- The infrastructure of the CRC 871 provides geometry data of each blade after welding, which are then used offline for an individual path planning and NC code generation process. This also includes tool-workpiece-intersection calculations. The virtual workpiece twin then contains all these data.
- Before machining, the process force prediction initially loads the planned tool path in the form of WCS-coordinates (xi, yi, zi) together with the calculated engagement conditions (depth of cut ap, entry angle φe of the cutting edge) from the virtual workpiece twin.
- At runtime, the process force prediction receives the latest cutter positions and process parameters from the NC control. The planned tool path data are synchronised with these values and extrapolated into the future within the prediction horizon.
- The corresponding future engagement conditions are then used to calculate process forces based on a suitable process force model. The output value may, for example, be a force value Fy, +3, which corresponds to the force prediction for a point in time that lies 3 ms in the future.
- The further application of this force value corresponds exactly to the reactive compensation, as described in the previous section.
4. Experimental Setup
5. Results
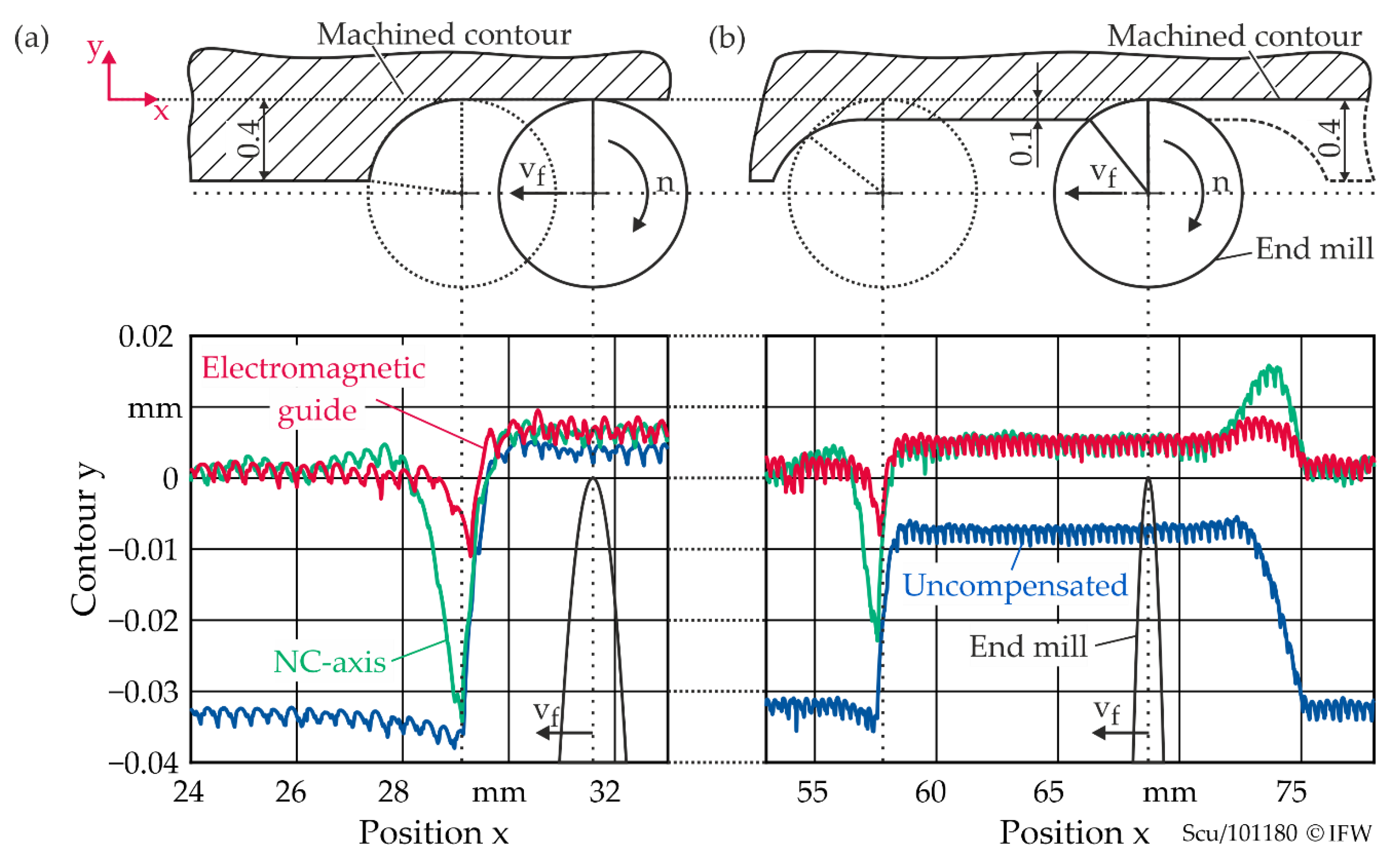
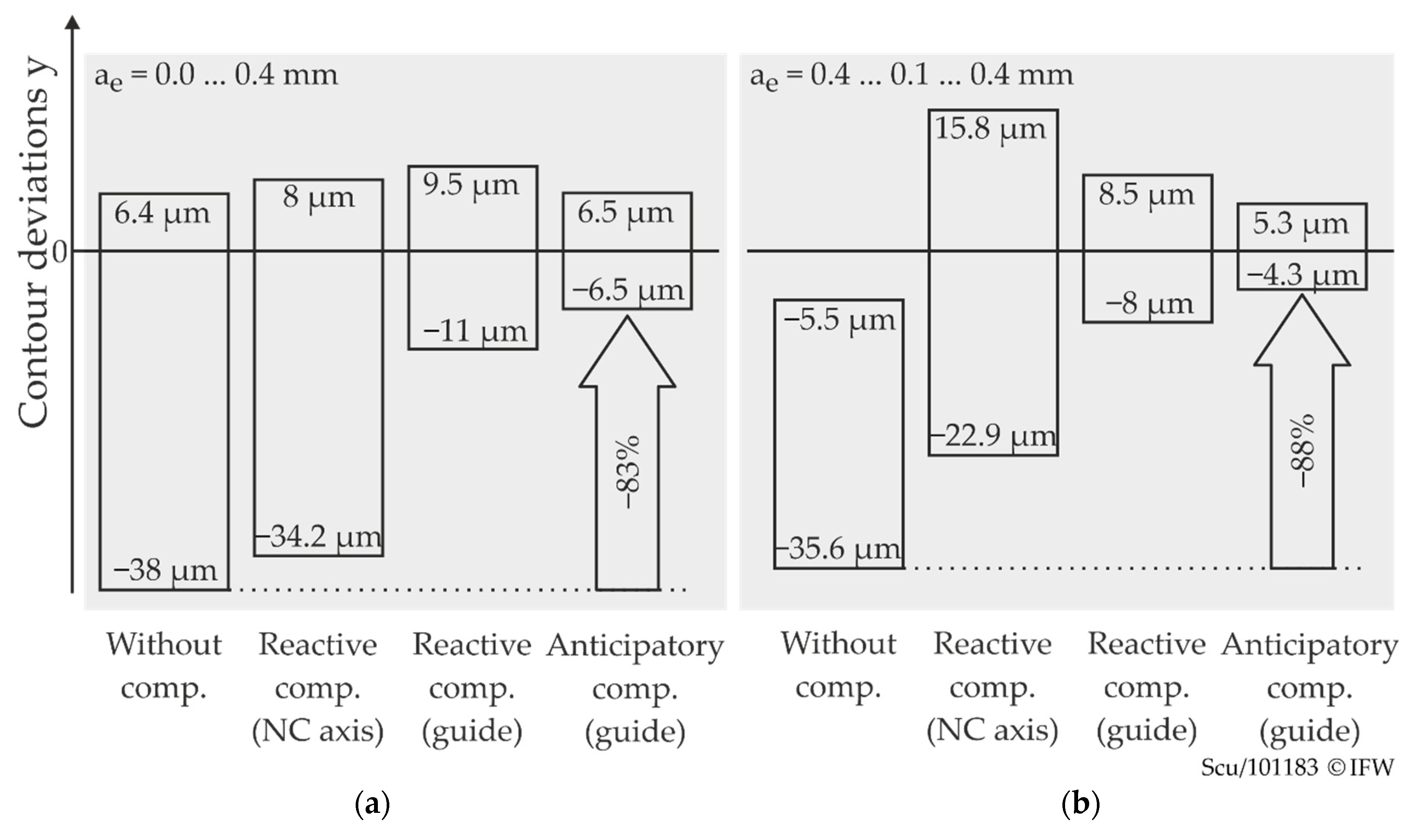
5.1. Reactive Deflection Compensation
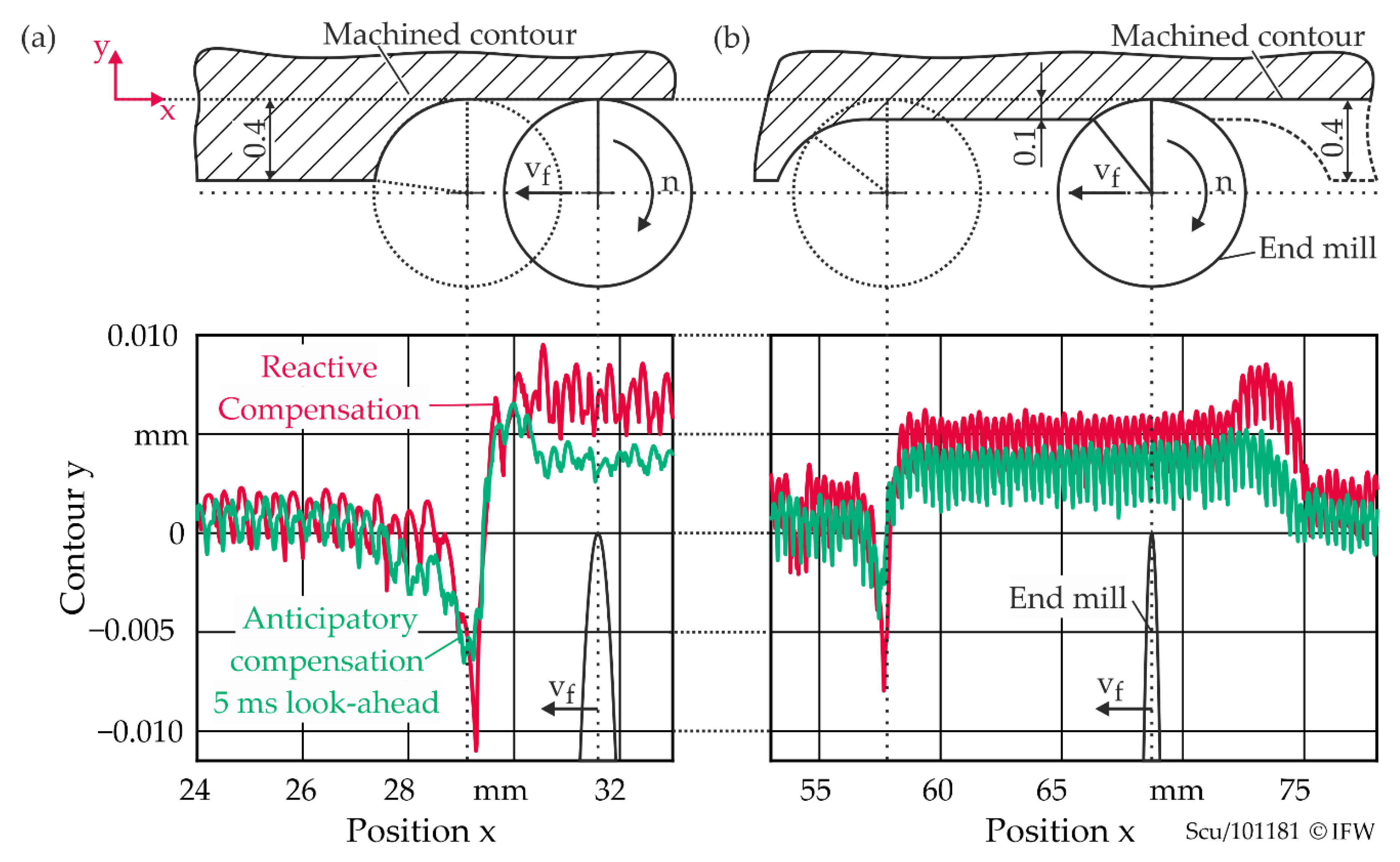
5.2. Anticipatory Deflection Compensation
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MTU Aero Engines AG. Aeroreport. 2017. Available online: https://aeroreport.de/media/pages/mediathek/ausgabe-01-2017-deutsch/ef0245217e-1615283755/01-2017-english.pdf (accessed on 8 April 2021).
- Aschenbruck, J.; Adamczuk, R.; Seume, J.R. Recent progress in turbine blade and compressor blisk regeneration. Procedia CIRP 2014, 22, 256–262. [Google Scholar] [CrossRef] [Green Version]
- Denkena, B.; Boess, V.; Nespor, D.; Floeter, F.; Rust, F. Engine blade regeneration: A literature review on common technologies in terms of machining. Int. J. Adv. Manuf. Technol. 2015, 81, 917–924. [Google Scholar] [CrossRef]
- Carter, T.J. Common failures in gas turbine blades. Eng. Fail. Anal. 2005, 12, 237–247. [Google Scholar] [CrossRef]
- Denkena, B.; Nyhuis, P.; Bergmann, B.; Nübel, N.; Lucht, T. Towards an autonomous maintenance, repair and overhaul process. Procedia Manuf. 2019, 40, 77–82. [Google Scholar] [CrossRef]
- Bremer, C. Data management and adaptive machining technology for efficient repair and manufacture of turbine components. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea and Air, Berlin, Germany, 9–13 June 2008; pp. 415–422. [Google Scholar]
- Jones, J.; McNutt, P.; Tosi, R.; Clinton, P.; Wimpenny, D. Remanufacture of turbine blades by laser cladding, machining and in-process scanning in a single machine. In Proceedings of the 23rd Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 6–8 August 2012; pp. 821–827. [Google Scholar]
- Tao, W.; Huapeng, D.; Jie, T.; Hao, W. Recent repair technology for aero-engine blades. Recent Pat. Eng. 2015, 9, 132–141. [Google Scholar] [CrossRef]
- Yilmaz, O.; Gindy, N.; Gao, J. A repair and overhaul methodology for aeroengine components. Robot. Comput. Integr. Manuf. 2010, 26, 190–201. [Google Scholar] [CrossRef]
- Su, C.; Jiang, X.; Huo, G.; Zou, Q.; Zheng, Z.; Feng, H.-Y. Accurate model construction of deformed aero-engine blades for remanufacturing. Int. J. Adv. Manuf. Technol. 2020, 106, 3239–3251. [Google Scholar] [CrossRef]
- Dittrich, M.-A.; Denkena, B.; Boujnah, H.; Uhlich, F. Autonomous machining—Recent advances in process planning and control. J. Mach. Eng. 2019, 19, 28–37. [Google Scholar] [CrossRef]
- Denkena, B.; Boujnah, H. Feeling machines for online detection and compensation of tool deflection in milling. CIRP Ann. 2018, 67, 423–426. [Google Scholar] [CrossRef]
- Altintas, Y.; Tuysuz, O.; Habibi, M.; Li, Z.L. Virtual compensation of deflection errors in ball end milling of flexible blades. CIRP Ann. 2018, 67, 365–368. [Google Scholar] [CrossRef]
- Boujnah, H. Kraftsensitiver Spindelschlitten zur Online Detektion und Kompensation der Werkzeugabdrängung in der Fräsbearbeitung. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2019. [Google Scholar]
- Brecher, C.; Wetzel, A.; Berners, T.; Epple, A. Increasing productivity of cutting processes by real-time compensation of tool deflection due to process forces. J. Mach. Eng. 2019, 19, 16–27. [Google Scholar] [CrossRef]
- Flöter, B.F. Potentiale einer Elektromagnetischen Führung in Fräsmaschinen und ihr Nutzen für die Reparaturbearbeitung. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2017. [Google Scholar]
- Hähn, F.; Weigold, M. Hybrid compliance compensation for path accuracy enhancement in robot machining. Prod. Eng. Res. Devel. 2020, 14, 425–433. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation; Cambridge University Press: Cambridge, UK, 2011; ISBN 9780511843723. [Google Scholar]
- Stemmler, S.; Abel, D.; Adams, O.; Klocke, F. Model predictive feed rate control for a milling machine. IFAC-PapersOnLine 2016, 49, 11–16. [Google Scholar] [CrossRef]
- Butz, M.V.; Sigaud, O.; Gérard, P. Anticipatory Behavior in Adaptive Learning Systems: Foundations, Theories, and Systems; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 3540404295. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denkena, B.; Bergmann, B.; Schumacher, T. Anticipatory Online Compensation of Tool Deflection Using a Priori Information from Process Planning. J. Manuf. Mater. Process. 2021, 5, 90. https://doi.org/10.3390/jmmp5030090
Denkena B, Bergmann B, Schumacher T. Anticipatory Online Compensation of Tool Deflection Using a Priori Information from Process Planning. Journal of Manufacturing and Materials Processing. 2021; 5(3):90. https://doi.org/10.3390/jmmp5030090
Chicago/Turabian StyleDenkena, Berend, Benjamin Bergmann, and Tim Schumacher. 2021. "Anticipatory Online Compensation of Tool Deflection Using a Priori Information from Process Planning" Journal of Manufacturing and Materials Processing 5, no. 3: 90. https://doi.org/10.3390/jmmp5030090
APA StyleDenkena, B., Bergmann, B., & Schumacher, T. (2021). Anticipatory Online Compensation of Tool Deflection Using a Priori Information from Process Planning. Journal of Manufacturing and Materials Processing, 5(3), 90. https://doi.org/10.3390/jmmp5030090




