1. Introduction
The continuous improvement of tools and machining processes in terms of product quality is essential in order to maintain competitiveness in the future and to save limited resources. Grinding is an energy-intensive hard machining process which is typically at the end of the manufacturing chain and which is used to produce the final workpiece quality [
1,
2,
3]. In hard machining of chuck components, such as bearing rings, the manufacturers aim is a high productivity and efficiency on the one hand, while on the other hand a good surface quality as well as a high product quality in terms of shape and dimensional accuracy are required [
1,
3]. The realisation of these demands, which partly contradict each other, is difficult to achieve with grinding processes widely used in industrial applications, such as internal plunge grinding (IPG) with vitrified-bonded grinding tools [
3,
4]. Internal plunge grinding is a machining process in which the full width of the grinding wheel is usually in contact with the workpiece bore length. The material removal takes place through a continuous radial infeed. Workpiece bores can be machined productively in this way, and a high surface quality can be produced due to a high coverage ratio between grinding wheel and workpiece [
4,
5,
6]. However, this grinding process is limited in terms of maximal material removal rate. Due to the large contact surface between grinding tool and workpiece, high normal forces arise even at low radial feed rates, so that rigid spindle systems are necessary [
6,
7,
8]. However, high-speed grinding spindles, which are required for internal cylindrical machining, exhibit low stiffness. In combination with slim tool holders, usually used in internal grinding operations so that the grinding tools can enter the bore, elastic deformations of tool and workpiece spindle are caused [
4]. Both spindle systems, the tool-side spindle as well as the workpiece-side spindle, shift relative to each other during the grinding process, and dimensional as well as shape deviations of the workpiece are the result [
6,
8,
9].
Various studies [
9,
10,
11] showed that internal traverse grinding has a high potential to achieve high material removal rates in combination with good surface quality in bore machining. Traverse grinding also offers high potential for external cylindrical and surface grinding operations [
12,
13]. High performance internal traverse grinding with electroplated cBN grinding tools is an established manufacturing process for the efficient internal machining of chuck components, such as gears or bearing rings. This manufacturing process uses bifunctional grinding tools with a tapered roughing zone and a cylindrical finishing zone. This allows a combined machining in a single axial stroke. While high material removal rates can be realised in the roughing zone, the finishing zone is used to smoothen the surface [
6,
10]. This manufacturing process combines the material removal rate of hard turning with the advantages of grinding, such as a high surface quality with low shape deviations. Using high speed conditions, these advantages can be further enhanced. The fundamental kinematics of ITG are shown in
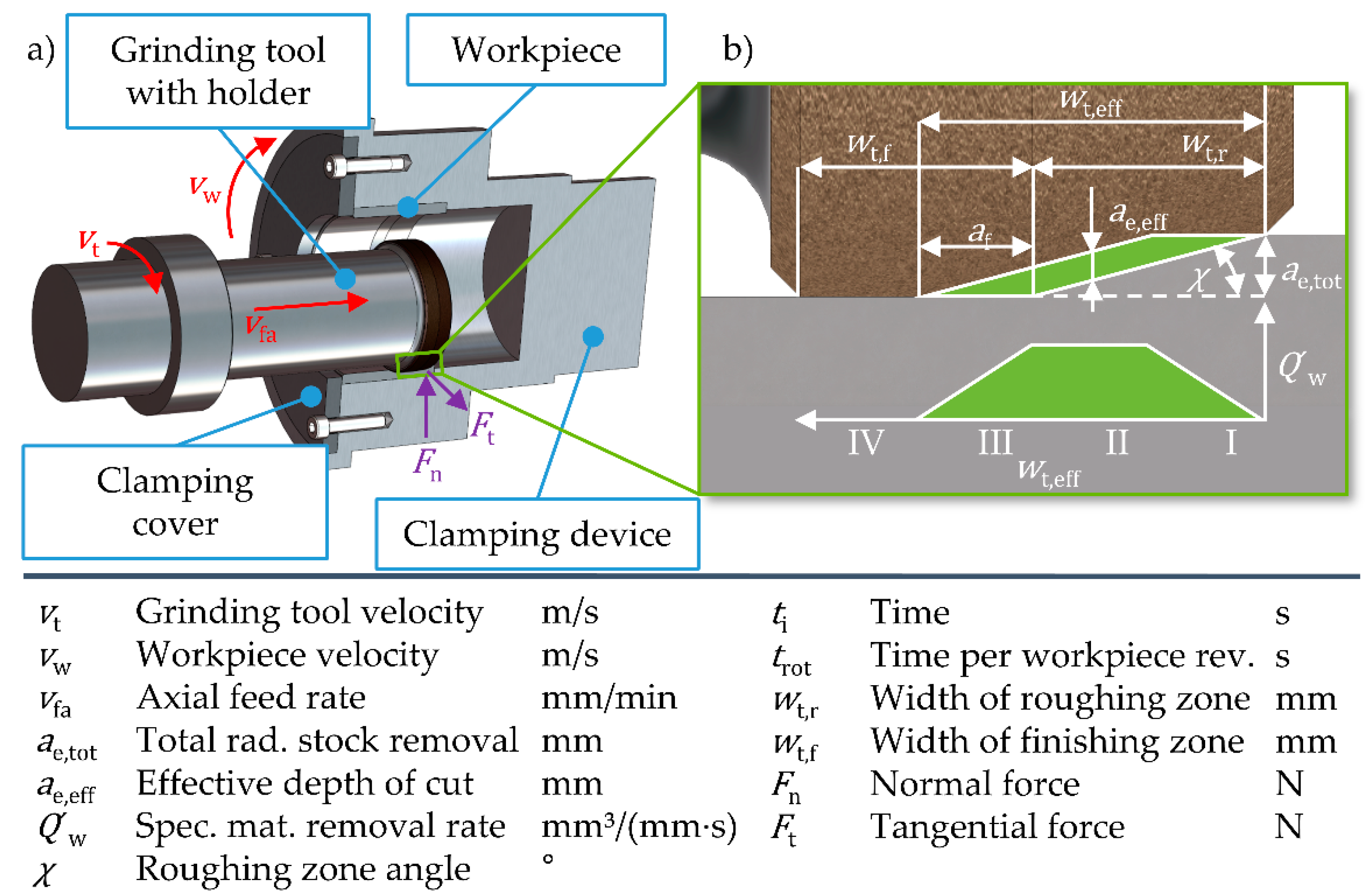
Figure 1.
Tool and workpiece rotate in the same direction with the circumferential velocities
and
. The total radial stock removal
is set prior to contact between tool and workpiece. In a single axial stroke, the grinding wheel moves parallel to the bore length with an axial feed rate
. Material removal mainly takes place in the conical roughing zone, while in the cylindrical finishing zone the surface is smoothened with minor material removal. In ITG, the material removal is distributed over four zones along the grinding wheel and its rate is only constant in zone 2, see
Figure 1b). In the first section (I) of the grinding wheel, the material removal rate increases. This is followed by a section (II) in which a continuous material removal occurs with an effective depth of cut
. In the transition area between roughing and finishing zone, in zone III, the material removal rate decreases until there is no significant material removal in the finishing zone [
10,
14]. During internal traverse grinding, there are significant differences in the acting normal force
at tool entry and exit. After the tool enters the workpiece, a normal force
is built up.
The normal force causes the workpiece and grinding wheel to be pressed apart due to the compliance of the workpiece spindle and tool spindle. As a result, the set radial stock removal is not fully achieved in the grinding process. An exception is the area of tool entry and exit along the bore length. This effect is much less pronounced at the tool entry, as the roughing zone of the tool is fully in contact after only a few revolutions of the workpiece. The dimensional deviation is much more evident in the exit area [
6]. At the exit of the roughing zone of the grinding wheel, the normal forces are strongly reduced when the roughing zone exits the workpiece, so that the spindle systems bounce back. Because the cylindrical finishing zone is still fully in contact, an increased material removal is generated in this zone, which leads to dimensional and form errors. Furthermore, the tool deflection varies along the bore length due to changing lever arms on the workpiece and tool parts during grinding, which causes additional shape deviations. The described shape errors due to the compliant spindle systems represent one of three major influencing factors that challenge the process control of internal traverse grinding. Other significant factors influencing the shape and dimensional deviations are the elastic deformation of the workpiece due to clamping and the high locally applied heat in grinding [
9].
Fundamental investigations were carried out regarding the influence of clamping and local thermal deformations on the resulting contour, and compensation strategies were developed [
6,
9,
15]. A multi-scale simulation system for the simulation of ITG processes was proposed in [
16], including the effects of workpiece clamping and thermal load during grinding based on earlier studies [
17,
18,
19]. Based on the simulations, compensation strategies were developed to reduce shape deviations. A similar simulation approach, incorporating the spindle compliances in a meta model of the process, was proposed in [
6], highlighting the relevance of the compliances for the accurate prediction of process results. Both [
6,
16] modelled the process forces on the level of individual grains, identifying the rake angle and the undeformed chip thickness as the most relevant parameters. While the force model was calibrated using experimental data in [
6], single grain finite element simulations were used in [
16].
Various extensions of the finite element method have been shown to yield good results for cutting processes. The arbitrary Lagrangian Eulerian (ALE) method was applied e.g., in [
20], while the coupled Eulerian–Lagrangian FEM (CEL) was applied to cutting simulations in [
21,
22,
23,
24]. Meshless methods for the simulation of cutting processes include smooth particle hydrodynamics (SPH) and the particle finite element method (PFEM), which were compared to classical Lagrangian FEM and ALE in [
25]. SPH was used to model an internal grinding process, similar to ITG, for the medical application of atherectomy in [
26].
The Johnson–Cook material model [
27] is widely used for metal cutting simulations, see e.g., [
23,
28,
29], but more complex material models were proposed to include additional effects such as phase transformations, see e.g., [
30]. Various analytical models for the prediction of process forces during grinding were proposed e.g., in [
31,
32,
33,
34]. A simplified model for the effective compliance of the grinding machine system, accompanied by a static analogy test for the experimental calibration, has recently been proposed in [
35].
Geometric physically-based simulations (GPS) are a proven concept for the simulation of machining processes such as e.g., milling and grinding [
36,
37]. The concept is characterised by short computation times for the simulation of whole machining processes, high precision in geometric approximation of the engagement situation plus the resulting workpiece and derivation of physical properties such as e.g., process forces from geometry using analytical or empirical surrogate models. Especially macroscopic grinding simulations are well established, for example to predict process forces [
38] and deflections [
39,
40]. Mesoscopic simulations, which model the interaction between the workpiece and the complete grinding wheel down to the engagement of every single grain, were also presented for grinding processes [
37,
41,
42] including internal traverse grinding [
6], but are in practice limited to the simulation of a few grinding wheel rotations because of the much higher computational effort that is required. An enhanced method developed by Siebrecht for face grinding [
43,
44] is computationally more efficient than older approaches and well suited to incorporate the changes in grain shapes due to wear. Nonetheless, both concepts presented in [
6,
44] require an additional macro-scale simulation tool to simulate a complete grinding process.
In this work, a simulation system that incorporates an FE-based force model and an empirical compliance model into a mesoscale GPS is proposed. The resulting ability to predict process forces and system deflections in a fully coupled manner, enables the prediction of compliance-based shape deviations without incorporating simulations at the macro scale. An efficient calculation of the undeformed chip geometry, based on [
44] and extended in this work, allows the simulation of the complete grinding process at the mesoscale. Furthermore, the simulation system is designed to be extensible for the inclusion of tool wear in the future. Simulation results are compared to experimental tests, performed on two different grinding machines, to validate the simulation system and to investigate the performance and transferability of the compliance and force models.
3. Results
In the following section, the calibration of the models for compliance and single grain forces is presented, and details of the implementation of the models into the GPS are discussed. Force curves and resulting workpiece shapes are then compared to the experimental findings.
3.1. Compliance Model Calibration
A total of 72 compliance tests were performed as described in
Section 2.1.
Figure 6a shows the distance
measured by the reference sensor at the headstock over the normal force
for an exemplary measurement.
The headstock moves approximately 10 μm away from the sensor at zero force (grey dots), until contact with the workpiece holder is established. Any additional movement of the headstock results in a deflection of the system and in a corresponding increase of the normal force (blue dots). Although the loading and unloading paths can be visually distinguished, a reasonable approximation of the effective system compliance
was obtained from a linear regression of the force-distance-data, neglecting data points where the measured force does not exceed a threshold of
. An extensive description of this approach can be found in [
35]. The linear fit exceeds a value of
for all but four measurements, which were excluded from the further evaluation.
Figure 6b shows the resulting values of compliance
for the three relative tool positions. Box boundaries represent the first and third quartile, while the whiskers extend to the datum furthest from the boxes, but not exceeding 1.5 times the interquartile range. No outliers beyond this range occur in the data. Whereas the first and third quartiles decrease for higher values of
, no clear trend is observed for the median. Mean values are presented in
Table 2 and decrease with increasing
.
For model (1), compliance
was determined from the average of all individual compliances
, while for model (2), the coefficients
and
of the function
were determined by a least-squares fit. All results are presented in
Table 3 and visualised in
Figure 6b.
While the results indicate a dependency of the effective system compliance on the relative tool position, the influence is comparatively small. Applying the simple model (1), which does not take the relative tool position into account, results in a maximum error of 4.9% at compared to model (2). Since other relevant factors, e.g., heat effects, are not yet included in the simulations and will likely induce an error of equal or higher magnitude, model (1) was applied for the simulations presented in this work.
3.2. Prediction of Single Grain Cutting Forces
Some representative force-displacement curves obtained from multiple single grain cutting simulations as described in
Section 2.5 are shown in
Figure 7. To compare the forces for varying undeformed chip thicknesses
, specific values per theoretical material removal rate
of the single grain were calculated, i.e.,
where the material removal rate is calculated based on unit width
, the undeformed chip thickness and on the relative cutting speed
for the single grain engagement as
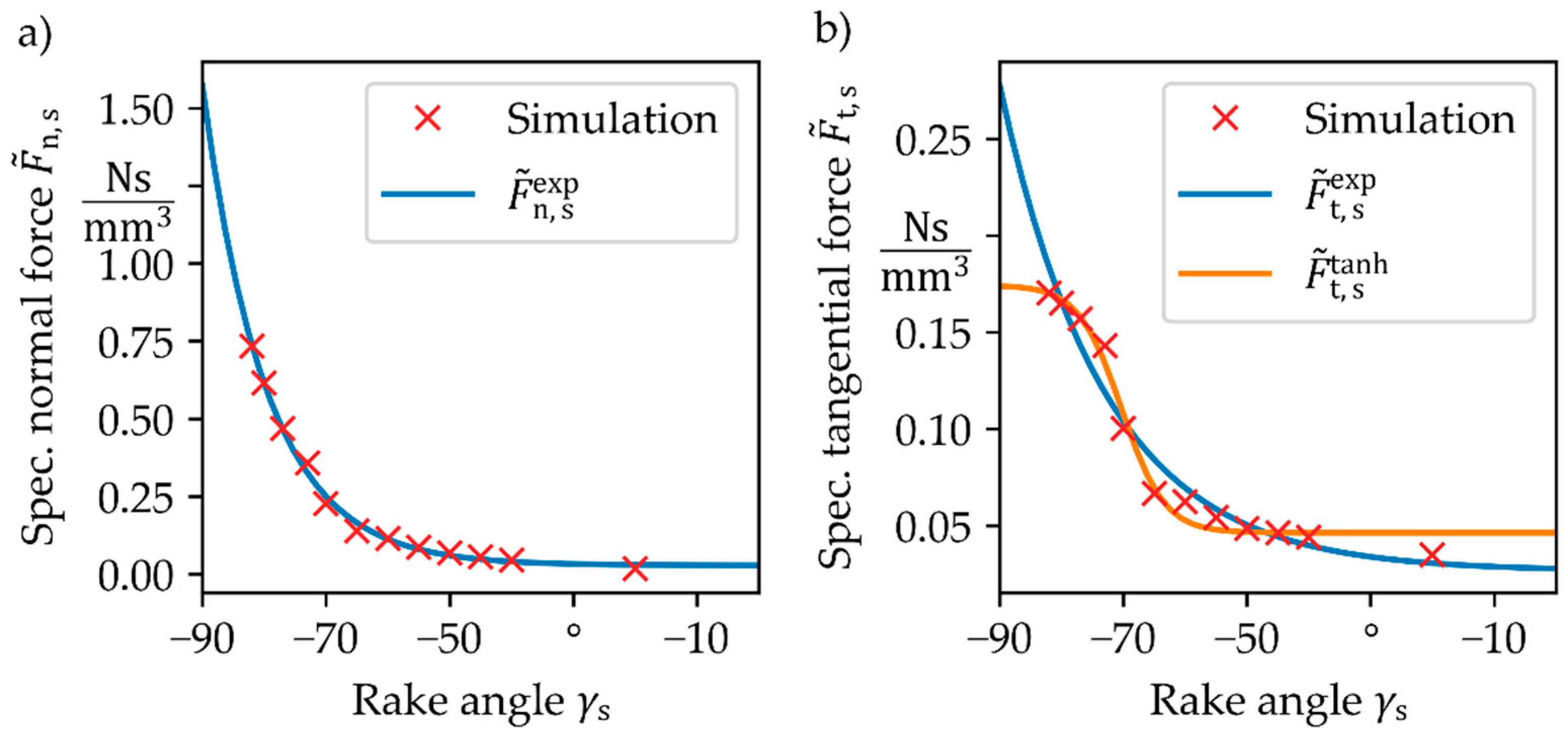
A pronounced dependency of the specific forces on the rake angle
can be observed: Large negative rake angles produce higher values for both normal and tangential forces. However, no significant influence of the undeformed chip thickness on the specific forces was found. Although only some exemplary curves are shown in
Figure 7, these trends held true for all simulations conducted.
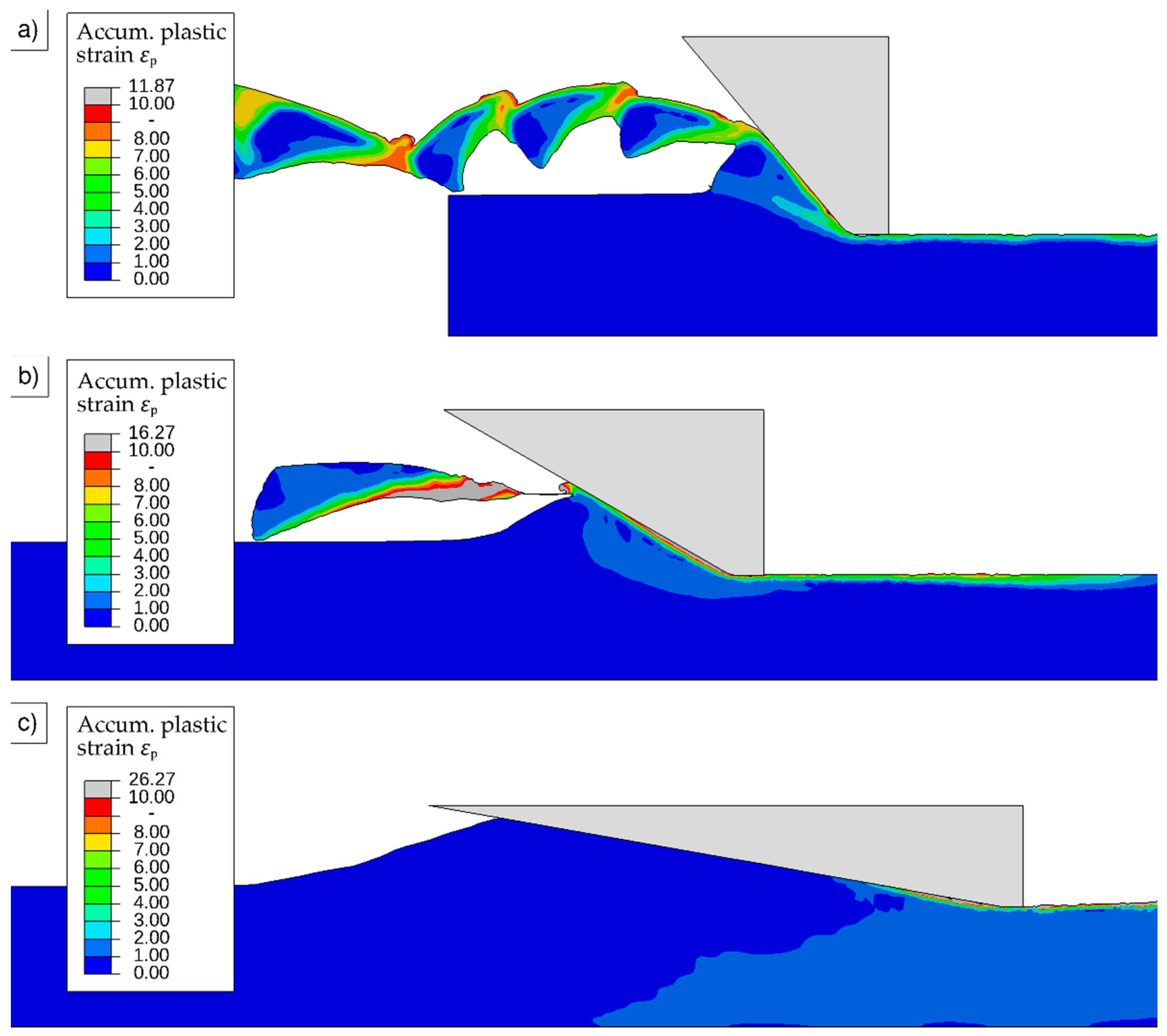
The force curves for rake angles closer to 0° show oscillations around an approximately constant value. Larger negative values of
lead to a reduced number of oscillations, and values below a certain threshold do not show any oscillations at all. This observation is linked to the emergence of shear bands in the workpiece material and resulting chip formation.
Figure 8 shows exemplary deformed workpiece geometries to demonstrate this effect. The segmented chip obtained for
coincides with the oscillations in the corresponding force curves. Only one distinct chip emerged for
before the simulation terminated because chip separation was not included in the model. For
, no chip formation was observed in the simulations.
Since the undeformed chip thickness
had no significant effect on the specific forces, the force model used in this work is parametrised only in terms of the rake angle
. To this end, a parameter study was conducted for a constant value of
and
. Based on [
6], it is assumed that predominantly large negative rake angles occur in the ITG process, and therefore the parameter study was focused on rake angles
. The restriction to angles
is due to numerical instabilities occurring in the single grain simulations past this value.
Force modelling for the GPS is based on a curve fit of the specific forces obtained from the single grain simulations. For the normal forces, the exponential ansatz function
was used, whereas for the tangential forces the functions
and
were compared. The results of the parameter study, as well as the force models resulting from the curve fits, are shown in
Figure 9, and the coefficients obtained for each ansatz function are presented in
Table 4It should be mentioned that, since the force curves did not saturate for large native rake angles in our simulations, a systematic underestimation of the predicted forces at large negative rake angles is expected. Not all simulations covered the same displacements due to numerical difficulties, e.g., chip separation as shown above. Nonetheless, the normal forces are predicted accurately by the exponential approach with a root-mean-squared error (RMSE) of , while the tangential forces seem to saturate for values of . A possible explanation for this behaviour is the underlying model assumption that only a finite shear stress can occur in the contact zone between grain and workpiece. The saturation of the tangential forces can be modelled through the ansatz based on the hyperbolic tangent function at the cost of a reduced accuracy especially for values of . Since the RMSE of for Equation (12) is lower than the RMSE of for Equations (11) and (12) is implemented in the GPS.
3.3. Geometric Physically-Based Grinding Simulation
A geometric physically-based simulation (GPS) was developed, based on the system presented by Siebrecht for face grinding [
44] and on a framework developed at the Institute of Machining Technology. The models and algorithms were replaced, modified and enhanced in various ways, described below.
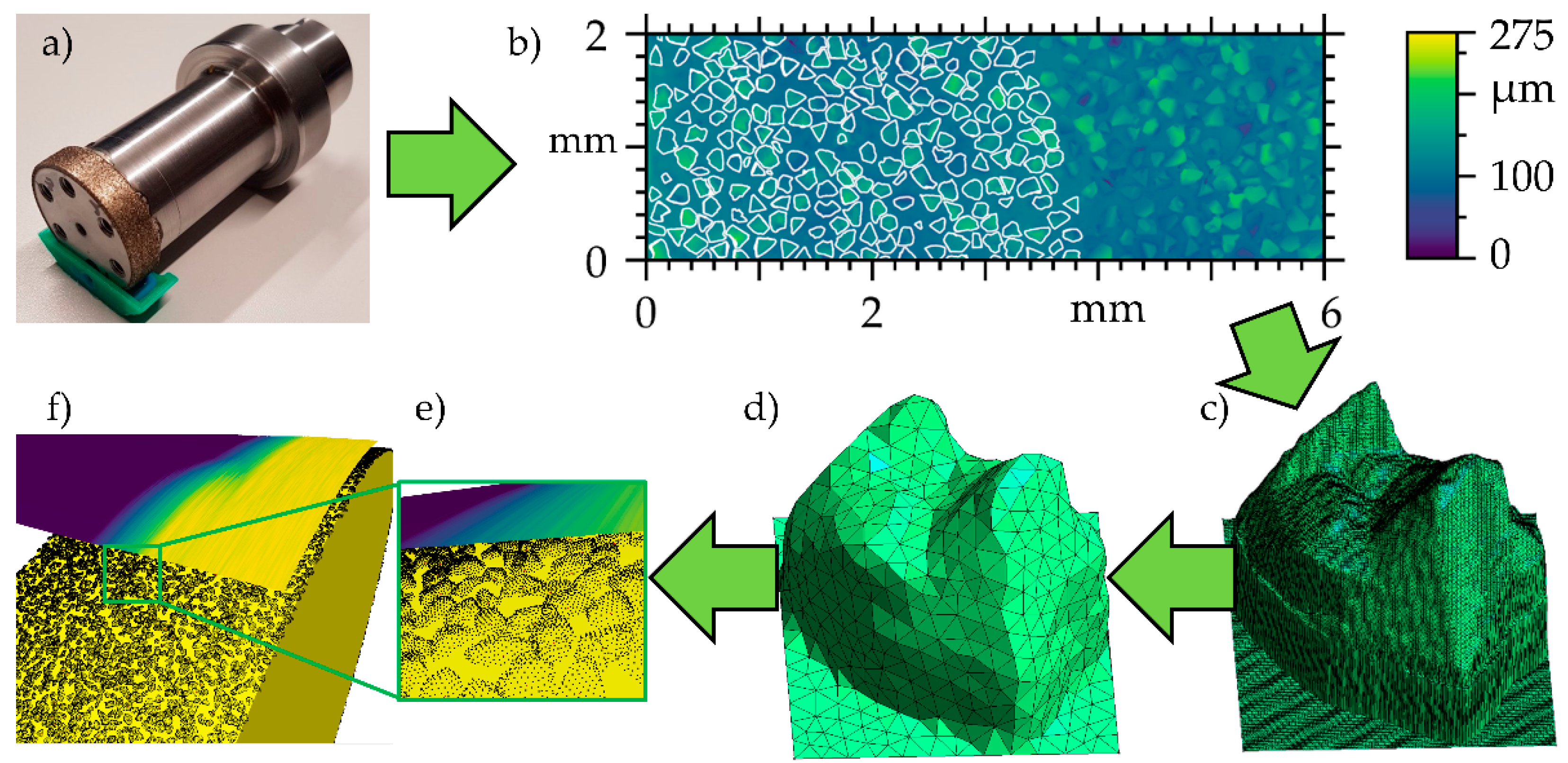
As the database of grain geometries (GDB) was created based on a new grinding wheel, there are some grains with an exceptional height. Especially at low axial feed rates, such outliers account for the main share of material removal and thus are subject to high wear levels. Another effect is that only a few grains get in contact with the workpiece at all, which leads to interrupted cutting, almost like e.g., in flank milling. Therefore, 15 grains have been excluded from the GDB of originally 417 grains. Paired with the GDB with realistic grains geometries, a suitable distribution of grains is important to create a realistic tool model. Following [
44], the grains were placed according to a Poisson disk sampling [
46]. Because the grain count of the tool is much higher than the size of the GDB, a uniformly distributed rotation around the surface normal of the grinding wheel at the grain position was applied to the orientation of each grain, therefore increasing variation between grains. The important parameter for the grain distribution is the grain density
. To approximate the grain density of the real grinding wheel, the sum of all grains in the digitised section, cf.
Figure 4b, where truncated grains were counted as half, was divided by the surface area.
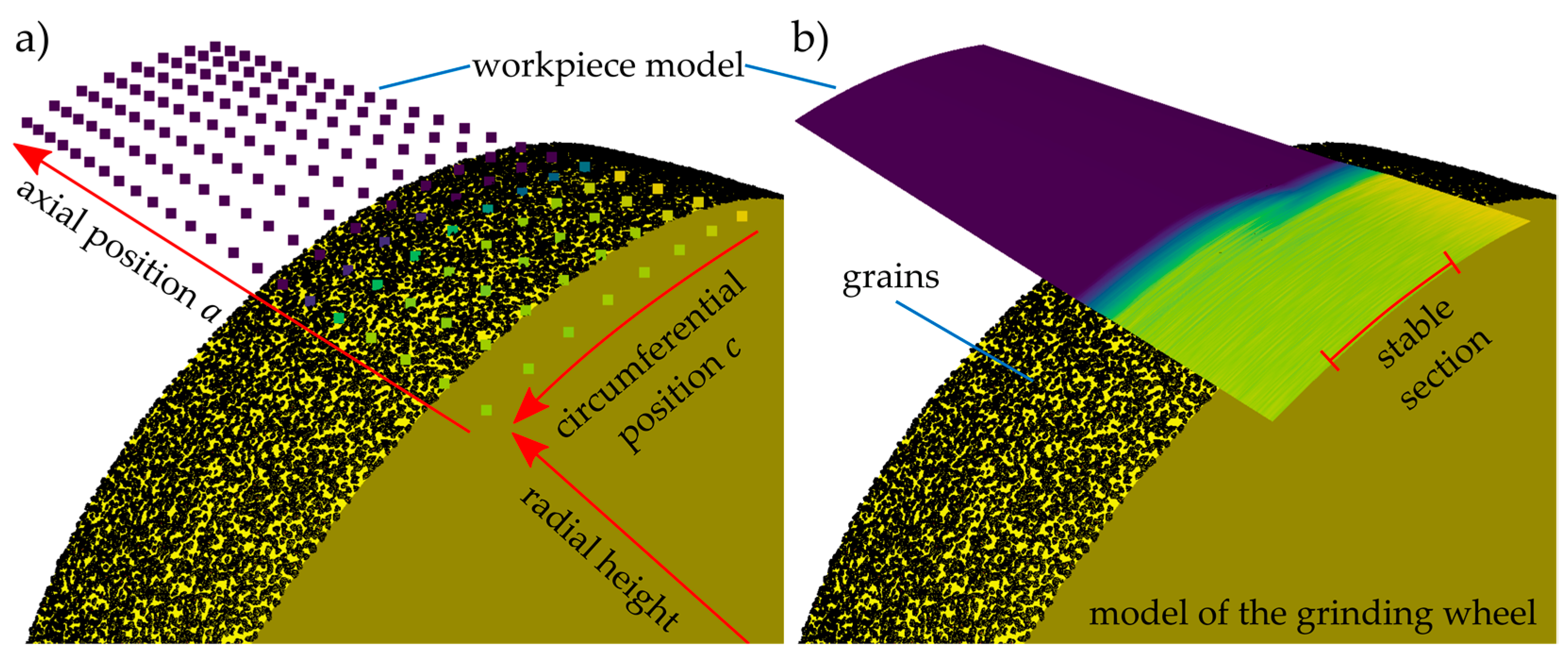
The second important component to be modelled, after describing the tool model above, is the workpiece. Because surfaces machined using ITG are typically roughly cylindrical, the workpiece was modelled as a cylindrical heightfield (cf.
Figure 10a). Traditional flat heightfields consist of a discrete grid describing a rectangle and a continuous height value for each position of the grid, i.e., every surface point is described by a point
ℕ in a plane and a height
. In contrast to a traditional heightfield, the grid of a cylindrical heightfield describes the lateral face of a cylinder, defined by an axial and a circumferential position
ℕ, and the height value describes the radial offset from the grid. The axial and circumferential distance
and
between the grid points, was chosen as 0.0071 mm. To shorten the simulation time, the cylindrical heightfield can be reduced to a circumferential section smaller than the full inner workpiece circumference. Because all process effects that are of interest in this study are rotationally symmetric, circumferential sections of less than 90° are sufficient to predict process forces and system deflections in a stable section. However, a short section to stabilise after each workpiece revolution is necessary, and the section of circumferential tool exit is not representative either; compare
Figure 10b.
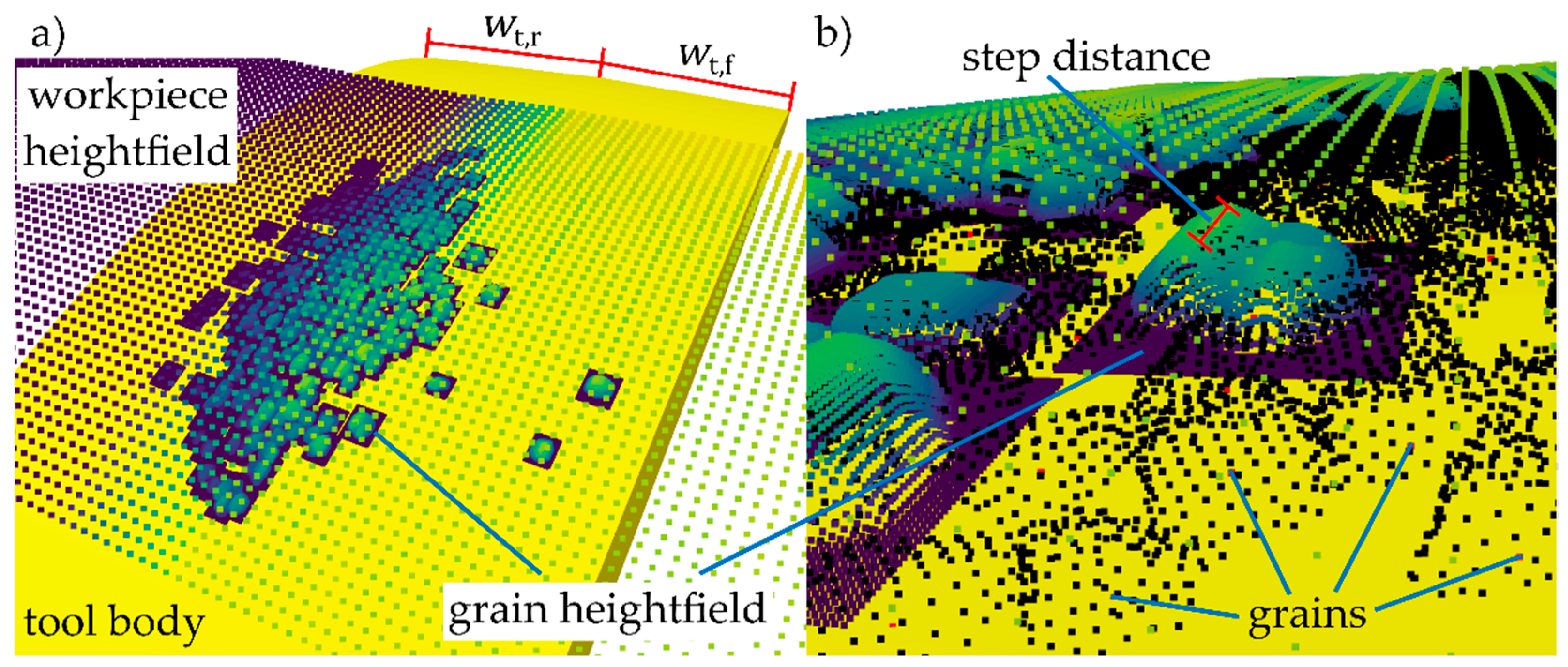
Simulation of the grinding process is performed in a time discrete manner. To reduce the overlap of the sweep volumes, the grains pass in a time step, the step duration
is calculated depending on the distance which each grain travels in a step. The step distance was chosen to be 0.1 mm. The engagement of a grain, i.e., the intersection of the grain and workpiece models is calculated according to the method presented by Siebrecht [
44]. The details can be found therein, but some important steps are described below. To approximate the volume a grain sweeps in a time step, a small local cylindrical heightfield is created for each grain that is located in proximity of the workpiece; see
Figure 11.
The grain heightfield is initialised with the radius of the workpiece before grinding, and all vertices of the grain mesh are intersected with the grain heightfield. The sweeping is achieved by intersecting the grain not only for the end point of a step, but also for multiple equidistant sub steps. In order to avoid missing any cutting volume at the connection between two steps, it is necessary to also add the end point of the last step again. To recreate the grain volume in the grain heightfield, in the next step, the morphological filters dilate with kernel size 3 and erode with kernel size 2 are applied to the heightfield, followed by a Gauss filter with kernel size 7 and . Smoothness of the sweep volume in cutting direction depends on the step length, the heightfield point distance, the parameters of the filtering and on the amount of sub steps. It was found that for the parameters given above, five sub steps are sufficient, so this number was chosen for all simulations.
To calculate material removal, the grain heightfields are subtracted from the workpiece. In detail: if the height of the grain heightfield
at grid position
is greater than the height
of the corresponding point of the workpiece, the difference is subtracted from the workpiece. The material removal rate
of a grain can directly be derived from the material removal and amounts to the sum of all subtracted heights multiplied by the axial and circumferential point distance, divided by the step duration, i.e.,
The undeformed chip thickness of a grain is approximated as the maximum height removed in a step.
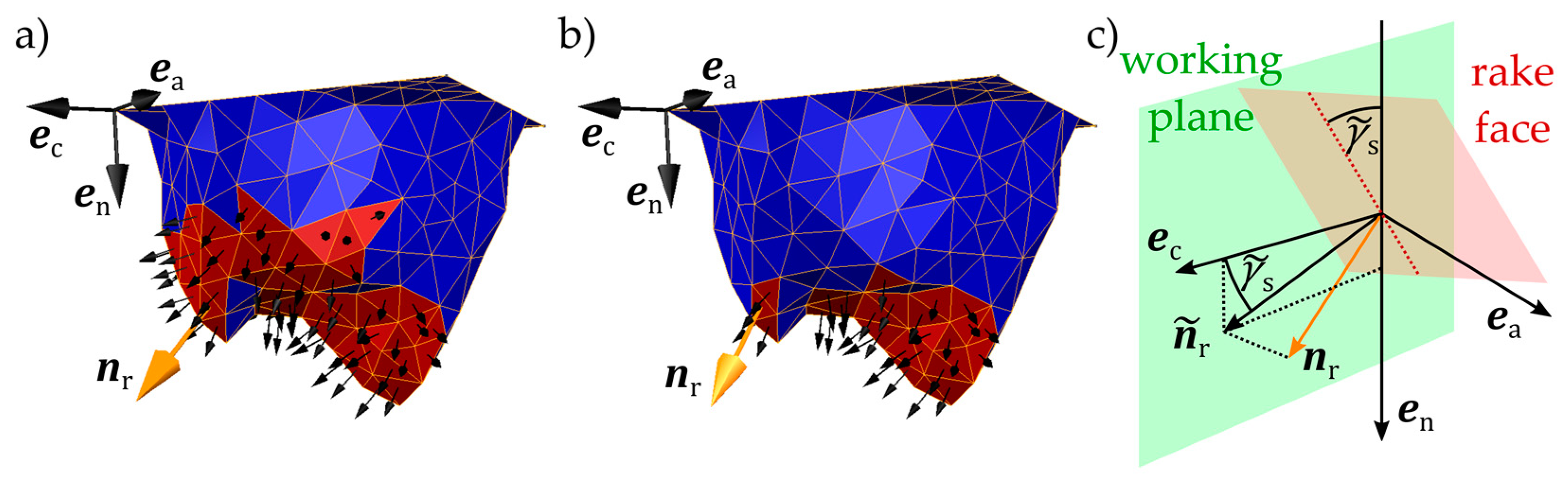
Since the force model for the individual grains is parametrised in terms of the rake angle
(cf.
Section 3.2), a method to approximate the effective rake angle for each grain, depending on the actual engagement, is required. The approximation scheme is visualised in
Figure 12.
The triangles of the grain mesh which are assumed to be engaged for a cutting direction
are depicted in
Figure 12a,b for two different undeformed chip thicknesses
. Triangles are considered only if they face in cutting direction, i.e., the projection of their normal onto the cutting direction
is positive. The effective normal vector
of a (virtual) plane rake face, see
Figure 12 is approximated by averaging the normals of the engaged triangles. The effective rake angle
is then approximated as
based on the projection
of the effective normal vector into the working plane.
To speed up the simulation,
is calculated in steps of 0.011 mm the first time a grain is engaged and interpolated linearly for the exact
of each engagement of the grain occurring during the entire grinding process. The cutting forces can now be calculated according to Equations (16) and (17) as
and the process forces amount to the sum of the single grain forces.
Using the compliance model described in
Section 3.1, the deflection of the system can be calculated for each step as the product of the process normal force multiplied with the compliance. To incorporate the deflection into the simulation, the tool is radially offset by the amount of the deflection. A slight damping of the radial tool movement is ensured, by applying an exponential moving average with weighting factor α = 0.1 to the forces. A detailed visualisation of the resulting workpiece surface which includes all effects discussed above can be found in
Figure 10b.
3.4. Validation of the Simulation System
To validate the simulation system, internal traverse grinding experiments were conducted using two machine tools with fundamentally different designs. The details of the experimental set-ups for the laboratory and industry settings are given in
Section 2.3 and the parameters are listed in
Table 1. The workpieces of the simulations for the laboratory setting were initialised according to the measured inner diameters after clamping (cf.
Section 2.3) with linear interpolation between the three measurement positions. A very rough approximation of the inverse workpiece deformation after unclamping was incorporated by subtracting the difference between the clamped and an unclamped workpiece from the simulation result. The workpiece models for the simulations of the industry setting were initialised with the constant diameter of an unclamped workpiece.
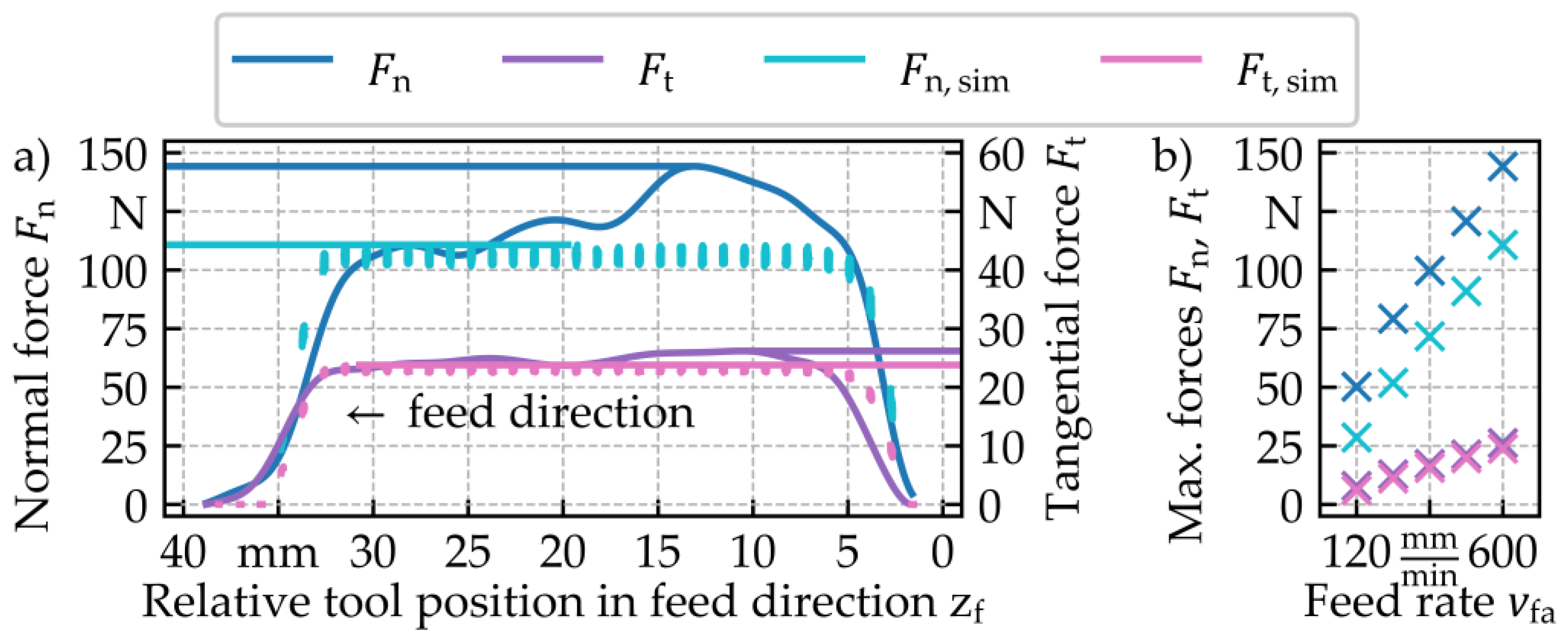
Figure 13 shows the measured and simulated process forces for an internal traverse grinding process at a feed rate of
= 600 mm/min, as well as the change in process forces over a variation of the feed rate for the industrial setup. The experimental conditions can be obtained from
Table 1. A strong increase of the process forces was observed in the simulated as well as the experimentally recorded forces in the tool entry section. Whereas the simulation predicted a subsequent quasi-stationary phase in both normal and tangential forces, the measured normal force decreased in this phase.
The measured and simulated forces showed good agreement at the tool exit, where all forces drop back to zero. The increase and drop of forces at the entry and exit zone are related to the progressive engagement and disengagement of the tool.
Figure 13b displays the maximum process forces for all tested feed rates. A linear increase depending on the feed rate was observed. Whereas the normal forces exhibited a difference between 21.7 N and 33.5 N, a good agreement was observed for the maximum tangential forces between simulation and experiment with a difference between 1.6 N and 2.4 N.
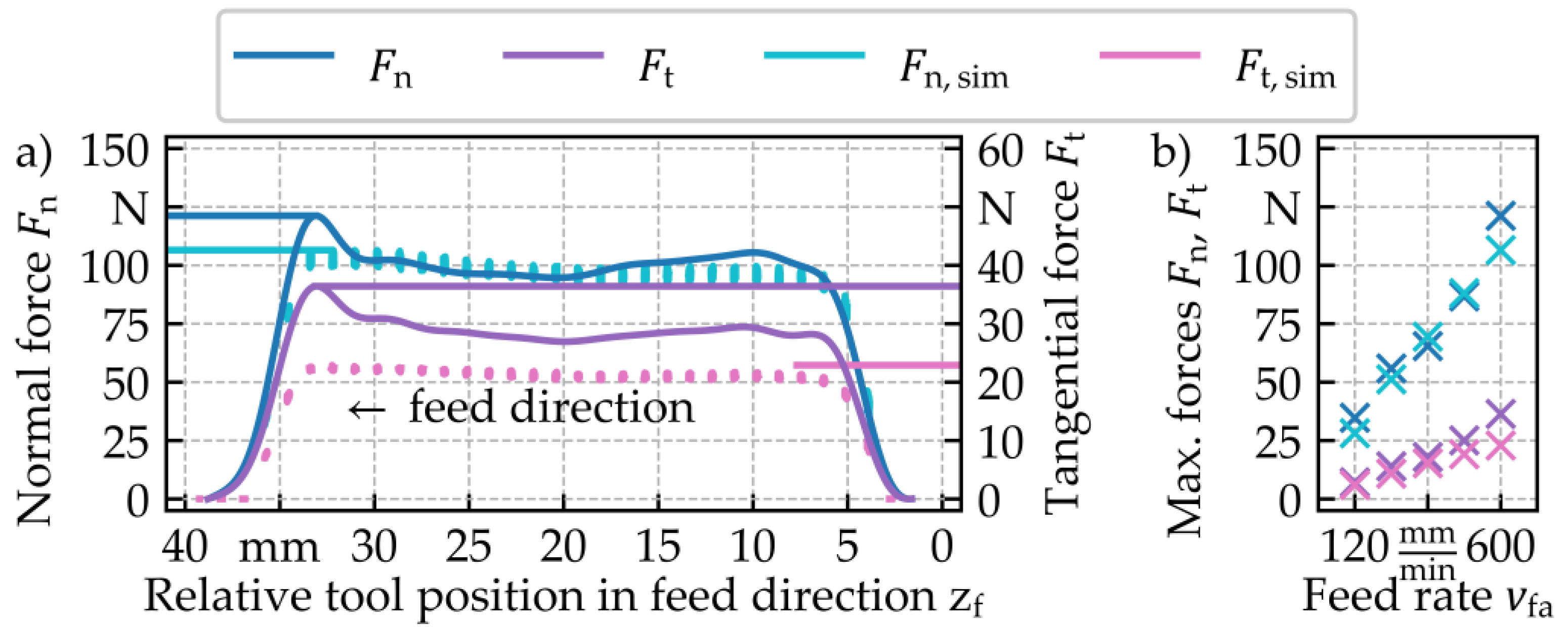
The process forces for the grinding tests in the laboratory setting, which were carried out analogously to the previous investigations, are presented in
Figure 14.
Figure 14a shows the force profile for the highest selected feed rate
= 600 mm/min. As for the tests in the industrial setting, the characteristic progression of process force, i.e., increase, quasi-stationary phase and process force decrease, was exhibited. In contrast to the results for the industrial setting, the measured process forces in the stationary zone showed a slight decrease in force, followed by a characteristic peak just before the exit zone. Good agreement between simulation and experiment was achieved for the normal forces aside from the peaks in the entry and exit zone, although the measured tangential forces were slightly higher than the simulated ones. A possible explanation for the measured force peaks is the workpiece deformation as a result of the axial clamping, which causes the workpiece wall to bulge in the radial direction against the clamping device. This causes a reduction of the radial stock
ae,tot in the middle section of the workpiece and reduces the process forces. By roughly incorporating this effect into the simulation, as described in the beginning of this section, the workpiece deformation and the resulting process forces were partly reproduced.
Figure 14b shows the comparison of maximum forces for the laboratory setting. In general, a high correspondence was observed between simulated and measured process normal forces as well as tangential forces with the exception of the parameter combination at the highest feed rate. Although the difference between the measured and simulated normal forces ranges from −5.0 N to +6.6 N for feed rates up to
= 480 mm/min, a difference of +14.7 N was observed for
= 600 mm/min. The results for the tangential forces exhibit a similar pattern. For the lowest four feed rates the difference ranges from 1.1 N to 5.9 N, whereas the difference at
= 600 mm/min amounts to 13.5 N.
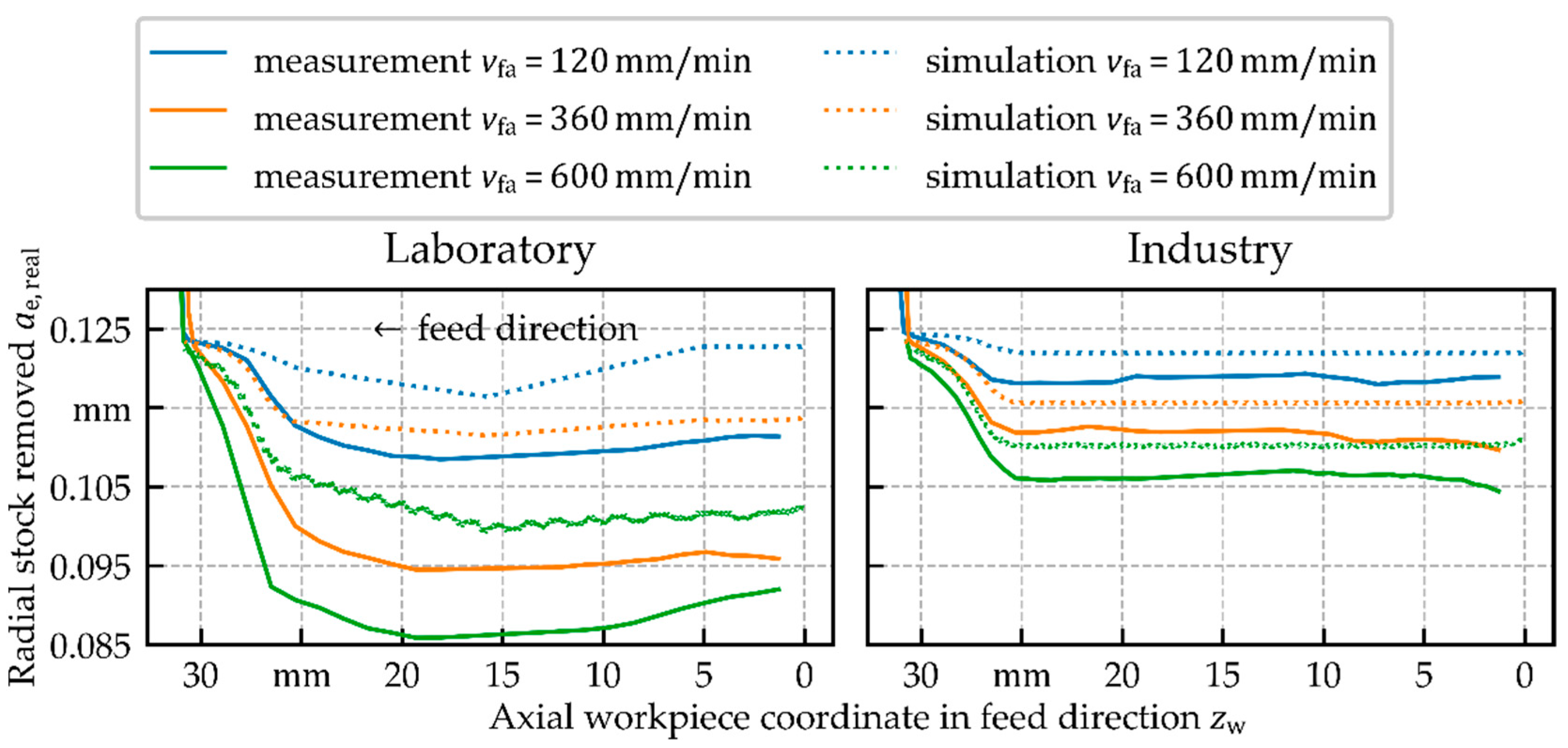
The comparison of workpiece inner contours measured after grinding experiments with the results obtained from the simulation showed a good qualitative accordance; see
Figure 15. The characteristic form of the step, generated on tool exit, was especially well reproduced by the simulation. The approximate incorporation of the clamping deformations in the laboratory setting largely influenced the resulting workpiece contour, because the deformation resulting from the clamping was in the same order of magnitude as the deflections resulting from the process normal force. In addition, the linear interpolation between only three points was clearly reproduced. In contrast, the results from the industry setting did not show a clear influence of deformations caused by workpiece clamping. On the other hand, it is worth mentioning that the global minima of the measured contours from the industry setting were located at the tool entry, which is counter intuitive because the lower forces and minima were not found in this section of the simulation results. While the simulation results qualitatively matched the measurements well, a distinct quantitative difference remained. The simulation systematically underestimated the difference between the achieved
and the set
.
4. Discussion
The quality of the results obtained in the GPS for process forces and shape deviations is tied to the models for the single grain forces and for the machine compliance. Although some discrepancies remained between the forces predicted by the combined FEM/GPS simulation system and the experimental measurements, the overall results were in good agreement. It should be noted that no experimental recalibration of the force model and the underlying FEM model was performed, despite the fact that the cooling lubricant supply differed between the two machine tools under examination and that the original calibration of the FEM model was performed for a different tool and workpiece. However, additional investigations into the material flow behaviour at small single grain cutting depths and large negative rake angles are advisable to further improve the force predictions, as is evident from the FEM results. It is also advisable to examine a possible integration of ploughing effects, such as a small portion of undeformed chip volume that is deformed, but not removed, into the GPS. Another possible area of improvement is the parametrisation of the force model in terms of cutting geometry. For example, a more complex description of the chip cross-section could lead to improvement. Additional investigation is necessary regarding the noticeable discrepancy between the simulated and the measured maximum normal force in the industrial setting. A possible explanation for this discrepancy is an inaccuracy of the custom measuring device [
35], depending on the axial contact position between tool and workpiece. This would also explain the unreasonably high change in the system compliance depending on the contact position found for the industrial setting [
35].
The reproduction of typical shape deviations in ITG processes, especially towards the entry and exit zones of the workpieces, is made possible by the incorporation of the compliance model in the GPS. While a qualitative prediction of the resulting shape errors was possible, the resulting shape deviations were consistently underestimated. A possible explanation is the determination of the compliances in static tests, indicating the need for further research into the influence of the system dynamics on the effective compliances. A definite issue in the laboratory setting is the elastic deformation of the workpiece due to axial clamping. While Holtermann et al. [
16] successfully modelled these deformations for a similar clamping mechanism, the deformations were not well reproducible in the current study. This inhibits direct modelling and requires a manual correction of the set radial stock removal which leads to additional variability. Precise measurement of the workpiece deformations after clamping within the machine tool, could mitigate these issues but is hard to achieve and would require special equipment. The aforementioned potential inaccuracy of the custom force measuring device, used to calibrate the compliance model, could be another possible explanation for the difference found between the measured and the simulated workpiece contours in the industrial setting.
Despite the remaining issues discussed above, which are partly related to potential measuring difficulties and hard to control variability in the laboratory setup, a good qualitative agreement for the predicted contours was achieved, and the process forces could be predicted very well for most of the experiments. It is especially worth noting that the single grain FEM model proved very good in transferability to two setups distinctly different than the process it was calibrated to. It could be shown that the approach for the compliance measurement and modelling is easily transferable between different machines, but further investigations are needed to judge the model quality, especially with respect to dynamic effects. To further enhance the simulation system, incorporating the modelling of thermo-mechanical workpiece deformations is planned. By using a flexible point-based grain geometry model, the simulation system is prepared, and also planned, for an integration of tool wear.