Numerical and Experimental Study of AlSi Coating Effect on Nugget Size Growth in Resistance Spot Welding of Hot-Stamped Boron Steels
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Work
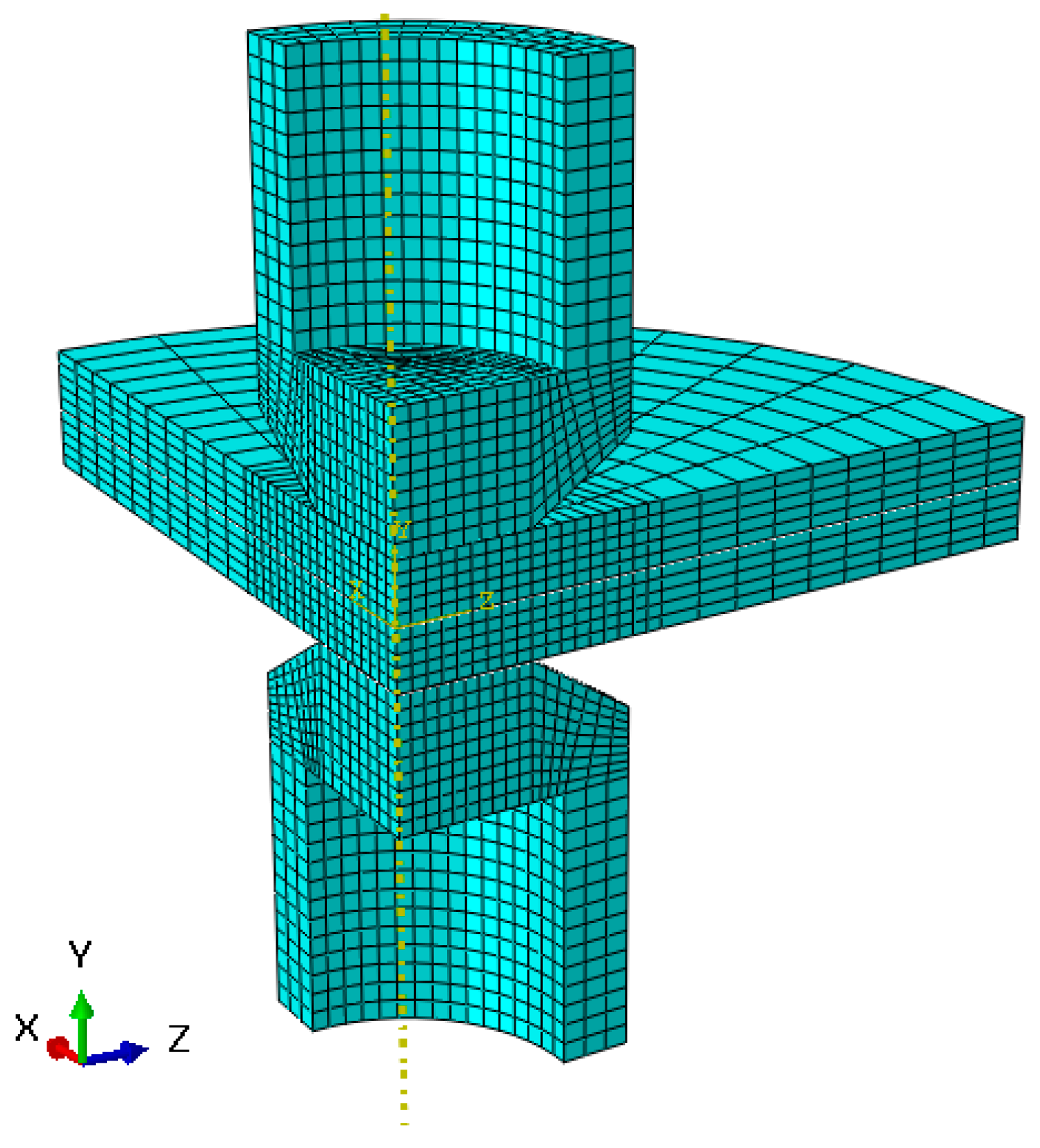
2.2. RSW Simulation
2.3. Governing Equation
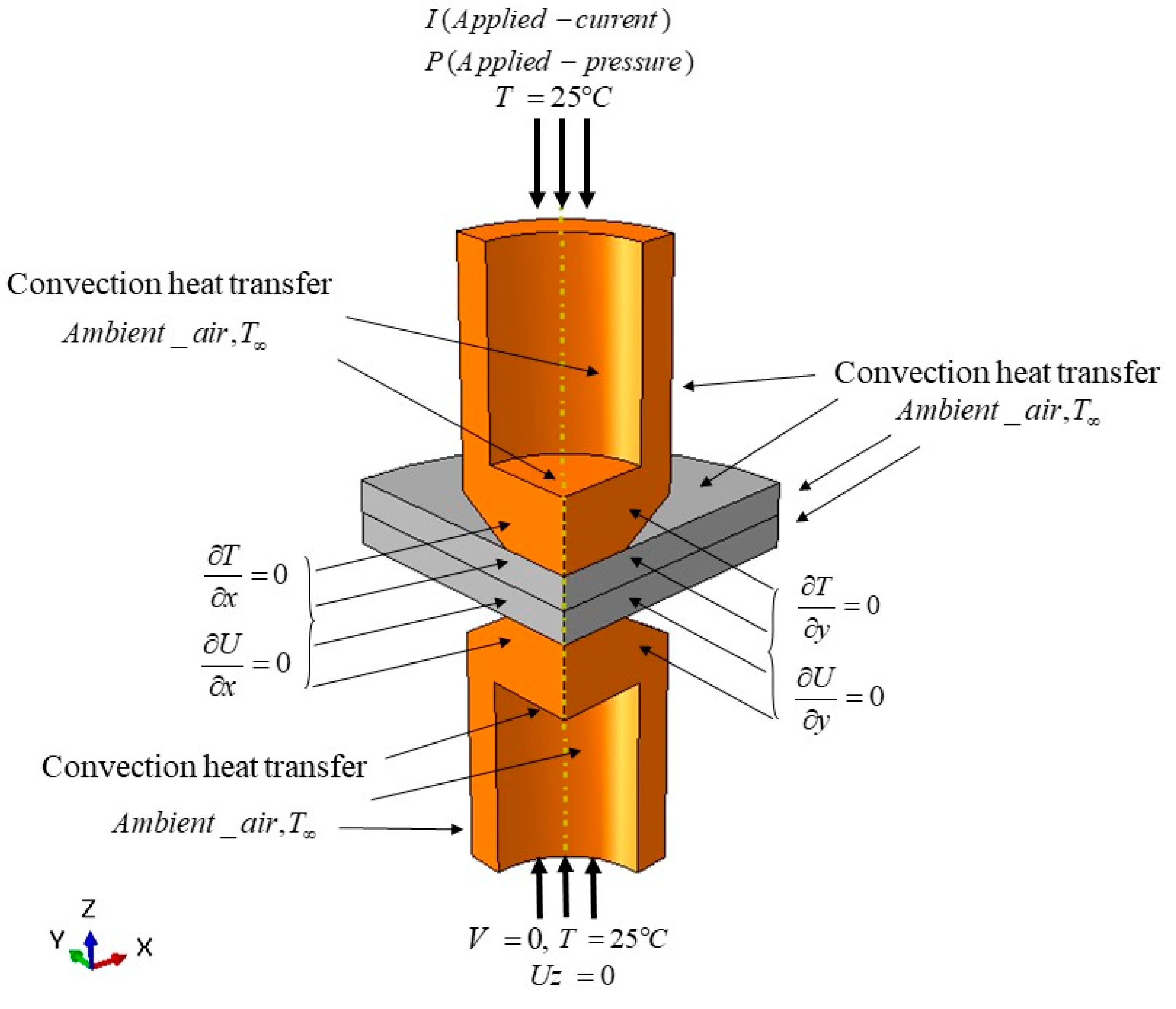
2.4. Boundary Conditions
2.4.1. Mechanical Boundary Condition
2.4.2. Electrical Boundary Condition
2.4.3. Thermal Boundary Condition
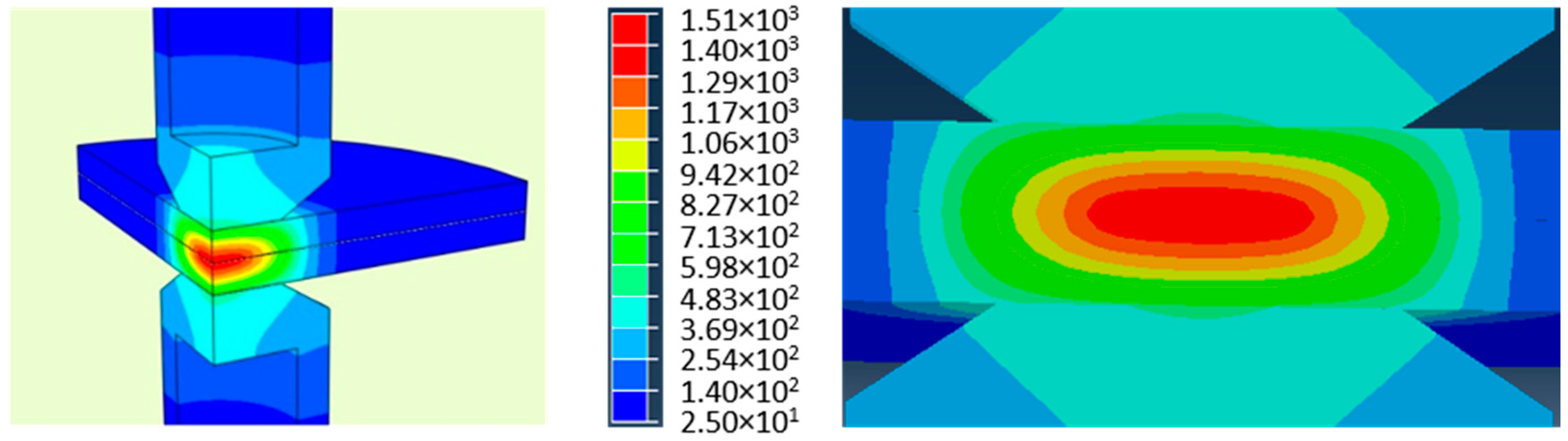
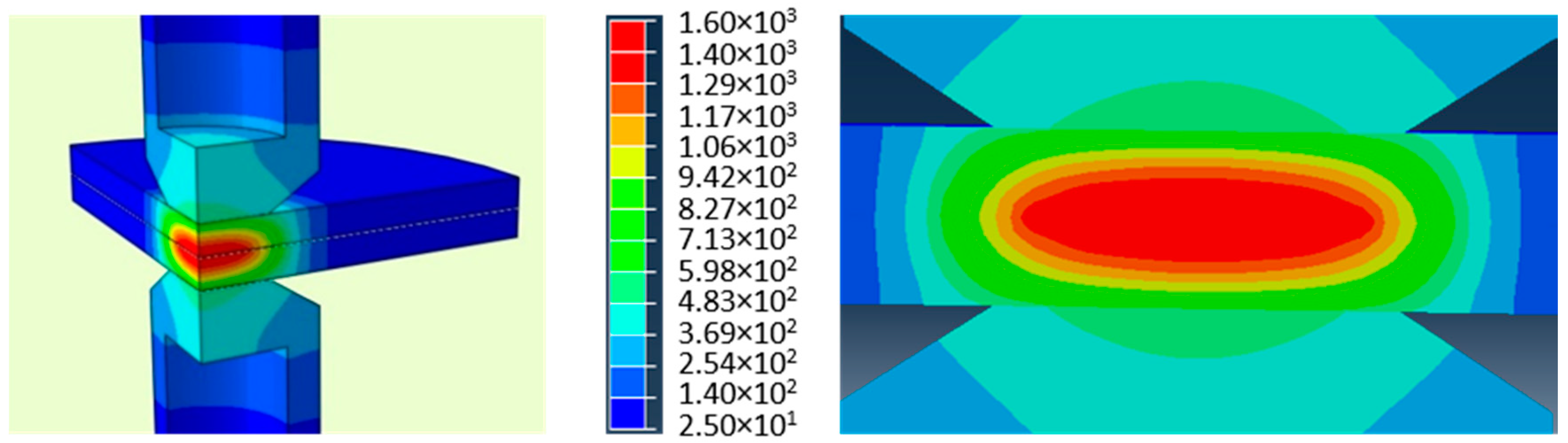
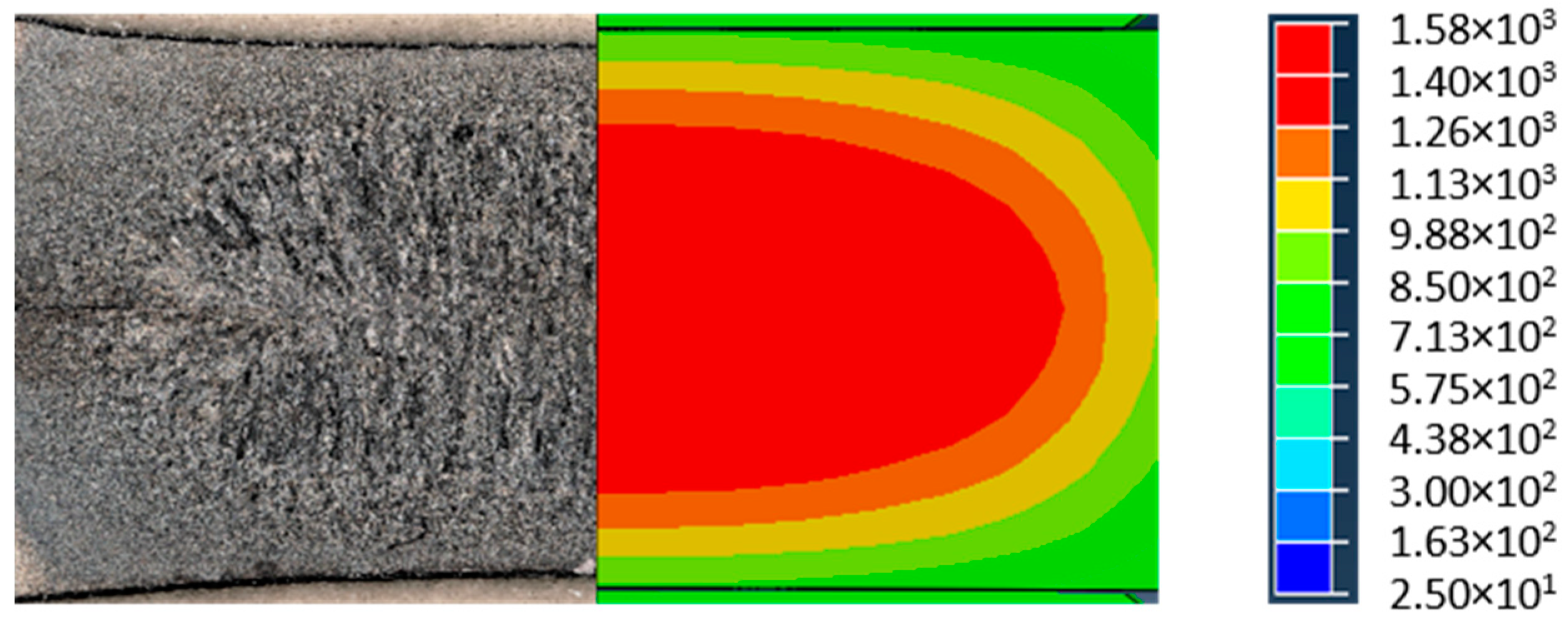
3. Results and Discussion
4. Conclusions
- 1-
- In the case of AlSi hot-stamped boron steel, because of the existence of some intermetallic phases in the coating, the electrical contact resistance at the faying interface increases. This plays a key role during RSW and affects the weldability of steel.
- 2-
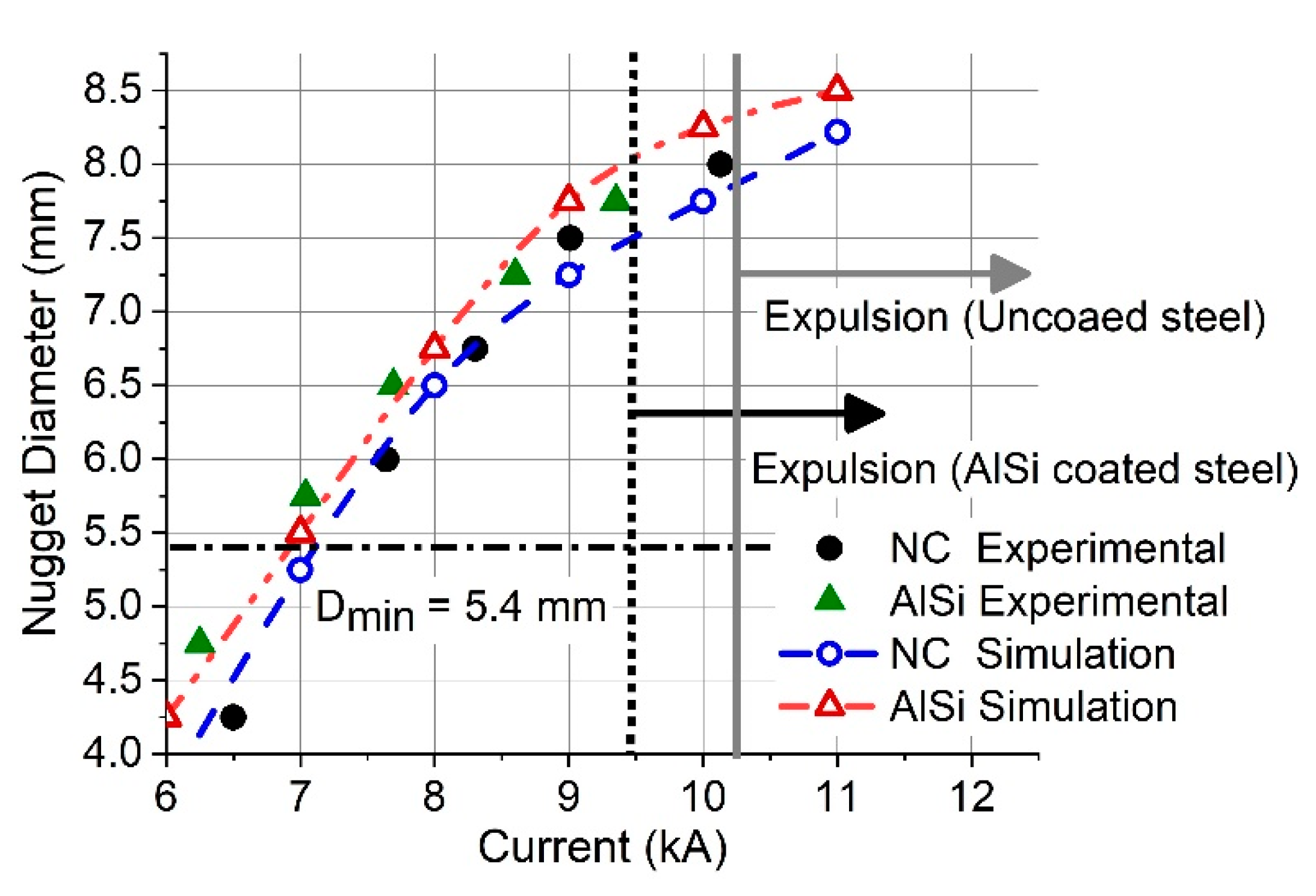
- At the same welding parameters, the dimensions of the formed nugget for AlSi-coated steel is larger than for uncoated steel.
- 3-
- AlSi coated steel requires a smaller electrical current for attaining the minimum nugget diameter in comparison with uncoated steel.
- 4-
- The maximum welding current for an expulsion-free welded joint for uncoated steel is higher than for AlSi-coated steel.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huh, H.; Kang, W. Electrothermal analysis of electric resistance spot welding processes by a 3-D finite element method. J. Mater. Process. Technol. 1997, 63, 672–677. [Google Scholar] [CrossRef]
- Chao, Y.J.; Wang, K.; Miller, K.; Zhu, X.-K. Dynamic separation of resistance spot welded joints: Part I—Experiments. Exp. Mech. 2010, 50, 889–900. [Google Scholar] [CrossRef]
- Kim, C.; Kang, M.; Park, Y. Laser welding of Al-Si coated hot stamping steel. Procedia Eng. 2011, 10, 2226–2231. [Google Scholar] [CrossRef]
- Suehiro, M.; Maki, J.; Kusumi, K.; Ohgami, M.; Miyakoshi, T. Properties of Aluminized Steels for Hot-Forming; 0148-7191; SAE Technical Paper: Warrendale, PA, USA, 2003. [Google Scholar]
- Karbasian, H.; Tekkaya, A.E. A review on hot stamping. J. Mater. Process. Technol. 2010, 210, 2103–2118. [Google Scholar] [CrossRef]
- Sun, X.; Khaleel, M.A. Dynamic strength evaluations for self-piercing rivets and resistance spot welds joining similar and dissimilar metals. Int. J. Impact Eng. 2007, 34, 1668–1682. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, H.; Hu, S. Relationships between quality and attributes of spot welds. Weld. J. N. Y. 2003, 82, 72-S. [Google Scholar]
- Zhang, H.; Senkara, J. Resistance Welding: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Cha, J. A Study on Resistance Spot Weldability of Aluminum Coated Sheet Steels. Master’s Thesis, Pukyong National University, Busan, Korea, 2002. [Google Scholar]
- Gould, J. An examination of nugget development during spot welding, using both experimental and analytical techniques. Weld. J. 1987, 66, 1s–10s. [Google Scholar]
- Tsai, C.; Papritan, J.; Dickinson, D.; Jammal, O. Modeling of resistance spot weld nugget growth. Weld. J. 1992, 71, 47. [Google Scholar]
- Tsai, C.; Jammal, O.; Dickinson, D. Study of nugget formation in resistance spot welding using finite element method. In Proceedings of the 2nd International Conference on Trends in Welding Research, Materials Park, OH, USA, 1–5 June 1998. [Google Scholar]
- Chang, B.; Zhou, Y. Numerical study on the effect of electrode force in small-scale resistance spot welding. J. Mater. Process. Technol. 2003, 139, 635–641. [Google Scholar] [CrossRef]
- Nied, H. The finite element modeling of the resistance spot welding process. Weld. J. 1984, 63, 123. [Google Scholar]
- Cho, H.; Cho, Y. A study of the thermal behavior in resistance spot welds. Weld. J. 1989, 68, 236s–244s. [Google Scholar]
- Eisazadeh, H.; Hamedi, M.; Halvaee, A. New parametric study of nugget size in resistance spot welding process using finite element method. Mater. Des. 2010, 31, 149–157. [Google Scholar] [CrossRef]
- Moshayedi, H.; Sattari-Far, I. Resistance spot welding and the effects of welding time and current on residual stresses. J. Mater. Process. Technol. 2014, 214, 2545–2552. [Google Scholar] [CrossRef]
- Nielsen, C.; Zhang, W.; Alves, L.; Bay, N.; Martins, P. Coupled Finite Element Flow Formulation. In Modeling of Thermo-Electro-Mechanical Manufacturing Processes; Springer: Berlin/Heidelberg, Germany, 2013; pp. 11–36. [Google Scholar]
- Nielsen, C.V.; Zhang, W.; Perret, W.; Martins, P.A.; Bay, N. Three-dimensional simulations of resistance spot welding. Proc. Inst. Mech. Eng. Part D: J. Automob. Eng. 2015, 229, 885–897. [Google Scholar] [CrossRef]
- Cheon, J.Y.; Vijayan, V.; Murgun, S.; Do Park, Y.; Kim, J.H.; Yu, J.Y.; Ji, C. Optimization of pulsed current in resistance spot welding of Zn-coated hot-stamped boron steels. J. Mech. Sci. Technol. 2019, 33, 1615–1621. [Google Scholar] [CrossRef]
- Ji, C.-W.; Jo, I.; Lee, H.; Choi, I.-D.; Do Kim, Y.; Park, Y.-D. Effects of surface coating on weld growth of resistance spot-welded hot-stamped boron steels. J. Mech. Sci. Technol. 2014, 28, 4761–4769. [Google Scholar] [CrossRef]
- Ighodaro, O.; Biro, E.; Zhou, Y. Comparative effects of Al-Si and galvannealed coatings on the properties of resistance spot welded hot stamping steel joints. J. Mater. Process. Technol. 2016, 236, 64–72. [Google Scholar] [CrossRef]
- Lövenborn, D. 3D FE Simulations of Resistance Spot Welding; KTH Royal Institute of Tchnology: Stockholm, Sweden, 2016. [Google Scholar]
- Zhang, P.; Zhu, L.; Xi, C.; Luo, J. Study on Phase Transformation in Hot Stamping Process of USIBOR® 1500 High-Strength Steel. Metals 2019, 9, 1119. [Google Scholar] [CrossRef]
- Moshayedi, H.; Sattari-Far, I. Numerical and experimental study of nugget size growth in resistance spot welding of austenitic stainless steels. J. Mater. Process. Technol. 2012, 212, 347–354. [Google Scholar] [CrossRef]
- Ji, C.-W.; Choi, I.; Kim, Y.D.; Park, Y.-D. Study on coating melting behavior on weld growth mechanism for Al-Si coated hot-stamped boron steels in resistance spot welding. Korean J. Met. Mater. 2014, 52, 931–941. [Google Scholar]
- Saha, D.; Ji, C.; Park, Y. Coating behaviour and nugget formation during resistance welding of hot forming steels. Sci. Technol. Weld. Join. 2015, 20, 708–720. [Google Scholar] [CrossRef]





| Steel | Chemical Composition in wt% | |||||
|---|---|---|---|---|---|---|
| Fe | C | Mn | Si | Cr | B | |
| Uncoated steel | 98 | 0.25 | 1.14 | 0.27 | 0.19 | 0.003 |
| Al-Si coated steel | 98 | 0.23 | 1.14 | 0.27 | 0.18 | 0.003 |
| Temp. (°C) | Density (kg/m3) | Electrical Resistivity µ·Ωm | Thermal Conductivity (W/m·K) | Specific Heat (J/kg·K) | Thermal Expansion Co. (10−6 × K−1) | Yield Stress (MPa) | Flow Stress at 0.4 of Strain (MPa) | Young’s Modulus (GPa) |
|---|---|---|---|---|---|---|---|---|
| 20 | 7900 | 0.36 | 26.2 | – | 17 | 1250 | 1840 | 200 |
| 100 | 7880 | 0.412 | 28.3 | 461 | 17.4 | 1210 | 1820 | 193 |
| 200 | 7830 | 0.463 | 31.5 | 495 | 18 | 1150 | 1800 | 185 |
| 400 | 7750 | 0.651 | 30.1 | 533 | 19.1 | 1080 | 1300 | 176 |
| 600 | 7660 | 0.908 | 27.1 | 648 | 19.6 | 700 | 1200 | 167 |
| 800 | 7560 | 1.12 | 25.2 | 675 | 20.2 | 480 | 900 | 159 |
| 1000 | 7510 | 1.19 | 27.4 | 500 | 20.4 | 400 | 800 | 151 |
| 1200 | 7370 | 1.23 | 31.3 | – | 20.7 | 200 | 400 | 60 |
| 1400 | 7320 | 1.27 | 34.7 | – | 21.3 | 90 | 200 | 20 |
| 1500 | 7320 | 1.282 | 36 | – | 21.6 | 20 | – | 10 |
| Temp. (°C) | Density (kg/m3) | Electrical Resistivity 10−9·Ωm | Thermal Conductivity (W/m·K) | Specific Heat (J/kg·K) | Thermal Expansion Co. (10−6 × K−1) | Yield Stress (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| 10 | 8900 | 26.4 | 390.3 | 397 | 16.5 | 83 | 124 | 0.32 |
| 93 | – | 30 | 380.6 | 402 | 16.7 | – | 105 | – |
| 204 | – | 40 | 370.1 | 419 | 17.1 | – | 93 | – |
| 316 | – | 50.5 | 355.1 | 431 | 17.5 | – | 82 | – |
| 427 | – | 61.9 | 345.4 | 440 | 17.8 | – | 55 | – |
| 538 | – | 69.9 | 334.9 | 465 | 18.4 | – | 38 | – |
| 649 | – | 80 | 320 | 477 | 18.5 | – | 25 | – |
| 760 | – | 89.8 | 315.5 | – | 18.9 | – | 16 | – |
| 871 | – | 94.8 | 310.3 | – | 19.3 | – | 14 | – |
| 982 | – | 99.8 | 305 | 502 | – | – | 7 | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afzal, A.; Hamedi, M.; Nielsen, C.V. Numerical and Experimental Study of AlSi Coating Effect on Nugget Size Growth in Resistance Spot Welding of Hot-Stamped Boron Steels. J. Manuf. Mater. Process. 2021, 5, 10. https://doi.org/10.3390/jmmp5010010
Afzal A, Hamedi M, Nielsen CV. Numerical and Experimental Study of AlSi Coating Effect on Nugget Size Growth in Resistance Spot Welding of Hot-Stamped Boron Steels. Journal of Manufacturing and Materials Processing. 2021; 5(1):10. https://doi.org/10.3390/jmmp5010010
Chicago/Turabian StyleAfzal, Ali, Mohsen Hamedi, and Chris Valentin Nielsen. 2021. "Numerical and Experimental Study of AlSi Coating Effect on Nugget Size Growth in Resistance Spot Welding of Hot-Stamped Boron Steels" Journal of Manufacturing and Materials Processing 5, no. 1: 10. https://doi.org/10.3390/jmmp5010010
APA StyleAfzal, A., Hamedi, M., & Nielsen, C. V. (2021). Numerical and Experimental Study of AlSi Coating Effect on Nugget Size Growth in Resistance Spot Welding of Hot-Stamped Boron Steels. Journal of Manufacturing and Materials Processing, 5(1), 10. https://doi.org/10.3390/jmmp5010010







