Improving Geometric Accuracy of 3D Printed Parts Using 3D Metrology Feedback and Mesh Morphing
Abstract
:1. Introduction
2. Proposed Method
2.1. Printing Sacrificial Parts Based on the Original CAD Model
2.2. Part Inspection
Registration and Deviation Measurement
- For each point of the scan data, find the closest vertex on the CAD (STL) model as its corresponding point.
- Find the rigid body transformation (translation and rotation) that minimizes the mean of squared distances between the corresponding pairs of scan point and CAD vertex.
- Apply the transformation of Step 2 to the scan data.
- If the change in the mean of squared distances between the scan points and CAD vertices falls below a pre-specified threshold, stop. Otherwise, iterate from 1.
2.3. Random Error Reduction Strategies
2.3.1. Smoothing
2.3.2. Averaging the Deviation Vector Fields
2.4. Morphing
- The algorithm does not move the points of the bottom surface, in order to allow a good printing surface. Their position remains the same as it was before the compensation.
- The algorithm eliminates the deviations on the mesh that are bigger than a realistic predetermined range. This range is fixed at 500 m as the range of deviations for FDM 3D printers is usually smaller [32].
3. Results and Discussion
3.1. Experimental Setup
3.2. Comparative Analysis
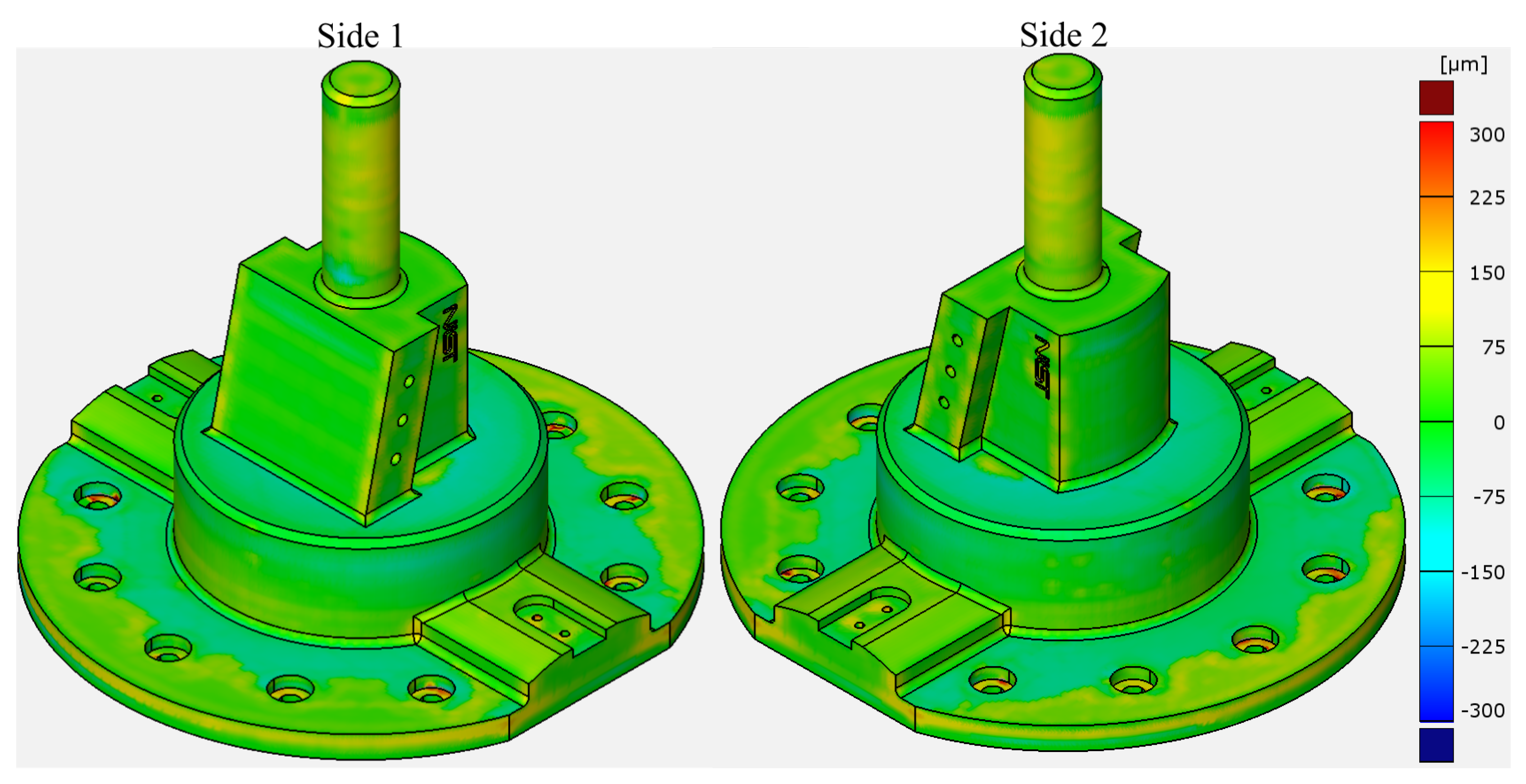
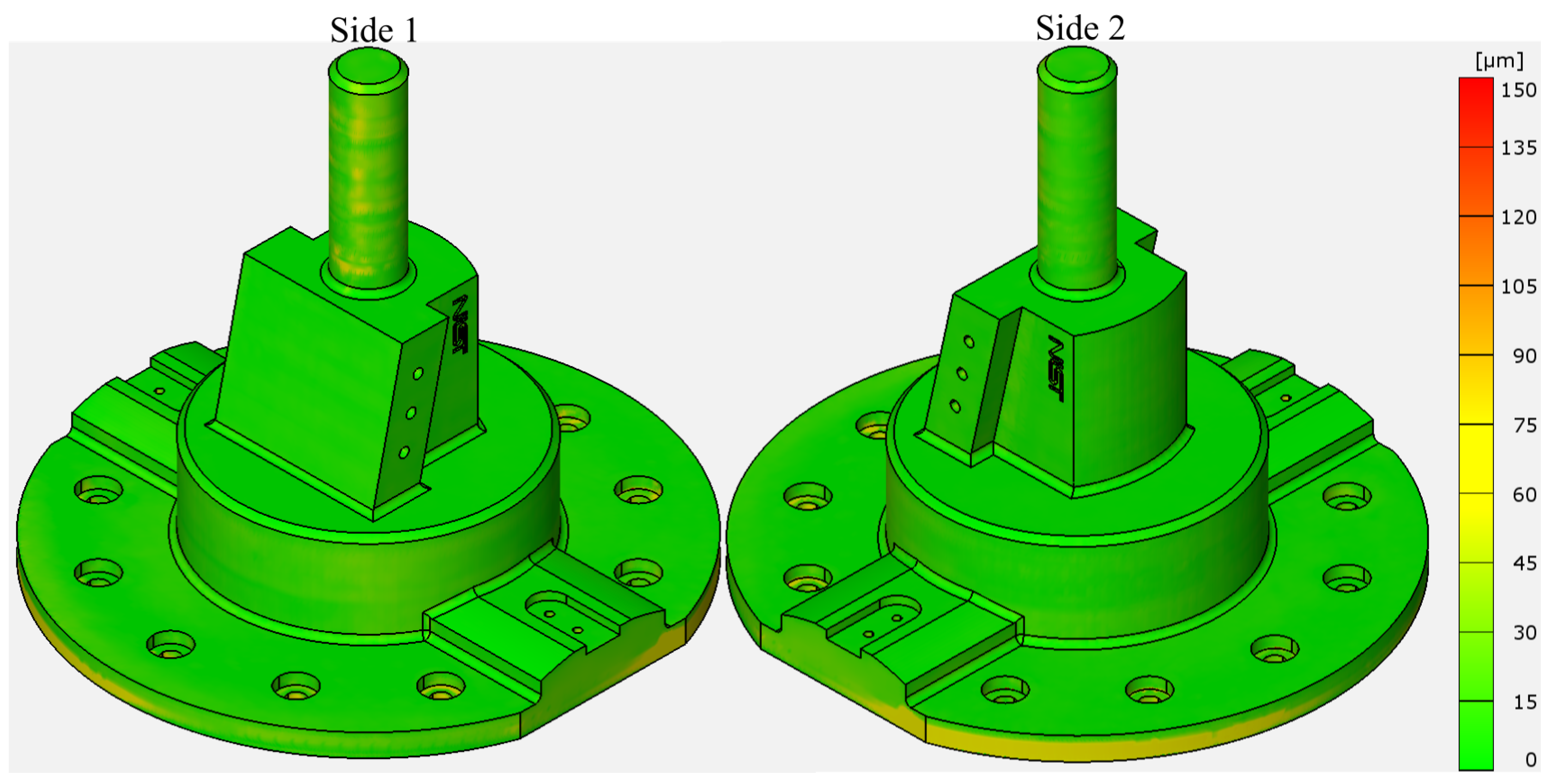
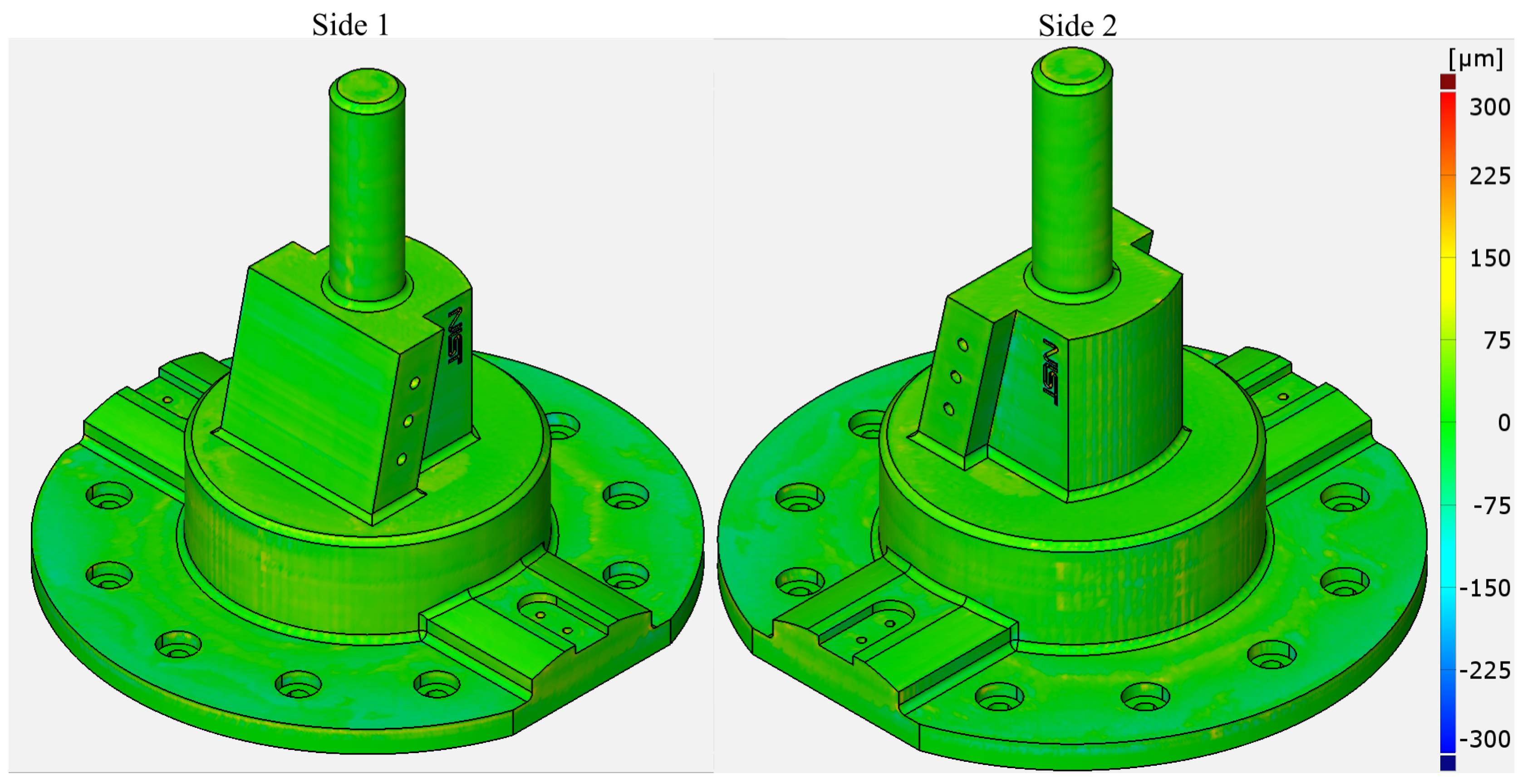
3.2.1. Deviation Analysis
3.2.2. Tolerance Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| PPE | Personal Protective Equipment |
| FDM | Fused Deposition Modelling |
| FFF | Fused Filament Fabrication |
| SLA | Stereolithography Apparatus |
| CAD | Computer Aided Design |
| FEA | Finite Element Analysis |
| ICP | Iterative Closest Point |
| STL | Standard Tessellation Language |
| GD&T | Geometric Dimensioning and Tolerancing |
| CMM | Coordinate Measuring Machine |
References
- Sachs, E.; Cima, M.; Williams, P.; Brancazio, D.; Cornie, J. Three Dimensional Printing: Rapid Tooling and Prototypes Directly from a CAD Model. J. Eng. Ind. 1992, 114, 481–488. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.C.L.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput. Aided Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Msallem, B.; Sharma, N.; Cao, S.; Halbeisen, F.S.; Zeilhofer, H.F.; Thieringer, F.M. Evaluation of the Dimensional Accuracy of 3D-Printed Anatomical Mandibular Models Using FFF, SLA, SLS, MJ, and BJ Printing Technology. J. Clin. Med. 2020, 9, 817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manero, A.; Smith, P.; Koontz, A.; Dombrowski, M.; Sparkman, J.; Courbin, D.; Chi, A. Leveraging 3D Printing Capacity in Times of Crisis: Recommendations for COVID-19 Distributed Manufacturing for Medical Equipment Rapid Response. Int. J. Environ. Res. Public Health 2020, 17, 4634. [Google Scholar] [CrossRef] [PubMed]
- Pearce, J.M. Distributed Manufacturing of Open Source Medical Hardware for Pandemics. J. Manuf. Mater. Process. 2020, 4, 49. [Google Scholar] [CrossRef]
- Bochmann, L.; Bayley, C.; Helu, M.; Transchel, R.; Wegener, K.; Dornfeld, D. Understanding error generation in fused deposition modeling. Surf. Topogr. Metrol. Prop. 2015, 3, 014002. [Google Scholar] [CrossRef]
- Akinsowon, V.; Nahirna, M. State of the 3D Printing Industry Survey 2019: AM Service Providers. Available online: https://amfg.ai/wp-content/uploads/2019/07/AMFG-State-of-the-Industry-Report_-AM-Service-Providers.pdf (accessed on 19 November 2020).
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Yang, H.J.; Hwang, P.J.; Lee, S.H. A study on shrinkage compensation of the SLS process by using the Taguchi method. Int. J. Mach. Tools Manuf. 2002, 42, 1203–1212. [Google Scholar] [CrossRef]
- Karalekas, D.; Aggelopoulos, A. Study of shrinkage strains in a stereolithography cured acrylic photopolymer resin. J. Mater. Process. Technol. 2003, 136, 146–150. [Google Scholar] [CrossRef]
- Wang, T.M.; Xi, J.T.; Jin, Y. A model research for prototype warp deformation in the FDM process. Int. J. Adv. Manuf. Technol. 2007, 33, 1087–1096. [Google Scholar] [CrossRef]
- Bourell, D.; Kruth, J.P.; Leu, M.; Levy, G.; Rosen, D.; Beese, A.M.; Clare, A. Materials for additive manufacturing. CIRP Ann. 2017, 66, 659–681. [Google Scholar] [CrossRef]
- Tong, K.; Amine Lehtihet, E.; Joshi, S. Parametric error modeling and software error compensation for rapid prototyping. Rapid Prototyp. J. 2003, 9, 301–313. [Google Scholar] [CrossRef]
- Tong, K.; Lehtihet, E.A.; Joshi, S. Software compensation of rapid prototyping machines. Precis. Eng. 2004, 28, 280–292. [Google Scholar] [CrossRef]
- Tong, K.; Joshi, S.; Amine Lehtihet, E. Error compensation for fused deposition modeling (FDM) machine by correcting slice files. Rapid Prototyp. J. 2008, 14, 4–14. [Google Scholar] [CrossRef]
- Lyu, J.; Manoochehri, S. Modeling Machine Motion and Process Parameter Errors for Improving Dimensional Accuracy of Fused Deposition Modeling Machines. J. Manuf. Sci. Eng. 2018, 140. [Google Scholar] [CrossRef]
- Huang, Q.; Nouri, H.; Xu, K.; Chen, Y.; Sosina, S.; Dasgupta, T. Statistical Predictive Modeling and Compensation of Geometric Deviations of Three-Dimensional Printed Products. J. Manuf. Sci. Eng. 2014, 136, 061008. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, J.; Sabbaghi, A.; Dasgupta, T. Optimal offline compensation of shape shrinkage for three-dimensional printing processes. IIE Trans. 2015, 47, 431–441. [Google Scholar] [CrossRef]
- Huang, Q. An Analytical Foundation for Optimal Compensation of Three-Dimensional Shape Deformation in Additive Manufacturing. J. Manuf. Sci. Eng. 2016, 138, 061010. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, Y.; Lyu, M.; Lin, W. Shape Deviation Generator—A Convolution Framework for Learning and Predicting 3D Printing Shape Accuracy. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1486–1500. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mhapsekar, K.; Anand, S. Part Build Orientation Optimization and Neural Network-Based Geometry Compensation for Additive Manufacturing Process. J. Manuf. Sci. Eng. 2018, 140. [Google Scholar] [CrossRef]
- McConaha, M.; Anand, S. Additive Manufacturing Distortion Compensation Based on Scan Data of Built Geometry. J. Manuf. Sci. Eng. 2020, 142. [Google Scholar] [CrossRef]
- Xu, K.; Kwok, T.H.; Zhao, Z.; Chen, Y. A Reverse Compensation Framework for Shape Deformation Control in Additive Manufacturing. J. Comput. Inf. Sci. Eng. 2017, 17, 021012. [Google Scholar] [CrossRef]
- Afazov, S.; Okioga, A.; Holloway, A.; Denmark, W.; Triantaphyllou, A.; Smith, S.A.; Bradley-Smith, L. A methodology for precision additive manufacturing through compensation. Precis. Eng. 2017, 50, 269–274. [Google Scholar] [CrossRef]
- Grimm, T. Users Guide to Rapid Prototyping; Society of Manufacturing Engineers: Dearborn, MI, USA, 2004. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Dowllng, M.M.; Griffin, P.M.; Tsui, K.L.; Zhou, C. Statistical issues in geometric feature inspection using coordinate measuring machines. Technometrics 1997, 39, 3. [Google Scholar] [CrossRef]
- Weyrich, T.; Pauly, M.; Keiser, R.; Heinzle, S.; Scandella, S.; Gross, M. Post-Processing of Scanned 3D Surface Data. In Proceedings of the First, Eurographics Conference on Point-Based Graphics, Zurich, Switzerland, 2–4 June 2004; pp. 85–94. [Google Scholar]
- Desbrun, M.; Meyer, M.; Schröder, P.; Barr, A.H. Implicit fairing of irregular meshes using diffusion and curvature flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH 99, Los Angeles, CA, USA, 8–13 August 1999. [Google Scholar] [CrossRef] [Green Version]
- Sharp, N.; Soliman, Y.; Crane, K. The Vector Heat Method. ACM Trans. Graph. 2019, 38, 24:1–24:19. [Google Scholar] [CrossRef]
- Bunge, A.; Herholz, P.; Kazhdan, M.; Botsch, M. Polygon Laplacian Made Simple. Comput. Graph. Forum 2020, 39, 303–313. [Google Scholar] [CrossRef]
- Minetola, P.; Calignano, F.; Galati, M. Comparing geometric tolerance capabilities of additive manufacturing systems for polymers. Addit. Manuf. 2020, 32, 101103. [Google Scholar] [CrossRef]
- Lipman, R.; Filliben, J. Testing Implementations of Geometric Dimensioning and Tolerancing in CAD Software. Comput. Aided Des. Appl. 2020, 17, 1241–1265. [Google Scholar] [CrossRef]
- Navangul, G.; Paul, R.; Anand, S. Error Minimization in Layered Manufacturing Parts by Stereolithography File Modification Using a Vertex Translation Algorithm. J. Manuf. Sci. Eng. 2013, 135. [Google Scholar] [CrossRef]
- Acceptance/Reverification According to VDI/VDE 2634, Part 3. Available online: https://www.zebicon.com/fileadmin/user_upload/2_Maaleudstyr/9_Certifikater/ATOS_Core_200_SN160300/2019-04-02_Acceptance_test_ATOS_Core_MV200_SN160300.pdf (accessed on 19 November 2020).
- Dawson-Haggerty, M. Trimesh. 2019. Available online: https://trimsh.org/ (accessed on 30 June 2020).
- Jacobson, A.; Panozzo, D. libigl: A Simple C++ Geometry Processing Library. 2018. Available online: https://libigl.github.io/ (accessed on 15 September 2020).
- ASME Y14.5—2018: Dimensioning and Tolerancing; American Society of Mechanical Engineers: New York, NY, USA, 2018.






| Printing temperature | 215 °C |
| Printing speed | 70 mm/s |
| Cooling | 100% |
| Support | None |
| Infill type | Triangles |
| Infill density | 10% |
| Plate adhesion | None |
| Layer height | 0.04 mm |
| Nozzle diameter | 0.4 mm |
| Average of Absolute Errors (m) | Standard Deviation (m) | 99th Percentile of Absolute Errors (m) | |
|---|---|---|---|
| Compensated part based on the average deviation of 5 parts | 23 | 20 | 98 |
| Compensated part based on deviation of part B | 52 | 48 | 221 |
| Part A | 52 | 62 | 330 |
| Part B | 53 | 60 | 318 |
| Part C | 51 | 57 | 309 |
| Part D | 49 | 54 | 288 |
| Part E | 48 | 54 | 309 |
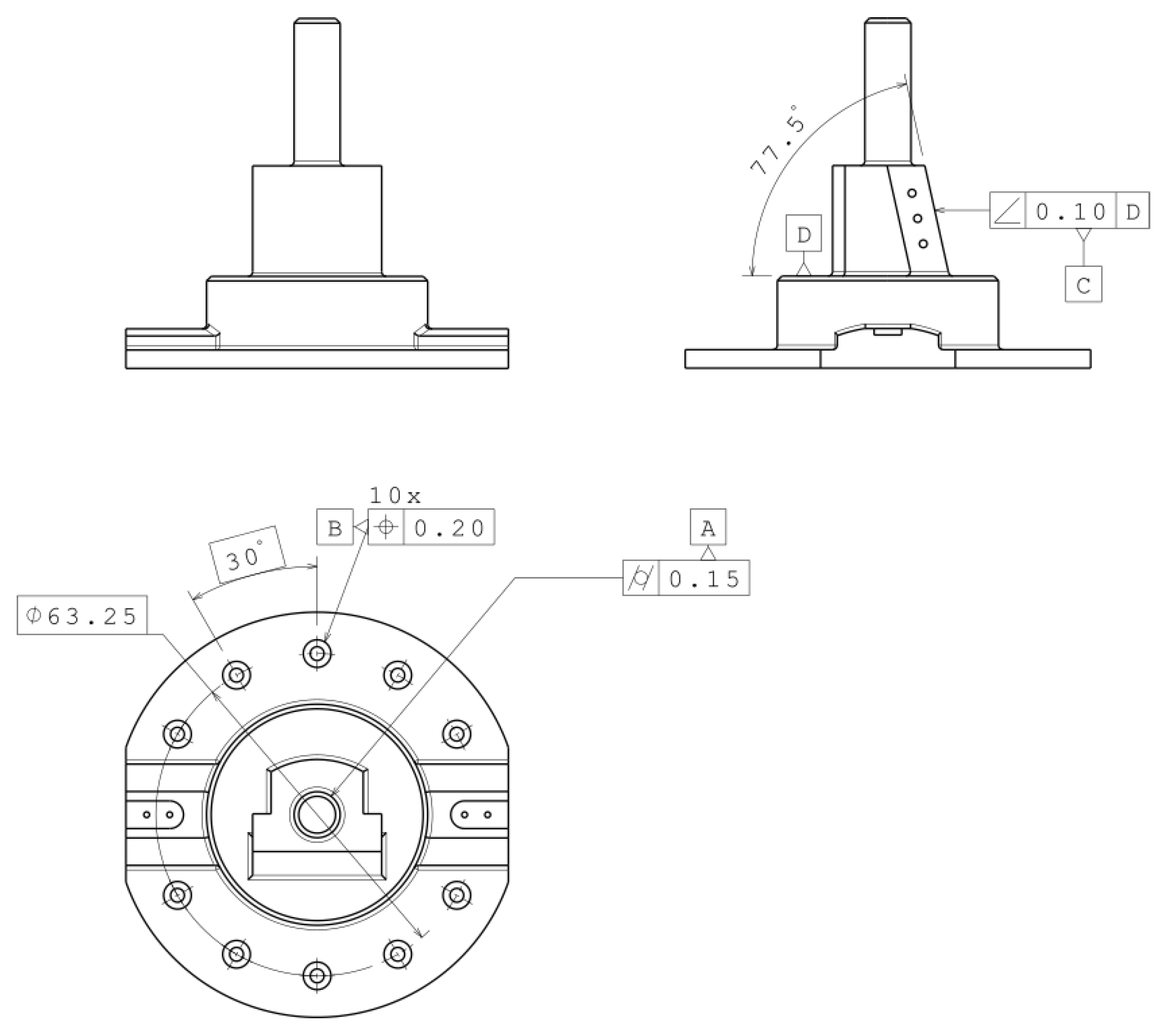
| Element | Cylinder A | Element Group B | Plane C |
|---|---|---|---|
| Datum | Plane D | ||
| Property | Cylindricity | Position | Angularity |
| Tolerance | 150 | 200 | 100 |
| Deviation of Compensated part based on the average deviation of five parts | 125 | 179 | 98 |
| Deviation of Compensated part based on part B | 165 | 194 | 156 |
| Deviation of part A | 285 | 499 | 108 |
| Deviation of part B | 282 | 455 | 103 |
| Deviation of part C | 244 | 499 | 117 |
| Deviation of part D | 179 | 502 | 125 |
| Deviation of part E | 273 | 471 | 122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jadayel, M.; Khameneifar, F. Improving Geometric Accuracy of 3D Printed Parts Using 3D Metrology Feedback and Mesh Morphing. J. Manuf. Mater. Process. 2020, 4, 112. https://doi.org/10.3390/jmmp4040112
Jadayel M, Khameneifar F. Improving Geometric Accuracy of 3D Printed Parts Using 3D Metrology Feedback and Mesh Morphing. Journal of Manufacturing and Materials Processing. 2020; 4(4):112. https://doi.org/10.3390/jmmp4040112
Chicago/Turabian StyleJadayel, Moustapha, and Farbod Khameneifar. 2020. "Improving Geometric Accuracy of 3D Printed Parts Using 3D Metrology Feedback and Mesh Morphing" Journal of Manufacturing and Materials Processing 4, no. 4: 112. https://doi.org/10.3390/jmmp4040112
APA StyleJadayel, M., & Khameneifar, F. (2020). Improving Geometric Accuracy of 3D Printed Parts Using 3D Metrology Feedback and Mesh Morphing. Journal of Manufacturing and Materials Processing, 4(4), 112. https://doi.org/10.3390/jmmp4040112






