Suppression of Polycrystalline Diamond Tool Wear with Mechanochemical Effects in Micromachining of Ferrous Metal
Abstract
1. Introduction
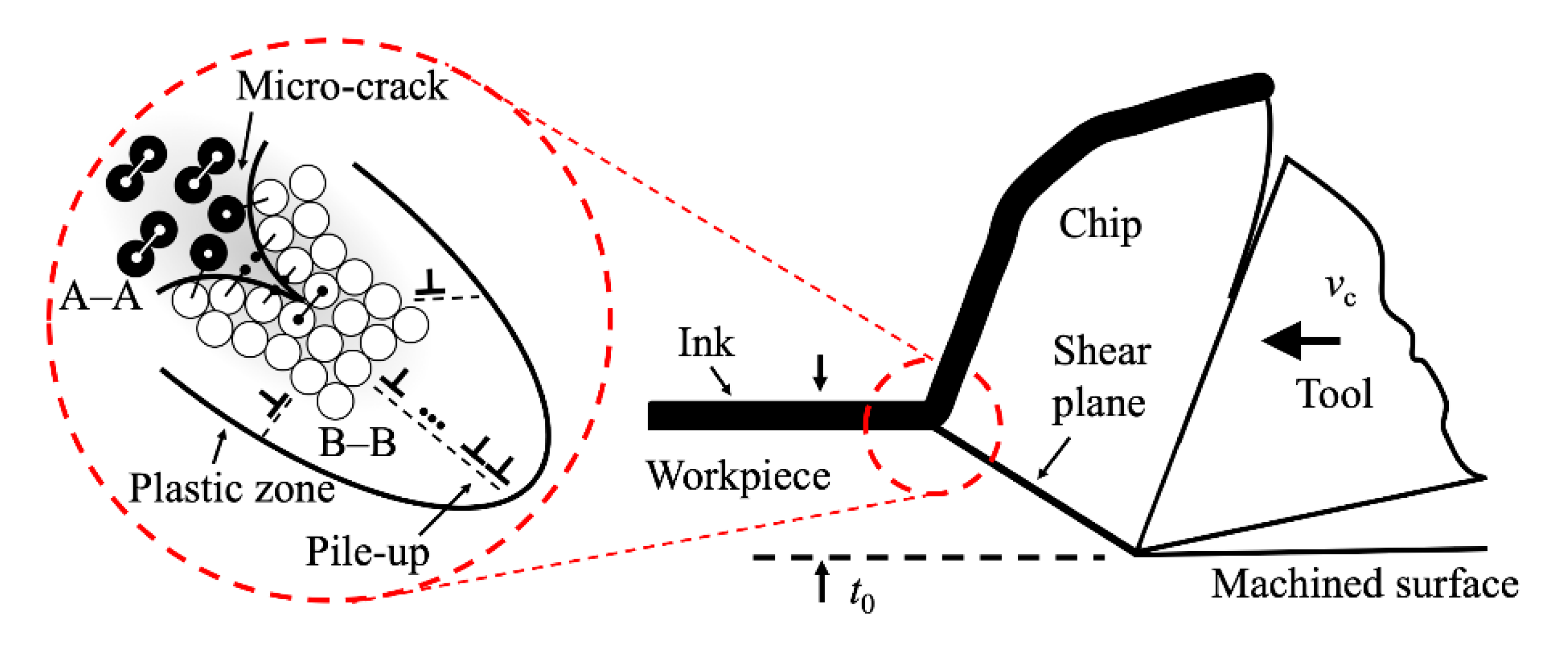
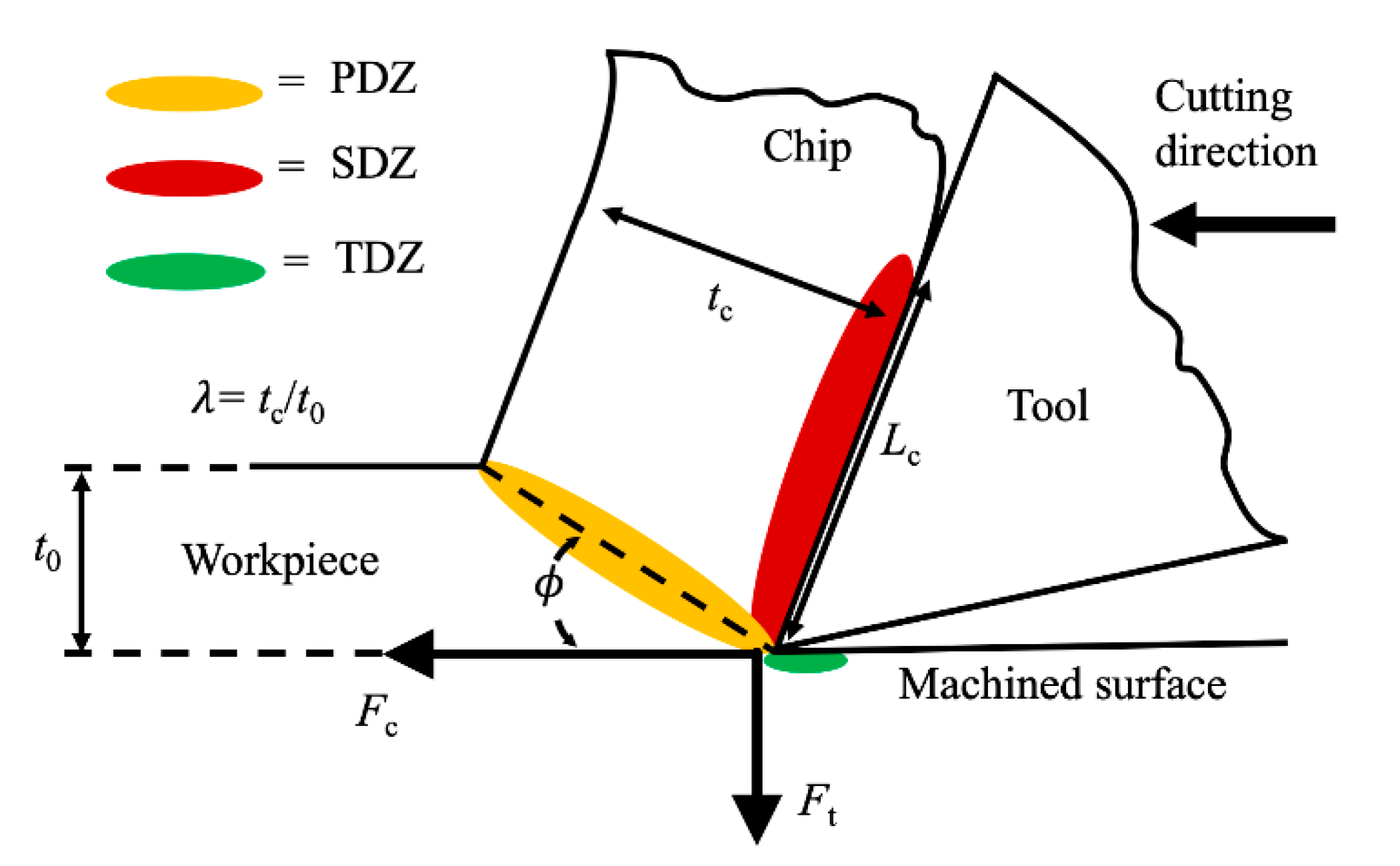
2. Mechanochemical Effect
3. Experiments
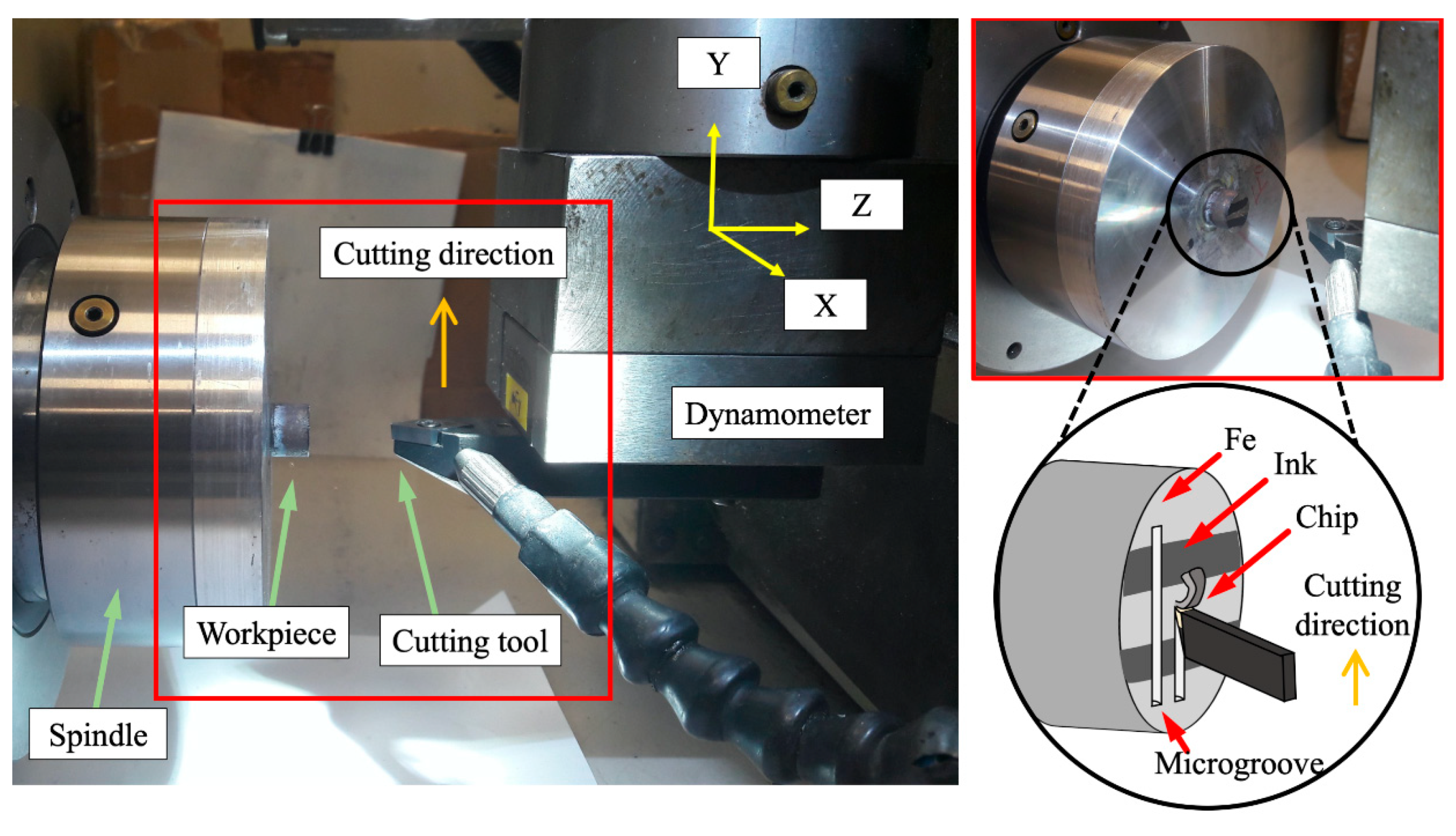
3.1. Mechanochemical Effect Validation
3.2. Diamond Turning Wear Tests
3.3. Surface Microhardness Tests
4. Experimental Results
4.1. Validation of Workpiece Modification
4.2. Diamond Tool Wear
5. Discussion
Influence of the Surface-Active Medium
6. Finite Element Analysis
6.1. Model Setup
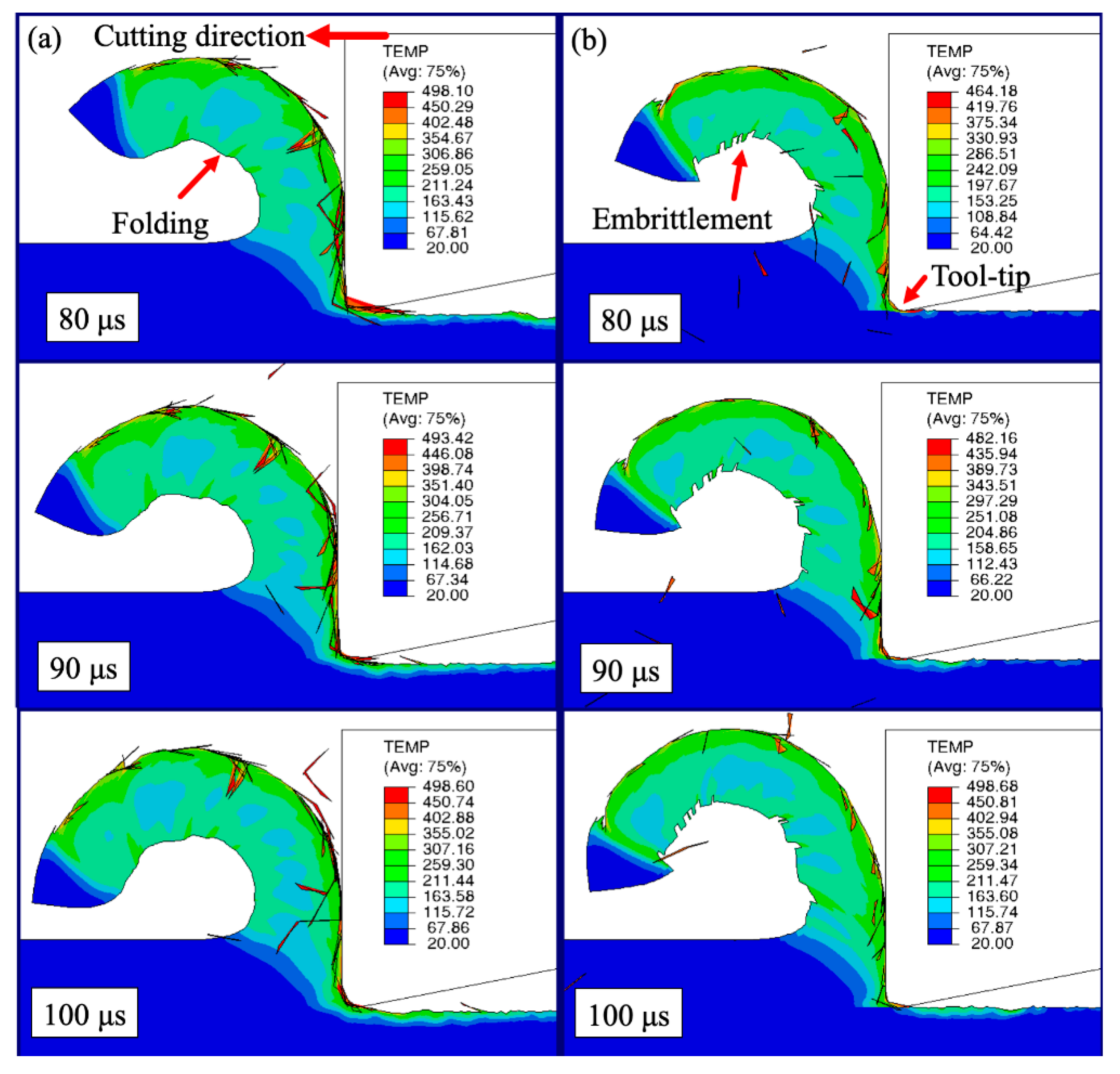
6.2. Simulated Mechanochemical Effect
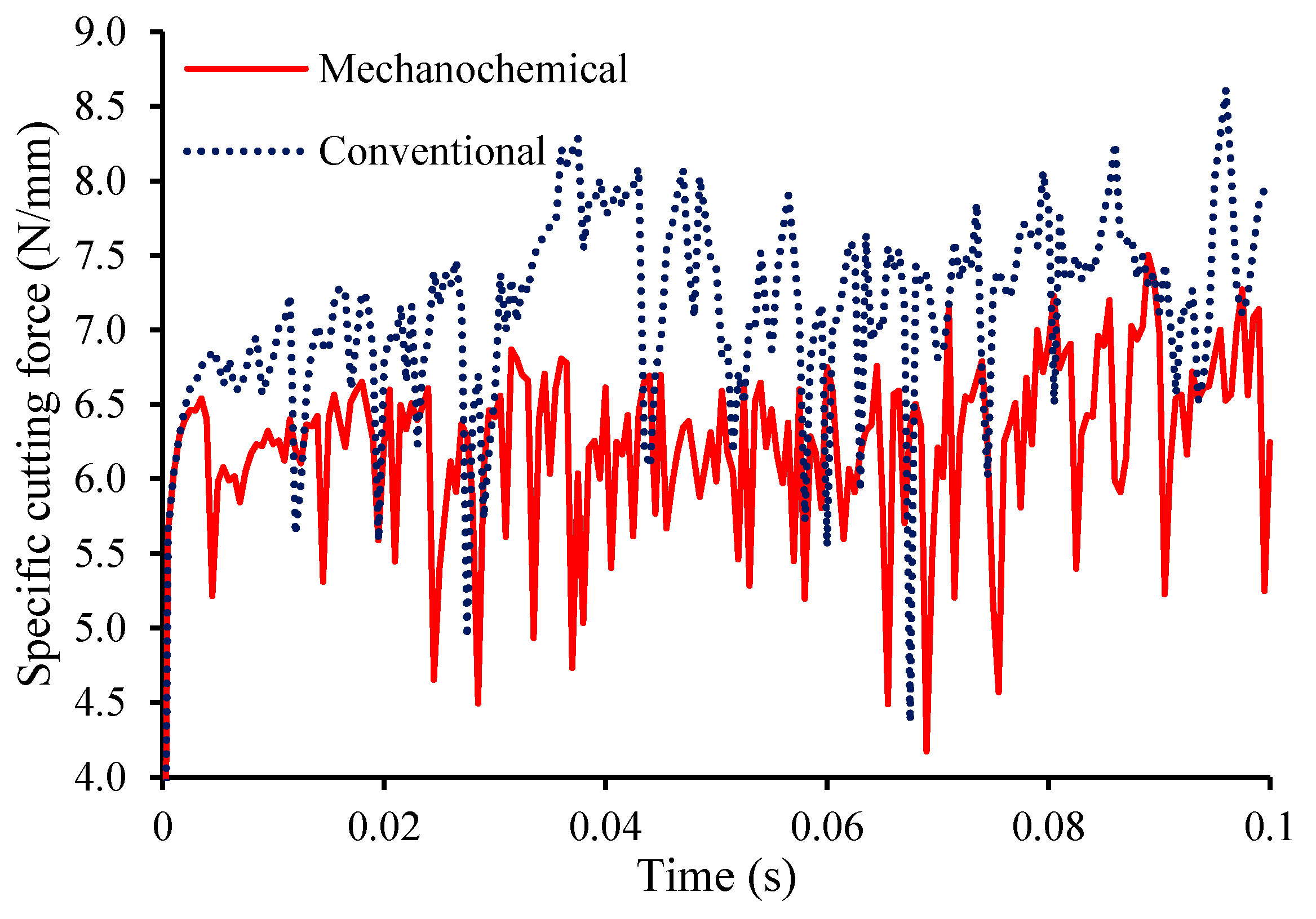
6.3. Simulation Results and Discussion
7. Conclusions
- The phenomenon is validated on iron by a 30% reduction in cutting forces and the production of thinner chips with embrittlement characteristics during orthogonal microcutting with a cubic boron nitride (CBN) cutting tool;
- Diamond turning with polycrsyalline diamond (PCD) on a chemisorbed workpiece can reduce flank wear by up to 56% and improve the surface roughness by 27% over a machining distance of 58.8 m;
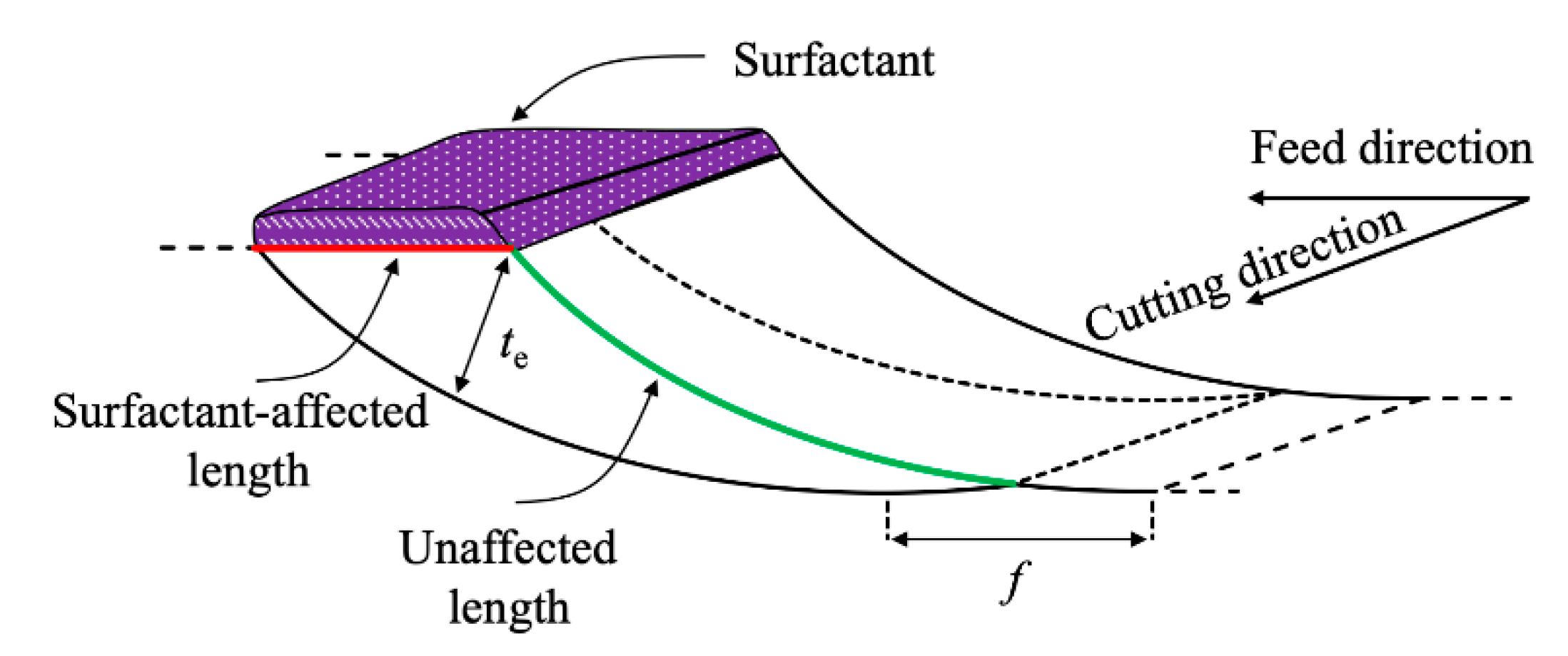
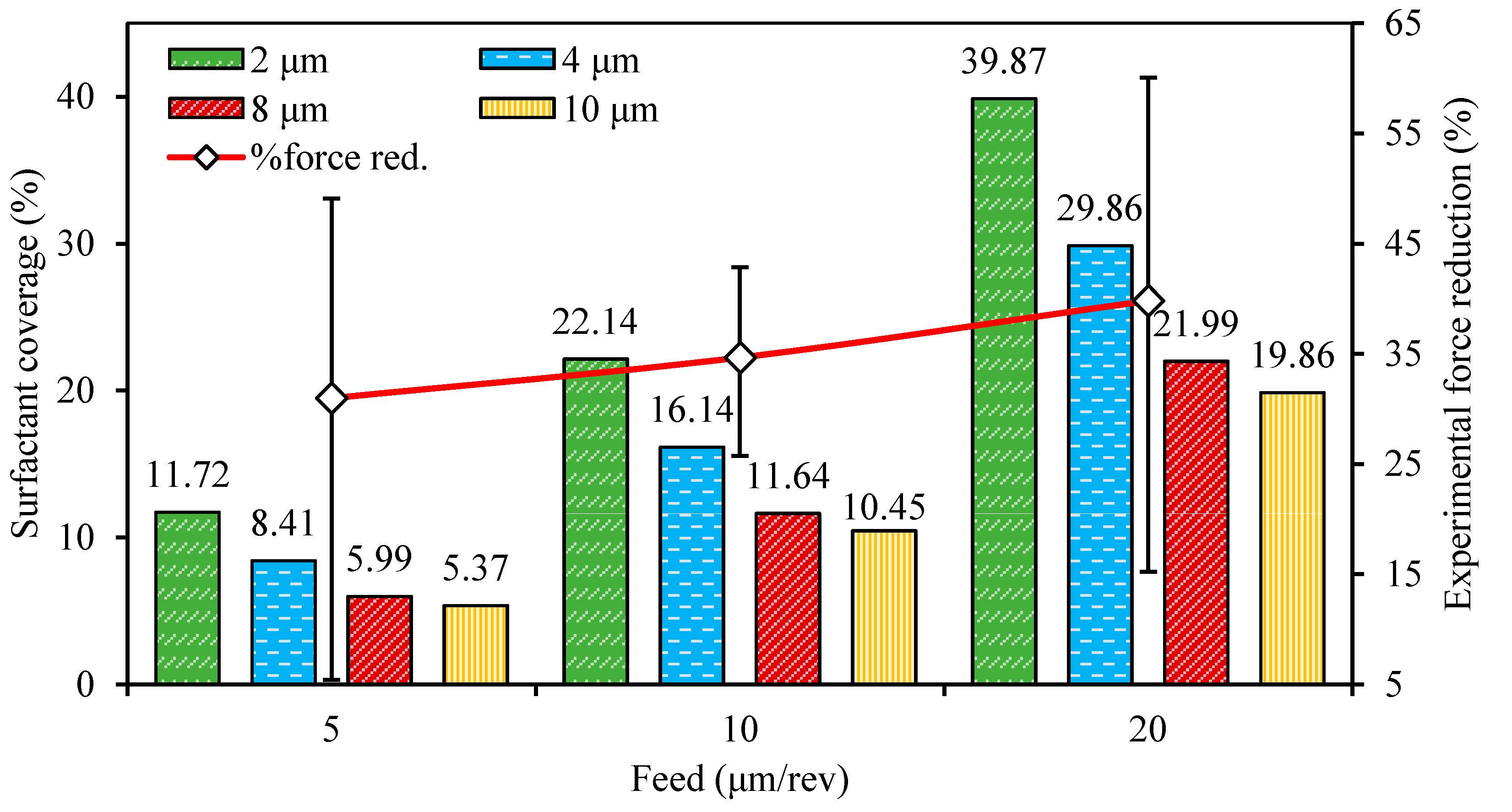
- The percentage reduction in cutting forces and tool wear during diamond turning with the mechanochemical effect increases with feed due to the enlargement of effective uncut chip thickness and surfactant-affected material;
- A finite element model utilizes the fracture energy parameter to simulate the chemisorption effect and demonstrate the reduction in chip thickness, shorter tool–chip contact, chip embrittlement, and the reduction in heat generation on the machined surface; and
- It is proposed that although heat generation can be reduced to mitigate diamond tool wear due to lower cutting energies under the mechanochemical effect, the heat generated during strain localization also contributes to the overall cutting temperature, to the extent that the reduction in tool wear does not coincide with the reduction in cutting forces or surfactant coverage.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Chen, Y.; Zhang, L. Understanding the material removal mechanisms. In Polishing of Diamond Materials: Mechanisms, Modeling and Implementation; Springer: London, UK, 2013; pp. 11–23. ISBN 1849964084. [Google Scholar]
- Zhang, X.Q.; Woon, K.S.; Rahman, M. Diamond turning. In Comprehensive Materials Processing; Elsevier: Amsterdam, The Netherlands, 2014; Volume 11, pp. 201–220. ISBN 9780080965338. [Google Scholar]
- Riemer, O. Advances in Ultra Precision Manufacturing. In Proceedings of the Japan Society for Precision Engineering, Kanazawa, Japan, 20–22 September 2011. [Google Scholar]
- Brinksmeier, E.; Preuss, W. Micro-Machining. Philos. Trans. R. Soc. A 2012, 370, 3973–3992. [Google Scholar] [CrossRef] [PubMed]
- Wilks, J. Performance of diamonds as cutting tools for precision machining. Precis. Eng. 1980, 2, 57–72. [Google Scholar] [CrossRef]
- Cheng, K.; Huo, D. Micro-Cutting: Fundamentals and Applications; Cheng, K., Huo, D., Eds.; John Wiley & Sons, Ltd.: West Sussex, UK, 2013; ISBN 9780470972878. [Google Scholar]
- Dewidar, M.M.; Khalil, K.A.; Lim, J.K. Processing and mechanical properties of porous 316L stainless steel for biomedical applications. Trans. Nonferr. Met. Soc. China 2007, 17, 468–473. [Google Scholar] [CrossRef]
- Niinomi, M. Recent metallic materials for biomedical applications. Metall. Mater. Trans. A 2002, 33, 477–486. [Google Scholar] [CrossRef]
- Li, Z.J.; Fang, F.Z.; Gong, H.; Zhang, X.D. Review of diamond-cutting ferrous metals. Int. J. Adv. Manuf. Technol. 2013, 68, 1717–1731. [Google Scholar] [CrossRef]
- Paul, E.; Evans, C.J.; Mangamelli, A.; Mcglauflin, M.L.; Polvanit, R.S. Chemical aspects of tool wear in single point diamond turning. Precis. Eng. 1996, 18, 4–19. [Google Scholar] [CrossRef]
- Casstevens, J.M. Diamond turning of steel in carbon-saturated atmospheres. Precis. Eng. 1983, 5, 9–15. [Google Scholar] [CrossRef]
- Evans, C.; Bryan, J.B. Cryogenic diamond turning of stainless steel. CIRP Ann. Manuf. Technol. 1991, 40, 571–575. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Gläbe, R. Advances in precision machining of steel. CIRP Ann. 2001, 50, 385–388. [Google Scholar] [CrossRef]
- Brinksmeier, E.; Gläbe, R. Precision Machining of Steel with Ultrasonically Driven Chilled Diamond Tools. In Proceedings of the American Society for Precision Engineering, St. Louis, MO, USA, 20–25 October 2002. [Google Scholar]
- Shamoto, E.; Moriwaki, T. Ultaprecision diamond cutting of hardened steel by applying elliptical vibration cutting. Ann. CIRP 1999, 48, 441–444. [Google Scholar] [CrossRef]
- Wang, Y.; Suzuki, N.; Shamoto, E.; Zhao, Q. Investigation of tool wear suppression in ultraprecision diamond machining of die steel. Precis. Eng. 2011, 35, 677–685. [Google Scholar] [CrossRef]
- Hartley, N.E.W. Mechanical property improvements on ion implanted diamond. Metastab. Mater. Form. Ion Implant. 1982, 7, 295–301. [Google Scholar] [CrossRef]
- Lee, Y.J.; Hao, L.; Lüder, J.; Chaudhari, A.; Wang, S.; Manzhos, S.; Wang, H. Micromachining of ferrous metal with an ion implanted diamond cutting tool. Carbon N. Y. 2019, 152, 598–608. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, K.; Kumar, A.S.; Rahman, M. A study of the diamond tool wear suppression mechanism in vibration-assisted machining of steel. J. Mater. Process. Technol. 2014, 214, 496–506. [Google Scholar] [CrossRef]
- Zhang, X.; Deng, H.; Liu, K. Oxygen-Shielded ultrasonic vibration cutting to suppress the chemical wear of diamond tools. CIRP Ann. 2019, 68, 69–72. [Google Scholar] [CrossRef]
- Grosskreutz, J.C. The effect of oxide films on dislocation-surface interactions in aluminium. Surf. Sci. 1967, 8, 173–190. [Google Scholar] [CrossRef]
- Shimada, S.; Tanaka, H.; Higuchi, M.; Yamaguchi, T.; Honda, S.; Obata, K. Thermo-Chemical wear mechanism of diamond tool in machining of ferrous metals. CIRP Ann. Manuf. Technol. 2004, 53, 57–60. [Google Scholar] [CrossRef]
- Lee, Y.J.; Wang, H. Current understanding of surface effects in microcutting. Mater. Des. 2020, 192, 108688. [Google Scholar] [CrossRef]
- Malkin, A.I. Regularities and mechanisms of the Rehbinder’s effect. Colloid J. 2012, 74, 223–238. [Google Scholar] [CrossRef]
- Rehbinder, P.A. On the effect of changes in the surface energy upon cleavage, hardness, and other crystal properties. In Proceedings of the VI-th Congress of Russian Physicists, Moscow, Russia, 5–16 August 1928; p. 29. [Google Scholar]
- Chaudhari, A.; Soh, Z.Y.; Wang, H.; Kumar, A.S. Rehbinder effect in ultraprecision machining of ductile materials. Int. J. Mach. Tools Manuf. 2018, 133, 47–60. [Google Scholar] [CrossRef]
- Udupa, A.; Viswanathan, K.; Saei, M.; Mann, J.B.; Chandrasekar, S. Material-Independent mechanochemical effect in the deformation of highly-strain-hardening metals. Phys. Rev. Appl. 2018, 10, 1. [Google Scholar] [CrossRef]
- Yeung, H.; Viswanathan, K.; Compton, W.D.; Chandrasekar, S. Sinuous flow in metals. Proc. Natl. Acad. Sci. USA 2015, 112, 9828–9832. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, A.; Wang, H. Effect of surface-active media on chip formation in micromachining. J. Mater. Process. Technol. 2019, 271, 325–335. [Google Scholar] [CrossRef]
- Atkins, A.G. Modelling metal cutting using modern ductile fracture mechanics: Quantitative explanations for some longstanding problems. Int. J. Mech. Sci. 2003, 45, 373–396. [Google Scholar] [CrossRef]
- Atkins, A.G.; Liu, J.H. Toughness and the transition between cutting and rubbing in abrasive contacts. Wear 2007, 262, 146–159. [Google Scholar] [CrossRef]
- Chan, C.Y.; Lee, W.B.; Wang, H. Enhancement of surface finish using water-miscible nano-cutting fluid in ultra-precision turning. Int. J. Mach. Tools Manuf. 2013, 73, 62–70. [Google Scholar] [CrossRef]
- Shchukin, E.D. The influence of surface-active media on the mechanical properties of materials. Adv. Colloid Interface Sci. 2006, 123, 33–47. [Google Scholar] [CrossRef]
- Simoneau, A.; Ng, E.; Elbestawi, M.A. Surface defects during microcutting. Int. J. Mach. Tools Manuf. 2006, 46, 1378–1387. [Google Scholar] [CrossRef]
- Simoneau, A.; Ng, E.; Elbestawi, M.A. Chip formation during microscale cutting of a medium carbon steel. Int. J. Mach. Tools Manuf. 2006, 46, 467–481. [Google Scholar] [CrossRef]
- Simoneau, A.; Ng, E.; Elbestawi, M.A. Grain size and orientation effects when microcutting AISI 1045 steel. CIRP Ann. 2007, 56, 57–60. [Google Scholar] [CrossRef]
- Lee, Y.J.; Chong, J.Y.; Chaudhari, A.; Wang, H. Enhancing ductile-mode cutting of calcium fluoride single crystals with solidified coating. Int. J. Precis. Eng. Manuf. Technol. 2019, 1–11. [Google Scholar] [CrossRef]
- Wang, H.; To, S.; Chan, C.Y. Investigation on the influence of tool-tip vibration on surface roughness and its representative measurement in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2013, 69, 20–29. [Google Scholar] [CrossRef]
- Rahman, M.A.; Amrun, M.R.; Rahman, M.; Kumar, A.S. Variation of surface generation mechanisms in ultra-precision machining due to relative tool sharpness (RTS) and material properties. Int. J. Mach. Tools Manuf. 2017, 115, 15–28. [Google Scholar] [CrossRef]
- Zhao, T.; Zhou, J.M.; Bushlya, V.; Ståhl, J.E. Effect of cutting edge radius on surface roughness and tool wear in hard turning of AISI 52100 steel. Int. J. Adv. Manuf. Technol. 2017, 91, 3611–3618. [Google Scholar] [CrossRef]
- Gavriljuk, V.G.; Shanina, B.D.; Shyvanyuk, V.N.; Teus, S.M. Electronic effect on hydrogen brittleness of austenitic steels. J. Appl. Phys. 2010, 108, 83723. [Google Scholar] [CrossRef]
- Teus, S.M.; Shanina, B.D.; Konchits, A.A.; Mogilny, G.S.; Gavriljuk, V.G. Mechanism of embrittlement of metals by surface-active elements. Metallofiz. Noveishie Tekhnologii 2018, 40, 201–218. [Google Scholar] [CrossRef]
- Wang, H.; To, S.; Chan, C.Y.; Cheung, C.F.; Lee, W.B. Elastic strain induced shear bands in the microcutting process. Int. J. Mach. Tools Manuf. 2010, 50, 9–18. [Google Scholar] [CrossRef]
- Abukhshim, N.A.; Mativenga, P.T.; Sheikh, M.A. Heat generation and temperature prediction in metal cutting: A review and implications for high speed machining. Int. J. Mach. Tools Manuf. 2006, 46, 782–800. [Google Scholar] [CrossRef]
- Toropov, A.; Ko, S.-L. Prediction of tool-chip contact length using a new slip-line solution for orthogonal cutting. Int. J. Mach. Tools Manuf. 2003, 43, 1209–1215. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part II: Temperature rise distribution due to frictional heat source at the tool-chip interface. Int. J. Mech. Sci. 2001, 43, 57–88. [Google Scholar] [CrossRef]
- Narulkar, R.; Bukkapatnam, S.; Raff, L.M.; Komanduri, R. Graphitization as a precursor to wear of diamond in machining pure iron: A molecular dynamics investigation. Comput. Mater. Sci. 2009, 45, 358–366. [Google Scholar] [CrossRef]
- Johnson, R.G.; Cook, W. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the Seventh International Symposium on Ballistics, The Hague, The Netherlands, 18–21 April 1983. [Google Scholar]
- Elango, P.; Marimuthu, K.P. Numerical validation of drilling of Al6061-T6 with experimental data. Mech. Mech. Eng. 2019, 23, 287–290. [Google Scholar] [CrossRef][Green Version]
- Akram, S.; Jaffery, S.H.I.; Khan, M.; Fahad, M.; Mubashar, A.; Ali, L. Numerical and experimental investigation of Johnson-Cook material models for aluminum (Al 6061-T6) alloy using orthogonal machining approach. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Atlati, S.; Haddag, B.; Nouari, M.; Zenasni, M. Analysis of a new Segmentation Intensity Ratio “SIR” to characterize the chip segmentation process in machining ductile metals. Int. J. Mach. Tools Manuf. 2011, 51, 687–700. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Mabrouki, T.; Nelias, D.; Gong, Y.D. Chip formation in orthogonal cutting considering interface limiting shear stress and damage evolution based on fracture energy approach. Finite Elem. Anal. Des. 2011, 47, 850–863. [Google Scholar] [CrossRef]
- Mabrouki, T.; Girardin, F.; Asad, M.; Rigal, J.-F. Numerical and experimental study of dry cutting for an aeronautic aluminium alloy (A2024-T351). Int. J. Mach. Tools Manuf. 2008, 48, 1187–1197. [Google Scholar] [CrossRef]







| Modification | Theoretical Approach | Application |
|---|---|---|
| Process | Reducing temperatures | Cryogenic turning [12,13,14] |
| Prohibition of chemical reactions | Machining in inert environments [10,11] | |
| Reducing tool–workpiece contact time | Ultrasonic vibration assisted machining [15,16] | |
| Tool | Prohibition of chemical reactions | Protective coatings [13] |
| Inhibiting reaction rates | Ion implantation [17,18] | |
| Workpiece | Prohibition of chemical reactions | Surface compound layer formation [13] |
| C | Mn | Si | P | S | Cr | Ni | V | Ti | Al | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.35 | 0.15 | 0.03 | 0.025 | 0.2 | 0.15 | 0.1 | 0.1 | 0.1 | Bal. |
| E (GPa) | v | ρ (g/cm3) | A (MPa) | B (MPa) | n | C | m | cp (J/g°C) | Tm (°C) | k (W/m°C) |
|---|---|---|---|---|---|---|---|---|---|---|
| 70 | 0.33 | 2.7 | 324.1 | 113.8 | 0.002 | 0.011 | 1.34 | 896 | 583 | 167 |
| D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|
| −0.77 | 1.45 | −0.47 | 0 | 1.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.J.; Shen, Y.-K.; Wang, H. Suppression of Polycrystalline Diamond Tool Wear with Mechanochemical Effects in Micromachining of Ferrous Metal. J. Manuf. Mater. Process. 2020, 4, 81. https://doi.org/10.3390/jmmp4030081
Lee YJ, Shen Y-K, Wang H. Suppression of Polycrystalline Diamond Tool Wear with Mechanochemical Effects in Micromachining of Ferrous Metal. Journal of Manufacturing and Materials Processing. 2020; 4(3):81. https://doi.org/10.3390/jmmp4030081
Chicago/Turabian StyleLee, Yan Jin, Yung-Kang Shen, and Hao Wang. 2020. "Suppression of Polycrystalline Diamond Tool Wear with Mechanochemical Effects in Micromachining of Ferrous Metal" Journal of Manufacturing and Materials Processing 4, no. 3: 81. https://doi.org/10.3390/jmmp4030081
APA StyleLee, Y. J., Shen, Y.-K., & Wang, H. (2020). Suppression of Polycrystalline Diamond Tool Wear with Mechanochemical Effects in Micromachining of Ferrous Metal. Journal of Manufacturing and Materials Processing, 4(3), 81. https://doi.org/10.3390/jmmp4030081







