Partition of Primary Shear Plane Heat in Orthogonal Metal Cutting
Abstract
1. Introduction
2. State of the Art on Heat Partition in Orthogonal Metal Cutting
2.1. Analytical Modeling Approaches
2.2. Numerical Modeling Approaches
2.3. Experimental Approaches
2.4. Conclusions from the State of the Art
3. Objectives and Procedure
4. Materials and Methods
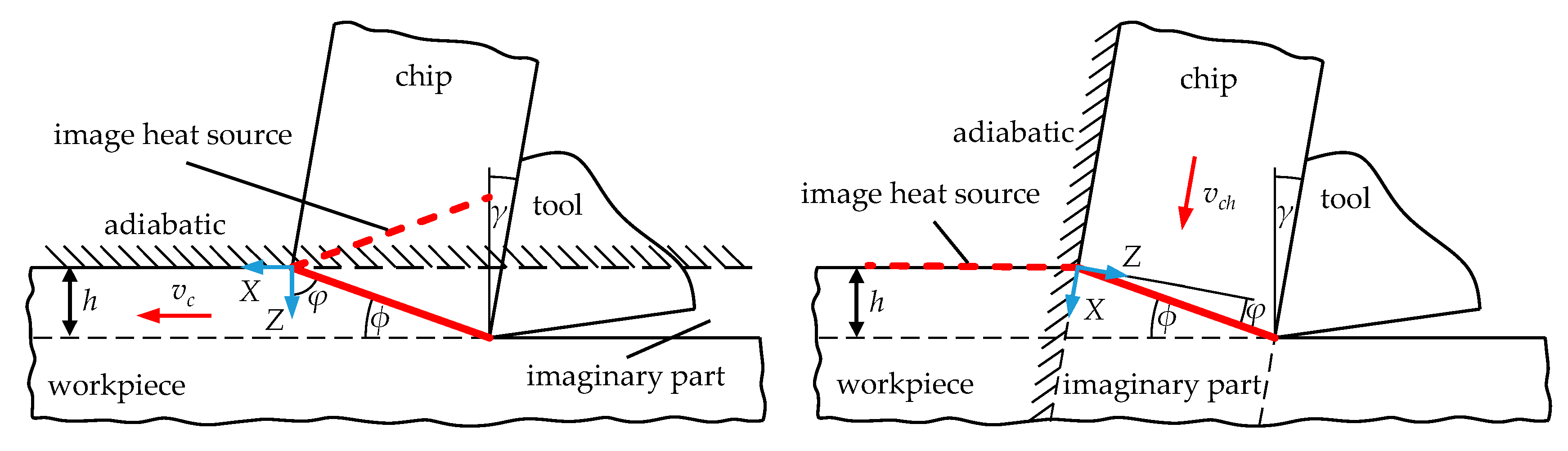
4.1. Implementation of the Analytical Model by Komanduri and Hou
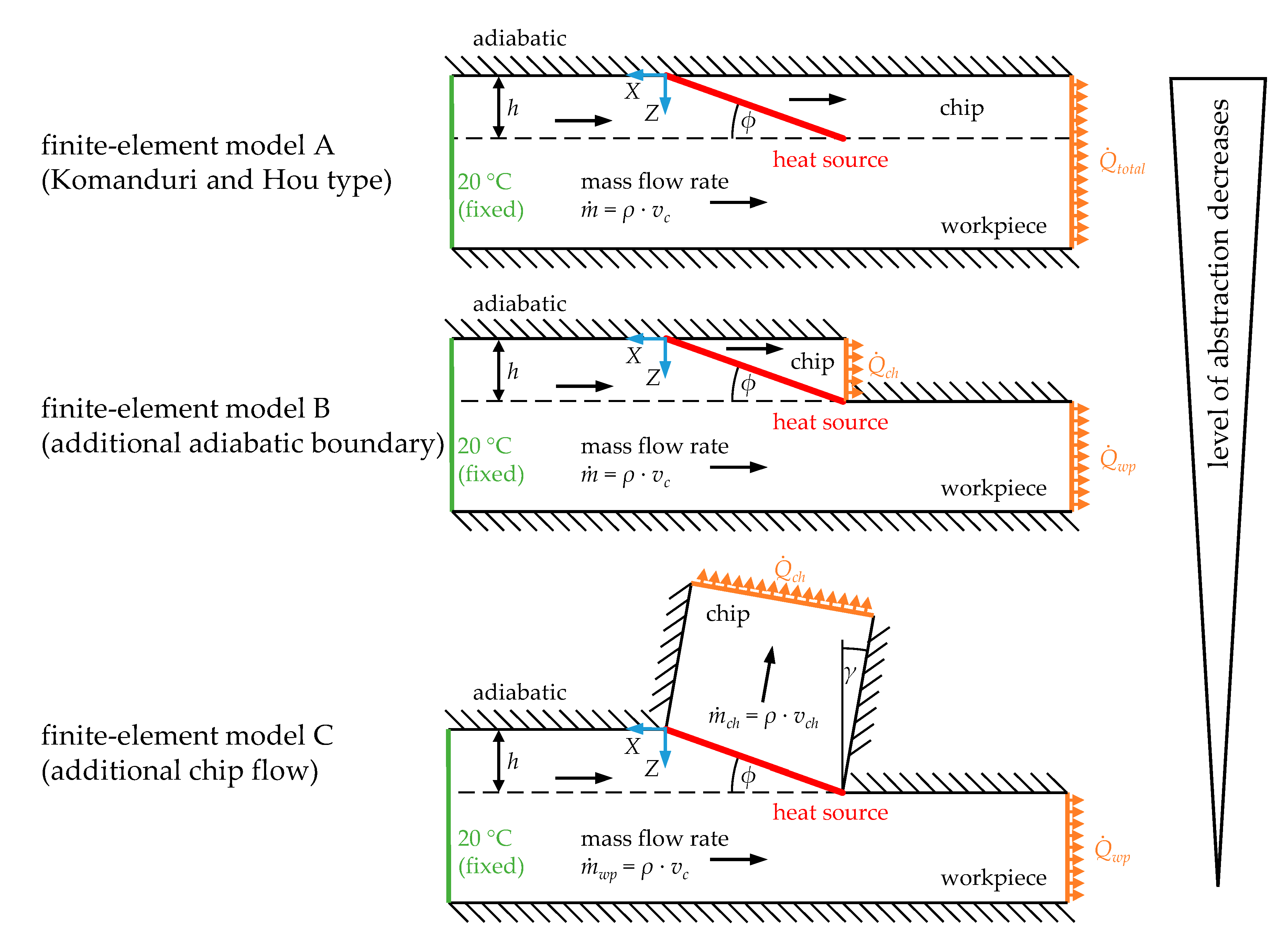
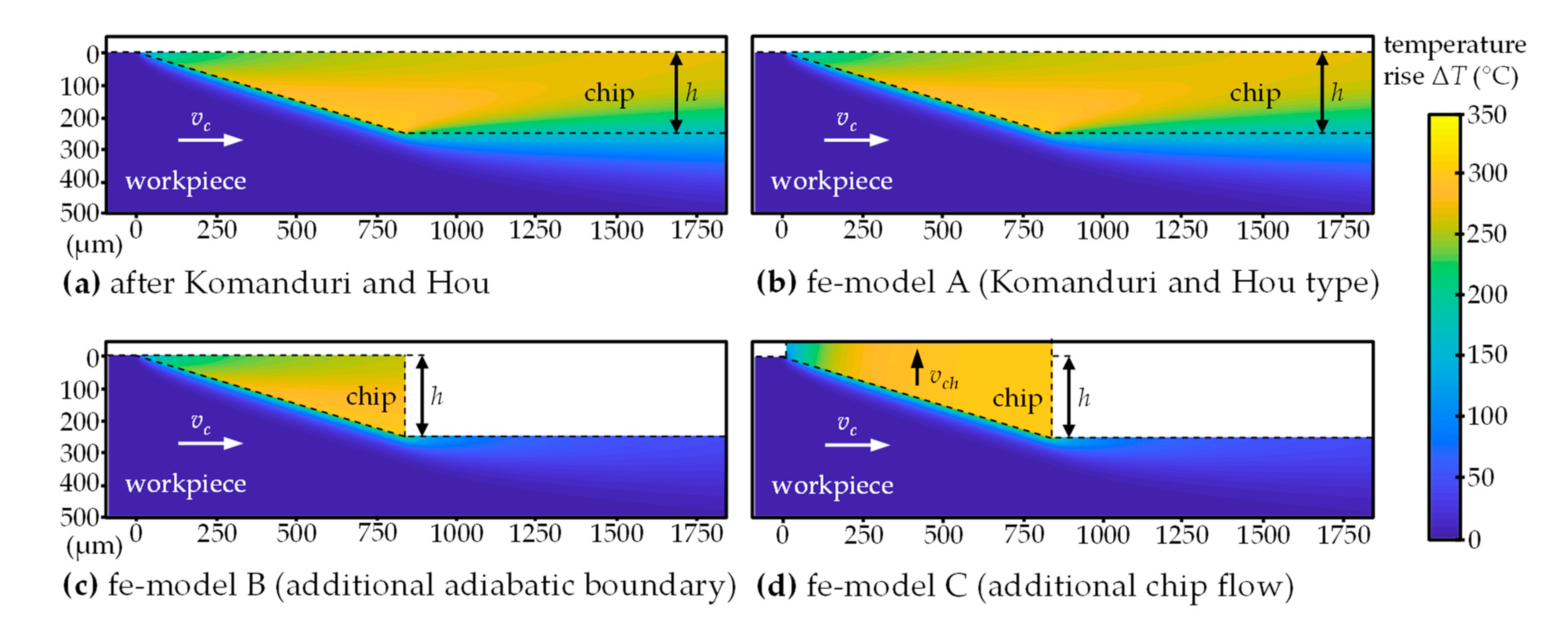
4.2. Development of a Finite-Element Model for Calculating Steady-State Temperature Fields
4.3. Calculation of Heat Partition Using Temperature Fields
4.4. Orthogonal Metal Cutting Data for Thermal Analysis
5. Results and Discussion
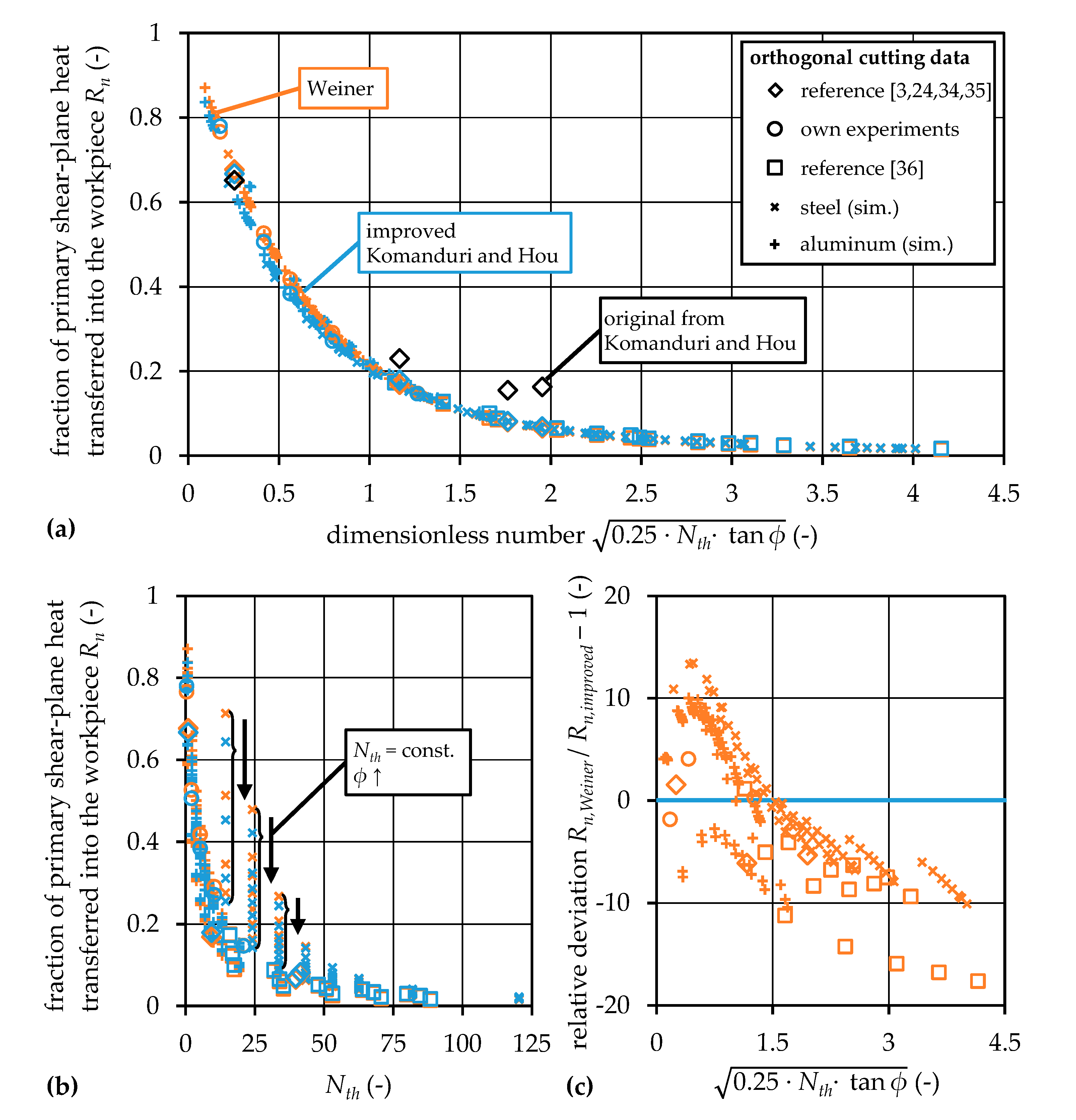
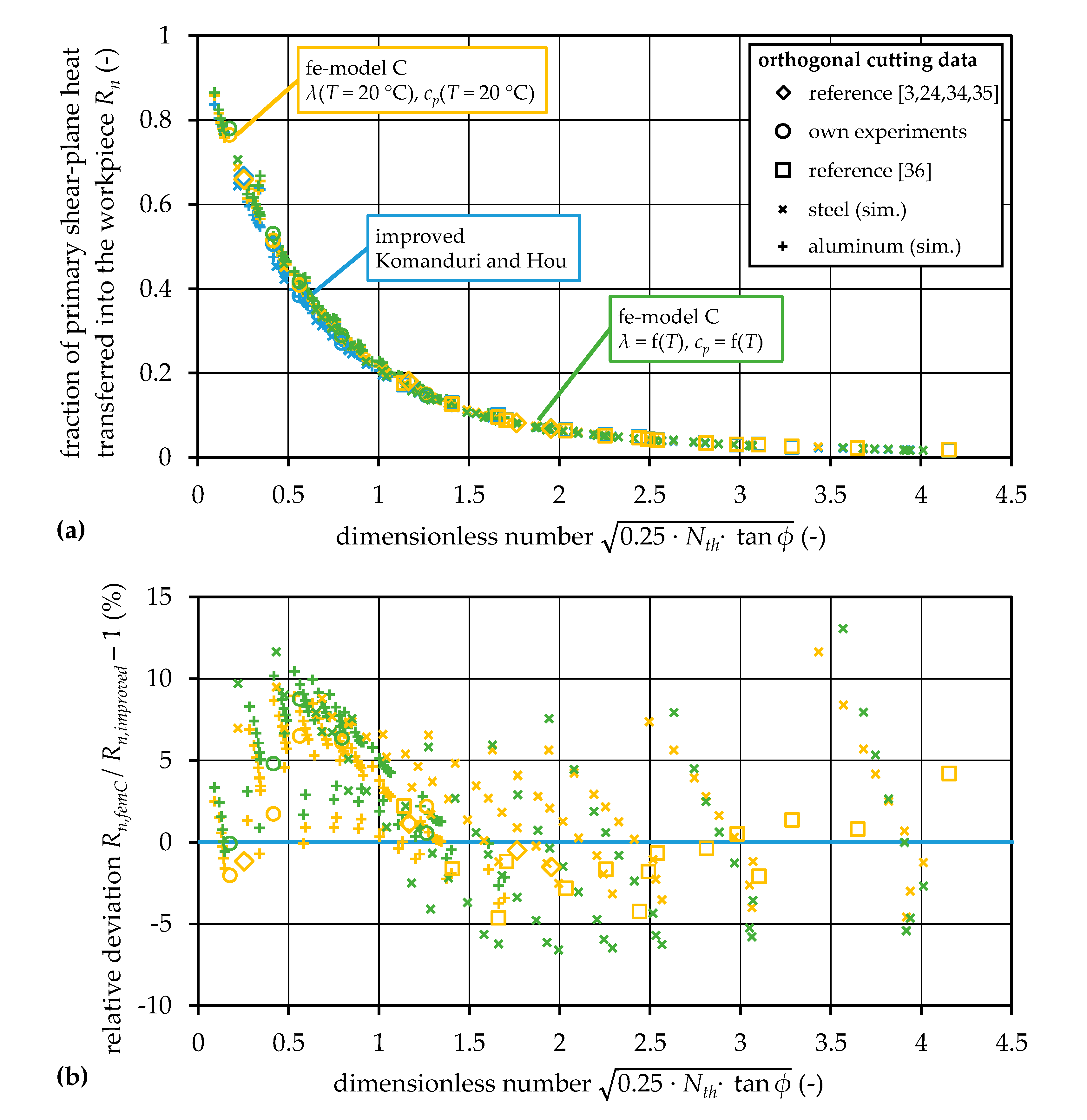
5.1. Improved Calculation of the Heat Partition for Komanduri and Hou’s Model
5.2. Orthogonal Metal Cutting Data for Thermal Analysis
5.3. Comparison of Heat Partition by Weiner and Improved Komanduri and Hou
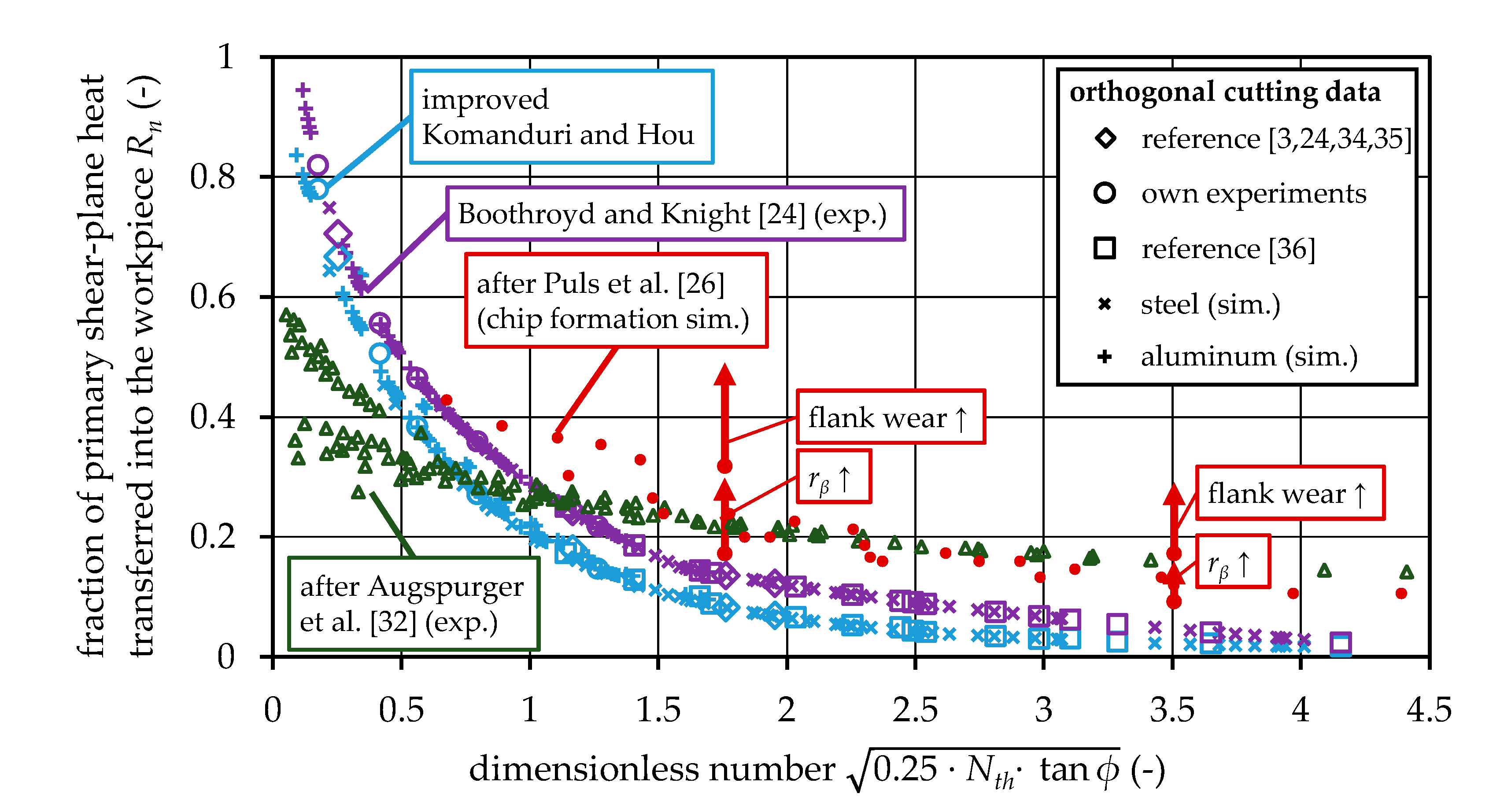
5.4. Investigation on Additional Influencing Factors on Heat Partition
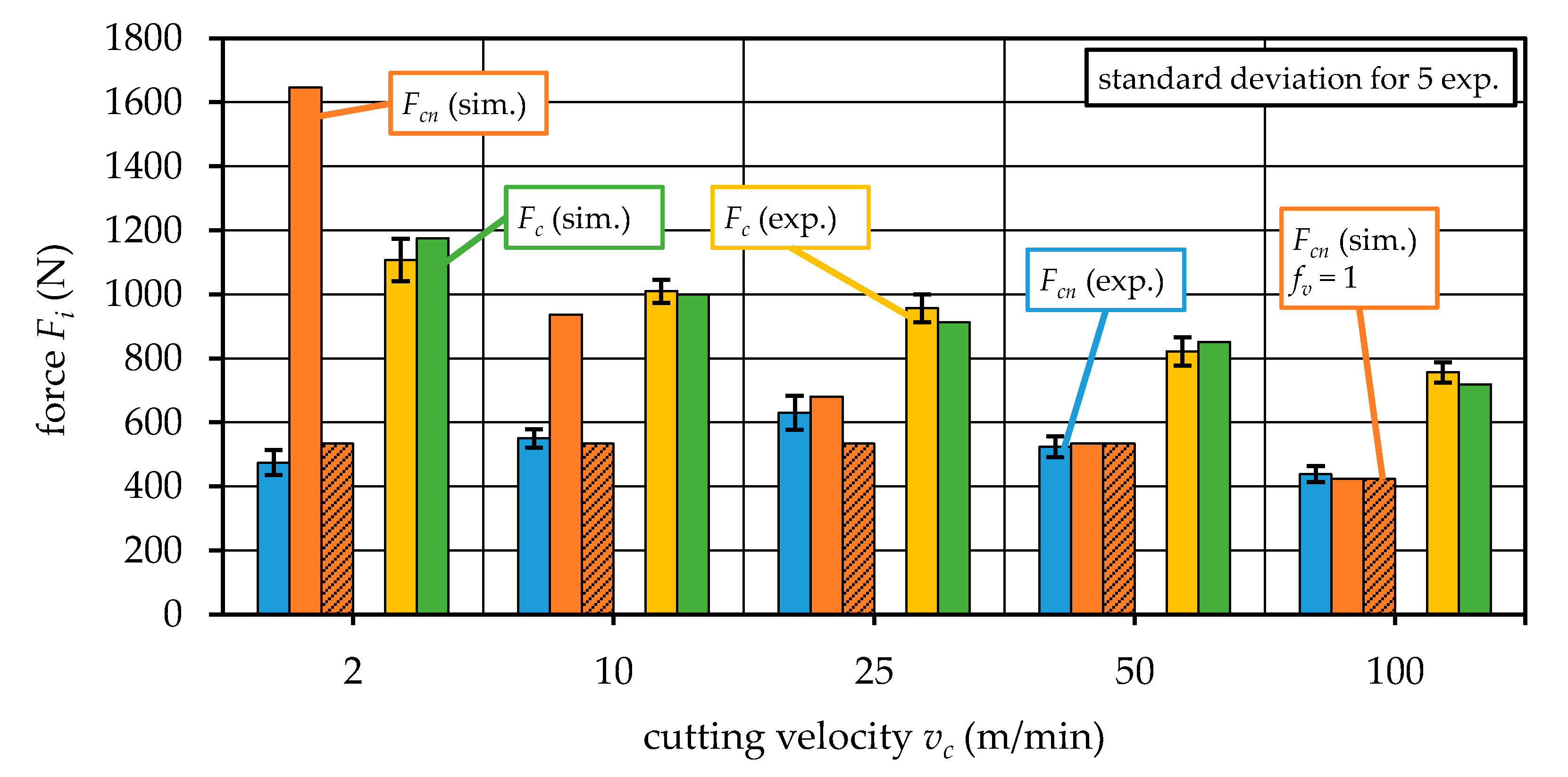
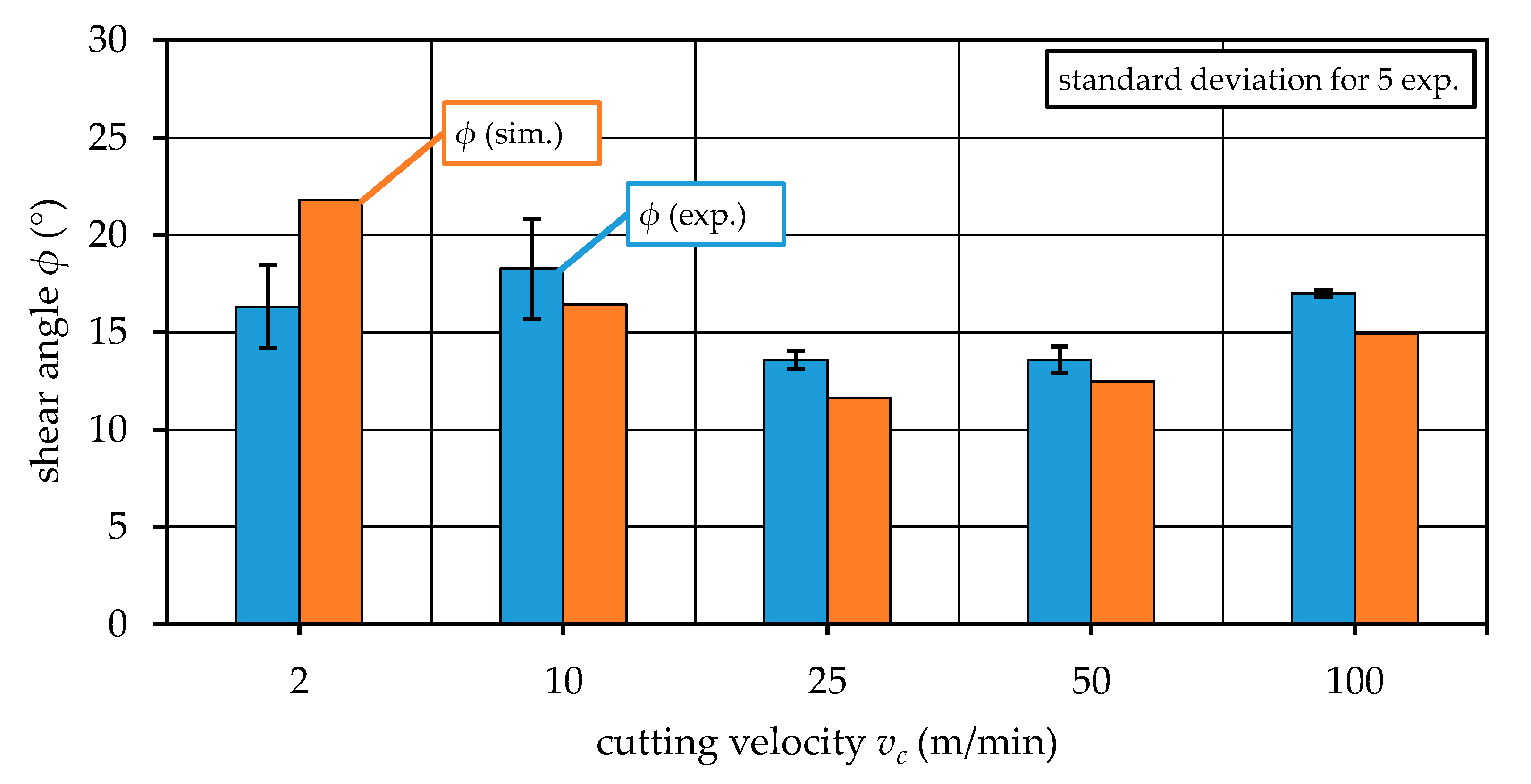
5.5. Comparison with Measurements
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Quantity |
| a | thermal diffusivity |
| cp | specific isobaric heat capacity |
| cv | specific isochoric heat capacity |
| erf | error function |
| erfc | complementary error function |
| Fc | cutting force |
| Fcn | thrust force |
| Fs | shear force |
| h | uncut chip thickness |
| hch | chip thickness |
| K0 | modified Bessel function of second kind of zero order |
| L | length of shear plane |
| lc | uncut chip length |
| lch | chip length |
| m | mass |
| mch | chip weight |
| mass flow rate | |
| mass flow rate in the chip | |
| mass flow rate in the workpiece | |
| Nth | thermal number |
| nX | total amount of elements in X-direction |
| nZ | total amount of elements in Z-direction |
| p | friction angle |
| Ps | total shear power |
| shear plane heat flux density | |
| Q | heat |
| heat flow rate into the chip | |
| total heat flow rate | |
| heat flow rate into the workpiece | |
| r2 | coefficient of determination |
| RAugspurger | fraction of total cutting power transferred into the workpiece from Augspurger |
| Rn | fraction of shear plane heat transferred into the workpiece |
| rβ | cutting edge radius |
| s | distance along shear plane |
| Δt | time period |
| T | temperature |
| ΔT | temperature rise |
| mean temperature rise in the chip | |
| ΔTM | temperature rise in point M(X,Z) in Komanduri and Hou’s model |
| tol | tolerance of temperature differences |
| v | velocity |
| vc | cutting velocity |
| vch | chip velocity |
| vs | shear velocity |
| V | volume |
| w | width |
| Δx | distance of grid points in X-direction |
| YL | auxiliary variable in Weiner’s model |
| Δz | distance of grid points in Z-direction |
| γ | rake angle |
| λ | thermal conductivity |
| λl | chip length ratio |
| ρ | density |
| φ | auxiliary angle in Komanduri and Hou’s model |
| ϕ | shear angle |
Appendix A
| Source | Nth | h (µm) | vc (m/min) | ϕ (°) | (W/mm2) | Source | Nth | h (µm) | vc (m/min) | ϕ (°) | (W/mm2) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [3] | 9.4 | 60.0 | 139.2 | 30.1 | 1182.9 | sim. | 10.1 | 90.8 | 450.0 | 30.8 | 3735.2 |
| [24] | 41.5 | 250.0 | 120.0 | 16.7 | 634.4 | sim. | 13.2 | 213.6 | 250.0 | 18.6 | 1136.0 |
| [33] | 39.7 | 248.9 | 91.4 | 21.0 | 11167.5 | sim. | 13.2 | 1068.1 | 50.0 | 15.7 | 174.0 |
| [34] | 0.9 | 10.0 | 517.8 | 15.5 | 2399.9 | sim. | 13.2 | 534.1 | 100.0 | 17.0 | 392.0 |
| [35] | 16.0 | 258.8 | 50.0 | 18.0 | 452.2 | sim. | 13.2 | 356.0 | 150.0 | 17.7 | 628.5 |
| [35] | 17.0 | 258.8 | 50.0 | 25.0 | 595.2 | sim. | 13.2 | 267.0 | 200.0 | 18.2 | 877.5 |
| [35] | 17.7 | 258.8 | 50.0 | 32.0 | 588.4 | sim. | 13.2 | 178.0 | 300.0 | 18.9 | 1402.3 |
| [35] | 31.9 | 258.8 | 100.0 | 20.0 | 948.5 | sim. | 13.2 | 89.0 | 600.0 | 25.1 | 4012.0 |
| [35] | 33.9 | 258.8 | 100.0 | 26.0 | 1140.3 | sim. | 13.2 | 152.6 | 350.0 | 29.8 | 2554.1 |
| [35] | 35.3 | 258.8 | 100.0 | 34.0 | 1172.9 | sim. | 13.2 | 118.7 | 450.0 | 30.8 | 3506.3 |
| [35] | 47.9 | 258.8 | 150.0 | 23.0 | 1564.2 | sim. | 14.5 | 62.8 | 150.0 | 2.9 | 373.5 |
| [35] | 50.9 | 258.8 | 150.0 | 26.0 | 1728.1 | sim. | 14.5 | 47.1 | 200.0 | 0.8 | 138.0 |
| [35] | 53.0 | 258.8 | 150.0 | 36.0 | 1755.5 | sim. | 14.5 | 94.2 | 100.0 | 7.4 | 632.0 |
| [35] | 63.9 | 258.8 | 200.0 | 22.0 | 2076.1 | sim. | 14.5 | 188.5 | 50.0 | 10.8 | 432.8 |
| [35] | 67.8 | 258.8 | 200.0 | 25.0 | 2204.0 | sim. | 19.4 | 523.6 | 150.0 | 19.3 | 634.7 |
| [35] | 70.7 | 258.8 | 200.0 | 37.0 | 2421.1 | sim. | 19.4 | 261.8 | 300.0 | 20.4 | 1407.3 |
| [35] | 79.9 | 258.8 | 250.0 | 24.0 | 2827.2 | sim. | 19.4 | 130.9 | 600.0 | 28.0 | 4062.2 |
| [35] | 84.8 | 258.8 | 250.0 | 27.0 | 2829.7 | sim. | 19.4 | 224.4 | 350.0 | 29.7 | 2331.6 |
| [35] | 88.4 | 258.8 | 250.0 | 38.0 | 2876.5 | sim. | 19.4 | 1570.8 | 50.0 | 17.4 | 177.9 |
| exp. | 0.4 | 120.0 | 2.0 | 16.3 | 36.1 | sim. | 19.4 | 785.4 | 100.0 | 18.6 | 397.5 |
| exp. | 2.1 | 120.0 | 10.0 | 18.3 | 171.1 | sim. | 19.4 | 392.7 | 200.0 | 19.8 | 883.8 |
| exp. | 5.2 | 120.0 | 25.0 | 13.6 | 316.1 | sim. | 19.4 | 314.2 | 250.0 | 20.1 | 1141.9 |
| exp. | 10.4 | 120.0 | 50.0 | 13.6 | 545.4 | sim. | 19.4 | 174.5 | 450.0 | 30.7 | 3201.6 |
| exp. | 20.9 | 120.0 | 100.0 | 17.0 | 1202.4 | sim. | 24.1 | 34.9 | 450.0 | 2.2 | 824.5 |
| sim. | 0.8 | 62.8 | 50.0 | 2.5 | 51.1 | sim. | 24.1 | 44.9 | 350.0 | 4.0 | 1148.3 |
| sim. | 0.8 | 31.4 | 100.0 | 4.0 | 168.6 | sim. | 24.1 | 52.4 | 300.0 | 5.2 | 1230.1 |
| sim. | 0.8 | 20.9 | 150.0 | 4.8 | 313.7 | sim. | 24.1 | 62.8 | 250.0 | 6.5 | 1252.0 |
| sim. | 0.8 | 15.7 | 200.0 | 5.4 | 477.3 | sim. | 24.1 | 104.7 | 150.0 | 10.2 | 1085.8 |
| sim. | 0.8 | 12.6 | 250.0 | 5.9 | 654.9 | sim. | 24.1 | 78.5 | 200.0 | 8.2 | 1207.1 |
| sim. | 0.8 | 10.5 | 300.0 | 6.3 | 844.1 | sim. | 24.1 | 157.1 | 100.0 | 13.1 | 925.9 |
| sim. | 0.8 | 9.0 | 350.0 | 30.6 | 4986.1 | sim. | 24.1 | 314.2 | 50.0 | 15.4 | 506.0 |
| sim. | 0.8 | 7.0 | 450.0 | 31.5 | 6832.5 | sim. | 33.7 | 36.7 | 600.0 | 4.9 | 2317.2 |
| sim. | 2.3 | 15.7 | 600.0 | 7.2 | 2007.6 | sim. | 33.7 | 73.3 | 300.0 | 10.0 | 2104.3 |
| sim. | 2.3 | 62.8 | 150.0 | 10.1 | 511.4 | sim. | 33.7 | 146.6 | 150.0 | 14.7 | 1417.1 |
| sim. | 2.3 | 31.4 | 300.0 | 11.5 | 1206.7 | sim. | 33.7 | 48.9 | 450.0 | 7.0 | 2372.6 |
| sim. | 2.3 | 188.5 | 50.0 | 7.8 | 125.3 | sim. | 33.7 | 62.8 | 350.0 | 8.9 | 2234.2 |
| sim. | 2.3 | 94.2 | 100.0 | 9.3 | 306.7 | sim. | 33.7 | 88.0 | 250.0 | 11.3 | 1928.9 |
| sim. | 2.3 | 47.1 | 200.0 | 10.7 | 731.9 | sim. | 33.7 | 110.0 | 200.0 | 12.8 | 1702.4 |
| sim. | 2.3 | 37.7 | 250.0 | 11.2 | 964.4 | sim. | 33.7 | 219.9 | 100.0 | 16.5 | 1049.2 |
| sim. | 2.3 | 26.9 | 350.0 | 30.3 | 3847.5 | sim. | 33.7 | 439.8 | 50.0 | 18.2 | 529.8 |
| sim. | 2.3 | 20.9 | 450.0 | 31.2 | 5276.0 | sim. | 43.4 | 80.8 | 350.0 | 12.3 | 2871.7 |
| sim. | 3.9 | 104.7 | 150.0 | 12.5 | 565.0 | sim. | 43.4 | 47.1 | 600.0 | 8.5 | 3674.8 |
| sim. | 3.9 | 26.2 | 600.0 | 13.2 | 3036.5 | sim. | 43.4 | 94.2 | 300.0 | 13.4 | 2618.3 |
| sim. | 3.9 | 62.8 | 250.0 | 13.5 | 1046.1 | sim. | 43.4 | 188.5 | 150.0 | 17.9 | 1612.4 |
| sim. | 3.9 | 52.4 | 300.0 | 13.8 | 1301.3 | sim. | 43.4 | 62.8 | 450.0 | 10.6 | 3278.9 |
| sim. | 3.9 | 44.9 | 350.0 | 30.1 | 3410.4 | sim. | 43.4 | 113.1 | 250.0 | 14.6 | 2327.4 |
| sim. | 3.9 | 34.9 | 450.0 | 31.1 | 4678.1 | sim. | 43.4 | 141.4 | 200.0 | 16.0 | 1994.3 |
| sim. | 3.9 | 314.2 | 50.0 | 10.3 | 146.4 | sim. | 43.4 | 282.7 | 100.0 | 19.0 | 1114.1 |
| sim. | 3.9 | 157.1 | 100.0 | 11.7 | 344.8 | sim. | 43.4 | 565.5 | 50.0 | 20.1 | 538.4 |
| sim. | 3.9 | 78.5 | 200.0 | 13.0 | 799.9 | sim. | 53.0 | 57.6 | 600.0 | 11.3 | 4575.8 |
| sim. | 5.4 | 146.6 | 150.0 | 14.0 | 590.5 | sim. | 53.0 | 76.8 | 450.0 | 13.3 | 3881.7 |
| sim. | 5.4 | 73.3 | 300.0 | 15.3 | 1344.6 | sim. | 53.0 | 115.2 | 300.0 | 15.9 | 2960.6 |
| sim. | 5.4 | 36.7 | 600.0 | 16.9 | 3469.5 | sim. | 53.0 | 230.4 | 150.0 | 20.2 | 1742.1 |
| sim. | 5.4 | 439.8 | 50.0 | 11.8 | 156.8 | sim. | 53.0 | 98.7 | 350.0 | 14.9 | 3296.2 |
| sim. | 5.4 | 219.9 | 100.0 | 13.2 | 363.2 | sim. | 53.0 | 138.2 | 250.0 | 17.1 | 2592.8 |
| sim. | 5.4 | 110.0 | 200.0 | 14.5 | 831.8 | sim. | 53.0 | 172.8 | 200.0 | 18.5 | 2188.5 |
| sim. | 5.4 | 88.0 | 250.0 | 14.9 | 1083.8 | sim. | 53.0 | 345.6 | 100.0 | 20.8 | 1152.3 |
| sim. | 5.4 | 62.8 | 350.0 | 30.1 | 3149.9 | sim. | 53.0 | 691.2 | 50.0 | 21.6 | 540.6 |
| sim. | 5.4 | 48.9 | 450.0 | 31.0 | 4321.7 | sim. | 62.6 | 68.1 | 600.0 | 13.5 | 5222.8 |
| sim. | 7.0 | 80.8 | 350.0 | 30.0 | 2968.3 | sim. | 62.6 | 116.7 | 350.0 | 17.0 | 3601.1 |
| sim. | 7.0 | 565.5 | 50.0 | 13.0 | 163.1 | sim. | 62.6 | 136.1 | 300.0 | 18.0 | 3206.4 |
| sim. | 7.0 | 282.7 | 100.0 | 14.3 | 374.1 | sim. | 62.6 | 204.2 | 200.0 | 20.4 | 2327.5 |
| sim. | 7.0 | 188.5 | 150.0 | 15.1 | 605.2 | sim. | 62.6 | 272.3 | 150.0 | 22.0 | 1834.5 |
| sim. | 7.0 | 141.4 | 200.0 | 15.6 | 849.9 | sim. | 62.6 | 408.4 | 100.0 | 22.3 | 1176.1 |
| sim. | 7.0 | 113.1 | 250.0 | 16.0 | 1105.0 | sim. | 62.6 | 816.8 | 50.0 | 22.8 | 539.8 |
| sim. | 7.0 | 94.2 | 300.0 | 16.4 | 1368.5 | sim. | 62.6 | 90.8 | 450.0 | 15.4 | 4314.8 |
| sim. | 7.0 | 47.1 | 600.0 | 19.4 | 3698.9 | sim. | 62.6 | 163.4 | 250.0 | 19.1 | 2783.1 |
| sim. | 7.0 | 62.8 | 450.0 | 30.9 | 4073.3 | sim. | 81.9 | 213.6 | 250.0 | 22.1 | 3038.3 |
| sim. | 8.5 | 230.4 | 150.0 | 15.9 | 614.5 | sim. | 81.9 | 89.0 | 600.0 | 16.9 | 6096.7 |
| sim. | 8.5 | 115.2 | 300.0 | 17.2 | 1383.0 | sim. | 81.9 | 118.7 | 450.0 | 18.7 | 4899.3 |
| sim. | 8.5 | 57.6 | 600.0 | 21.3 | 3834.7 | sim. | 81.9 | 152.6 | 350.0 | 20.2 | 4011.8 |
| sim. | 8.5 | 76.8 | 450.0 | 30.9 | 3885.2 | sim. | 81.9 | 178.0 | 300.0 | 21.1 | 3536.9 |
| sim. | 8.5 | 691.2 | 50.0 | 13.9 | 167.2 | sim. | 81.9 | 267.0 | 200.0 | 23.2 | 2513.0 |
| sim. | 8.5 | 345.6 | 100.0 | 15.2 | 381.1 | sim. | 81.9 | 534.1 | 100.0 | 24.4 | 1201.1 |
| sim. | 8.5 | 172.8 | 200.0 | 16.5 | 861.2 | sim. | 81.9 | 1068.1 | 50.0 | 24.6 | 534.3 |
| sim. | 8.5 | 138.2 | 250.0 | 16.9 | 1118.0 | sim. | 81.9 | 356.0 | 150.0 | 24.7 | 1956.8 |
| sim. | 8.5 | 98.7 | 350.0 | 29.9 | 2830.9 | sim. | 120.4 | 130.9 | 600.0 | 21.4 | 7061.5 |
| sim. | 10.1 | 816.8 | 50.0 | 14.6 | 170.2 | sim. | 120.4 | 224.4 | 350.0 | 24.2 | 4459.4 |
| sim. | 10.1 | 408.4 | 100.0 | 15.9 | 385.9 | sim. | 120.4 | 261.8 | 300.0 | 25.0 | 3894.9 |
| sim. | 10.1 | 272.3 | 150.0 | 16.6 | 620.9 | sim. | 120.4 | 523.6 | 150.0 | 28.1 | 2084.1 |
| sim. | 10.1 | 204.2 | 200.0 | 17.1 | 868.8 | sim. | 120.4 | 174.5 | 450.0 | 22.9 | 5540.9 |
| sim. | 10.1 | 136.1 | 300.0 | 17.9 | 1392.3 | sim. | 120.4 | 314.2 | 250.0 | 25.9 | 3312.5 |
| sim. | 10.1 | 68.1 | 600.0 | 22.8 | 3920.2 | sim. | 120.4 | 392.7 | 200.0 | 26.9 | 2709.9 |
| sim. | 10.1 | 116.7 | 350.0 | 29.9 | 2721.3 | sim. | 120.4 | 1570.8 | 50.0 | 27.0 | 519.3 |
| sim. | 10.1 | 163.4 | 250.0 | 17.5 | 1126.5 | sim. | 120.4 | 785.4 | 100.0 | 27.3 | 1213.6 |
References
- Kuschel, S.; Kolkwitz, B.; Sölter, J.; Brinksmeier, E.; Heinzel, C. Experimental and numerical analysis of residual stress change caused by thermal loads during grinding. Procedia CIRP 2016, 45, 51–54. [Google Scholar] [CrossRef]
- Novovic, D.; Aspinwall, D.K.; Dewes, R.C.; Bowen, P.; Griffiths, B. The effect of surface and subsurface condition on the fatigue life of Ti–25V–15Cr–2Al–0.2C %wt alloy. CIRP Ann. 2016, 65, 523–528. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles, 2nd ed.; Oxford University Press: New York, NY, USA, 2005; ISBN 0195142063. [Google Scholar]
- Segurajauregui, U.; Arrazola, P.J. Heat-flow determination through inverse identification in drilling of aluminium workpieces with MQL. Prod. Eng. Res. Dev. 2015, 9, 517–526. [Google Scholar] [CrossRef]
- Fleischer, J.; Pabst, R.; Kelemen, S. Heat flow simulation for dry machining of power train castings. CIRP Ann. 2007, 56, 117–122. [Google Scholar] [CrossRef]
- Sölter, J.; Frohmüller, R.; Wirbser, H. Temperature measurements and heat partitioning in machining processes. In Thermal Effects in Complex Machining Processes: Final Report of the DFG Priority Programme 1480: Lecture Notes in Production Engineering; Biermann, D., Hollmann, F., Eds.; Springer Internat. Publ: Cham, Switzerland, 2018; pp. 5–21. ISBN 978-3-319-57120-1. [Google Scholar]
- Langenhorst, L.; Cihan, M.; Sölter, J. A three dimensional calculation approach for the heat flux density distribution in face milling. Procedia CIRP 2019, 82, 8–13. [Google Scholar] [CrossRef]
- Merchant, M.E. Mechanics of the metal cutting process. I. Orthogonal cutting and a type 2 chip. J. Appl. Phys. 1945, 16, 267–275. [Google Scholar] [CrossRef]
- Jaeger, J.C. Moving sources of heat and the temperature of sliding contacts. Proc. R. Soc. N. S. W. 1942, 76, 203–224. [Google Scholar]
- Loewen, E.G.; Shaw, M.C. On the analysis of cutting tool temperatures. Trans. ASME 1954, 71, 217–231. [Google Scholar]
- Grzesik, W.; Nieslony, P. Physics based modelling of interface temperatures in machining with multilayer coated tools at moderate cutting speeds. Int. J. Mach. Tools Manuf. 2004, 44, 889–901. [Google Scholar] [CrossRef]
- Sölter, J.; Gulpak, M. Heat partitioning in dry milling of steel. CIRP Ann. 2012, 61, 87–90. [Google Scholar] [CrossRef]
- Malkin, S.; Guo, C. Thermal analysis of grinding. CIRP Ann. 2007, 56, 760–782. [Google Scholar] [CrossRef]
- Hahn, R.S. On the temperature developed at the shear plane in the metal cutting process. In Proceedings of the First U.S. National Congress of Applied Mechanics, Chicago, IL, USA, 11–16 June 1951; pp. 661–666. [Google Scholar]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process Part I—Temperature rise distribution due to shear plane heat source. Int. J. Mech. Sci. 2000, 42, 1715–1752. [Google Scholar] [CrossRef]
- Chao, B.T.; Trigger, K.J. The significance of thermal number in metal machining. Trans. ASME 1953, 75, 109–120. [Google Scholar]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part II: Temperature rise distribution due to frictional heat source at the tool-chip interface. Int. J. Mech. Sci. 2001, 43, 57–88. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part III: Temperature rise distribution due to the combined effects of shear plane heat source and the tool-chip interface frictional heat source. Int. J. Mech. Sci. 2001, 43, 89–107. [Google Scholar] [CrossRef]
- Karpat, Y.; Özel, T. Predictive analytical and thermal modeling of orthogonal cutting process—part i: Predictions of tool forces, stresses, and temperature distributions. J. Manuf. Sci. Eng. 2006, 128, 435–444. [Google Scholar] [CrossRef]
- Grzesik, W. Heat in metal cutting. In Advanced Machining Processes of Metallic Materials: Theory, Modelling and Applications, 2nd eds.; Grzesik, W., Ed.; Elsevier: Oxford, UK; Boston, MA, USA, 2017; pp. 163–182. ISBN 9780444637116. [Google Scholar] [CrossRef]
- Akbar, F.; Mativenga, P.T.; Sheikh, M.A. Prediction of heat partition in metal cutting: A State-of-the-art Review of conventional to high-speed machining. In Metal cutting: Research Advances; Davim, J.P., Ed.; Nova Science Publishers: New York, NY, USA, 2010; pp. 23–75. ISBN 978-1-60876-207-1. [Google Scholar]
- Deshpande, A.; Madhavan, V. Study of heat partition at the primary shear plane using finite element analysis of heat and mass transfer. In Transactions of the North American Manufacturing Research Institution of SME; Society of Manufacturing Engineers: Dearborn, MI, USA, 2007; Volume 35. [Google Scholar]
- Xia, Q.; Gillespie, D.R.H. Quasi-static finite element modelling of thermal distribution and heat partitioning for the multi-component system of high speed metal cutting. J. Mater. Proc. Technol. 2020, 275, 116389. [Google Scholar] [CrossRef]
- Boothroyd, G.; Knight, W.A. Fundamentals of Machining and Machine Tools, 3rd ed.; CRC Taylor & Francis: Boca Raton, FL, USA, 2006; ISBN 9781574446593. [Google Scholar]
- Arrazola, P.J.; Özel, T.; Umbrello, D.; Davies, M.A.; Jawahir, I.S. Recent advances in modelling of metal machining processes. CIRP Ann. 2013, 62, 695–718. [Google Scholar] [CrossRef]
- Puls, H.; Klocke, F.; Veselovac, D. FEM-based prediction of heat partition in dry metal cutting of AISI 1045. Int. J. Adv. Manuf. Technol. 2016, 86, 737–745. [Google Scholar] [CrossRef]
- Davies, M.A.; Ueda, T.; M’Saoubi, R.; Mullany, B.; Cooke, A.L. On the measurement of temperature in material removal processes. CIRP Ann. 2007, 56, 581–604. [Google Scholar] [CrossRef]
- Boothroyd, G. Temperatures in orthogonal metal cutting. Proc. Inst. Mech. Eng. 1963, 177, 789–810. [Google Scholar] [CrossRef]
- Lazoglu, I.; Altintas, Y. Prediction of tool and chip temperature in continuous and interrupted machining. Int. J. Mach. Tools Manuf. 2002, 42, 1011–1022. [Google Scholar] [CrossRef]
- Ulutan, D.; Erdem Alaca, B.; Lazoglu, I. Analytical modelling of residual stresses in machining. J. Mater. Process. Technol. 2007, 183, 77–87. [Google Scholar] [CrossRef]
- Lazoglu, I.; Bugdayci, B. Thermal modelling of end milling. CIRP Ann. 2014, 63, 113–116. [Google Scholar] [CrossRef]
- Augspurger, T.; Bergs, T.; Döbbeler, B. Measurement and modeling of heat partitions and temperature fields in the workpiece for cutting inconel 718, AISI 1045, Ti6Al4V, and AlMgSi0.5. J. Manuf. Sci. Eng. 2019, 141, 061007. [Google Scholar] [CrossRef]
- Weiner, J.H. Shear-plane temperature distribution in orthogonal cutting. Trans. ASME 1955, 77, 1331–1341. [Google Scholar]
- Trigger, K.J.; Chao, B.T. An analytical evaluation of metal cutting temperature. Trans. ASME 1951, 73, 58–68. [Google Scholar]
- Ueda, T. Cutting temperature. In CIRP Encyclopedia of Production Engineering; Laperrière, L., Reinhart, G., Eds.; Springer: Berlin, Germany, 2014; pp. 334–345. ISBN 978-3-642-20616-0. [Google Scholar]
- Childs, T.H.C.; Rahmad, R. Modelling orthogonal machining of carbon steels. Part II: Comparisons with experiments. Int. J. Mech. Sci. 2009, 51, 465–472. [Google Scholar] [CrossRef]
- Spittel, M.; Spittel, T. Steel symbol/number: 100Cr6/1.3505. In Numerical Data and Functional Relationships in Science and Technology: New Series; Spittel, M., Spittel, T., Warlimont, H., Landolt, H., Börnstein, R., Martienssen, W., Eds.; Springer: Berlin, Germany, 2009; pp. 552–557. ISBN 978-3-540-44758-0. [Google Scholar]
- Kienzle, O. Die Bestimmung von kräften und leistungen an spanenden werkzeugen und werkzeugmaschinen. VDI-Z 1952, 94, 299–305. [Google Scholar]
- König, W.; Essel, K. Spezifische Schnittkraftwerte für die Zerspanung Metallischer Werkstoffe. Specific Cutting Force Data for Metal-Cutting; Verl. Stahleisen: Düsseldorf, Germany, 1973; ISBN 3514002401. [Google Scholar]
- Spittel, M.; Spittel, T. Steel symbol/number: 42CrMo4/1.7225. In Numerical Data and Functional Relationships in Science and Technology: New Series; Spittel, M., Spittel, T., Warlimont, H., Landolt, H., Börnstein, R., Martienssen, W., Eds.; Springer: Berlin, Germany, 2009; pp. 1050–1055. ISBN 978-3-540-44758-0. [Google Scholar]
- Spittel, M.; Spittel, T. AlZn5.5MgCu. In Numerical Data and Functional Relationships in Science and Technology: New Series; Spittel, M., Spittel, T., Warlimont, H., Landolt, H., Börnstein, R., Martienssen, W., Eds.; Springer: Berlin, Germany, 2011; pp. 480–485. ISBN 978-3-642-13863-8. [Google Scholar]

| Research Question 1 | Do heat partition results by Komanduri and Hou improve when the amount of grid points in the calculation of temperature fields is increased? |
| Research Question 2 | Does the fraction of primary shear plane heat transferred into the workpiece depend on the shear angle in addition to the thermal number? |
| Research Question 3 | Do further adjustments to reality, implemented in numerical models, have a relevant influence on the heat partition? |
| Research Question 4 | Do the idealized conditions in the utilized models have a relevant influence on heat partition in comparison to experimental results? |
| Machining Parameters | Material Properties | Process Quantities |
|---|---|---|
| cutting velocity vc | thermal conductivity λ | shear plane heat flux density |
| uncut chip thickness h | specific heat capacity cp | shear angle ϕ |
| density ρ |
| Source | Thermal Number Nth |
|---|---|
| Shaw [3] | 9.38 |
| Boothroyd and Knight [24] | 41.46 |
| Trigger and Chao [34] | 39.72 |
| Ueda et al. [35] | 0.94 |
| Childs and Rahmad [36] | 15.97–88.37 |
| Parameter | Value |
|---|---|
| fluid supply | none |
| cutting edge inclination | 0° |
| tool cutting edge angle | 90° |
| feed rate | 0.12 mm |
| cutting velocity | 2, 10, 25, 50, 100 m/min |
| depth of cut | 2 mm |
| cutting edge radius | 8.5 µm |
| rake angle | 9.3° |
| clearance angle | 5.7° |
| Parameter | Value |
|---|---|
| cutting edge inclination | 0° |
| tool cutting edge angle | 90° |
| cutting velocity | 50–1250 m/min |
| uncut chip thickness | 6.98–1570.80 µm |
| rake angle | 0° |
| Orthogonal Cutting Data | Komanduri and Hou Rn,impr. | Deviation to fe Model A Rn,femA/Rn,impr. −1 | Deviation to fe Model B Rn,femB/Rn,impr. −1 | Deviation to fe Model C Rn,femC/Rn,impr. −1 | |
|---|---|---|---|---|---|
| 0.25 | ref. [35] | 0.6667 | 0.97% | −1.27% | −1.17% |
| 1.17 | ref. [3] | 0.1795 | 3.30% | −0.24% | 1.16% |
| 1.76 | ref. [24] | 0.0821 | 0.92% | −0.51% | −0.50% |
| 1.95 | ref. [34] | 0.0690 | 1.29% | −0.79% | −1.51% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Langenhorst, L.; Sölter, J.; Kuschel, S. Partition of Primary Shear Plane Heat in Orthogonal Metal Cutting. J. Manuf. Mater. Process. 2020, 4, 82. https://doi.org/10.3390/jmmp4030082
Langenhorst L, Sölter J, Kuschel S. Partition of Primary Shear Plane Heat in Orthogonal Metal Cutting. Journal of Manufacturing and Materials Processing. 2020; 4(3):82. https://doi.org/10.3390/jmmp4030082
Chicago/Turabian StyleLangenhorst, Lars, Jens Sölter, and Sven Kuschel. 2020. "Partition of Primary Shear Plane Heat in Orthogonal Metal Cutting" Journal of Manufacturing and Materials Processing 4, no. 3: 82. https://doi.org/10.3390/jmmp4030082
APA StyleLangenhorst, L., Sölter, J., & Kuschel, S. (2020). Partition of Primary Shear Plane Heat in Orthogonal Metal Cutting. Journal of Manufacturing and Materials Processing, 4(3), 82. https://doi.org/10.3390/jmmp4030082





