Development of a Novel Tuning Approach of the Notch Filter of the Servo Feed Drive System
Abstract
:1. Introduction
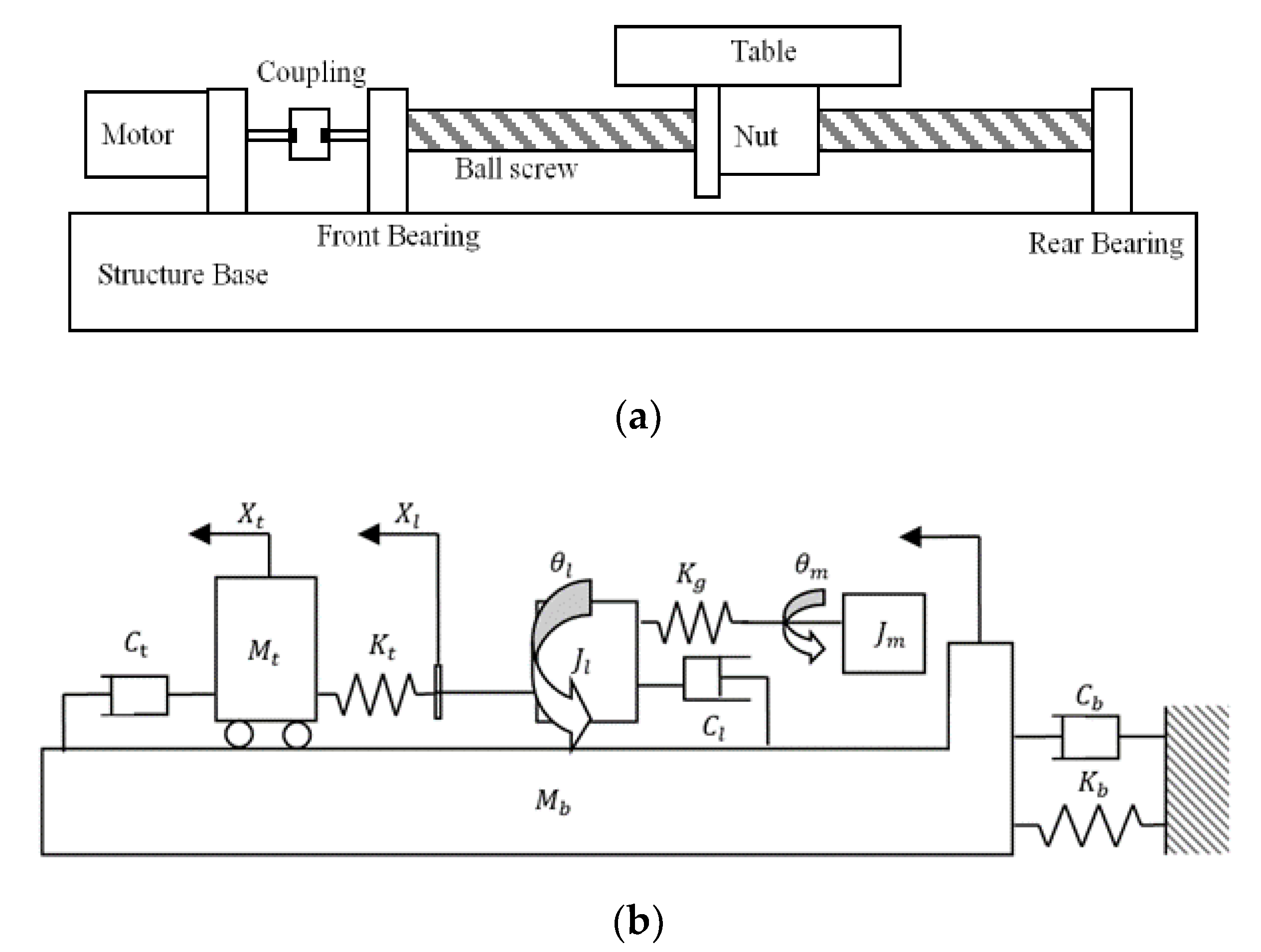
2. The Dynamic Model of the Feed Drive System
2.1. The Derivation of the Feed Drive System
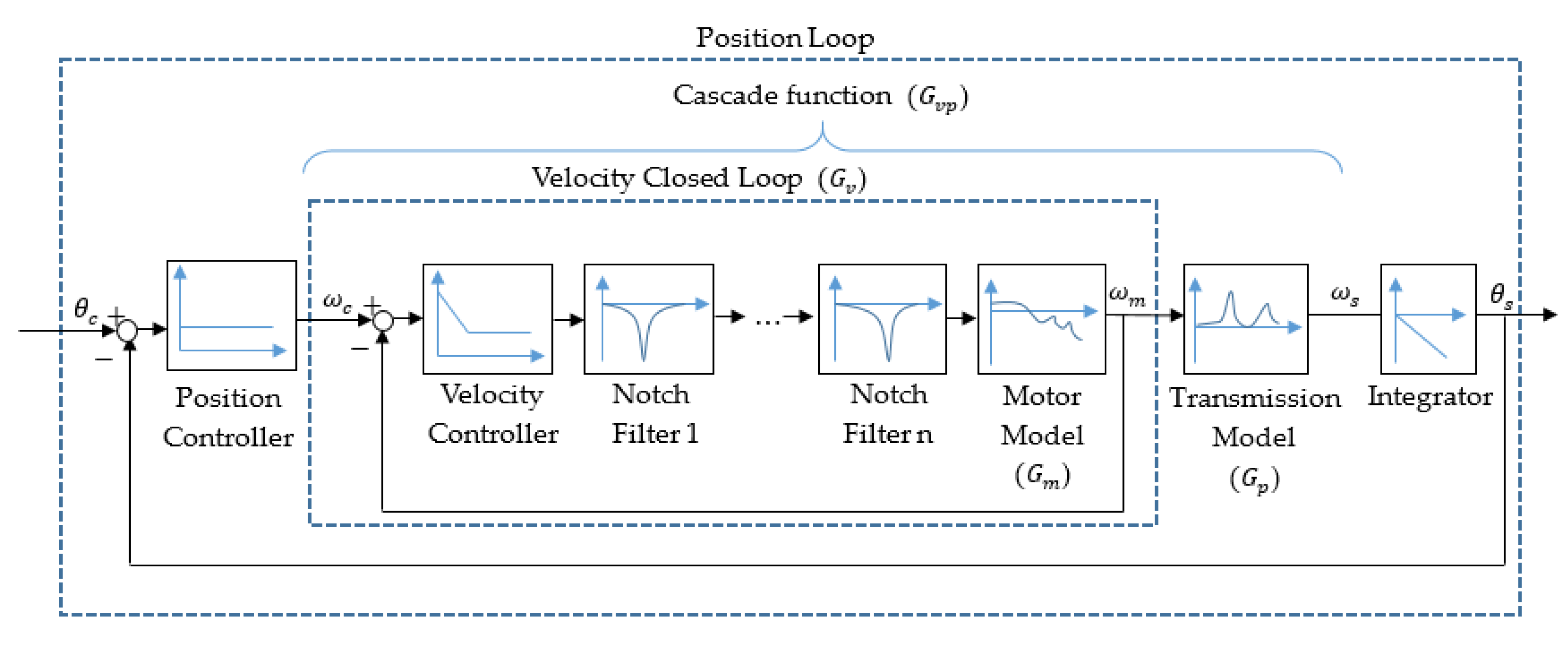
2.2. Transformed Representation of the Servo Feed Drive System
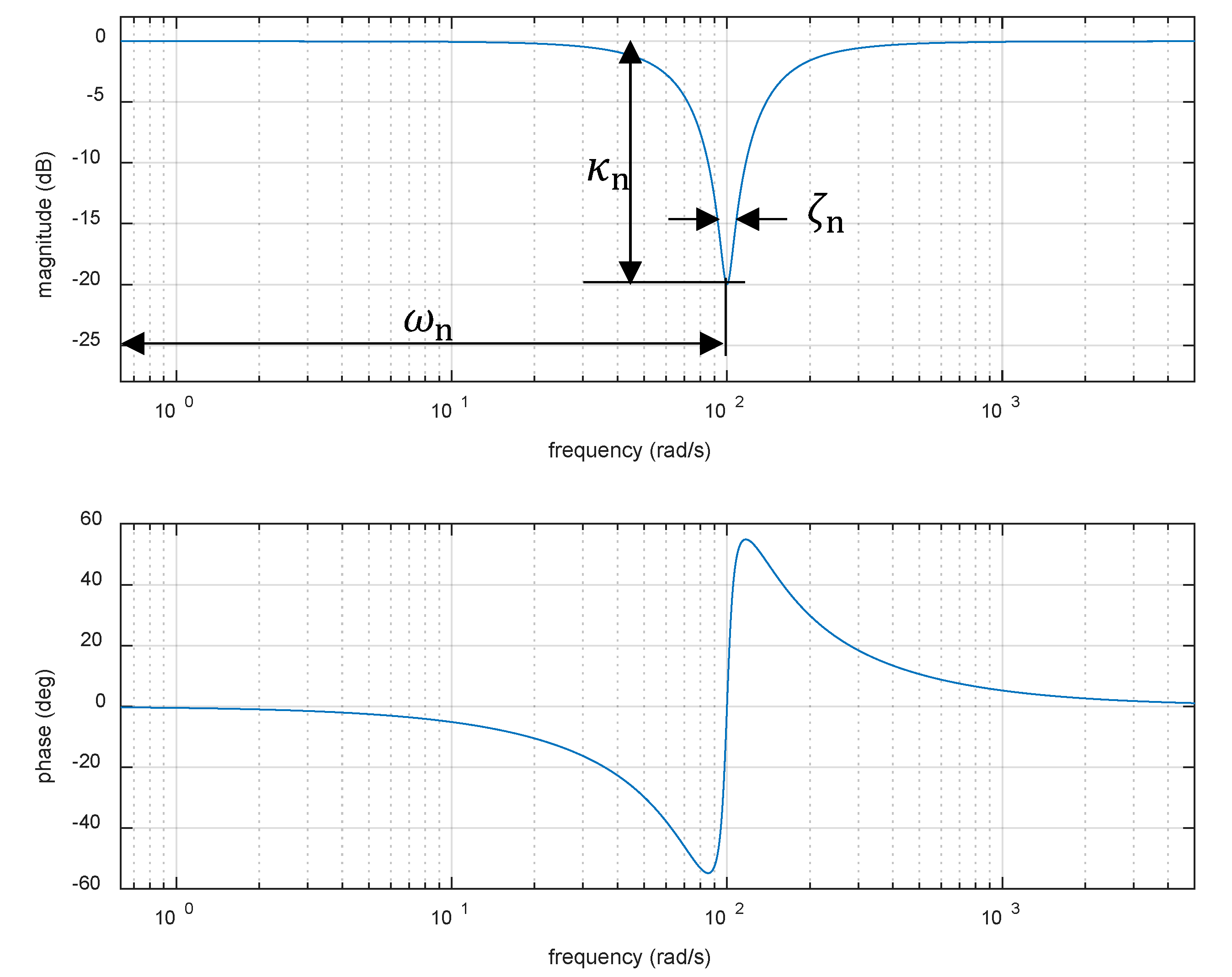
2.3. Traditional Tuning Method of Notch Filter
3. The Notch Filter Tuning Approach Using the Optimization
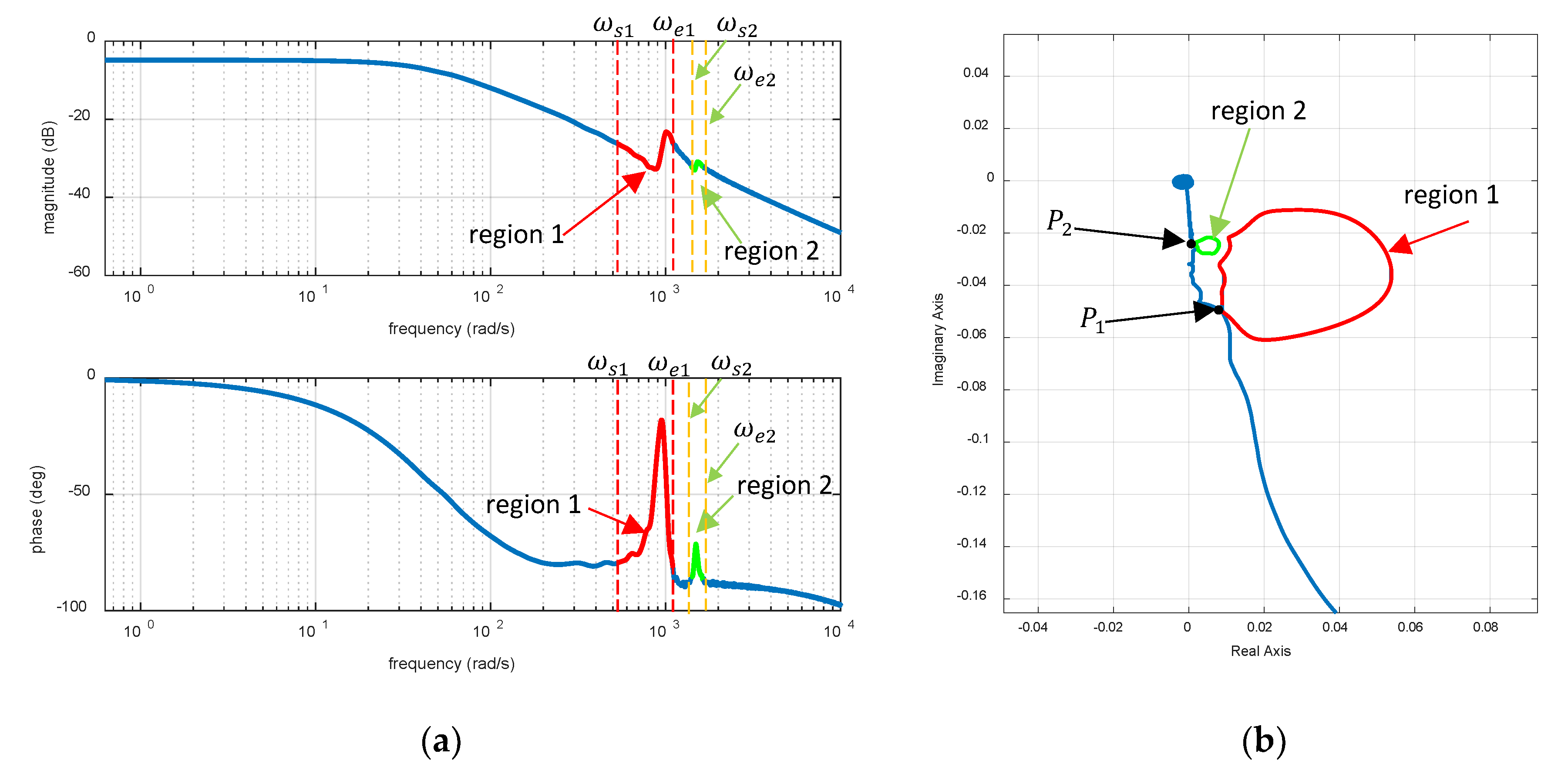
3.1. The Determination of the Range of the Center Frequency by Nyquist Plot
3.2. Optimal Approach for Tuning Notch Filter
- Determine the start frequency and end frequency of each closed path using the searching method in Section 3.1.
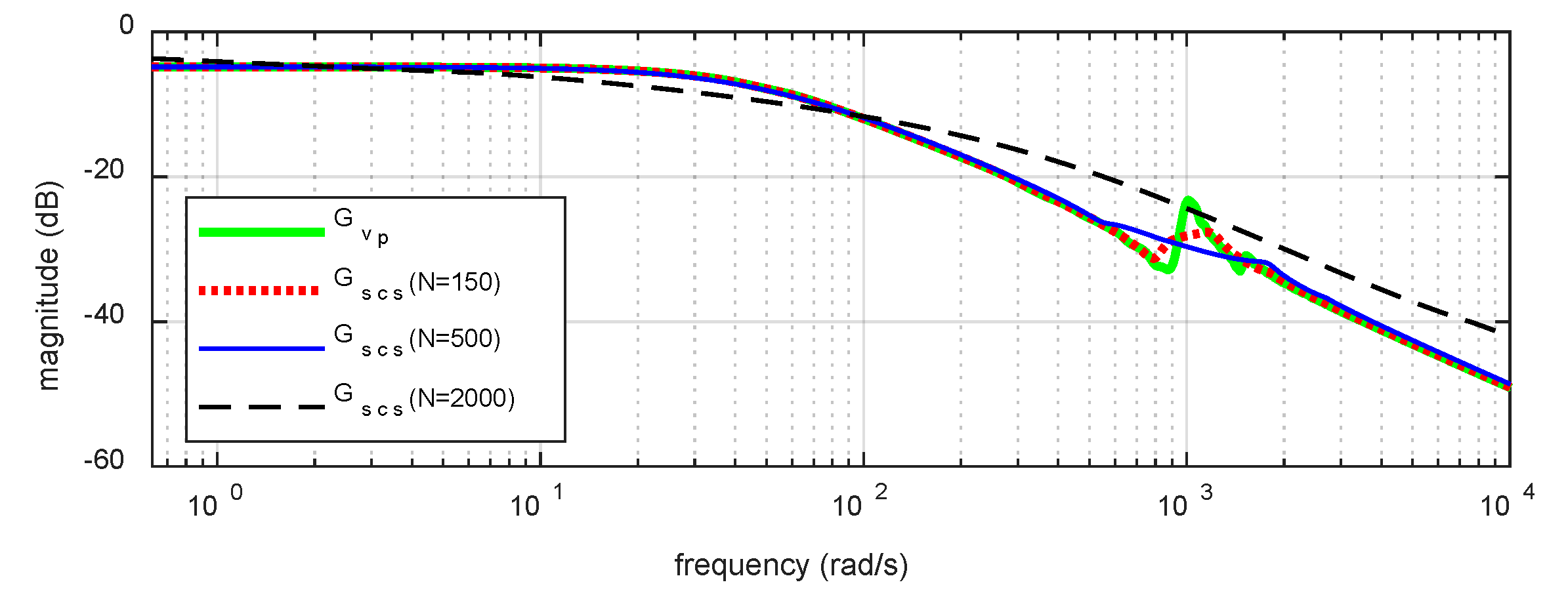
- Smooth by applying the moving average filter given as the following.Here is the smoothed transfer function of . The magnitude plot of and three cases of with different are shown in Figure 6. In the figure, it can be observed that with smaller has a worse result; however, with larger are changed completely and also have an unsuitable result. Hence, here the is selected as 500 to remain the main profile of and smooth the peak parts of .
- The notch filter such that the resulting can approach the by minimizing the following objective function. The lower and upper bounds are obtained from step 1.
4. Results and Discussion
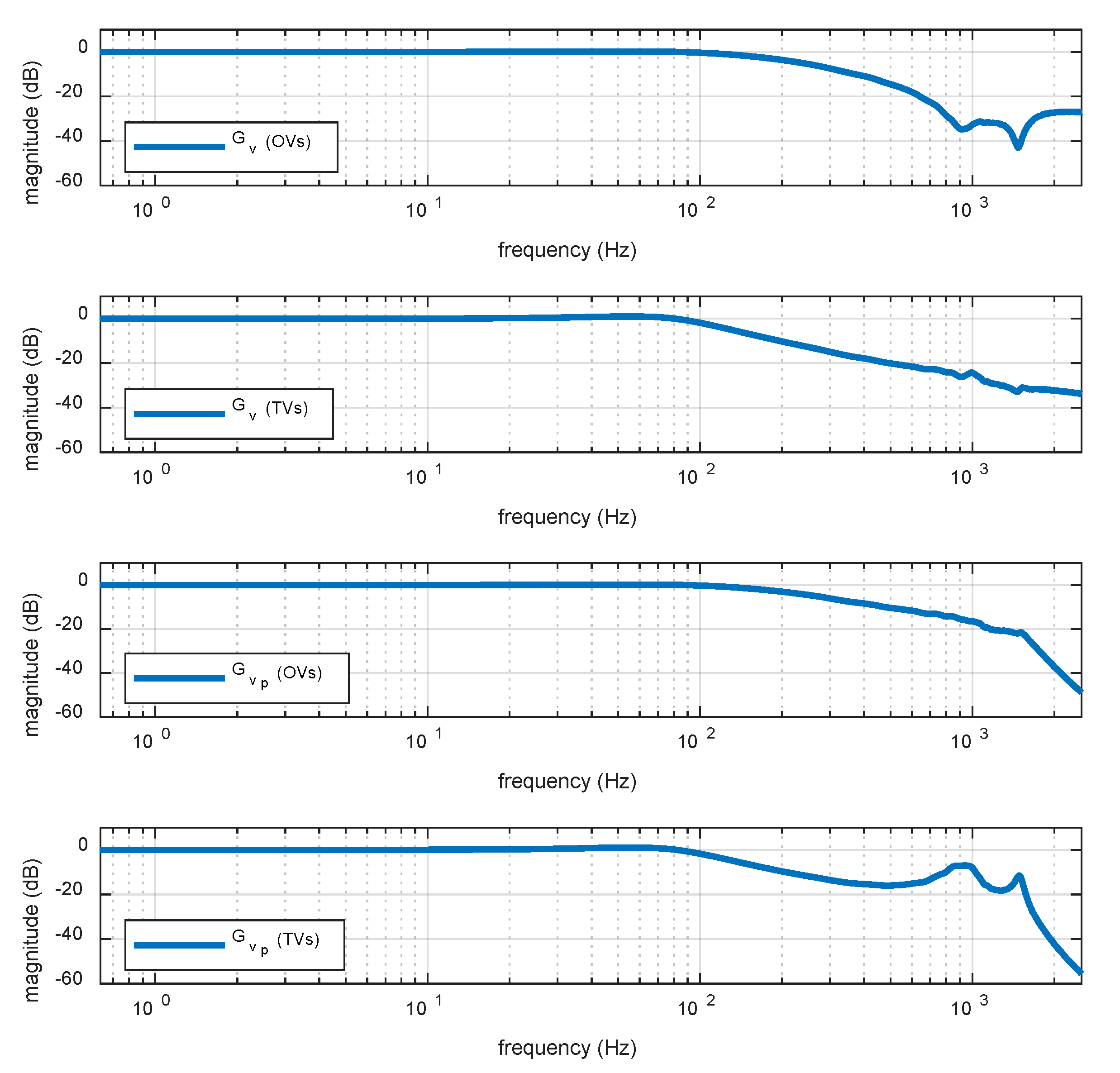
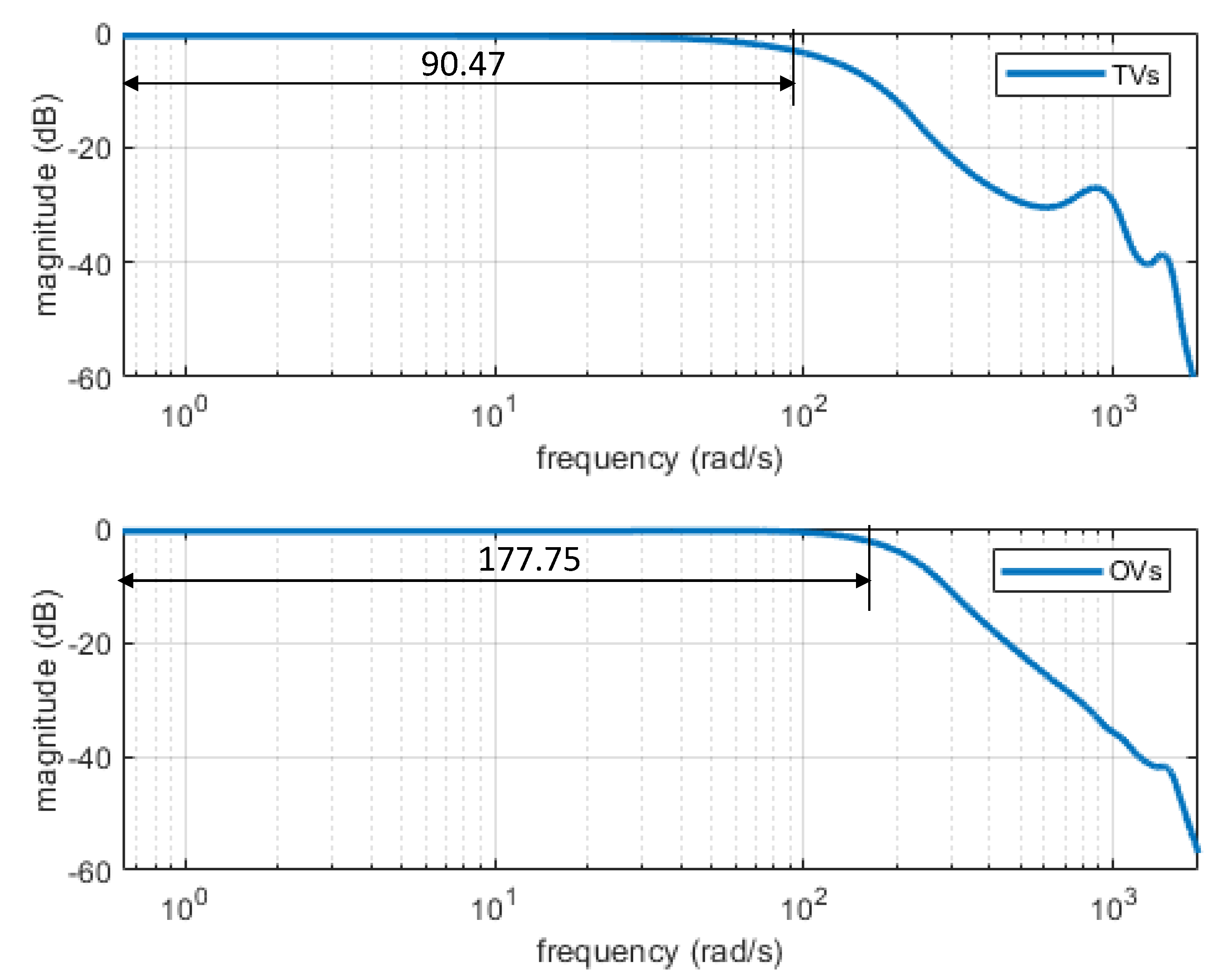
4.1. The Comparisons of Frequency Response Functions Using Traditional and Optimal Approaches
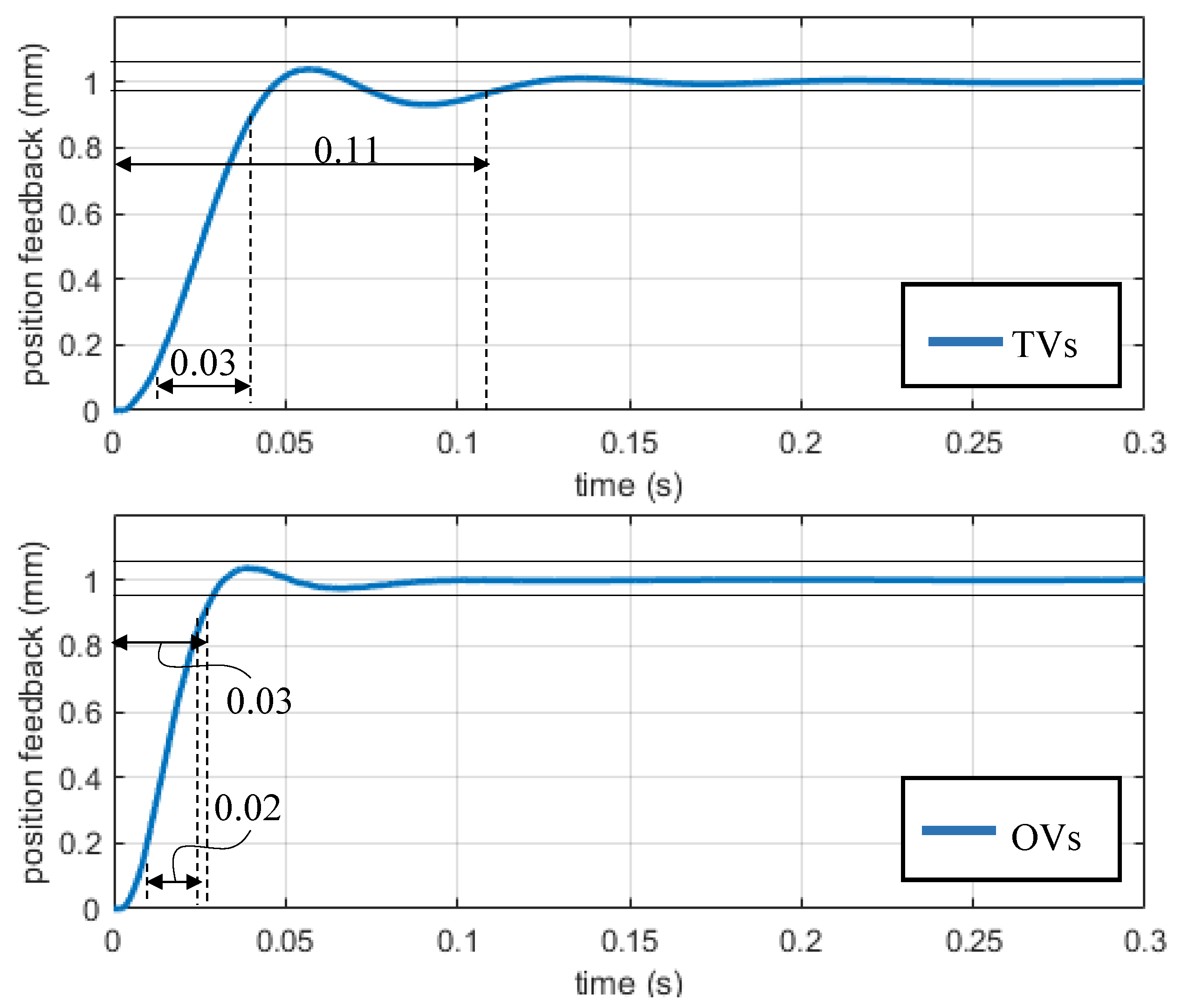
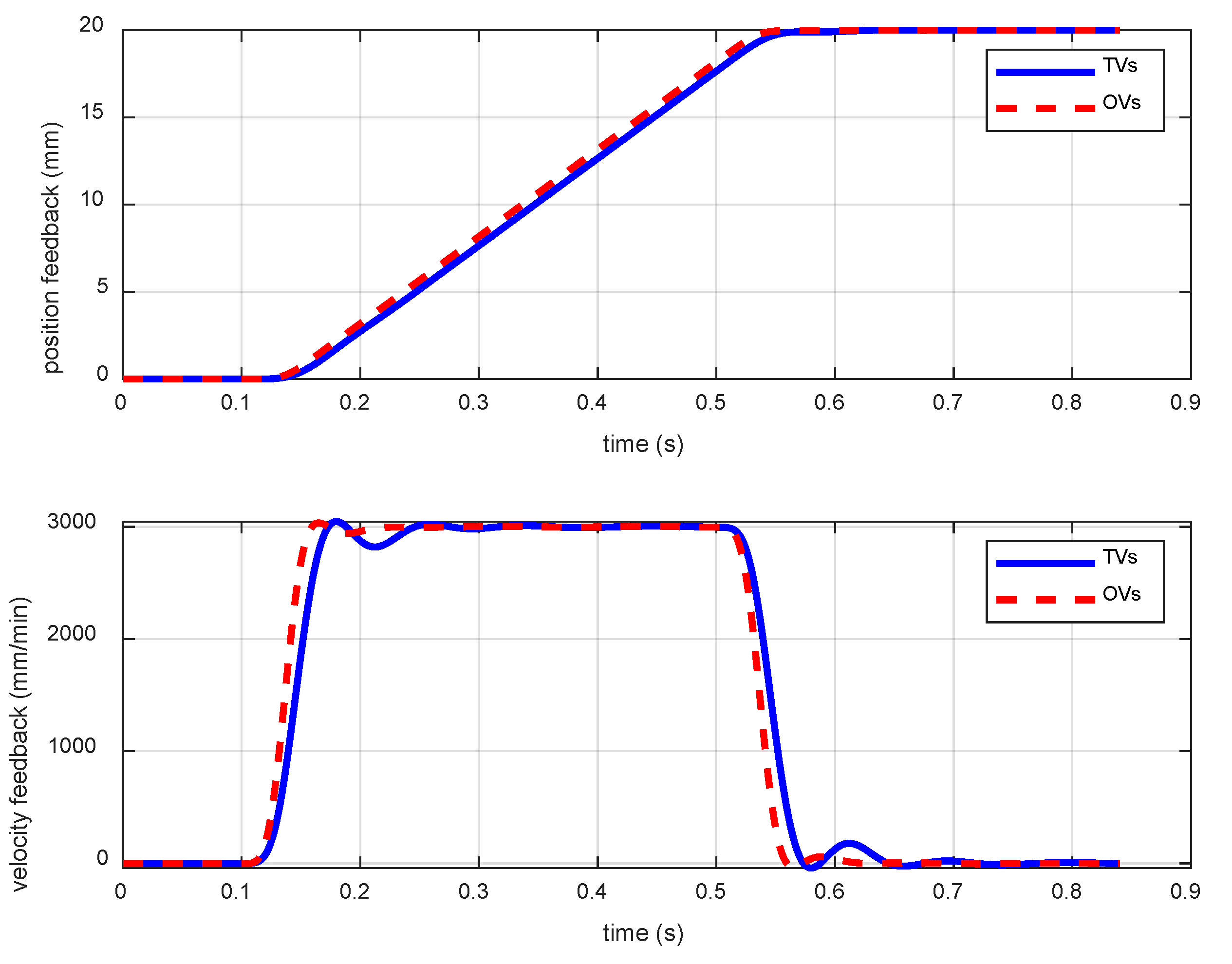
4.2. The Comparision of Simulation Results with Traditional and Optimal Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pritschow, G. On the Influence of the Velocity Gain Factor on the Path Deviation. Ann. CIRP 1996, 45, 367–371. [Google Scholar] [CrossRef]
- Chen, Y.C.; Tlusty, J. Effect of Low-Friction Guideways and Lead-Screw Flexibility on Dynamics of High-Speed Machines. Ann. CIRP 1995, 44, 353–356. [Google Scholar] [CrossRef]
- Pritschow, G. A Comparison of Linear and Conventional Electromechanical Drives. Ann. CIRP 1998, 47, 541–548. [Google Scholar] [CrossRef]
- Tsai, M.S.; Huang, Y.C.; Lin, M.T.; Wu, S.K. Integration of Input Shaping Technique with Interpolation for Vibration Suppression of Servo-feed Drive System. J. Chin. Inst. Eng. 2017, 40, 284–295. [Google Scholar] [CrossRef]
- Jones, S.D.; Ulsoy, A.G. An Approach to Control Input Shaping with Application to Coordinate Measuring Machines. ASME J. Dyn. Syst. Meas. Control 1999, 121, 242–247. [Google Scholar] [CrossRef]
- Cole, M.O.T.; Shinonawanik, P.; Wongratanaphisan, T. Time-domain Prefilter Design for Enhanced Tracking and Vibration Suppression in Machine Motion Control. Mech. Syst. Signal Process. 2018, 104, 106–119. [Google Scholar] [CrossRef]
- Symens, W.; Van Brussel, H.; Swevers, J. Gain-Scheduling Control of Machine Tools with Varying Structural Flexibility. Ann. CIRP 2004, 52, 321–324. [Google Scholar] [CrossRef]
- Zheng, H.; Qin, H.; Ren, M.; Zhang, Z. Active Vibration Control for the Time-Varying Systems with a New Adaptive Algorithm. J. Vib. Control 2020, 26, 200–213. [Google Scholar] [CrossRef]
- Ast, A.; Braun, S.; Eberhard, P.; Heisel, U. An Adaptronic Approach to Active Vibration Control of Machine Tools with Parallel Kinematics. Prod. Eng. 2009, 3, 207–215. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Inman, D.J. Active Vibration Control of Flexible Cantilever Plates using Piezoelectric Materials and Artificial Neural Networks. J. Sound Vib. 2016, 363, 33–53. [Google Scholar] [CrossRef]
- Yousefi, H.; Hirvonen, M.; Handroos, H. Application of Neural Network in Suppressing Mechanical Vibration of a Permanent Magnet Linear Motor. Control Eng. Pract. 2008, 16, 787–797. [Google Scholar] [CrossRef]
- Edalath, S.; Kukreti, A.R.; Cohen, K. Enhancement of a Tuned Mass Damper for Building Structures using Fuzzy Logic. J. Vib. Control 2012, 19, 1763–1772. [Google Scholar] [CrossRef]
- Thenozhi, S.; Yu, W. Active Vibration Control of Building Structures using Fuzzy Proportional-derivative/Proportional-integral-derivative Control. J. Vib. Control 2015, 21, 2340–2359. [Google Scholar] [CrossRef]
- Yiǧit, I. Model Free Sliding Mode Stabilizing Control of a Real Rotary Inverted Pendulum. J. Vib. Control 2017, 23, 1645–1662. [Google Scholar] [CrossRef]
- Wang, J.; Jin, F.; Zhou, L. Implementation of Model-free Motion Control for Active Suspension Systems. Mech. Syst. Signal Process. 2019, 119, 589–602. [Google Scholar] [CrossRef]
- Smith, A.D. Wide Bandwidth Control of High-Speed Milling Machine Feed Drives. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 1999. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Int. Conf. Neural Netw. IEEE 1995, 4, 1942–1948. [Google Scholar]

| Parameters | Value (Unit) | Parameters | Value (Unit) |
|---|---|---|---|
| 800 (Ns/m) | 8520 (Nm/rad) | ||
| 1.95 (Ns/m) | 1.95 × (N/m) | ||
| 500 (Ns/m) | 138 (kg) | ||
| 0.00823 ( | 570 (kg) | ||
| 0.04 ( | 0.0032 (m/rad) | ||
| 1.83 × (N/m) | 0.003342 (Nms/rad) | ||
| 1.38 () |
| Transfer Function | Parameter | Initial Value | Minimum Value | Maximum Value | Unit |
|---|---|---|---|---|---|
| Notch Filter 1 | 534 | 534 | 1100 | rad/s | |
| 0.1 | 0.1 | 10 | - | ||
| 0.1 | 0.1 | 50 | - | ||
| Notch Filter 2 | 534 | 534 | 1100 | rad/s | |
| 0.1 | 0.1 | 10 | - | ||
| 0.1 | 0.1 | 50 | - | ||
| Notch Filter 3 | 1400 | 1400 | 1628 | rad/s | |
| 0.1 | 0.1 | 10 | - | ||
| 0.1 | 0.1 | 50 | - |
| Parameter | Traditional Value | Optimal Value | Unit |
|---|---|---|---|
| 92.47 | 298.41 | 1/s | |
| 223.46 | 280.65 | Nm /rad | |
| 1.78 | 4.46 | Nms/rad | |
| 1012.13 | 1099.92 | rad/s | |
| 0.10 | 0.17 | - | |
| 13.28 | 4.60 | - | |
| 884.33 | 988.31 | rad/s | |
| 1.11 | 0.05 | - | |
| 0.10 | 2.97 | - | |
| 1570.05 | 1485.52 | rad/s | |
| 0.1 | 0.03 | - | |
| 1.2 | 5.48 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-C.; Tsai, M.-S.; Hong, M.-Q.; Tang, P.-Y. Development of a Novel Tuning Approach of the Notch Filter of the Servo Feed Drive System. J. Manuf. Mater. Process. 2020, 4, 21. https://doi.org/10.3390/jmmp4010021
Liu C-C, Tsai M-S, Hong M-Q, Tang P-Y. Development of a Novel Tuning Approach of the Notch Filter of the Servo Feed Drive System. Journal of Manufacturing and Materials Processing. 2020; 4(1):21. https://doi.org/10.3390/jmmp4010021
Chicago/Turabian StyleLiu, Chung-Ching, Meng-Shiun Tsai, Mao-Qi Hong, and Pu-Yang Tang. 2020. "Development of a Novel Tuning Approach of the Notch Filter of the Servo Feed Drive System" Journal of Manufacturing and Materials Processing 4, no. 1: 21. https://doi.org/10.3390/jmmp4010021
APA StyleLiu, C.-C., Tsai, M.-S., Hong, M.-Q., & Tang, P.-Y. (2020). Development of a Novel Tuning Approach of the Notch Filter of the Servo Feed Drive System. Journal of Manufacturing and Materials Processing, 4(1), 21. https://doi.org/10.3390/jmmp4010021





