Automated Unsupervised 3D Tool-Path Generation Using Stacked 2D Image Processing Technique
Abstract
1. Introduction
2. State of the Art
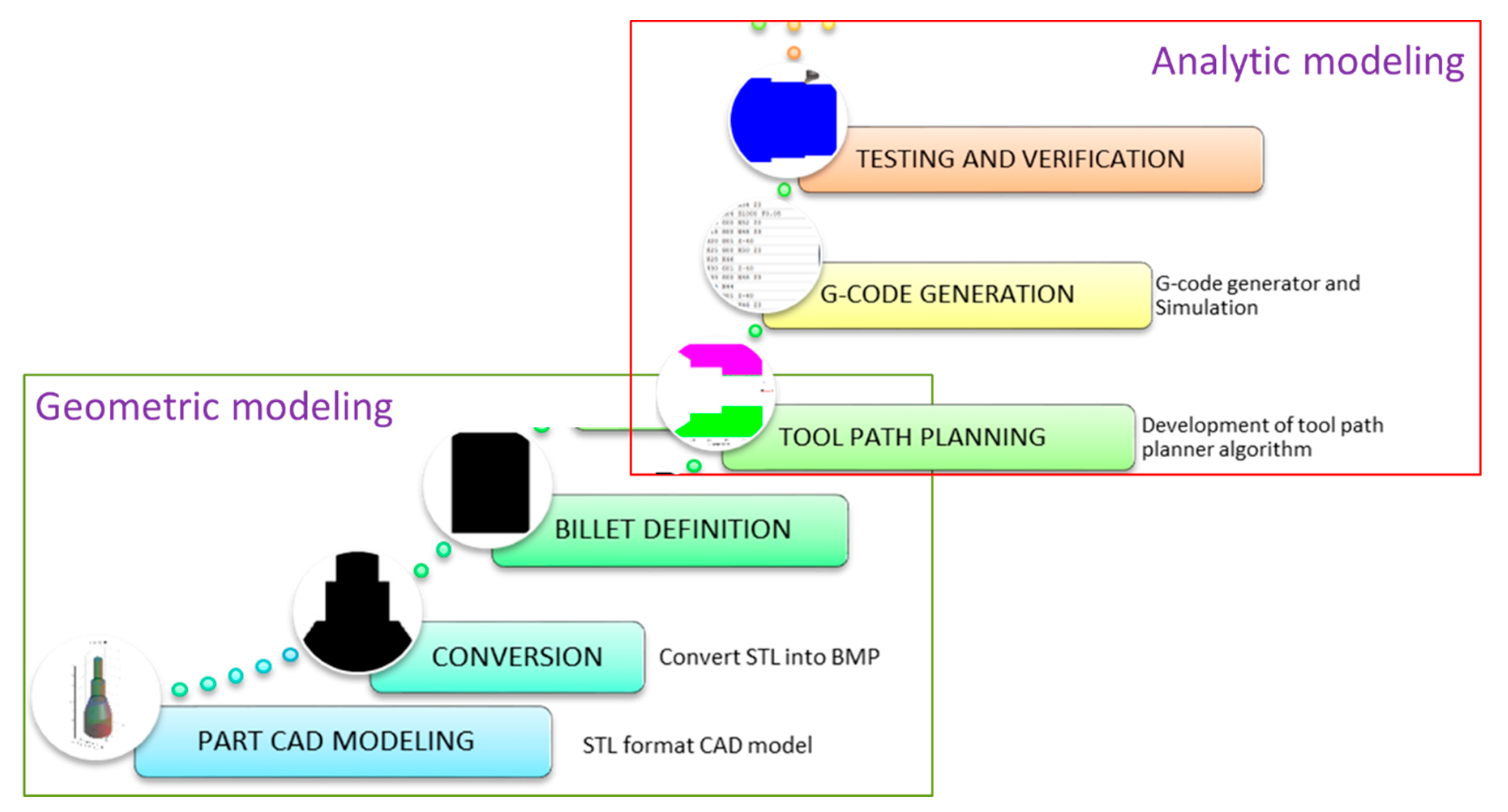
3. Materials and Methods
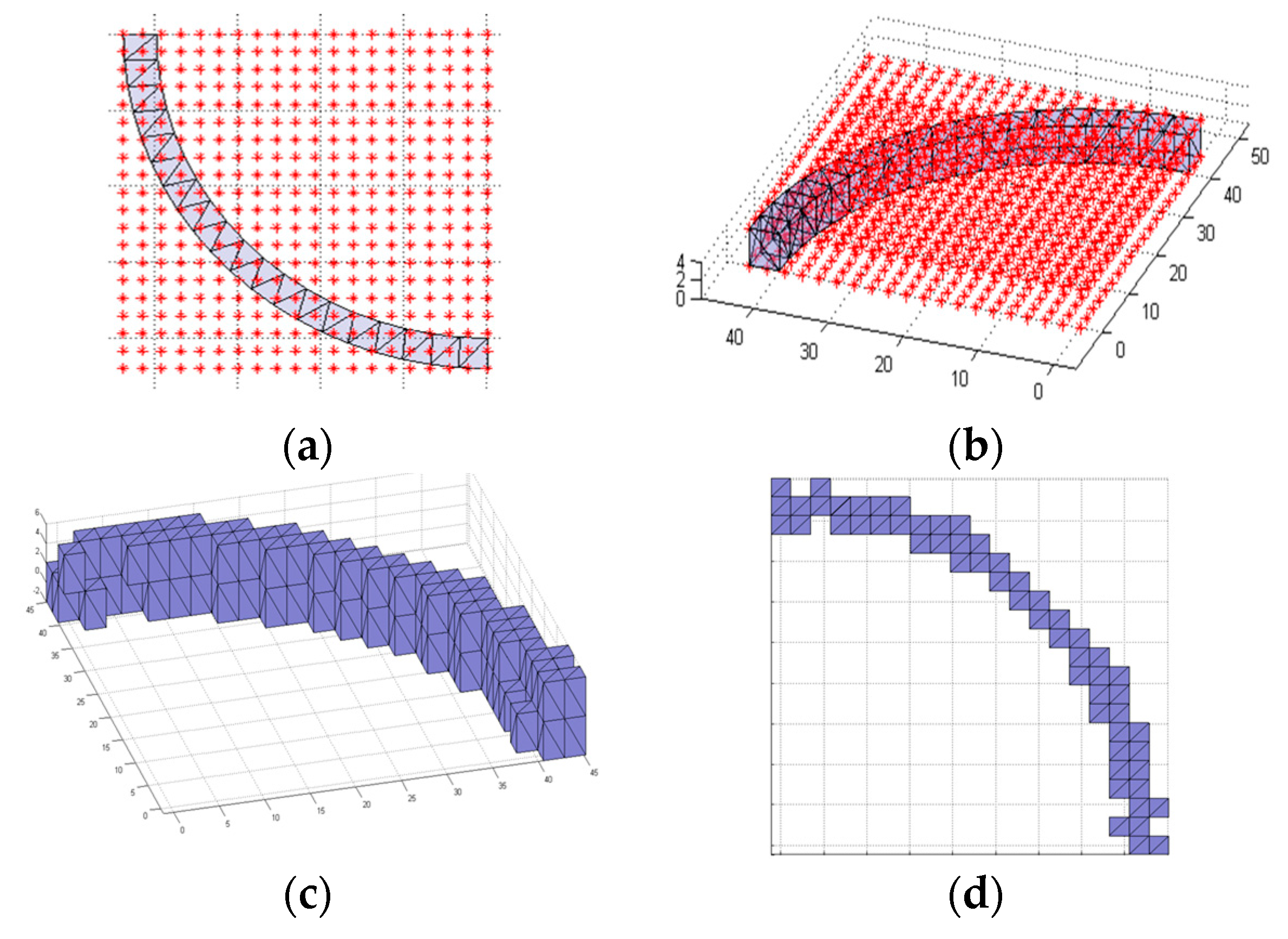
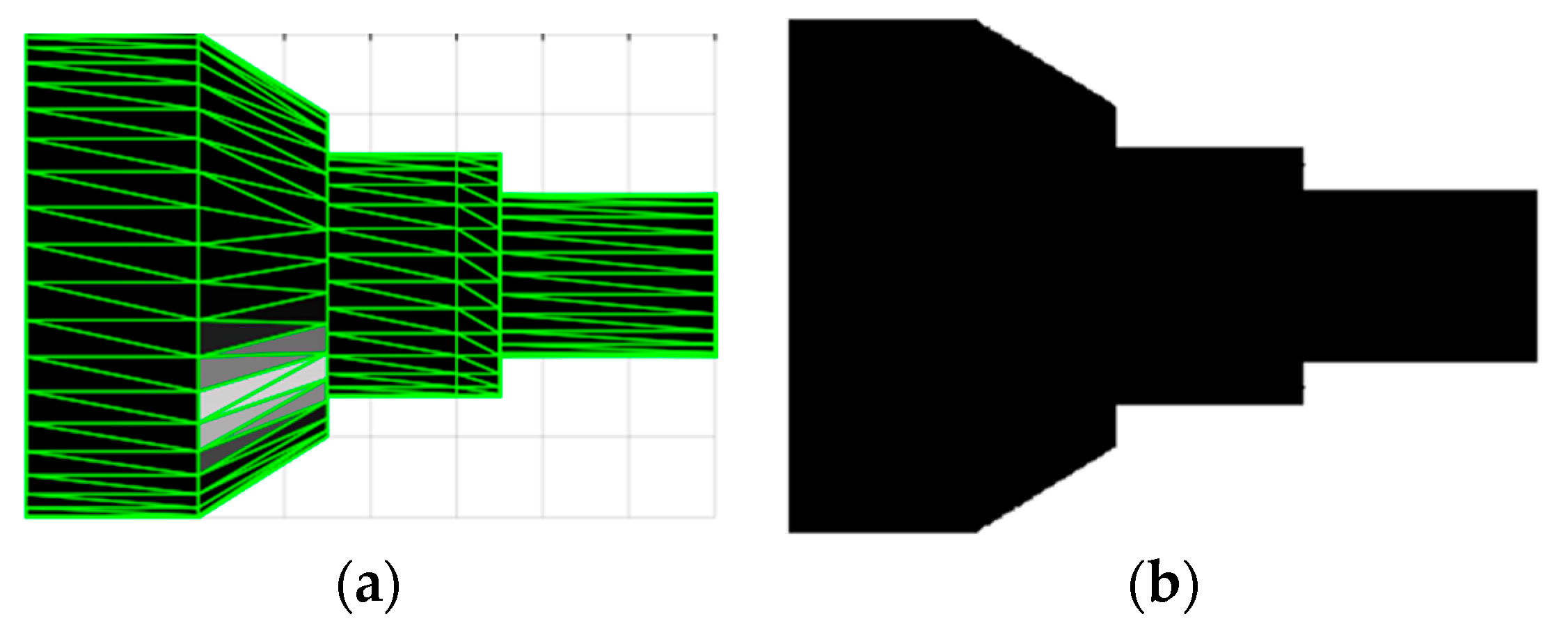
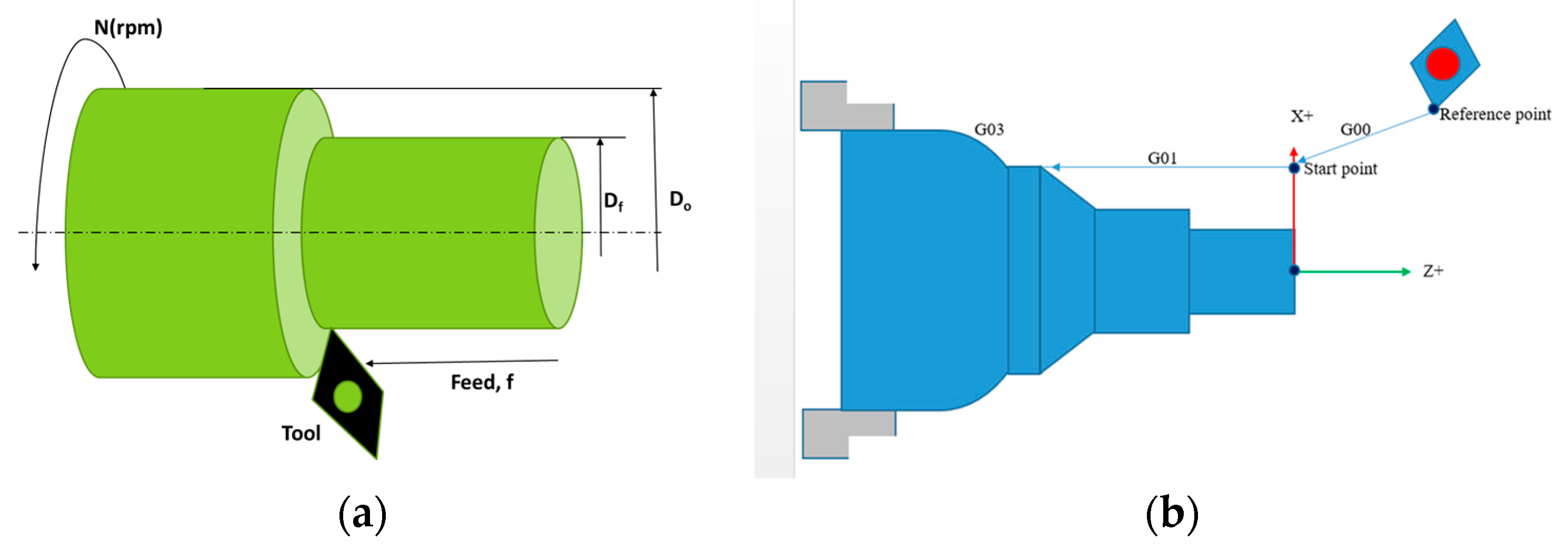
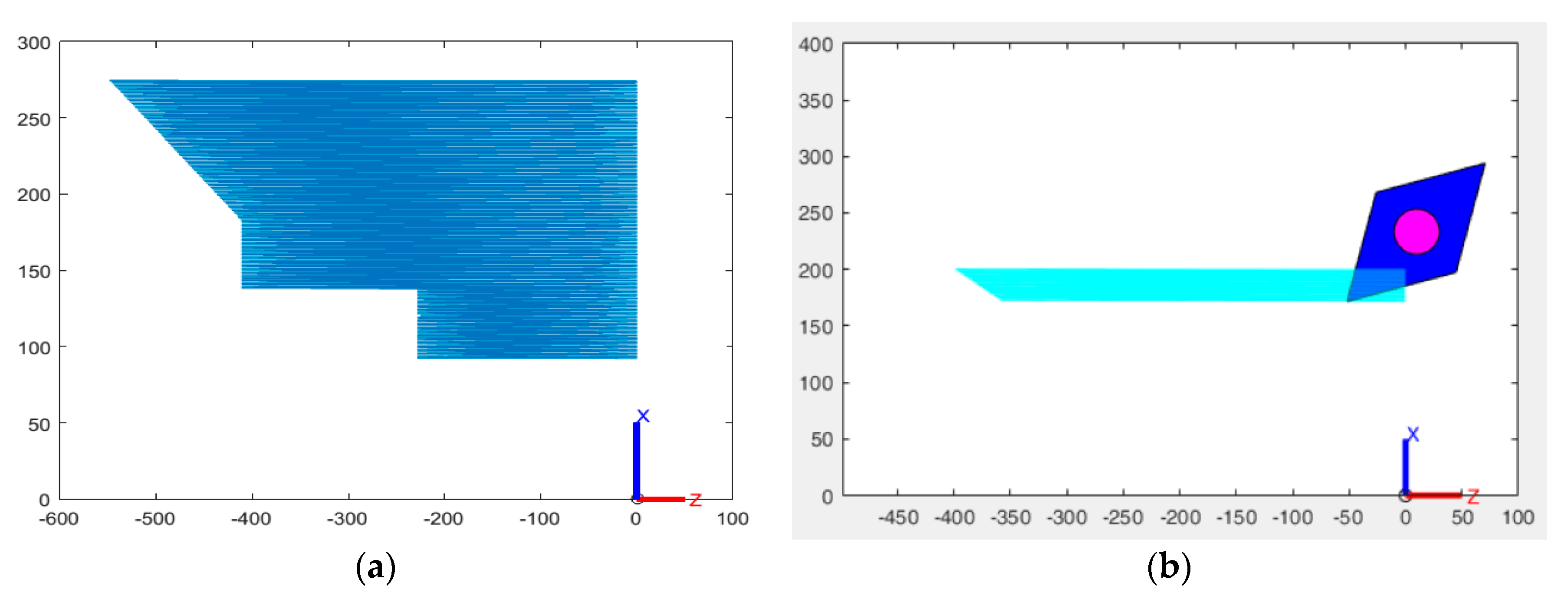
3.1. Geometric Modeling and Parameter Identification
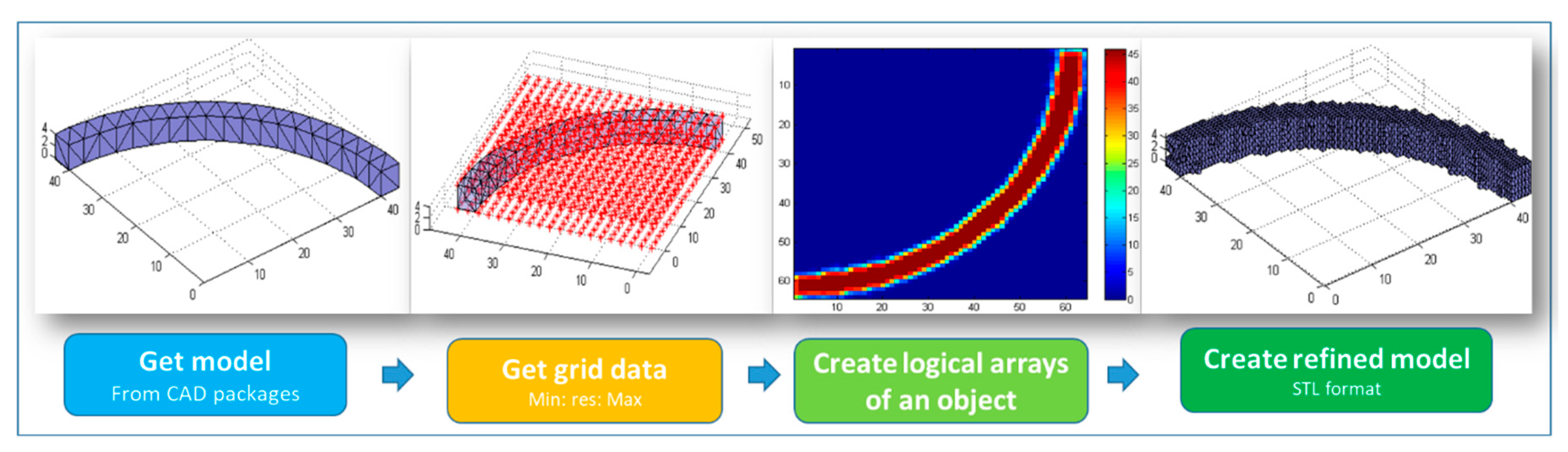
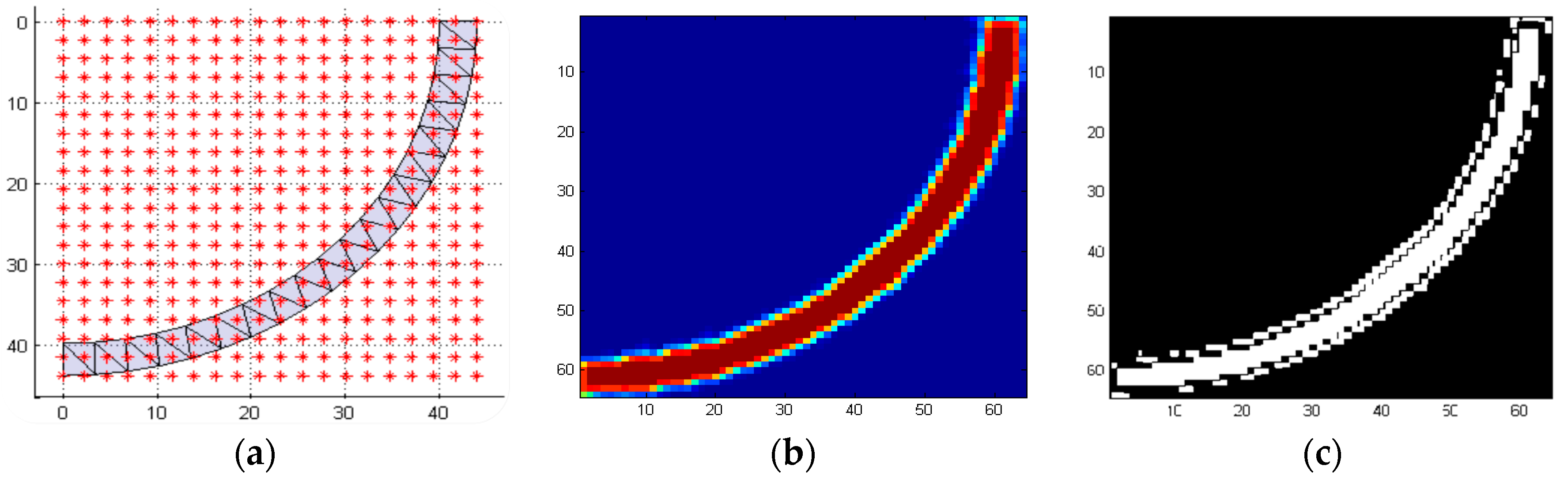
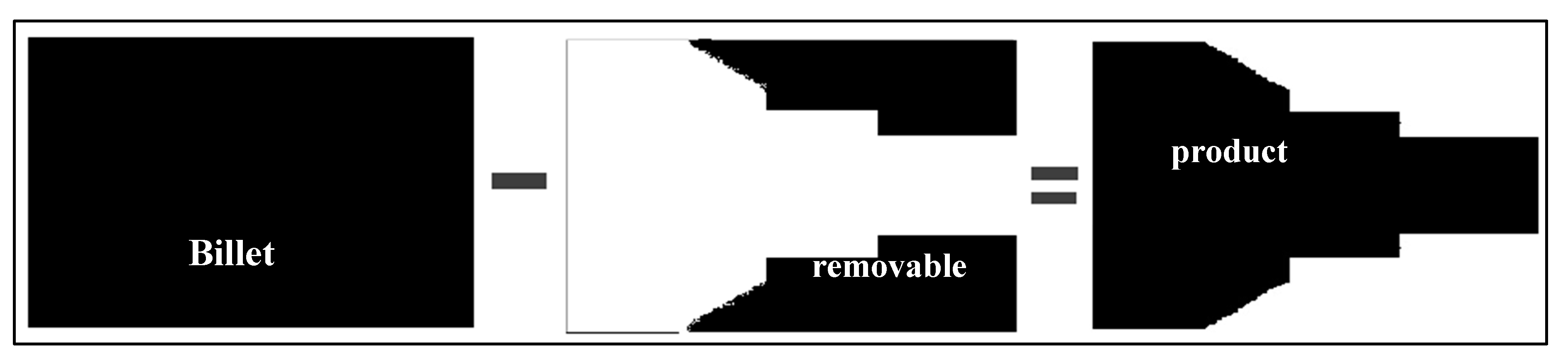
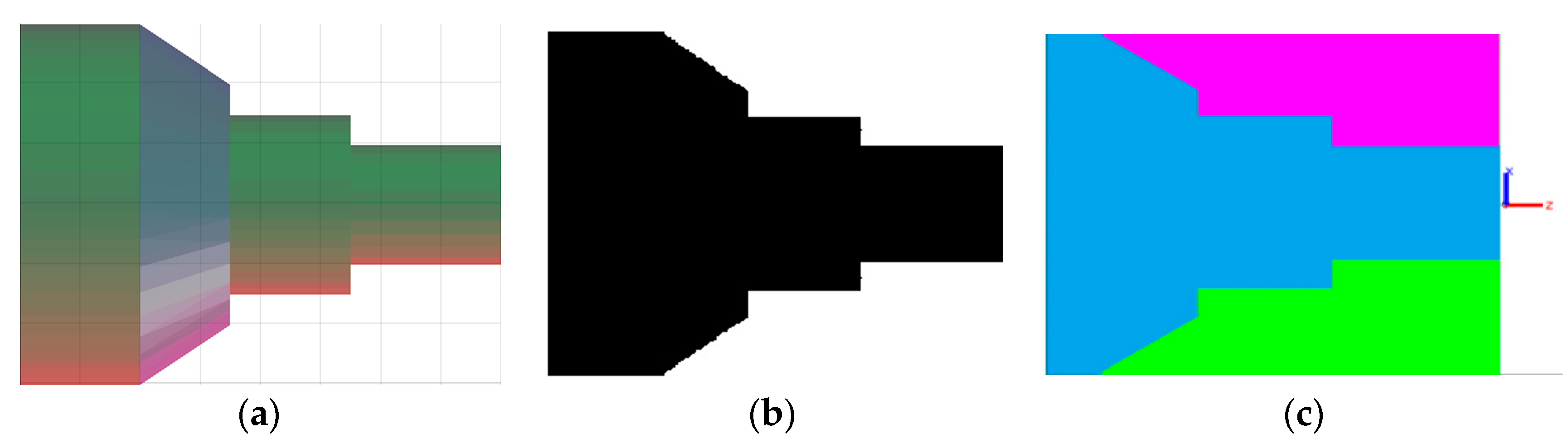
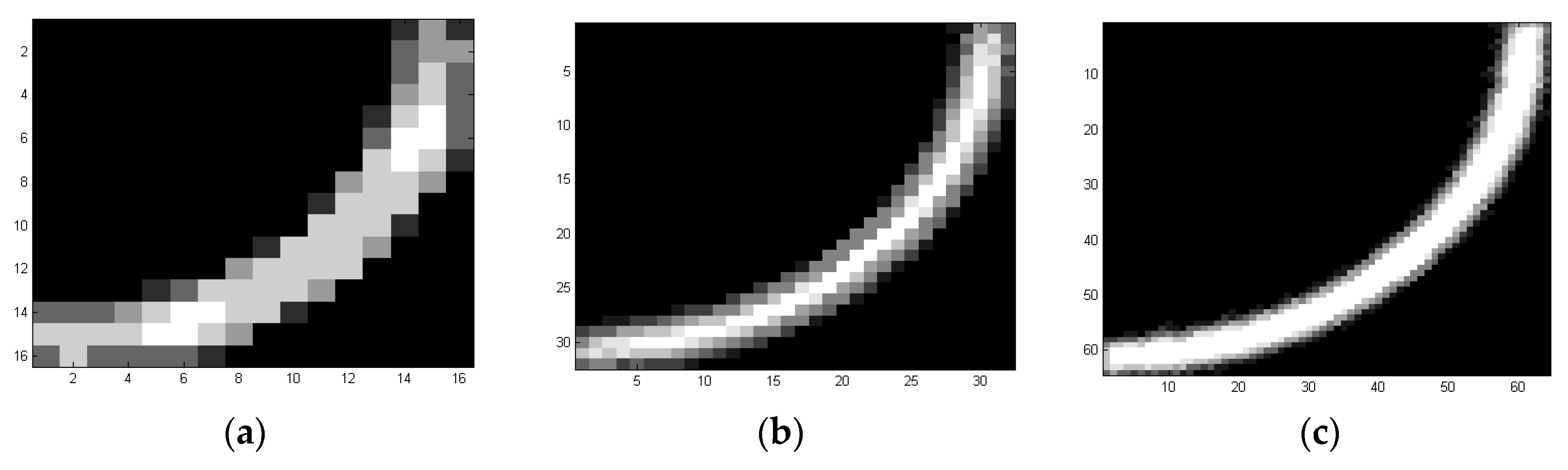
3.2. Model Segmentation and Reconstruction
| Algorithm 1: Pseudocode for voxelization as a binary logic |
| grid_data = zeros(rx,ry,rz); |
| P0 = Facet position |
| Nf = Array for normal facets |
| for nz = 1 : rz |
| for ny = 1 : ry |
| for nx = 1 : rx |
| % Get the point |
| p = [ xa(nx) ; ya(ny) ; za(nz) ]; |
| % Find the closest Facet |
| vertices_distance = ∑(([ P0(1,:)-p(1) ; P0(2,:)-p(2) ; P0(3,:)-p(3) ])2); |
| [v,ind] = min(vertices_distance); |
| % Add Point if it is enclosed inside an object |
| data = dot(N_f(:,ind),p-P0(:,ind)); |
| grid_data(nx,ny,nz) = (data>=0);% logical array size of NxMxK |
| end |
| end |
| end |
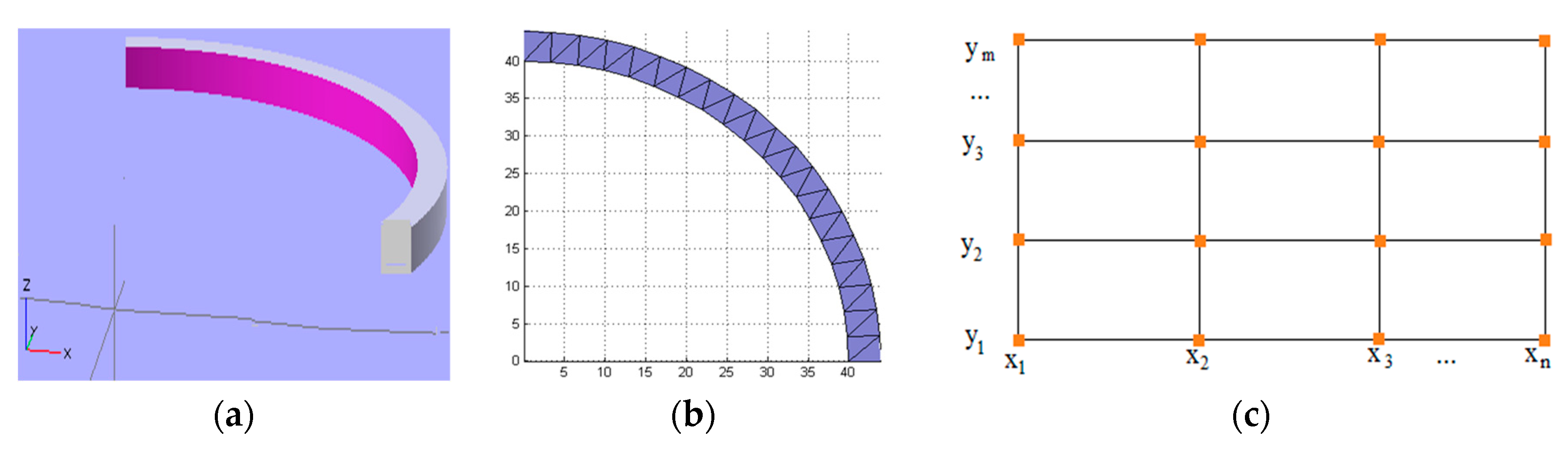
3.3. Point Cloud Generation Using Image Processing Techniques
3.4. Tool Path Motion Parameters
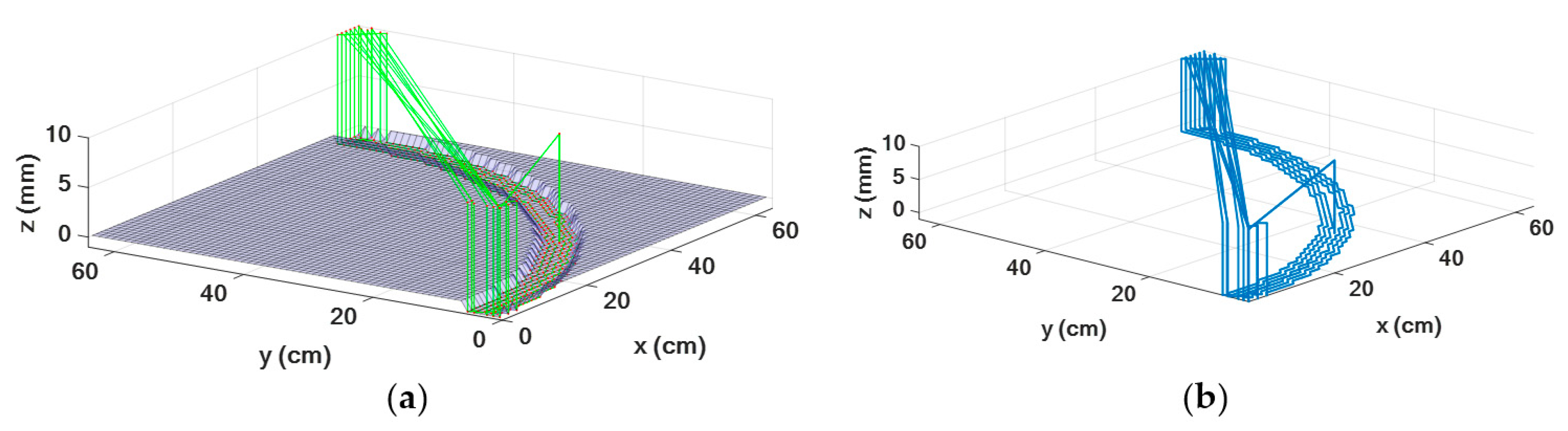
3.5. Tool-Path Generation and Parsing
| Algorithm 2: Pseudocode for image processed path generator | |
| [z,x] = pixels data from image along(z,x) axis | |
| Pcor = []; | % Initializing the dynamic coordinate array |
| k = 0; | % Counter |
| t = 0; | % Counter |
| for i = From Zo to Zf | |
| t = t + 1; | % Able to count the number of tool passes |
| for j = From Xf to Xo | % Holds true for materials to be removed |
| if image(i,j)>0; | |
| Pnew = [j,i]; | |
| k = k + 1; | % Counts the true pixels to be removed |
| else | |
| Pnew = []; | % Final product pixels |
| end | |
| P = Pnew; | |
| Pcor = [Pcor;P]; | % Creates a vector of tool path |
| end | |
| end | |
3.6. G-Code Generation
- G00 X45 Y20 Z00: Rapid movement to coordinates of (45, 20, 0)
- G01 X45 Y20 Z00 F3.5: Linear movement to coordinates of (45, 20, 0)
- G02/G03 X45 Y20 R1.0: Circular motion to coordinates of (45, 20) with a radius of 1.0
4. Result and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Altintas, Y. Manufacturing Automation by Yusuf Altintas. Camb. Core 2012. [Google Scholar] [CrossRef]
- Zhou, M.; Zheng, G.; Chen, Z.C. An automated CNC programming approach to machining pocket with complex islands and boundaries by using multiple cutters in hybrid tool path patterns. Int. J. Adv. Manuf. Technol. 2016, 83, 407–420. [Google Scholar] [CrossRef]
- Wang, X.; Fu, X.; Li, C.; Kang, M. Tool path generation for slow tool servo turning of complex optical surfaces. Int. J. Adv. Manuf. Technol. 2015, 79, 437–448. [Google Scholar] [CrossRef]
- Filice, L.; Ambrogio, G.; Gaudioso, M. Optimised tool-path design to reduce thinning in incremental sheet forming process. Int. J. Mater. Form. 2013, 6, 173–178. [Google Scholar] [CrossRef]
- Lechevalier, D.; Shin, S.-J.; Rachuri, S.; Foufou, S.; Lee, Y.T.; Bouras, A. Simulating a virtual machining model in an agent-based model for advanced analytics. J. Intell. Manuf. 2019, 30, 1937–1955. [Google Scholar] [CrossRef] [PubMed]
- Jouandeau, N. Rapidly-exploring Sorted Random Tree: A Self Adaptive Random Motion Planning Algorithm. In Informatics in Control, Automation and Robotics: Selected Papers from the International Conference on Informatics in Control, Automation and Robotics 2007; Filipe, J., Cetto, J.A., Ferrier, J.-L., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 63–73. [Google Scholar]
- Liu, Y.; Guo, X.; Li, W.; Yamazaki, K.; Kashihara, K.; Fujishima, M. An intelligent NC program processor for CNC system of machine tool. Robot. Comput. Integr. Manuf. 2007, 23, 160–169. [Google Scholar] [CrossRef][Green Version]
- Ridwan, F.; Xu, X.; Ho, F.C.L. Adaptive execution of an NC program with feed rate optimization. Int. J. Adv. Manuf. Technol. 2012, 63, 1117–1130. [Google Scholar] [CrossRef]
- Tönshoff, H.K.; Janocha, H.; Seidel, M. Image Processing in a Production Environment. CIRP Ann. 1988, 37, 579–590. [Google Scholar] [CrossRef]
- Reduction of Production Cycle Time by Optimising Production and Non-Production Components of Time in the Metalworking Industry: A Case Study. Available online: http://www.scielo.org.za/scielo.php?script=sci_arttext&pid=S2224-78902016000100015 (accessed on 10 August 2019).
- Ullah, A.S.; Harib, K.H. Tutorials for Integrating CAD/CAM in Engineering Curricula. Educ. Sci. 2018, 8, 151. [Google Scholar] [CrossRef]
- Mikołajczyk, T.; Kłodowski, A.; Mrozinski, A. Camera-based Automatic System for Tool Measurements and Recognition. Procedia Technol. 2016, 22, 1035–1042. [Google Scholar] [CrossRef][Green Version]
- Posada, J.R.D.; Schneider, U.; Sridhar, A.; Verl, A. Automatic Motion Generation for Robotic Milling Optimizing Stiffness with Sample-Based Planning. Machines 2017, 5, 3. [Google Scholar] [CrossRef]
- Dupont, P.E.; Derby, S. An Algorithm for CAD-Based Generation of Collision-Free Robot Paths. In CAD Based Programming for Sensory Robots; Springer: Berlin/Heidelberg, Germany, 1988; pp. 433–465. [Google Scholar]
- Xu, K.; Li, Y.; Xiang, B. Image processing-based contour parallel tool path optimization for arbitrary pocket shape. Int. J. Adv. Manuf. Technol. 2019, 102, 1091–1105. [Google Scholar] [CrossRef]
- Chitsaart, C.; Rianmora, S.; Rattana-Areeyagon, M.; Namjaiprasert, W. Automatic Generating CNC-Code for Milling Machine. World Acad. Sci. Eng. Technol. J. Ind. Manuf. Eng. 2013, 7, 2607–2613. [Google Scholar]
- Konobrytskyi, D. Automated CNC Tool Path Planning and Machining Simulation on Highly Parallel Computing Architectures. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 2013. [Google Scholar]
- Zhao, Q.; Huang, X.; Wang, C.; Yao, Y.; Hu, Q. NC tool path generation approach based on STL. In Proceedings of the 2011 IEEE International Symposium on IT in Medicine and Education, Guangzhou, China, 9–11 December 2011; pp. 228–231. [Google Scholar]
- Qu, X. Raster milling tool-path generation from STL files. Rapid Prototyp. J. 2006, 12, 4–11. [Google Scholar] [CrossRef]
- Hassaballah, M.; Abdelmgeid, A.A.; Alshazly, H.A. Image Features Detection, Description and Matching. In Image Feature Detectors and Descriptors: Foundations and Applications; Awad, A.I., Hassaballah, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 11–45. [Google Scholar]
- Vatani, M.; Rahimi, A.R.; Brazandeh, F. An Enhanced Slicing Algorithm Using Nearest Distance Analysis for Layer Manufacturing. Proc. World Acad. Sci. Eng. Technol. 2009, 3, 6. [Google Scholar]
- Eragubi, M. Slicing 3D CAD Model in STL Format and Laser Path Generation. Int. J. Innov. Manag. Technol. 2013, 4, 410–413. [Google Scholar] [CrossRef]
- Szucki, M.; Suchy, J. A voxelization based mesh generation algorithm for numerical models used in foundry engineering. Metall. Foundry Eng. 2012, 38, 43. [Google Scholar] [CrossRef]
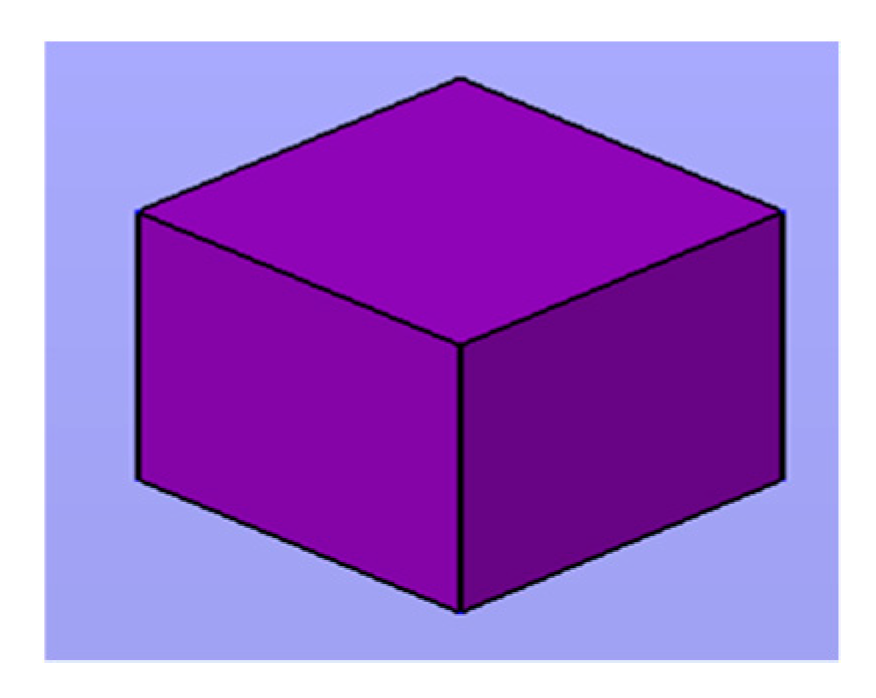
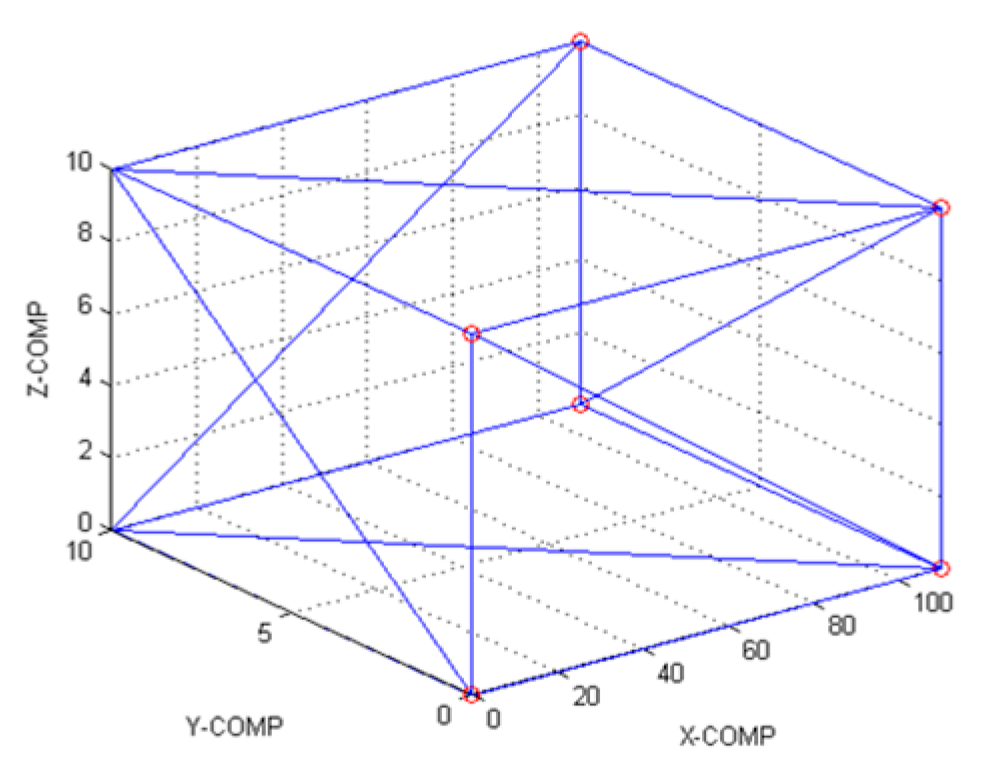

| Parameter | STEP | STL | IGES |
|---|---|---|---|
| Memory (Bytes) | 16.7 K | 684 | 21.3 K |
| 3D | Yes | Yes | Yes |
| Vertices | 18 | 36 | 18 |
| Faces | 6 | 12 | 6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuli, T.B.; Cesarini, A. Automated Unsupervised 3D Tool-Path Generation Using Stacked 2D Image Processing Technique. J. Manuf. Mater. Process. 2019, 3, 84. https://doi.org/10.3390/jmmp3040084
Tuli TB, Cesarini A. Automated Unsupervised 3D Tool-Path Generation Using Stacked 2D Image Processing Technique. Journal of Manufacturing and Materials Processing. 2019; 3(4):84. https://doi.org/10.3390/jmmp3040084
Chicago/Turabian StyleTuli, Tadele Belay, and Andrea Cesarini. 2019. "Automated Unsupervised 3D Tool-Path Generation Using Stacked 2D Image Processing Technique" Journal of Manufacturing and Materials Processing 3, no. 4: 84. https://doi.org/10.3390/jmmp3040084
APA StyleTuli, T. B., & Cesarini, A. (2019). Automated Unsupervised 3D Tool-Path Generation Using Stacked 2D Image Processing Technique. Journal of Manufacturing and Materials Processing, 3(4), 84. https://doi.org/10.3390/jmmp3040084





