Abstract
In this work, we introduce an analytical expression for approximating the transient melting radius during powder melting in Selective Laser Melting (SLM) assumed with a stationary laser heat source. The purpose of this work is to evaluate the suggested analytical approach in determining the melt pool geometry during laser processing, by considering heat transfer and phase change effects. This will allow for the rendering of the first findings on the way to a quasi-real time calculation of the melt pool during laser melting, which will contribute significantly to the process design and control, especially when new powders are applied. Initially, we consider the heat transfer process associated with a point heat source, releasing a continuous and constant power (in a semi-infinite powder bed. On the point of the heat source the temperature is infinite, and the material starts to melt spherically outwards, creating an interface that separates the solid from the molten material; we assume different properties between the two phases. Unlike the cases of the cartesian and cylindrical coordinates, (in a cartesian coordinate the heat source is over a plane, i.e., W/m2, and in cylindrical along a line, i.e., W/m), where the melting process is proportional to the square root of time, in spherical coordinates the melting stops at a finite radius, i.e., a maximum radius, which depends only on the heat source, the conductivity of the solid and the difference between the far-field temperature and the melting temperature of the material. Here we should also point out that to achieve continuous melting in spherical coordinates the power of the source must increase with the square root of the time. The obtained analytical expression for the maximum melting radius and the approximate expression for its dependence on the time compare well with the numerical results obtained by a finite element analysis.
1. Introduction
Melting due to a heat source is very significant in thermal manufacturing processes such as Selective Laser Melting (SLM) [1,2,3,4,5,6] and Selective Laser Sintering (SLS) [7,8], spot welding, torch welding [9,10,11], and arc welding [12], to name a few. In these processes, an understanding of the melting process is very important due to the many other physical phenomena taking place simultaneously, such as Marangoni effects and the internal flow in the molten material.
The fundamentals of the thermodynamic change phase of solids are presented comprehensively by Tosun [13], whereas in the work of Berveiller & Fischer [14] a deeper insight into the influence of the change phase on the mechanical properties of solids is outlined. Here, kinematic models to describe the phase change effects in metals during melting and solidification, especially in the case of steel alloys, are expedient [15]. During the phase change from solid to liquid and back to solid, thermal and plastic stresses occur due to a lower yield strength in metals at higher temperatures [16]. After a cooling down to an ambient temperature due to a non-linear interaction of thermal, elastic and plastic stresses and the phase change, rest stresses are formed in the solid structure, so called residual stresses [17,18]. In particular in the case of SLM processes, a residual stresses formation is of great importance since residual stresses are dominated by the actual process parameters [19]. Modeling methods are applied in order to simulate the formation of residual stresses that have a significant impact in process feasibility and product properties [20,21]. A deeper insight into the characterization and evaluation of residual stresses by means of experimental measurements and analytical models is presented by Ghidelli et al. [22].
Fundamental work on phase change dates back to Lamè & Clapeyron [23] and to Stefan [24] who consider the problem of ice formation. Phase change in cylindrical and spherical coordinates were later considered by Frank [25], Paterson [26], and Cho & Sunderland [27]. Paterson [26] addressed the problem of a line heat source in cylindrical coordinates and obtained an expression for the propagation of the melting interface. The temperature along the line heat source is infinite, and an interface separates the material into two regions: the molten phase and the solid phase. The velocity of the interface is proportional to the square root of time, and the proportionality constant is obtained through a characteristic equation by employing the boundary condition describing the energy conservation along the boundary of fusion. The analytical expression for the process was obtained by employing a similarity variable that reduced the partial differential equations (PDE) into ordinary differential equations (ODE). Finally, the characteristic algebraic equation is obtained.
Analytical expressions for the phase change process can be also obtained in one-dimensional cartesian coordinates in the case of the solidification of a supercooled liquid, and the melting or solidification in a half-space with a constant temperature along the boundary [28]. As mentioned before, a common characteristic of many one-dimensional problems, particularly in cartesian coordinates, is the reduction of the PDE to an ODE using the characteristic variable x/√ t. Detailed accounts of many problems with different configurations in solidification and melting are described in Alexiades & Solomon [29], Carslaw & Jaeger [30], Ghez [31] and Hu & Argyropoulous [32], along with the methodologies for addressing more complicated problems, both analytically and approximately.
An analytical solution for solidification/melting in spherical coordinates is not available. The physical reason for this is that the temperature drops rapidly enough along the radius, and after a certain point the solidification/melting cannot be sustained due to the reduction of the temperature gradient. Mathematically, the situation can be easily understood by considering the problem of one dimensional heat conduction in an infinite medium in the three basic coordinate systems, i.e., cartesian, cylindrical and spherical. Although for steady-state conditions there is an analytical solution in spherical coordinates and the temperature is proportional to the inverse radius 1/r, this is not the case in cylindrical and cartesian coordinates; in cylindrical coordinates, the temperature is proportional to the log[r] and in artesian coordinates it is proportional to x [33], i.e., for cartesian and cylindrical coordinates the only possible solution is time dependent. Hence Paterson [26], who considered the problems of phase change in cylindrical and spherical coordinates, and was able to obtain an analytical solution in spherical coordinates only under the assumption that the power of the heat source increases with the square root of time; hence, this solution is of less practical importance.
In the existing literature, time-intensive thermal models of the transient temperature distribution during SLM processing are presented using equivalent heat sources on the basis of the finite element analysis [34,35]. In this work, we focus exclusively on the transient heat transfer effects during the phase change, i.e., the melting, of solid powder to liquid, by proposing an analytical model. We consider the problem of phase change in spherical coordinates assuming a continuous but constant heat source at a single point. This simplifies the problem, as the solution is spherically symmetric. In what follows, we present the problem, the steady-state solution and a transient approximate analytical solution, and compare them with a numerical simulation obtained using a finite element analysis. Here, the main goal is to appraise the proposed analytical solution, which provides a quasi-real time estimation of the melt pool. Future enhancements are intended to assist the SLM process, as well as the product design and control, especially due to the recent rising industrial application of additive manufacturing (AM) technologies [36].
2. Problem Statement and Solution
Consider the case of semi-infinite solid material, i.e., powder beds, that we wish to melt in order to subsequently produce a solid component. A point laser beam provides a heat source of power that melts the material with a spherical symmetry. The configuration is shown in Figure 1. We assume that the solid and the molten material have the same density, so the shape of the configuration remains the same, i.e., no annulus is created. However, we assume that the heat capacity and the conductivity of the two phases are different. This leads to a discontinuity of the temperature gradient at the interface (R[t]) between the solid and the liquid (molten material). The interface (R[t]) separates the solid from the molten material and is a function of time.
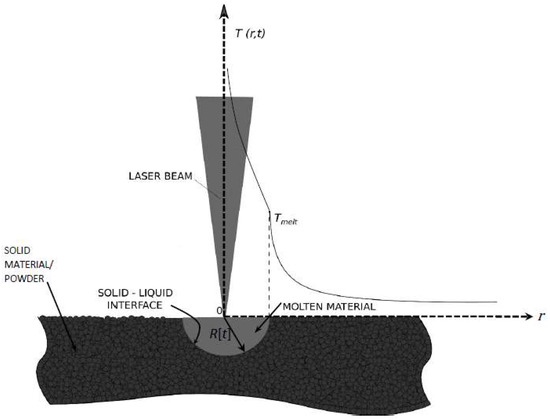
Figure 1.
Schematic representation of a cross section of the physical problem, which is spherically symmetric. The molten material has the shape of a hemisphere with radius R[t] that denotes the location of the interface. The melting is due to a laser delivering a power at the point 0 of the semi-infinite solid material (powder).
The equations that describe the two phase-problem are as follows [28]:
(i) The liquid phase:
(ii) The solid phase:
(iii) Energy balance on the interface:
where α is the thermal diffusivity, k is the thermal conductivity, L is the latent heat, ρ is the density that is constant, i.e., ρs = ρl, and Tmelt is the melting temperature of the material. In the above equations, the subscript l denotes the liquid phase (molten material) and s the solid (powder).
The above system of equations and boundary conditions (Equations (1)–(7)) have no analytical solution. There is only an analytical/similarity solution if the heat source increases with the square root of time [26], i.e.,
However, if we assume steady-state conditions, i.e., we drop the time derivative terms from the system of Equations (1)–(7), and we obtain the following steady-state solutions: , , and for the temperature fields and the radius, respectively:
and
It is important to point out that the above steady-state solutions must also be valid in the case of different densities between the solid and the liquid. This is justified because at a steady-state the terms related to convection must be zero, and the system of Equations (1)–(7) would be applicable.
3. Approximation Solutions
3.1. Approximate Analytical Solution
An approximate solution for the interface R[t] can be obtained by considering that the process is controlled by diffusion in the solid phase. This is justified because (i) the powder has a smaller thermal diffusivity than the molten material, (ii) the melt pool is confined in a small radius and (iii) the steady-state solution of the interface R (Equation (10)) is independent of the properties of the liquid. Hence, for the case of a constant, continuous, thermal energy source at the origin of a semi-infinite, homogeneous medium, the temperature distribution is obtained as [37]:
Hence, the location of the interface R[t] with the temperature T = Tmelt is given by numerically solving the implicit equation:
3.2. Numerical Solution
The finite element simulation was performed on the commercial software ANSYS Workbench [38]. For the properties of the solid material, we have used the properties of the powder IN718 [2], i.e., ks = 0.37 W/(mK), αs = 2.76 × 10−7 m/s2, = 20 °C and Tmelt = 1300 °C. For a heat source of power = 4 W, using Equation (10), we obtain that at a steady-state the interface is located at R = 0.13 mm. In the FE simulation, the heat power was defined on an infinitesimal surface of radius 0.01 mm in order to replicate the point heat source. This dimension represents 7.7% of the computed melt pool of radius 0.13 mm, even at a very short time duration (0.01 s) after the simulation starts. The significance of the heat source dimension in the FE analysis drops to a theoretical zero, i.e., the point source is approximated, especially when compared to the expected final melt pool radius of 1.3 mm, i.e., at steady state, reaching a value of solely 0.77%. Based on these dimensional observations, the mesh density in the heat source area was estimated to have a value of 0.005 mm and in the expected melt pool area a value of 0.05 m. This geometrical discretization enables a fast convergence during the transient thermal analysis, with an adequate computation of the temperature gradients, as shown in Figure 2. The very high temperature of 3.4 × 105 °C in the center of the melt pool, i.e., on the approximated point heat source, represents the theoretical infinity of the analytical solution.

Figure 2.
Mesh discretization and melt pool computation with the semi-spherical interface for a large time of 10,000 s, i.e., the steady-state has been reached. The numerical software employed is ANSYS [38].
3.2.1. Numerical Results with no Phase Change
To verify the numerical analysis, we first addressed the problem of the continuous release of heat at single point on a homogeneous semi-infinite medium, i.e., without considering the varying material properties at the melt pool interface (Equation (7)). We have used the properties of the solid mentioned earlier. The analytical solution for this problem is given by Equation (11), hence we expect the numerical solution to match Equation (12). In Figure 3, we compare the results of the simulation with Equation (12). The figure shows the location of the radius where the temperature is at Tmelt for the two cases, i.e., numerical (dashed curve) and analytical (solid curve, Equation (12)). For the given data, the steady-state radius is R = 0.00134 m. As expected, the results are very accurate, and the error is less than 1%.
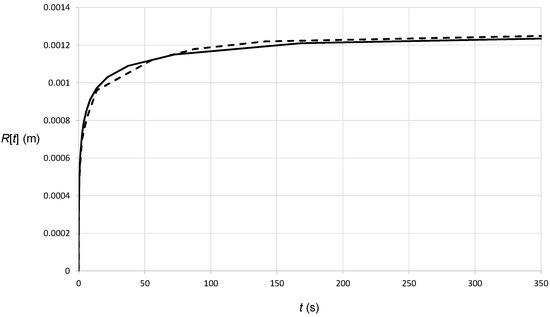
Figure 3.
Heat transfer in a homogeneous, semi-infinite material with a continuous heat release at a single point. The curves show the radius (semi-spherical interface) where the temperature has the constant value Tmelt, as a function of time. The solid curve is the analytical solution (Equation (12)), and the dashed curve is the numerical solution obtained using the finite element analysis (ANSYS [38]).
3.2.2. Numerical Results with Phase Change
The numerical analysis is enhanced with the definition of the varying, i.e., non-linear specific heat capacity between the solid and liquid phases, implying that the phase change from the solid to liquid state requires the latent heat at the melting temperature. We have assumed a pure material, i.e., the phase change occurs at the distinct temperature Tmelt. The liquid phase and the solid phase are characterized by different properties of the heat capacity, specifically cps = 351 J/(kg·K) and cpl = 643 J/(kg·K), resulting in a latent heat of 4.59 × 105 J/kg. In addition, the density of the liquid is ρl = 7756 kg/m3 and kl = 26.63 W/(m·K). A parameter sensitivity analysis shows that the thermal conductivity variation due to the phase change does not influence the melt pool creation significantly, i.e., the dominant material property in this case is the heat capacity, as justified by literature findings [39]. In Figure 4, we show the results of the numerical simulation, and we compare them with the approximate transient analytical result (Equation (12)). It is evident that both the numerical and approximate results (Equation (12)) approach the steady-state solution (Equation (10)), the only difference being the rate at which this is approached. It is interesting, however, that although the approximate solution (Equation (12)) assumes a single material, in particular solid powder, it provides results close to the numerical solution, the maximum error being approximately 10%. This is not surprising as the melt pool is isolated in a small region.
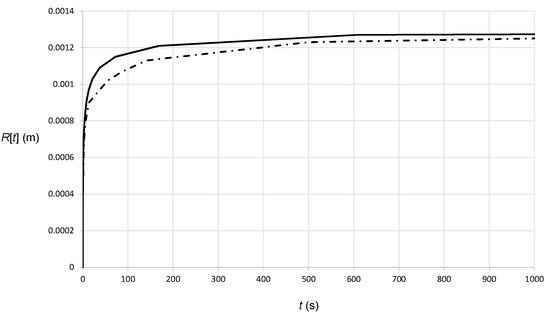
Figure 4.
Heat transfer with phase change in a semi-infinite powder bed with continuous heat release at a single point. The curves show the melt pool radius (semi-spherical interface) where the temperature has the constant value Tmelt. The solid curve is the analytical solution obtained assuming a single material, i.e., homogeneous powder (Equation (12)), and the dashed curve is the numerical solution. In the latter, we assume that there are two phases: solid and liquid.
In addition, because of the latent heat and the higher heat capacity, the interface obtained by the numerical solution requires more time to achieve a certain radius, hence the radius obtained from the analytical solution is always higher than the one obtained from the numerical solution.
4. Conclusions
The findings of our work are summarized as follows:
- (1)
- We consider the heat conduction problem associated with a continuous source of power at a single point in a semi-infinite material. At the point of the heat source, the temperature is infinite, and the melting process is spherically symmetric. Unlike cartesian and cylindrical coordinates, there is no analytical solution; there is, however, a steady-state solution, i.e., the melting process reaches a maximum radius. The radius is proportional to the power of the heat source and inversely proportional to the conductivity of the solid and the difference between the melting temperature and the temperature at infinity, as proposed in the work of [26].
- (2)
- An approximate analytical solution of the melting radius as a function of time is obtained by assuming a single material, i.e., solid powder, and by locating the radius where the temperature is at the melting temperature, as in [37].
- (3)
- This simple approximation has the same steady-state result as the numerical solution, and also provides transient results close to the numerical solution, although the numerical solution includes the latent heat, and a higher heat capacity and conductivity for the fluid similar to the finite element analyses conducted by [34,35] for a moving heat source (Figure 4). The reason for this is that the heat conduction process is controlled by the material with the lower thermal diffusivity, i.e., the solid powder, and that the melt pool has small dimensions. The difference between the two is that the numerical result requires more time to achieve the steady-state solution because of the extra energy required due to the latent heat and the non-linear heat capacity of the molten material.
Author Contributions
Conceptualization, M.M.F. and L.P.; Data curation, L.P.; Formal analysis, M.M.F.; Investigation, M.M.F. and L.P.; Methodology, M.M.F. and L.P.; Resources, M.M.F. and L.P.; Software, M.M.F. and L.P.; Supervision, M.M.F.; Validation, M.M.F. and L.P.; Visualization, M.M.F. and L.P.; Writing—original draft, M.M.F. and L.P.; Writing—review & editing, L.P.
Funding
The work presented in this paper was partially performed in the framework of the AMable Project which has received funding from the European Union Horizon 2020 research and innovation program under grant agreement No 768775. Project website: http://www.amable.eu [36]. The work was partially funded by Porfyrios Chap Glass Ltd., CYPRUS. The author Marios M. Fyrillas was partially supported by CRoNoS—IC1408 COST Action.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, B.; Chou, K. Melt Pool Evolution Study in Selective Laser Melting. In Proceedings of the 26th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 10–12 August 2015; pp. 1182–1194. [Google Scholar]
- MERLIN Project “Development of Aero Engine Component Manufacture Using Laser Additive Manufacturing”, 7th Framework Programme FP7, 2007–2013. Available online: http://www.merlin-project.eu/ (accessed on 15 November 2018).
- Li, Y.; Zhou, K.; Tor, S.B.; Chua, C.K.; Leong, K.F. Heat transfer and phase transition in the selective laser melting process. Int. J. Heat Mass Transfer 2017, 108, 2408–2424. [Google Scholar] [CrossRef]
- Kruth, J.P.; Duou, J.; Mercelis, P.; Van Vaerenbergh, J.; Craeghs, T.; De Kuester, J. On-line monitoring and process control in selective laser melting and laser cutting. In Proceedings of the 5th Lane Conference, Laser Assisted Net Shape Engineering, Erlangen, Germany, 25–28 September 2007; pp. 23–37. [Google Scholar]
- Papadakis, L.; Loizou, A.; Risse, J.; Bremen, S.; Schrage, J. A computational reduction model for appraising structural effects in selective laser melting manufacturing: A methodical model reduction proposed for time-efficient finite element analysis of larger components in Selective Laser Melting. J. Virtual Phys. Prototyp. 2014, 9, 17–25. [Google Scholar] [CrossRef]
- Xuezhi, S.; Shuyuan, M.; Changmeng, L.; Cheng, C.; Qianru, W.; Xianping, C.; Jiping, L. Performance of High Layer Thickness in Selective Laser Melting of Ti6Al4V Materials. Materials 2016, 9, 975. [Google Scholar]
- Polivnikova, T. Study and Modelling of the Melt Pool Dynamics during Selective Laser Sintering and Melting. Ph.D. Thesis, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 2015. [Google Scholar]
- Ioannou, Y.; Doumanidis, C.; Fyrillas, M.M.; Polychronopoulou, K. Analytical model for geometrical characteristics control of laser sintered surfaces. Int. J. Nanomanufacturing 2010, 6, 300–311. [Google Scholar] [CrossRef]
- Doumanidis, C.; Fourligkas, N. Temperature Distribution Control in Scanned Thermal Processing of Thin Circular Parts. IEEE Trans. Control Syst. Technol. 2001, 9, 708–717. [Google Scholar] [CrossRef]
- Doumanidis, C. Modeling and control of timeshared and scanned torch welding. ASME J. Dyn. Syst. Meas. Control 1994, 116, 387–395. [Google Scholar] [CrossRef]
- Doumanidis, C. Simulation for control of sequential and scanned thermal processing. Int. J. Modeling Simul. 1997, 17, 169–177. [Google Scholar]
- Doumanidis, C.; Hardt, D.E. Simultaneous in-process control of heat-affected zone and cooling rate during arc welding. Weld. Res. Suppl. 1990, 69, 186–196. [Google Scholar]
- Tosun, I. The Thermodynamics of Phase and Reaction Equilibria; Elsevier: Oxford, UK, 2013. [Google Scholar]
- Berveiller, M.; Fischer, F.D. Mechanics of Solids with Phase Changes; Springer: Vienna, Austria, 1997. [Google Scholar]
- Leblond, J.B. A new kinetic model for anisothermal metallurgical transformations in steels including effect of austenite grain size. Acta Metall. 1984, 2, 137–146. [Google Scholar] [CrossRef]
- Radaj, D. Heat Effects of Welding; Springer: Berlin, Germany, 1992. [Google Scholar]
- Mercelis, P.; Kruth, J.P. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Vrancken, B. Study of Residual Stresses in Selective Laser Melting. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2016. [Google Scholar]
- Mugwagwa, L.; Dimitrov, D.; Matope, S.; Yadroitsev, I. Evaluation of the impact of scanning strategies on residual stresses in selective laser melting. Int. J. Adv. Manuf. Technol. 2019, 102, 2441–2450. [Google Scholar] [CrossRef]
- Zaeh, M.F.; Branner, G. Investigations on residual stresses and deformations in selective laser melting. Prod. Eng. 2010, 4, 35–45. [Google Scholar] [CrossRef]
- Megahed, M.; Mindt, H.W.; N’Dri, N.; Duan, H.; Desmaison, O. Metal additive-manufacturing process and residual stress modeling. Integr. Mater. Manuf. Innov. 2016, 5, 61–93. [Google Scholar] [CrossRef]
- Ghidelli, M.; Sebastiani, M.; Collet, C.; Guillemet, R. Determination of the elastic moduli and residual stresses of freestanding Au-TiW bilayer thin films by nanoindentation. Mater. Des. 2016, 106, 436–445. [Google Scholar] [CrossRef]
- Lamè, G.; Clapeyron, B.P. Memoire sur la solidification par refroidissement d’un globe solide. Ann. Chem. Phys. 1831, 47, 250–256. [Google Scholar]
- Stefan, J. Ueber die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Ann. Phys. Chemie (Wiedemannsche Annalen) 1891, 278, 269–286. [Google Scholar] [CrossRef]
- Frank, F.C. Radially symmetric phase growth controlled by diffusion. Proc. R. Soc. A 1950, 201, 586–599. [Google Scholar]
- Paterson, S. Propagation of a boundary of fusion. Proc. Glasg. Math. Assoc. 1952, 1, 42–47. [Google Scholar] [CrossRef]
- Cho, S.H.; Edward, J.E. Phase change of spherical bodies. Int. J. Heat Mass Transfer 1970, 13, 1231–1233. [Google Scholar]
- Özişik, M.N. Heat Conduction; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Alexiades, V.; Solomon, A.D. Mathematical Modelling of Melting and Freezing Processes; Hemisphere Publishing Corporation; Taylor & Francis Group: Washington, DC, USA, 1993. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1946. [Google Scholar]
- Ghez, R. Diffusion Phenomena, Case and Studies; Kluwer Academic: New York, NY, USA, 2001. [Google Scholar]
- Hu, H.; Argyropoulos, A.S. Mathematical modelling of solidification and melting: A review. Model. Simul. Mater. Sci. Eng. 1996, 4, 371–396. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 5th ed.; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Mirkoohi, E.; Ning, J.; Bocchini, P.; Fergani, O.; Chiang, K.N.; Liang, S.Y. Thermal Modeling of Temperature Distribution in Metal Additive Manufacturing Considering Effects of Build Layers, Latent Heat, and Temperature-Sensitivity of Material Properties. J. Manuf. Mater. Process. 2018, 2, 63. [Google Scholar] [CrossRef]
- De Moraes, D.A.; Czekanski, A. Parametric Thermal FE Analysis on the Laser Power Input and Powder Effective Thermal Conductivity during Selective Laser Melting of SS304L. J. Manuf. Mater. Process. 2018, 2, 47. [Google Scholar] [CrossRef]
- AMable Project “AdditiveManufacturABLE: Enabling SME and Mid-Cap Uptake of Additive Manufacturing by Bridging Gaps in the Digital Process Chain”, Horizon 2020. Available online: https://www.amable.eu/ (accessed on 10 January 2019).
- Yilbas, B.S.; Sahin, A.Z. Friction Welding. In Springer Briefs in Manufacturing and Surface Engineering; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- ANSYS Engineering Simulation & 3D Design Software. ANSYS Workbench Products Release Notes; ANSYS, Inc.: Cononsburg, WA, USA, 2005. [Google Scholar]
- Papadakis, L. Simulation of the Structural Effects of Welded Frame Assemblies in Manufacturing Process Chains. Ph.D. Thesis, Technische Universität München, München, Germany, 2008. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).