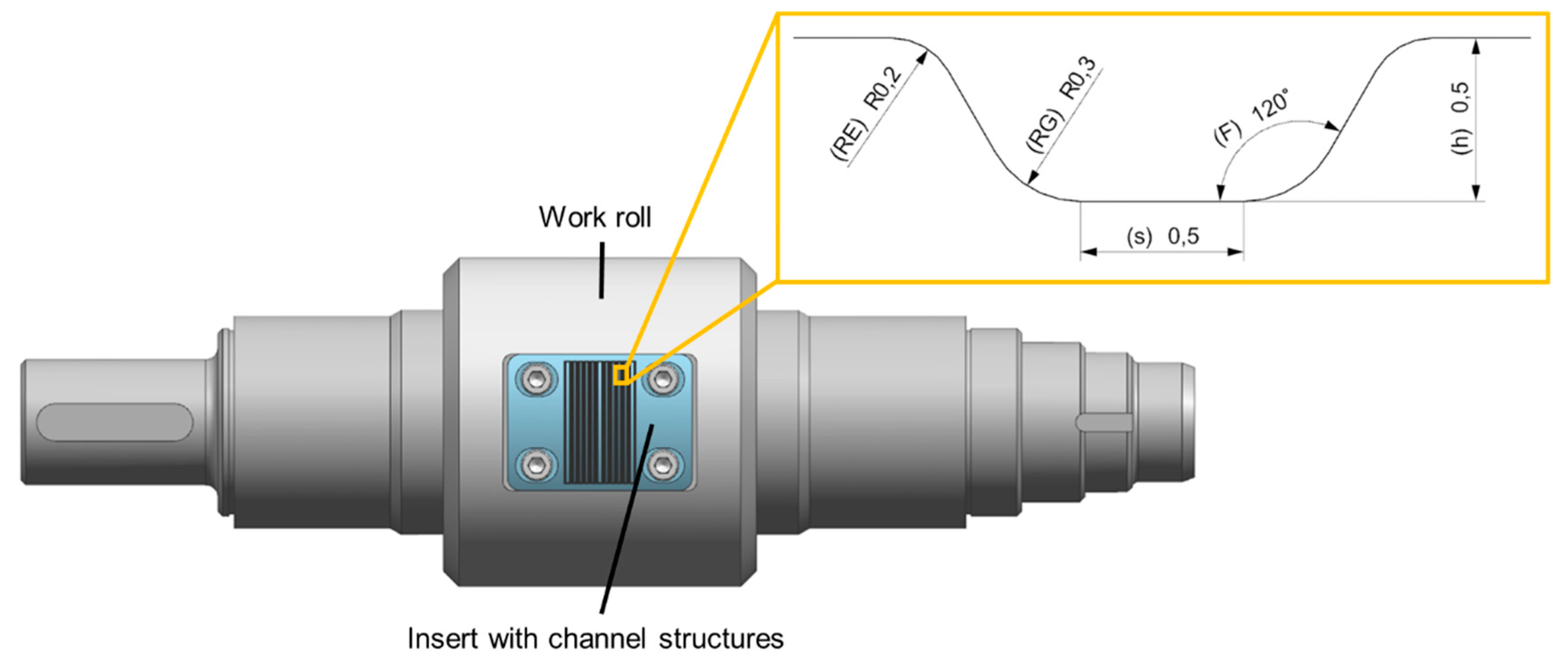
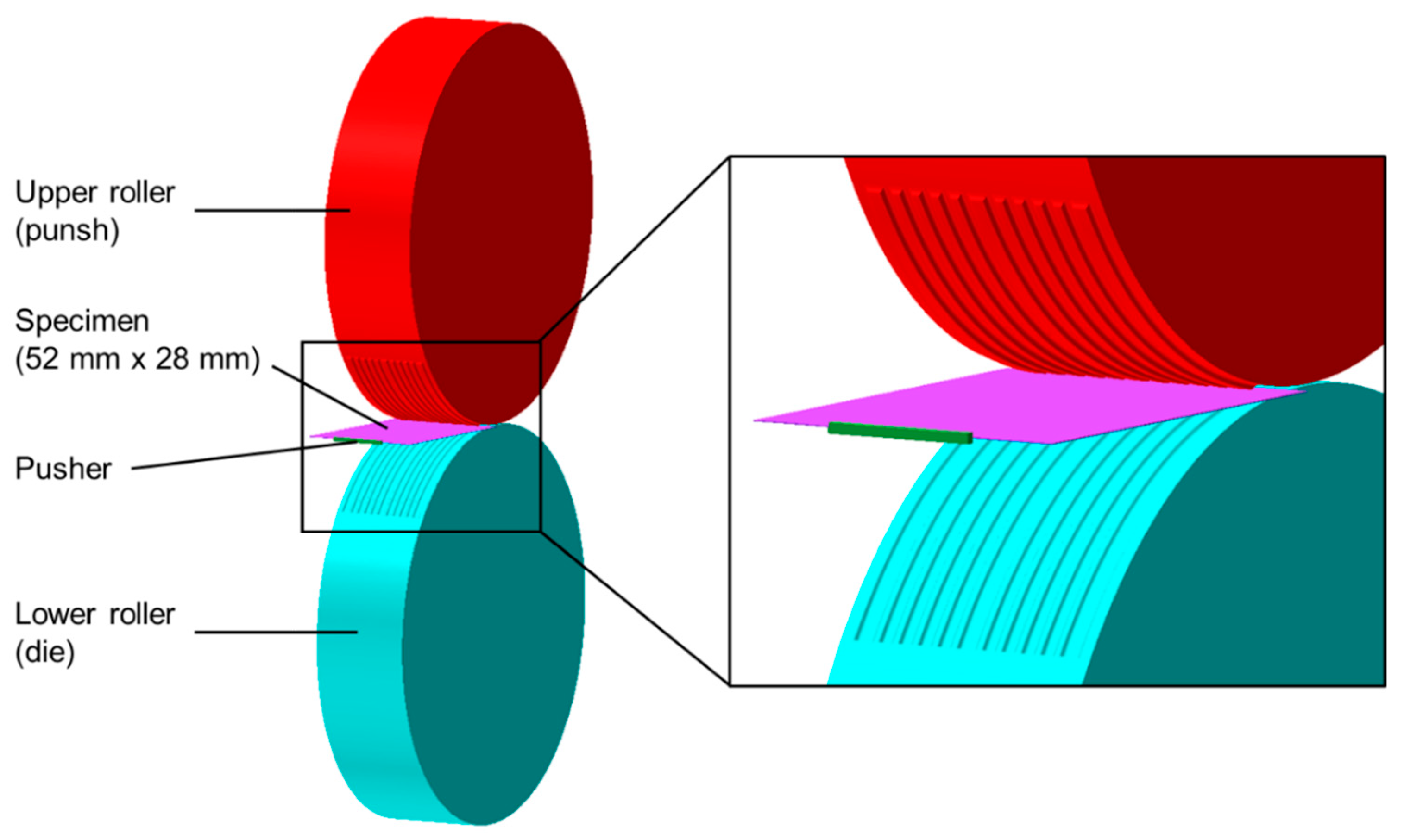
3.1. Preliminary Numerical Analysis and Experimental Studies of the Roll Forming Process
The numerical simulation in advance to the experimental tests has demonstrated the feasibility of the roll forming process for the forming of relevant bipolar plate channel geometries. The specimen was processed successfully by the roller geometries and first characteristics were visible (
Figure 5).
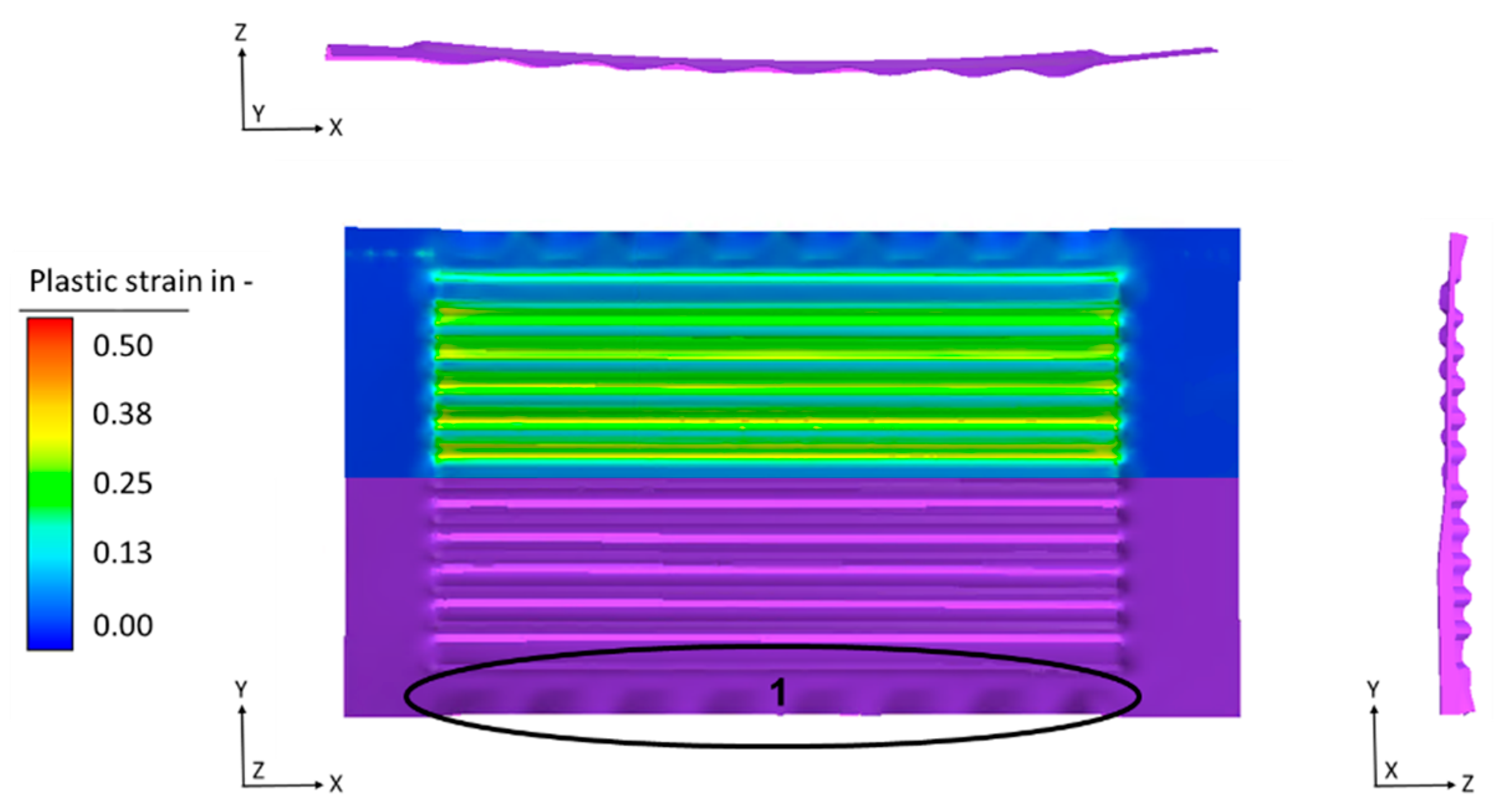
The macroscopic geometrical shape shows that the roll forming of the channels has been successful and the designed properties are clearly formed in the initial metal foil. The evaluation of the equivalent plastic strain shows some maximum values of φ = 0.36 and an average of φ = 0.27 for the radii and channel flanks (
Figure 5). Furthermore, eight first type wrinkles were visible on each side in x-direction within the peripheral areas next to the flow field of the specimen (
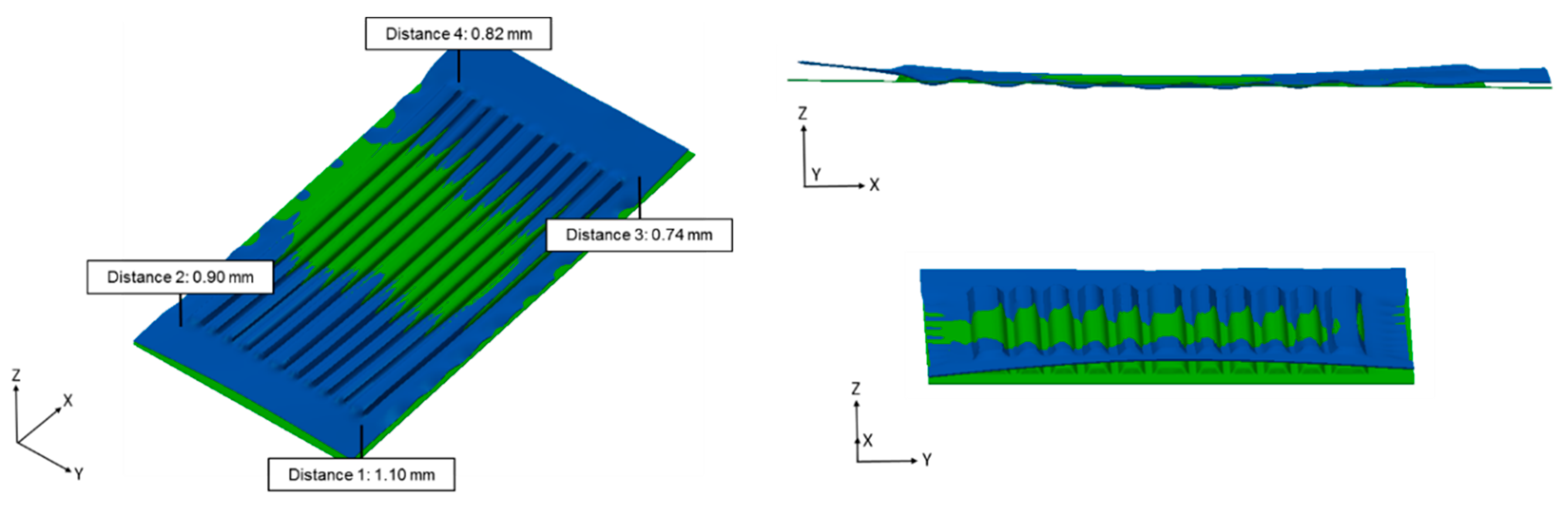
Figure 5(1)). Another phenomenon in sheet metal forming processes is the springback effect, which can be seen in both, x-direction and y-direction. This kind of springback effect is typical for the forming of metal foils by deep drawing and leads to an uneven specimen geometry, where problems in further operations like welding or assembling can occur. One further geometric uncertainty is the bending of the specimen, which normally appears within rolling processes and which in this case is caused by the small diameter of the work rolls (105 mm) and the rotational rolling kinematic. Compared to the CAD construction, the deviation in four defined points at the edges of the flow field (0.5 mm diagonal from the outer channel geometries) becomes clearly visible with a maximum distance of 1.10 mm between construction and simulated result and can be seen in the different views too (
Figure 6).
However, the numerical simulation proved, that the process of rolling this industrial shape bipolar plate channels in general works good, which leads to the conclusion that experimental tests have to be done, to prove the feasibility for the real process too.
In accordance to the geometries and parameters described above, the experimental tests were performed. The experiments showed equivalent results to the numerical simulations, which leads to the fact that the prediction of the numerical simulations worked very well. The channel geometries were successfully formed in the 0.1 mm metal foils by rolling, while the other geometrical characteristics, which can be seen in the numerical results (
Figure 5), occurred in the experiments too (
Figure 7).
A first optical analysis offers an almost identical look, as seen in the FEM results. The eight first grade wrinkles (
Figure 7(1)), spread over the peripheral areas on each side over the length of the specimen, occur in the same way, as in the numerical prediction. Other forming effects, which were visible for the simulation and the experiments, are the springback effect after the release of the tools and the bending of the specimen, which directly appears during the roll forming. One effect, which is not visible in the numerical simulation are the wrinkles over the width of the specimen (
Figure 7(2)). These wrinkles are limited to the experiments because there is a small offset in the radial position of the rollers, which leads to the effect that the gap in the entry area of the inserts is smaller, than in the outlet area. This means that the material in the outlet area is less restricted by geometrical boundaries and can deform in an undefined way, which also results in small wrinkles. A further challenge is given by the exact positioning of the specimen in front of the rollers. Minimal variances of the position in width and length lead to oblique or incompletely formed specimen.
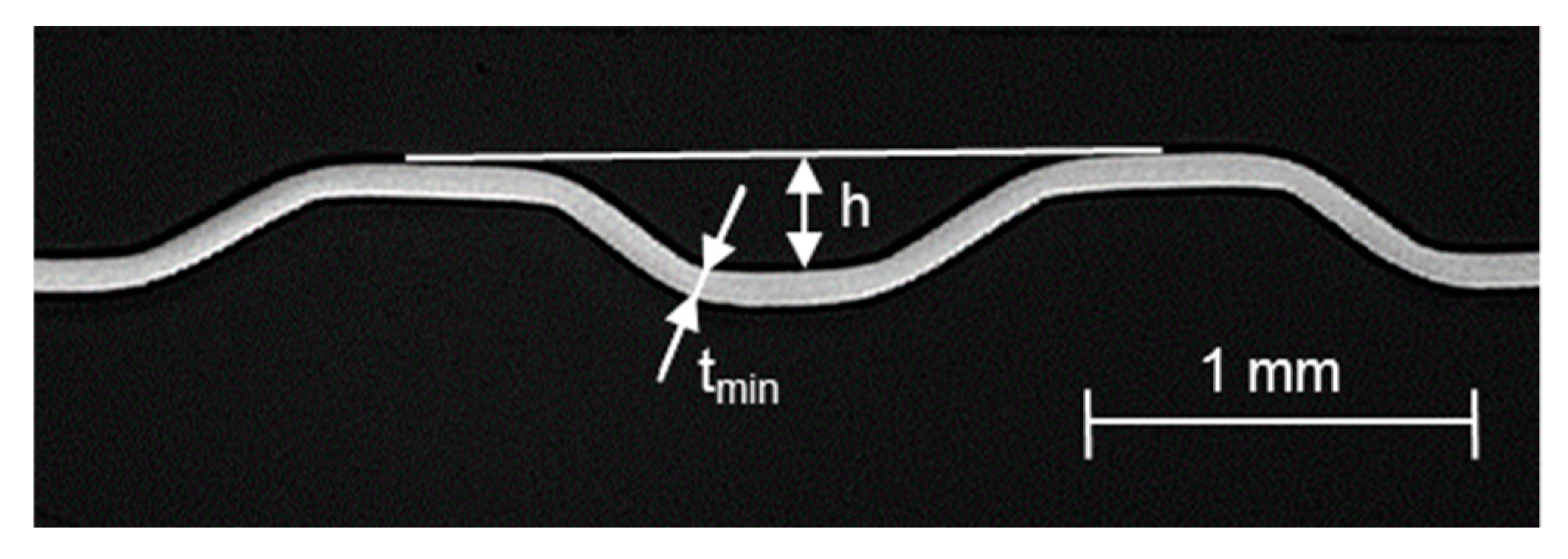
Other important geometrical values are the channel height and the remaining thickness of the formed workpiece. For the influence on the channel height, the rolling gap can be adjusted. In this case, the rolling gap was set to the initial thickness of the metal foils added with 20 µm offset (0.12 mm). Another characteristic of these forming processes is the thinning effect in the radii and flanks of the channel structures. To examine the detailed effects, microsections were made and analysed under the microscope. The results show channel cross-sections, with an average height (h) of 0.32 mm and even plateaus at the tops and bottom of the channels (
Figure 8).
Additionally it can be seen, that the formed structure of this setup developed without any significant thinning in the radii and flank areas and a minimum thickness (t
min) of 84.8 µm in one of the measured bottom radii (
Figure 8). This means, that the roll forming process with the used parameters is in a very safe area regarding possible damage effects like cracks. Additionally, it has to be said, that a reduced rolling gap (< 0.12 mm) can lead to more extensive thinning.
3.2. Verification of the Numerical Roll Forming Model
For a further predictive use of the roll forming FEM model, an exact calibration has to be done. A general conformity between the simulated and the experimental geometries was directly visible for the comparison of the forming results (
Figure 9).
As already stated, the wrinkles appear in the same amount and at the same location, which is again visible within
Figure 9. For another more exact statement, the experimental samples were measured according to the macroscopic geometry and the thinning; to compare the values with the ones gained from the FEM. The results are shown in
Table 2.
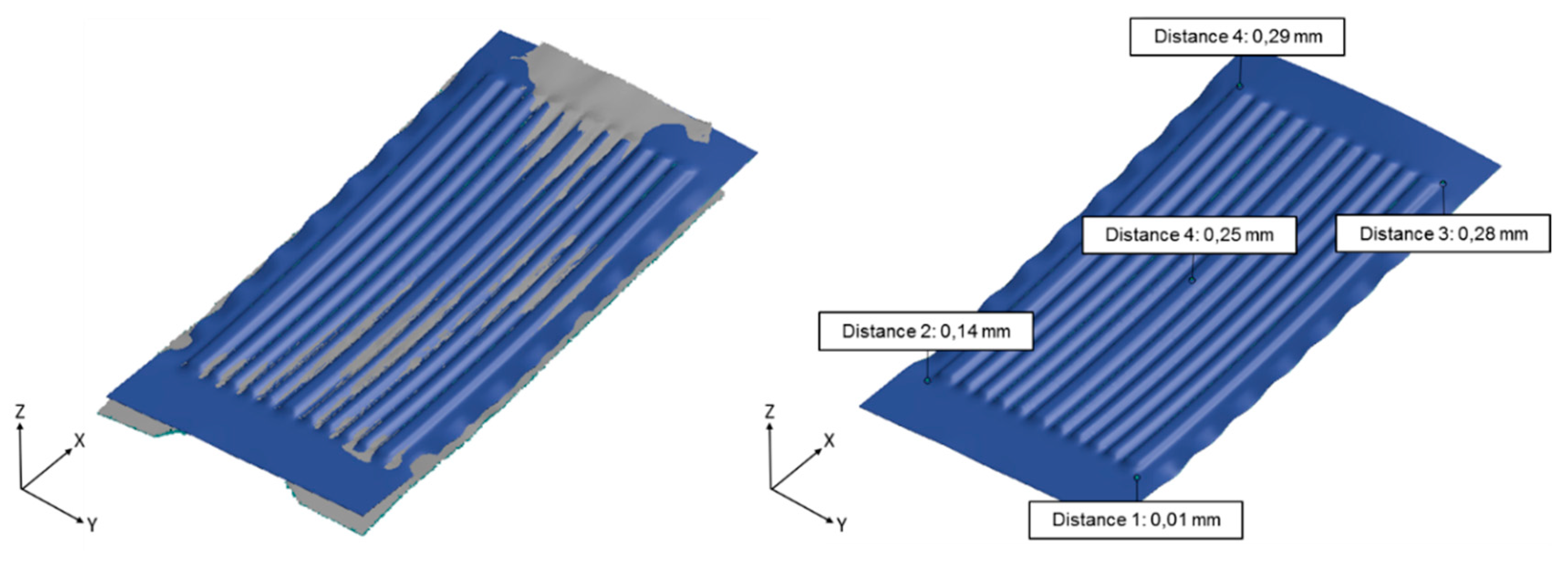
An additional measurement was done by means of the photogrammetry method (GOM ATOS Core, Braunschweig, Germany). This enables a direct comparison between the calculated numerical forming result (blue) and the experimental specimen (grey).
Figure 10 shows a very good conformity for the geometrical shape, with a maximum deviation in the distance between both results of 0.29 mm.
To sum it all up, a good congruence was found between the numerical simulation and the experimental tests. The maximum deviation in the height of the channels (12.5%) seems to be relatively high concerning the percentage but in total difference, it is just 40 µm too. Nevertheless, especially the global geometrical accordance and the thickness development show a noticeably better conformity, which means, that the FE-model can be used for further process improvements. The remaining problems with the macroscopic shape of the specimen (wrinkles and bending) should be solved to improve the roll forming results.
3.3. Roll Forming Process Improvements
First of all, it was tested how the roll forming results develop if the material is processed with the initial rolling direction of the metal foil perpendicular to the roll forming direction (90°RD). It is relevant to know if it is necessary to consider the initial rolling direction of the 316L (1.4404) metal foils in the process setup, especially if it is planned to produce bipolar plates directly from the coil. The investigation was done directly in the numerical simulation with the calibrated model setup. So the rolling direction of the initial workpiece had to be changed while all of the other parameters remained the same. The forming results were compared with the numerical model, where the initial rolling direction of the metal foil is the same as the roll forming direction (0°RD).
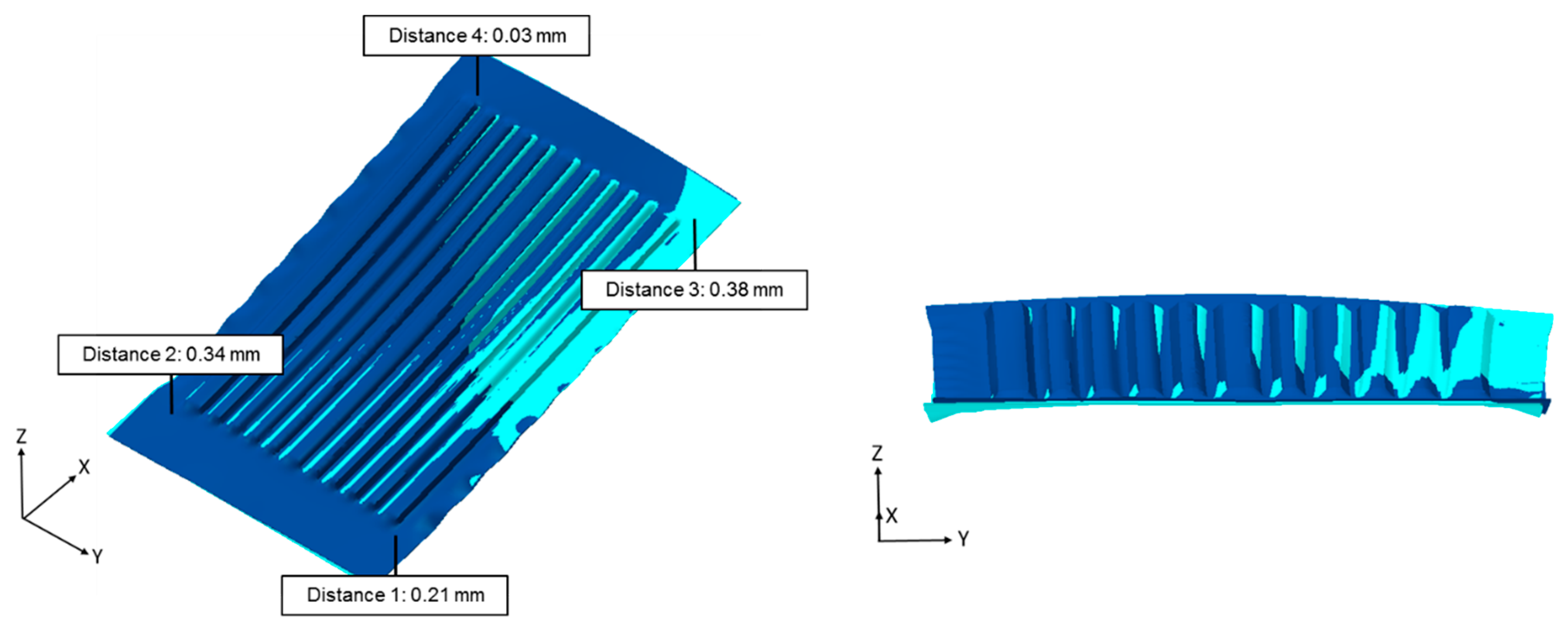
Figure 11 shows an almost identical geometry for the direct comparison.
A more detailed look at the distances between both geometries clarifies the identical forming results with a maximum deviation of 0.38 mm. This means that the geometries show a slightly different springback effect after the release of the tools, but in general behave in the same way during the forming process. Therefore, the results show that the anisotropic characteristics of the initial material have no significant impact on the process results of the roll forming technology. For this reason, it can be stated that a production directly from the coil is possible with the used material and without any additional treatments or processes. Further improvement has to be done regarding the undesirable geometrical forming behaviour like wrinkles and the bent global structure of the workpieces.
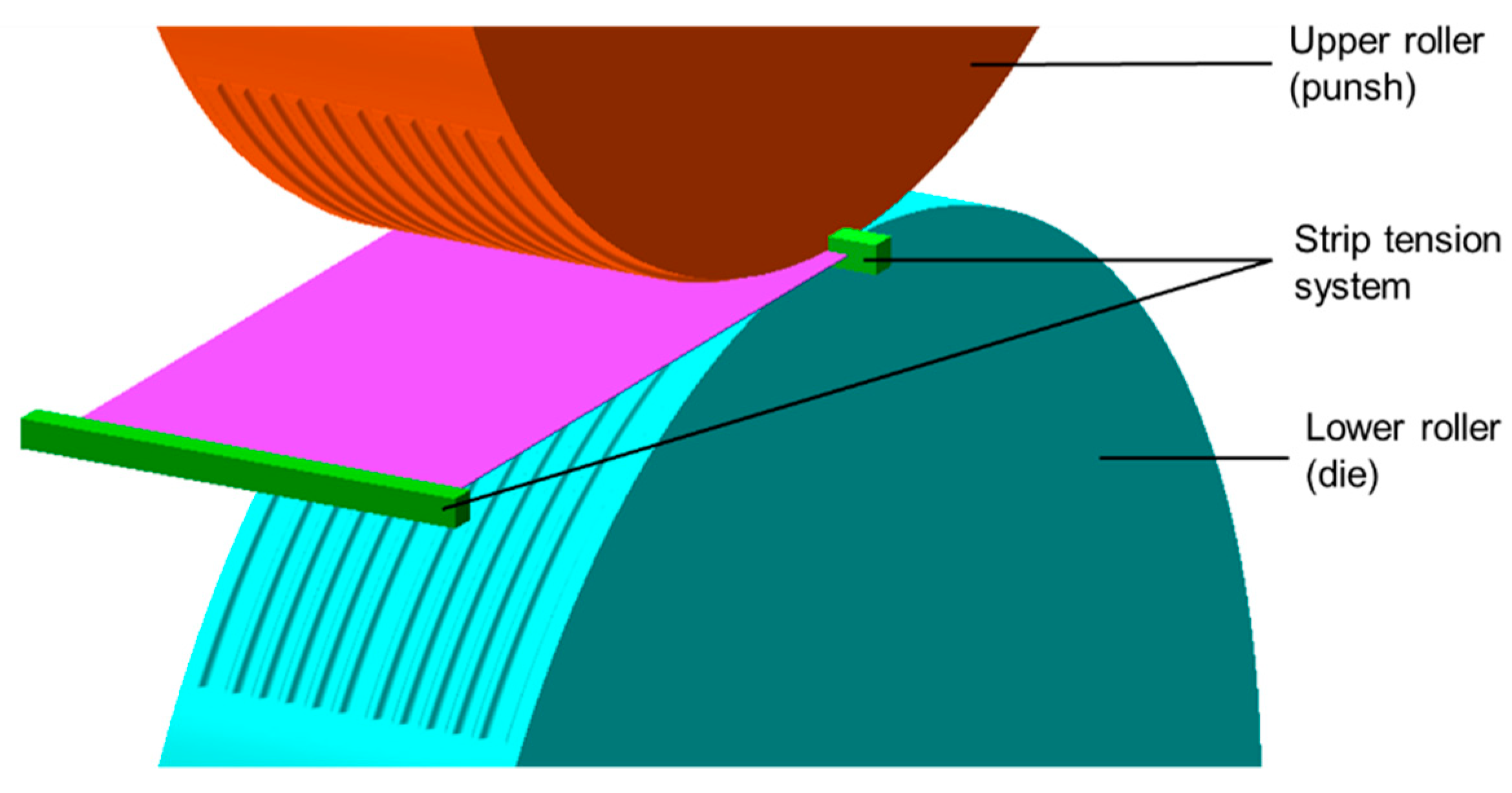
Within deep drawing processes of metal foils, a binder can be used to enhance the quality of the products. For the roll forming process, this is not feasible. For this reason, a strip tension system was implemented numerically, to reduce the effects of wrinkling and bending within the roll forming process (
Figure 12).
Therefore, the speed of the workpiece was measured on both sides of the rolling process within the FE simulation, in front of the working rolls (entrance side) and behind the working rolls (outlet side). Both sides had to be measured because there is a different velocity of the unformed and formed material parts in conventional rolling processes. Normally the velocity for rolled products is lower on the entrance side, than on the outlet side, where the thickness is reduced. The reason is that the reduction in thickness and the related material displacement leads to a higher speed, when the thinner product leaves the rolling mill. Within the roll forming process, a different effect occurs. The material on the entrance side in front of the rolling gap shows a higher velocity (8.4 mm/s) than on the outlet side, after the forming of the specimen (8.2 mm/s). This is probably caused by the process characteristics of roll forming, where no thickness reduction of the initial material takes place, while the channel geometry is formed into the metal foil. This kind of forming process slows the velocity on the outlet side because the material flow does not take place in length direction but in height and width. For this purpose, the part of the geometry on the outlet side has a lower velocity than on the entrance side. However, to get a taut metal strip, the velocity of both strip tension elements was set to 8.2 mm/s, while all other process parameters stayed the same, like for the real process. A constant velocity of 8.2 mm/s causes tensile stresses during the roll forming process (
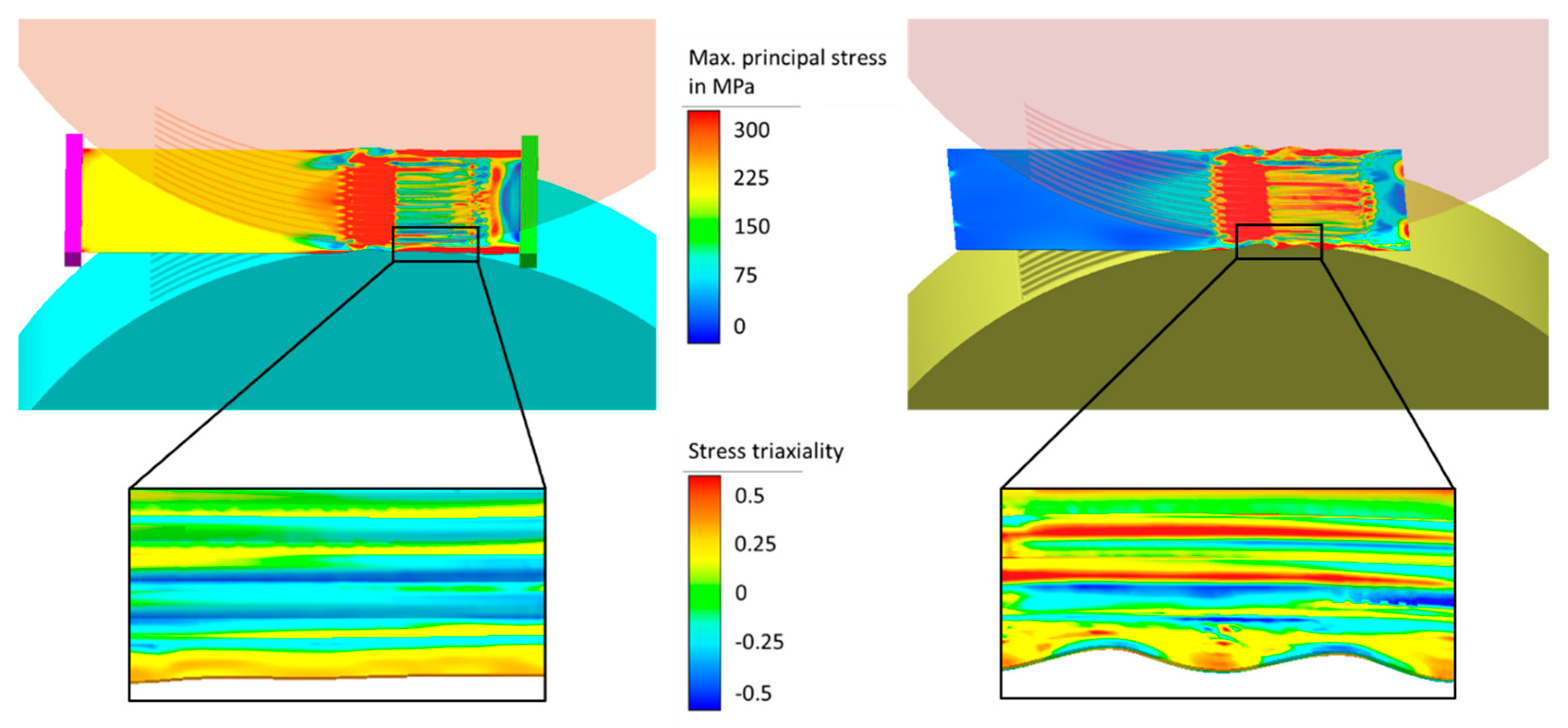
Figure 13).
These tensile stresses, shown by the maximum principal stress in
Figure 13 enable a superposition with the compressive stresses in the wrinkled areas of the specimen, which occur during the roll forming process. While the specimen without strip tension shows values of around 5 MPa, the strip tension system increases the tensile stresses to 200 MPa. A closer look at the stress triaxiality in
Figure 13 (enlargements) clarifies the mechanics behind the effects of stress superposition. On the one side, the roll forming without strip tension shows wrinkles with changing triaxiality values (−0.35: uniaxial compressive stresses and 0.43: almost uniaxial tensile stresses). On the other side, it can be seen that the roll forming setup with strip tension system only indicates positive values for the triaxiality (0.33: uniaxial tensile stresses). Therefore, it can be concluded that the superposition within the strip tension model causes a higher amount of constant tensile stresses to eliminate the compressive stresses, which occurs during wrinkling. For this reason, the strip tension also enlarges the stability of the whole specimen against distortion.
The numerical results show, that significant improvements were archived using the numerical simulated strip tension system. A look at the simulated geometry development shows an even result with just a few slight wrinkles over the length in the peripheral areas and without noticeable springback effects after the release from the tools (
Figure 14).
Especially the fact, that the final bipolar plates were cut from the metal sheets after the forming process leads to the conclusion that the remaining small wrinkles in the outer areas of the specimen were of minor relevance regarding to the final product. The equivalent plastic strain develops in the same way, as seen for the roll forming without strip tension system with some peaks of φ = 0.39 at the channels front and back edges and an average of φ = 0.32 at the channel flanks. Furthermore, a small increase of thinning can be measured in the radii (thickness: 79.3 µm) and the channel flanks (thickness: 84.3 µm) compared to the forming process without strip tension system (thickness radii: 83.5 µm, channel flanks: 89.9 µm). This effect is also caused by the additional tensile stresses; applied for the process with strip tension system and therefore lead to the increased thinning. A more detailed analysis of the global geometry with a comparison to the CAD construction is shown in
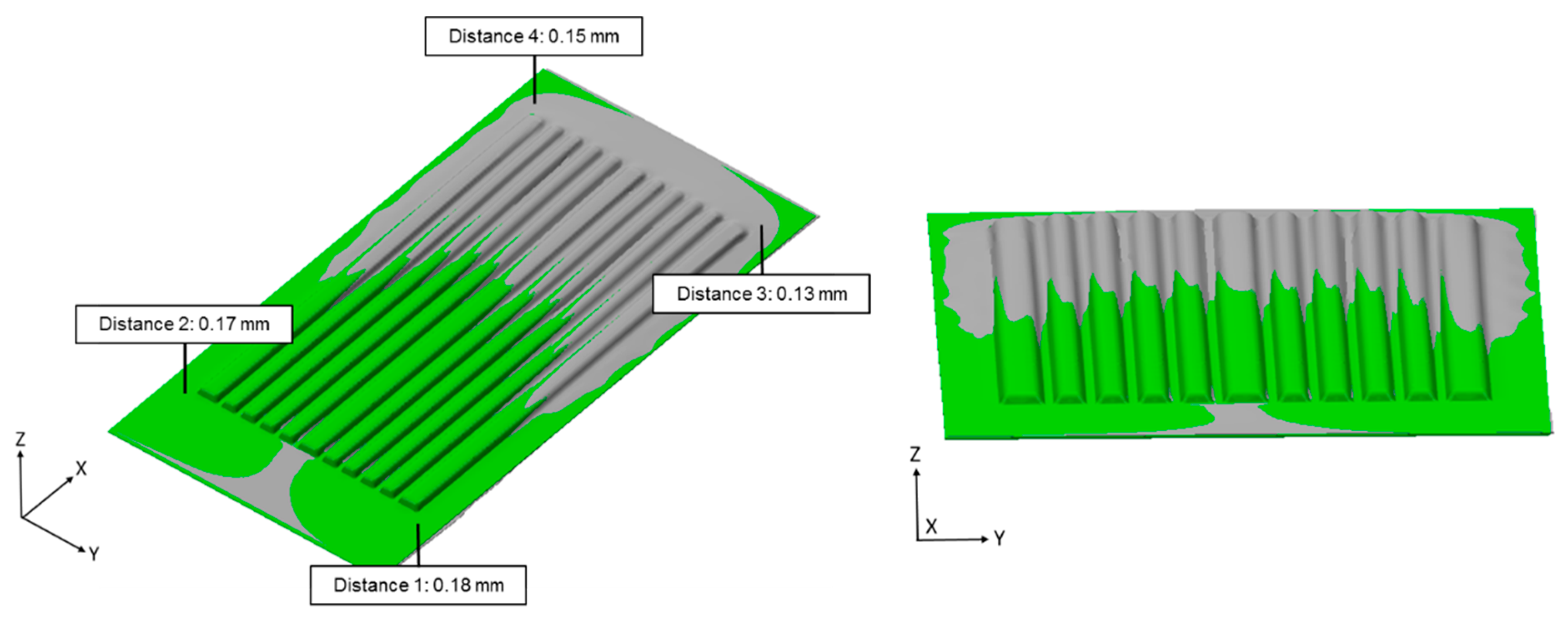
Figure 15.
It is clearly visible that the geometry, which was generated within the numerical calculation for the roll forming process with applied strip tension system, is in very good accordance to the constructed CAD geometry. A maximum deviation of 0.18 mm is noticeable less than the values, which were measured for the roll forming without strip tension. The exact comparison can be seen in
Table 3.
Overall, it can be concluded that the use of a strip tension system can clearly improve the workpiece quality of the roll forming process. This means that the roll forming process with strip tension system leads to results, which are comfortable to handle in subsequent operations like welding or the assembly of fuel cell stacks due to the geometrical improvements, which were achieved.