Finite Element Modeling of Orthogonal Machining of Brittle Materials Using an Embedded Cohesive Element Mesh
Abstract
1. Introduction
2. Finite Element Model Setup
2.1. Model Configuration
2.2. Damage Criteria
2.3. Other Material Properties
2.4. Scaling Factor
2.5. Sensitivity Study
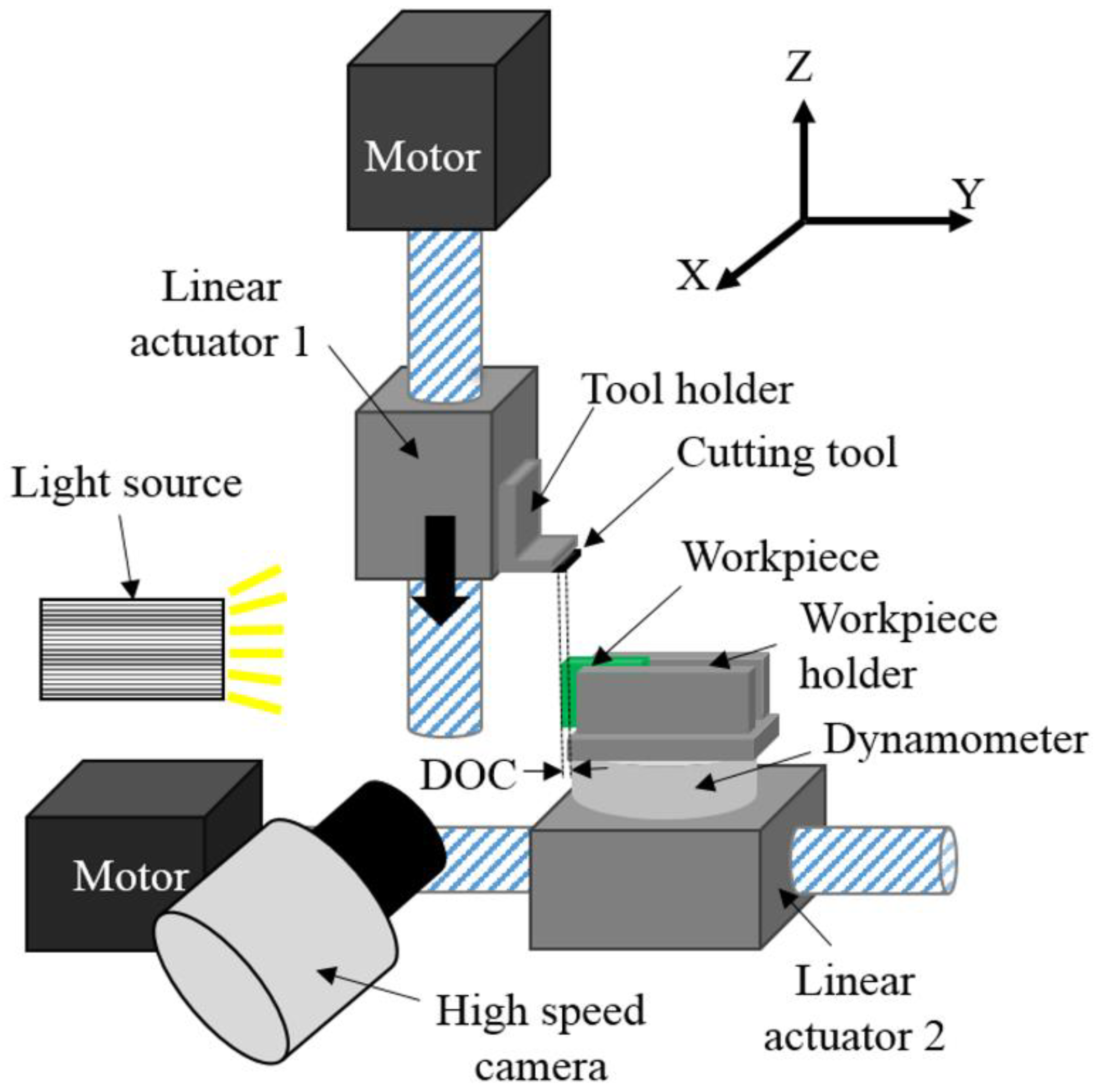
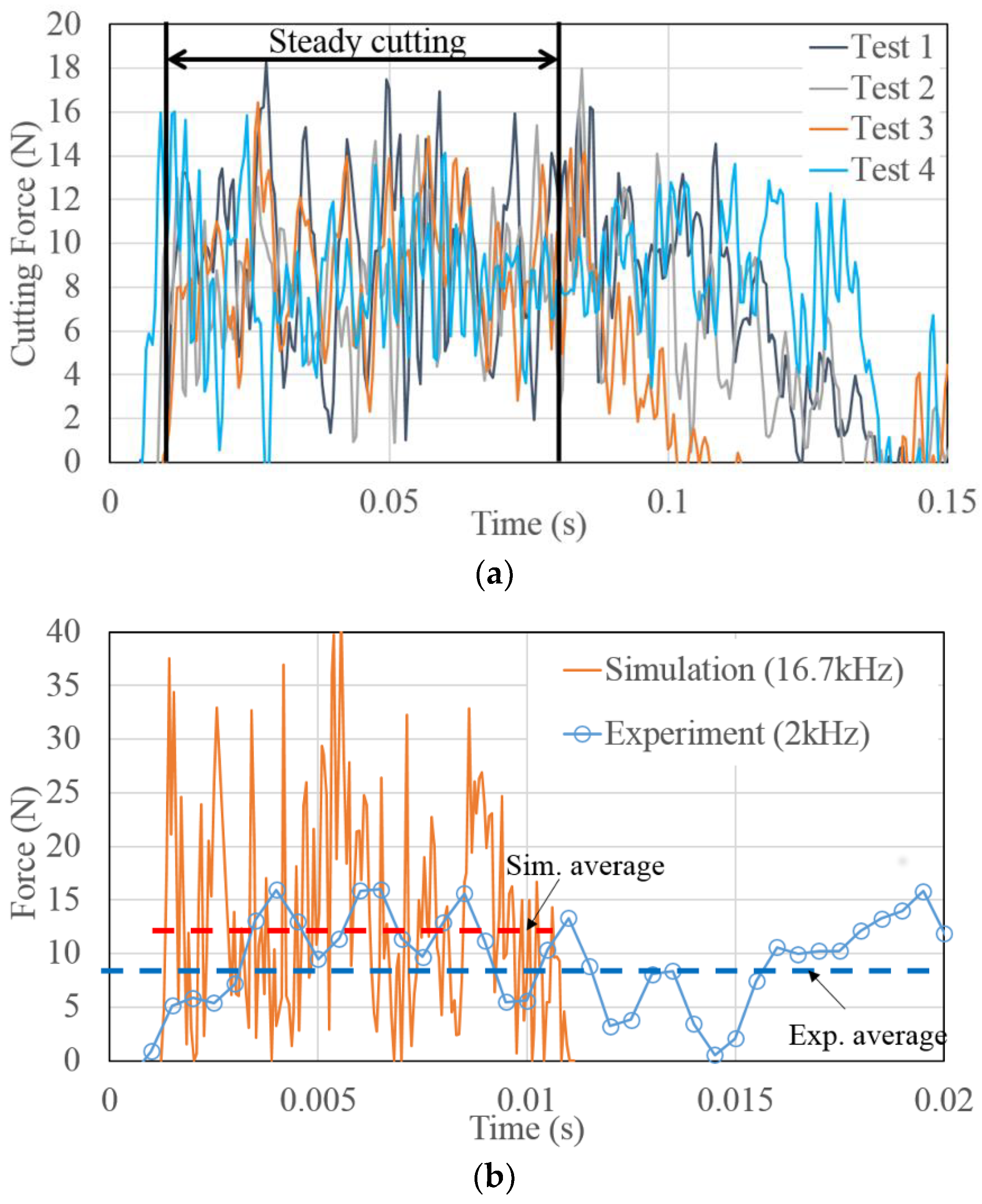
3. Experiment Setup for Model Validation
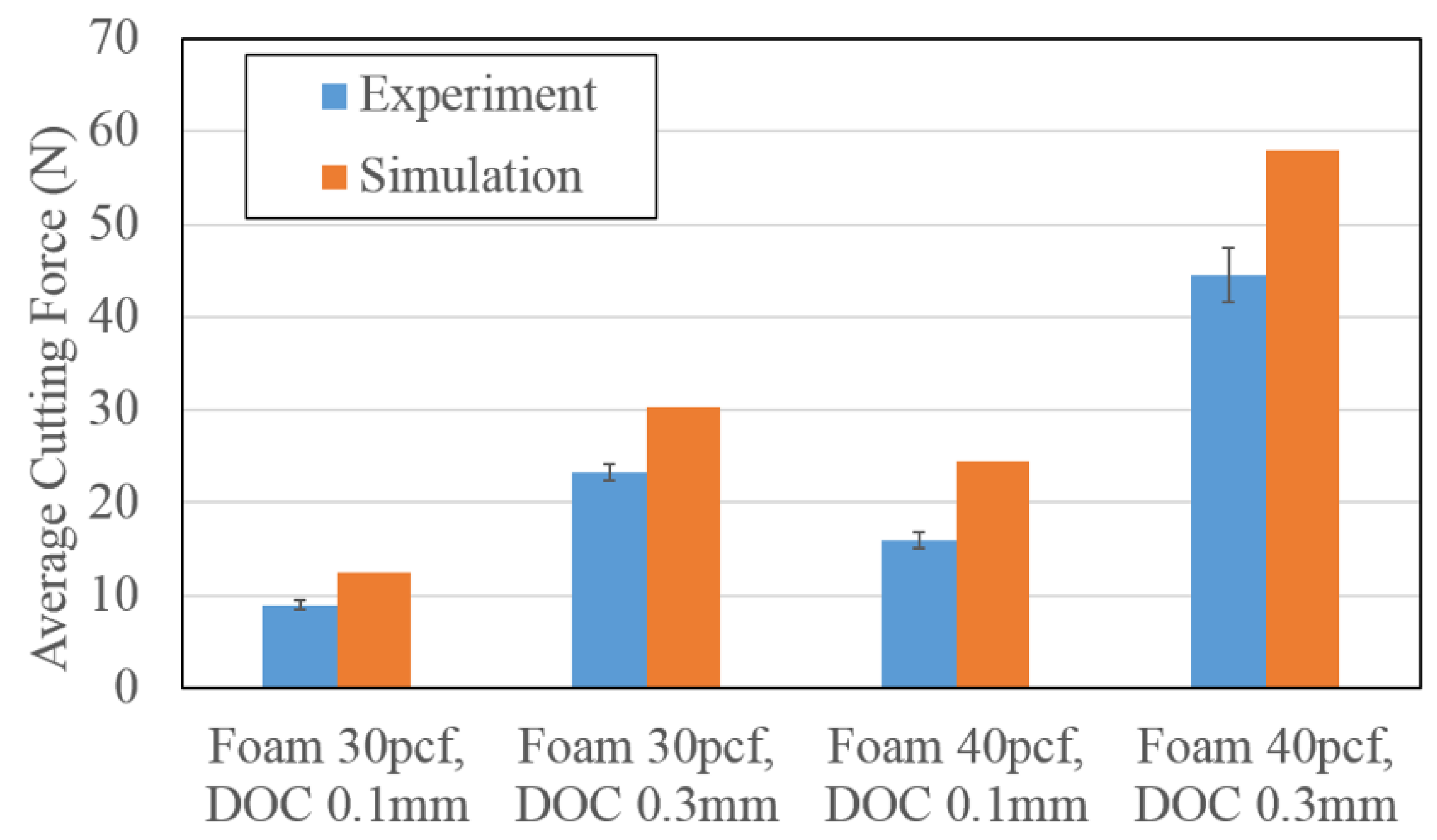
4. Simulation and Experiment Results
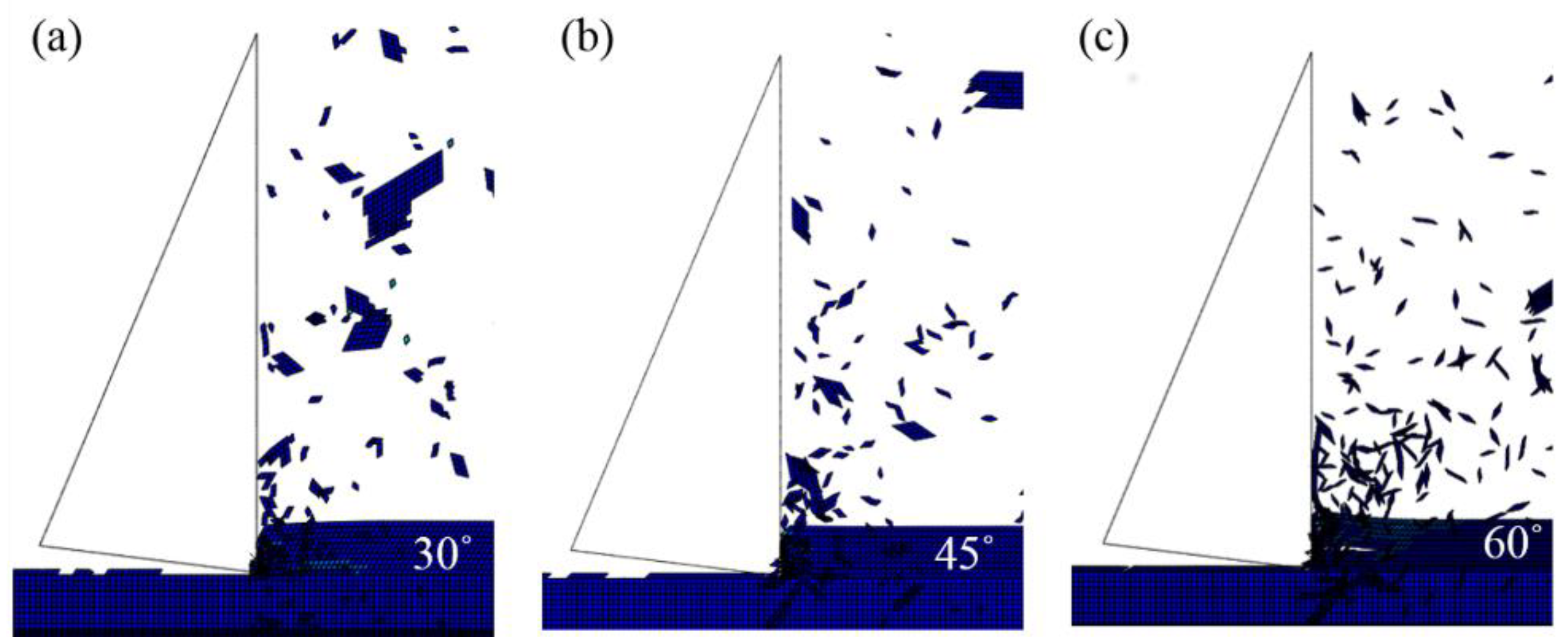
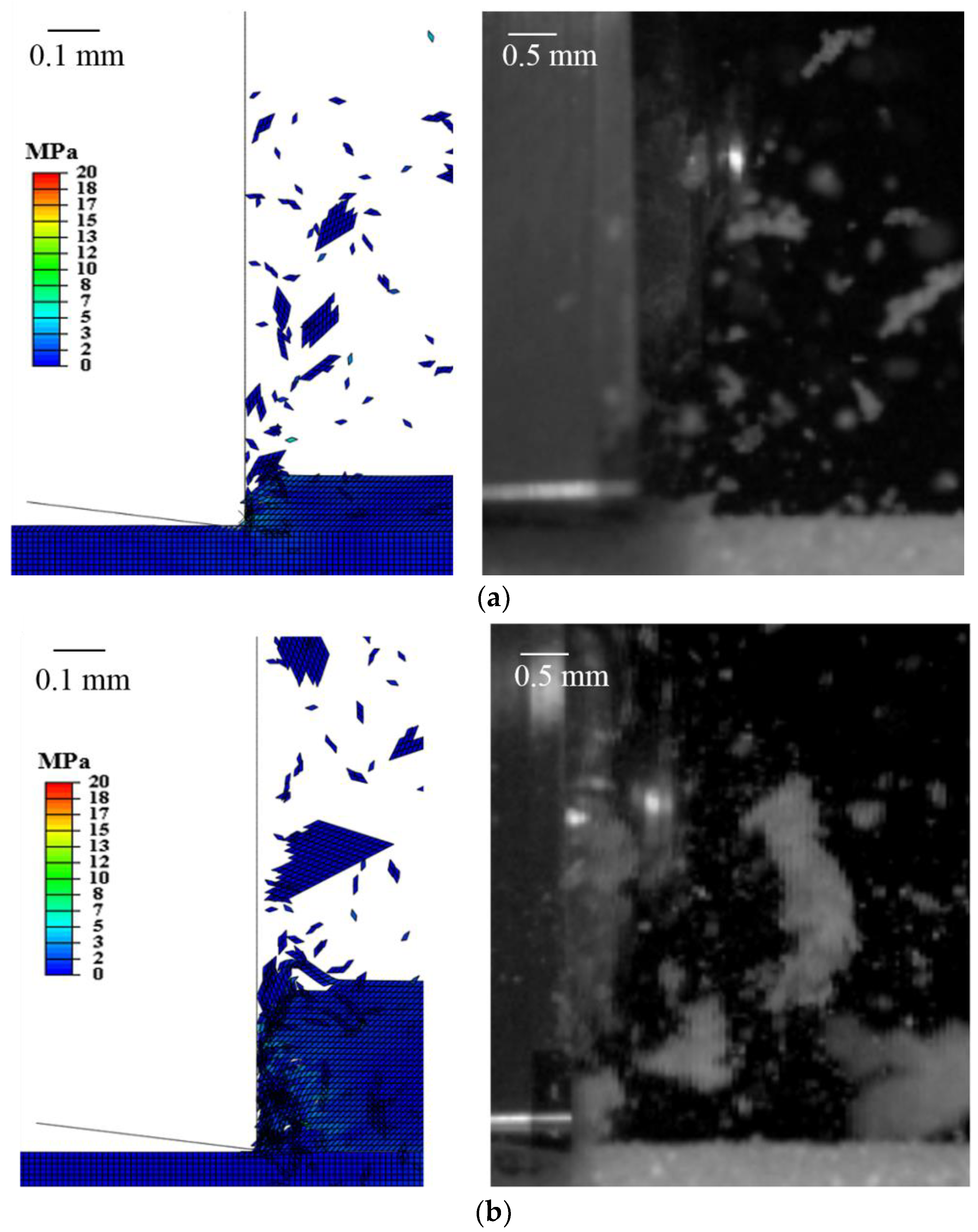
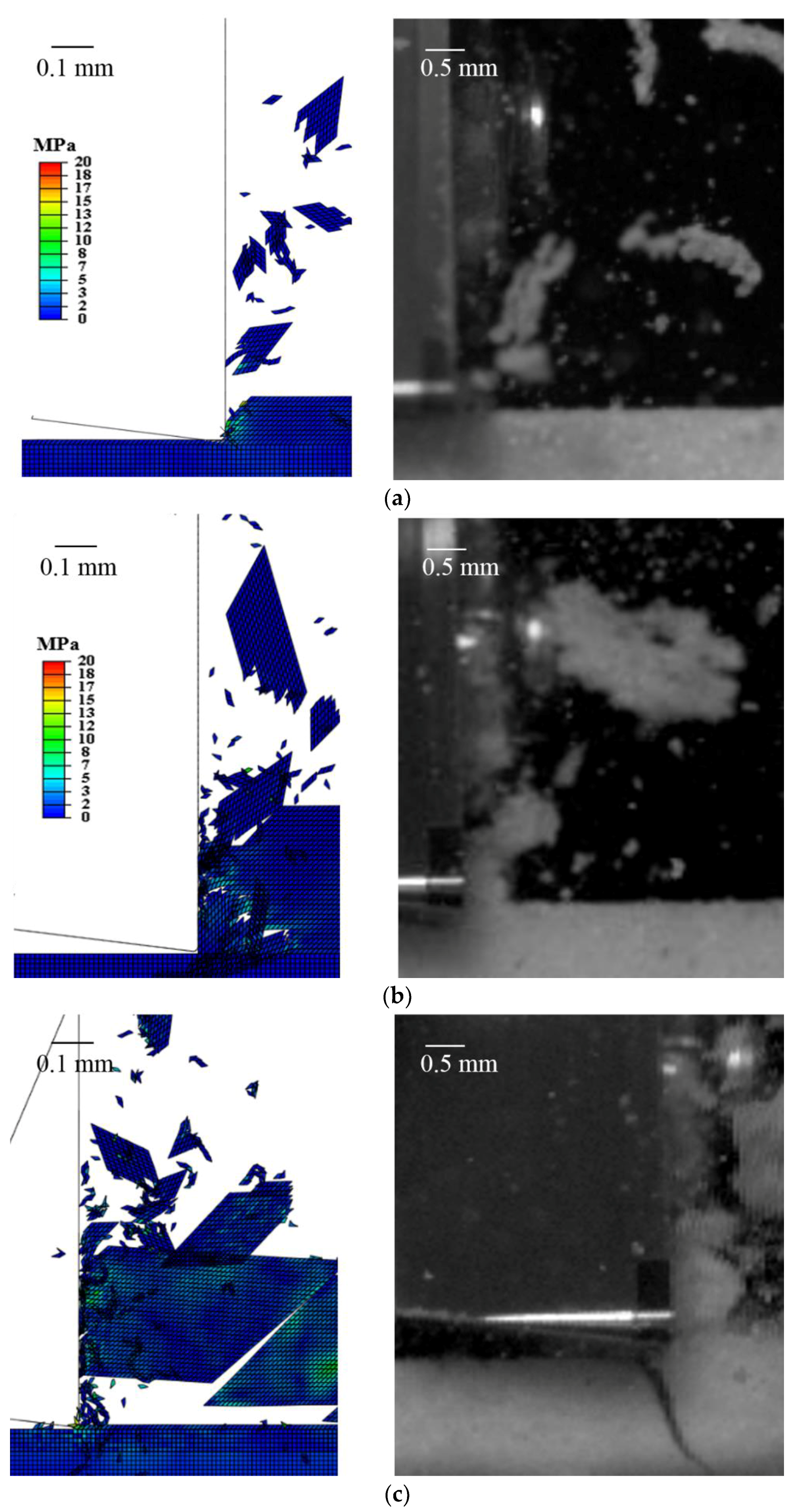
4.1. Chip Formation
4.2. Cutting Force
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, D.F.; Cong, W.L.; Pei, Z.J.; Tang, Y.J. A cutting force model for rotary ultrasonic machining of brittle materials. Int. J. Mach. Tools Manuf. 2012, 52, 77–84. [Google Scholar] [CrossRef]
- Rao, G.V.G.; Mahajan, P.; Bhatnagar, N. Micro-mechanical modeling of machining of FRP composites–Cutting force analysis. Compos. Sci. Technol. 2007, 67, 579–593. [Google Scholar] [CrossRef]
- Umer, U.; Ashfaq, M.; Qudeiri, J.; Hussein, H.; Danish, S.; Al-Ahmari, A. Modeling machining of particle-reinforced aluminum-based metal matrix composites using cohesive zone elements. Int. J. Adv. Manuf. Technol. 2015, 78, 1171–1179. [Google Scholar] [CrossRef]
- Santiuste, C.; Soldani, X.; Miguélez, M.H. Machining FEM model of long fiber composites for aeronautical components. Compos. Struct. 2010, 92, 691–698. [Google Scholar] [CrossRef]
- Usui, S.; Wadell, J.; Marusich, T. Finite element modeling of carbon fiber composite orthogonal cutting and drilling. Procedia CIRP 2014, 14, 211–216. [Google Scholar] [CrossRef]
- Yan, X.; Reiner, J.; Bacca, M.; Altintas, Y.; Vaziri, R. A study of energy dissipating mechanisms in orthogonal cutting of UD-CFRP composites. Compos. Struct. 2019, 220, 460–472. [Google Scholar] [CrossRef]
- Umbrello, D.; M’saoubi, R.; Outeiro, J. The influence of Johnson–Cook material constants on finite element simulation of machining of AISI 316L steel. Int. J. Mach. Tools Manuf. 2007, 47, 462–470. [Google Scholar] [CrossRef]
- Shrot, A.; Bäker, M. Determination of Johnson–Cook parameters from machining simulations. Comput. Mater. Sci. 2012, 52, 298–304. [Google Scholar] [CrossRef]
- Shi, J.; Liu, C.R. The influence of material models on finite element simulation of machining. J. Manuf. Sci. Eng. 2004, 126, 849–857. [Google Scholar] [CrossRef]
- Takabi, B.; Tai, B.L. A review of cutting mechanics and modeling techniques for biological materials. Med. Eng. Phys. 2017, 45, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Takabi, B.; Tajdari, M.; Tai, B.L. Numerical study of smoothed particle hydrodynamics method in orthogonal cutting simulations–Effects of damage criteria and particle density. J. Manuf. Processes 2017, 30, 523–531. [Google Scholar] [CrossRef]
- Turon, A.; Davila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Dong, X.; Shin, Y.C. Multi-scale genome modeling for predicting fracture strength of silicon carbide ceramics. Comput. Mater. Sci. 2018, 141, 10–18. [Google Scholar] [CrossRef]
- Paulino, G.; Zhang, Z. Cohesive modeling of propagating cracks in homogeneous and functionally graded composites. In Proceedings of the 5th GRACM International Congress on Computational Mechanics, Limassol, Cyprus, 29 June–1 July 2005. [Google Scholar]
- Liang, S.Y.; Shih, A.J. Analysis of Machining and Machine Tools; Springer: Boston, MA, USA, 2016. [Google Scholar]
- Liu, J.; Bai, Y.; Xu, C. Evaluation of ductile fracture models in finite element simulation of metal cutting processes. J. Manuf. Sci. Eng. 2014, 136, 011010. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Zavattieri, P.D. A grain level model for the study of failure initiation and evolution in polycrystalline brittle materials. Part II: Numerical examples. Mech. Mater. 2003, 35, 365–394. [Google Scholar] [CrossRef]
- Feng, J.; Chen, P.; Ni, J. Prediction of surface generation in microgrinding of ceramic materials by coupled trajectory and finite element analysis. Finite Elem. Anal. Des. 2012, 57, 67–80. [Google Scholar] [CrossRef]
- Sawbones Inc., General Catalog. Available online: https://www.sawbones.com/wp/wp-content/uploads/2017/07/Gen-393 Catalog-ReVamp-V1.pdf (accessed on 13 March 2019).
- Kobayashi, A.; Mall, S. Dynamic fracture toughness of Homalite-100. Exp. Mech. 1978, 18, 11–18. [Google Scholar] [CrossRef]
- Kobayashi, T.; Yamamoto, I.; Niinomi, M. Introduction of a new dynamic fracture toughness evaluation system. J. Test. Eval. 1993, 21, 145–153. [Google Scholar]
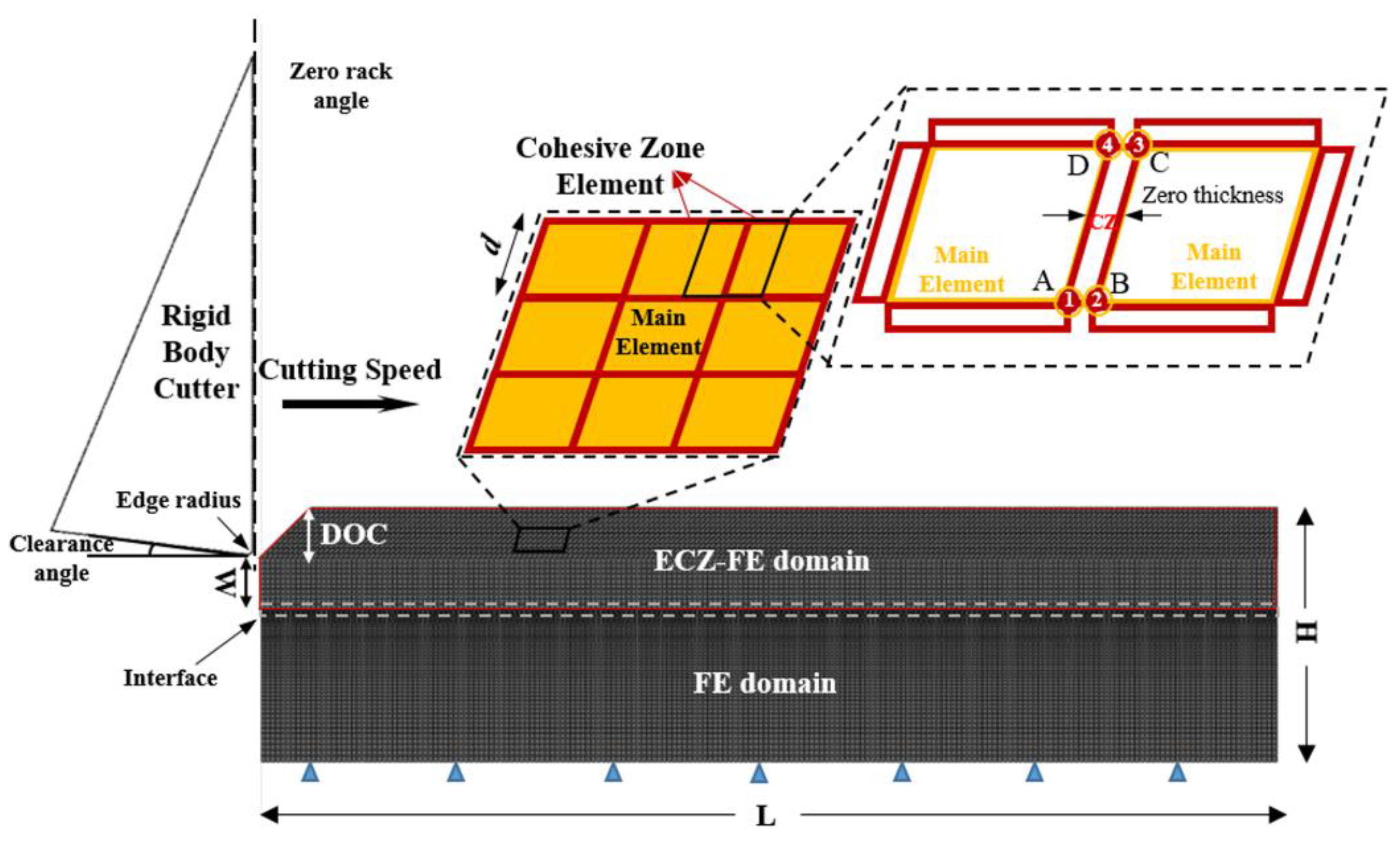
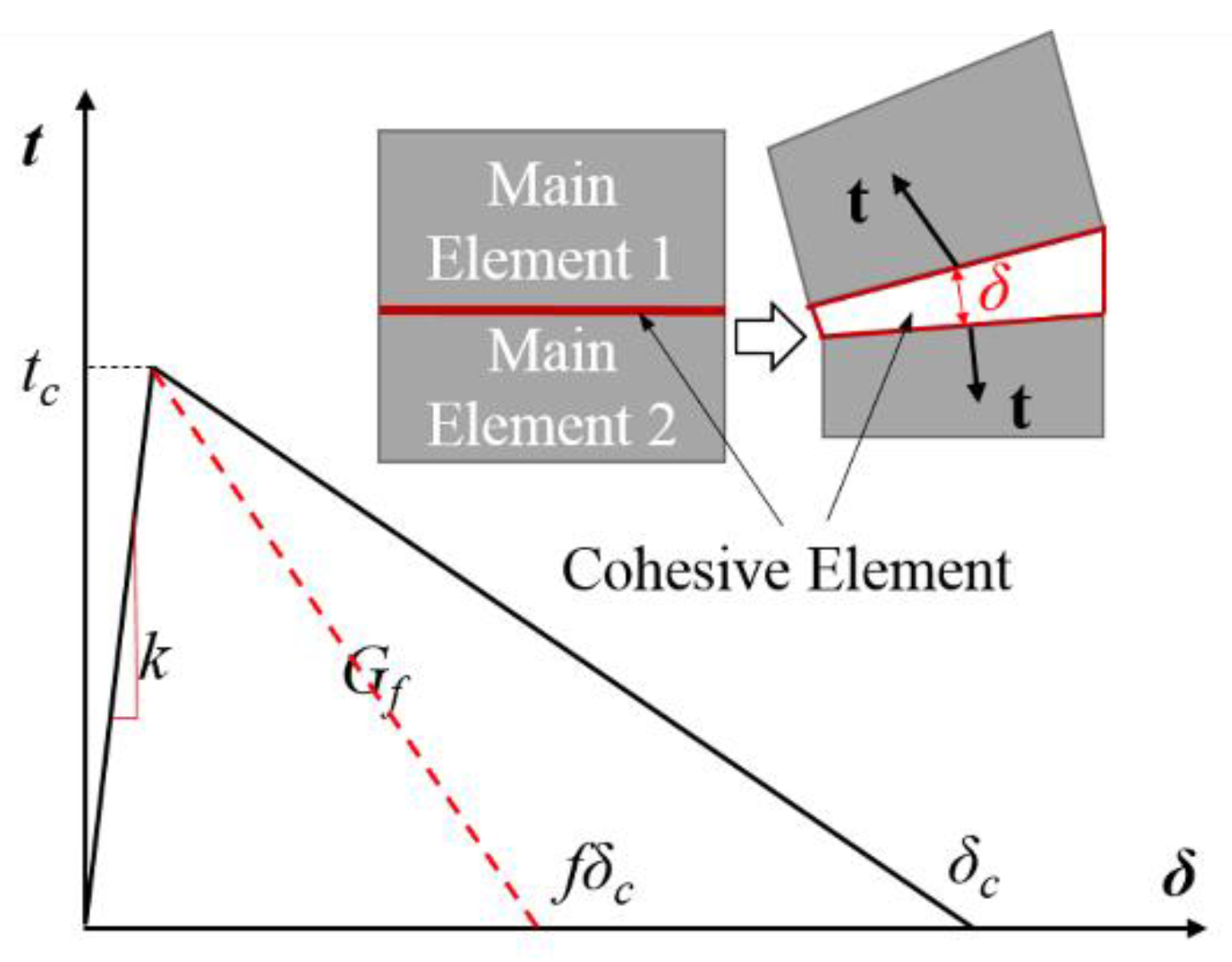
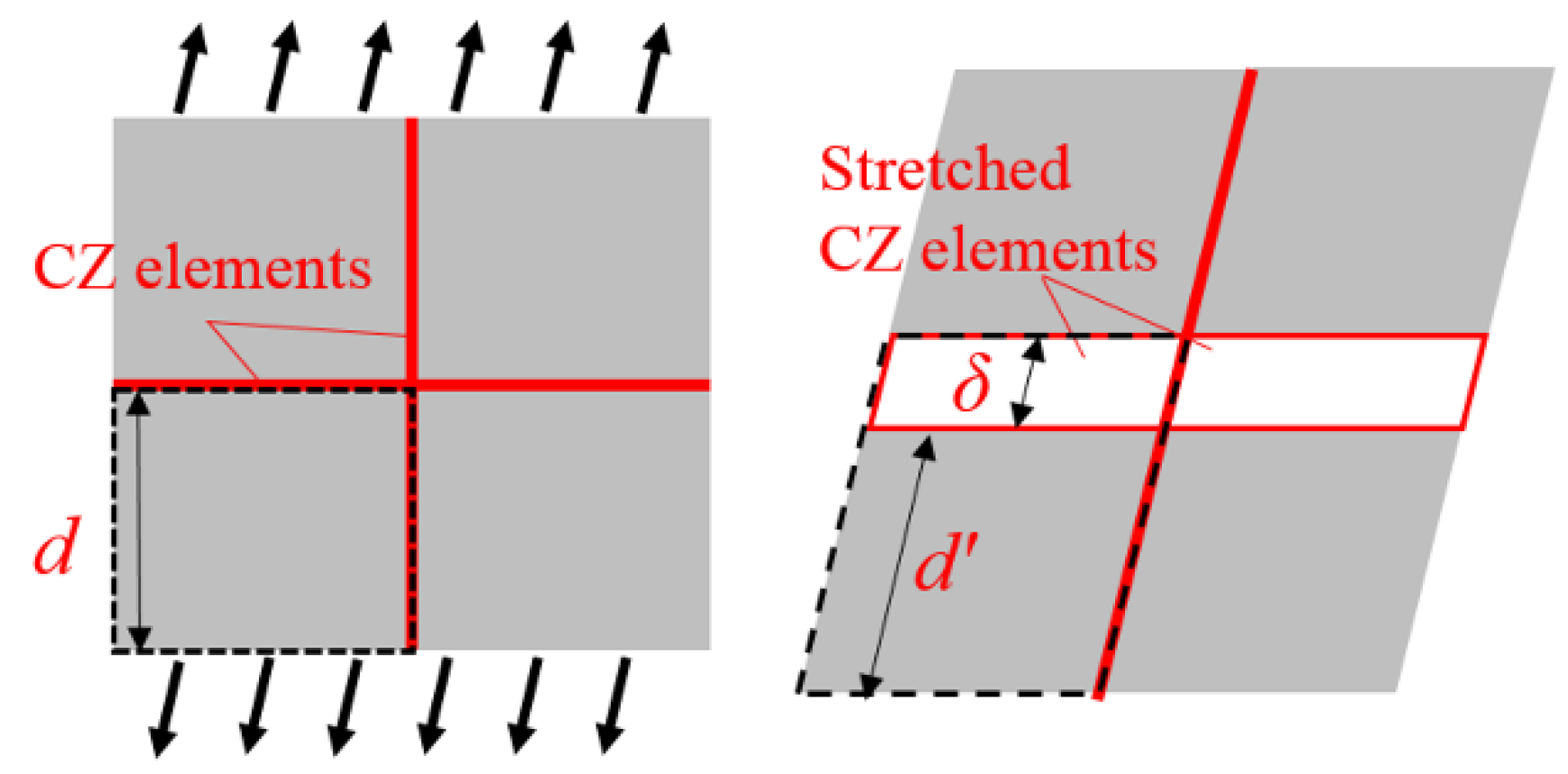
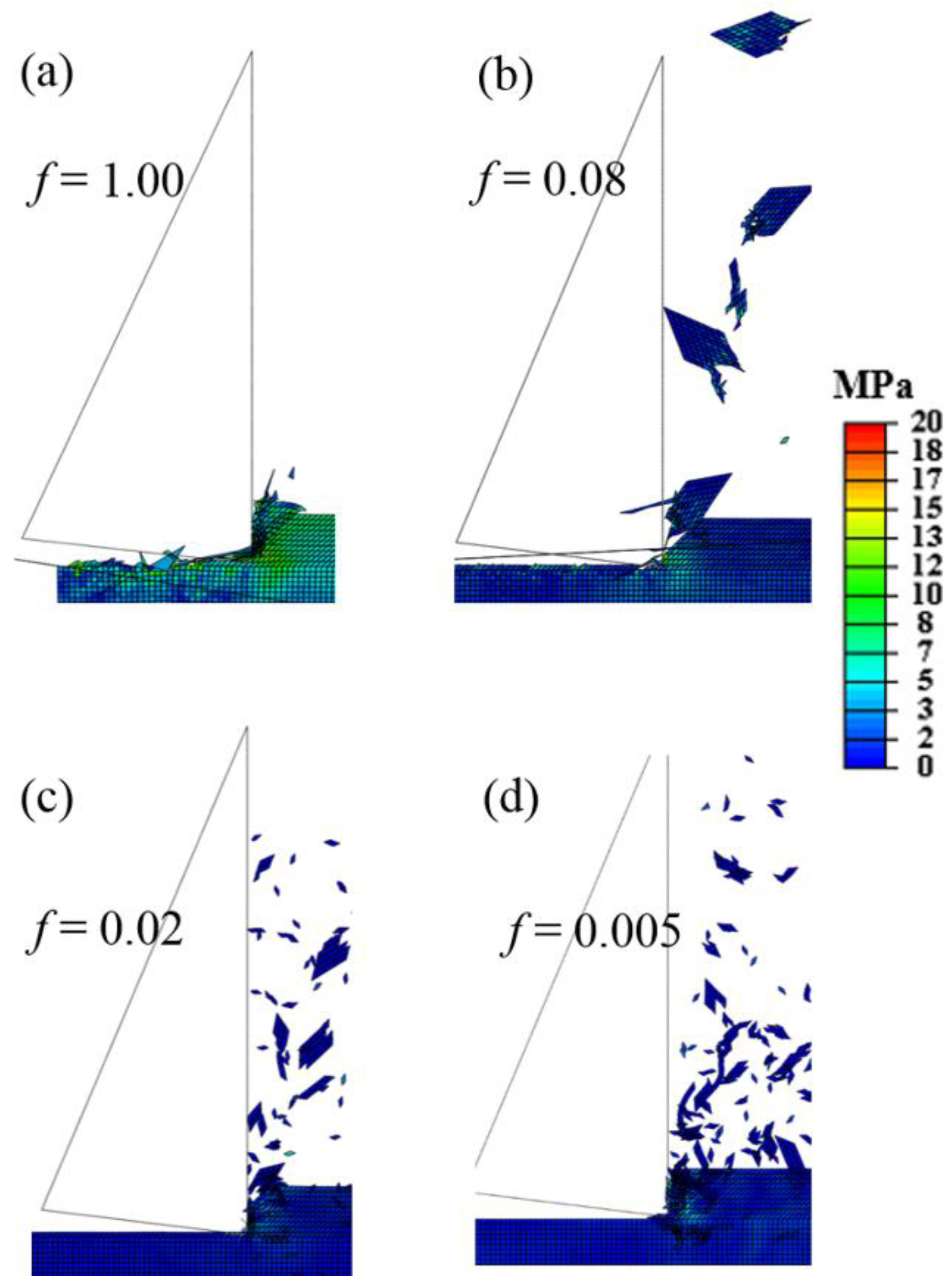
| DOC (mm) | L (mm) | H (mm) | W (mm) | |
|---|---|---|---|---|
| Case 1 | 0.1 | 2 | 0.5 | 0.1 |
| Case 2 | 0.3 | 5 | 0.85 | 0.1 |
| Samples | tc (N/mm2) | k (N/mm3) | Gf (N/mm) | δ (mm) |
|---|---|---|---|---|
| 30 pcf | 9.6 | 59,200 | 0.31 | 0.064 |
| 40 pcf | 15.2 | 100,000 | 1.12 | 0.147 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takabi, B.; Tai, B.L. Finite Element Modeling of Orthogonal Machining of Brittle Materials Using an Embedded Cohesive Element Mesh. J. Manuf. Mater. Process. 2019, 3, 36. https://doi.org/10.3390/jmmp3020036
Takabi B, Tai BL. Finite Element Modeling of Orthogonal Machining of Brittle Materials Using an Embedded Cohesive Element Mesh. Journal of Manufacturing and Materials Processing. 2019; 3(2):36. https://doi.org/10.3390/jmmp3020036
Chicago/Turabian StyleTakabi, Behrouz, and Bruce L. Tai. 2019. "Finite Element Modeling of Orthogonal Machining of Brittle Materials Using an Embedded Cohesive Element Mesh" Journal of Manufacturing and Materials Processing 3, no. 2: 36. https://doi.org/10.3390/jmmp3020036
APA StyleTakabi, B., & Tai, B. L. (2019). Finite Element Modeling of Orthogonal Machining of Brittle Materials Using an Embedded Cohesive Element Mesh. Journal of Manufacturing and Materials Processing, 3(2), 36. https://doi.org/10.3390/jmmp3020036






