Effect of Deformation Path on the Microstructure and Mechanical Behavior of TWIP980 Steel
Abstract
1. Introduction
2. Materials and Methods
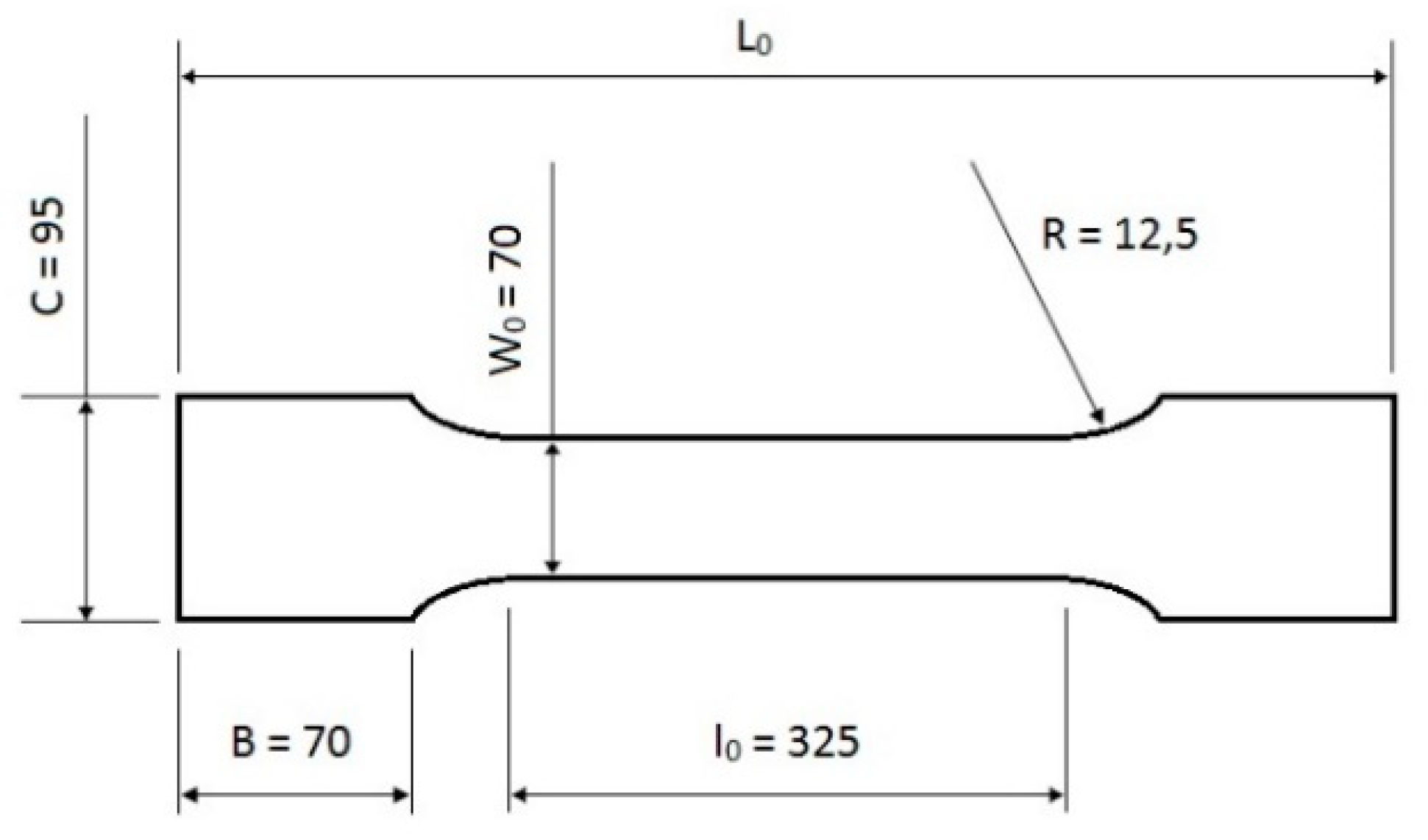
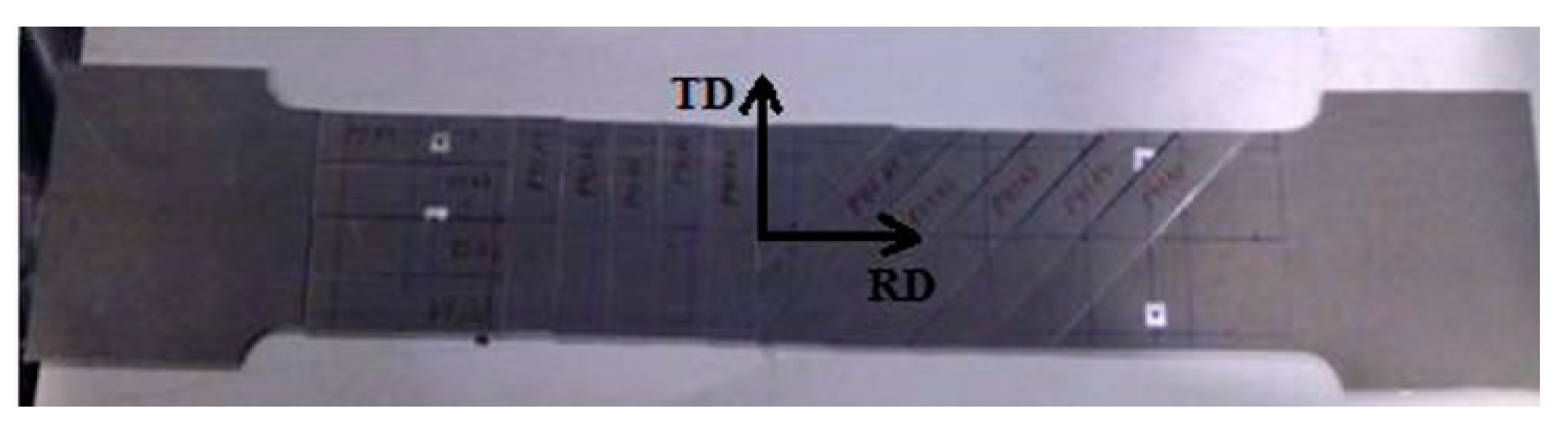
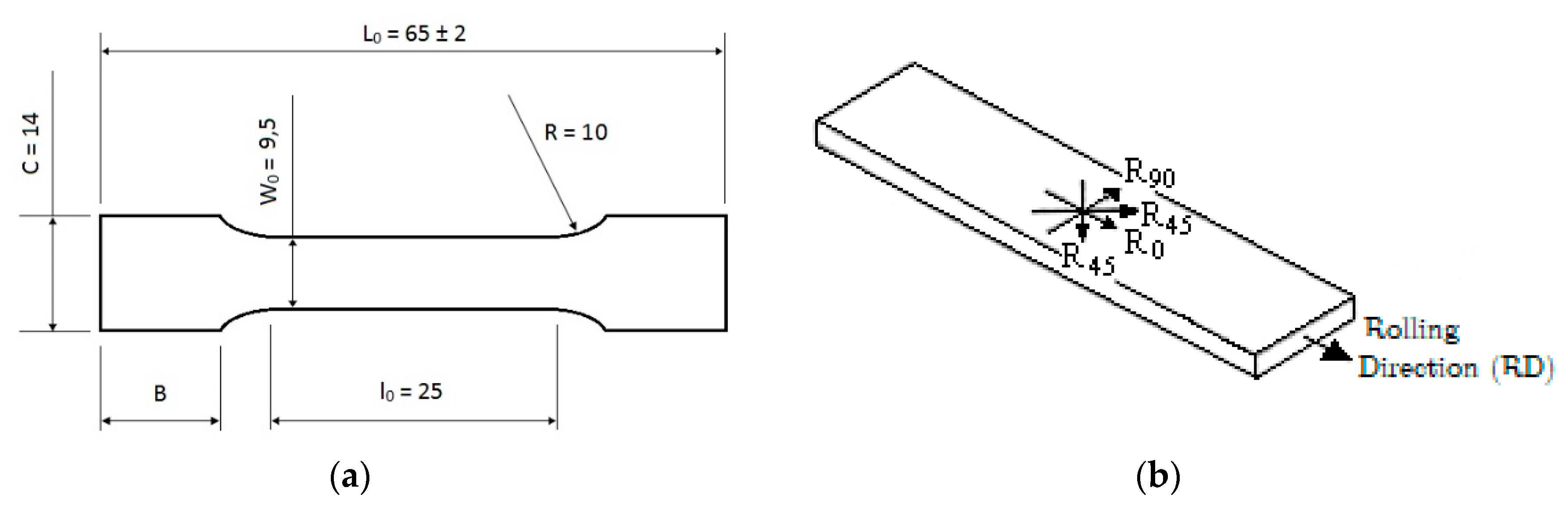
2.1. Two-Step Tensile Testing
2.1.1. First Step
2.1.2. Second Step
2.2. Microstructural Analysis
3. Results
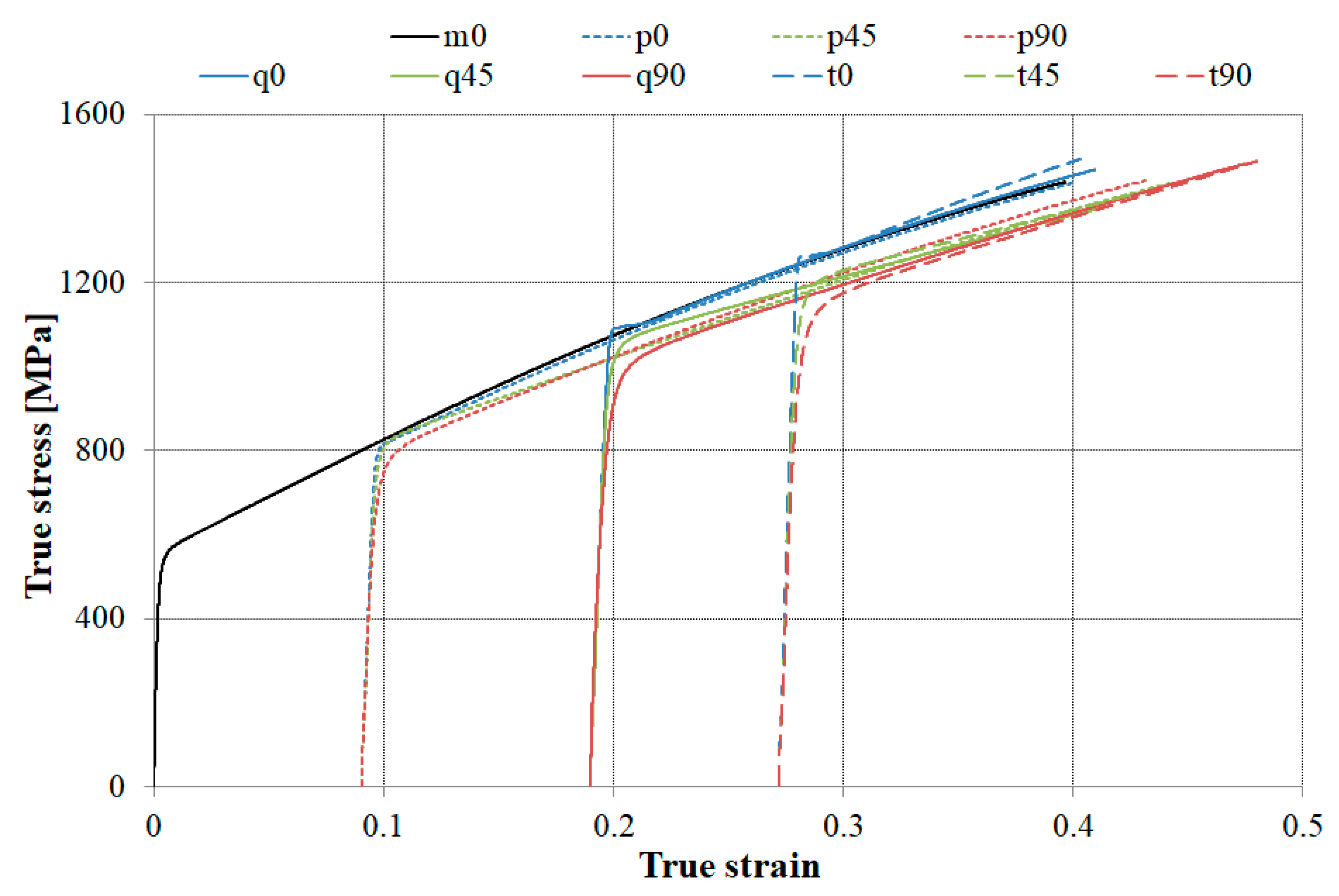
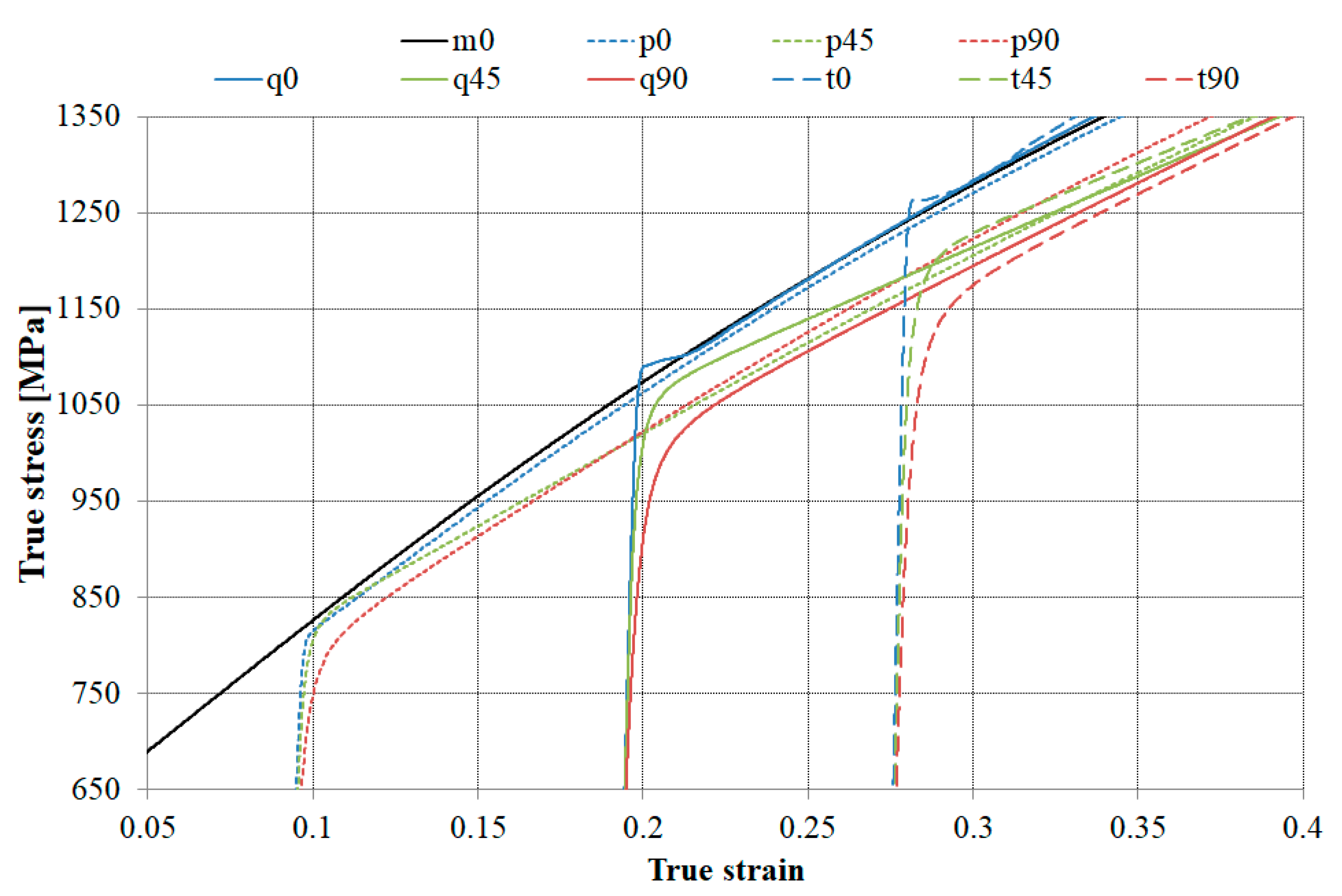
3.1. Tensile Testing
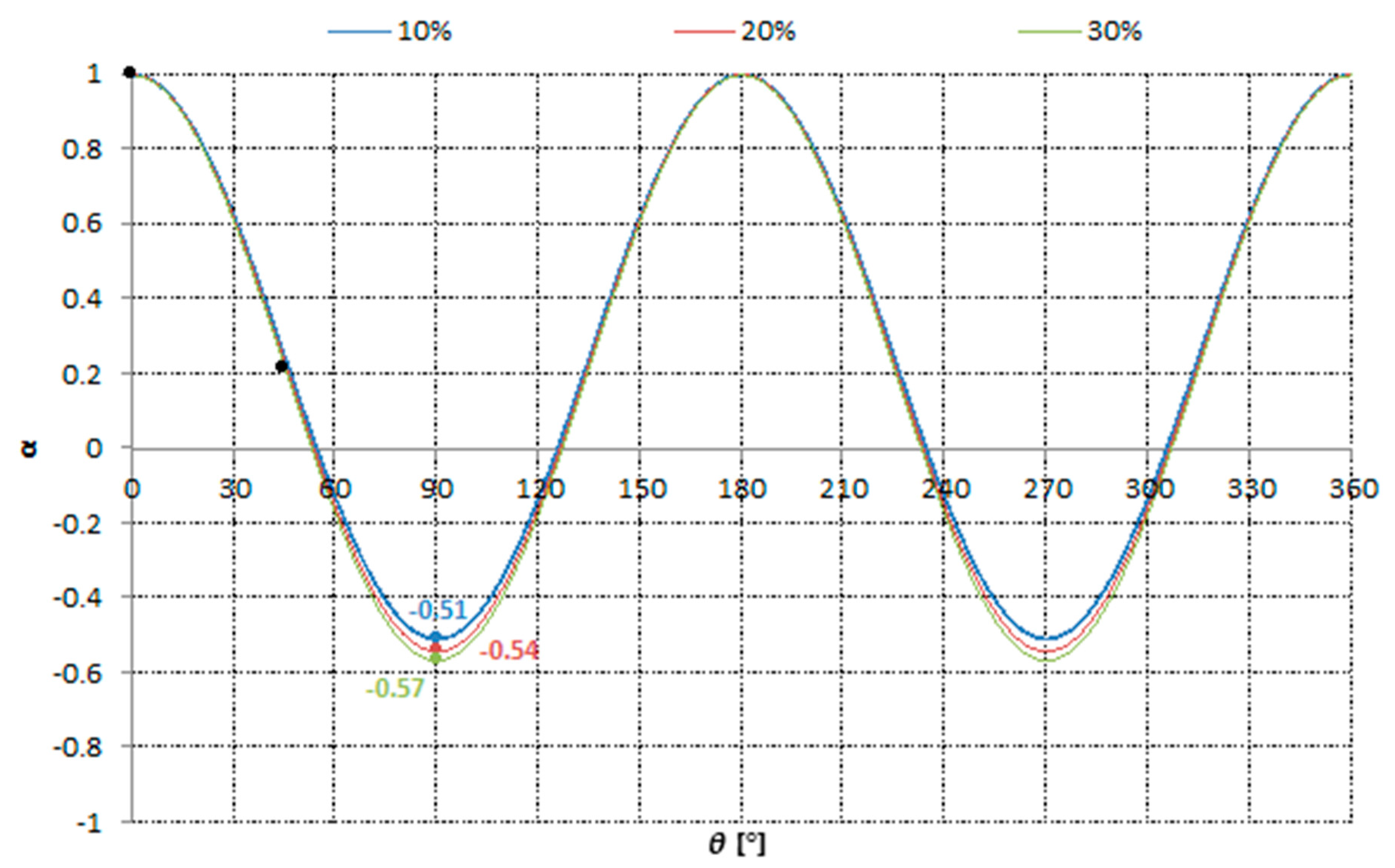
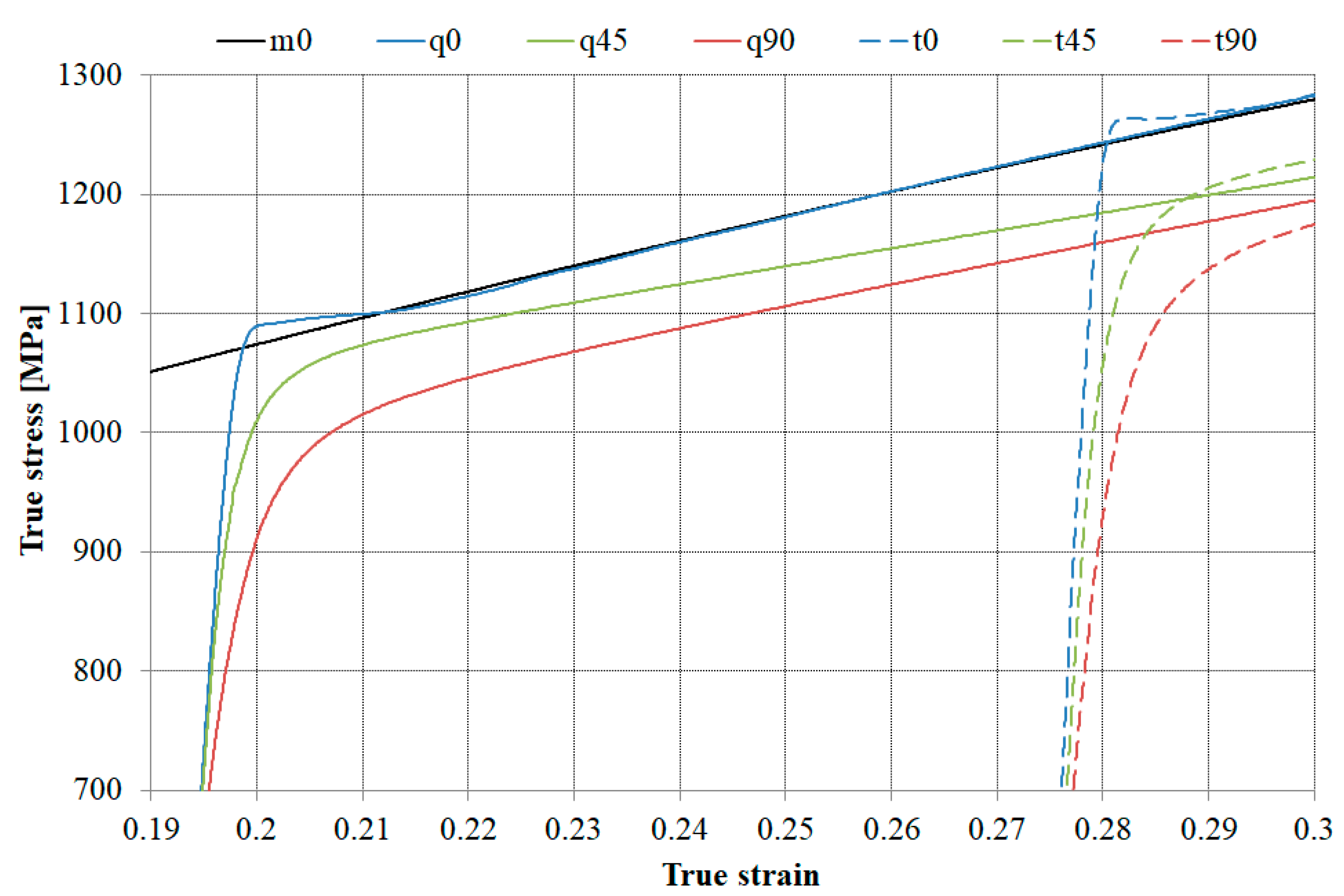
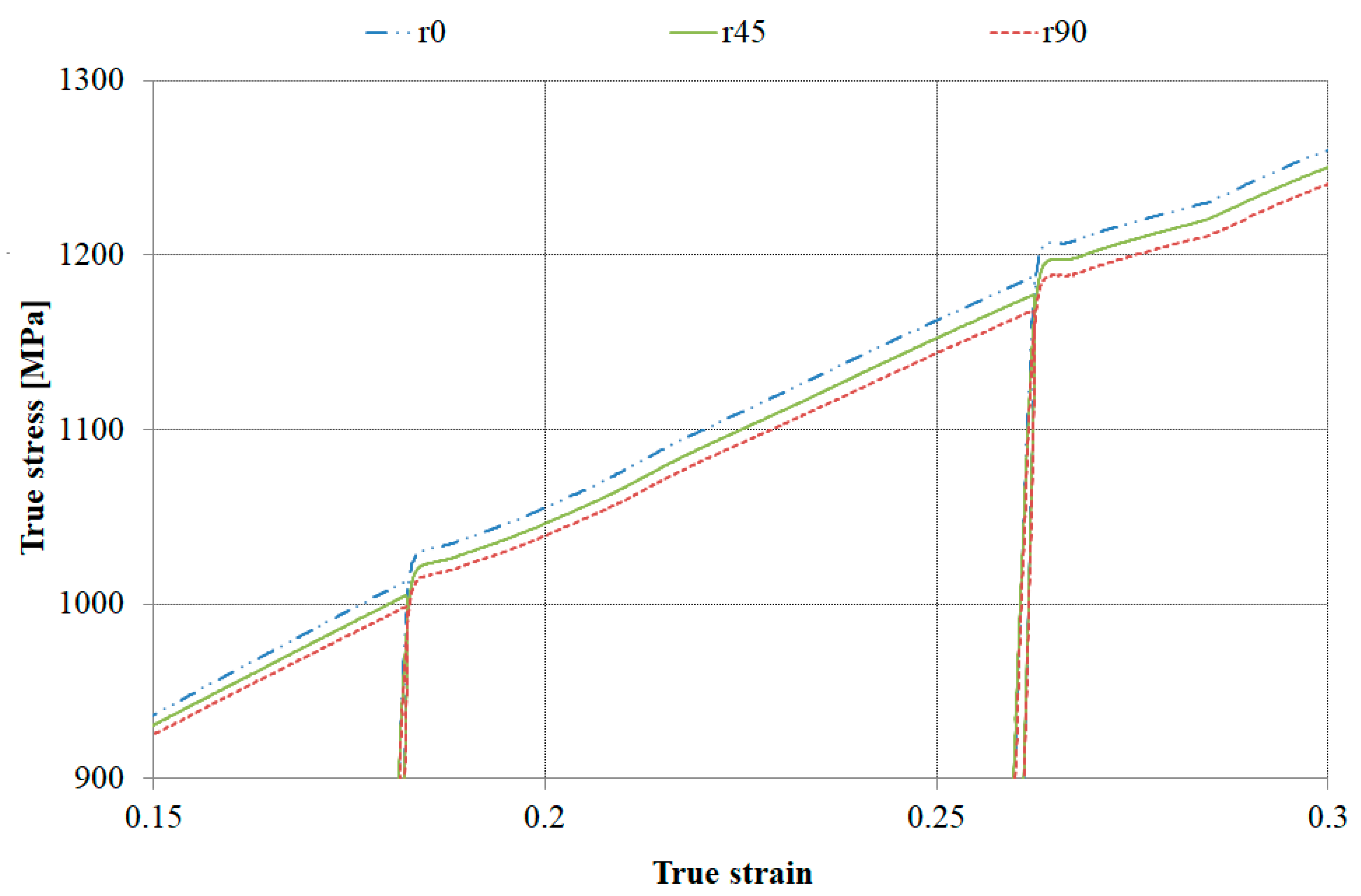
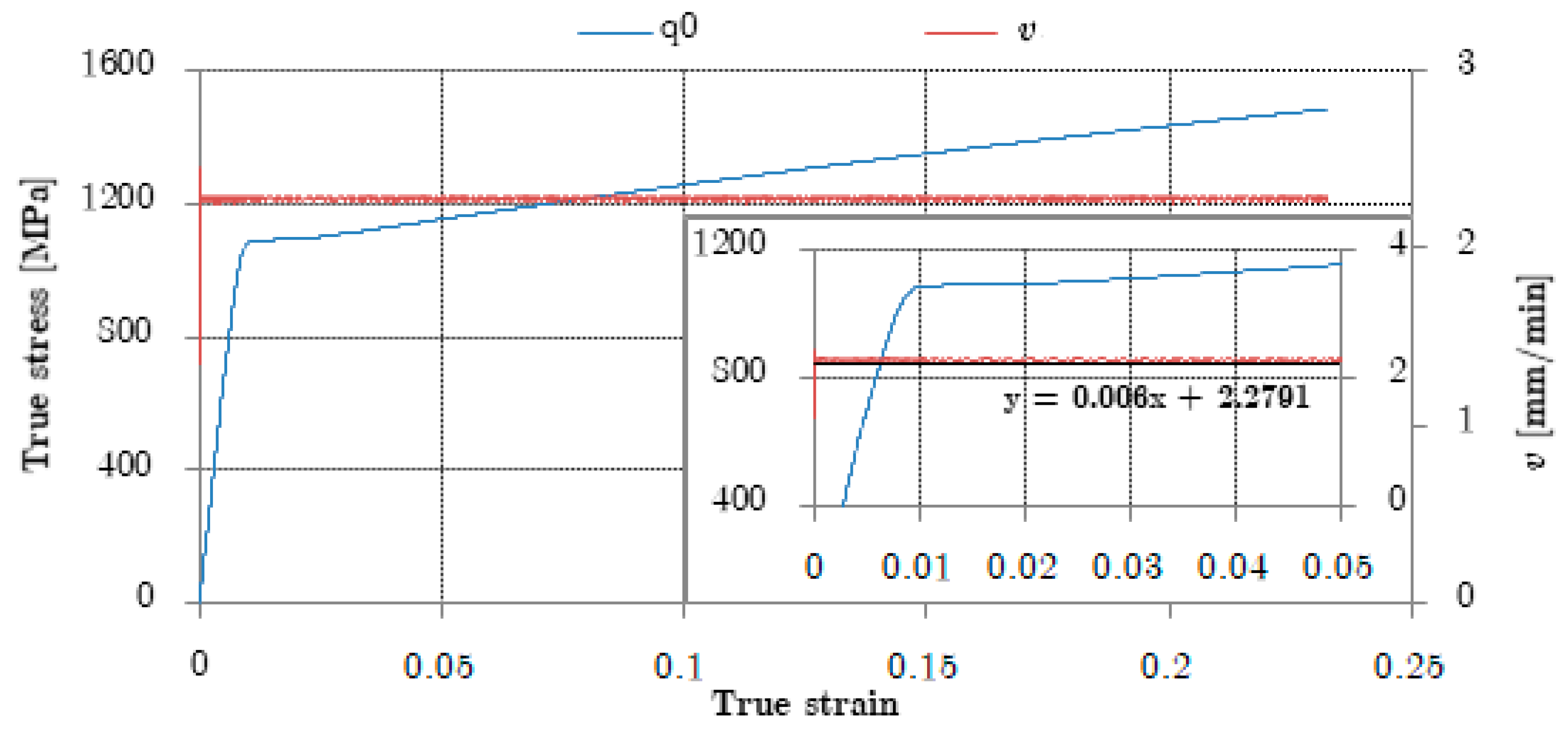
3.1.1. Pre-Deformations and Strain Path Change
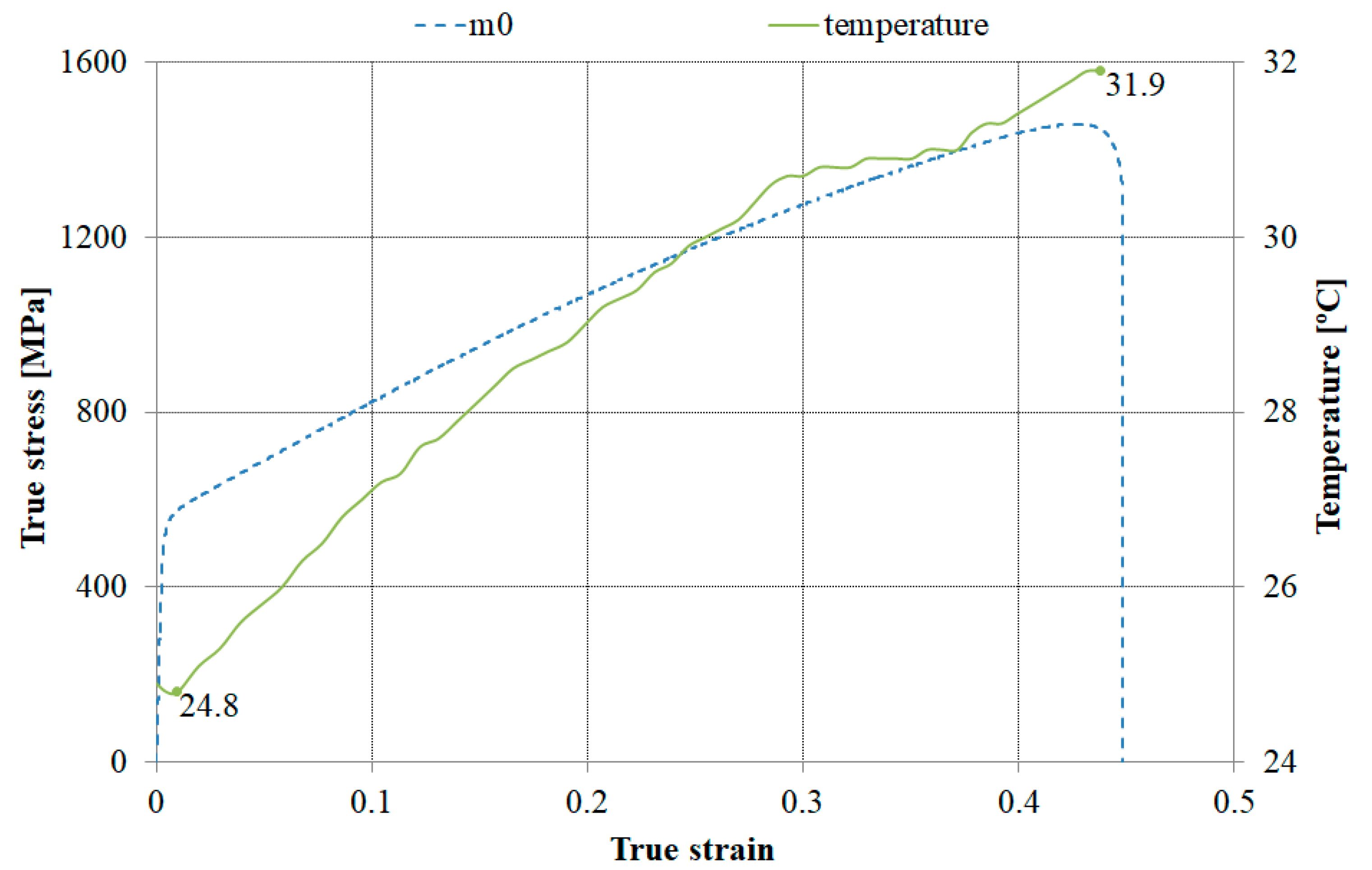
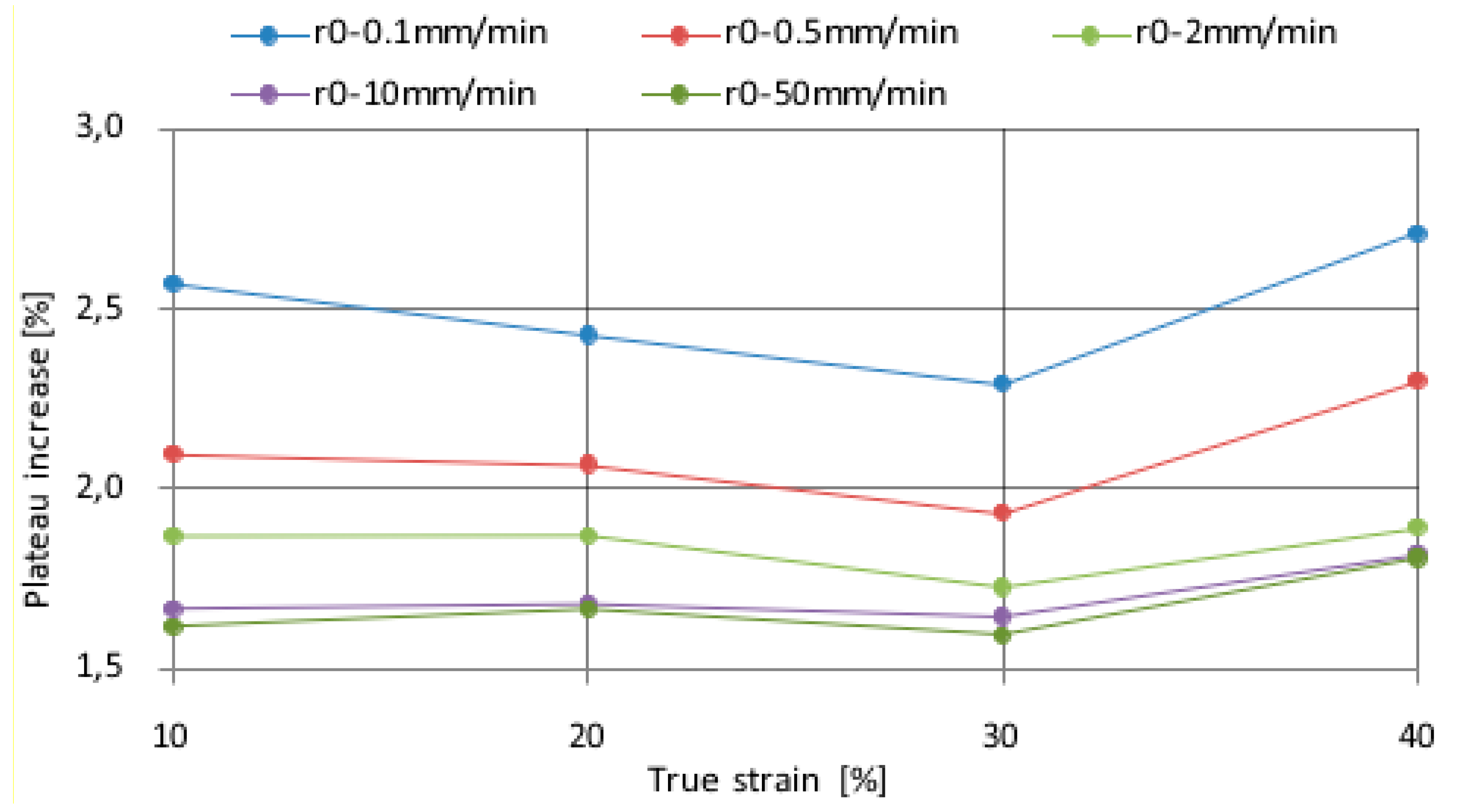
3.1.2. Influence of Deformation Path, Strain Rate, and Sample Temperature on the Yield Plateau
3.1.3. Mechanical Properties
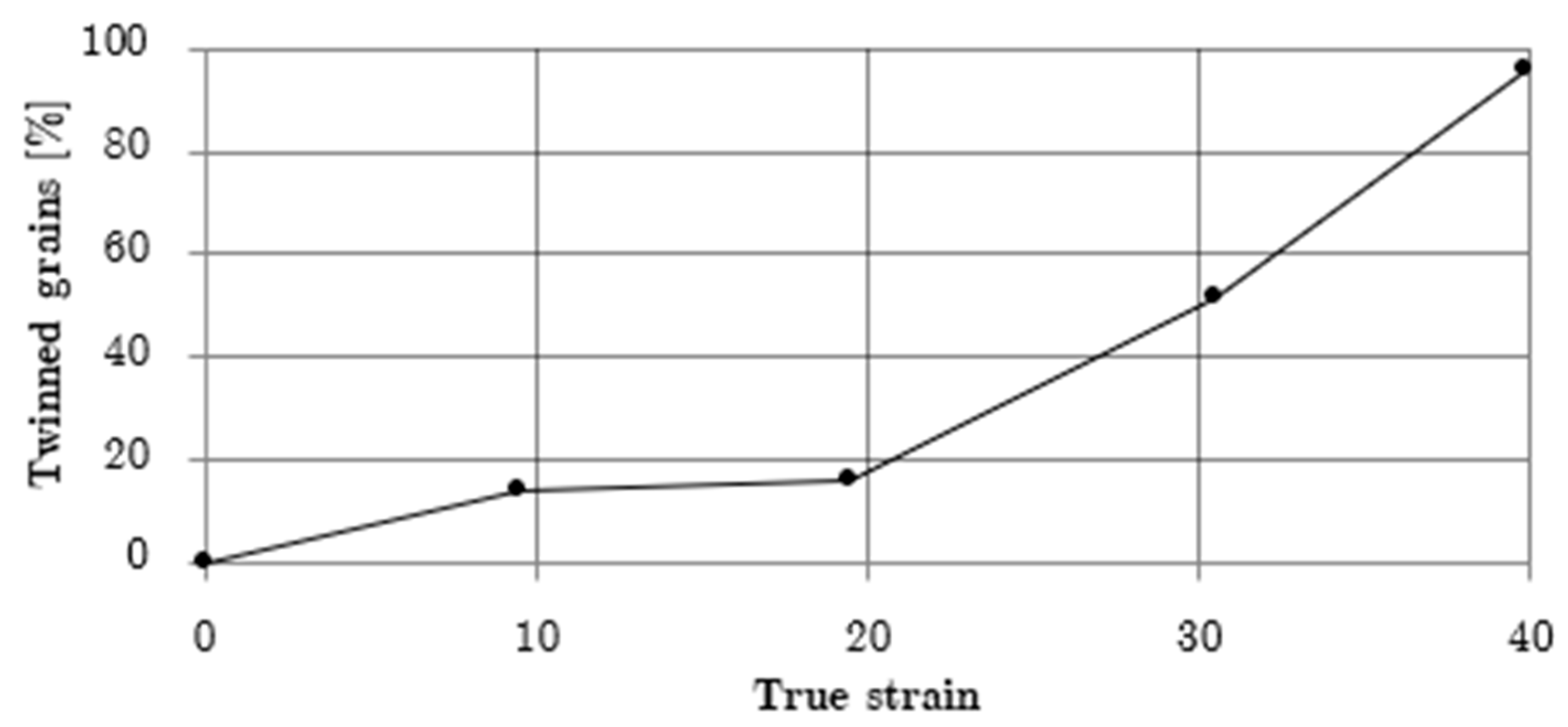
3.2. Microstructure
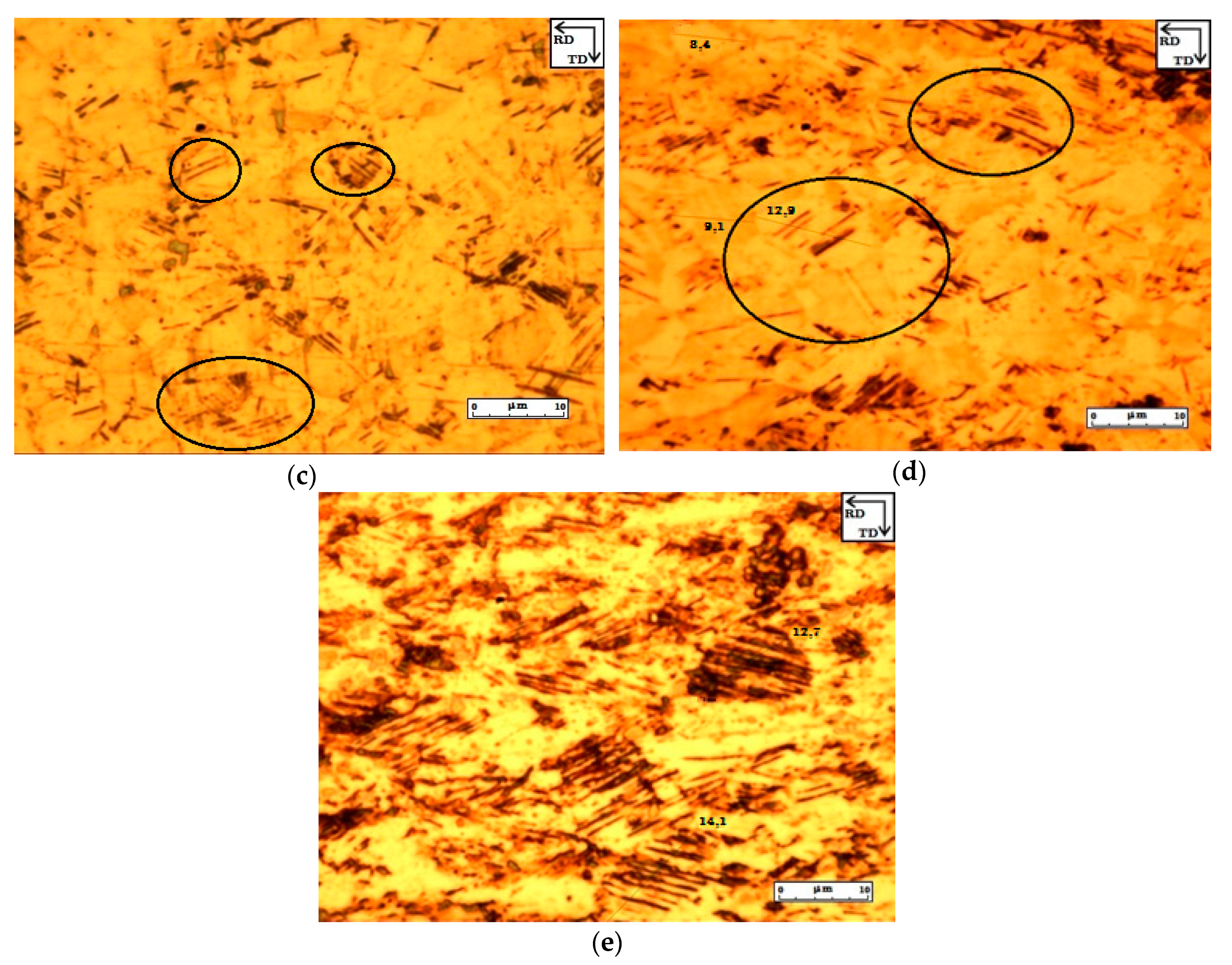
3.2.1. Optical Microscopy
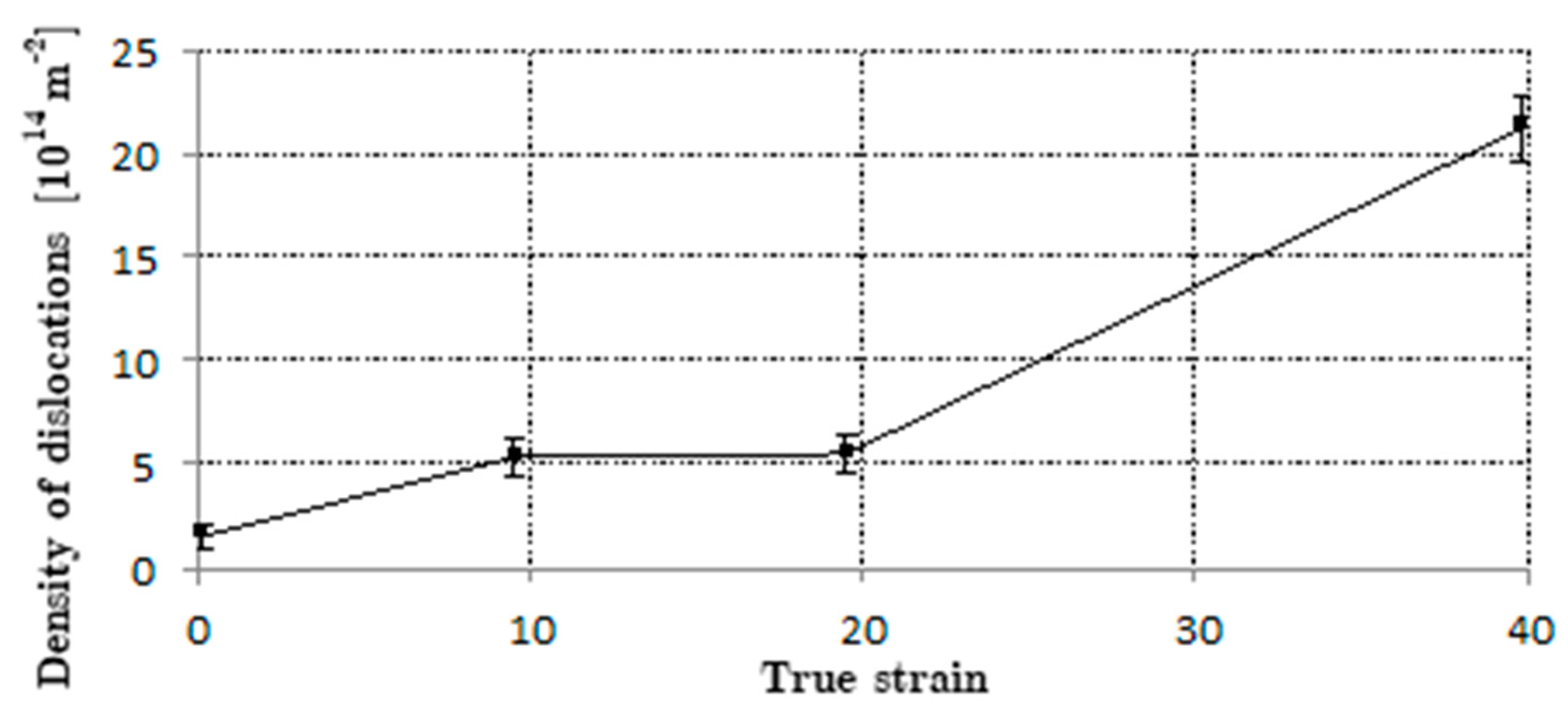
3.2.2. Transmission Electron Microscopy
3.2.3. Scanning Electron Microscopy
4. Discussions and Conclusions
- The yield stress increased with the level of deformation, independent of the loading direction;
- The highest yield stress was obtained for a θ = 0°, followed by 45°, and lastly by 90°, mainly due to back stress;
- Yield plateaus occur for cases of reloading in the same direction (α = 1).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gutierrez-Urrutia, I.; Raabe, D. Dislocation and twin substructure evolution during strain hardening of an Fe–22 wt.% Mn–0.6 wt.% C TWIP steel observed by electron channeling contrast imaging. Acta Mater. 2011, 59, 6449–6462. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C.P.; Cugy, P.; Barbier, D. High manganese austenitic twinning induced plasticity steels: A review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 2011, 15, 141–168. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Chin, K.; Kim, J. High Mn TWIP Steels for Automotive Applications. New Trends Dev. Automot. Syst. Eng. 2011. [Google Scholar] [CrossRef]
- Bouaziz, O.; Guelton, N. Modelling of TWIP effect on work-hardening. Mater. Sci. Eng. A 2001, 319–321, 246–249. [Google Scholar] [CrossRef]
- Karaman, I.; Sehitoglu, H.; Gall, K.; Chumlyakov, Y.; Maier, H. Deformation of single crystal Hadfield steel by twinning and slip. Acta Mater. 2000, 48, 1345–1359. [Google Scholar] [CrossRef]
- Bracke, L.; Kestens, L.; Penning, J. Direct observation of the twinning mechanism in an austenitic Fe-Mn-C steel. Scr. Mater. 2009, 61, 220–222. [Google Scholar] [CrossRef]
- Idrissi, H.; Renard, K.; Ryelandt, L.; Schryvers, D.; Jacques, P.J. On the mechanism of twin formation in Fe–Mn-C TWIP steels. Acta Mater. 2010, 58, 2464–2476. [Google Scholar] [CrossRef]
- Liu, J.B.; Liu, X.H.; Liu, W.; Zeng, Y.W.; Shu, K.Y. Transmission electron microscopy observation of a deformation twin in TWIP steel by an ex situ tensile test. Philos. Mag. 2011, 91, 4033–4044. [Google Scholar] [CrossRef]
- Mahato, B.; Shee, S.K.; Sahu, T.; Ghosh Chowdhury, S.; Sahu, P.; Porter, D.A.; Karjalainen, L.P. An effective stacking fault energy viewpoint on the formation of extended defects and their contribution to strain hardening in a Fe-Mn-Si-Al twinning-induced plasticity steel. Acta Mater. 2015, 86, 69–79. [Google Scholar] [CrossRef]
- Kim, J.-K.; Kwon, M.-H.; De Cooman, B.C. On the deformation twinning mechanisms in twinning-induced plasticity steel. Acta Mater 2017, 141, 444–455. [Google Scholar] [CrossRef]
- Fernandes, F.A.O.; Oliveira, D.F.; Pereira, A.B. Optimal parameters for laser welding of advanced high-strength steels used in the automotive industry. Procedia Manuf. 2017, 13. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Kwon, O.; Chin, K.-G. State-of-the-knowledge on TWIP steel. Mater. Sci. Technol. 2012, 28, 513–527. [Google Scholar] [CrossRef]
- Li, F.; Bate, P.S. Strain path change effects in cube textured aluminium sheet. Acta Metall. Mater. 1991, 39, 2639–2650. [Google Scholar] [CrossRef]
- Wen, W.; Borodachenkova, M.; Tomé, C.N.; Vincze, G.; Rauch, E.F.; Barlat, F.; Grácio, J.J. Mechanical behavior of Mg subjected to strain path changes: Experiments and modeling. Int. J. Plast. 2015, 73, 171–183. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Tomé, C.N. Modeling transients in the mechanical response of copper due to strain path changes. Int. J. Plast. 2007, 23, 640–664. [Google Scholar] [CrossRef]
- Nesterova, E.; Bacroix, B.; Teodosiu, C. Experimental observation of microstructure evolution under strain-path changes in low-carbon IF steel. Mater. Sci. Eng. A 2001, 309–310, 495–499. [Google Scholar] [CrossRef]
- Liao, J.; Sousa, J.A.; Lopes, A.B.; Xue, X.; Pereira, A.B. Mechanical, microstructural behaviour and modelling of dual phase steels under complex deformation paths. Int. J. Plast. 2017, 93, 269–290. [Google Scholar] [CrossRef]
- Wen, W.; Borodachenkova, M.; Pereira, A.; Barlat, F.; Gracio, J. Hardening behavior and texture evolution of TWIP steel during strain path change. IOP Conf. Ser. Mater. Sci. Eng. 2015, 82, 012089. [Google Scholar] [CrossRef]
- Lapovok, R.; Timokhina, I.; Mester, A.-K.; Weiss, M.; Shekhter, A. Influence of the Strain History on TWIP Steel Deformation Mechanisms in the Deep-Drawing Process. Metall. Mater. Trans. A 2018, 49, 2069–2083. [Google Scholar] [CrossRef]
- Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature (ISO 6892-1:2009). Available online: https://infostore.saiglobal.com/preview/is/en/2009/i.s.eniso6892-1-2009.pdf?sku=1141079 (accessed on 17 January 2019).
- Bilby, B.; Entwisle, A. The formation of mechanical twins. Acta Metall. 1954, 2, 15–19. [Google Scholar] [CrossRef]
- He, B.B.; Hu, B.; Yen, H.W.; Cheng, G.J.; Wang, Z.K.; Luo, H.W.; Huang, M.X. High dislocation density-induced large ductility in deformed and partitioned steels. Science 2017, 357, 1029–1032. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, J.H.; Shen, E.L.; Raphanel, J.L. A parameter for measuring the magnitude of a change of strain path: Validation and comparison with experiments on low carbon steel. Int. J. Plast. 1994, 10, 535–551. [Google Scholar] [CrossRef]
- Dieter, G. Mechanical Metallurgy; McGraw-hill: New York, NY, USA, 1961; pp. 370–371. [Google Scholar]
- Bintu, A.; Vincze, G.; Picu, C.R.; Lopes, A.B.; Grácio, J.J.; Barlat, F. Strain hardening rate sensitivity and strain rate sensitivity in TWIP steels. Mater. Sci. Eng. A 2015, 629, 54–59. [Google Scholar] [CrossRef]
- Liang, Z.Y.; Wang, X.; Huang, W.; Huang, M.X. Strain rate sensitivity and evolution of dislocations and twins in a twinning-induced plasticity steel. Acta Mater. 2015, 88, 170–179. [Google Scholar] [CrossRef]
- Kim, J. Dislocation Density-Based Constitutive Modeling of the Tensile Behavior of TWIP Steels; Pohang University of Science and Technology: Pohang, South Korea, 2012. [Google Scholar]





| m | p | q | t | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 45° | 90° | 0° | 45° | 90° | 0° | 45° | 90° | 0° | 45° | 90° | |
| σy [MPa] | 520 | 480 | 400 | 715 | 635 | 540 | 960 | 840 | 640 | 1232 | 1100 | 820 |
| σmax [MPa] | 1456 | 1448 | 1495 | 1445 | 1433 | 1467 | 1489 | 1406 | 1494 | 1531 | 1422 | 1562 |
| σy/σmax | 0.38 | 0.33 | 0.27 | 0.49 | 0.43 | 0.37 | 0.65 | 0.60 | 0.43 | 0.80 | 0.77 | 0.52 |
| e | 0.39 | 0.40 | 0.43 | 0.31 | 0.34 | 0.35 | 0.21 | 0.23 | 0.28 | 0.20 | 0.24 | 0.25 |
| n | 0.34 | 0.33 | 0.35 | 0.22 | 0.21 | 0.23 | 0.14 | 0.11 | 0.15 | 0.11 | 0.08 | 0.12 |
| K [MPa] | 1993 | 1935 | 1995 | 1870 | 1772 | 1881 | 1815 | 1651 | 1803 | 1874 | 1621 | 1829 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, A.B.; Fernandes, F.A.O.; Filipe, B. Effect of Deformation Path on the Microstructure and Mechanical Behavior of TWIP980 Steel. J. Manuf. Mater. Process. 2019, 3, 12. https://doi.org/10.3390/jmmp3010012
Pereira AB, Fernandes FAO, Filipe B. Effect of Deformation Path on the Microstructure and Mechanical Behavior of TWIP980 Steel. Journal of Manufacturing and Materials Processing. 2019; 3(1):12. https://doi.org/10.3390/jmmp3010012
Chicago/Turabian StylePereira, António B., Fábio A.O. Fernandes, and Bruno Filipe. 2019. "Effect of Deformation Path on the Microstructure and Mechanical Behavior of TWIP980 Steel" Journal of Manufacturing and Materials Processing 3, no. 1: 12. https://doi.org/10.3390/jmmp3010012
APA StylePereira, A. B., Fernandes, F. A. O., & Filipe, B. (2019). Effect of Deformation Path on the Microstructure and Mechanical Behavior of TWIP980 Steel. Journal of Manufacturing and Materials Processing, 3(1), 12. https://doi.org/10.3390/jmmp3010012







