Intelligent Fault Diagnosis of Bearings Based on Energy Levels in Frequency Bands Using Wavelet and Support Vector Machines (SVM)
Abstract
:1. Introduction
2. Wavelet Transform
- A)
- The integral of the wavelet function is equal to zero in the time domain.In other words, the mean value of is zero.
- B)
- In addition, one of the following conditions exists:
3. Multi-Resolution Analysis
4. Support Vector Machine (SVM) Technique
- A)
- a polynomial kernel function:
- B)
- an RBF kernel function:
5. Data Acquisition of Vibration Signals
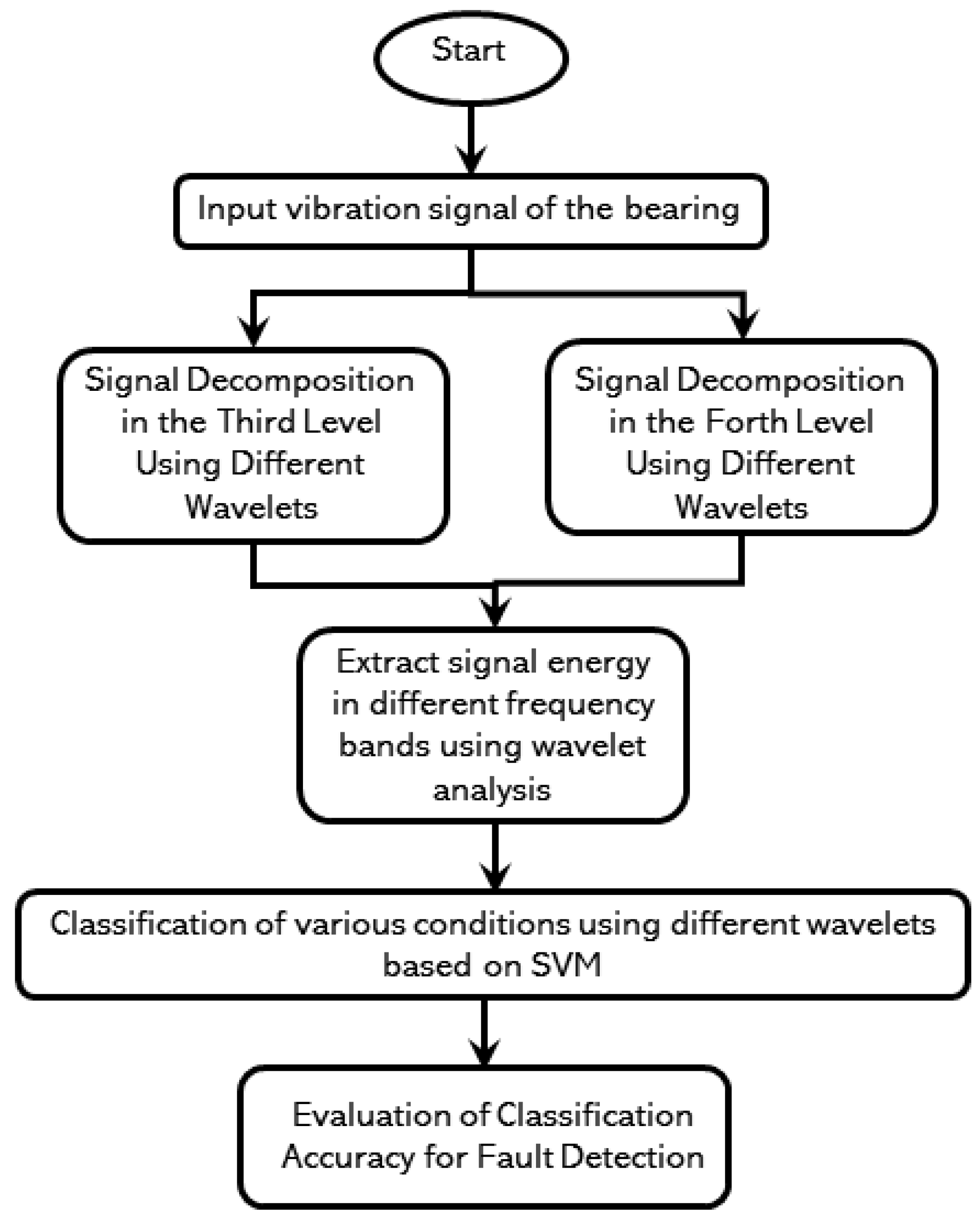
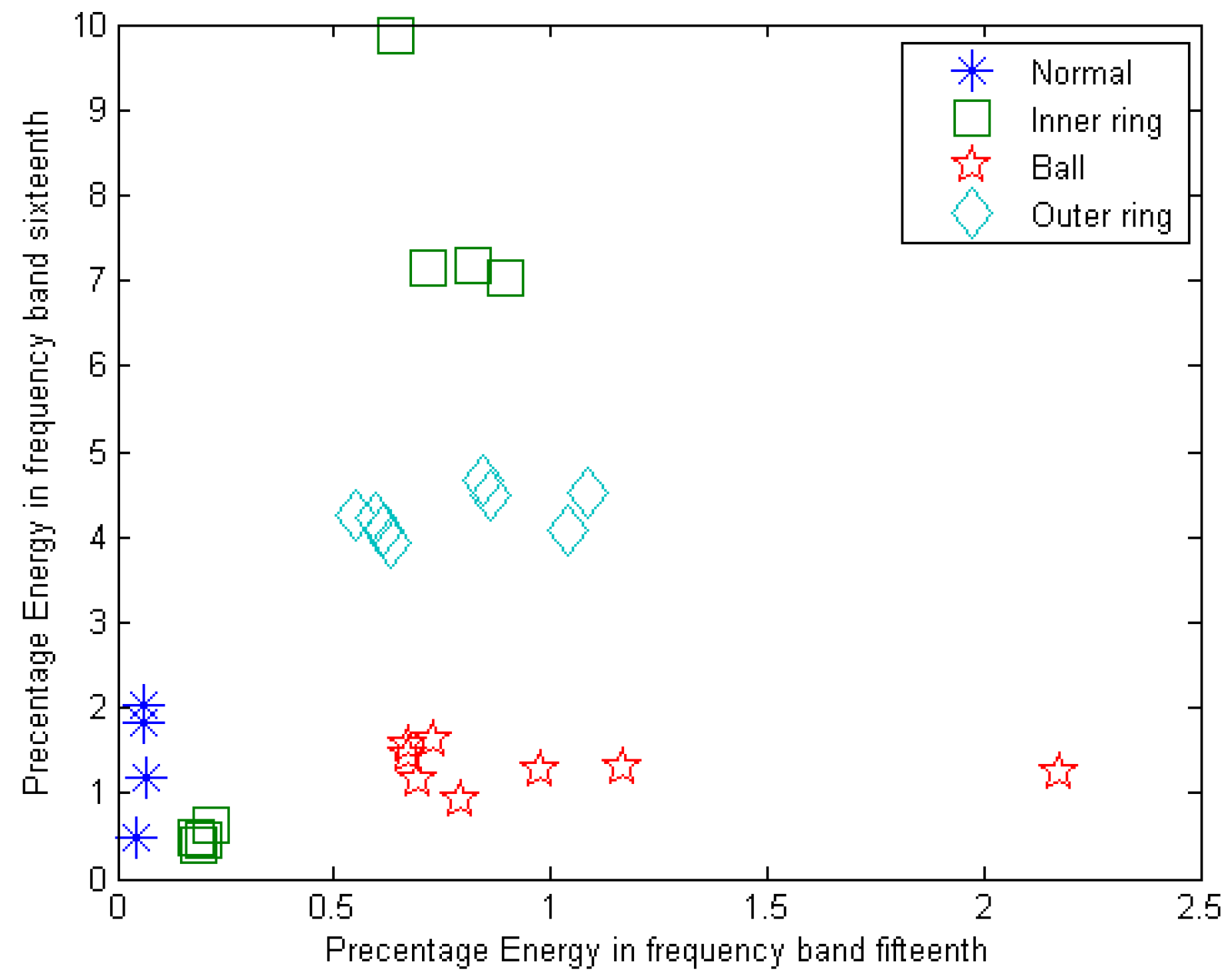
6. Feature Extraction
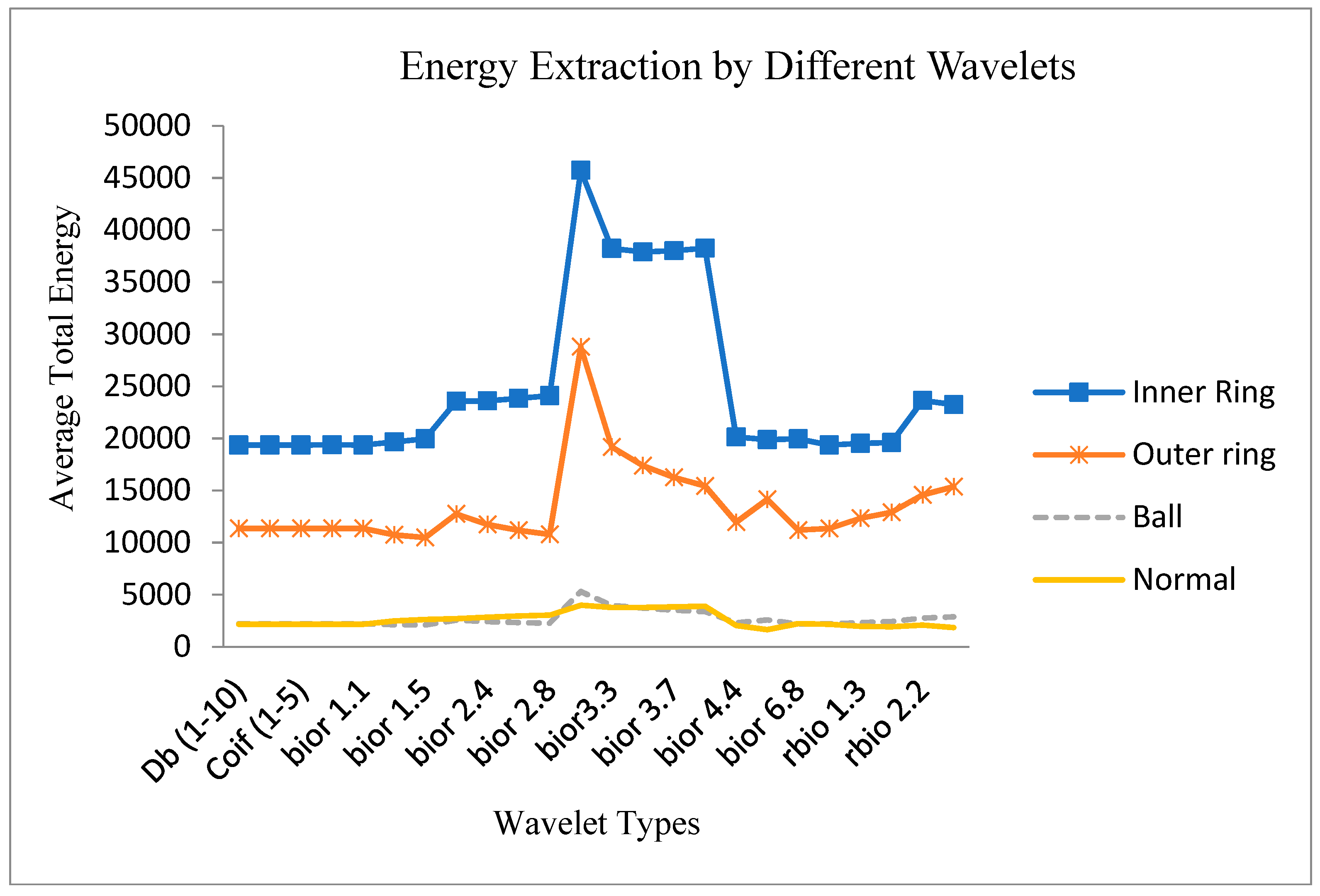
7. Signal Decomposition in the Third Level Using Different Wavelets
8. Signal Decomposition in the Fourth Level Using Different Wavelets
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, J.; Shao, Y. Overview of dynamic modelling and analysis of rolling element bearings with localized and distributed faults. Nonlinear Dyn. 2018, 93, 1765–1798. [Google Scholar] [CrossRef]
- Mehrabi, A.B.; Farhangdoust, S. A Laser-Based Non-Contact Vibration Technique for Health Monitoring of Structral Cables: Background, Success, and New Developments. Adv. Acoust. Vib. 2018, 2018, 1–13. [Google Scholar]
- Lim, T.C.; Singh, R. Vibration transmission through rolling element bearings, part IV: Statistical energy analysis. J. Sound Vib. 1992, 153, 37–50. [Google Scholar] [CrossRef]
- Martin, H.R.; Honarvar, F. Application of statistical moments to bearing failure detection. Appl. Acoust. 1995, 44, 67–77. [Google Scholar] [CrossRef]
- Parey, A.; el Badaoui, M.; Guillet, F.; Tandon, N. Dynamic modelling of spur gear pair and application of empirical mode decomposition-based statistical analysis for early detection of localized tooth defect. J. Sound Vib. 2006, 294, 547–561. [Google Scholar] [CrossRef]
- Antoni, J. Cyclic spectral analysis of rolling-element bearing signals: Facts and fictions. J. Sound Vib. 2007, 304, 497–529. [Google Scholar] [CrossRef]
- Chebil, J.; Noel, G.; Mesbah, M.; Deriche, M. Wavelet Decomposition for the Detection and Diagnosis of Faults in Rolling Element Bearings. Jordan J. Mech. Ind. Eng. 2009, 3, 260–267. [Google Scholar]
- Tang, Y.Y. Wavelet Theory and Its Application to Pattern Recognition, 2nd ed.; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 2009. [Google Scholar]
- Li, Z.; Feng, Z.; Chu, F. A load identification method based on wavelet multi-resolution analysis. J. Sound Vib. 2014, 333, 381–391. [Google Scholar] [CrossRef]
- He, Q.; Wang, X. Time–frequency manifold correlation matching for periodic fault identification in rotating machines. J. Sound Vib. 2013, 332, 2611–2626. [Google Scholar] [CrossRef]
- Lin, J.; Qu, L. Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Nikravesh, S.M.Y.; Taheri, H.; Wagstaff, P. Identification of Appropriate Wavelet for Vibration Study of Mechanical Impacts. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013; Volume 14, p. V014T15A022. [Google Scholar]
- Nikravesh, S.M.Y.; Taheri, H. Onset of Nucleate Boiling Detection in a Boiler Tube by Wavelet Transformation of Vibration Signals. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2018, 1, 31005–31007. [Google Scholar]
- Liu, X.; Bo, L.; He, X.; Veidt, M. Application of correlation matching for automatic bearing fault diagnosis. J. Sound Vib. 2012, 331, 5838–5852. [Google Scholar] [CrossRef]
- Peng, Z.K.; Tse, P.W.; Chu, F.L. An improved Hilbert–Huang transform and its application in vibration signal analysis. J. Sound Vib. 2005, 286, 187–205. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; He, Z. Multi-stable stochastic resonance and its application research on mechanical fault diagnosis. J. Sound Vib. 2013, 332, 5999–6015. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.; Zhou, L.; Nian, Y.; Shao, Y. A statistical feature investigation of the spalling propagation assessment for a ball bearing. Mech. Mach. Theory 2019, 131, 336–350. [Google Scholar] [CrossRef]
- Lu, W.; Jiang, W.; Yuan, G.; Yan, L. A gearbox fault diagnosis scheme based on near-field acoustic holography and spatial distribution features of sound field. J. Sound Vib. 2013, 332, 2593–2610. [Google Scholar] [CrossRef]
- Kar, C.; Mohanty, A.R. Vibration and current transient monitoring for gearbox fault detection using multiresolution Fourier transform. J. Sound Vib. 2008, 311, 109–132. [Google Scholar] [CrossRef]
- Nikravesh, S.M.Y.; Chegini, S.N. Crack identification in double-cracked plates using wavelet analysis. Meccanica 2013, 48, 2075–2098. [Google Scholar] [CrossRef]
- Li, B.; Chen, X.F.; Ma, J.X.; He, Z.J. Detection of crack location and size in structures using wavelet finite element methods. J. Sound Vib. 2005, 285, 767–782. [Google Scholar] [CrossRef]
- Kim, E.-Y.; Lee, Y.-J.; Lee, S.-K. Heath monitoring of a glass transfer robot in the mass production line of liquid crystal display using abnormal operating sounds based on wavelet packet transform and artificial neural network. J. Sound Vib. 2012, 331, 3412–3427. [Google Scholar] [CrossRef]
- Rucka, M.; Wilde, K. Application of continuous wavelet transform in vibration based damage detection method for beams and plates. J. Sound Vib. 2006, 297, 536–550. [Google Scholar] [CrossRef]
- Rafiee, J.; Rafiee, M.A.; Tse, P.W. Application of mother wavelet functions for automatic gear and bearing fault diagnosis. Expert Syst. Appl. 2010, 37, 4568–4579. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Lu, C. Rolling bearing fault detection based on the teager energy operator and elman neural network. Math. Probl. Eng. 2013, 2013, 10. [Google Scholar] [CrossRef]
- Newland, D.E. An Introduction to Random Vibrations, Spectral & Wavelet Analysis, 3rd ed.; Dover Publications: New York, NY, USA, 1993. [Google Scholar]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Supprot-Vector Networks. Mach. Learn. 1995, 297, 273–297. [Google Scholar] [CrossRef]
- CWRU. Case Western Reserve University Bearing Data Center. Available online: http://www.eecs.case.edu/labratory/bearing/download.html (accessed on 4 December 2012).
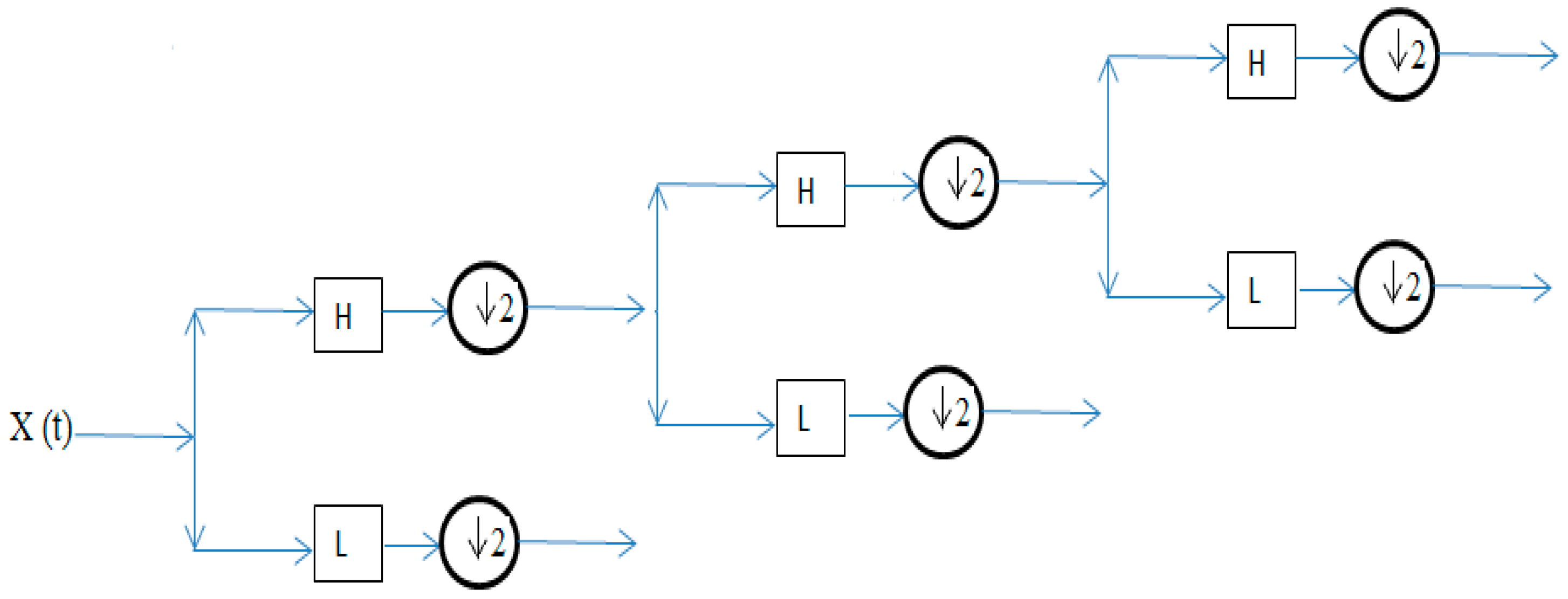
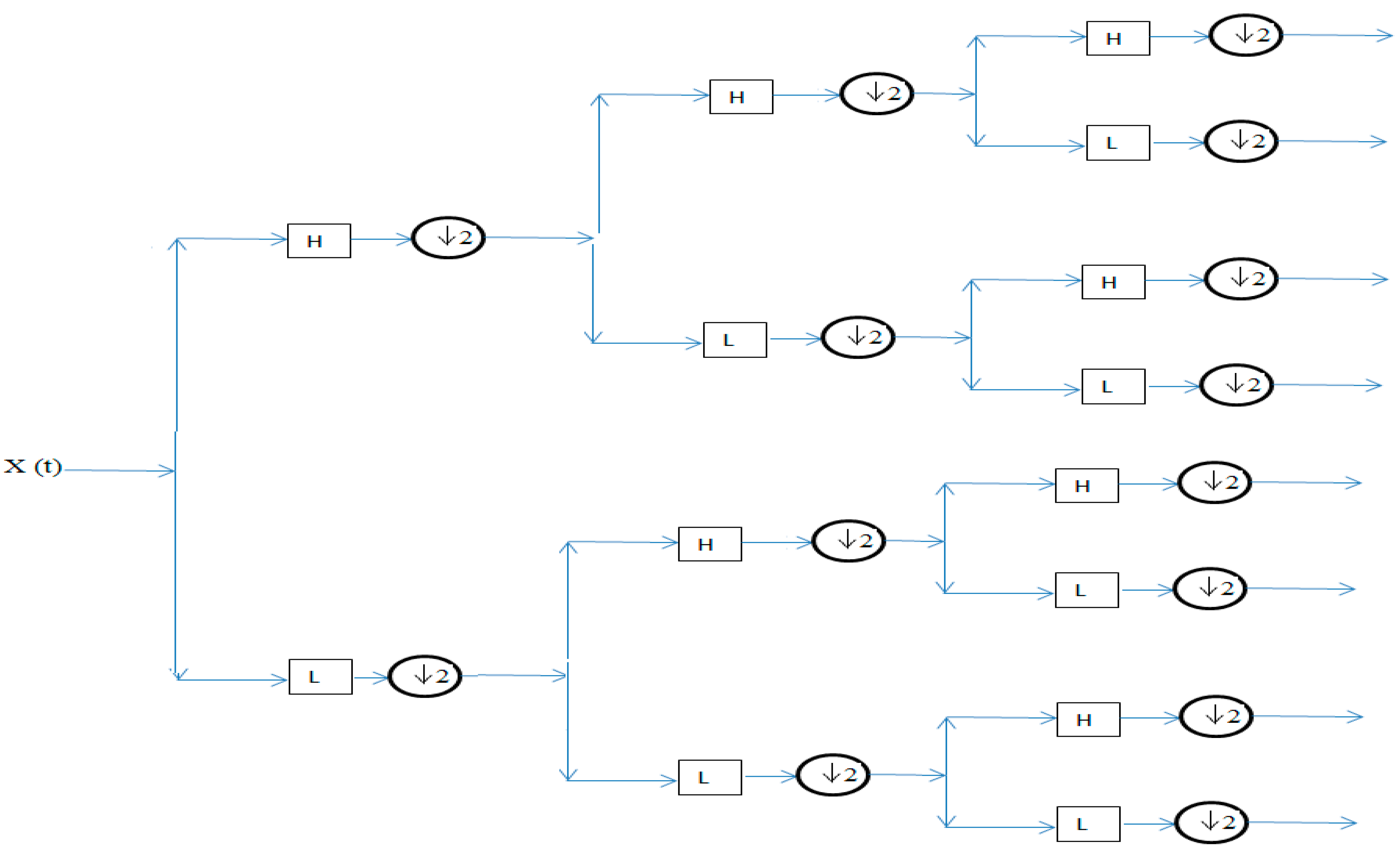
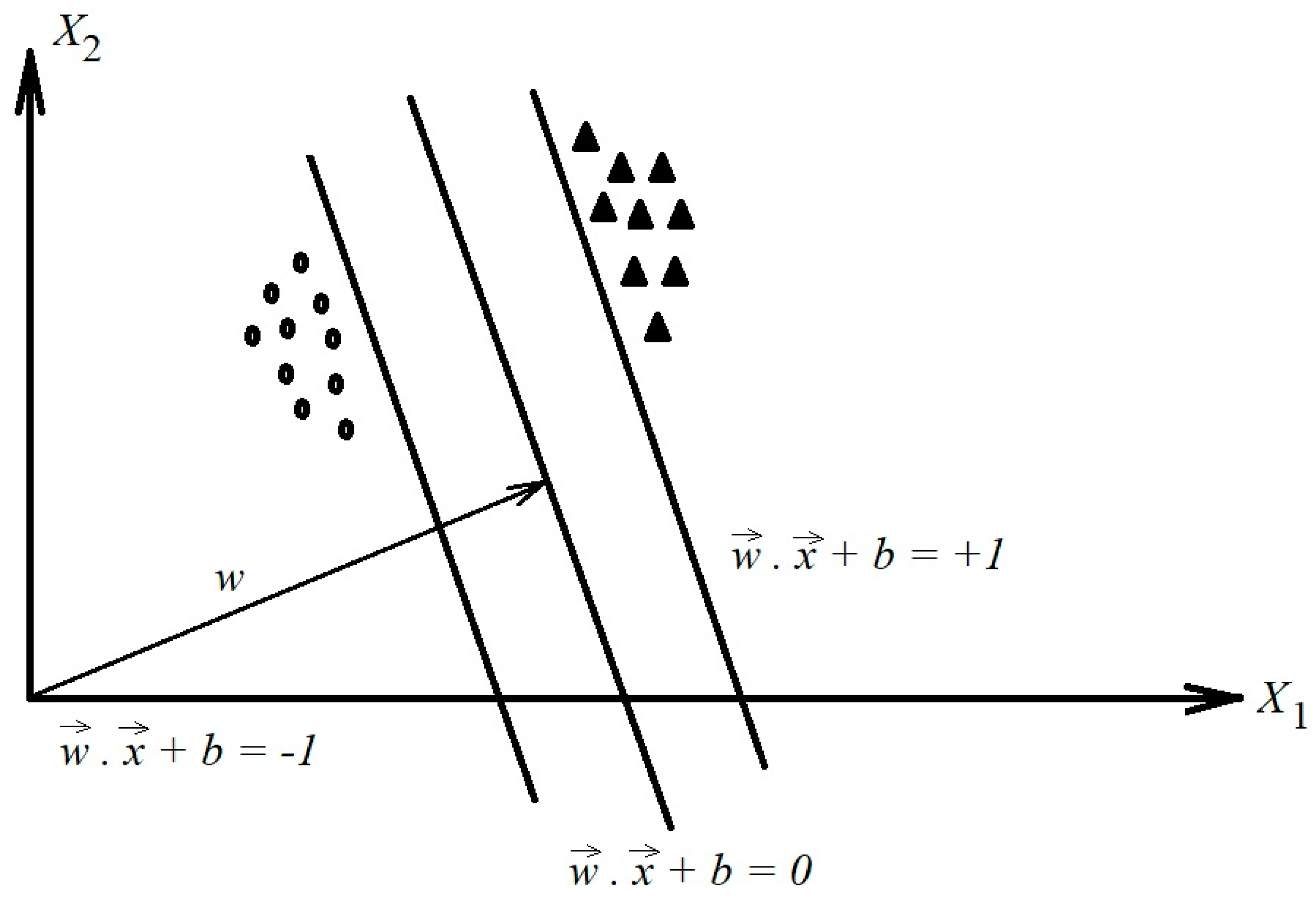

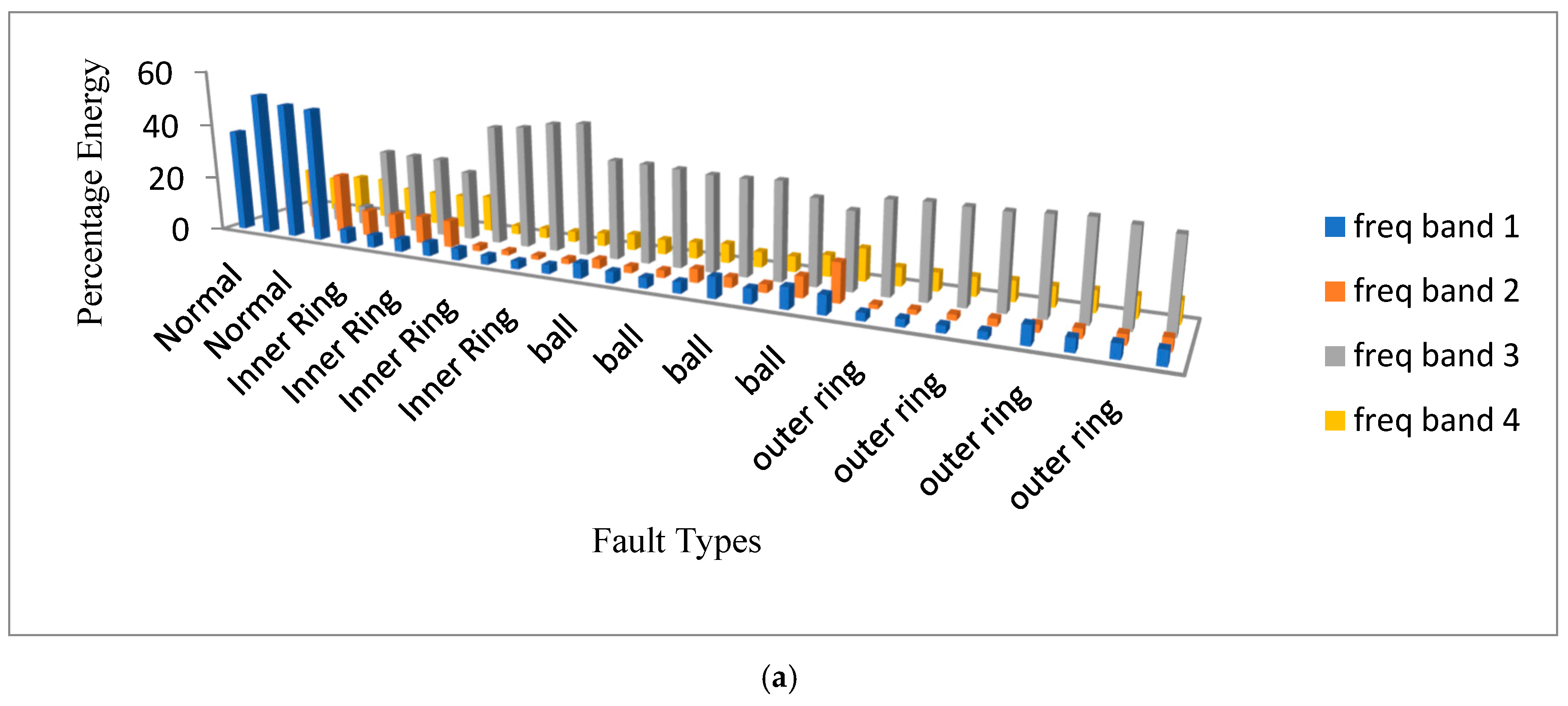
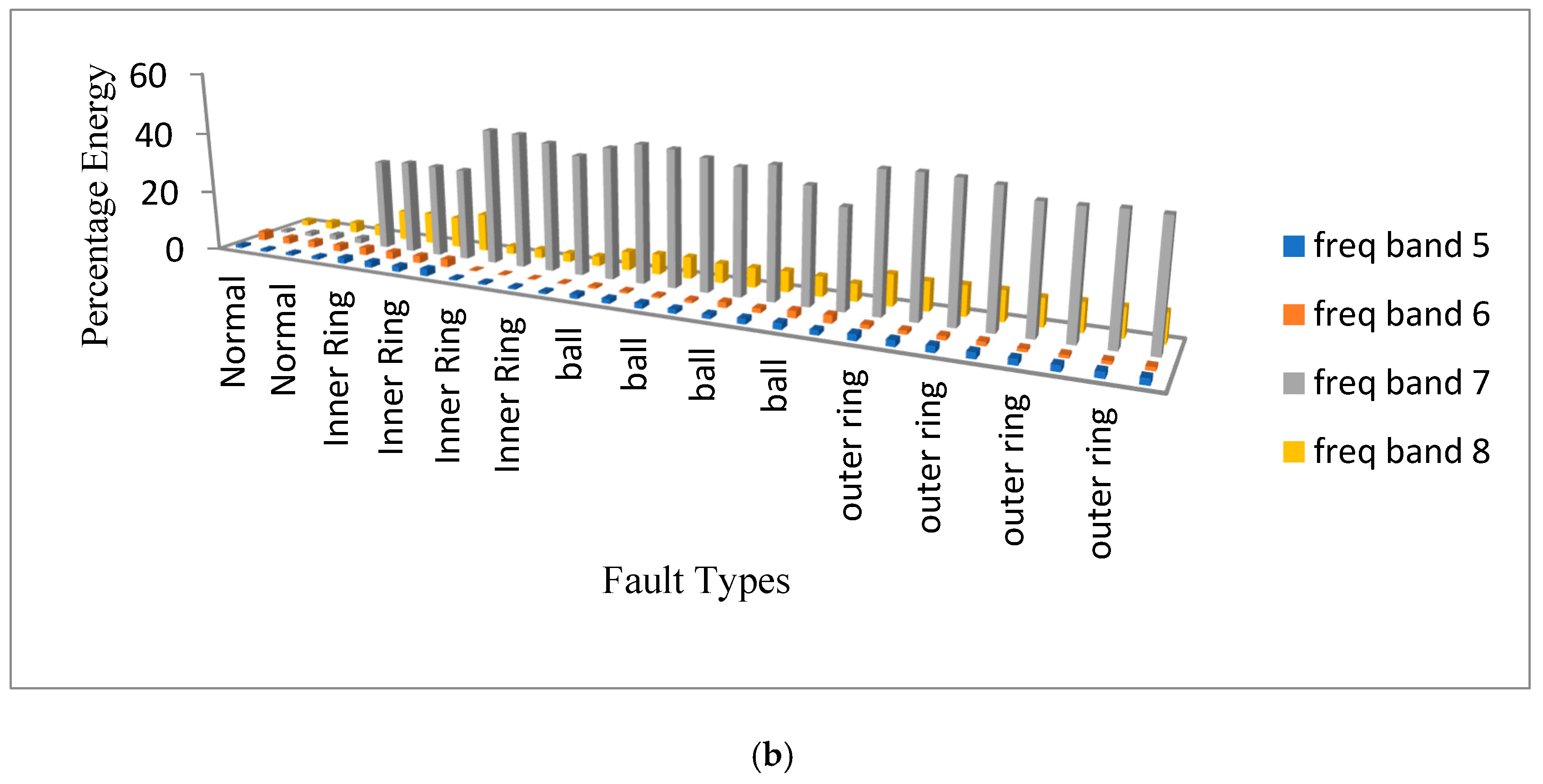
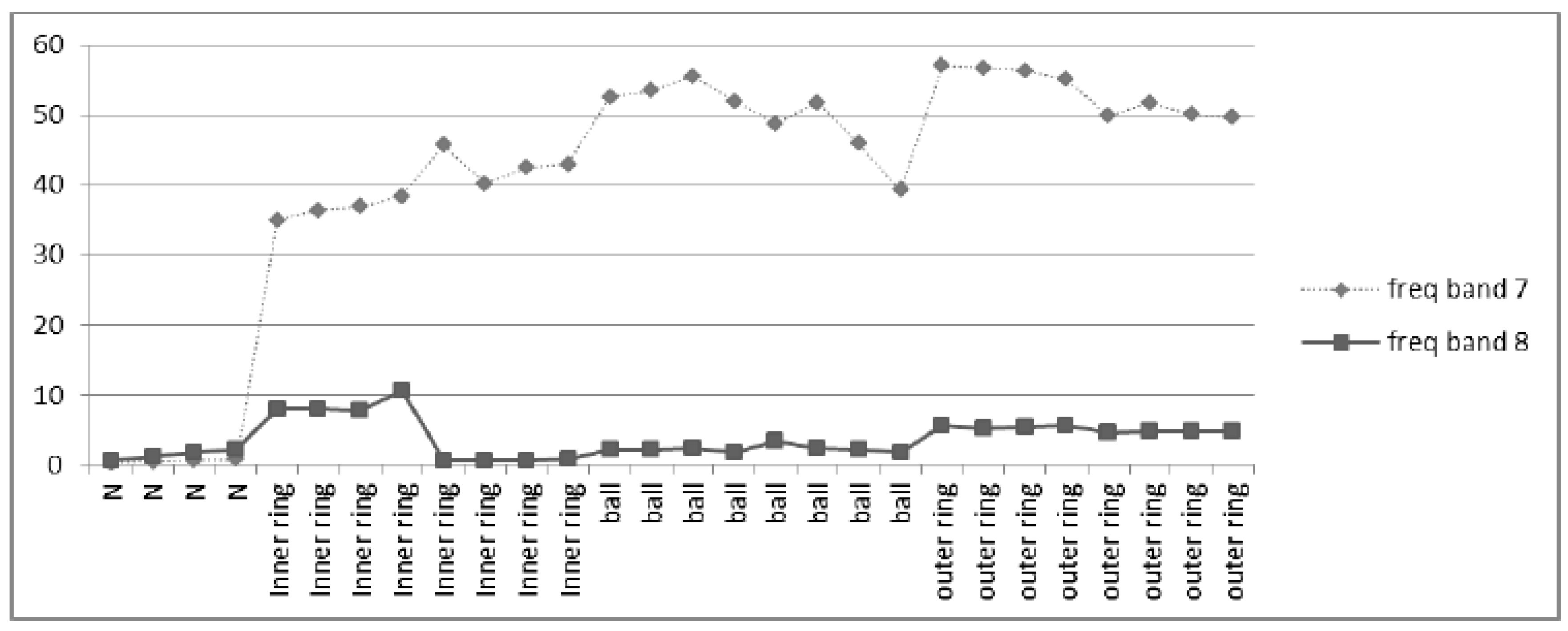
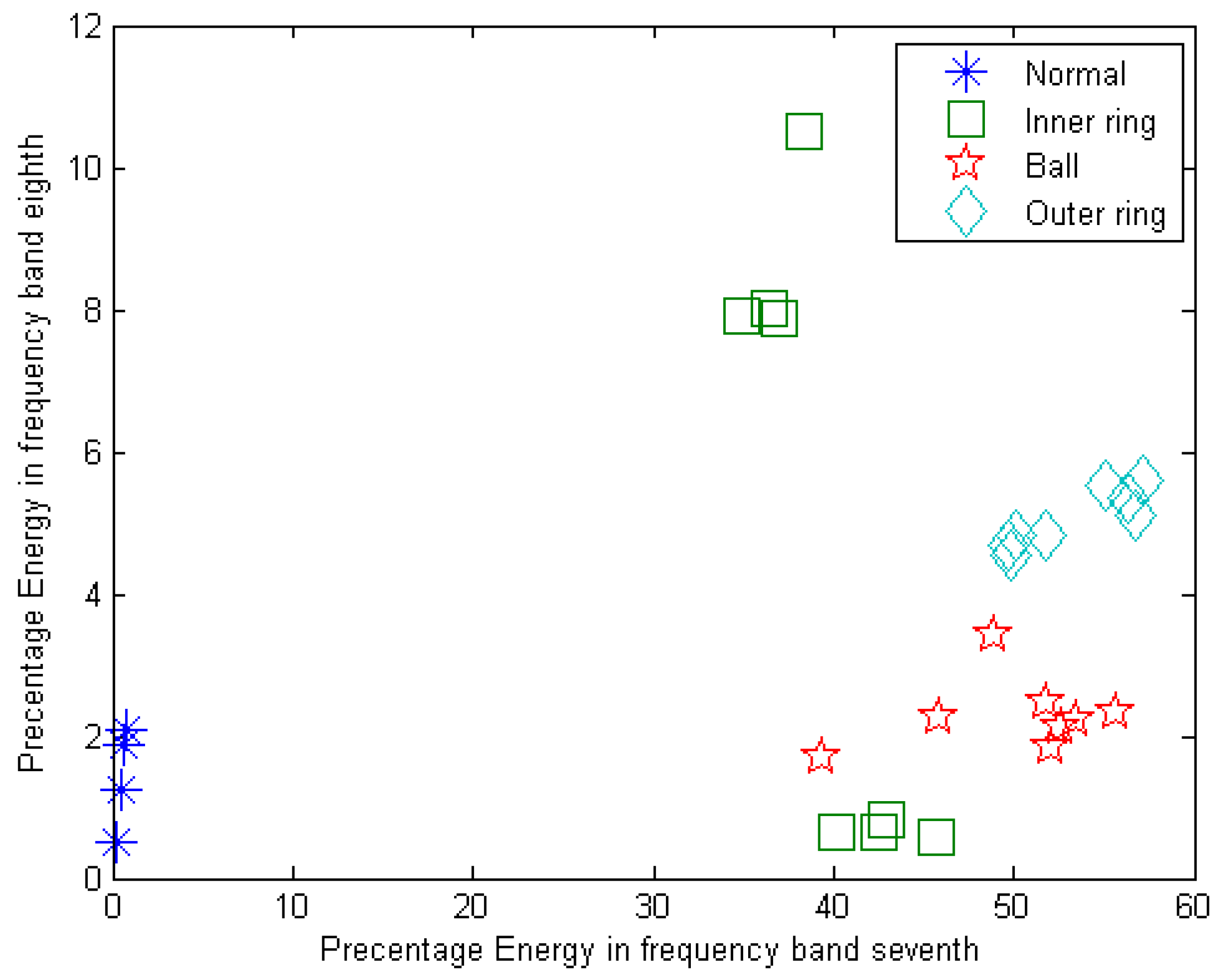
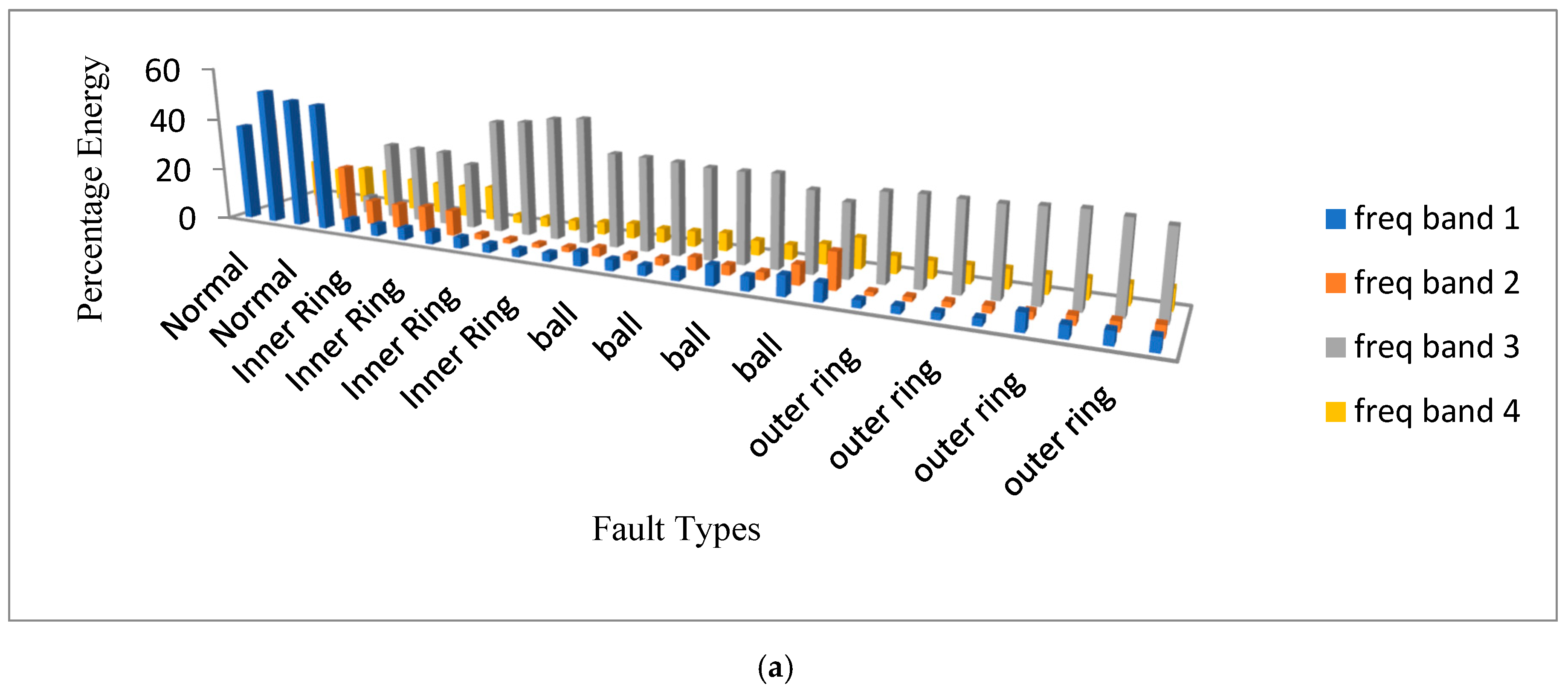
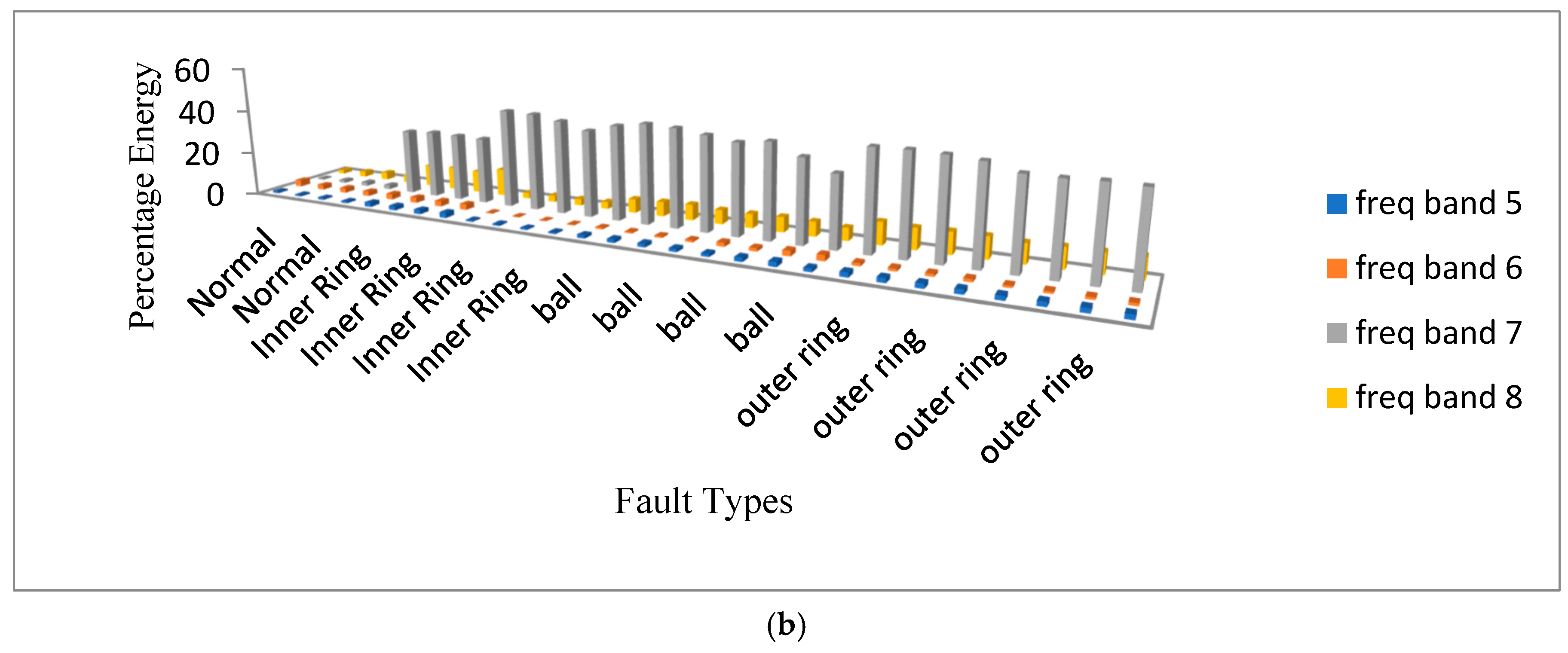
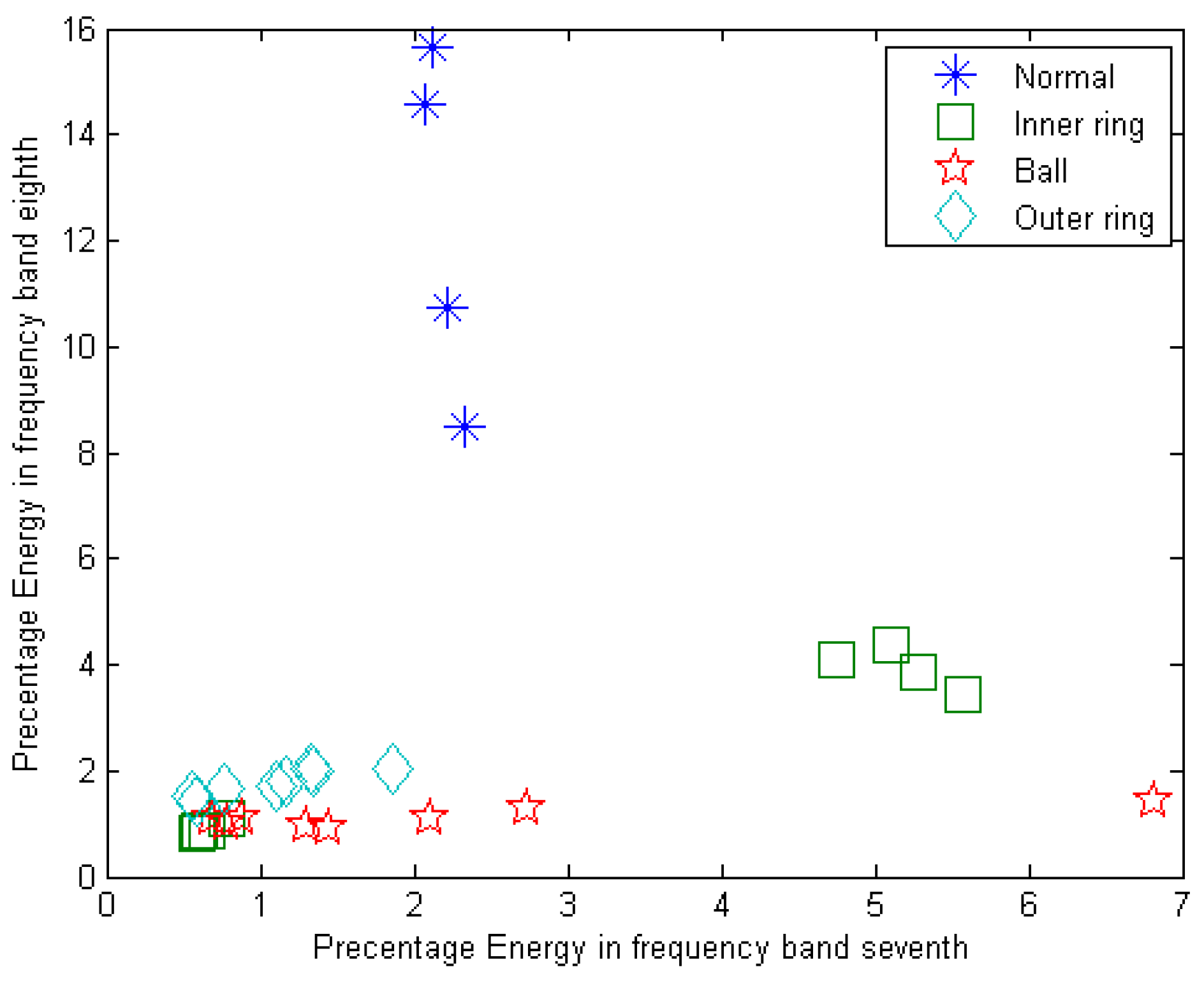
| Frequency Range (Hz) | Frequency Bands | Frequency Range (Hz) | Frequency Bands |
|---|---|---|---|
| (3000–3750) | Freq Band 5 | (0–750) | Freq Band 1 |
| (3750–4500) | Freq Band 6 | (750–1500) | Freq Band 2 |
| (4500–5250) | Freq Band 7 | (1500–2250) | Freq Band 3 |
| (5250–6000) | Freq Band 8 | (2250–3000) | Freq Band 4 |
| Frequency Range (Hz) | Frequency Bands | Frequency Range (Hz) | Frequency Bands |
|---|---|---|---|
| (3000–3375) | Freq Band 9 | (0–375) | Freq Band 1 |
| (3375–3750) | Freq Band 10 | (375–750) | Freq Band 2 |
| (3750–4125) | Freq Band 11 | (750–1125) | Freq Band 3 |
| (4125–4500) | Freq Band 12 | (1125–1500) | Freq Band 4 |
| (4500–4875) | Freq Band 13 | (1500–1875) | Freq Band 5 |
| (4875–5250) | Freq Band 14 | (1875–2250) | Freq Band 6 |
| (5250–5625) | Freq Band 15 | (2250–2625) | Freq Band 7 |
| (5625–6000) | Freq Band 16 | (2625–3000) | Freq Band 8 |
| Wavelet Type | Normal Conditions | Inner Ring | Outer Ring | Balls | Wavelet Type | Normal Conditions | Inner Ring | Outer Ring | Balls |
|---|---|---|---|---|---|---|---|---|---|
| Db (1–10) | 2157.11 | 19,367.78 | 11,358.25 | 2200.625 | bior 5.5 | 1646.074 | 19,875.59 | 14,148.54 | 2582.225 |
| Sym (2–8) | 2157.12 | 19,368.15 | 11,358.69 | 2200.63 | bior 6.8 | 2220.009 | 19,964.09 | 11,197.79 | 2189.105 |
| Coif (1–5) | 2157.13 | 19,368.43 | 11,358.56 | 2200.65 | rbio 1.1 | 2157.112 | 19,367.79 | 11,358.25 | 2200.554 |
| dmey | 2158.01 | 19,383.33 | 11,362.88 | 2202.375 | rbio 1.3 | 1968.818 | 19,517.14 | 12,327.03 | 2327.723 |
| bior 1.1 | 2157.112 | 19,367.79 | 11,358.25 | 2200.554 | rbio 1.5 | 1928.785 | 19,601.41 | 12,917.27 | 2416.57 |
| bior 1.3 | 2471.467 | 19,652.07 | 10,742.81 | 2132.575 | rbio 2.2 | 2080.56 | 23,640.36 | 14,581.46 | 2763.02 |
| bior 1.5 | 2627.541 | 19,954.79 | 10,477.61 | 2095.307 | rbio 2.4 | 1834.783 | 23,242.51 | 15,360.39 | 2873.272 |
| bior 2.2 | 2697.638 | 23,563.8 | 12,754.69 | 2561.615 | rbio 2.6 | 1742.075 | 23,080.8 | 16,037.67 | 2982.819 |
| bior 2.4 | 2844.135 | 23,600.42 | 11,734.45 | 2419.893 | rbio 2.8 | 1697.09 | 23,004.08 | 16,639.32 | 3083.27 |
| bior 2.6 | 2954.414 | 23,842.13 | 11,182.01 | 2329.608 | rbio 3.1 | 3709.718 | 40,385.17 | 22,977.3 | 4467.429 |
| bior 2.8 | 3039.554 | 24,100.1 | 10,784.85 | 2260.565 | rbio 3.3 | 2278.809 | 37,702.51 | 23,492.65 | 4455.607 |
| bior 3.1 | 3986.502 | 45,741.43 | 28,792.2 | 5301.835 | rbio 3.5 | 1890.008 | 36,741.06 | 24,388.36 | 4596.692 |
| bior3.3 | 3767.156 | 38,241.26 | 19,187.21 | 3980.502 | rbio 3.7 | 1710.69 | 36,158.9 | 25,240.45 | 4744.515 |
| bior 3.5 | 3768.738 | 37,900.59 | 17,383.33 | 3708.362 | rbio 3.9 | 1617.109 | 35,760.62 | 26,009.97 | 4884.884 |
| bior 3.7 | 3832.379 | 38,021.93 | 16,253.48 | 3519.478 | rbio 4.4 | 2321.09 | 20,025.55 | 11,591.45 | 2264.359 |
| bior 3.9 | 3902.459 | 38,245.49 | 15,448.34 | 3372.755 | rbio 5.5 | 3175.766 | 20,351.78 | 9854.393 | 2047.906 |
| bior 4.4 | 2050.796 | 20,143.06 | 11,956.86 | 2298.285 | rbio 6.8 | 2104.933 | 19,875.52 | 12041.18 | 2326.006 |
| Wavelet Type | Normal Conditions | Inner Ring | Outer Ring | Balls | Wavelet Type | Normal Conditions | Inner Ring | Outer Ring | Balls |
|---|---|---|---|---|---|---|---|---|---|
| Db1 | 100% | 100% | 100% | 100% | Coif2 | 100% | 92% | 92% | 100% |
| Db2 | 100% | 92% | 100% | 92% | Coif3 | 100% | 100% | 92% | 92% |
| Db3 | 100% | 78% | 100% | 92% | bior 1.1 | 100% | 100% | 100% | 100% |
| Sym2 | 100% | 92% | 100% | 92% | bior 1.3 | 100% | 92% | 100% | 100% |
| Sym3 | 100% | 92% | 100% | 92% | bior 1.5 | 100% | 71% | 100% | 100% |
| Sym4 | 100% | 85% | 100% | 92% | rbio 1.1 | 100% | 71% | 100% | 92% |
| Coif1 | 100% | 78% | 100% | 92% | rbio 1.3 | 100% | 100% | 100% | 92% |
| Wavelet Type | Normal Conditions | Inner Ring | Outer Ring | Balls | Wavelet Type | Normal Conditions | Inner Ring | Outer Ring | Balls |
|---|---|---|---|---|---|---|---|---|---|
| Db1 | 85% | 92% | 100% | 85% | Coif2 | 92% | 78% | 71% | 64% |
| Db2 | 85% | 92% | 100% | 92% | Coif3 | 85% | 64% | 64% | 50% |
| Db3 | 100% | 92% | 92% | 57% | bior 1.1 | 85% | 92% | 100% | 85% |
| Sym2 | 85% | 100% | 100% | 57% | bior 1.3 | 100% | 78% | 85% | 42% |
| Sym3 | 100% | 85% | 100% | 50% | bior 1.5 | 85% | 85% | 85% | 64% |
| Sym4 | 100% | 78% | 100% | 64% | rbio 1.1 | 92% | 100% | 100% | 71% |
| Coif1 | 85% | 85% | 100% | 85% | rbio 1.3 | 85% | 78% | 100% | 78% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadavar Nikravesh, S.M.; Rezaie, H.; Kilpatrik, M.; Taheri, H. Intelligent Fault Diagnosis of Bearings Based on Energy Levels in Frequency Bands Using Wavelet and Support Vector Machines (SVM). J. Manuf. Mater. Process. 2019, 3, 11. https://doi.org/10.3390/jmmp3010011
Yadavar Nikravesh SM, Rezaie H, Kilpatrik M, Taheri H. Intelligent Fault Diagnosis of Bearings Based on Energy Levels in Frequency Bands Using Wavelet and Support Vector Machines (SVM). Journal of Manufacturing and Materials Processing. 2019; 3(1):11. https://doi.org/10.3390/jmmp3010011
Chicago/Turabian StyleYadavar Nikravesh, Seyed Majid, Hossein Rezaie, Margaret Kilpatrik, and Hossein Taheri. 2019. "Intelligent Fault Diagnosis of Bearings Based on Energy Levels in Frequency Bands Using Wavelet and Support Vector Machines (SVM)" Journal of Manufacturing and Materials Processing 3, no. 1: 11. https://doi.org/10.3390/jmmp3010011
APA StyleYadavar Nikravesh, S. M., Rezaie, H., Kilpatrik, M., & Taheri, H. (2019). Intelligent Fault Diagnosis of Bearings Based on Energy Levels in Frequency Bands Using Wavelet and Support Vector Machines (SVM). Journal of Manufacturing and Materials Processing, 3(1), 11. https://doi.org/10.3390/jmmp3010011






